Bayesian Regularization Applied to Ultrasound Strain Imaging

Abstract

Noise artifacts due to signal decorrelation and reverberation are a considerable problem in ultrasound strain imaging. For block-matching methods, information from neighboring matching-blocks has been utilized to regularize the estimated displacements. We apply a recursive Bayesian regularization algorithm developed by Hayton et al. (1999) to phase-sensitive ultrasound radiofrequency signals to improve displacement estimation. The parameter of regularization is reformulated, and its meaning examined in the context of strain imaging. Tissue-mimicking experimental phantoms and radiofrequency data incorporating finite element models for the tissue deformation and frequency-domain ultrasound simulations are used to compute the optimal parameter with respect to nominal strain and algorithmic iterations. The optimal strain regularization parameter was found to be twice the nominal strain and did not vary significantly with algorithmic iterations. The technique demonstrates superior performance over median filtering in noise reduction at strains 5% and higher for all quantitative experiments performed. For example, the strain signal-to-noise ratio was 11 dB higher than that obtained using a median filter at 7% strain. It has to be noted that for applied deformations lower than 1%, since signal decorrelation errors are minimal, using this approach may degrade the displacement image.

INTRODUCTION

Ultrasound strain imaging algorithms can generally be divided into two independent stages, namely: estimation of the local displacements from a pre-deformation to a post-deformation state and computation of local strain from these estimated displacements. The first stage can be considered to be an instance of the general deformable image registration problem [1], [2]. Approaches to the registration problem include differential methods of estimating optical flow [3], [4], optimization of a global deformation model’s parameters [5]–[7], and block-matching methods [8]–[12] While global deformational models are popular for registration in other imaging modalities, the pixel dimensions and high frequency speckle content of ultrasonic signals lead to a significant computational burden, along with a difficult to navigate optimization parameter space with abundant local extrema [7], [13]. Block-matching methods are not as computationally expensive, but only local information determines displacement estimated from a matching-block. This makes it difficult to enforce diffeomorphic deformation, and it puts block-matching techniques at a disadvantage compared to methods that simultaneously incorporate information from the entire image space. In order to improve the quality of block-matching based motion tracking, regularization strategies are employed that fuse information from neighboring matching-blocks [13]–[16].

In ultrasonic displacement estimation, signal decorrelation during block-matching introduces peak hopping errors and degrades the quality of the resulting strain or modulus image [17], [18]. Signal decorrelation may be due to large axial deformations distorting the signal, elevational motion of the probe, or unwanted physiological motion [19], [20].

There are primarily two strategies employed in the peer-reviewed literature to correct for displacement estimation errors. One strategy aims to reduce peak hopping by restricting the search area of a matching-block. Smaller search areas are feasible when the center of the search region is initialized appropriately, where the search may propagate away from a region of known displacement such as the face of the transducer [8], [21] or lines or points with high confidence [22], [23]. Alternatively, a coarse-to-fine scheme may be employed where displacements from a large matching-block or low-pass filtered and subsampled matching-block initializes the center of the search region at progressively smaller matching-block sizes to achieve a high resolution strain image [8], [13], [24]–[27].

The other commonly employed strategy used to reduce noise in ultrasound displacement estimation is to incorporate displacements from neighboring blocks into the displacement estimation equation. Filtering approaches, such as a median [28] or Kalman filter [16], remove noise but come at the cost of reduced strain dynamic range and spatial resolution. Alternatively, motion within tissue may be assumed to be continuous, and displacements may be estimated by minimizing a cost function incorporating a term involving a similarity metric and a term involving displacement continuity between adjacent matching-blocks. This cost function can then be minimized with iterative techniques [15], [16], [29] or application of the Viterbi algorithm [14] or in a multiscale context [13].

In this article, we examine a regularization approach that attempts to optimize the displacement using both the block similarity metric and the motion of neighboring blocks. However, unlike the aforementioned algorithms, we do not explicitly formulate the problem as the minimization of a cost function. Instead, we follow the approach proposed by Hayton et al. [30] where the similarity metric is viewed in a probabilistic framework. Iterative Bayesian regularization is applied based on the similarity metric observed in neighboring blocks. Hayton et al. [30] originally applied this method for deformable image registration of magnetic resonance images obtained during breast imaging. Xiao et al. have also applied this method to the registration of three-dimensional (3D) B-Mode ultrasound subvolumes [31]. In the remaining sections, we first review the theoretical aspects of the algorithm and derive extensions that are relevant to strain imaging. Next, we describe the evaluation of the performance of this algorithm on tissue-mimicking (TM) phantoms and finite element based simulation experiments. Example images from a liver ablation, carotid atheroma, and breast carcinoma are examined. We also evaluate the characteristics of the main algorithmic parameter, the strain regularization sigma (SRS). This parameter imposes a Gaussian distribution on the estimated strain. Finally, we conclude with a discussion of the algorithm’s application in potential improvement of clinical strain imaging algorithms.

MATERIALS AND METHODS

Algorithm

In block-matching methods, a small matching-block from the pre-deformation image is compared to the post-deformation image using a similarity metric [11], [32]. We assume the comparison is made on a regular grid of points by translating the matching-block within a specified search region. The grid of similarity metric values located at the matching-block’s center define a similarity metric image associated with the matching-block utilized for displacement estimation. Examples of similarity metrics include sum of absolute difference, sum of squared differences, normalized cross correlation, phase correlation, or mutual information [1], [2].

We can treat the similarity metric image as a probability density image for the displacement of the matching-block by applying a few basic transformations. First, the similarity must be inverted, if necessary, such that the maximum value corresponds the region with the greatest similarity. Next, the metric must be shifted by the negative of the metric’s theoretical minimum so the smallest resulting value is zero. In the case of normalized cross correlation, 1.0 is added to the similarity metric since its bounds are [−1, 1]. For most other similarity metrics, this is a null operation. Finally, the similarity metric values are normalized by their sum such that integral of all values is unity. The similarity metric image can now be treated as a probability density image for displacement estimation that a discrete form with sample spacing equal to the input images’ sample spacing. A value of zero in the probability density image occurs at the metric’s theoretical minimum with the sum of discrete probabilities being unity.

The probability density images obtained are prior probability density estimates, Pr(u_x), in a Bayesian framework.

$$\mathit{\text{Pr}}({\mathbf{u}}_{\mathbf{x}}|{\mathbf{u}}_{{𝒩}_x})=\frac{\mathit{\text{Pr}}({\mathbf{u}}_{{𝒩}_x}|{\mathbf{u}}_{\mathbf{x}})\mathit{\text{Pr}}({\mathbf{u}}_{\mathbf{x}})}{\mathit{\text{Pr}}({\mathbf{u}}_{{𝒩}_x})}$$

where u_x is the displacement of the matching-block at location x and u_𝒩x is the displacement at neighboring matching-blocks. In this 2D case, we use the four neighbors, two axial and two lateral. The notation u_𝒩x is shorthand for {u_x′: x′ ∈ 𝒩_x}. The denominator, Pr(u_𝒩x), serves at as a normalizing constant. This factor is accounted for by renormalization at the end of every iteration of the algorithm.

We assume that Pr(u_𝒩x|u_x) can be modeled by the probability densities of the displacements estimated at immediate neighbors, i.e. four neighbors in 2D. In addition, we assume that these neighbors are independent.

$$\mathit{\text{Pr}}({\mathbf{u}}_{{𝒩}_x}|{\mathbf{u}}_{\mathbf{x}})={\displaystyle \prod _{\mathbf{x}\prime \in {𝒩}_x}\mathit{\text{Pr}}({\mathbf{u}}_{\mathbf{x}}\prime |{\mathbf{u}}_{\mathbf{x}})}$$

Here Pr(u_x′|u_x) is the probability that a neighboring block at x′ has a displacement u_x′ given a displacement u_x at x. The assumption of independence is usually invalid, but iterative application of the algorithm is intended to account for some of the expected correlation between neighboring displacement estimates.

We model Pr(u_x′|u_x) as the maximum of the neighboring probability density image modulated by a Gaussian term.

$$\mathit{\text{Pr}}({\mathbf{u}}_{\mathbf{x}}\prime |{\mathbf{u}}_{\mathbf{x}})\propto \underset{{\mathbf{v}}_{\mathbf{x}}\prime }{\text{max}}\left[\mathit{\text{Pr}}({\mathbf{v}}_{\mathbf{x}}\prime )\text{ exp}(\frac{-{\Vert {\mathbf{v}}_{\mathbf{x}}\prime -{\mathbf{u}}_{\mathbf{x}}\Vert }^2}{2{{\sigma }_{\mathbf{u}}}^2})\right]$$

Here v_x′ is the displacement at x′. The proportionality is addressed in the re-normalization step of the algorithm. The displacement v_x′ is evaluated over a subset of the region where u_x′ is evaluated. We restrict the above to ‖v_x′ − u_x‖ < ε, where ε is a threshold. The σ_u is a vector that determines the width of Gaussian-like term for each direction. If δ_x is the spacing between matching-blocks in one direction, then σ _ε = σ_u/δ_x, the SRS, represents the algorithm’s parameter in terms of a factor related to the expected strain. Spacing between matching-blocks can be decreased by increasing matching-block overlap or decreasing their dimension.

A likelihood term for the Bayesian model can then be written as,

$$\begin{array}{cc}\mathit{\text{Pr}}({\mathbf{u}}_{{𝒩}_x}|{\mathbf{u}}_{\mathbf{x}})\hfill & \propto {\displaystyle \prod _{\mathbf{x}\prime \in {𝒩}_x}\mathit{\text{Pr}}({\mathbf{u}}_{\mathbf{x}}\prime |{\mathbf{u}}_{\mathbf{x}})}\hfill \\ \hfill & \propto {\displaystyle \prod _{\mathbf{x}\prime \in {𝒩}_x}\underset{{\mathbf{v}}_{\mathbf{x}}\prime }{\text{max}}\left[\mathit{\text{Pr}}({\mathbf{v}}_{\mathbf{x}}\prime )\text{ exp}(\frac{-{\Vert {\mathbf{v}}_{\mathbf{x}}\prime -{\mathbf{u}}_{\mathbf{x}}\Vert }^2}{2{{\sigma }_{\mathbf{u}}}^2})\right]}\hfill \end{array}$$

The influence of neighbors beyond adjacent blocks can be achieved by recursively applying the entire regularization procedure.

The displacement of the matching-block is taken according to the maximum a posteriori principle.

$${\mathbf{u}}_{\mathbf{x}}=\text{arg }\underset{{\mathbf{u}}_{\mathbf{x}}}{\text{max}}\mathit{\text{ Pr}}({\mathbf{u}}_{\mathbf{x}}|{\mathbf{u}}_{{𝒩}_x})$$

Subsample precision of the displacement is achieved using interpolation of the posterior probability density.

Implementation

A multi-threaded version of the described algorithm was implemented with the Insight Toolkit [33] using normalized cross-correlation as the similarity metric for the results presented in this article. The search region was 17 A-lines in the lateral direction along with sufficient data points along the axial direction to capture the maximum displacement. A simple unguided search was used, which is sufficient for the following analysis but not computationally efficient. A computationally efficient implementation will follow in future work. The quantity ε, where ‖v_x′ − u‖ < ε was taken to be 3σ_u.

The steps of the algorithm can be summarized as follows:

1. Calculate a normalized cross-correlation image for every matching-block by translating it within its search region.

2. Add 1.0 to the similarity metric (normalized cross-correlation) image.

3. Normalize the similarity metric images (prior probability density) so the values sum to 1.0.

4. Calculate the posterior probability density for every similarity metric image’s four neighbors.

5. Repeat steps (3) and (4) for the desired number of iterations.

6. Calculate subsample displacements from the posterior probability density images.

Validation on Experimental TM Phantoms

A TM ultrasound elastography phantom subject to uniform deformation was imaged using a clinical ultrasound scanner. The 10×10×10 cm gelatin phantom had a 1.0 cm spherical inclusion near its center. This type of phantom is common in the elastography literature because of its simple, well known behavior and resemblance to an isolated tumor within background tissue. Frames of data were continuously collected as the unconstrained phantom was deformed with an acrylic plate. The plate was fitted with a transducer at the center and translated using a linear motion table. The phantom was scanned using a Siemens S2000 (Siemens Ultrasound, Mountain View, CA, USA) clinical ultrasound system equipped with a VFX9-4 transducer and the plane through the center of the sphere imaged. The transducer was excited at 8.9 MHz and radiofrequency (RF) data sampled at 40 MHz to a depth of 5.5 cm.

Twenty independent deformation experiments were performed by varying the pre-deformation frame index within the continuous loop to obtain statistically significant results. The frame average strain was controlled by the frame skip between pre-deformation and post-deformation frames. Displacement estimation error for comparison with the median filter and optimization of SRS was computed as follows. The estimated displacements were interpolated with cubic B-spline interpolation such that the sampling of the displacement image matched that of the RF data. The inverse displacement was applied to each pixel in the pre-deformation image, and windowed-sinc interpolation applied to find the corresponding RF value in the post-deformation image. A mean absolute RF difference (MARD) is reported excluding the edges of the image where edge effects or out-of-bounds conditions may occur.

$$\mathit{\text{MARD}}=\frac{{\displaystyle {\sum }_{i=1}^n|I_m({\mathbf{x}}_i-{\mathbf{u}}_{x,i})-I_f({\mathbf{x}}_i)|}}{n}$$

where I_m is the interpolated RF value in the post-deformation (moving) image and I_f is the RF value in pre-deformation (fixed) image.

Experiments were also performed on a uniform TM phantom. Displacement estimation error was also quantified using the elastographic signal-to-noise (SNRe) ratio in the axial direction [32]

$${\mathit{\text{SNR}}}_e[\mathit{\text{dB}}]=20\text{ log }10(\frac{m_{\epsilon }}{s_{\epsilon }})$$

where m_ε and s_ε are the mean and standard deviation of the axial strain, respectively. Calculation of the SNRe was restricted to the area around the transducer’s focus.

Numerical Simulation

Numerical ultrasound simulations were designed to mimic the ultrasound propagation and solid body mechanics present in the phantom. RF data was generated using an ultrasound frequency domain simulation program developed in our laboratory [34]. Uniformly distributed collections of randomly positioned acoustic scatterers were generated and their response to a linear array transducer over a range of frequencies calculated. A particular ultrasound transducer was simulated by multiplying the phantom response in the frequency domain with the spectrum for the ultrasound transducer of interest. A single row of 128 elements was the aperture, with a spacing of 0.2 mm between elements. An individual element had a size of 0.15 mm laterally and 10 mm elevationally. The beamspacing was 0.2 mm, and the transmit focus was located at a depth of 20 mm. This yielded the Fourier Transform of the RF data of interest. For these experiments, the simulated transducer’s spectrum was modeled as Gaussian with a center frequency of 8.0 MHz and a 40% fractional bandwidth. The simulated transducer array had a channel count of 128 elements. Displacements were applied to the individual scatterers that made up each numerical phantom, to produce a set of post-deformation numerical phantoms and the accompanying RF data. A 40×40×10mm volume of scatterers was simulated.

Displacement fields were generated by specifying the mechanical properties of interest, and applying uniform displacements as boundary conditions using commercially available finite element software, ANSYS (ANSYS Inc, Pittsburgh, PA, USA). Displacement fields were simulated for a phantom having a uniform background modulus of 2kPa and a circular inclusion with a modulus of 8 kPa. The inclusion’s diameter was 8 mm. Boundary conditions were as follows. Uniform displacements were applied across the top surface of each phantom in the axial direction such that the nominal strain produced in the phantom was equal to 0.5%, 1.0%, 3.0%, 5.0%, 7.0%, and 9.0%. The bottom of each phantom was constrained to have no axial displacement, and a single node was fixed in the lateral direction at the bottom, central node to ensure uniqueness of the solution. Displacement fields from a nearly incompressible (Poisson’s ratio of 0.495) material model in a plane stress state were simulated and applied to the numerical phantoms. The mechanical model represents a cylindrical inclusion in an unconstrained background, which is similar in its deformation to a spherical inclusion phantom [35].

Deformation estimation statistics on n=30 randomly generated collections of scatterers were collected for both the circular inclusion phantoms and the uniform phantoms. Displacement estimation error for comparison with the median filter and optimization of SRS were computed as follows. Output displacements from the finite element simulation were interpolated with cubic B-spline interpolation at locations where displacement estimation occurred. A mean absolute axial displacement difference (MADD) is reported excluding the edges of the image, where edge effects may occur.

$$\mathit{\text{MADD}}=\frac{{\displaystyle {\sum }_{i=1}^n|{\widehat{u}}_a-u_a|}}{n}$$

where û_a is the estimated axial displacement and u_a is the known axial displacement. Simulations of a uniformly elastic TM phantom were similarily examined and evaluated for variations in the SNRe with applied deformation.

In-vivo Imaging

In order to examine the performance from data closer to what is expected in clinical application, we examine strain images obtained in-vivo from porcine liver, human arterial tissue, and a for a patient with breast cancer. The first set of images correspond to a radiofrequency ablation performed on an open-abdominal in vivo porcine model with a healthy liver. The study was approved by the research animal care use committee at the University of Wisconsin-Madison. Details about this study are presented in [36]. The second set of images examined was generated from ultrasound RF data acquired on an atherosclerotic in vivo carotid artery. A different transducer was used, namely, the Siemens 18L6 linear array (Siemens Ultrasound, Mountain View, CA, USA). The source of deformation in this case is blood pressure. The study was approved by the UW-Madison institutional review board (IRB), and patient consent was obtained prior to the ultrasound scans of the carotid artery. The third set of images are strain images generated from a patient with invasive ductal carcinoma in the breast [37] from a study also approved by the UW-Madison IRB. Patient consent was obtained prior to ultrasound scanning.

Experimental Protocol

In order to visualize the effectiveness of recursive Bayesian regularization, we quantified errors at 0.5%, 1.0%, 3.0%, 5.0%, 7.0%, and 9.0% strain in the TM phantom and numerical simulation images. We present estimated axial strain images with and without regularization at 5.0% strain. We also generated strain images after filtering the displacements with a 3×3, 5×5, and 7×7 pixel median filter for comparison. Matching-block size used was 41 points (0.8 mm) in the axial direction and 9 points (1.1 mm) in the lateral direction. A two-point central difference method is used calculate the strain images from the displacement images.

Liver, carotid, and breast B-mode images are displayed along with axial strain images with no regularization, 3×3 median filtering, and three iterations of Bayesian regularization. As with the spherical inclusion phantom, the MARD was calculated to quantify the quality of motion tracking.

An optimal SRS under different conditions was extracted by minimizing the described error measure for both TM phantom and numerical simulation images. Brent’s Method for scalar minimization [38] was performed to a tolerance of 0.001. The optimal SRS was examined over a range of strains, matching-block overlaps, and algorithm iterations. Unless otherwise noted, strain examined was 5%, matching-block overlap was 0%, and the number of iterations was set to three. Although SRS can be specified independently in all directions, SRS reported is the parameter’s value along the axial direction. The value in the lateral direction was taken to be half the value in the axial direction since unconstrained compression of nearly incompressible elastic materials lead to strains in orthogonal planes that are half that along the loading axis, i.e. the incompressibility assumption. Note, however, the parameters for each direction can be specified independently, and strain in one direction does not directly influence strain in the other directions.

RESULTS

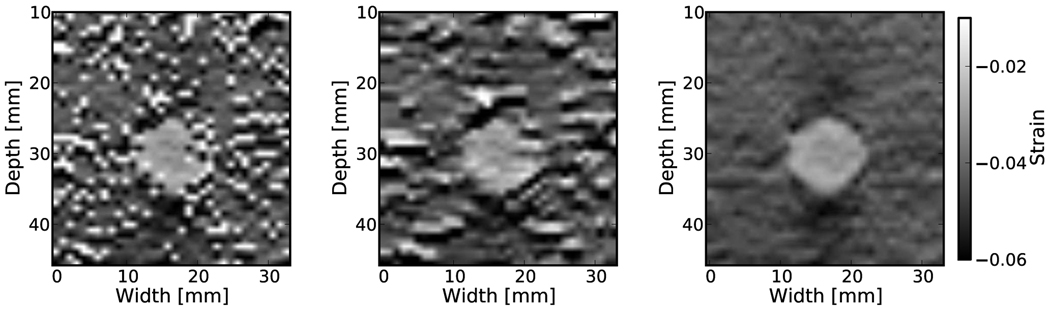
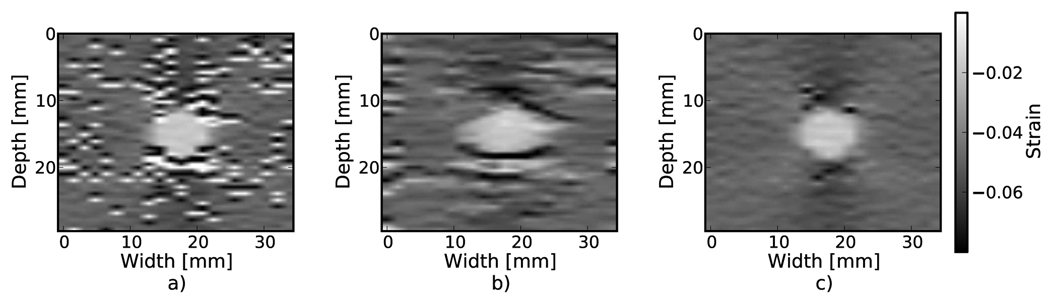
Examples of the algorithm’s effectiveness are shown in Fig. 1 and Fig. 2. Fig. 1 shows axial strain images of the phantom data with no regularization (a), median filtering of the displacements (b), and recursive Bayesian regularization (c). With no regularization, there are considerable peak hopping errors limiting the ability of median filtering to remove these errors. Instead, these errors are “smeared”, which arguably makes the regularized image worse than the original because the peak hopping errors are more likely to be interpreted as artifactual tissue structures. The proposed Bayesian regularization on the other hand, does an excellent job of removing these noise artifacts from the image. Results are similar for the numerical simulation results, shown in the Fig. 2. Again, considerable decorrelation noise is present in the uncorrected image. Median filtering removes a good portion of the noise, but it also results in a noticeable loss of resolution at the boundary of the inclusion. The Bayesian regularization does a better job of removing noise while increasing the observable strain pattern surrounding the inclusion. However, a few peak hopping errors are not removed as illustrated in Fig. 2(c).

Figure 1.

Phantom axial strain images with different types of regularization applied. a) No regularization. b) 3×3 median filter applied to the displacements. c) Three iterations of the proposed regularization algorithm.

Figure 2.

Simulation axial strain images with different types of regularization applied. a) No regularization. b) 3×3 median filter applied to the displacements. c) Three iterations of the proposed regularization algorithm.

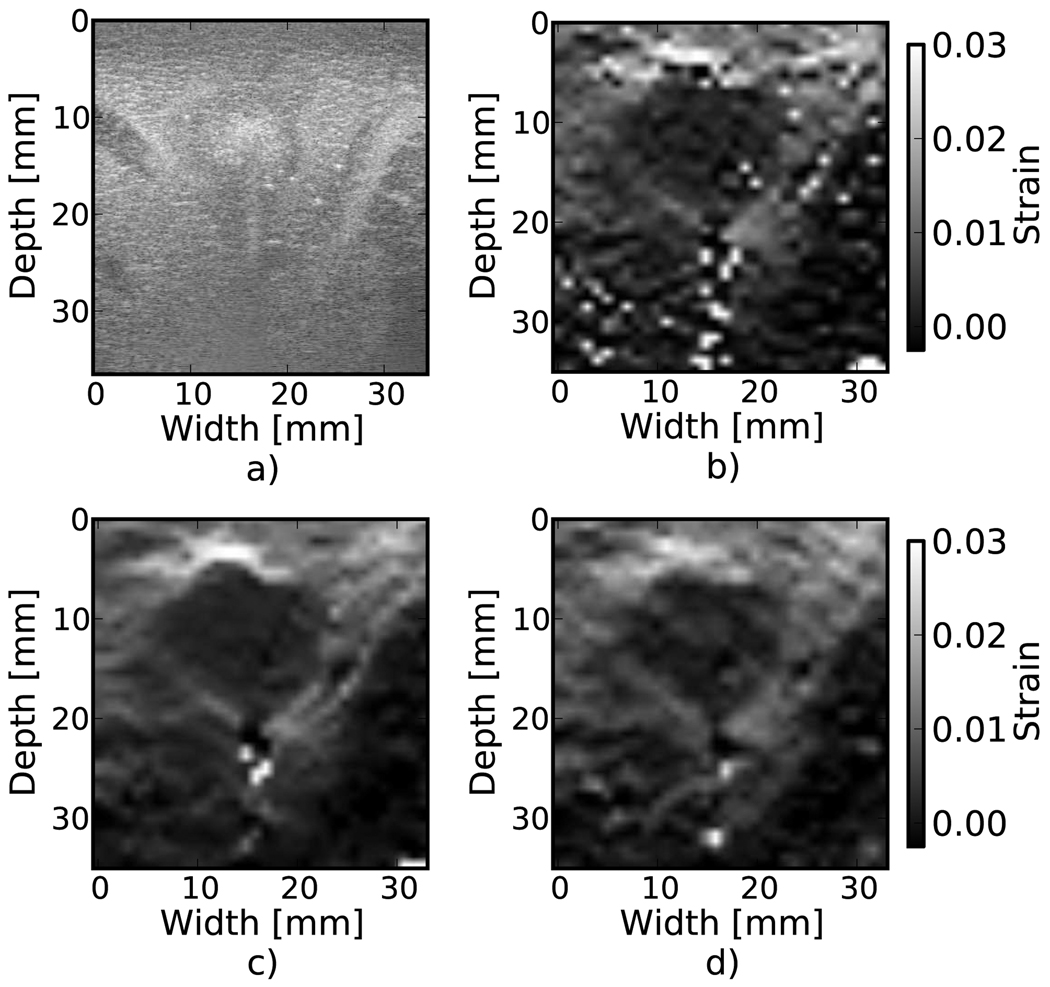
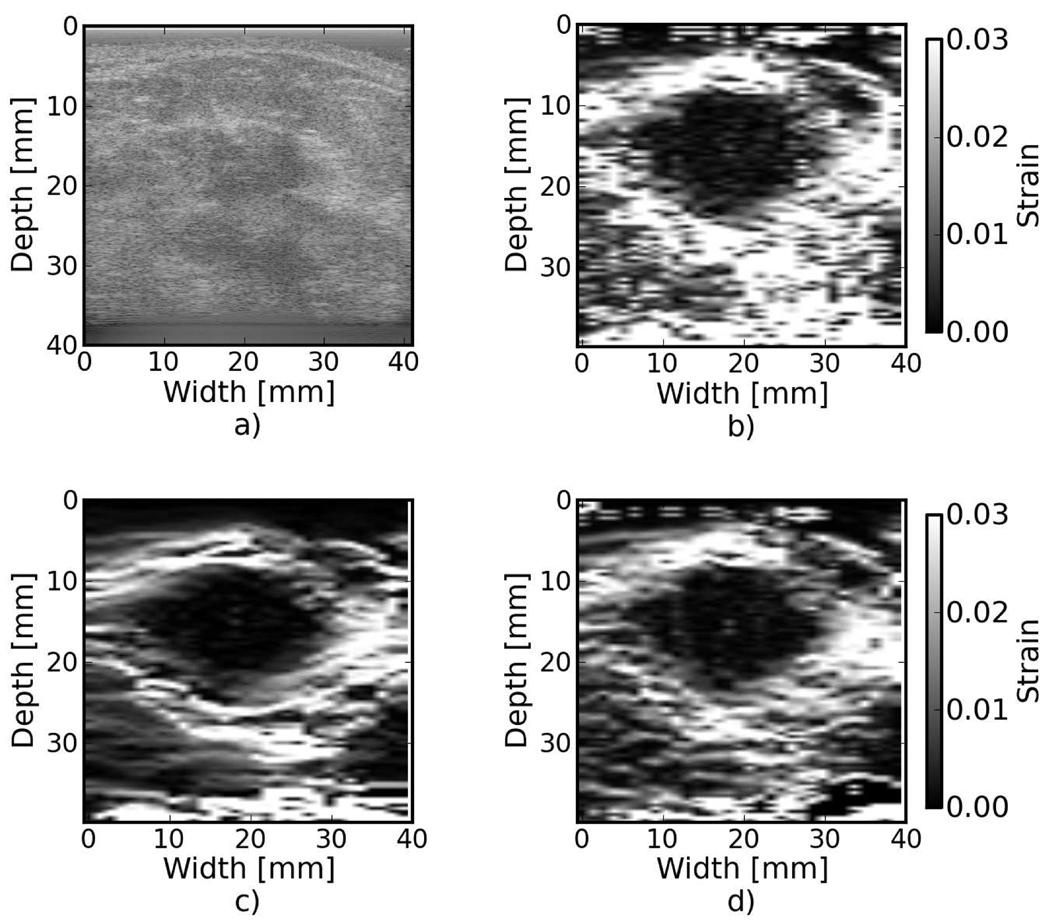
Results from tracking tissue RF echo signals are shown in Fig. 3, Fig. 4, and Fig. 5. The ablated liver tissue observable in Fig. 3(a) causes the reduced strain region in the strain images. Both median filtering and Bayesian regularization remove the majority of peak hopping errors. The median filtered image appears smoother while the Bayesian regularization image has more detail, although the true underlying strain is unknown, so it is difficult to associate a correct image from appearance. Bayesian regularization does slightly better at handling shadowing from the electrode ablation needle at the bottom of the ablated region. The MARD values were 150.0, 127.6, and 124.1 for no regularization, median filtering, and Bayesian regularization, respectively. Figure 4 shows an atherosclerotic artery undergoing compression during systole. Bayesian regularization removes many of the peak hopping artifacts in the areas of high strain, roughly 3% and higher. However, note that in areas distant from the vessel wall, where there is little to no deformation, Bayesian regularization introduces additional artifacts compared to the case with no regularization. The MARD values were 55.6, 50.5, and 46.6 for no correction, median filtering, and Bayesian regularization, respectively. In the breast cancer image (Fig. 5), the MARD values were 88.0, 73.39, and 68.7 for no regularization, median filter, and Bayesian regularization. The MARD and the appearance of the image suggest that the regularization is likely more accurate. However, depending on the situation, accuracy might not be the only criteria for a ’better’ image. For example, consistent appearance of inclusion and background gray-levels may qualify an image as ’better’. According to that criterion, the median filter may be considered better in this case.

Figure 3.

Strain images from an in vivo porcine liver undergoing RF electrode ablation. a) B-Mode. b) No regularization. c) 3×3 median filter applied to the displacements. d) Three iterations of the proposed regularization algorithm.

Figure 4.

Strain images of an atherosclerotic carotid bulb during systole, in vivo. a) B-Mode. b) No regularization. c) 3×3 median filter applied to the displacements. d) Three iterations of the proposed regularization algorithm.

Figure 5.

In vivo strain images of a patient with invasive ductal carcinoma of the breast. a) B-Mode. b) No regularization. c) 5×5 median filter applied to the displacements. d) One iteration of the proposed regularization algorithm.

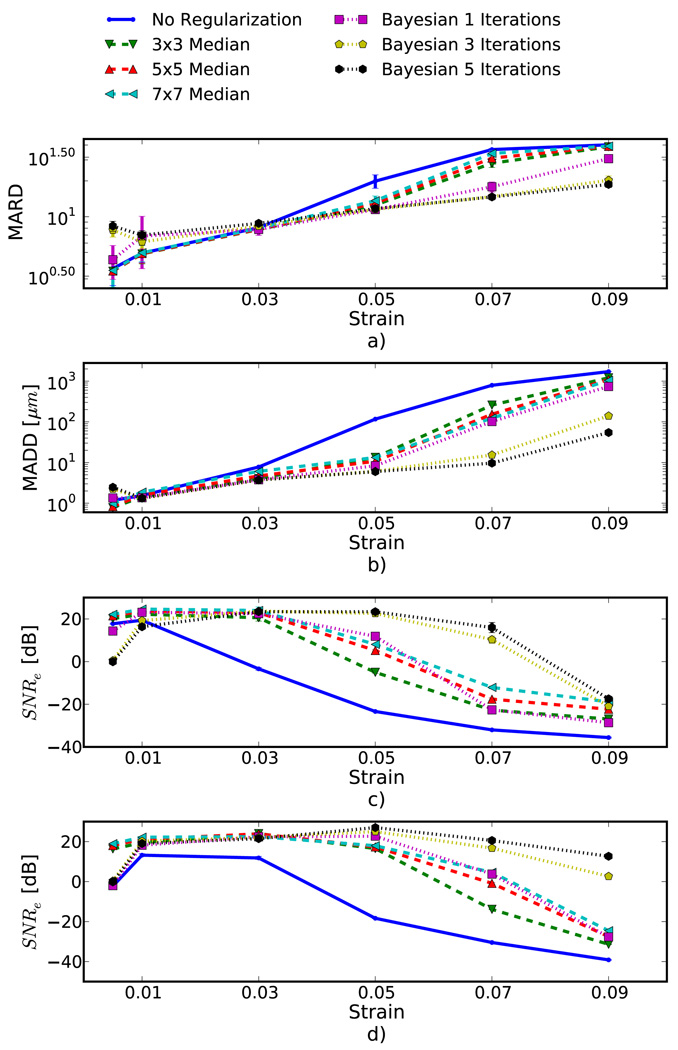
Quantification of the results observed visually in Fig. 1, are shown in Fig. 6(a) and the corresponding simulation results indicated visually in Fig. 2 are plotted in Fig. 6(b). Mean error metrics for the inclusion experiments and SNRe for the uniform strain experiments are plotted against strain for each regularization method. Error bars here denote two standard errors of the error measures corrected for repeated measure means [39]. Results are consistent across strain content, simulation and phantom data, and method for measuring the tracking quality of the estimated displacement. Bayesian regularization greatly improves motion tracking performance over no regularization and median filtering at large strains, 5.0% and higher. Improvement is on par with median filtering at moderate strains, 3.0%. For small strains, <1.0%, Bayesian regularization may decrease performance relative to no regularization. This is consistent with the carotid strain image shown in Fig. 4. In general, increased iterations of the proposed algorithm result in greater improvement, but the relative improvement from three iterations to five iterations is much smaller than one iteration to three iterations. In contrast, the ideal median filter size varies depending on the strain content and the amount of applied deformation. This is consistent with our visual observation of the algorithm’s behavior; images improve up to approximately three iterations after which the improvement is not as noticeable.

Figure 6.

Motion tracking quality versus applied strain for four different experiments, a) spherical inclusion phantom, b) spherical inclusion phantom simulation, c) uniform phantom, and d) uniform simulation. Different quality metrics are applied to the appropriate experiment. a) Mean absolute RF phantom image RF difference (MARD) versus regularization method (lower is better). b) Mean absolute displacement difference (MADD) between the simulated and estimated displacements (lower is better). c) and d) are the mean strain over the standard deviation of the strain (higher is better).

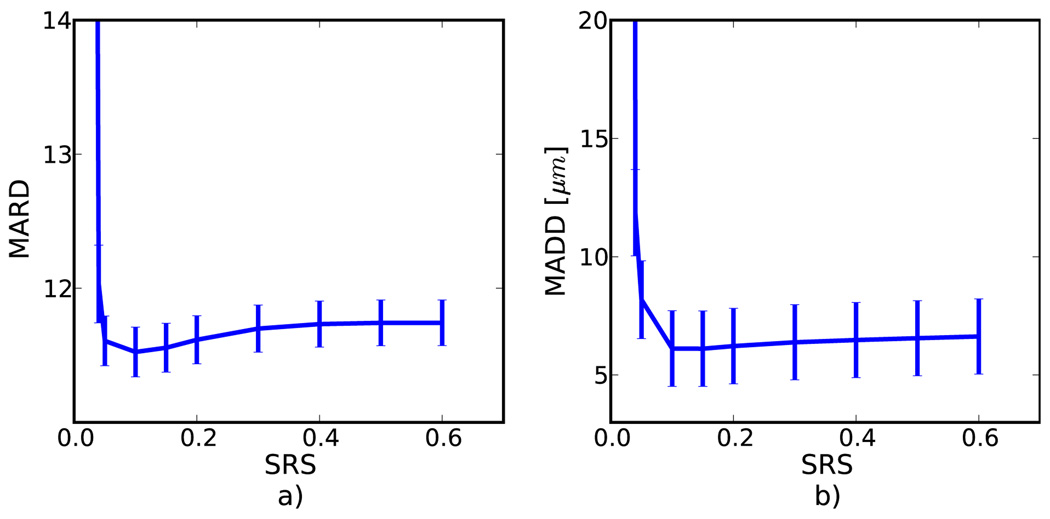
Figure 7 depicts the MARD for displacement tracking in the TM phantom along with MADD for the numerical simulation studies, respectively. The SRS is the only input parameter to the algorithm, and this graph reveals roughly where the optimal value exists, i.e. the location of smallest error. It also demonstrates the robustness of the algorithm, i.e. how well the algorithm performs when a non-optimal SRS’s is used. There is significant variation in the error measure, but the results suggest that as the SRS is lowered, the effectiveness increases slightly until the parameter approaches the strain in image (0.05) after which the error increases dramatically. Both the simulation and phantom display similar patterns.

Figure 7.

Error measures on a) phantom and b) simulation versus the regularization parameter. The nominal strain in both cases was 5 %.

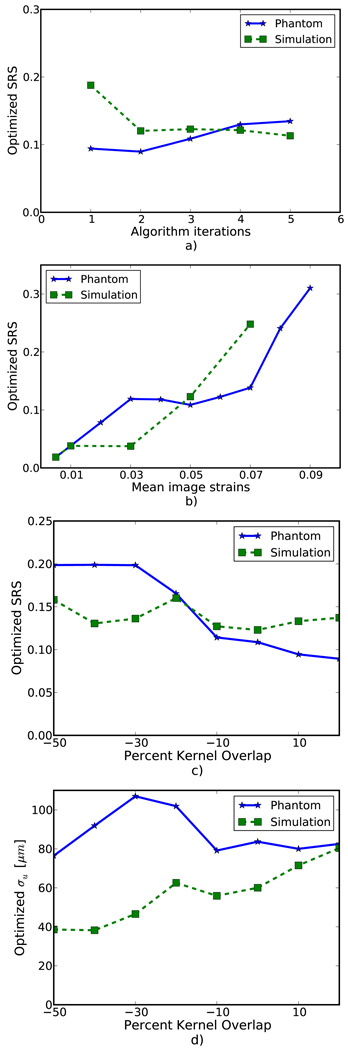
Figure 8(a) shows optimized SRS versus the number of algorithm iterations. No consistent pattern is observed. This suggests the optimization parameters do not strongly depend on the number of iterations. As expected, Fig. 8(b) demonstrates the optimal SRS increases with increasing image strain. The optimal parameter is approximately twice the image strain. A decrease in SRS is seen in Fig. 8(c) with phantom images, but a consistent trend is absent from the simulation images. The deviation in optimized parameters in either case is relatively small given the flatness of the error metric shown in Fig. 7. Figure 8(d), which plots σ_u as opposed to SRS, is shown to contrast with Fig. 8(c). Phantom images again demonstrate a downward trend while simulation images suggest an upward trend. Optimized parameters for phantom images and simulation images are more consistent in Fig. 8(c) than Fig. 8(d), which suggest SRS may be a more consistent parameter than σ_u.

Figure 8.

Variation in the optimized regularization parameter with a) the number of algorithm iterations, b) image strain, and c) matching-block overlap. To contrast with c) the optimized regularization parameter multiplied by matching-block spacing versus matching-block overlap is shown in d).

DISCUSSION

Block matching based displacement tracking methods can regularize the estimated displacement to reduce noise artifacts by enforcing the diffeomorphic transformation expected in images of solid tissue. Filtering methods such as median filtering take into account displacements of neighboring matching-blocks and can reduce noise artifacts, but come at the cost of spatial resolution. Better regularization performance is possible when incorporating similarity metric values from neighboring blocks prior to displacement estimation.

The method described in this article is analogous to regularization algorithms that minimize a cost function involving the similarity metric and the continuity assumption [13]–[15]. However, transforming the similarity metric image into a probability distribution allows use of the similarity metric’s weight in determining displacements to vary dynamically depending on the local uncertainty. The weight of the similarity metric does not depend on its absolute value. Instead, weight of the similarity metric is adjusted locally to the noise conditions in a matching-block’s search region. This independence of local or global noise improves robustness of the local estimated displacements.

Due to its statistical nature, the algorithm encourages a continuous solution, but it still allows discontinuous motion when it is strongly suggested by the data. This is important for Fig. 4, where opposing arterial walls move in opposite directions.

The form of the likelihood term in the Bayesian model suggests that a Gaussian distribution in the estimated strain distribution is expected since it involves the difference in displacements and the matching-block spacing is constant. The actual strain distribution depends on the modulus distribution and boundary conditions of the tissue imaged, but a Gaussian distribution is an appropriate generic form because of the Central Limit Theorem. As long as the regularization parameter is large enough, the algorithm performs across a wide range of strains. This robustness can be inferred from the flatness in the latter portion of Fig. 7. If the variance of the Gaussian is presumed to be too small, large strains are not possible, and regularization will degrade the quality of motion tracking. Furthermore, we have shown that the parameter does not have to be chosen arbitrarily because of its meaningful interpretation in terms of the expected strain. In Hayton’s original article, he remarked on the complex interaction of the Gaussian likelihood standard deviation with matching-block spacing [30]. The term σ_u controls the probability of δu in δu/δx but the matching-block spacing scales δx in δu/δx. When we formulate σ_ε as σ_u/δ_x the algorithm’s parameters are decoupled into a single parameter with a meaningful interpretation. A good SRS can be determined analytically as opposed to heuristically with a rough knowledge of the expected strain. Figure 8(b) shows that the optimal parameter increases with the image strain. However, the relationship is not expected to be strictly linear. A strain image will contain a distribution of strain amplitudes, and signal decorrelation varies with the applied strain [40], which will also affect the optimal parameter. In an approximate sense, the SRS can be viewed as the standard deviation of a function that modulates the estimated strain.

As seen in Fig. 6, Bayesian regularization can greatly increase the quality of motion tracking and dynamic range of strains that can be imaged. This improvement is mostly seen at higher applied deformations, i.e. 5% and above. For very small strains, application of the algorithm can decrease image quality compared to no regularization. The source of noise at small strains is predominately electronic and quantization noise [40], and quantization noise may prevent the algorithm from being effective at these levels. This behavior along with the additional computational expense, suggest it may be desirable to limit application to high strain situations when applied to a clinical setting.

Various methods, given in the subplots of Fig. 6, were used to to validate the algorithm. The SNRe is a common metric used to evaluate strain imaging algorithms in the literature that characterizes the dynamic range and peak SNRe available [40]. Typically, an algorithm has difficulty at low strains and high strains, which gives the curve a ’bandpass filter’ shape [40], observable in Fig. 6. The regularization greatly increases the dynamic range at the higher end, but slightly compresses it at the lower end. Since the SNRe is calculated on a uniform target, it does not demonstrate the ability of the algorithm to faithfully reproduce structures, which is often the purpose of creating the image. For this reason, we also evaluted performance with an inclusion target. For the simulation case, we have perfect knowledge of the true underlying displacement, so we can calculate the MADD. The MADD is a measure of the estimated displacement’s fidelity over the entire image. In the phantom case, the true displacement is not precisely known, so the MARD error measurement is used. The MARD similarly measures the estimated displacement’s fidelity if the motion of the RF can be assumed to follow the motion of the tissue from which it is generated. Since the shape of the MARD curves coincide well with the other error measures, its use in providing a quantitative assessment of the in vivo examples is justified. The in vivo examples demonstrate the algorithms effectiveness in more realistic clinical conditions.

Application of regularization of course comes at a computational expense. The authors have not attempted a real-time implementation, but the following observations were made on the computational complexity. First, the algorithm is easily parallizable and was implemented as a multi-threaded filter on a CPU. The shifting, normalization, and logarithm operations are all parallelizable. Computation of the likelihood term is parallizable on a per displacement basis in a given iteration. Particular computational expense comes in the calculation of the likelihood term, which is a convolution-like operation. This has the following implications. Although Fig. 7 suggests a safe choice of SRS is higher, this will come at an additional computation expense because the Gaussian term becomes larger. Also, the size of the search region should be minimal to reduce calculation of the likelihood terms. Approaches such as a multi-resolution pyramid [24] where subsampled search regions that cover a large area of physical space are used to initialize smaller search regions may be helpful.

The algorithm is 2D, but analysis in this article focused on the performance along the ultrasound beam axis. Although lateral strains and shear strains are also expected to be improved, the relatively poor point spread function and sampling in the lateral direction still create very noisy strain images. Combination of the algorithm with other techniques, such as the multi-resolution pyramid [24], will be necessary before an informative analysis can be performed on this data.

CONCLUSION

We propose the application of a recursive Bayesian regularization algorithm for ultrasound strain imaging. This algorithm applies a probabilistic model to the similarity metric and imposes a Gaussian distribution on the estimated strain when incorporating the results of neighboring matching-blocks. Results from in vivo, TM phantom and numerical simulations were presented, and the proposed algorithm was proven to be an effective method of improving displacement estimates.

Biographies

Matthew McCormick (S’2010) received a B.S. in biomedical engineering from Marquette University in 2005. He received a M.S. degree in biomedical engineering from the University of Wisconsin-Madison in 2008, where he is currently a PhD candidate. His research interests include signal processing for ultrasound strain image and high-frequency ultrasound tissue characterization. These techniques are applied towards stroke prevention by characterizing carotid artery plaques.

Nicholas Rubert (S’2010) was born in Sayre, Pennsylvania in 1985. He received the B.S. degree in physics from the Pennsylvania State University in 2008. He is currently a graduate student in medical physics at the University of Wisconsin. His current interests include elastography and inverse problems.

Tomy Varghese (S’92-M’95-SM’00) received the B.E. degree in Instrumentation Technology from the University of Mysore, India in 1988, and the M.S. and Ph.D in electrical engineering from the University of Kentucky, Lexington, KY in 1992 and 1995, respectively. From 1988 to 1990 he was employed as an Engineer in Wipro Information Technology Ltd. India. From 1995 to 2000, he was a post-doctoral research associate at the Ultrasonics laboratory, Department of Radiology, University of Texas Medical School, Houston, TX. He is currently an Associate Professor in the Department of Medical Physics at the University of Wisconsin-Madison, Madison, WI. His current research interests include elastography, ultrasound imaging, ultrasonic tissue characterization, detection and estimation theory, statistical pattern recognition and signal and image processing applications in medical imaging. Dr. Varghese is a fellow of the American Institute of Ultrasound in Medicine (AIUM), Senior member of the IEEE, and a member of the American Association of Physicists in Medicine (AAPM) and Eta Kappa Nu.