Virtual Screening Using Molecular Simulations

Abstract

Effective virtual screening relies on our ability to make accurate prediction of protein-ligand binding, which remains a great challenge. In this work, utilizing the molecular-mechanics Poisson-Boltzmann (or Generalized Born) Surface Area approach, we have evaluated the binding affinity of a set of 156 ligands to seven families of proteins, trypsin β, thrombin α, cyclin-dependent kinase (CDK), cAMP-dependent kinase (PKA), urokinase-type plasminogen activator, β-glucosidase A and coagulation factor Xa. The effect of protein dielectric constant in the implicit-solvent model on the binding free energy calculation is shown to be important. The statistical correlations between the binding energy calculated from the implicit-solvent approach and experimental free energy are in the range 0.56~0.79 across all the families. This performance is better than that of typical docking programs especially given that the latter is directly trained using known binding data while the molecular mechanics is based on general physical parameters. Estimation of entropic contribution remains the barrier to accurate free energy calculation. We show that the traditional rigid rotor harmonic oscillator approximation is unable to improve the binding free energy prediction. Inclusion of conformational restriction seems to be promising but requires further investigation. On the other hand, our preliminary study suggests that implicit-solvent based alchemical perturbation, which offers explicit sampling of configuration entropy, can be a viable approach to significantly improve the prediction of binding free energy. Overall, the molecular mechanics approach has the potential for medium to high-throughput computational drug discovery.

Introduction

It takes on average 11.4 to 13.5 years to develop a new small-molecule drug based on the statistics from 2000 to 2007 ¹. With an approximate $50 billion annual R&D spending by top pharmaceutical companies, the average cost to bring an innovated drug to market is estimated to be $1.8 billion. A series of technologies, from functional genomics ² to combinational chemistry ³ and high-throughput screening ⁴, are utilized to accelerate the drug discovery process. With the rapid development of computing technology, computer-aided drug design, has attracted a great deal of attention due to its promise for high efficiency and low cost. With the aid of computers, candidates are searched or designed in silico and thus the need for the more expensive and time-consuming experimental synthesis and characterization is reduced. Since 1995 when the computer-designed drug (carbonic anhydrase inhibitor dorzolamide ⁵) was first introduced, numerous successful cases were reported, e.g. Imatinib, a tyrosine kinase inhibitor designed specifically for the Bcr-Abl fusion protein that is characteristic for Philadelphia chromosome-positive leukemias ⁶, Zanamivir, for therapeutic or prophylactic treatment of influenza infection ⁷, and Dorzolamide, a carbonic anhydrase inhibitor used to treat glaucoma ⁸.

A key step in drug discovery is to identify novel chemical molecules (hits and leads) that interact with specific biomolecular targets, in most cases, proteins such as enzymes, ion channels and transmembrane receptors ^{9, 10}. However, the pharmaceutical industry is facing an “innovation deficit” in which an insufficient number of new chemical entities are discovered each year even with billions of research dollars spent ^{1, 11}. Virtual screening techniques such as molecular docking have been developed to facilitate the rapid identification of potential leads. In docking, with the structure of protein targets obtained from either X-ray or NMR, a library of ligands are brought to the proximity of the specific binding site of the target and possible poses and conformations of the ligands are sampled. For each pose a “score”, which is the measure of the empirical binding free energy of the receptor-ligand system, is calculated in accordance to the “scoring function”, which is typically constructed based on an over-simplified empirical force field for the sake of computational speed ⁹.

Although efficient, molecular docking has a series of inherent limitations ¹². In typical docking approaches, ligands are allowed to make conformational changes while proteins are treated either as rigid or with limited flexibility. A binding score is assigned to each static pose even though the binding free energy is an ensemble-averaged thermodynamic quantity including vibrational, rotational and conformational contributions. The treatment of solvent effects is often inadequate even though solvent plays a crucial role in the binding. In addition, the scoring function contains a set of empirically determined parameters which are derived from its training set, a series of complexes with known binding structures and affinities. The choice of training set affects the resultant parameters and thereafter the score; a ligand that is chemically different from those in the training set may not be accurately described. Although consensus enrichment may improve docking reliability, it seems to mostly improve the accuracy of structure rather than the binding affinity ¹³. In a previous work which evaluated a series of popular scoring functions on a set of 100 protein-ligand complexes, only 4 out of 11 scoring functions were able to give correlation coefficients over 0.50 with experimentally measured binding affinities ¹⁴. Limited accuracy of binding affinity prediction remains a problem for molecular docking because true hits may be eliminated even when docking poses are correctly predicted. Other studies provide a similar conclusion that scores generated by docking programs are barely correlated with experimental data and weakly predictive of binding affinity across a series of systems ^15–17. The over-simplification of the solvent model, negligence of configurational entropy, and insufficiency in conformational space sampling ¹⁸, all limit current docking approaches from a promising future virtual screening tool.

Molecular mechanics simulation and analysis, a more rigorous and ab initio method broadly used in computational chemistry since 1970s, may be a prospective candidate for the next generation virtual screening tool. It overcomes the conceptual flaw in molecular docking by generating a sequence of “snapshots” with physical methods (e.g. molecular dynamics or Monte Carlo) to represent the ensemble of accessible microstates of a system, followed by computing the ensemble-average of a particular thermodynamic quantity of interest, including binding thermodynamics. Furthermore, the parameters used in molecular mechanics simulation, originated either from quantum mechanics calculation or experiments, are typically atomistic and more transferred than those used in empirical scoring functions that are derived from fitting in training set. Molecular mechanics approaches have been shown to be effective for virtual lead optimization ^{9, 18, 19}. However, alchemical approaches, in which a molecule is gradually transferred into another, offer detailed sampling of configurational space in response to perturbations in protein binding sites, ligands and water dynamics. However, they are computationally too expensive for high throughput application.

Recently, more and more advanced molecular simulations and free energy calculations have been successfully applied to the optimization of lead compounds, such as the search of non-nucleoside inhibitors of HIV reverse transcriptase and inhibitors of the binding of the proinflammatory cytokine macrophage migration inhibitory factor to its receptor CD74 applying free energy perturbation calculations in conjunction with Monte Carlo statistical mechanics simulations for protein–inhibitor complexes in aqueous solution, “double decoupling”—a method to calculate the free-energy changes associated with making the inhibitor ‘disappear’ from the complex with the enzyme and for making the inhibitor disappear in bulk water, a recent approach called “steered molecular dynamics” to compute the force that is required to extract inhibitors from complexes with enzymes, in which molecular-dynamics simulations are employed to predict the energy changes for a harmonic-spring-attached inhibitor being pulled at constant velocity into the surrounding water ^19–21. S.P. Brown and S.W. Muchmore applied an implicit solvent molecular mechanics simulation in the context of a distributed-computing paradigm to estimate relative binding affinities to three targets: urokinase, PTP-1B, and Chk-1 ²². The so called molecular-mechanics Poisson-Boltzmann Surface Area (MM-PBSA), first introduced by Kollman and colleagues ²³, was used. The observed correlation coefficients with experiments are in the range of 0.72–0.83. While this is a small data set, the results seem to be significantly better than those typically reported from docking when using a scoring function ^15–17. C. Gao and et al ²⁴ adopted a method based on perturbation theory using a quasi-harmonic model as reference to account for the free energy change originated from 1) enthalpic change; 2) entropic loss due to different and more restricted configurations of a bound ligand relative to its free solvated state, which is often neglected or treated crudely in predicting binding affinity. For the 16 protein pocket targets tested, in most cases, the ligand conformation in the bound state was significantly different from the most favorable conformation in solution. Both entropic and enthalpic contributions to this free energy change are significant. And in general, the correlation between measured and calculated ligand binding affinities, including the free energy change due to ligand conformational change is comparable to or better than that obtained by using an empirically-trained docking score. The molecular mechanics method has its weakness too. For example, these calculations are computationally intense compared to molecular docking and are often imprecise for large targets and compounds as large as typical drugs ^{21, 24}.

Although there have been many studies of protein-ligand binding using implicit solvent based molecular mechanics approaches with various parameters and settings ^25–29, systematic investigations of its potential as a semi-high throughput screening tool on a series of reliable experimental data is still lacking. In this work, we apply molecular mechanics to calculate the binding affinities of 7 protein families with a total of 156 ligands. With explicit solvent MD simulation, conventional MM-PBSA and MM-GBSA (molecular-mechanics Generalized-Born Surface Area) ²³ were applied to estimate the binding free energy. The entropic contribution, including ligand conformational restriction, to protein-ligand binding was evaluated using different methods. The effect of solute dielectric constant on the calculated affinity was carefully examined. The overall efficiency and accuracy found from this study suggest that a molecular simulation is a viable approach for medium-throughput virtual screening. Future directions to further improvement were also presented.

Materials and Methods

Systems selection

The complexes of proteins and ligands were chosen from the refined set of PDBBind database ³⁰. Experimental crystal structures and binding affinities were reported for all the systems. We selected seven disparate families of proteins, i.e. trypsin β, thrombin α, cyclin-dependent kinase (CDK), cAMP-dependent kinase (PKA), urokinase-type plasminogen activator, β-glucosidase A and coagulation factor Xa, with the numbers of ligands in corresponding families being 57, 28, 11, 8, 19, 18 and 15, separately (see Table-S1 for details). We combined data of cyclin-dependent kinase and cAMP-dependent kinase which results to 6 groups in reality (in the following we use “CDK+PKA” for this group). We selected ligands from each family according to the following rules: a) the number of heavy atoms of the ligand is less than 50; b) the number of rings in the ligand is no greater than 5; c) the maximum number of atoms in a ring is no greater than 30; and d) the number of rotatable bonds in the ligand is no greater than 10.

Amber simulation

Molecular dynamics simulations using Amber ³¹ version 9 were performed to generate an ensemble of conformations for each protein-ligand complex in water, followed by MM-GBSA/MM-PBSA ²³ calculations to estimate the binding free energy.

In the MD simulations, the entire protein from PDB rather than only the pocket was included. Missing protein residues were added using Modeller ³² version 9.4 with sequences given by experiments. The Amber ff99SB force field ³³ was used for proteins. The generalized AMBER force field force field parameters were assigned to the small molecules ³⁴. The ligands’ atomic partial charges were generated by the empirical charge model—AM1-BCC ³⁵ by using the Antechamber module ³⁶ version 1.27. The protonation of proteins was assigned by the LEaP module of Amber 9 ³⁷, which was also used to generate the parameters and coordinates files for PMEMD (Particle Mesh Ewald Molecular Dynamics) simulations. Each complex was solvated in a TIP3P water box ³⁸ with a minimum distance 10.0 Å from the surface of the complex to the edge of the simulation box. Each system was neutralized by adding Na⁺ or Cl^- ions. Scripts were used to automate the above process of converting PDB and MOL2 formatted experimental structures to Amber simulation input files ³⁹.

The solvated complex was subject to an initial energy minimization with solute restrained followed by a complete minimization with no restrains. Each energy minimization consisted of a 2,500-step steepest descent minimization and then another 2,500-step conjugated gradient. Subsequently, a 100-ps MD simulation was performed with the complex subject to positional restraint. The 100-ps MD simulation was used to heat the system from 0 to 300 K in NVT ensemble. Finally, a 2-ns unrestrained NPT simulation was performed, with temperature and pressure controlled at 300 K and 1 atm, respectively, by applying Berendsen weak-coupling algorithm ⁴⁰. The particle mesh Ewald (PME) method ^{41, 42} was used to treat the long-range electrostatic interactions. The cutoff distances for the real-space of PME and the Van der Waals interactions were set to 10 Å. All bonds involving hydrogen atoms were constrained using the SHAKE algorithm ⁴³. An integration time step of 2.0 fs was used. Atom coordinates were recorded every picosecond. The snapshots generated in the 2-ns MD simulation were input into the post-simulation MM-GBSA/MM-PBSA calculations of binding free energy.

MM-GB(PB)SA calculation

In MM-GBSA/MM-PBSA method, the binding free energy is computed as the following ⁴⁴:

$$\mathrm{\Delta }{G}_{\mathit{bind},\mathit{solv}}=\mathrm{\Delta }{G}_{\mathit{bind},\mathit{vac}}+\mathrm{\Delta }{G}_{\mathit{complex},\mathit{solv}}-\mathrm{\Delta }{G}_{\mathit{protein},\mathit{solv}}-\mathrm{\Delta }{G}_{\mathit{ligand},\mathit{solv}}$$ (1)

where ΔG_bind,solv and ΔG_bind,vac are the binding free energies in solvated state and in vacuum, respectively. ΔG_complex,solv, ΔG_protein,solv and ΔG_ligand,solv are solvation free energies of complex, protein and ligand, respectively. The solvation free energy, based on the implicit solvent models, include the polar and the non-polar contributions:

$$\mathrm{\Delta }{G}_{\mathit{solv}}=\mathrm{\Delta }{G}_{\mathit{solv},\mathit{polar}}+\mathrm{\Delta }{G}_{\mathit{solv},\mathit{non}-\mathit{polar}}$$ (2)

The polar component of solvation free energy ΔG_solv,polar was calculated by either Generalized Born (GB) or Poisson Boltzmman (PB) approach. GB is developed to approximate the exact or linearized PB solutions ⁴⁵. The non-polar solvation part ΔG_{solv,non-polar} was computed from the surface area (SA) of the molecule of concern ⁴⁶. The first term on the right hand side of Eq. (1), i.e. vacuum binding free energy ΔG_bind,vac can be decomposed into the enthalpic and entropic:

$$\mathrm{\Delta }{G}_{\mathit{bind},\mathit{vac}}=\mathrm{\Delta }{E}_{\mathit{bind},\mathit{vac}}-T\mathrm{\Delta }S$$ (3)

where ΔE_bind,vac is the gas-phase potential energy (including valence, electrostatic and Van der Waals terms) change upon binding. In the second term on the right hand side, ΔS is the entropy change upon binding in vacuum. Therefore, the binding free energy in solution can be reformulated as:

$$\mathrm{\Delta }{G}_{\mathit{bind},\mathit{solv}}=\mathrm{\Delta }{E}_{MM}+\mathrm{\Delta }{G}_{GB}(\text{or}\mathrm{\Delta }{G}_{PB})+\mathrm{\Delta }{G}_{SA}-T\mathrm{\Delta }S$$ (4)

in which ΔE_MM = ΔE_bind,vac since the latter is also called molecular mechanics (MM) energy. The Δ symbol refers to the difference between the complex and the protein and ligand in isolation.

The MM-PBSA module ²³ of Amber 9 was utilized to calculate ΔG_bind,solv from Eq. (4). The vacuum state as mentioned above is, in reality, a “reference state”, which means it does not need to have the characteristics of “vacuum” in its ordinary sense. Hence, the relevant parameter, i.e. relative dielectric constant of the reference state is not necessarily “1” as defined in real vacuum. As long as dielectric constant of the reference is used consistently in each and every component of MM, GB (or PB), SA and entropy, the choice of values has flexibility. For simplicity we require that the reference dielectric constant equals that of the solute in our MM-GB(PB)SA calculation such that solvation energy of solutes in the reference medium is zero. As a result, the GB reaction field energy of the complex, for example, is simply:

$$\mathrm{\Delta }{G}_{GB,\mathit{comp}}=\frac{1}{8\pi }\left(\frac{1}{\epsilon }-\frac{1}{{\epsilon }_{\mathit{solv}}}\right)\sum _{i\ne j}\frac{q_i{q}_j}{f_{ij}}$$ (5)

In Eq. (5) ε and ε_solv are dielectric constants of complex (or “vacuum”, equivalently) and solvent, respectively. q_i and q_j are atomic charges. f_ij is a function of distance between atoms i and j, and their effective Born radii ^{45, 47}. In this work, the dielectric constant of solvent is always and uniformly 78.0. However, the solute’s dielectric constant is a quantity to be specified. We let it vary between 1.0 and 10.0 which is a typical range for binding pockets ^{48, 49}. In MM-PBSA the Amber 9 PB solver was used and the lattice spacing was specified as 0.25 Å ⁵⁰. Energy estimations with GB were made with the Onufriev’s parameters (igb = 2 which is the default value in Amber 9’s MM-PBSA module) ⁵¹. For each of complex, protein and ligand, the non-polar solvation term Δ G_{solv,non-polar} was calculated from the solvent-accessible surface area (SASA), for example,

$$\mathrm{\Delta }{G}_{\mathit{complex},\mathit{solv},\mathit{non}-\mathit{polar}}=\gamma {\mathit{SASA}}_{\mathit{complex}}$$ (6)

where SASA was determined with the molsurf method using a probe radius of 1.4 Å. A constant γ = 0.0072 kcal mol⁻¹ Å⁻² was used with Amber PB/GB polar solvation energies ^{46, 52, 53}.

The change in solute entropy ΔS during ligand association was estimated by a normal mode analysis with the “nmode” module of Amber, which computes the molecular mass, principal moments of inertia, symmetry factor and vibrational frequencies to derive translational, rotational and vibrational entropies for each of the complex, the protein and ligand ^{54, 55}. Before normal mode calculations, the complexes were energy minimized with distance-dependent dielectric constant using a maximum of 50,000 steps and a convergence criterion for the energy gradient less than 10⁻⁴ kcal mol⁻¹ Å⁻¹. The dielectric constant in nmode had an r² dependence with distance.

We also performed alchemical free energy calculations with implicit solvent to elucidate the effects of configurational change due to binding that are not addressed properly. The free energy difference of binding between two ligands to a common protein is depicted by a thermodynamic cycle ⁴⁴. The relative binding energy then is computed as with the explicit solvent calculations by mutating one ligand into another in 10 steps. The difference is that here implicit solvent is used. The Bennett Acceptance Ratio (BAR) ^56,57, a free energy estimation method that minimizes variance by utilizing forward and reverse perturbations was applied to perturb and calculate the free energy difference between neighboring perturbation states. Snapshots for free energy calculations were generated with TINKER molecular dynamics ⁵⁸ using the AMOEBA polarizable force field ⁵⁹. The electrostatic contribution to solvation energy was calculated implicitly using the polarizable Generalized-Kirkwood (GK) model developed by Schnieders et al ⁶⁰. The nonpolar contributions to solvation energy are composed of cavitation and dispersion terms ^61–64. The soft-core ⁶⁵ buffered 14-7 potential ⁶⁶ was used to prevent energetic instabilities as annihilated atoms could be penetrated by other atoms. This interaction replaces Halgren’s buffered 14-7 interaction only between annihilated and non-annihilated atoms. In addition to the soft-core treatment, the radii of annihilated atoms still need to be scaled to zero to annihilate its contribution to implicit polar and nonpolar solvation energy. The RATTLE algorithm ⁶⁷ was used to constrain bonds involving hydrogen atoms. The time step was 1.5 fs and each simulation at the intermediate perturbation states was run for 150 ps. Since the configurational degrees of freedom of water are already incorporated in the implicit solvation contribution, less simulation time is required.

Results and Discussion

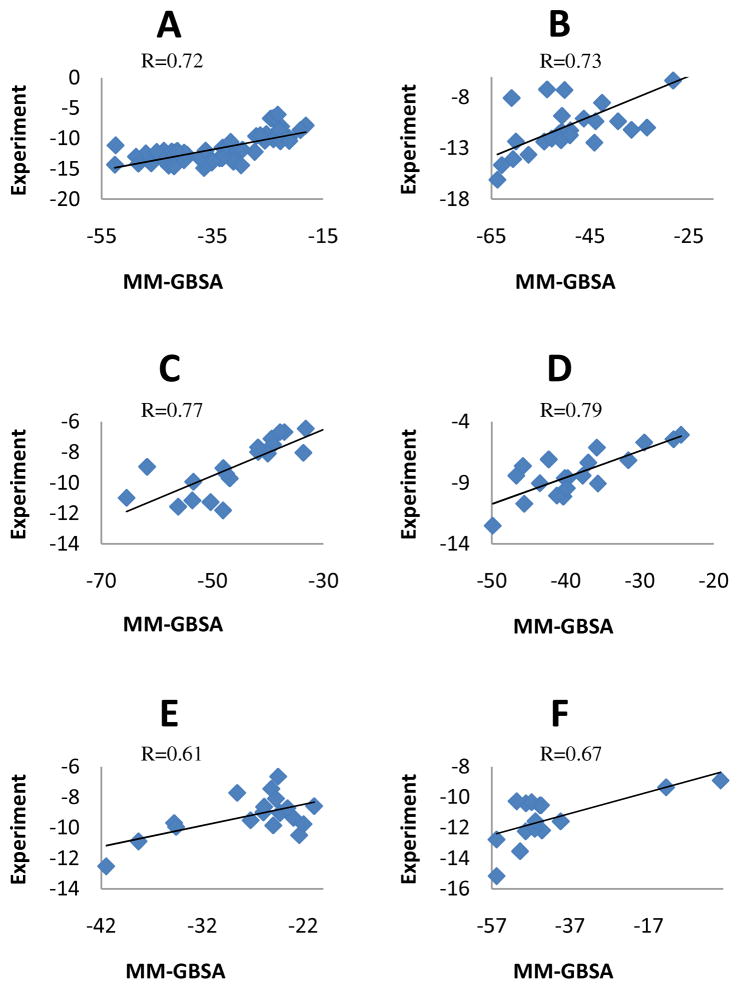
The binding free energies calculated by MM-GB(PB)SA analysis have been compared with experimental data. The quality of the computational prediction has been evaluated by the Pearson product-moment correlation coefficient (PMCC), R. According to its definition R falls in the range [−1, 1]. Figures 1A-F give illustrations of correlations between MM-GBSA (entropic contribution excluded) and experimental pKa’s for all the protein families we have investigated. The solute dielectric constant 4.0 has been used. Overall all predicted binding affinities display visible correlations with the experimental data. Four families, trypsin β, thrombin α, CDK+PKA, urokinase-type and plasminogen activator all have PMCC greater than 0.7 while the other two, β-glucosidase A and coagulation factor Xa show slightly worse R values but still sufficiently larger than 0.5—a number that only sophisticated molecular docking can achieve ^{14, 17, 68}. Although there is clearly room for improvement, e.g. β-glucosidase A (see Figure 1E) has a cluster at the top right which seems to give a different correlation, the overall results are encouraging. Note that unlike docking, the molecular simulation approaches we adopted here utilized general and transferable force fields that were not parameterized against any known binding data.

Figure 1.

Correlation between MM-GBSA predicted and experimental binding free energy. The R values shown in the figures are the Pearson product-moment correlation coefficients. The protein dielectric constant in MM-GBSA calculation was set to 4.0. A through F refer to the following protein targets, respectively: trypsin β, thrombin α, CDK+PKA, urokinase-type plasminogen activator, β-glucosidase A and coagulation factor Xa. The average standard deviations for MM-GBSA(MM-PBSA) calculations are 3.7(9.0), 2.0(5.6), 1.5(2.3), 1.4(2.0), 1.0(1.8) and 1.2(1.5) kcal/mol for trypsin β, thrombin α, CDK+PKA, urokinase-type plasminogen activator, β-glucosidase A and coagulation factor Xa, respectively.

When comparing calculation with experiment, one must pay attention to the quality of experimental data. With careful examination, it turns out the majority of the “K_i” values for coagulation factors under investigation are actually “apparent” values, as they were measured in complex biological environments such as blood and living organisms, rather than true thermodynamic K_i values obtained in biochemical assays. We have labeled such apparent K_i’s in the supporting material (see Table-S1). It is possible there is a systematic correlation between the apparent and true K_i if the experiments are done under the same condition. However given the different sources of these experimental data, this is unlikely to be the case. This may explain the inferior performance we see for the coagulation factor family. We present the comparison here but readers need to be cautious about the quality of these “experimental data”.

In addition, the sequences can be somewhat different among proteins within the same family. According to Binding MOAD (mother of all databases) data ^{69, 70}, we divided each protein family into subfamilies based on the criterion of 90% homology (see Table-S1). For example, trypsin β can be split into three sub-families and coagulation factor Xa four. The PMCC for each sub-family consisted of no less than 3 members is calculated for ε=4.0 using MM-GBSA. For example, the R values are 0.74 and 0.79 for two trypsin subfamilies respectively, 0.94 and 0.55 for coagulation factor (note the issue with apparent Ki), 0.80 and 0.77 for urokinase. To ensure the statistical significance of our results, we report the correlation for the whole protein families below.

The effect of dielectric constant

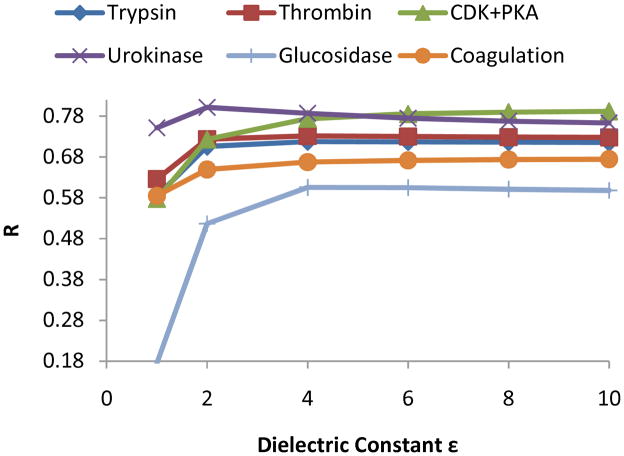
The dielectric constant ε of a solute (including protein and ligand) is a predetermined parameter chosen by users in MM-GB(PB)SA calculation. This is an approximation since ε is only applicable to macroscopic systems and is unlikely a constant from one solute to another. However for high-throughput virtual screening with molecular simulations, specifying individual dielectric constants for a huge number of complexes is not practical. So here we examine carefully in this section how the theoretical prediction depends on the values of ε. Again, the free energy of binding excludes the entropic contribution, i.e. –TΔS (see Eq. 4). As is shown in Table I, for both GB and PB, a dielectric constant of 4.0 results in predictions significantly better than 1.0 for all the protein families. The β-glucosidase A is the most affected system, for which calculations display rather poor correlation with experiments for both GB (0.18) and PB (0.16) when the dielectric constant of the complex was set to 1.0. Overall, PB and GB methods give similar results.

Table I.

Correlation Coefficients (R) between MM-GBSA or MM-PBSA Calculations and Experimental Binding Free Energies for Dielectric Constant ε=1.0 or 4.0.

Protein Targets (# of Ligands)	MM-GBSA (ε=4.0)	MM-GBSA (ε=1.0)	MM-PBSA (ε=4.0)	MM-PBSA (ε=1.0)
trypsin β (57)	0.72	0.58	0.70	0.40
thrombin α (28)	0.73	0.63	0.74	0.42
CDK+PKA (19)	0.77	0.58	0.78	0.62
urokinase-type plasminogen activator (19)	0.79	0.75	0.78	0.68
β-glucosidase A (18)	0.61	0.18	0.56	0.16
coagulation factor Xa (15)	0.67	0.58	0.67	0.45

To further examine how the dielectric constant affects the binding prediction, we expanded ε from 1.0 to 10.0. Figure 2 shows how the correlation coefficient between MM-GBSA evaluations and experimental binding free energy respond to the variation of dielectric constant. The steeper change takes place only for ε=1.0 to 4.0 for all the families. When ε is beyond 4.0, the curves all saturate and each stays at a quasi-steady level. The MM-PBSA displays exactly the same trend as GB (curves not shown here). As can be seen from Eq. (5), when the dielectric constant is far less than 78.0, i.e., that of water, the GB reaction field energy scales roughly inversely with ε. And the “vacuum” electrostatic energy scales exactly with inverse ε. The two components typically have opposite signs and the residue contributes only a minor portion to the binding free energy when solute dielectric constant is relative large, e.g. > 4.0. This is why all the curves saturate beyond 4.0. However, if the solute dielectric constant is reduced, e.g. ε=1.0, meaning the screening effect is very weak, the addition of reaction field and “vacuum” electrostatic energies becomes a significant contribution. In addition, it is found that enhanced correlation with experiments does not promise better absolute values of binding free energies (data not shown here). Negligence of entropic contribution may be an important attribution. But relative binding potency is of more interest than the accurate value of absolute binding free energy at the current stage. Figure 2 indicates that ε=4.0 provides the best prediction in the MM-GB(PB)SA calculations of relative binding affinity for 5 out of 6 protein groups in the current study. For urokinase, 2.0 performs slightly better that 4.0. Hou and et al did similar study using MM-GB(PB)SA to a) compute binding free energies of 59 ligands interacting to 6 proteins and b) rescore a set of 98 multi-family protein-ligand complexes that underwent previous molecular docking evaluation ^{14, 26, 27}. They also computed MM-GB(PB)SA correlation coefficients with experiments. It is found that for some families, e.g. the cytochrome C peroxidase family, ε=4.0 gives a worse R than ε=1.0 and ε=2.0. And ε=2.0 outperforms ε=4.0 in linear correlation coefficient, using MM-PBSA on the study of the 98 complexes. They also defined a polar solvent accessible surface difference that is roughly correlated with best interior dielectric constant in all the protein families they studied. The set of proteins in the current study seems to be more “polar” than those investigated by Hou et al. Dong et al studied electrostatic interactions in the binding stability of Barnase and Barstar by performing Poisson-Boltzmann calculations, also specifying protein dielectric constant ε_p=4 ⁷¹. However, aside from employing “solvent-exclusion” (SE) surface determined by solvent probe as we did, they addressed the dielectric boundary using the van der Waals (vdW) surface of the protein. The major difference between the vdW and SE surfaces lies in the many small crevices around the interface, which are left as part of the low protein dielectric in the SE specification but treated as part of the high solvent dielectric in the vdW surface specification. The authors suggested that vdW surface is a solution to reduce the desolvation cost and charge-charge interaction strength that is typically overestimated when a single static structure is used, and the “vdW + ε_p=4” protocol results in quantitative agreement with experimental data. In this work, we have performed molecular dynamics simulations to sample many configurations of the protein complex which effectively provides more electrostatic screening and thus we believe that the use of SE surface is appropriate.

Figure 2.

Correlation between experimental binding free energies and MM-GBSA calculations using different dielectric constants for the families of trypsin β, thrombin α, CDK+PKA, urokinase-type plasminogen activator, β-glucosidase A and coagulation factor Xa.

The β-glucosidase A family shows distinctively poor correlation when the protein dielectric constant was set to 1.0. Figure 3 is the binding pocket for PDB I.D. 1oif. In the vicinity of the ligand, there are two GLU residues (GLU 351 and GLU 166) with their carboxyl groups pointing to each other. The contribution of these acidic groups to electrostatic potential is sensitive to the pre-assigned dielectric constant as well as the protonation states. PropKa calculation ⁷² gives pKa values 9.72 for GLU 166 and 5.13 for GLU 351. So GLU 166 has a high possibility of being protonated and GLU 351 deprotonated at neutral pH. The results we reported so far were determined by protonating GLU 166 and keeping GLU 351 charged. Note that the LEaP module in Amber leaves the choice of protonation either to user or by default, the latter deprotonated both GLUs. We performed MD simulation and MM-GBSA calculations for both situations. The correlation coefficients between MM-GBSA predictions and experiments, when both the GLUs deprotonated are: -0.109, 0.167, 0.547, 0.615, 0.623 and 0.622 for dielectric constant ε being 1.0, 2.0, 4.0, 6.0, 8.0 and 10.0, respectively. For comparison, the corresponding values when GLU 166 is deprotonated are: 0.175, 0.517, 0.605, 0.605, 0.601 and 0.598. The computational prediction does improve when the charges are correctly assigned, especially at low solute dielectric constant where electrostatic interaction is stronger, e.g. ε=1.0 or 2.0. On the other hand, by using large dielectric constants, the “error” due to incorrect protonation assignments seems to have “smeared” out. Nonetheless, before the simulation and MM-GB(PB)SA calculation, it is paramount to assure that the protonation states are reasonable, otherwise the results would be unpredictable.

Figure 3.

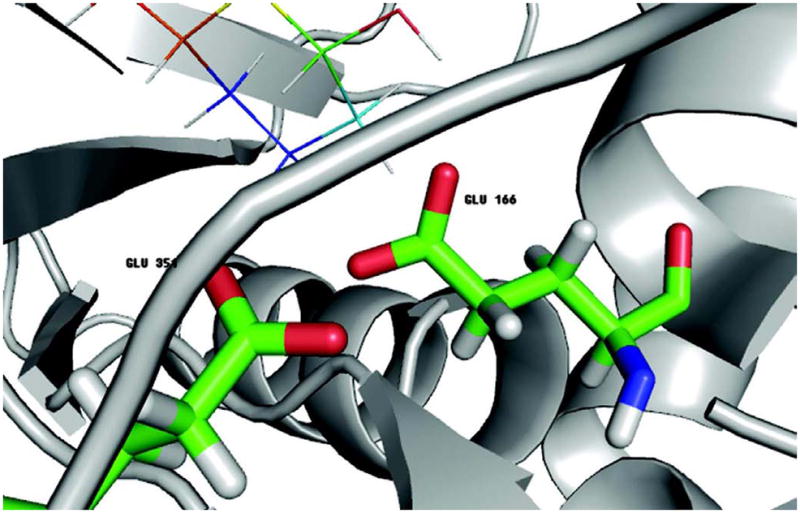
Binding Pocket of PDB ID 1oif. The ligand is shown as lines. The two GLU residues close to each other are represented in sticks. According to PropKa ⁷², GLU166 has a pKa value 9.72 and GLU351 5.13.

The introduction of a global dielectric constant is a convenient but coarse treatment to account for the diminishment of electrostatic interactions screened by environment. Solvent water has an extremely high dielectric constant, but mostly due to the orientational response of water molecules. Since our simulations have explicitly sampled protein-ligand motion, this dielectric component is arguably unnecessary. However, electrostatic distortion by polarization effects also contributes to dielectric response. A previous study employing a polarizable force field ⁷³ showed that polarization results in significant screening in the charge-charge interaction between benzamidine and trypsin. Thus, the use of a high dielectric constant is effectively “picking up” the missing polarization effect in fixed-charge models. In Figure 2, it is also noted that both β-glucosidase A and CDK+PKA families require ε=4.0 and above, while the others saturate earlier at 2.0. It is likely that stronger polarization occurs in the β-glucosidase A and CDK+PKA binding pockets.

Incorporation of entropic contribution

In the binding pocket, the vibration motion and conformation of ligands and protein are likely more restricted. The entropic term –TΔS is non-negligible in general. In the calculations performed so far, we are relying on the assumption that this term remains constant throughout a wide range of ligands for the same protein. We have investigated the possibility of improving the prediction by accounting for entropic contributions explicitly. In our first approach, the entropy change upon binding was estimated using the rigid rotor, harmonic oscillator approximation ^{74, 75} via the normal mode module of Amber 9. The results are collected to Table II. The inclusion of the entropic contribution calculated by normal mode appears to make both GB and PB predictions worse. Similar findings were reported previously that entropy estimation based on computationally expensive normal mode analysis tends to have a large margin of error that introduces significant uncertainty in the result ⁷⁶.

Table II.

Correlations Coefficients (R) between Experiments and MM-GBSA or MM-PBSA Predictions with (e.g. MM-PBSA + N.M.) and without Entropic Contribution estimated from Normal Mode Analysis. All data presented are calculated at ε=4.0.

Protein Targets (# of Ligands)	MM-GBSA	MM-GBSA + N.M.	MM-PBSA	MM-PBSA + N.M.
trypsin β (57)	0.72	0.64	0.70	0.61
thrombin α (28)	0.73	0.65	0.74	0.64
CDK+PKA (19)	0.77	0.65	0.78	0.69
urokinase-type plasminogen activator (19)	0.79	0.70	0.78	0.68
β-glucosidase A (18)	0.61	0.61	0.56	0.55
coagulation factor Xa (15)	0.67	0.61	0.67	0.61

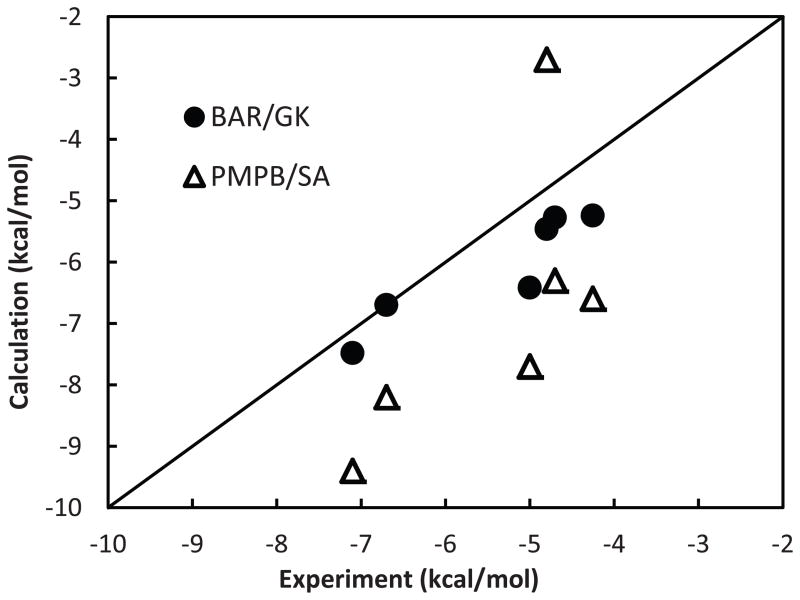
C. Gao et al ²⁴ suggested a sophisticated method to account for the effect of ligand conformational restriction to protein-ligand binding free energy, in which both entropic and enthalpic energy changes are addressed. The two combined, gives the so-called configurational free energy change ΔG_conf. Multiple conformational energy wells of the isolated ligand were sampled, followed by the calculation of configuration integral applying free energy perturbation based on quasi-harmonic approximation of each well. The complexes investigated in the current study have overlap with those by C. Gao. For these common systems, we compare the correlation coefficients of computational predictions after including configurational free energy change ΔG_conf from C. Gao et al (our binding free energy without – TΔS but plus Gao’s ΔG_conf). Unlike the normal mode entropic estimation which leads to inferior correlation with experiment, the configurational free energy can worsen correlation (e.g. R of the thrombin α family decreases by ~0.15 for both GB and PB), improve it (e.g. R of urokinase-type plasminogen activator gains ~0.17), or have negligent effect (e.g. trypsin β, β-glucosidase A and coagulation factor Xa) (see Table III). To achieve better correlation, more sophisticated techniques beyond Quasi-harmonic approximation may be necessary. We have further investigated an alchemical perturbation approach to rigorously sample the configuration entropy in implicit solvent. In our previous study ⁴⁴, we examined the binding free energy of 5 benzamine analogs to trypsin using a PMPB/SA (Polarizable Multipole Possion Boltzmann/Surface Area) method that is similar to MM-PBSA. The binding free energy calculated via PMPB/SA with and without entropic terms, estimated based on harmonic approximation, compared to experimental values ^77–82 yielded correlations of 0.667 and 0.708, respectively. Here we recomputed the relative binding free energy by perturbing one ligand into another in 10 steps. At each step, 150 ps MD simulations in Generalized Kirkwood (GK) implicit solvent were performed to sample the protein-ligand configuration. The free energy changes between the neighboring steps were computed using Bennett Acceptance Ratio (or BAR, see Method section for additional computational details), and the total relative binding free energy is the sum of contributions from the intermediate steps. Thus, in this approach, relative binding free energy including its entropic contribution was explicitly sampled. The “only” approximation is the continuum solvation model. The addition of intermediate steps, which is completely ignored by traditional end-state only MM-PBSA approaches, apparently has a significant effect. A correlation of 0.933 between the calculated and experimental binding free energy was achieved using the implicit solvent based GK/BAR alchemical perturbation (see Figure 4). The calculated relative binding free energies have been offset by absolute binding free energy of trypsin-benzamidine calculated from explicit water simulation ⁷³. Note this offset has no effect on the correlation we are reporting here. The most significant improvement is the slope of the calculated binding free energy, which is typically exaggerated by both MM-PBSA and PMPB/SA. This suggests that the “slower” perturbation between end-states in the GK/BAR method helps capture the configurational entropy, nonetheless with a ten-time increase in computational cost. The trypsin-benzamidine systems are relatively “rigid” and sampling is somewhat easier to converge. The general applicability of implicit solvent based perturbation approaches requires further investigation of a broad range of protein complexes, using polarizable and fixed charge force field.

Table III.

Correlation Coefficients (R) of MM-GBSA or MM-PBSA Predictions with Experiments Including and Excluding Configuration Free Energy ΔG_conf. All data presented are calculated at ε=4.0.

Protein Targets (# of Ligands)	MM-GBSA	MM-GBSA +ΔGconf	MM-PBSA	MM-PBSA +ΔGconf
trypsin β (37)	0.69	0.67	0.67	0.63
thrombin α (17)	0.81	0.65	0.83	0.68
CDK+PKA (9)	0.73	0.90	0.74	0.92
β-glucosidase A (14)	0.40	0.39	0.36	0.34
coagulation factor Xa (14)	0.59	0.61	0.58	0.59

Figure 4.

Comparison of experimental ⁷⁷–⁸² and calculated binding free energies from BAR/GK and PM-PB/SA calculations for trypsin-benzamidine analogs.

Effect of simulation length

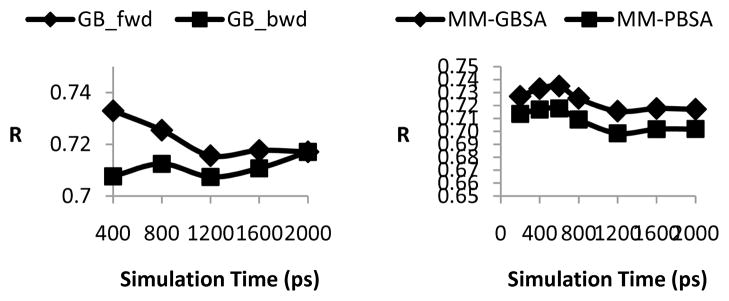
In the above sections, free energy calculated in MM-GB(PB)SA has been averaged on the entire snapshots across the entire 2 ns MD simulation, starting from the crystal structures. It is of interest to discern whether shorter simulations will provide similar prediction and how the R values vary over the period of simulations. We choose trypsin family as an example. Figure 5-A shows the correlation coefficient R between GB predicted and experimental binding free energies using the 400, 800, 1,200, 1,600 and up to 2,000 ps MD trajectory segments, either in the forward (starts from the beginning of simulation) or backward (starts from the end of simulation) direction. The comparison indicates that the earlier simulation snapshots gave better predictions, but only slightly. Given that our simulations started with crystal structures, it is understandable that the conformations close to initial structures tend to offer better results than those relatively dissimilar. However the difference is non-substantial, which suggests the initial and later conformations are structurally alike. Figure 5-B compares two free energy calculation methods: MM-GBSA and MM-PBSA. The family of concern is also trypsin. The two analysis methods display a highly analogous trend. The same examinations were applied to all the other families, GB and PB predictions consistently have similar trends, in both the forward and backwards directions (results not shown here). In general, no significant difference (< 2% in R values) was found when different segments of the 2 ns simulation trajectories were used except for urokinase. For urokinase, the correlation coefficient dropped from 0.78 (2-ns trajectory) to 0.70 if the last 400-ps trajectory was used. Therefore, if starting from or near crystal structure, a reduced simulation time, e.g. 200–400 ps, could lead to reliable prediction of rankings of different ligands as demonstrated by the correlation coefficient. This result is consistent with a previous work on 3 kinases where 10-ps simulations seemed to work reasonably well when starting from crystal structures ²². However, for a novel system with unknown initial structure, long simulations would become necessary to obtain equilibrium binding structures.

Figure 5.

The effect of MD simulation lengths on the calculated binding affinity of the trypsin family. A) correlation coefficients between MM-GBSA calculation and experimental values. One configuration snapshot was recorded every picosecond. The forward direction (diamond markers) starts with the first snapshot recorded and is along the trajectory of the simulation. The backward (square markers) starts from the last snapshot and is along the time-reversed direction. B) Comparison of MM-GBSA (diamonds) and MM-PBSA predictions. Both use trajectory segments in forward direction starting from the beginning of simulations.

Computational Cost

The Amber simulation was executed using PMEMD. The PMEMD simulation was performed on the supercomputer—Ranger, at Texas Advanced Computing Center (TACC), each complex is allocated with a compute node of 16 cores total except the glucosidase family which has a significantly longer backbone hence was allocated 48 cores. The wall-clock time for the 2-ns simulation of one complex is roughly 20 hours.

For each complex in explicit solvent, a 2-ns MD simulation was performed and the system configurations were recorded every pico second leading to 2,000 snapshots. MM-GB(PB)SA were adopted to ensemble-average all the 2,000 snapshots except the computation-intense normal mode computation where snapshots from every 20 ps were used. For each complex with water molecules removed, it took about 15 hours to complete the MM-PBSA calculations of all the 2,000 snapshots using a single CPU core. The cost of MM-GBSA is much lower, which is about 3 hours. The entropy calculation was split into 2 steps: minimization and normal mode entropy calculation. The frequency to extract snapshots is every 20 ps, so a total of 100 snapshots were accounted for. For each snapshot, complex, protein and ligand were treated separately. The ligand computation time is prompt. For complex and protein, it took ~6 hours to minimize each snapshot, followed by ~4 hours to perform the normal mode calculation. As we discussed earlier, the expensive entropy estimation based on normal mode analysis may not improve the prediction. If we neglect the entropy estimation, and use 200-ps MD simulation trajectory, the cost of evaluating each protein-ligand complex using MM-GBSA binding would be around 40 hours in a ~2.3 GHz compute core.

In the configurational entropy calculation reported by Gao et al ²⁴, most CPU time was spent on MD simulation of the ligands in the multiple wells representing the free-state. The actual simulation time was case-dependent. For example, for a 38-atom ligand with 30 wells, the calculation took ~6 hours on a single AMD Opteron 246 (2.0 GHz) processor. In our implicit-solvent alchemical perturbation approach, the computationally expensive part is the ten-step perturbation to change one ligand to another. Each of the ten steps is a 150 ps long TINKER MD simulation in GK solvent using AMOEBA polarizable force field. It takes roughly 27 hours to run a 150 ps simulation of trypsin complex on 10 CPU-cores (AMD Opteron 2.4 GHz).

Conclusions

From the study of binding to all the families of protein targets, we show that the molecular mechanics approach, explicit-solvent MD simulations followed by MM-GB(PB)SA free energy calculation, provides fairly reasonable prediction of experimental binding free energy (R > 0.55 for all the protein families). Also we show that applying molecular mechanics to virtual screening is practical on today’s regular computing clusters. MM-GB(PB)SA seems robust for the analysis of a range of protein targets as well as ligands if the correlation with experiment, rather than the absolute binding affinity, is of concern. We find that the specification of solute (protein-ligand) dielectric constant is important in the MM-GB(PB)SA calculation—for the families we studied, 4.0 appeared to give better correlated binding energy. Previously high dielectric values and vdW surface instead of solvent exposed surface has been found necessary to screen the electrostatic interactions in protein-protein interactions ⁷¹. While in the current approach MD simulations are utilized to obtain many snapshots for the subsequent PB and GB calculations, we still find a dielectric constant of 4 is desirable for the complex. This high dielectric constant is likely needed to account for the dielectric response due to the electronic polarization effect that is missing in the fix-charge model. The entropic contribution to binding estimated using a rigid rotor harmonic oscillator approximation, which computationally is rather expensive, actually deteriorates the predictions. On the other hand, our preliminary results demonstrate that employing implicit-solvent based alchemical perturbation is promising for incorporation of entropy. Also, we show that if starting from a crystal structure, the length of explicit-solvent MD simulation does not seem to affect the prediction, and therefore short simulations are sufficient to provide meaningful results. In summary, our work shows that physics-based molecular mechanics models are promising for the next generation of medium to high-throughput virtual screening. In continuation of this work, we plan to combine the current molecular mechanics scheme with conventional docking method to eliminate the initial dependence on the known protein-ligand complex crystal structure and to explore treatment of entropic effect utilizing implicit-solvent based alchemical perturbation.