MfSAT: Detect simple sequence repeats in viral genomes

Abstract

Simple sequence repeats (SSRs) are ubiquitous short tandem repeats, which are associated with various regulatory mechanisms and have been found in viral genomes. Herein, we develop MfSAT (Multi-functional SSRs Analytical Tool), a new powerful tool which can fast identify SSRs in multiple short viral genomes and then automatically calculate the numbers and proportions of various SSR types (mono-, di-, tri-, tetra-, penta- and hexanucleotide repeats). Furthermore, it also can detect codon repeats and report the corresponding amino acid.

Background

Simple sequence repeats (SSRs) or microsatellites are tandemly repeated tracts consisting of 1-6 base pair (bp) long units [1, 2]. Comprehensive analysis of SSRs in 8619 pre-miRNAs indicates SSRs are widely present in these very small non-coding RNA sequences [3]. It has been demonstrated that SSRs can affect gene expression and the corresponding gene products and even cause phenotypic changes or diseases [4, 5]. Correspondingly, computational tools for detection of SSRs and their related information from whole genome sequences are increasing as well [6]. The growing number of analytical tools for SSRs has greatly assisted the understanding of SSRs at the genome-wide level. Our examination of the available tools reveals certain faults. In order to efficiently screen viral genome sequences for SSRs, we have developed a new tool called MfSAT.

Methodology

Consider a sequence or multiple sequences over a finite alphabet {(a, t, g, c) or (a, u, g, c)}. A tract at a given locus will be defined as a microsatellite if that tract can be expressed as a tandem repeat of a motif of 1−6 bp size [6]. Our goal is to efficiently detect SSRs in a sequence or multiple sequences given an arbitrary motif size or minimum repeat number. The proposed algorithm has two parameters, maximum motif and minimum repeat number which are independent. When you run according to the first parameter, the minimum number is three, whereas if you run by use of another parameter, the maximum motif is “hexa”. If users select the “HexaÆmono” tag, MfSAT progressively scans for nucleation sites starting from hexanucleotide repeat to mononucleotide repeat at a given locus. If no hexanucleotide repeat tract is detected, then pentanucleotide repeat nucleation site will be searched for and so on. This algorithm is the same with IMEx [6, 7]. However, if users select another tag, “MonoÆhexa”, in contrast to above step, in this section we assume the algorithm advances the shortest repeats. Given a candidate trinucleotide repeat motif k and its starting position j together with the starting position d of coding sequence of analyzed genome sequences, the verification formula determines whether an SSR is a codon repeat. The formula is as follows: S = (j-d)/3 (1) If S is an integer, the trinucleotide repeat is a codon repeats. It remains to judge what its corresponding amino acid is.

Software Requirements

MfSAT can be used in any computer with windows system

Input

MfSAT uses a advanced and power algorithm ‘regular expressions’ to screen one or multiple viral DNA/RNA sequences in fast format for SSRs and reports the motif, repeat number, genomic location, abundance of each of six classes SSRs and many other features useful for SSRs’ studies.

Output

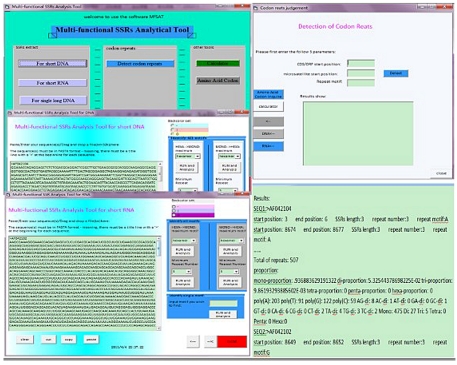
We have developed a new tool that can be successfully used to identify SSRs in viral genomes consisting of viral DNA or RNA sequences for escaping statistical troubles. Judging according to its performance, MfSAT is a definite advance compared to other available tools. A stand-alone software with several videos is available online at http://hudacm11.mysinamail.com/hunan.html. This tool is also available from authors Zhongyang Tan and Guangming Zeng on request (zhongyang@hnu.cn; zgming@hnu.cn). The output is composed of three parts: the first part consists of a list of SSRs, each with information such as repeat motif content, repeat number, starting position, end position, SSR length; the second part is the numbers of proportions of each of the six classes of SSRs (mono-, di-, tri-, tetra-, penta- and hexanucleotide repeats); the third part comprises the numbers of poly(A), poly (T/U), poly(G), poly(C), and 12 classes of dinucleotide repeats including AG, GA, GT (GU), TG (UG), AC, CA, CT (CU), TC (UC), AT (AU), TA (UA), GC and CG repeats. It is clear from the results that MfSAT is more attractive in terms of consideration. Figure 1 shows the software interface and output results of MfSAT.

Figure 1.

Software Interface and Output Results of MfSAT.

Future Work

Development of a linux version of MfSAT is in process.