Abstract
In several neurodegenerative disorders, including Huntington's disease, aspects concerning the earliest of protein structures that form along the aggregation pathway have increasingly gained attention because these particular species are likely to be neurotoxic. We used time-resolved small-angle neutron scattering to probe in solution these transient structures formed by peptides having the N-terminal sequence context of mutant huntingtin exon 1. We obtained snapshots of the formed aggregates as the kinetic reaction ensued to yield quantitative information on their size and mass. At the early stage, small precursor species with an initial radius of gyration of 16.1 ± 5.9 Å and average mass of a dimer to trimer were monitored. Structural growth was treated as two modes with a transition from three-dimensional early aggregate formation to two-dimensional fibril growth and association. Our small-angle neutron scattering results on the internal structure of the mature fibrils demonstrate loose packing with ∼1 peptide per 4.75 Å β-sheet repeat distance, which is shown to be quantitatively consistent with a β-helix model. This research provides what we believe to be new insights into the structures forming along the pathway of huntingtin exon 1 aggregation and should assist in determining the role that precursors play in neuronal toxicity.
Introduction
Cognitive deficits and psychiatric symptoms associated with random, jerky, and uncontrollable movements are characteristics of Huntington's disease (HD), a fatal late-onset autosomal polyglutamine (polyQ) neurodegenerative disorder. Examination of patients' brains shows region-specific neuronal degeneration with severe cortical-striatal atrophy. Similar to other polyQ disorders (1), HD is linked to the presence of an abnormally long sequence of glutamine repeats (Q > 36) in the disease protein. The involved protein, huntingtin (Htt), contains ∼3144 amino acids corresponding to the expression of the 67 exons of the HTT gene (2). However, only the first exon with the polyQ stretch seems to be required to reproduce HD pathogenesis in cell and animal models (3).
Recent work shows that cleavage of the full Htt protein releasing a proteolytic fragment containing exon 1 is an obligatory step to initiate cellular toxicity (4,5). This cleaved fragment containing the expanded polyQ region has a strong tendency to misfold toward a stable three-dimensional conformation enriched in β-sheet structure with self-assembly resulting in fibrillar aggregates. Although the link with polyQ length, aggregation, and disease is inescapable—the longer the polyQ repeat, the earlier the age of onset and the more severe the symptoms—numerous studies in HD cell and animal models show a strong dichotomy between aggregate presence and neuronal toxicity (6–8). Some results even imply that aggregates are, in fact, beneficial for neuronal survival.
To address the question “what makes an aggregate toxic?” an increasing number of reports in the amyloid field have appeared over the last decade focusing on the mechanism of aggregation implicated in a variety of neurodegenerative diseases, including Alzheimer's and Parkinson's diseases, and in which the importance of protein oligomerization in pathogenesis has been emphasized (9).
Various biophysical methods, including atomic force microscopy (AFM) (10,11) and analytical ultracentrifugation (12), have been applied toward the identification and structural characterization of early oligomers formed during Htt fibrillization with the smallest structures detected being spherical oligomers of 50 Å diameter (10). Small-angle neutron and x-ray scattering have been efficiently applied to various aggregation systems including amyloid-β fibrils (13–16). Here, we utilize small-angle neutron scattering (SANS) in a time-resolved fashion to pinpoint the various transient intermediates that form along the aggregation pathway for a truncated mutant Htt exon 1 peptide. This peptide contains the 17 N-terminal residues of Htt followed by a 42-glutamine repeat, a 10-proline stretch, and two lysines on the C-terminus for enhanced solubility (NtQ42P10 for short). With SANS, the structures of biological macromolecules can be directly measured in solution without radiation degradation. We are reporting what we believe to be new quantitative and detailed structural information on the aggregation of NtQ42P10 by monitoring the growth of early-formed species into eventual fibrils.
Materials and Methods
Materials
The peptide with sequence MATLEKLMKAFESLKSFQ42P10K2 (NtQ42P10) and molecular mass 8583 Da was synthesized by solid-phase Fmoc chemistry (performed at the Keck-Yale facility, New Haven, CT) and then purified by reverse phase high-performance liquid chromatography (HPLC). Mass spectrometry confirmed the purified peptide contained 42 glutamines. Trifluoroacetic acid (TFA) (>99.5%; Thermo Fisher Scientific, Waltham, MA), 1,1,1,3,3,3-hexafluoro-2-isopropanol (HFIP) (99.5+%; Acros Organics, Geel, Belgium), 10× phosphate-buffered saline (PBS) powder (Thermo Fisher Scientific), and D2O (99.9% D, Cambridge Isotope Laboratories, Andover, MA) were used without further purification.
Peptide solubilization and disaggregation
The NtQ42P10 peptide was solubilized and disaggregated similar to established procedures (17). Briefly, the purified peptide was dissolved in 50:50 TFA/HFIP, incubated for 3 h, and then dried under Argon gas. For HPLC kinetics, the peptide was first solubilized into 0.05% TFA D2O, ultracentrifuged at 356k × g at 4°C for 2 h, and the supernatant brought up to 1× PBS D2O to initiate the reaction.
High performance liquid chromatography
A model No. 1100 series HPLC equipped with a C3 column (Agilent Technologies, Santa Rosa, CA) was used with a reverse phase water (+ 0.05% TFA) / acetonitrile (+ 0.05% TFA) gradient. The peptide concentration was determined by HPLC using a standard curve generated from NtQ22P10 peptide (same sequence as NtQ42P10 but with 22 glutamines) and amino-acid analysis. To overcome the 40-min HPLC runtime per sample, NtQ42P10 aliquots removed from the reaction vessel were quench-frozen in liquid nitrogen and stored at –80°C. The time-point aliquots were then individually thawed, ultracentrifuged at 356k × g at 4°C for 20 min, and supernatant injected onto the HPLC for monomer concentration measurement.
Thioflavin T fluorescence
The fluorescence of Thioflavin T (ThT) was monitored using a model No. LS 55 fluorescence spectrometer (Perkin-Elmer, Waltham, MA) with excitation and emission wavelengths, λex = 450 nm and λem = 482 nm, respectively. Sample aliquots of 20 μL were removed from the reaction vessel, diluted with 130 μL 1× PBS, and then 5 μL of 2 μM ThT solution was added to give 64.5 μM ThT final. Equivalent background runs of ThT in 1× PBS were performed and subtracted from the sample signal.
Congo Red birefringence
An aliquot of the NtQ42P10 fibril sample grown in 1× PBS D2O and measured by SANS was placed on a microscope slide and dried at 37°C overnight. The sample was fixed with 10% formalin, rinsed with deionized water, stained with 1% Congo Red solution for 30 min at room temperature, rinsed again with deionized water, and then mounted with a coverslip after drying. Images were collected using a microscope (40×; Leica, Solms, Germany) and cross-polarizers.
Transmission electron microscopy
Transmission electron microscopy (TEM) was performed using a model No. H-600 electron microscope (Hitachi, Tokyo, Japan) in the Biological Sciences Division, University of Tennessee. Aliquots of the NtQ42P10 fibril sample grown in 1× PBS D2O and measured by SANS were fixed to collodion/carbon grids and stained with a 1% uranyl acetate solution for imaging. Single fibril diameter was measured at 21 different positions on the TEM image using the software program ImageJ (18) and converted from pixels to nanometers using the image scale bar. The fibril radius in Ångstroms was then calculated to directly compare with the SANS results.
Small-angle neutron scattering
SANS experiments were performed on the CG-3 Bio-SANS instrument at the High Flux Isotope Reactor at Oak Ridge National Laboratory (Oak Ridge, TN). Neutrons of wavelength, λ = 6.0 Å with a wavelength spread, Δλ/λ = 0.14 were used. Time-resolved measurements were made with a 6.9 m sample/detector distance with static sample measurements also made at 1.2 and 15.4 m to obtain data at higher and lower respective wavevector transfer, Q = 4π sin(θ)/λ, where 2θ is the scattering angle. Samples were loaded into 2 mm pathlength rectangular-shaped quartz cuvettes (Hellma USA, Plainville, NY).
For the time-resolved measurements, 15-min neutron exposure intervals were collected where structural changes taking place over this time were integrated to reflect the average structure. Samples with sedimenting aggregates were dispersed by inverting the cuvette several times to ensure sample homogeneity and then measured for 15 min. It was found that no significant sample settling occurred over this timeframe as gauged by comparing the total integrated intensity on the detector for consecutive 5-min exposures. For static measurements on NtQ42P10 fibrils, 0.5, 1, and 2 h exposure times were collected at 1.2, 6.9, and 15.4 m, respectively. These longer exposure times were achieved by binning multiple 15-min exposures obtained upon first dispersing the sample to homogeneity. Scattered neutrons were detected with a 1 × 1 m two-dimensional position-sensitive detector with 192 × 192 pixels.
NtQ42P10 was solubilized and disaggregated following the above procedures except the Argon-dried film was resuspended first in 0.05% TFA D2O to dissolve the peptide, brought up in PBS D2O, and then centrifuged at 16.1k × g for 2 min to remove any particulates. The NtQ42P10 fibril sample was prepared in the same manner and allowed to aggregate for >500 h at 22°C before measurement. The final NtQ42P10 concentration was determined by HPLC to be 0.93 mg/mL (108 μM) in PBS D2O for the kinetics sample and 0.76 mg/mL (89 μM) for the fibril sample. All neutron scattering experiments were conducted at 20°C.
Data reduction was accomplished using IgorPro software (WaveMetrics, Lake Oswego, OR) with SANS macros developed by Dr. Ken Littrell (Oak Ridge National Laboratory). The total two-dimensional scattering was corrected for the scattering from the quartz cell and from stray neutrons in the room and for nonuniform detector response. Then, the scattering was normalized by the incident beam flux, radially averaged to obtain I(Q) versus Q, and then I(Q) was placed on absolute scale intensity using porasil B as a calibration standard with known scattering cross section. Background scattering from the buffer, Ibg(Q), and the Q-independent excess incoherent scattering, Iinc(0), were subtracted from the total scattering, Itot(Q), to obtain the protein sample scattering, , with Iinc(0) determined from Q > 0.35 Å−, assuming the residual difference in intensity is completely incoherent scattering.
Fitting procedures for the SANS data followed a Guinier analysis (19). Within the Guinier regime, with the low-Q region of the scattering profile where Qmax·Rg ≤ 1.3, the scattering intensity can be described as
| (1) |
with
| (2) |
The value M was calculated from I(0) = scattering intensity at zero angle, where c = peptide concentration, Δρ = contrast in scattering length density between protein and D2O buffer solution (= ρprot – ρbuf), = protein partial specific volume (= 0.73 mL/g), and NA = Avogadro's number. The peptide scattering length density, ρprot = 3.564 × 1010 cm−2 was calculated from the atomic composition using the program CRYSON (20) that accounts for H/D exchange. The D2O scattering length density used was ρD2O = 6.404 × 1010 cm−2.
Modified Guinier fits were made by plotting ln[Q·I(Q)] versus Q2 to obtain the , where Rc is the cross-sectional radius of gyration and related to the cylindrical radius by . Then, from the intercept (Ic(0)), the mass per length was calculated
| (3) |
Values for ρprot, ρbuf, and were the same as above.
Results and Discussion
NtQ42P10 aggregates formed at high concentration are amyloidlike
Using equivalent conditions to our SANS experiments, which require peptide concentrations in the mg/mL range, we performed kinetic studies on NtQ42P10 aggregation with 93 μM monomer in phosphate-buffered saline (PBS) D2O at 22°C. Monomer disappearance was followed by reverse phase HPLC and fibril production monitored by the fluorescence of ThT, an amyloidophilic dye. Fig. 1 A shows that the aggregation reaction proceeds rapidly with the amount of soluble monomer decreasing in the absence of a noticeable lag phase and a single exponential rate constant kmon = 1.28 ± 0.09 h−1. Only 10% monomer remained in solution after 2 h and was completely consumed by 6.5 h. Concurrently, the ThT fluorescence signal, indicative of the presence of amyloidlike structures, also lacks an observable lag phase and reaches a plateau at ∼2 h with an exponential rate constant kfib = 1.1 ± 0.3 h−1 similar to kmon (Fig. 1 A).
Figure 1.
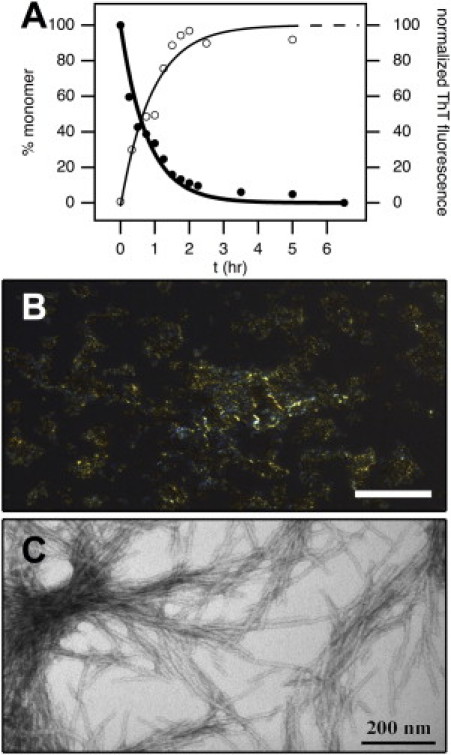
Aggregation kinetics of NtQ42P10 and the resulting fibrils. (A) Disappearance of monomeric NtQ42P10 (93 μM) from the supernatant solution (solid circles) and increasing ThT fluorescence (open circles) corresponding to the formation of ThT-binding amyloidlike aggregates. (Solid lines) Single-exponential fits to the data with an extrapolation of the ThT fluorescence fit (dashed line). (B) NtQ42P10 fibrils stained with Congo Red exhibit birefringence by polarizing optical microscopy (scale bar = 50 μm), which is indicative of amyloidlike aggregates. (C) TEM image of the fibrils formed by NtQ42P10 with a calculated fibril radius, R = 40 ± 8 Å and range of 28–56 Å.
The inverse dependence of the lag phase duration on monomer concentration is a phenomenon already known from other amyloid proteins (21), and an observed lag phase recently was reported for a F17W mutant NtQ30P6 peptide (22). Once formed, the NtQ42P10 aggregates were characterized by Congo Red birefringence and TEM. Aggregates stained with Congo Red and viewed by polarized light microscopy display a gold/apple-green birefringence characteristic of amyloidlike fibrils (Fig. 1 B). Likewise, TEM shows the fibrillar nature of the NtQ42P10 aggregates (Fig. 1 C), where both individual fibrils and fibril bundles were observed. The radii of individual fibrils range from 28 to 56 Å with an average radius of R = 40 ± 8 Å.
The substitution of D2O for H2O can influence protein aggregation processes (16,23). For the kinetic assays performed above, we did not observe any dramatic difference in the aggregation rate for D2O compared to H2O and found the resulting fibrils to have the same structure as those grown in H2O within the resolution of TEM (data not shown). Their similarity also can be assessed by comparing the aggregates in Fig. 1 C with TEM of NtQ30P6 fibrils grown in H2O (22). In summary, we find that NtQ42P10 aggregation at high monomer concentrations in D2O buffer does not drastically affect the amyloid properties of the resulting fibrils, only the kinetics of formation—namely, leading to faster aggregation rates and shortened lag phase times in the ThT assay.
Quantifying the NtQ42P10 aggregates by SANS
With the scattering vector range chosen for the time-resolved SANS measurements, 0.01 < Q < 0.1 Å−1, we monitored size changes that occur from hundreds down to tens of Ångstroms, respectively. To optimize the time-resolved measurements for sample kinetic rate, data binning, and instrumental signal/noise, we first performed several experiments at different starting monomer concentrations and varied the neutron exposure time binning. From these initial experiments, we confirmed reproducibility and the direct dependence of the kinetic rate on peptide concentration. We also found that 15-min neutron exposures and 50–100 μM NtQ42P10 provide a sufficient balance between time resolution and SANS signal/noise ratio for adequately following structural changes in time.
Therefore, after 11 min to load NtQ42P10 into the instrument and acquire a transmission measurement, time-resolved SANS profiles were acquired every 15 min. Fig. 2 A shows selected SANS profiles that illustrate how the scattering intensity (I(Q)) increases and changes shape over the time-course of the aggregation reaction. Changes in the shape of the scattering profiles are emphasized in the Kratky plot representation, Q2·I(Q) versus Q (Fig. 2 A, inset), which correspond to changes in overall aggregate structure. The formation of a maximum at Q ≈ 0.03 Å−1 in the Kratky plot reveals a conformational transition over time toward increased folding with greater structural rigidity.
Figure 2.
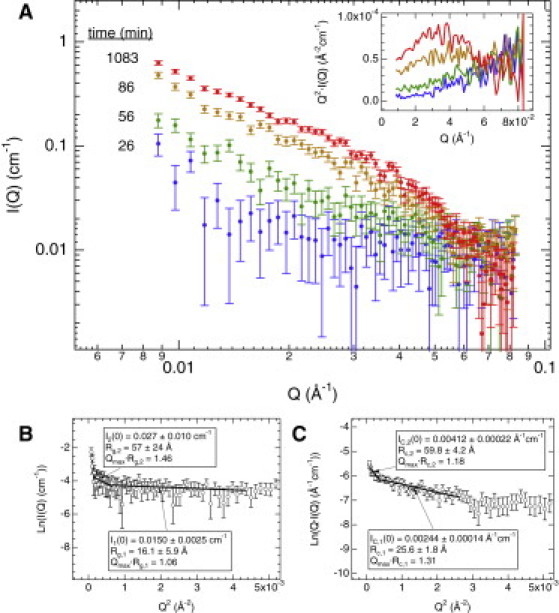
Time-resolved SANS on NtQ42P10 and analysis. Peptide concentration was 108 μM. (A) Select time-resolved SANS profiles, I(Q) versus Q, of NtQ42P10 at 26 (blue), 56 (green), 86 (yellow), and 1083 min (red). Kratky plots, Q2·I(Q) versus Q (inset, colors correspond to the same times in the main plot, error bars omitted for clarity) show the formation of a maximum about Q ≈ 0.03 Å−1 with time, which is indicative of an increase in folding and structural rigidity. (B) A representative Guinier plot and fits to the SANS curve for 26 min. (C) A representative modified Guinier plot and fits to the SANS curve for 86 min. (Error bars) Standard errors from the radial average of the intensity data on the neutron area detector.
Guinier analysis (see Materials and Methods) (19) was applied to each of the radially averaged SANS profiles by plotting ln[I(Q)] versus Q2 to obtain quantitative information on the size (via the radius of gyration, Rg) and oligomerization state (via the apparent molecular mass, M) of NtQ42P10. Fig. 2 B displays a representative Guinier plot to the SANS curve obtained at 26 min (= 11 min + 15 min), where obtained linear fits within Qmax·Rg ≤ 1.3 correspond to slope = −R2g/3. We found two linear fit regions—a proper one (Qmax·Rg,1 = 1.06) corresponding to a distinct population of small species (Rg,1 = 16.1 ± 5.9 Å) and a second approximate one (Qmax·Rg,2 = 1.46) that is indicative of larger species with Rg,2 = 57 ± 24 Å. The dimensions obtained for the larger aggregates were affected by additional influences including polydispersity and favorable interactions between smaller species. The continuous upturn in the Guinier plot at small Q also indicates the presence of aggregates larger than the Q-range of the instrument configuration.
Eventually, during the course of aggregation, the increasing anisotropy of the forming fibrils resulted in the fibril length exceeding our SANS measurements such that only the two-dimensional fibril cross section was monitored. The advantage is that cross-sectional measurements were unaffected by fibril length polydispersity. At this point, the conventional Guinier analysis was no longer valid and the data were treated by modified Guinier plots as previously performed for SANS on amyloid-β fibrils (13). The cross-sectional radius of gyration (Rc) and mass per length (ML) were obtained from the fits (see Materials and Methods).
Fitting errors (∼5%) were the major source of error for ML and taken into consideration. Slight variations in the partial specific volume (), which depend on protein type and folding state (24), can contribute an additional ∼3% error. Including other errors conservatively results in ∼10% total error propagated into the determination of ML, which underscores the strength of the technique and allows us to interpret these values with high confidence. Fig. 2 C shows a representative modified Guinier fit to the SANS curve for 86 min, where two distinct linear fit regions were observed. The first one reveals a size of Rc,1 = 25.6 ± 1.8 Å (Qmax·Rc,1 = 1.31), which corresponds to growing individual fibrils and closely matches the TEM-calculated radius. The second linear region with a larger radius of cross section, Rc,2 = 59.8 ± 4.2 Å (Qmax·Rc,2 = 1.18), correlates to fibril bundles formed by attractive fibril-fibril interactions.
Early-stage aggregate structural growth
As stated previously, SANS data for NtQ42P10 early aggregates forming within 71 min were analyzed using Guinier fits to obtain Rg and M, and we focus on the smaller aggregates having a true Guinier regime. When plotted as a function of time, Rg,1 and M1 (Fig. 3, A and B) show a progressive increase in growth. Dividing M by the peptide monomer molecular mass yields the average number of peptides (n) incorporated into an aggregate species (Fig. 3 B, right axis). We identified the earliest species to have dimensions intermediate between a dimer and trimer (n = 2.6 ± 0.4 peptides) having Rg = 16.1 ± 5.9 Å. Although no distinct scattering signal from the monomer itself was detected, the HPLC data in Fig. 1 A show the monomer amount decreased from 60 to 25% over 30–75 min of the aggregation reaction. Because scattering is weight-averaged, the oligomer scattering signal dominates and obscures the monomer scattering contribution. For comparison, the radius of gyration of a monomer with a random coil conformation, Rg,rc, can be predicted from the relation
| (4) |
where N = number of residues (25). In our case, the 71-amino-acid NtQ42P10 has a predicted Rg,rc = 26 Å, pointing out that the earliest species we observe here are smaller and more compact relative to a monomer random coil. These initial dimer and trimer species grow into oligomers of n = 14 ± 2 peptides with Rg = 46.4 ± 4.2 Å by 71 min of the aggregation reaction. It is worth noting that small mutant Htt oligomers composed of 5–15 proteins recently have been observed in a HD cell model (26). From a linear fit to the change in the number of peptides with time (dn/dt), we found that 6 ± 2 peptides/h are incorporated into the growing oligomers, a rate which then rapidly accelerates after 56 min.
Figure 3.
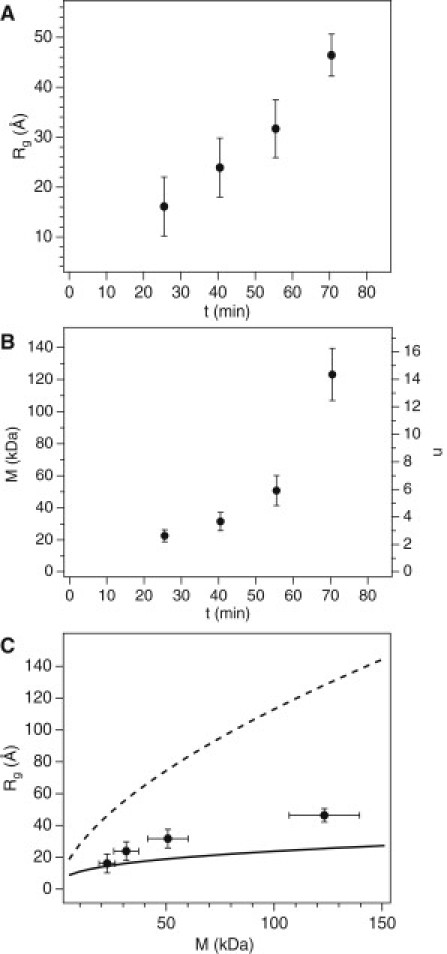
Early aggregates of NtQ42P10 formed within the first 71 min. (A) The smallest species progressively grow from an initial Rg,1 of 16–46 Å over this time. (B) The corresponding change in molecular mass with time for the smaller aggregates, M1 = 22.6 to 123 kDa, with the number of NtQ42P10 peptides per aggregate, n (right axis) calculated from M1. (C) A plot of Rg,1 versus M1 compared to model calculations for a random coil (dashed line) using Eq. 4 and a solid sphere (solid line) using Eq. 5. (Error bars) Standard error from the Guinier fits.
Again, these growing oligomers are in the presence of larger structures, which we approximated from Guinier fits to obtain Rg,2 and M2 (1.46 ≤ Qmax·Rg,2 ≤ 2.21). During the initial 71 min, Rg,2 increases from 60 to 90 Å with M2 ≈ 41 to 370 kDa (n ≈ 5 to 43), respectively. For comparison, TEM on Htt exon 1 Q44 identified 40–50 Å diameter oligomers after 30-min aggregation (27), and AFM on Htt exon 1 Q53 showed spherical oligomers with diameters of 50–650 Å within 1 h with fibrils present by this time (10). Spherical oligomers of similar size were also observed by TEM for NtQ30P6 by 15 min of the aggregation reaction (22). These reported spherical oligomers range from comparable in size up to much larger than the oligomers we detected by SANS. This is consistent with our analysis that aggregates larger than the size window of our time-resolved SANS configuration are simultaneously present.
By plotting Rg versus M (Fig. 3 C) to remove the time component of growth, correlations between the two parameters were discerned. To compare with the experimental results, two different cases were calculated and plotted: 1), an equivalent random coil; and 2), a solid sphere. The equivalent random coil Rg,rc was calculated using Eq. 4 with N = M/120.9, where 120.9 Da is the average molecular mass per residue of NtQ42P10. The solid sphere Rg,sphere was calculated from M and = 0.73 mL/g by
| (5) |
The initial NtQ42P10 dimer and trimer structures closely agree with the sphere model M and Rg. Because a sphere is the shape of minimal volume, this indicates that these earliest and smallest species are spherical and compact. As the aggregates become larger in mass and radius, they slightly diverge from the sphere model but are always distant from the random coil model. The increasing anisotropy of the aggregates during growth can account for this divergence from the sphere model.
Although formation of fibrils by monomer addition driven by aggregation of the polyQ region has been demonstrated and recognized for some time now (28,29), recent work by Thakur et al. (22) proposed an aggregation model where the 17-residue N-terminus of Htt fragments guides the initial assembly into oligomers. This is consistent with AFM studies by Legleiter et al. (11) that showed mutant Htt fragments first form oligomers before fibrils (11). Our results above on NtQ42P10 illuminate the structural details of the oligomerization process with evidence for the initial formation of compact spherical dimers and trimers. These directly identified, early intermediates progressively grow in mass and size anisotropy toward becoming predominantly fibrillar structures. At this point, fibril growth dominates and is now discussed.
Later-stage two-dimensional fibril growth
SANS data for NtQ42P10 fibril growth were fit using modified Guinier plots (see Fig. 2 C) to obtain the Rc and ML as a function of time (Fig. 4, A and B). Both the single fibril, with Rc,1 and ML,1, and fibril-fibril aggregates, with Rc,2 and ML,2, were properly treated by modified Guinier analysis. The open symbols in Fig. 4 A were from measurements with aggregate sedimentation, which affected accurate determination of ML (omitted from Fig. 4, B and C) for these times but did not appreciably affect Rc,1 and Rc,2 as seen by their close agreement with the encompassing data. Samples were redispersed to homogeneity just before measurement of the last three time points to ensure accurate ML values. During the time-course for fibrillization, the larger aggregates were about twice the size and mass of the individual fibrils (Rc,2 ≈ 2Rc,1 and ML,2 ≈ 1.5ML,1), suggesting the larger aggregates are two aligned and favorably interacting fibrils.
Figure 4.
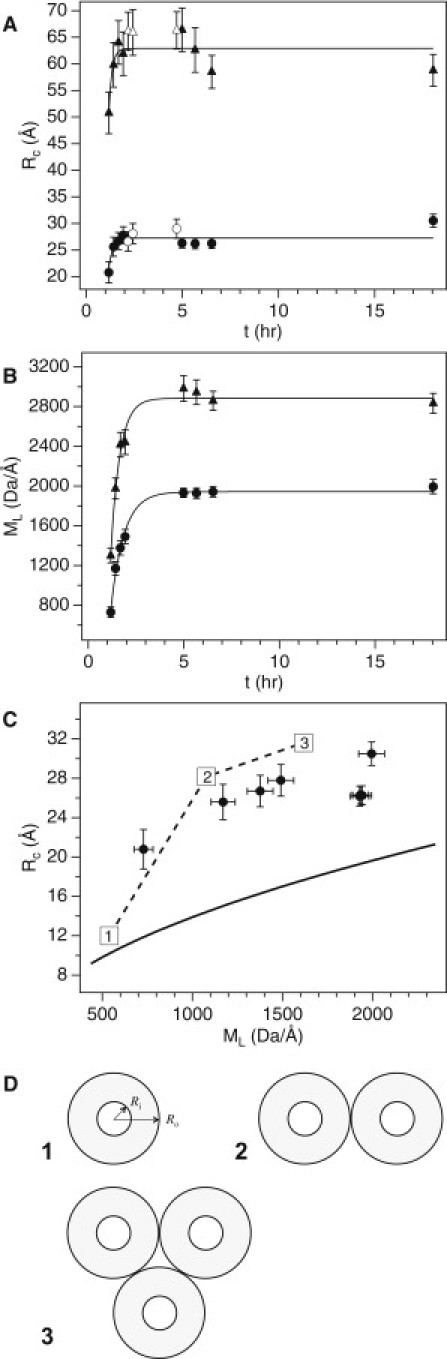
Aggregates of NtQ42P10 beyond 1 h are predominately fibrillar and their two-dimensional cross section is analyzed. (A) Change in the two characteristic length-scales, Rc,1 (circles) and Rc,2 (triangles), with time. (Open symbols) Rc measurements where sample sedimentation was observed. (Solid lines) Single-exponential fits to the data. (B) Corresponding changes in ML,1 (circles) and ML,2 (triangles). (Solid lines) Single-exponential fits to the data. (C) A plot of Rc,1 versus ML,1 compared to model calculations for a solid cylinder cross section (solid line) using Eq. 6 and the Perutz hollow cylinder β-helix cross section for one, two, and three filaments per fibril (numbered squares) using Eqs. 7a, 7b, and 7c, respectively. (Dashed line) Guide to the eye. The corresponding points to the open-symbol data in panel A are omitted from panels B and C, because sample sedimentation influenced ML values. (Error bars) Standard error from the modified Guinier fits. (D) Schematics of the hollow cylinder models for one, two, and three filaments per fibril used to calculate Rc in panel C. The inner and outer radii of a single filament, Ri and Ro, respectively, are indicated on model 1.
Single-exponential fits to Rc growth with time (Fig. 4 A) yield saturating cross-sectional radius of gyration values, Rc,1(∞) = 27.2 ± 0.4 Å and Rc,2(∞) = 63 ± 1 Å.
Single-exponential fits to the corresponding ML changes with time (Fig. 4 B) yield reliable rates, kML,1 = 1.5 ± 0.2 h−1 and kML,2 = 2.1 ± 0.3 h−1, with saturating mass per length values, ML,1(∞) = 1940 ± 30 Da/Å and ML,2(∞) = 2880 ± 50 Da/Å. Most notably, the single fibril kML,1 closely matches the kinetic rates for monomer loss (kmon = 1.28 ± 0.09 h−1) and fibril formation (kfib = 1.1 ± 0.3 h−1) obtained from the HPLC and ThT assays, respectively. Indeed, the NtQ42P10 aggregation kinetics describing monomer loss, formation of ThT-positive aggregates, and structural growth in Rc and ML are in agreement with ∼2 h to reach saturation. This importantly demonstrates that the peptide monomer pool is depleted by about the same time as structural changes in Rc and ML reach a plateau. Because SANS is insensitive to the fibril length, it is unknown from the SANS data alone whether fibril elongation via monomer addition to the growing fibril-ends continues well beyond the observed plateau in structural changes. Monomer loss followed by HPLC confirms this is not the case.
By plotting Rc,1 versus ML,1 (Fig. 4 C), we removed the time component to assess how these two parameters are related for the single NtQ42P10 fibril. For comparison, we calculated from ML and = 0.73 mL/g the cross-sectional radius of gyration for a solid cylinder,
| (6) |
We also calculated the cross-sectional radius of gyration for three hollow cylinder models representing one, two, and three filaments of the Perutz β-helix model (30) (Fig. 4 D) from the mass moment of inertia and parallel axis theorem (see the Supporting Material for derivations):
| (7a) |
| (7b) |
| (7c) |
In the Perutz model, each filament has an internal and external radius of Ri = 5.9 Å and Ro = 15.9 Å, respectively. Also, each filament consists of 20 glutamines per 4.75 Å β-sheet repeat cross section (30) yielding ML,f1 = 538.95 Da/Å with ML,f2 = 2ML,f1 and ML,f3 = 3ML,f1.
The discrepancy observed between the experimental data and the solid cylindrical cross-section model suggests that the peptide is not optimally packed within the growing NtQ42P10 fibrils—Rc,1 is always ∼1.6Rc,cyl. In fact, we found excellent agreement with the hollow cylinder models, where even the ML for NtQ42P10 contains an additional 364.5 Da/Å compared to the calculated Q20 hollow cylinder ML values that would make the two- and three-filament models superimpose with the experimental data. Although this does not directly prove that NtQ42P10 fibrils are β-helix structures, the model is consistent with our results. The implications for the internal fibril structure are discussed below within the context of the formed mature fibrils.
Fibril structure determined from SANS
A more complete scattering vector range (0.004 < Q < 0.18 Å−1) was utilized to carefully probe the final structure of the NtQ42P10 mature fibrils by SANS (Fig. 5). The fibril sample prepared at 89 μM was allowed to aggregate for >500 h at 22°C before taking measurements. The resulting scattering profile was fit with a long-cylinder form factor shape (31), which treats the single fibril as a simple cylindrical cross section of infinite length to reveal a radius of 47 ± 1 Å. The observed scattering at Q < 0.02 Å−1 is due to attractive fibril-fibril interactions, where deviations are seen between the experimental data and the extrapolated fit.
Figure 5.
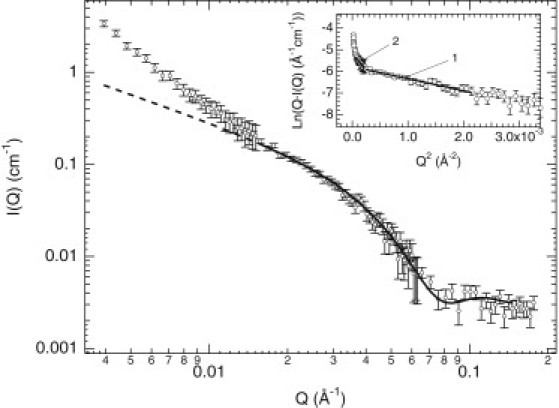
SANS data obtained over a larger Q-range allow the NtQ42P10 fibril structure to be more carefully probed. Peptide concentration was 89 μM. A long-cylinder form factor fit (solid line) accounts for the SANS profile at high and intermediate Q values. Deviations observed between the experimental scattering data and the extrapolated fit (dashed line) at Q < 0.02 Å−1 are due to favorable fibril-fibril interactions. The modified Guinier plot of the SANS profile (inset) shows two linear fit regions, denoted as 1 and 2, with the resulting Rc and ML values given in the text. (Error bars) Standard errors from the radial average of the intensity data on the neutron area detector.
From the modified Guinier analysis (see Fig. 5, inset), we found Ic,1(0) = 0.00308 ± (9 × 10−5) Å−1 cm−1 and Rc,1 = 33 ± 1 Å (Qmax·Rc,1 = 1.55), which yielded ML,1 = 1800 ± 50 Da/Å and 47 ± 1 Å, respectively. The obtained fibril radius R1 matches both the cylinder form factor fit radius and the average single fibril radius determined by TEM (R = 40 ± 8 Å). Also, from the modified Guinier analysis, we found Ic,2(0) = 0.0057 ± (3 × 10−4) Å−1 cm−1, which yielded ML,2 = 3300 ± 200 Da/Å, and Rc,2 = 77 ± 4 Å (Qmax·Rc,2 = 1.17). All of these values are also comparable to those from the NtQ42P10 kinetic end-state fibrils, demonstrating reproducibility.
Measurements of both the NtQ42P10 fibril radius and mass per length provide constraints on the internal structural arrangements of the peptides within the fibril. Thus, to determine the number of peptides per fibril, we constructed a simple volume element to describe the fibril cross section and compare the maximum and actual number of peptides filling this volume. With a β-sheet structure having a 4.75 Å repeat distance and the peptide chains oriented normal to the fibril direction, we calculated the maximum number of peptides per β-sheet repeat distance (nL,max) from the fibril radius as
| (8) |
where L = 4.75 Å, = 0.73 mL/g, and Mpep = peptide molecular mass (= 8583 Da). The actual number of peptides per 4.75 Å (nL) was directly calculated from ML,
| (9) |
Interestingly, the mature fibrils have three times less peptide than expected for a laminated β-sheet structure with nL,max = 3.2 ± 0.1 peptides and nL = 1.00 ± 0.03 peptides. From the time-resolved SANS data with a saturating radius R1(∞) = 38.5 ± 0.6 Å and mass per length ML,1(∞) = 1940 ± 30 Da/Å, we found nL,max = 2.13 ± 0.07 and actual nL = 1.07 ± 0.02, respectively. Again, our results are quantitatively consistent with the Perutz β-helix structural model. Because 40 glutamines are required to stabilize the β-helix structure with two full turns to form a filament (30), only 0.5 peptide/4.75 Å for NtQ42P10 is needed. Thus, a single fibril of 2–3 filaments would have 1–1.5 peptides/4.75 Å. In addition, the hollow cylinder models above have Rc,f2 = 28 Å and Rc,f3 = 32 Å, values matching the measured fibril Rc,1. Extending the idea of 2–3 filaments composing a single fibril, we noted the smallest detected species are dimers and trimers and could serve as the basic building blocks for the growing fibrils, although this could be fortuitous.
Evidence against the β-helix model for polyQ has been reported (32,33). However, we emphasize that the sequence context of NtQ42P10 appears to play an important role in the resulting fibril structure. Also, polymorphisms in fibril structure are a common characteristic, as demonstrated for amyloid-β (34). Different peptide concentrations and growth conditions can result in structural variations and if any structural heterogeneity is present, SANS will give an average structure. One consideration that may help to satisfy both Rc and ML values is that either or both the 17-residue N-terminal and P10 regions of NtQ42P10 maintain extended or disordered conformations whereas the Q42 region forms the β-sheet core of the fibril.
X-ray crystallography experiments on Htt exon 1 Q17 show the N-terminal region is capable of adopting an α-helix conformation whereas the proline-rich C-terminus forms a polyproline helix (35). X-ray fiber diffraction on Htt exon 1 Q51 also suggests that the flanking polyproline region is not part of the ordered fibril structure (36). Our results on NtQ42P10 fibrils underscore the need to further investigate the effects of sequence context, polyQ length, and growth conditions on Htt fibrils. More detailed knowledge concerning the fibrils would aid in determining the aggregation pathways undertaken by monomeric and oligomeric species to construct the resulting fibrils.
Conclusions
With time-resolved SANS, we are capable of pinpointing and characterizing the smallest of mutant Htt species as they exist in solution at a given time during the aggregation process. These species can be distinguished from the presence of the larger aggregates that are simultaneously present. Our results provide a detailed view where aggregation of the mutant Htt exon 1 peptide, NtQ42P10, begins with compact spherical dimers and trimers coexisting with larger, quickly forming oligomer species. Monomer depletion and ThT-positive aggregate formation ensues with no observed lag phase. The dimers and trimers grow into 14-mers within 71 min, which matches the 5- to 15-mer oligomers recently observed in a HD cell model (26).
Beyond this point, the aggregates in solution become predominately fibrillar. The late-stage fibrillization process reaches a plateau in cross-sectional radius and mass per length within ∼2 h, concurrent with full monomer depletion and saturation of ThT-positive aggregate development. These formed fibrils are amyloidlike but interestingly, the peptide is assembled within these fibrils at only ∼31–50% of the capable packing efficiency. This packing arrangement is quantitatively consistent with the Perutz β-helix structural model as opposed to any compact β-sheet-rich structural arrangements (32,33,37).
The detailed structural information provided here for the early-stage oligomers, forming fibrils, and end-state fibrils should be of great value in more carefully discerning their respective structures and roles in the aggregation pathway. Implications for the toxicity of early oligomers to neuronal cells now can be discussed within the context of the structural details we provide. This time-resolved SANS approach to capture the structures of transient amyloidlike aggregates in solution establishes a strong method that should prove useful in the further study of aggregates pertaining to HD as well as the study of other protein aggregation processes like those involved in Alzheimer's and Parkinson's diseases.
Acknowledgments
We gratefully acknowledge Drs. H. M. O'Neill, A. Osmand, and D. C. Rau for valuable discussions and suggestions.
This research at Oak Ridge National Laboratory's Center for Structural Molecular Biology was supported by the Office of Biological and Environmental Research, using facilities supported by the U.S. Department of Energy, managed by UT-Battelle, LLC under contract No. DE-AC05-00OR22725. This research was also supported by the Clifford Shull Fellowship Program at Oak Ridge National Laboratory (to C.B.S.) and by National Institutes of Health grant No. 1R21NS056325-01A1 (to V.B.).
Contributor Information
Christopher B. Stanley, Email: stanleycb@ornl.gov.
Valerie Berthelier, Email: vberthel@mc.utmck.edu.
Supporting Material
References
- 1.Shao J., Diamond M.I. Polyglutamine diseases: emerging concepts in pathogenesis and therapy. Hum. Mol. Genet. 2007;16:R115–R123. doi: 10.1093/hmg/ddm213. [DOI] [PubMed] [Google Scholar]
- 2.MacDonald M.E. Huntingtin: alive and well and working in middle management. Sci. STKE. 2003;2003:pe48. doi: 10.1126/stke.2003.207.pe48. [DOI] [PubMed] [Google Scholar]
- 3.Bates G., Harper P., Jones L. Oxford University Press; Oxford, UK: 2002. Huntington's Disease. [Google Scholar]
- 4.Sawa A., Nagata E., Snyder S.H. Huntingtin is cleaved by caspases in the cytoplasm and translocated to the nucleus via perinuclear sites in Huntington's disease patient lymphoblasts. Neurobiol. Dis. 2005;20:267–274. doi: 10.1016/j.nbd.2005.02.013. [DOI] [PubMed] [Google Scholar]
- 5.Graham R.K., Deng Y., Hayden M.R. Cleavage at the caspase-6 site is required for neuronal dysfunction and degeneration due to mutant huntingtin. Cell. 2006;125:1179–1191. doi: 10.1016/j.cell.2006.04.026. [DOI] [PubMed] [Google Scholar]
- 6.Saudou F., Finkbeiner S., Greenberg M.E. Huntingtin acts in the nucleus to induce apoptosis but death does not correlate with the formation of intranuclear inclusions. Cell. 1998;95:55–66. doi: 10.1016/s0092-8674(00)81782-1. [DOI] [PubMed] [Google Scholar]
- 7.Kuemmerle S., Gutekunst C.A., Ferrante R.J. Huntington aggregates may not predict neuronal death in Huntington's disease. Ann. Neurol. 1999;46:842–849. [PubMed] [Google Scholar]
- 8.Slow E.J., Graham R.K., Hayden M.R. Absence of behavioral abnormalities and neurodegeneration in vivo despite widespread neuronal huntingtin inclusions. Proc. Natl. Acad. Sci. USA. 2005;102:11402–11407. doi: 10.1073/pnas.0503634102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Chiti F., Dobson C.M. Protein misfolding, functional amyloid, and human disease. Annu. Rev. Biochem. 2006;75:333–366. doi: 10.1146/annurev.biochem.75.101304.123901. [DOI] [PubMed] [Google Scholar]
- 10.Wacker J.L., Zareie M.H., Muchowski P.J. Hsp70 and Hsp40 attenuate formation of spherical and annular polyglutamine oligomers by partitioning monomer. Nat. Struct. Mol. Biol. 2004;11:1215–1222. doi: 10.1038/nsmb860. [DOI] [PubMed] [Google Scholar]
- 11.Legleiter J., Mitchell E., Muchowski P.J. Mutant huntingtin fragments form oligomers in a polyglutamine length-dependent manner in vitro and in vivo. J. Biol. Chem. 2010;285:14777–14790. doi: 10.1074/jbc.M109.093708. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Olshina M.A., Angley L.M., Hatters D.M. Tracking mutant huntingtin aggregation kinetics in cells reveals three major populations that include an invariant oligomer pool. J. Biol. Chem. 2010;285:21807–21816. doi: 10.1074/jbc.M109.084434. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Burkoth T.S., Benzinger T.L.S., Lynn D.G. Structure of the β-amyloid(10–35) fibril. J. Am. Chem. Soc. 2000;122:7883–7889. [Google Scholar]
- 14.Hamill A.C., Wang S.C., Lee C.T., Jr. Solution structure of an amyloid-forming protein during photoinitiated hexamer-dodecamer transitions revealed through small-angle neutron scattering. Biochemistry. 2007;46:7694–7705. doi: 10.1021/bi700233k. [DOI] [PubMed] [Google Scholar]
- 15.Vestergaard B., Groenning M., Svergun D.I. A helical structural nucleus is the primary elongating unit of insulin amyloid fibrils. PLoS Biol. 2007;5:e134. doi: 10.1371/journal.pbio.0050134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Nayak A., Sorci M., Belfort G. A universal pathway for amyloid nucleus and precursor formation for insulin. Proteins. 2009;74:556–565. doi: 10.1002/prot.22169. [DOI] [PubMed] [Google Scholar]
- 17.Berthelier V., Wetzel R. An assay for characterizing in vitro the kinetics of polyglutamine aggregation. Methods Mol. Biol. 2003;217:295–303. doi: 10.1385/1-59259-330-5:295. [DOI] [PubMed] [Google Scholar]
- 18.Rasband, W. S. 1997–2004. ImageJ. U.S. National Institutes of Health, Bethesda, MD. http://rsb.info.nih.gov/ij/.
- 19.Guinier A., Fournet G. Wiley; New York: 1955. Small-Angle Scattering of X-Rays. [Google Scholar]
- 20.Svergun D., Barberato C., Koch M.H.J. CRYSOL—a program to evaluate x-ray solution scattering of biological macromolecules from atomic coordinates. J. Appl. Crystallogr. 1995;28:768–773. [Google Scholar]
- 21.Lee C.C., Nayak A., McRae G.J. A three-stage kinetic model of amyloid fibrillation. Biophys. J. 2007;92:3448–3458. doi: 10.1529/biophysj.106.098608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Thakur A.K., Jayaraman M., Wetzel R. Polyglutamine disruption of the huntingtin exon 1 N-terminus triggers a complex aggregation mechanism. Nat. Struct. Mol. Biol. 2009;16:380–389. doi: 10.1038/nsmb.1570. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Verheul M., Roefs S.P., de Kruif K.G. Aggregation of β-lactoglobulin and influence of D2O. FEBS Lett. 1998;421:273–276. doi: 10.1016/s0014-5793(97)01581-0. [DOI] [PubMed] [Google Scholar]
- 24.Chalikian T.V., Bresiauer K.J. On volume changes accompanying conformational transitions of biopolymers. Biopolymers. 1996;39:619–626. doi: 10.1002/(sici)1097-0282(199611)39:5<619::aid-bip1>3.0.co;2-z. [DOI] [PubMed] [Google Scholar]
- 25.Fitzkee N.C., Rose G.D. Reassessing random-coil statistics in unfolded proteins. Proc. Natl. Acad. Sci. USA. 2004;101:12497–12502. doi: 10.1073/pnas.0404236101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Ossato G., Digman M.A., Gratton E. A two-step path to inclusion formation of huntingtin peptides revealed by number and brightness analysis. Biophys. J. 2010;98:3078–3085. doi: 10.1016/j.bpj.2010.02.058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Poirier M.A., Li H., Ross C.A. Huntingtin spheroids and protofibrils as precursors in polyglutamine fibrilization. J. Biol. Chem. 2002;277:41032–41037. doi: 10.1074/jbc.M205809200. [DOI] [PubMed] [Google Scholar]
- 28.Scherzinger E., Sittler A., Wanker E.E. Self-assembly of polyglutamine-containing huntingtin fragments into amyloid-like fibrils: implications for Huntington's disease pathology. Proc. Natl. Acad. Sci. USA. 1999;96:4604–4609. doi: 10.1073/pnas.96.8.4604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Chen S., Berthelier V., Wetzel R. Polyglutamine aggregation behavior in vitro supports a recruitment mechanism of cytotoxicity. J. Mol. Biol. 2001;311:173–182. doi: 10.1006/jmbi.2001.4850. [DOI] [PubMed] [Google Scholar]
- 30.Perutz M.F., Finch J.T., Lesk A. Amyloid fibers are water-filled nanotubes. Proc. Natl. Acad. Sci. USA. 2002;99:5591–5595. doi: 10.1073/pnas.042681399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Pedersen J.S. Analysis of small-angle scattering data from colloids and polymer solutions: modeling and least-squares fitting. Adv. Colloid Interface Sci. 1997;70:171–210. [Google Scholar]
- 32.Sharma D., Shinchuk L.M., Kirschner D.A. Polyglutamine homopolymers having 8–45 residues form slablike β-crystallite assemblies. Proteins. 2005;61:398–411. doi: 10.1002/prot.20602. [DOI] [PubMed] [Google Scholar]
- 33.Sikorski P., Atkins E. New model for crystalline polyglutamine assemblies and their connection with amyloid fibrils. Biomacromolecules. 2005;6:425–432. doi: 10.1021/bm0494388. [DOI] [PubMed] [Google Scholar]
- 34.Paravastu A.K., Leapman R.D., Tycko R. Molecular structural basis for polymorphism in Alzheimer's β-amyloid fibrils. Proc. Natl. Acad. Sci. USA. 2008;105:18349–18354. doi: 10.1073/pnas.0806270105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Kim M.W., Chelliah Y., Bezprozvanny I. Secondary structure of huntingtin amino-terminal region. Structure. 2009;17:1205–1212. doi: 10.1016/j.str.2009.08.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Perutz M.F., Pope B.J., Scherzinger E. Aggregation of proteins with expanded glutamine and alanine repeats of the glutamine-rich and asparagine-rich domains of Sup35 and of the amyloid β-peptide of amyloid plaques. Proc. Natl. Acad. Sci. USA. 2002;99:5596–5600. doi: 10.1073/pnas.042681599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Sawaya M.R., Sambashivan S., Eisenberg D. Atomic structures of amyloid cross-β spines reveal varied steric zippers. Nature. 2007;447:453–457. doi: 10.1038/nature05695. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


