MATHEMATICAL MODELS OF SUBCUTANEOUS INJECTION OF INSULIN ANALOGUES: A MINI-REVIEW

Abstract

In the last three decades, several models relevant to the subcutaneous injection of insulin analogues have appeared in the literature. Most of them model the absorption of insulin analogues in the injection depot and then compute the plasma insulin concentration. The most recent systemic models directly simulate the plasma insulin dynamics. These models have been and/or can be applied to the technology of the insulin pump or to the coming closed-loop systems, also known as the artificial pancreas. In this paper, we selectively review these models in detail and at point out that these models provide key building blocks for some important endeavors into physiological questions of insulin secretion and action. For example, it is not clear at this time whether or not picomolar doses of insulin are found near the islets and there is no experimental method to assess this in vivo. This is of interest because picomolar concentrations of insulin have been found to be effective at blocking beta-cell death and increasing beta-cell growth in recent cell culture experiments.

1. Introduction

Diabetes mellitus is a syndrome of disordered metabolism resulting in hyperglycemia. This is caused by a combination of hereditary and acquired factors. Type 1 diabetes develops due to a diminished production of insulin. Type 2 diabetes and gestational diabetes occur when the insulin is not used effectively, called insulin resistance, in combination with a defect in the pancreatic β-cells. Diabetes has become an epidemic disease worldwide, with the population of diabetic patients growing rapidly in almost all countries. It has been a major focus for researchers to seek an efficient and effective approach to help people with diabetes to improve their daily life.

All forms of diabetes have been treatable since insulin became medically available in 1921, but a real cure to this disease has been elusive. Type 2 diabetes can be treated by a combination of medications, insulin supplementation and dietary adjustment. The basic treatment for type 1 diabetes is the subcutaneous injection of insulin through a syringe or insulin pump when needed. Due to the technological difficulties, effective ways to monitor plasma glucose concentration non-invasively have lagged behind other developments. Thus, all current therapies are open-loop treatment that is not able to use the feedback of glucose concentration automatically. For example, an insulin pump is operated manually by the patients and it is the patients themselves that calculate the dose of insulin to be injected according to the calorie of the food to be eaten. When an accurate non-invasive glucose monitoring technique is developed, the open-loop treatment can become closed-loop, that is, the so called artificial pancreas that delivers insulin automatically according to the variation of the glucose level in the blood will be available for patients. Patient groups and researchers working on an artificial pancreas believe they are just a few years away from a nearly carefree way for people with diabetes to monitor blood and inject insulin as needed (www.jdrf.org).

One of the important nodes in the artificial pancreas is the algorithm of accurately delivering insulin doses. The insulin delivery includes injecting human insulin, rapid-acting insulin analogues, and long-acting insulin analogues. The modes of subcutaneous injection include bolus injection and continuous injection. In the last three decades, several mathematical models have been proposed to simulate the plasma insulin concentration after subcutaneous injection ([17], [23], [35], [42]). These models either describe the insulin and insulin absorption in the injection depot ([21], [35], [38], [39]), or model the insulin concentrations in different compartments ([30], [32], [42]). The models also target different types of insulin and insulin analogues, for example, regular insulin ([4]), rapid acting insulin analogues ([17], [23], [30], [32], [38], [39], [35]) and long acting insulin analogues ([17], [21], [23], [35]). An internet-based software, DiasNet ([29]), implemented some of these models ([38], [39]) to provide decision services for patients and healthcare professionals. The most recently proposed models ([17]) are systemic, that is, the models consider both the dissolving of the insulin analogues in the depot and transport to the plasma under the hypothesis that the dissolving from dimer to monomer is reverse proportional.

In this article, we will review recent models of subcutaneous insulin injection. We organize this paper as follows. In the next section, we review the models of the absorption of insulin analogues at the injection depot, followed by Section 3 where we will focus on the compartmental models and systemic models. We will also propose two new models in this section. Some simulations are also given. In Section 4, we will conclude this paper with a discussion.

2. Modeling the absorption of insulin analogues in injection depot

It is widely accepted that the process of insulin absorption is complex ([23]). The absorption is affected by the temperature, the concentration of the insulin, and the location of the injection ([23]). Nevertheless, the chemical reaction can be depicted by the following diagram:

$$H\underset{\mathit{\text{pq}}}{\overset{p}{\rightleftharpoons }}3D$$ (2.1)

where H stands for hexamer and D for dimer, p is the transform rate from one hexameric molecule to three dimeric molecules, and pq is the transform rate from three dimeric molecules to one hexameric molecule. A dimer can be divided into two monomeric molecules of insulin. Both forms of dimer and monomer can penetrate the capillary boundary and reach the blood stream ([6]). To model the absorption, the above reaction has to be incorporated in the model according to the Law of Mass Action.

2.1. Modeling the rapid-acting insulin analogues

To model the absorption of human insulin and intermediate-acting insulin analogues in the injection depot, Mosekilde et al. ([21]) proposed following model

$$\{\begin{array}{c}\frac{\partial H(r,t)}{\partial t}=-p(H(r,t)-{\mathit{\text{qD}}}^3(r,t))+d{\nabla }^{2}H(r,t)\hfill \\ \frac{\partial D(r,t)}{\partial t}=p(H(r,t)-{\mathit{\text{qD}}}^3(r,t))+d{\nabla }^{2}D(r,t)-\mathit{\text{bD}}(r,t)-S[C-B(r,t)]D(r,t)+\frac{B(r,t)}{T}\hfill \\ \frac{\partial B(r,t)}{\partial t}=S[C-B(r,t)]D(r,t)-\frac{B(r,t)}{T}\hfill \end{array}$$ (2.2)

where t is the time (min), r is the radial distance from the injection point, H,D and B are the hexameric, dimeric and bound insulin concentration (U/ml) in the subcutaneous tissue at (r, t), b is the absorption rate constant, q is the chemical constant between the different insulin states, p the corresponding rate constant, d is the diffusion constant, C the volumetric binding capacity, T the bound insulin lifetime and S the binding rate constant.

The authors assumed that only the dimeric insulin form can penetrate the capillary membrane and thus be absorbed into plasma. In addition to that, the fraction of soluble insulin dissociating into a monomeric form is negligible. The state B in this model is an imaginary state to mimic the self-association of the insulin analogues.

Human insulin and various insulin analogues are different in their structures ([1], [17]). For rapid acting insulin analogues, the time spent in the bound state is extremely short, thus the binding state B can be omitted in the model. In addition, the slow absorption occurs only at very low concentrations (4 Uml⁻¹ and 0.01 ml, or 0.4 Uml⁻¹ and less than 1 ml) ([5]), which is much less than the therapeutic concentrations (40 Uml⁻¹ and 100 Uml⁻¹) and doses (1 U) ([39]). This model was simplified by Trajanoski et al. ([38]) after the binding state B was neglected. The resulting model becomes

$$\{\begin{array}{c}\frac{\partial H(r,t)}{\partial t}=-p(H(r,t)-{\mathit{\text{qD}}}^3(r,t))+d{\nabla }^{2}H(r,t)\hfill \\ \frac{\partial D(r,t)}{\partial t}=p(H(r,t)-{\mathit{\text{qD}}}^3(r,t))+d{\nabla }^{2}D(r,t)-\mathit{\text{bD}}(r,t)\hfill \end{array}$$ (2.3)

This simplification enables an easy numerical computation. Both [38] and [39] gave the same iterative algorithm ((14) and (15) in [38]; and (6a) and (6b) in [39]) except for a misprint in sign in [38]. In the numerical computation, the injection depot is assumed to be a ball and to be divided into 15 spheres and then to be integrated ([39]). Trajanoski et al. ([38]) also pointed out that the insulin in monomeric form has less tendency of self-association and thus the monomer equation can be modeled by

$$\frac{\partial m(r,t)}{\partial t}=D{\nabla }^{2}m-\mathit{\text{BM}}$$ (2.4)

where m is the concentration of monomers.

Model (2.4) is further modified by Wach et al. ([39]) and resulted in

$$\frac{\partial m(r,t)}{\partial t}=D\frac{1}{r^2}\frac{\partial }{\partial r}\left(r^2\frac{m}{r}\right)-\mathit{\text{BM}}$$ (2.5)

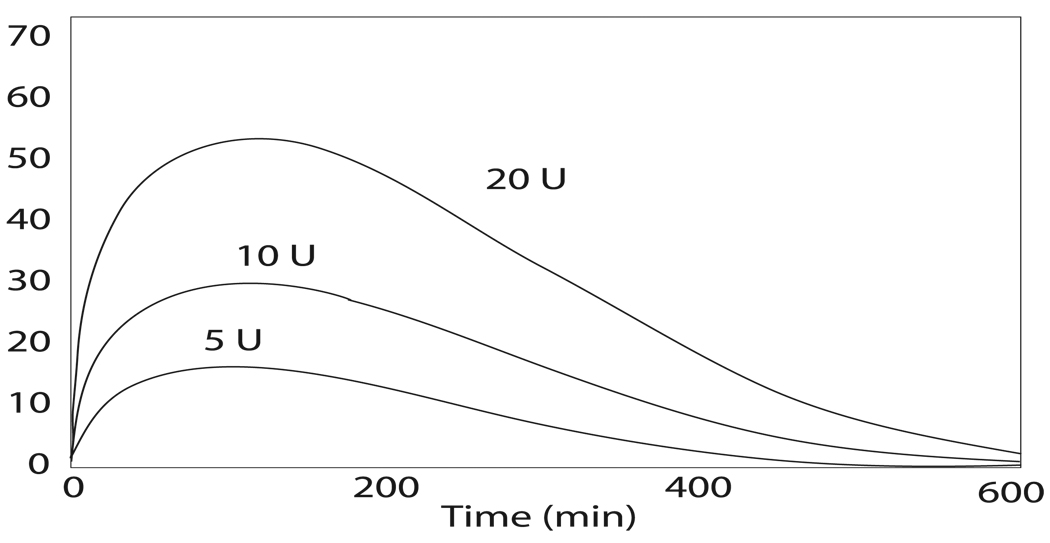
where r is the radius of the polar coordinate, and D is the diffusion rate. The significant advantage of this modification is that the equation (2.5) is analytically solvable by applying the method of Fourier transform (see [39] for the solution). This model (2.2) has the feature of showing the inverse responses to the initial doses (refer to Figure 1). All three models demonstrate profiles of absorptions that are in agreement with the experimental data for human insulin or the insulin analogues being considered.

FIGURE 1.

Dose dependency of plasma insulin concentration simulated by the model (2.3). (Adapted from [23]).

In the point of view of treating diabetes, the ultimate purpose of the subcutaneous injection of insulin analogues is to increase the plasma insulin concentration and thus lower blood glucose to maintain normal glycemia. Thus additional calculation is necessary after the absorption is modeled. To this end, the authors assume the local concentration in the depot to be the whole body insulin concentration and compute the concentration by integrating the multilayered depot.

$$I\prime (t)=-k_{e}I(t)+\frac{1}{V_d}{\displaystyle {\int }_{V_{\mathit{\text{SC}}}}(\mathit{\text{bD}}(r,t))\mathit{\text{dV}}},$$ (2.6)

where k_e is the rate constant for insulin elimination, V_SC is the subcutaneous depot volume and V_d is the plasma insulin distribution volume ([38], [39]).

2.2. Modeling the long-acting insulin analogues

Based on the models in [21] and [38], Tarin et al. ([35]) reinforced the imaginary bound state B(r, t) with diffusion and proposed a model to study the dynamics of long-acting insulin analogues, e.g., Glargine. The model is given by

$$\{\begin{array}{c}\frac{\partial B(r,t)}{\partial t}=-\kappa B(r,t)(C_{\mathit{\text{max}}}-H(r,t))+d_{B}d{\nabla }^{2}B(r,t)\hfill \\ \frac{\partial H(r,t)}{\partial t}=-p(H(r,t)-{\mathit{\text{qD}}}^3(r,r,t))+\kappa B(r,t)(C_{\mathit{\text{max}}}-H(r,t))+d{\nabla }^{2}H(r,t)\hfill \\ \frac{\partial D(r,t)}{\partial t}=p(H(r,t)-{\mathit{\text{qD}}}^3(r,t))-\mathit{\text{bD}}(r,t)+d{\nabla }^{2}D(r,t)\hfill \end{array}$$ (2.7)

where C_max, a parameter to be identified, is the maximum concentration of hexamer in the injection depot, κ > 0 is the proportional factor of disengagement of insulin analogue in the depot, b is the absorption rate, d_B ∈ [0, 1] is a non-dimensional factor that reduces the diffusion effect, and all other notations remain the same as in model (2.2).

In a similar approach to that in [38] and [39], the computation of plasma insulin concentration is obtained by integration over the subcutaneous volume

$$I(t)=b{\displaystyle {\int }_{V_{\mathit{\text{SC}}}}D(r,t)\mathit{\text{dV}},}$$ (2.8)

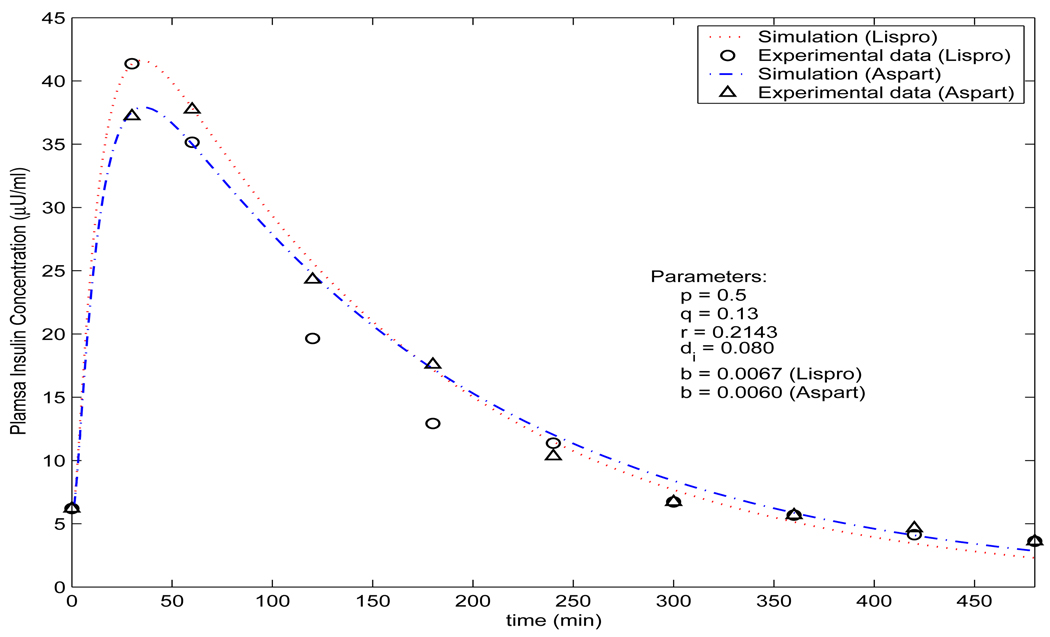
with discretization of the depot volume into multiple spheres ([35]). The calculated plasma insulin concentration is the dotted line given in Figure 3.

FIGURE 3.

Profile of plasma insulin concentration by the model (3.11) (lower/green solid curve), the model (3.12) (upper/red solid curve) (p = 0.5, q = 3.04, r = 0.2143, c = 15, b = 0.025, k = 2.35 ×10⁻⁵ and d_i = 0.0215), and the model (2.7) (dotted curve) with the measured data (circle ○) from [15].

3. Modeling the dynamics of plasma insulin concentration

The computation results by (2.6) and (2.8) give rough estimates of plasma insulin concentration. To estimate the plasma insulin concentration more accurately, a compartmental modeling approach is widely used, for example in the models proposed in [14], [30], [32], and [42]. Furthermore, Li and Kuang ([17]) proposed two ordinary differential equation models systemically to model the plasma insulin concentration after the injected insulin is dissolved in the injection depot. The models can be classified as (a) bolus injection model, and (b) continuous injection model. We will review them separately below.

3.1. Modeling the bolus insulin injection

Shimoda et al. ([32]) proposed a compartment-based model to study the dynamics of a short-acting insulin analog (Insulin Lispro) injected subcutaneously, and developed an insulin infusion algorithm. The authors used the first-order delay for the transfer function in the injection depot. The model is given as follows:

$$\{\begin{array}{c}{x}_1^{\prime }(t)=-k_{21}{x}_1(t)+u(t)\hfill \\ x_2^{\prime }(t)=k_{21}{x}_1(t)-(k_d+k_a)x_2(t)\hfill \\ I\prime (t)=\frac{k_a}{V_d}{x}_2(t)-k_{e}I(t),\hfill \end{array}$$ (3.9)

where x₁ is the subcutaneous insulin mass in the injection depot, x₂ is the subcutaneous insulin mass proximal to plasma and I is the plasma insulin concentration and u(t) is the input function. The parameters k_d and k_e are the degradation rate in the depot and plasma respectively, and V_d is the volume of plasma.

Notice this model is a linear non-autonomous system. The solutions can be explicitly expressed in terms of the initial conditions, the input function u(t), and the parameters. By applying the algorithm with regular insulin, the episodes of postprandial hyperglycemia and delayed hyperinsulinemia and accompanied hypoglycemia occurred. However, these episodes disappear when using rapid acting insulin lispro. This is because the regular insulin does not dissolve as quickly as lispro in the depot and the first order delay is not enough to simulate the slow dissolving process. Refer to the subsection 2.2 in this paper for how the slow process is modeled for long acting insulin.

All previous compartment based models ([14], [23], [30], [32]) have used the first order delay to mimic the dissolving process of regular insulin and insulin analogues for simplicity. In doing so the accuracy of the concentrations of the insulin in different forms was lost. Li and Kuang ([17]) considered the process given in the reaction diagram (2.1) and hypothesize that the insulin absorption in depot is inversely proportional to the concentration of insulin in plasma. They propose the following model:

$$\{\begin{array}{c}H\prime (t)=-p(H(t)-{\mathit{\text{qD}}}^3(t))\hfill \\ D\prime (t)=p(H(t)-{\mathit{\text{qD}}}^3(t))-\frac{\mathit{\text{bD}}(t)}{1+I(t)}\hfill \\ I\prime (t)=\frac{\mathit{\text{rbD}}(t)}{1+I(t)}-d_{i}I(t),\hfill \end{array}$$ (3.10)

with H(0) > 0,D(0) = 0, and I(0) ≥ 0, where H(t) (U/ml) stands for the concentration of insulin analogue in its hexameric form, D(t) (U/ml) for the concentration of the insulin analogue in the dimeric form, and I(t) (U/ml) for plasma insulin concentration at time t ≥ 0.

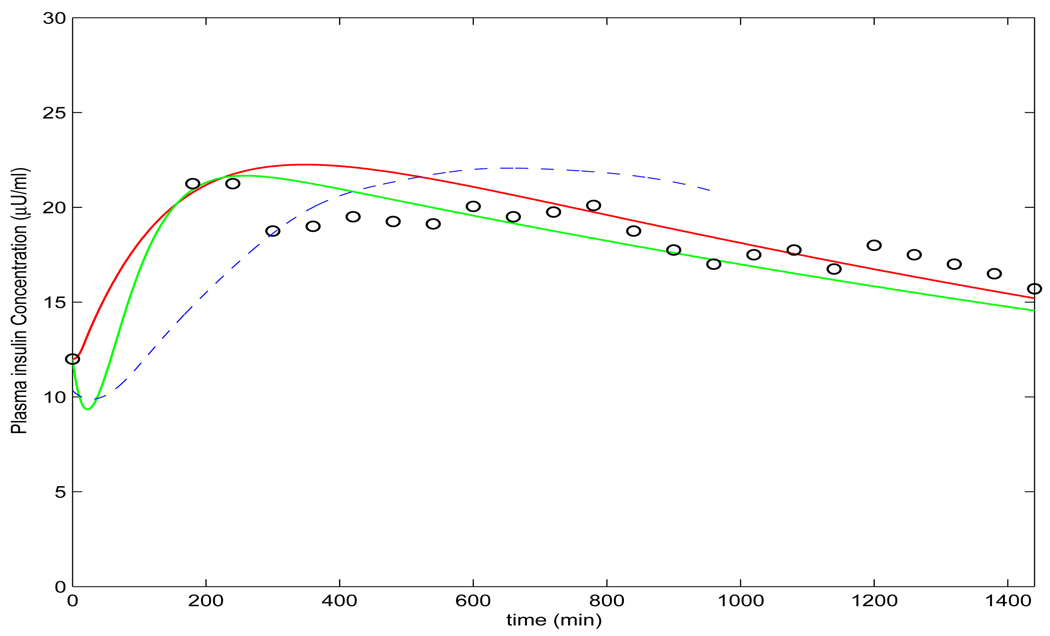
This hypothesis serves as a bridge between the local injection of insulin analogue and plasma insulin concentration in the whole body, which are depicted by the term bD(t)/(1 + I(t)) in the second equation and the term rbD(t)/(1 + I(t)) in the third equation of model (3.10), where b (U/min) is a constant parameter ([21], [39] and [35]), and r ≤ 1, as only fractional molecules can become plasma insulin ([35]). The constant d_i (min⁻¹) in the third equation is the insulin degradation rate that has been assumed as linear ([7], [8], [16], [18], [19], [22], [25], [26], [34], [37], [40]) but was enhanced to the form of Michaelis-Menten by [41]. With this hypothesis, using the same parameters in previous models, the profile resulting from the simulation of the model (3.10) matches the experimental data (refer to Figure 2).

FIGURE 2.

Profiles of plasma insulin concentration produced by model (3.10) and the measured data for insulin aspart and for insulin lispro from [9]. This figure is adapted from [17].

To model the slow dissolving, long acting insulins, e.g., glargine and the newly created insulin analogue glulisine ([1]), Li and Kuang ([17]) propose the following model by simulating the slow process with the binding state as in the model (2.2) by [21]:

$$\{\begin{array}{c}B\prime (t)=-\mathit{\text{kB}}(t)\frac{C_{\mathit{\text{max}}}}{1+H(t)}\hfill \\ H\prime (t)=-p(H(t)-{\mathit{\text{qD}}}^3(t))+\mathit{\text{kB}}(t)\frac{C_{\mathit{\text{max}}}}{1+H(t)}\hfill \\ D\prime (t)=p(H(t)-{\mathit{\text{qD}}}^3(t))-\frac{\mathit{\text{bD}}(t)}{1+I(t)}\hfill \\ I\prime (t)=\frac{\mathit{\text{rbD}}(t)}{1+I(t)}-d_{i}I(t),\hfill \end{array}$$ (3.11)

with initial condition B(0) = B₀ > 0,H(0) = 0,D(0) = 0, and I(0) = I₀ ≥ 0, where B(t) (U/ml) is the concentration at the bound state for the insulin analogue in hexermeric form, H(t) (U/ml) is the concentration of insulin analogue in hexameric form, D(t) (U/ml) is the concentration of insulin analogue in dimeric form, and I(t) (U/ml) for insulin concentration at time t ≥ 0. The term kB(t)C_max/(1 + H(t)) is because the insulin analogue in the depot formed near the injection site is transferred to hexamer gradually and the transfer is inversely proportional to the concentration of the insulin in hexameric form with the maximum transformation capacity C_max ([21], [35]), where constant k (min⁻¹) is the absorption rate. This modification prevents the unpredictable behavior of the model (2.2) and the model (2.7) if H(t) > C_max. The profile of the insulin dynamics produced by the model (3.11), using the parameters in the model (2.2) and the model (2.7), is well in agreement with the experimental data in [15] (refer to Figure 3. These two models proposed in [17] not only feature systemic modeling, thereby allowing the plasma insulin concentration to be obtained directly, but they also model multiple doses as the initial condition I(0) ≥ 0. Previous models ([21], [23], [35], [38], [39], [42]) lack this feature. However, it is important since the residual insulin can never be zero ([31]).

Notice that the imaginary state B in the model does not really exist in the absorption process. It is mainly to mimic the delayed process of the absorption by adding the zinc ions in the analogues. So it is intuitive to consider the delayed effect by modeling with delay differential equations (DDE). So we propose the following model for the long acting insulin analogues by adding an explicit delay τ > 0 for hexamers to transfer to dimers in the model (3.10). Thus, the new model is given by

$$\{\begin{array}{c}H\prime (t)=-p(H(t)-{\mathit{\text{qD}}}^3(t))\hfill \\ D\prime (t)=p(H(t-\tau )-{\mathit{\text{qD}}}^3(t))-\frac{\mathit{\text{bD}}(t)}{1+I(t)}\hfill \\ I\prime (t)=\frac{\mathit{\text{rbD}}(t)}{1+I(t)}-d_{i}I(t).\hfill \end{array}$$ (3.12)

The mathematical analysis is almost the same as that for the model (3.10) in [17]. For example, it is easy to show that the trivial solution is the unique equilibrium and it is globally asymptotically stable. Figure 3 demonstrates the dynamics of the plasma insulin concentration with comparison to the profiles generated by the model (3.11), (2.7) and the experimental data. Clearly, comparing with the experimental data, the simulation result by the DDE model (3.12) is slightly better than the profile by the model (3.11), which itself is much better than the simulation result by the model (2.7).

3.2. Modeling continuous subcutaneous insulin injection

Besides the commonly used bolus injection of insulin, continuous subcutaneous injection is another effective regimen for insulin delivery. Insulin is secreted from the pancreas in two oscillatory manners. Both pulsatile oscillations with small amplitude and short period (5–15 minutes, [16], [19], [28], [34]), and ultradian oscillations with large amplitude and long period (50–150 minutes, [16], [19], [33], [34]) are observed. Since the pulsatile secretion is small and the period of secretion is short, its secretion rate can be simulated by a positive constant u > 0. The aim of the continuous subcutaneous insulin injection is to mimic the pulsatile secretion of insulin.

Wilinska et al. ([42]) proposed eleven compartment-based models to simulate the continuous subcutaneous insulin injection (CSII). According to the authors ([42]), the best model within the eleven models is the tenth model, which is based on the model diagram in Figure 3.2 and given by

$$\{\begin{array}{c}{Q}_{1a}^{\prime }(t)=\mathit{\text{ku}}-k_{a1}{Q}_{1a}-\frac{V_{\mathit{\text{MAX}},\mathit{\text{LD}}}{Q}_{1a}}{k_{M,\mathit{\text{LD}}}+Q_{1a}}\hfill \\ Q_{1b}^{\prime }(t)=(1-k)u-k_{a2}{Q}_{1b}-\frac{V_{\mathit{\text{MAX}},\mathit{\text{LD}}}{Q}_{1b}}{k_{M,\mathit{\text{LD}}}+Q_{1b}}\hfill \\ Q_2^{\prime }(t)=k_{a1}{Q}_{1a}-k_{a1}{Q}_2\hfill \\ Q_3^{\prime }(t)=k_{a1}{Q}_2+k_{a2}{Q}_{1b}-k_e{Q}_3\hfill \end{array}$$ (3.13)

where u is the insulin infusion rate, Q_1a and Q_1b represent the insulin mass (mU) delivered in slow and fast channels at proportion k and 1 − k, respectively; Q₂ (mU) is the insulin mass in slow channel; Q₃ represents insulin mass (mU) in the plasma compartment; k_a1, k_a2 and k_e are transfer rate (min⁻¹; V_MAX,LD is the maximal saturation level (mUmin⁻¹) of the Michaelis-Menten kinetics of insulin degradation; k_MD (mU) is the half saturation value; and LD_a and LD_b stand for the local degradation at the injection site (mUmin⁻¹), respectively. When u is a positive constant, the model simulates the pulsatile secretion; when u is a function of t, it can be used to simulate the case that the secretion rate varies along the time t. With appropriate selection of u(t) and parameters, the model (3.13) can simulate bolus injection as well.

The model output fits the experimental data well after parameter estimation. The molecular process in (2.1) is not completely reflected in the model (3.13). The authors stated that “The idea of two absorption channels does not have an immediate physiological interpretation” ([42]). In fact, the addition of the slow channel mimics the dissolving process for the proportion ku. In the model fitting, 67% of insulin passes through the slow channel ([42]). In addition, considering the local degradation LD_a and LD_b helps the model output, although the local degradation is still controversial ([5], [3], [12], [13], [14], [42]). In the model (3.13), assuming the continuous injection is at a constant rate u, we can modify the model (3.10) as follows to model CSII:

$$\{\begin{array}{c}H\prime (t)=u-p(H(t)-{\mathit{\text{qD}}}^3(t))\hfill \\ D\prime (t)=p(H(t)-{\mathit{\text{qD}}}^3(t))-\frac{\mathit{\text{bD}}(t)}{1+I(t)}\hfill \\ I\prime (t)=\frac{\mathit{\text{rbD}}(t)}{1+I(t)}-d_{i}I(t).\hfill \end{array}$$ (3.14)

Clearly, the system (3.14) assumes a unique steady state E* = (H*,D*, I*) that is in the interior of the first quadrant, where

$$\begin{array}{ccc}{I}^{*}\hfill & =\hfill & d_i^{-1}\mathit{\text{ru}}\hfill \\ D^{*}\hfill & =\hfill & r^{-1}{b}^{-1}{d}_i{I}^{*}(1+I^{*})=b^{-1}u(1+d_i^{-1}\mathit{\text{ru}})\hfill \\ H^{*}\hfill & =\hfill & p^{-1}u+q{(D^{*})}^3=p^{-1}u+{\mathit{\text{qb}}}^{-3}{u}^3{(1+d_i^{-1}\mathit{\text{ru}})}^3.\hfill \end{array}$$

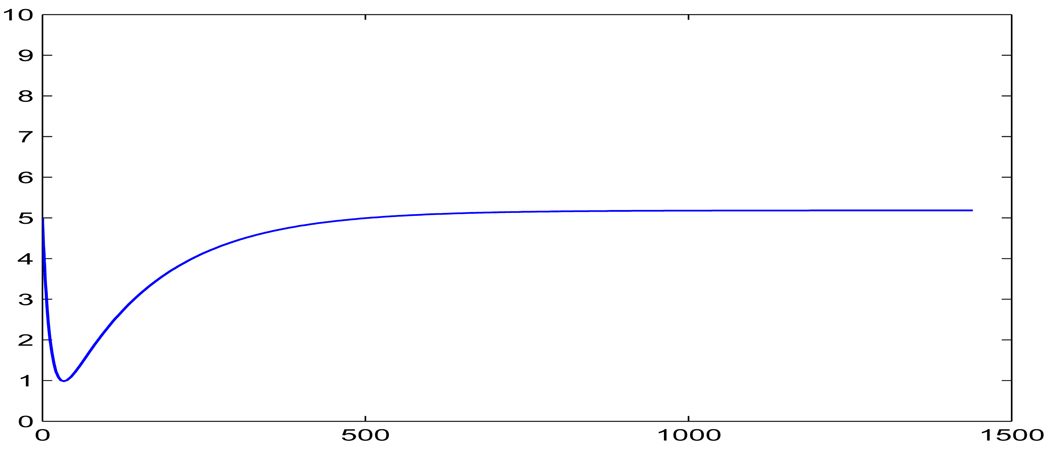
Preliminary simulation (3.2) demonstrates that the model (3.14) produces ideal insulin concentration for basal insulin. We will further analyze this model in future work.

4. Discussions

In this paper, we reviewed multiple models of subcutaneous injection of regular insulin and insulin analogues. Some models (model (2.2), model (3.9), model (2.3), and model (2.5)) have been reviewed by Nucci and Cobelli ([23]). Nucci and Cobelli([23]) also reviewed the model proposed by Berger and Rodbard ([4]) and pointed out that the model (2.3) ([38]) and the model in [4] “stand out as the better descriptors of insulin subcutaneous absorption kinetics” ([23]). Nucci and Cobelli also pointed out that the model proposed by Berger and Rodbard ([4]) has not been scientifically validated, and it is not suitable for rapid insulin. The model (2.3) requires a high burden in computation and it is not suitable for the intermediate and long-acting insulin ([23]). From a different perspective, both model (2.3) and model (2.2) are well built models from the view of pharmacokinetics as the physico-chemical process is considered. These models feature an accurate description of the injection depot including the important inverse relationship between the doses of the injected insulin analogue and the absorption rate of dissolved monomeric insulin form (refer to Figure 1). To estimate the plasma insulin concentration, not only the computation burden is large as pointed out in [23], but also the way of the computation is actually relative to the concentration of insulin in dimeric (and monomeric) form in the local depot instead of the concentration in plasma.

To get more accurate quantitative estimation and qualitative behavior of the concentration of plasma insulin, the plasma insulin as a compartment has to be included in the model. However, a gap between the plasma compartment and the injection depot can not be easily filled. There is little knowledge regarding how the dimers and monomers penetrate the capillary membranes and enter the plasma. The model (3.10) and the model (3.11) proposed by Li and Kuang ([17]) make a hypothesis on this relationship: the transfer rate of dimers into plasma insulin is inversely proportional to the concentration of the plasma insulin. Then, with the same or fine-tuned parameter values used by other models ([21], [38], [35], [39], [42]), these models produce the best profiles comparing with the experimental data given by [15] and [35]. Thus the hypothesis seems reasonable, although clinical experiments are necessary to validate it. One should also notice that these two models do not aim to model the insulin absorption in the injection depot. So a key phenomenon, inverse dose response, is not observed in the model (3.10) and the model (3.11).

The model (3.13) (the tenth model in [42]) considered local degradation of insulin at the injection depot and maintaining the two pathways of insulin absorption, i.e., fast absorption and slow absorption. The degradation term is taken as in Michaelis-Menten kinetics by assuming that the process is saturable. According to the Akaike criterion (AIC) ([42]), this model is the best model of all the eleven models in [42]. The authors ([42]) concluded that this model suggests the presence of fast and slow absorption channels and the presence of local insulin degradation.

All the compartment-based models do not maintain the inverse relationship of doses, except the model #5 in [42] for insulin lispro. We suspect the loss of this feature in compartment models is due to the lack of diffusion terms in the equations. Considering the diffusion effect in the depot, the models will be reaction-diffusion equations and become the models in [21], [38] and [39].

For many individuals, insulin injection can now be performed periodically though an insulin pump. This can be modeled by a forced periodic function of time t. Thus, some models in this review could be extended to include such a forced term so that the models become non-autonomous nonlinear differential equation systems. For both mathematics and insulin management, it would be interesting to study such non-autonomous differential equations.

Modeling is an important tool in our quest to better understand the properties of insulin and its analogues in vivo. These studies have important implications for current insulin therapy as well as for the eventual adoption of a closed-loop artificial pancreas that can perfectly mimic the normal release kinetics of insulin from the pancreatic beta-cell. Parker et al. ([27]) reviewed the existing algorithms in closed-loop blood glucose regulation, which use the intravenous route for insulin delivery. The authors discussed the advantages and disadvantages of those algorithms in insulin delivery through this route. As pointed out by the authors, “a key tenet from robust control theory is that controller performance is directly linked to model accuracy”, and “the stability of insulin preparations is also important” ([27], pp. 71). The stability is achieved in the process of the transformation from hexamers to monomers. Li and Kuang ([17]) not only proved the stability analytically for the model (3.10) and the model (3.11), but also these models demonstrate more accurate profiles comparing with experimental data.

These studies also have the potential to inform us about the kinetics by which endogenous insulin hexamers released from the body’s own pancreatic beta-cells to become biologically active monomers. While the kinetics of the conversion from hexamer to monomer are unlikely to play a significant role in the peripheral circulation, there is increasing evidence that insulin may have critical local paracrine actions within the islets ([24]; reviewed by Johnson and Alejandro ([10])). Although picomolar doses of insulin were found to be effective at blocking beta-cell death and increasing beta-cell growth in vitro (Johnson et al. [11]; Beith et al. [2]), it remains unclear whether such concentrations of insulin are found in the islet in vivo. Answering this and other key questions will require models that take into account the delay required for insulin crystals and hexamers to dissolve into active hormones. The models reviewed herein provide key building blocks for this and other important endeavors.

FIGURE 4.

Model diagram of the tenth model in [42]. LD_a = V_MAX,LDQ_1a/(k_M,LD + Q_1a) and LD_b = V_MAX,LDQ_1b/(k_M,LD + Q_1b) are in the form of Michaelis-Menten kinetics as in the model (3.13). (The model diagram is adapted from [42].)

FIGURE 5.

Profile of the continuous subcutaneous insulin injection model (3.14), where u = 0.002µU/ml per minute and I(0) = 0.005µU/ml.