Abstract
The purposes of this study were to create a three-dimensional representation of strain during isometric contraction in vivo and to interpret it with respect to the muscle fiber direction. Diffusion tensor MRI was used to measure the muscle fiber direction of the tibialis anterior (TA) muscle of seven healthy volunteers. Spatial-tagging MRI was used to measure linear strains in six directions during separate 50% maximal isometric contractions of the TA. The strain tensor (E) was computed in the TA's deep and superficial compartments and compared with the respective diffusion tensors. Diagonalization of E revealed a planar strain pattern, with one nonzero negative strain (εN) and one nonzero positive strain (εP); both strains were larger in magnitude (P < 0.05) in the deep compartment [εN = −40.4 ± 4.3%, εP = 35.1 ± 3.5% (means ± SE)] than in the superficial compartment (εN = −24.3 ± 3.9%, εP = 6.3 ± 4.9%). The principal shortening direction deviated from the fiber direction by 24.0 ± 1.3° and 39.8 ± 6.1° in the deep and superficial compartments, respectively (P < 0.05, deep vs. superficial). The deviation of the shortening direction from the fiber direction was due primarily to the lower angle of elevation of the shortening direction over the axial plane than that of the fiber direction. It is concluded that three-dimensional analyses of strain interpreted with respect to the fiber architecture are necessary to characterize skeletal muscle contraction in vivo. The deviation of the principal shortening direction from the fiber direction may relate to intramuscle variations in fiber length and pennation angle.
Keywords: diffusion tensor magnetic resonance imaging, muscle mechanics, deformation, human, imaging
many treatments of muscle-tendon mechanics assume that a muscle's fibers shorten along their longitudinal axes in a spatially uniform manner and that tendons and aponeuroses undergo an equal-magnitude, spatially uniform lengthening (12, 53); however, recent studies have demonstrated additional complexity during in vivo contractions. Fiber rotation during contraction causes shortening velocities of aponeuroses to exceed those of muscle fibers, a “gear ratio” effect that decreases as a function of contraction intensity (2, 6). MRI data have revealed spatially heterogeneous strain patterns in muscle tissue during contraction (38, 43, 55) that may result from nonuniformity in fiber length and curvature (4) and/or spatial variability in the distribution or material properties of tissues involved in myofascial force transmission (31, 51, 52). Nonuniform fiber lengths and curvature may also lead to shear strain across and between muscle fibers (4). Other MRI data have demonstrated strain heterogeneity along the superficial and deep aponeuroses of the soleus muscle (16, 26, 43), implying a spatially variable gear ratio (43). Finally, muscles operate under a constraint of almost complete volume preservation during contraction (3); therefore, if a muscle shortens in one direction, it must expand in at least one other direction. Collectively, these findings indicate that the intramuscular patterns of strain development during contraction are multidimensional and spatially heterogeneous and, thus, require characterization with reference to the local fiber geometry using imaging methods that have three-dimensional (3D) sensitivity.
Phase-contrast (14, 15) and spatial-tagging (54) MRI are methods for quantifying the strain characteristics of muscle in vivo. While phase-contrast techniques have excellent spatial resolution, the acquisition of a full data set may involve as many as 50 contractions per motion-encoding direction. To avoid subject fatigue, studies are restricted to low contraction intensities and/or characterize motion in a single direction only (38, 43, 44). In spatial-tagging MRI, the tissue magnetization is saturated in a spatially dependent manner prior to acquisition of a series of images, resulting in a line or grid pattern of “tags” (areas of low signal intensity) in each image. Tissue displacement during the image acquisition period is revealed as the interimage motion of the tags. Spatial-tagging methods can accurately portray tissue displacement in any direction (50). Moreover, only a single contraction is required to acquire one motion-encoding direction of spatially tagging data; therefore, higher-intensity contractions and/or more motion-sensitized strain directions can be studied. Strain-mapping methods for spatial-tagging MRI that are based on distance measurements between manually detected tag positions may be more subjective and time-consuming than the methods employed in the analysis of phase-contrast MRI and have a spatial resolution that is limited to the intertag distance. An alternative approach, harmonic phase analysis (37), provides pixel-wise spatial resolution of strain by investigating the phase information of the tagged image; however, this analysis method may be confounded in skeletal muscle because of the presence of an internal aponeurosis, which creates lines of signal dropout in the image unrelated to the tagging sequence.
Analyses of skeletal muscle strain with respect to an external, arbitrary frame of reference have limited applicability, however, since muscle architecture may vary within muscles (21, 23, 28, 42), between muscles (46, 47), and between individuals. In the tibialis anterior (TA) muscle, the fibers in the superficial and deep compartments originate on the crural fascia and tibia, respectively, and project inferiorly and centrally to insert onto a central aponeurosis. Within each compartment, the fibers are consistently oriented in the laboratory frame of reference (28). However, variations in muscle shape and aponeurosis orientation cause intramuscular heterogeneity in fiber length and pennation angle (21, 23, 28). These architectural patterns can be quantified in vivo using diffusion tensor MRI (DT-MRI). DT-MRI identifies the principal direction of water diffusion, which is collinear to the longitudinal axis of skeletal and cardiac muscle fibers (8, 11, 24, 40). By combination of DT-MRI measurements of the direction of greatest diffusion throughout the muscle with appropriate data-processing methods, a whole muscle's architecture can be reconstructed and quantified in 3D (11, 20–22, 28).
In this study, we used spatial-tagging MRI to measure linear strains in six directions due to submaximal isometric contraction of the TA muscle. Computation of a strain tensor and its comparison with the diffusion tensor in the same region of muscle were used to test the hypothesis that the direction of principal shortening would differ from the principal fiber direction. We also conducted an exploratory analysis of the direction of principal elongation and its relationship to the diffusion tensor. Finally, we tested for compartment-specific variations in the strain patterns.
METHODS
Subjects
Seven healthy subjects (4 men) participated in the study; their descriptive characteristics were as follows (means ± SD): 23.6 ± 3.3 yr old, 168.4 ± 12.7 cm height, and 76.1 ± 20.5 kg body mass. The study was approved by the Vanderbilt University Institutional Review Board, and all subjects provided written informed consent prior to participation.
Experimental Protocol
Each subject came to the laboratory for an orientation session and a testing session. During the orientation session, the study procedures were explained and each subject completed a health history questionnaire to ensure that he/she had no known history of physician-diagnosed disease. The subject then lay supine on an exercise bench, to which an MRI-compatible isometric exercise device was secured. The subject's self-reported dominant foot (in all cases, the right foot) was placed in the exercise device, and a strap was placed over the metatarsal bones. The subject performed two or more 3-s, isometric maximal voluntary contractions (MVCs) of the dorsiflexor muscles. During each contraction, the largest force range was recorded. This procedure was repeated until two of the force ranges were within 5% of each other; the MVC was recorded as the higher of the two. The subject then practiced submaximal isometric dorsiflexion contractions at 50% MVC.
On the testing day, the isometric exercise device was bolted to a grid plate on the patient bed of the imager. The subject lay supine with the foot in the exercise device. A radiofrequency coil was placed around the leg. To minimize gross movement of the leg, foam pads were packed around the leg in the coil and the subject's thighs were strapped to the patient bed. Structural and diffusion-weighted MRI data sets were acquired. Then the subject performed twelve to fifteen 15- to 20-s isometric dorsiflexion contractions at 50% MVC while spatially tagging data were acquired.
Data Acquisition
Force.
The force acquisition system has been previously described (35). Briefly, the isometric exercise device contained a load cell, the signals from which were differentially amplified, conditioned using a bridge circuit, digitized at 1,000 Hz, and recorded by an in-house written LabVIEW version 7.1 (National Instruments, Austin, TX) program. Real-time, 20-Hz visual feedback concerning relative force production was provided in the form of a simulated light panel on a computer screen during contractions performed in the laboratory and on a pair of MRI-compatible goggles during contractions performed in the MRI scanner.
MRI acquisition: general.
Imaging data were obtained with a 3-T magnetic resonance imager (Intera Achieva, Philips Medical Imaging, Best, The Netherlands) and an eight-channel phased-array knee coil (Philips Medical Imaging). The subject lay supine, with the foot strapped into the isometric exercise device; the maximum girth of the TA was centered in the knee coil. Three-plane, gradient-echo scout images were acquired to determine the superior extent of the TA's central aponeurosis. Subsequent images were acquired with their center 2 cm inferior to this point.
Structural images.
Ti-weighted images were acquired in all three standard anatomic planes using repetition time (TR)/echo time (TE) = 500/16 ms, three slices (sagittal and coronal) or five slices (axial) with slice thickness = 7.1 mm, field of view (FOV) = 179 × 179, number of excitations (NEx) = 2, and acquired matrix = 128 × 128 (reconstructed at 256 × 256).
DT-MRI.
Diffusion-weighted images were acquired over five axial slices using a pulsed-gradient spin-echo echo-planar imaging sequence with the same offsets and FOV as the other axial acquisitions, TR/TE = 5,000/46 ms, NEx = 4, diffusion encoding in 15 directions with a diffusion weighting (b−) value of 450 s/mm2, and one b = 0 s/mm2 image.
Spatially tagged images.
Spatially tagged images, consisting of 2 series of 20 dynamically acquired images, were acquired using a binomial spatial-tagging sequence employing a single-shot, gradient-echo readout and TR/TE = 10 s/22 ms with an acquired matrix of 128 × 116 (reconstructed at 128 × 128) and FOV = 179 × 179. Single-shot images were used to decrease the total number of contractions the subjects had to perform; each image acquisition required 70 ms. To create isotropic resolution in the strain measurements, the slice thickness was 7.1 mm and the tags were applied 7.1 mm apart.1
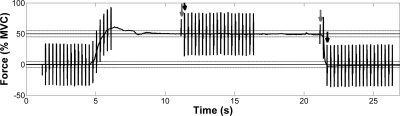
Figure 1 depicts the relationship between the contraction and the acquisition of the tagging data. Briefly, the first set of tags was applied and imaged after the subject had achieved a steady force level; the second set of tags was applied at the end of the contraction and imaged following relaxation. Tissue displacement during the ramp-down in force was studied, because pilot studies showed that the subjects were able to relax more quickly and reproducibly than they were able to contract and attain a submaximal target force. While hysteresis that affects the area under the stress-strain curve may occur, the total displacement during the force ramp-up and -down phases of isometric contractions differs only in sign (33).
Fig. 1.
Force tracing and artifacts from magnetic field gradients during tag application and image acquisition. Image series began with 2 “dummy scans,” in which the imaging sequence was run but data were not acquired; the 2nd of these scans is shown. At ∼5 s into each contraction, spatial tags were applied and a series of 20 images were acquired as the subject maintained a steady force level, representing the position of the muscle during contraction. Each image acquisition required 70 ms, and acquisitions were separated by 0.26 s. At 10 s after the 1st set of tags was applied, a 2nd set of tags was applied. Then the subject relaxed and a 2nd set of 20 images, reflecting deformation of the tibialis anterior (TA) muscle due to relaxation, was acquired. Gray arrows indicate times of tag application; black arrows in middle and right sections of the trace indicate image analyzed for contraction and relaxation, respectively. Gray lines at 45% and 55% maximal voluntary contraction (MVC) indicate range of acceptable contraction intensities for tag application and contraction image acquisition. Gray lines at −5% and 5% MVC indicate acceptable range of forces for the image analyzed as the relaxation image.
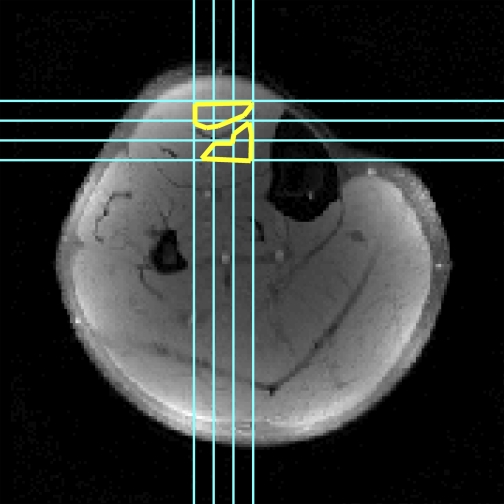
A total of 12–15 contractions were performed, with displacement encoding and/or slice acquisition in a different direction each time. The laboratory frame of reference is defined, such that, for the right leg of a supine subject, the +x direction of the imager points toward the medial aspect of the leg, the +y direction points anteriorly, and the +z direction points toward the head. In separate axial image acquisitions, displacement encoding occurred in the x, y, and xy directions. Sagittal image acquisitions were used to encode displacement in the z and yz directions. For displacement encoding in the xz direction, coronal image acquisitions were performed. Three separate contractions were required when sagittal and coronal images were acquired, with one slice acquired per contraction. The three slices were sufficient to image the entire region of muscle in line with the aponeurosis (Fig. 2).
Fig. 2.
Axial structural image illustrating locations of sagittal and coronal slices (blue lines) and regions of interest (ROIs, yellow lines). Mean linear strains were calculated for each direction in ROIs and used to form the strain tensor; mean signals in the ROI from each of the diffusion-weighted images and the nondiffusion weighted image were used to calculate the diffusion tensor.
Data Analysis
Force.
Unfiltered force data acquired during each contraction (Fig. 1) were analyzed to determine the contraction intensities at which the tags were applied and imaged. Magnetic field gradient switching caused artifacts in the force data, allowing the force during tag application and image acquisition to be determined as the average of the pre- and postartifact forces. The first image following application of the first set of tags was used to reflect the contracted state. The first image acquisition in which the force was within 5% of the postcontraction baseline was used to reflect the relaxed state.
Structural MRI.
Image analysis was performed using Matlab version 7.6.0 (Mathworks, Natick, MA). Regions of interest (ROIs) in the superficial and deep compartments of the central TA were defined in axial structural images near the aponeurosis and excluded voxels that contained signals from both compartments, resolved connective tissues, and/or blood vessels. The same ROI was used for DT-MRI and spatial-tagging data analysis. Accounting for slice offsets and thicknesses allowed identification of the corresponding positions in sagittal and coronal images (Fig. 2).
DT-MRI.
The diffusion-weighted images were registered to the b = 0 s/mm2 image using an affine transformation. The mean signal intensity (SI) in the superficial and deep ROIs was computed in the b = 0 s/mm2 image and each of the diffusion-weighted images. The diffusion tensor (D) was formed using a weighted least-squares algorithm, as described elsewhere (27). D was diagonalized, the principal diffusivities were computed as the eigenvalues of D and magnitude-sorted, and the D eigenvector matrix (V) was calculated. V represents the rotation of the muscle fibers from the laboratory frame of reference. The eigenvectors corresponding to the first, second, and third eigenvalues of V are denoted  ,
, 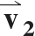 , and
, and 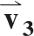 , respectively.
, respectively.
Spatially tagged MRI.
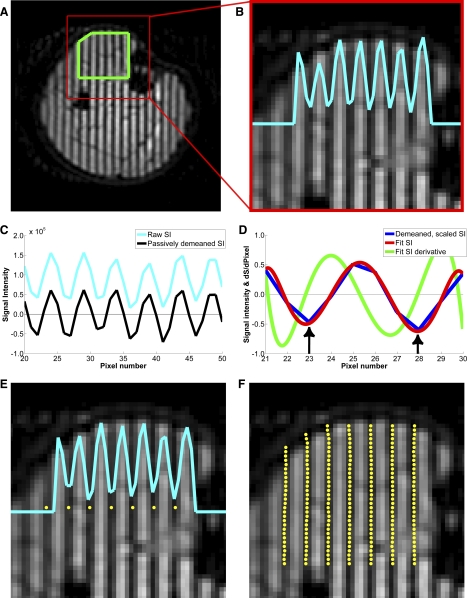
Manual determination of spatial tag location is time-consuming and subjective and may lead to uncertainty if a distinct minimum in SI is not present between neighboring pixels. Therefore, a semiautomated method was developed and used to detect the tag positions. The method was based on fitting the SI data along lines perpendicular to the tags to a polynomial function and using an inflection in the derivative of this polynomial to detect local minima. These procedures are illustrated in Fig. 3.
Fig. 3.
Axial tagged images illustrating the semiautomated tag detection method. Central portion of the TA was defined in sagittal, coronal, and axial tagged images (A) and used to restrict subsequent analyses to this area. The raw signal intensity (SI) along lines perpendicular to the applied tags was measured (B). Raw SI data were passively demeaned (baseline D–C shift was subtracted) and scaled to ±1 (C). The 1st minimum was manually defined as the initial reference point (left arrow in D). Ten local data points along a line perpendicular to the tag were fitted to a 7th-order polynomial. Order of the polynomial was chosen, because a 7th-order polynomial minimized residual errors between the fit and the demeaned and scaled SI data while not producing extraneous minima. The next minimum in SI was identified as the inflection point of the derivative of the fitted SI values (right arrow in D). This pixel index was recorded and defined as the next reference point; locations of subsequent tags in that line were determined in the same manner. Steps described for B–D were repeated for E and F. In E, the 1st minimum was used as the initial reference point. Final tag positions were plotted on the tagged image; any erroneously placed tags were identified by visual inspection and corrected (F).
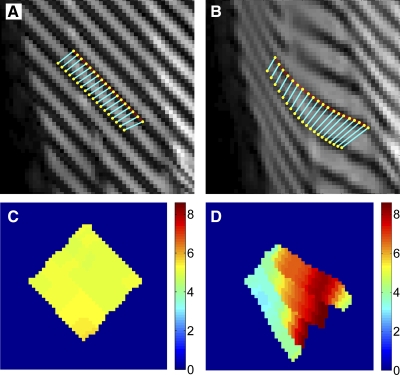
The intertag distance (d) was measured between corresponding points on adjacent tags. For tags applied parallel to a cardinal axis of the image, d was measured along the row or column connecting corresponding points. For tags applied obliquely to a cardinal axis of the image, additional processing was required to measure d. A line (a 1st-order polynomial for images acquired during the contraction and a 5th-order polynomial for images acquired during relaxation) was fitted to the detected tag positions and interpolated at an initial density of four points per voxel using low-pass interpolation. The corresponding points between two adjacent lines of tags were identified using a robust point-matching (RPM) algorithm (7). RPM iteratively identifies the closest point match between two lines and then optimizes the match using a nonrigid transform. The nonrigid transform was constrained, such that corresponding points on the neighboring lines of tags did not overlap the previous or subsequent pair of corresponding points. A salient advantage of RPM is its superior tolerance to noise and outliers resulting from errors in tag identification. Sample curve-matching results are presented in Fig. 4, A and B.
Fig. 4.
Sample curve-matching data during contraction (A) and relaxation (B) and the corresponding distance maps (C and D). After tags were detected, a 1st-order (contraction images) or 5th-order (relaxation images) polynomial was fitted to the detected tags in neighboring tag lines. A robust point-matching algorithm was used to determine the corresponding points on the lines. Distance between the points was measured using the Pythagorean theorem and mapped for visualization of tag distances (C and D). Contraction distance map (C) was homogeneous, as the applied tag distance was 5.08 pixels (7.1 mm). In the relaxation distance map (D), there is intercompartmental heterogeneity in the detected tag distance, as the muscle nonuniformly deformed during relaxation. These data were combined with those from the other tagging directions by axial reformatting of all data.
For each tagging direction, d was calculated using the Pythagorean theorem and plotted; sample results for a sagittal slice are shown in Fig. 4, C and D. For sagittal and coronal images, the data were also plotted in an axially reformatted image. For each tagging direction, the mean value for d in the ROI was measured and the strain (ε) was calculated as
| 1 |
where the subscripts c and r indicate the contraction and relaxation tag distances, respectively. Defined this way, a negative strain would indicate that the muscle shortened during contraction and elongated during relaxation. For each of the six tagging directions, the mean strain was calculated in the same ROIs that were used to calculate D. These six linear strains were used to create a strain tensor (E), defined as
| 2 |
E was diagonalized, the principal strains were computed as the eigenvalues of E and magnitude-sorted, and the strain tensor eigenvector matrix (U) was calculated. U represents the rotation of the strain tensor from the laboratory frame of reference.
The first and second eigenvalues of E contained one negative and one positive value; the third eigenvalue was always approximately zero (see results). Since the first eigenvalue was not consistently positive or negative, the largest negative eigenvalue and the largest positive eigenvalue were grouped together for subsequent analysis and are described below as the negative and positive principal strains (εN and εP, respectively). The eigenvectors corresponding to εN and εP are denoted 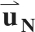 and
and 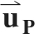 , respectively.
, respectively.
Comparison of the diffusion and strain tensors.
Descriptive and comparative analyses of the orientations of D and E were performed. Descriptive analyses for D included calculation of the elevation and azimuth angles of  ,
, 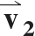 , and
, and 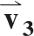 . As defined here, the elevation angle is a vector's angle above or below the xy (axial anatomic) plane and the azimuth angle is the polar angle within the xy plane. Elevation angles were calculated as the complement angle of cos−1(
. As defined here, the elevation angle is a vector's angle above or below the xy (axial anatomic) plane and the azimuth angle is the polar angle within the xy plane. Elevation angles were calculated as the complement angle of cos−1( ·ẑ), where ẑ is a unit vector in the +z direction. Azimuth angles are presented using the conventions that an angle between 0 and +180° reflects a rotation of the eigenvector from the +x-axis toward or past the −y-axis (i.e., positioned posteriorly to the left-right axis of the body) and an angle between 0 and −180° reflects a rotation of the eigenvector from the +x-axis toward or past the +y-axis (i.e., positioned anteriorly to the left-right axis of the body). The elevation and azimuth angles for
·ẑ), where ẑ is a unit vector in the +z direction. Azimuth angles are presented using the conventions that an angle between 0 and +180° reflects a rotation of the eigenvector from the +x-axis toward or past the −y-axis (i.e., positioned posteriorly to the left-right axis of the body) and an angle between 0 and −180° reflects a rotation of the eigenvector from the +x-axis toward or past the +y-axis (i.e., positioned anteriorly to the left-right axis of the body). The elevation and azimuth angles for 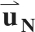 and
and 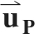 were also calculated. The angular deviation between
were also calculated. The angular deviation between 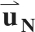 and
and  (θE−D) was calculated as cos−1(
(θE−D) was calculated as cos−1(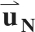 ·
· ).
).
Statistical Analysis
The accuracy and precision of the tag detection method were measured by constructing a 95% confidence interval (CI) around dc and calculating the coefficient of variation (CV) of dc, respectively. To test the hypothesis that the principal shortening direction would differ from the fiber direction, a 95% CI was constructed around θE−D. Also the elevation and azimuth angles of  and
and 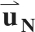 were compared using a two-tailed, paired Student's t-test. Two-tailed, paired Student's t-tests were also used to compare the elevation and azimuth angles of
were compared using a two-tailed, paired Student's t-test. Two-tailed, paired Student's t-tests were also used to compare the elevation and azimuth angles of 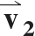 and
and 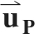 . These comparisons were made separately for each muscle compartment. Intercompartmental comparisons of the mean values for the diffusivities, θE−D, εN, and εP were made using two-tailed, paired Student's t-tests. Data are presented as means ± SE.
. These comparisons were made separately for each muscle compartment. Intercompartmental comparisons of the mean values for the diffusivities, θE−D, εN, and εP were made using two-tailed, paired Student's t-tests. Data are presented as means ± SE.
RESULTS
Force
The mean MVC force was 467.0 ± 54.0 N. The relative contraction intensity was 49.4 ± 0.6% MVC during the first tag application and 49.5 ± 0.6% MVC during acquisition of the contraction image. The relative contraction intensity was 49.6 ± 0.9% MVC during the second tag application and 0.5 ± 1.1% MVC during acquisition of the relaxation image. The image analyzed as the relaxation image was between the 1st and 7th dynamic image; the tags were detectable through the 10th image of the dynamic image series.
Spatial-Tagging Data
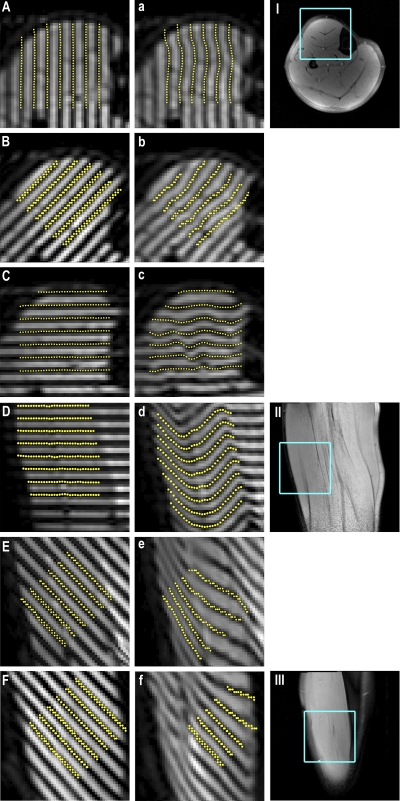
Figure 5 shows spatially tagged images acquired during contraction and relaxation and the corresponding structural images. The axial contraction (Fig. 5, A–C) and relaxation (Fig. 5, a–c) images illustrate displacement encoding in the x, xy, and y directions; the corresponding structural image is shown in Fig. 5I. The sagittal images illustrate displacement encoding in the z direction (Fig. 5, D and d) and the yz direction (Fig. 5, E and e); the sagittal structural image is shown in Fig. 5II. Figure 5, F and f, shows coronal images with displacement encoding in the xz direction; the structural image is shown in Fig. 5III.
Fig. 5.
Left column: tagged images with displacement encoding in the x (A), xy (B), y (C), z (D), yz (E), and xz (F) directions, acquired in the contracted state. Middle column: corresponding images acquired following relaxation. Yellow points indicate automatically detected tag positions. Right column: corresponding axial (I), sagittal (II), and coronal (III) anatomic images, with displayed regions in the right and middle columns outlined in blue.
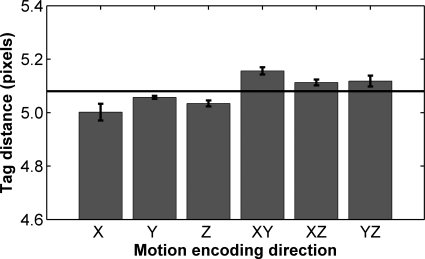
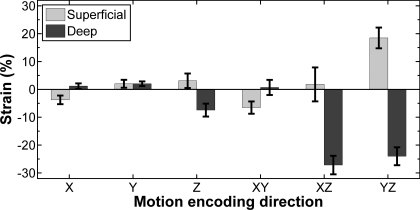
Figure 6 shows accuracy and precision data for all directions of tag application. Averaged over all directions, the method had a mean tag distance of 5.08 pixels (7.10 mm), corresponding to a relative error of <0.01% and a CV of 1.4%. For each displacement-encoding direction, the 95% CI of detected tag distances contained the applied tag distance. The average linear strains in the deep and superficial compartments in each displacement-encoding direction are shown in Fig. 7.
Fig. 6.
Average detected tag distance in contraction images (n = 7). Horizontal line indicates known tag distance of 5.08 pixels; error bars indicate SE. Over all directions, the tag position detection method had a relative error of 0.5% with a coefficient of variation of 1.4%. Note that n = 6 for z and yz directions because of an error in specifying the tag distance in 1 subject (5.0, rather than 5.08, pixels). Mean relative error and precision were unchanged by exclusion of these data.
Fig. 7.
Average linear strains in superficial and deep compartments of the TA for each direction. Error bars indicate SE. Linear strains were highly variable, with qualitative intercompartmental differences in the nature of the strain (shortening or elongation).
Diffusion Tensor and Strain Tensor Results
The first, second, and third eigenvalues of D in the deep compartment of the muscle did not differ from their respective values in the superficial compartment (P = 0.62, 0.33, and 0.91, respectively); the mean values for the whole muscle were 2.02 ± 0.02, 1.75 ± 0.03, and 1.49 ± 0.02 × 10−5 cm2/s. The elevation and azimuth angles for  ,
, 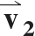 , and
, and 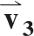 are given in Table 1 and illustrated in Fig. 8.
are given in Table 1 and illustrated in Fig. 8.
Table 1.
Angles of elevation and azimuth for the eigenvectors of D and the negative and positive principal strains of E
| Compartment | Angle | |||||
|---|---|---|---|---|---|---|
| Deep | Elevation | 69.3 ± 2.3 | 48.2A ± 1.5 | −20.2 ± 2.3 | −41.4B ± 1.6 | −0.6 ± 1.7 |
| Azimuth | 34.8 ± 4.7 | 40.5 ± 6.2 | 37.1 ± 3.8 | 42.6 ± 5.6 | −53.1 ± 3.6 | |
| Superficial | Elevation | 66.1 ± 6.6 | 40.4A ± 1.7 | −21.4 ± 6.7 | −42.8B ± 2.0 | −0.9 ± 2.7 |
| Azimuth | −144.9 ± 7.7 | −105.8 ± 18.3 | −135.7 ± 3.7 | −91.6C ± 16.8 | −44.7 ± 2.7 |
All angles are given in degrees. Superscripts denote levels of statistical significance. Figure 8 provides a graphical illustration of the data for εN, εP,  ,
, 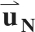 ,
, 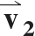 , and
, and 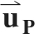 and a depiction of the sign conventions for the elevation and azimuth angles.
and a depiction of the sign conventions for the elevation and azimuth angles.
P < 0.001 vs. mean elevation angle for  ;
;
P < 0.001 vs. mean elevation angle for 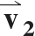 ;
;
P < 0.001 vs. mean azimuth angle for 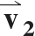 .
.
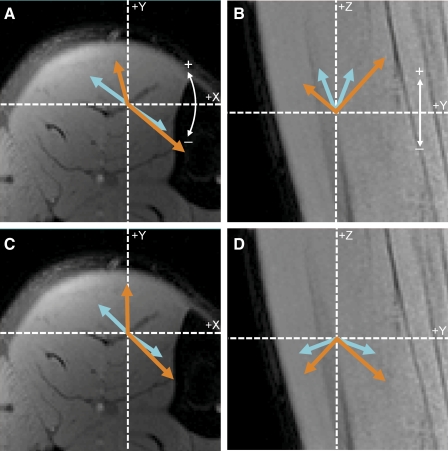
Fig. 8.
Average eigenvalue and eigenvector data for D (blue arrows) and E (orange arrows). Laboratory frame of reference is indicated by dashed lines; white arrows indicate angle conventions for the eigenvectors. Direction of the arrows represents azimuth angles (A and C) or elevation angles (B and D); length of the arrows represents eigenvalue's magnitude. Left and right arrows represent data from the superficial and deep compartments, respectively. A and B: data for  and
and 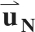 . Elevation angles of
. Elevation angles of  and
and 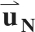 differed significantly in both compartments (P < 0.001), but azimuth angles did not (P = 0.50 and 0.11 for deep and superficial compartments, respectively). C and D: azimuth and elevation angles, respectively,
differed significantly in both compartments (P < 0.001), but azimuth angles did not (P = 0.50 and 0.11 for deep and superficial compartments, respectively). C and D: azimuth and elevation angles, respectively, 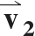 and
and 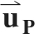 . Azimuth angles of
. Azimuth angles of 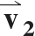 and
and 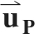 did not differ significantly in the deep compartment (P < 0.05) but differed significantly in the superficial compartment (P < 0.05). Elevation angles of
did not differ significantly in the deep compartment (P < 0.05) but differed significantly in the superficial compartment (P < 0.05). Elevation angles of 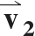 and
and 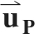 differed significantly in both compartments (P < 0.001).
differed significantly in both compartments (P < 0.001).
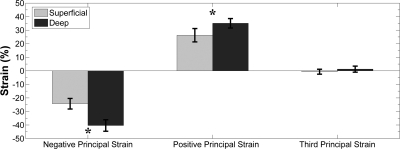
In every subject, the first two principal strains contained one large-magnitude, negative value and one large-magnitude, positive value; the third eigenvalue of E was near zero. Figure 9 shows the three principal strains in the superficial and deep compartments of the TA. εN and εP in the deep compartment were greater in magnitude than the corresponding values in the superficial compartment (P = 0.018 and 0.048, respectively).
Fig. 9.
Positive and negative principal strains in superficial and deep compartments of the TA muscle. Both strains were larger in magnitude in the deep compartment than in the superficial compartment: *P = 0.018 and 0.049 for negative and positive strains, respectively. Third principal strain did not differ significantly from zero in either compartment.
In both compartments, the direction of εN was closest to, but deviated from, the fiber direction. In the deep compartment, the mean value of θE−D was 24.0 ± 1.7°; its 95% CI was (19.8–28.2°). In the superficial compartment, θE−D was 39.8 ± 6.8°; its 95% CI was (23.1–56.5°). This value is greater than the corresponding value for the deep compartment (P = 0.049). In both compartments, the elevation angle for 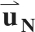 differed significantly from the elevation angle for
differed significantly from the elevation angle for  , but these vectors' azimuth angles did not differ (Table 1, Fig. 8). Among
, but these vectors' azimuth angles did not differ (Table 1, Fig. 8). Among  ,
, 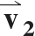 , and
, and 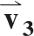 , the direction of εP was always most closely aligned to
, the direction of εP was always most closely aligned to 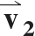 . In each compartment, the elevation angle for
. In each compartment, the elevation angle for 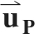 differed significantly from the elevation angle for
differed significantly from the elevation angle for 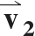 , but the vectors' azimuth angles did not differ (Table 1, Fig. 8).
, but the vectors' azimuth angles did not differ (Table 1, Fig. 8).
DISCUSSION
This is the first study of which we are aware that has measured the resting architecture and contraction-induced strain patterns in an extremity muscle using methods that have 3D sensitivity and that share an absolute, fixed frame of reference. Below, we will show that the DT-MRI and spatial-tagging MRI methods are sufficiently accurate and precise for measuring these elements of muscle structure and function. Then we will argue that the rotation of E from D in the deep compartment of the muscle results from intramuscle heterogeneity in muscle architecture. We also offer tentative explanations for the differences in the strain patterns in the two muscle compartments.
Accuracy and Precision of Architecture and Strain Measurements
We previously used numerical (10) and experimental (21) methods to investigate the noise sensitivity and repeatability of muscle architecture measurements using DT-MRI. For our fiber-tracking protocols, the within-day 95% CI of pennation angle measurements is ±8° (21). However, these measurements averaged data from only 5 DT-MRI data points (resulting in less noise reduction than the larger ROI sizes used in the present study) and were based on diffusion measurements in 10 noncollinear directions (rather than the 15 directions used in the present study). Also, pennation angle measurements by DT-MRI-based fiber tracking require digitization and shape modeling of the aponeurosis of fiber insertion, resulting in some error propagation; for the signal-to-noise ratio levels observed in the present study (∼80–100), the variability in fiber orientation measurements due to noise alone is SD ≅ 8° for single voxels and SD ≅ 3° for ROIs (10). Thus we expect the contribution of experimental error to the 95% CI for the fiber orientation measurements made in the present study to be significantly less than the ±8° reported previously (21). Within each of the TA's compartments, the fiber orientations in the laboratory frame of reference are consistent throughout the muscle (28). Therefore, we further conclude that the use of a single-slice, compartmental ROI-based approach for measurement of the fiber orientation did not reduce any natural variation in the data, while it increased the accuracy and precision of the fiber orientation estimates.
Regarding the accuracy and precision requirements for the strain measurements, the expected linear strain during submaximal contractions is 4–5% along the aponeurosis and ∼1.5% in the external tendon (16, 34). The expected strains are higher in the muscle proper (∼50%) than for the aponeurosis and tendon but vary along muscle fascicles (43, 55). These small strains in the connective tissues and the spatial variability in strain in the muscular tissue create the need for high accuracy and precision in linear strain measurements. When using multiple measurements to assess 3D strain, error propagation should also be considered. Other potential sources of error are motion during the image acquisition period and losses of natural variability in strain patterns due to averaging of the data from the entire ROI.
First, we note that the tag distances measured by the semiautomated detection method did not differ significantly from their known values and had a mean CV of 1.4% (Fig. 6); error propagation suggests that the contribution of tag detection error to total CV in E is 3.5% of the mean values for the principal strains (25–40%). Therefore, our method provided accurate and precise measurements of E. Regarding the possibility of motion during the image acquisition period, we note first that the image acquisition time for these single-shot images was only 70 ms. Also, objective criteria were established to ensure that the images that were analyzed were acquired while the muscle was stationary. Finally, single-shot imaging allowed us to collect all the necessary data over 12–15 contractions per subject, rather than the hundreds that would have been required with multishot approaches. As a result, the variability in contraction intensity at the time of tag application and in the contraction and relaxation images was very low, with 95% CIs of less than ±3% of the MVC force. We did not deem it necessary to analyze a second image in each state (contracted or relaxed) because of the high accuracy and precision levels already observed and because the recovery of longitudinal magnetization as the dynamic image series continues progressively reduces the contrast between tagged and untagged structures, making tag detection less precise. Nor did we deem it necessary to analyze all the adjacent tags, as an analysis of variance performed on adjacent intertag distances in the z direction yielded no significant differences between the neighboring intertag distances and d in the contracted and relaxed states (P = 0.86 and 0.82 for superficial and deep compartments, respectively). Finally, the ROI-based approach employed in the calculation of strain likely served to decrease noise effects in a manner similar to the analysis of the DT-MRI data. The ROI approach is justified, because the ROIs were specified very close to the aponeurosis in a 7.1-mm-thick slice, meaning that they were unlikely to have been influenced by along-fascicle (43) or along-aponeurosis (16, 38, 43, 55) spatial heterogeneity in strain.
Relationship of Strain Patterns to Muscle Fiber Architecture
We begin by noting some general features of the 3D strain patterns. First, for some of the linear strain directions, there was considerable variability in the magnitude and even the nature (shortening or elongation) of the strain between subjects. However, formation and diagonalization of a 3D strain tensor revealed a consistent, planar pattern of strain development characterized by one shortening direction and one elongation direction [an elongation direction being a consequence of nearly complete volume preservation during contraction (3) and similar to a recent finding based on multiplanar ultrasound imaging (30)]. Also it is likely that there are active and passive components to the fibers' motion during a submaximal muscle contraction, as only a subset of the TA's motor units are recruited during submaximal contractions (9), motor units' fibers are distributed throughout the muscle (5), and fibers are linked by a shared intramuscular connective tissue network (45) that would tend to couple the motion of adjacent fiber and cause these active and passive components to be similar in magnitude and direction.
The high strains that we observed were similar in magnitude to those previously observed for contracting muscle (30, 43, 55) and were larger in magnitude in the deep compartment than in the superficial compartment. One possible explanation for the intercompartmental differences in εN and εP relates to the structural properties of the components of the deep and superficial compartments of the TA. Because the pennation angles and fascicle lengths of the two compartments are similar (21, 23, 28, 32) and both sets of fibers share a common aponeurosis and tendon of insertion, these architectural features are unlikely to explain the differences in strain patterns between the compartments. However, the material properties of the tissues of fiber origin differ. The superficial compartment muscle fibers originate from a more compliant structure [the crural fascia, with an elastic modulus of ∼280 MPa (48)] than the deep compartment fibers [the tibia, with an elastic modulus of ∼18 GPa (36)]. During contraction, the compliant crural fascia may permit the superficial compartment and central aponeurosis to be displaced medially toward the noncompliant tibia, leading to higher-magnitude strains in the deep compartment and intercompartmental differences in the signs of εxz and εyz (Fig. 7). An alternative or additional explanation lies in the separate neural control that exists over the compartments of the TA (49); this explanation has been posited to lead to different levels of neural activation in the two compartments during submaximal contractions (1). These proposed explanations are not mutually exclusive and are amenable to testing using models that account for differences in material properties of the tissue of fiber origin and activation levels. In either case, a consequence of the differences in strain magnitude would be the development of shear strain within the aponeurosis itself.
Regarding the strain directions, a consistent and important finding was that 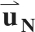 was not collinear with
was not collinear with  and, thus, the fiber orientation; this indicates the presence of shear strain in the muscle tissue. We consider first the possibility that this misalignment resulted from the fact that DT-MRI data were acquired from relaxed muscle, while the strain data reflect the deformation that occurs during the transition to and from the contracted state. It is well known that resting and contracting muscle architecture differs; for example, Maganaris and Baltzopoulos (32) found that, during MVC, the mean pennation angle increased from 11° to 20° in the deep compartment and from 14° to 19° in the superficial compartment of the TA. It is therefore conceivable that
and, thus, the fiber orientation; this indicates the presence of shear strain in the muscle tissue. We consider first the possibility that this misalignment resulted from the fact that DT-MRI data were acquired from relaxed muscle, while the strain data reflect the deformation that occurs during the transition to and from the contracted state. It is well known that resting and contracting muscle architecture differs; for example, Maganaris and Baltzopoulos (32) found that, during MVC, the mean pennation angle increased from 11° to 20° in the deep compartment and from 14° to 19° in the superficial compartment of the TA. It is therefore conceivable that 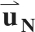 would be collinear with
would be collinear with  in the contracted state and that the misalignment was due only to the change in fiber orientation. However, the subjects in our study performed a 50% MVC; by linear interpolation, a 3–5° change in pennation angle would be expected. As this change in pennation angle is much less than θE−D (24–40°), the deviation between
in the contracted state and that the misalignment was due only to the change in fiber orientation. However, the subjects in our study performed a 50% MVC; by linear interpolation, a 3–5° change in pennation angle would be expected. As this change in pennation angle is much less than θE−D (24–40°), the deviation between 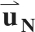 and
and  could not have been due to the change in fiber orientation alone. Rather, we argue that the rotation of
could not have been due to the change in fiber orientation alone. Rather, we argue that the rotation of 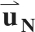 away from
away from  is more likely to have resulted from heterogeneity in fiber length and pennation [such that pennation angles tend to be larger, and fibers tend to be shorter, in the superior portion than in the inferior portion of the TA (20, 21, 23, 28)]. The results of the model of Blemker et al. (4) suggest that architectural heterogeneity could have contributed to the rotation of
is more likely to have resulted from heterogeneity in fiber length and pennation [such that pennation angles tend to be larger, and fibers tend to be shorter, in the superior portion than in the inferior portion of the TA (20, 21, 23, 28)]. The results of the model of Blemker et al. (4) suggest that architectural heterogeneity could have contributed to the rotation of 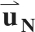 away from
away from  ; Zhong et al. (55) reached a similar conclusion after observing that, during minimally loaded shortening contractions, the direction of the principal shortening is noncollinear to the longitudinal axis of the biceps brachii muscle (the presumptive fiber direction). The present results confirm and extend these observations by also elucidating the nature of the rotation of E from D for the deep compartment: the azimuth angles of the eigenvectors were aligned, but the elevation angles were not (Fig. 8, Table 1).
; Zhong et al. (55) reached a similar conclusion after observing that, during minimally loaded shortening contractions, the direction of the principal shortening is noncollinear to the longitudinal axis of the biceps brachii muscle (the presumptive fiber direction). The present results confirm and extend these observations by also elucidating the nature of the rotation of E from D for the deep compartment: the azimuth angles of the eigenvectors were aligned, but the elevation angles were not (Fig. 8, Table 1).
One possible explanation for the role of architectural heterogeneity in causing the misalignment of 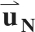 and
and  is as follows. Let us assume a population of different-length fibers that undergo the same relative shortening. The result will be spatial variability in the absolute length change of the fibers and, thus, a deviation of the direction of the ensemble-averaged strain away from the fiber direction and toward the longest fibers (inferiorly, in the case of the TA). This would be permitted to occur by the interfiber connections formed by the intramuscular connective tissue network (45). Similarly, heterogeneity in pennation angle would cause forces to be applied to the aponeurosis with spatially varying orientations with respect to the local tangent to the aponeurosis; this would cause spatially variable aponeurosis motion.
is as follows. Let us assume a population of different-length fibers that undergo the same relative shortening. The result will be spatial variability in the absolute length change of the fibers and, thus, a deviation of the direction of the ensemble-averaged strain away from the fiber direction and toward the longest fibers (inferiorly, in the case of the TA). This would be permitted to occur by the interfiber connections formed by the intramuscular connective tissue network (45). Similarly, heterogeneity in pennation angle would cause forces to be applied to the aponeurosis with spatially varying orientations with respect to the local tangent to the aponeurosis; this would cause spatially variable aponeurosis motion.
In addition to the nearest alignment of 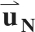 to
to  ,
, 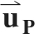 was aligned closely to
was aligned closely to 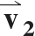 . Also, using DT-MRI and phase-contrast MRI, Dou et al. (13) analyzed the architecture and strain patterns in the heart and observed a close correspondence between the orientations of E and D. In the heart, as in skeletal muscle,
. Also, using DT-MRI and phase-contrast MRI, Dou et al. (13) analyzed the architecture and strain patterns in the heart and observed a close correspondence between the orientations of E and D. In the heart, as in skeletal muscle,  indicates the fiber direction (24, 40); however,
indicates the fiber direction (24, 40); however, 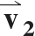 and
and 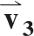 also have identified structural bases in the heart, with
also have identified structural bases in the heart, with 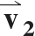 reflecting direction of myocardial sheets and
reflecting direction of myocardial sheets and 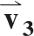 reflecting cross-fiber diffusion perpendicular to the sheets (41). The small intersubject variability in the elevation and azimuth angles of
reflecting cross-fiber diffusion perpendicular to the sheets (41). The small intersubject variability in the elevation and azimuth angles of 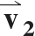 and
and 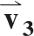 , the close alignment of
, the close alignment of 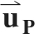 to
to 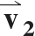 (Table 1, Fig. 8), and the different behaviors of the second and third eigenvalues of D during muscle elongation (18) and muscle damage (19) collectively argue that there may be distinct structural bases for the second and third eigenvalues of D (and their eigenvectors) in skeletal muscle as well. While several models have been proposed (17, 25), this structural basis has yet to be definitively identified experimentally. Therefore, while there is a clear relationship between the orientations of
(Table 1, Fig. 8), and the different behaviors of the second and third eigenvalues of D during muscle elongation (18) and muscle damage (19) collectively argue that there may be distinct structural bases for the second and third eigenvalues of D (and their eigenvectors) in skeletal muscle as well. While several models have been proposed (17, 25), this structural basis has yet to be definitively identified experimentally. Therefore, while there is a clear relationship between the orientations of 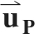 and
and 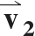 , suggesting that some higher-order aspect of muscle architecture may determine the direction of principal elongation, the details of why this relationship exists are unclear and merit additional study.
, suggesting that some higher-order aspect of muscle architecture may determine the direction of principal elongation, the details of why this relationship exists are unclear and merit additional study.
Perspectives and Significance
The principal contribution of this work is the quantitative characterization of the relationship between the magnitude and direction of negative and positive strains and the underlying muscle architecture during isometric contraction in vivo. Muscles affected by diseases such as Duchenne muscular dystrophy experience architectural disruption due to fat infiltration and muscle fiber degeneration and regeneration processes and may have decreased lateral force transmission because of the mutation or absence of dystroglycan complex proteins. These disruptions to muscle architecture and force transmission, together with the strong relationship between strain development and architecture observed in the present study, suggest that architectural derangement may be in part responsible for decreased stress development during isometric twitch and tetanic (39) contractions observed in dystrophic skeletal muscle and the decreased strain development observed in dystrophic cardiac muscle (29).
GRANTS
This study was supported by National Institutes of Health Grants R01 AR-050101 and UL1 RR-024975.
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the authors.
ACKNOWLEDGMENTS
We thank Dr. Anneriet Heemskerk, Dr. Amanda Wake, and Prof. Michael Miga for helpful comments and the subjects for their participation.
Footnotes
In one subject, a data entry error resulted in a tag spacing of 7.0 mm in the images sensitized to motion in the y and yz directions. Because strain reflects relative, rather than absolute, length changes and this error was equally represented in the images used to represent the contracted and relaxed states, this error did not affect calculation of E.
REFERENCES
- 1. Akima H, Ito M, Yoshikawa H, Fukunaga T. Recruitment plasticity of neuromuscular compartments in exercised tibialis anterior using echo-planar magnetic resonance imaging in humans. Neurosci Lett 296: 133–136, 2000 [DOI] [PubMed] [Google Scholar]
- 2. Azizi E, Brainerd EL. Architectural gear ratio and muscle fiber strain homogeneity in segmented musculature. J Exp Zool A Ecol Genet Physiol 307: 145–155, 2007 [DOI] [PubMed] [Google Scholar]
- 3. Baskin RJ, Paolini PJ. Volume change and pressure development in muscle during contraction. Am J Physiol 213: 1025–1030, 1967 [DOI] [PubMed] [Google Scholar]
- 4. Blemker SS, Pinsky PM, Delp SL. A 3D model of muscle reveals the causes of nonuniform strains in the biceps brachii. J Biomech 38: 657–665, 2005 [DOI] [PubMed] [Google Scholar]
- 5. Bodine SC, Garfinkel A, Roy RR, Edgerton VR. Spatial distribution of motor unit fibers in the cat soleus and tibialis anterior muscles: local interactions. J Neurosci 8: 2142–2152, 1988 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Brainerd EL, Azizi E. Muscle fiber angle, segment bulging and architectural gear ratio in segmented musculature. J Exp Biol 208: 3249–3261, 2005 [DOI] [PubMed] [Google Scholar]
- 7. Chui H, Rangarajan A. A new point matching algorithm for non-rigid registration. Comp Vis Image Understand 89: 114–141, 2003 [Google Scholar]
- 8. Cleveland GG, Chang DC, Hazlewood CF, Rorschach HE. Nuclear magnetic resonance measurement of skeletal muscle: anisotropy of the diffusion coefficient of the intracellular water. Biophys J 16: 1043–1053, 1976 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Connelly DM, Rice CL, Roos MR, Vandervoort AA. Motor unit firing rates and contractile properties in tibialis anterior of young and old men. J Appl Physiol 87: 843–852, 1999 [DOI] [PubMed] [Google Scholar]
- 10. Damon BM. Effects of image noise in muscle diffusion tensor (DT)-MRI assessed using numerical simulations. Magn Reson Med 60: 934–944, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Damon BM, Ding Z, Anderson AW, Freyer AS, Gore JC. Validation of diffusion tensor MRI-based muscle fiber tracking. Magn Reson Med 48: 97–104, 2002 [DOI] [PubMed] [Google Scholar]
- 12. Delp SL, Loan JP, Hoy MG, Zajac FE, Topp EL, Rosen JM. An interactive graphics-based model of the lower extremity to study orthopaedic surgical procedures. IEEE Trans Biomed Eng 37: 757–767, 1990 [DOI] [PubMed] [Google Scholar]
- 13. Dou J, Tseng WY, Reese TG, Wedeen VJ. Combined diffusion and strain MRI reveals structure and function of human myocardial laminar sheets in vivo. Magn Reson Med 50: 107–113, 2003 [DOI] [PubMed] [Google Scholar]
- 14. Drace JE, Pelc NJ. Measurement of skeletal muscle motion in vivo with phase-contrast MR imaging. J Magn Reson Imaging 4: 157–163, 1994 [DOI] [PubMed] [Google Scholar]
- 15. Drace JE, Pelc NJ. Skeletal muscle contraction: analysis with use of velocity distributions from phase-contrast MR imaging. Radiology 193: 423–429, 1994 [DOI] [PubMed] [Google Scholar]
- 16. Finni T, Hodgson JA, Lai AM, Edgerton VR, Sinha S. Nonuniform strain of human soleus aponeurosis-tendon complex during submaximal voluntary contractions in vivo. J Appl Physiol 95: 829–837, 2003 [DOI] [PubMed] [Google Scholar]
- 17. Galban CJ, Maderwald S, Uffmann K, de Greiff A, Ladd ME. Diffusive sensitivity to muscle architecture: a magnetic resonance diffusion tensor imaging study of the human calf. Eur J Appl Physiol 93: 253–262, 2004 [DOI] [PubMed] [Google Scholar]
- 18. Hatakenaka M, Matsuo Y, Setoguchi T, Yabuuchi H, Okafuji T, Kamitani T, Nishikawa K, Honda H. Alteration of proton diffusivity associated with passive muscle extension and contraction. J Magn Reson Imaging 27: 932–937, 2008 [DOI] [PubMed] [Google Scholar]
- 19. Heemskerk A, Strijkers G, Drost M, van Bochove G, Nicolay K. Skeletal muscle degeneration and regeneration following femoral artery ligation in the mouse: diffusion tensor imaging monitoring. Radiology 243: 413–421, 2007 [DOI] [PubMed] [Google Scholar]
- 20. Heemskerk AM, Sinha TK, Wilson KJ, Ding Z, Damon BM. Quantitative assessment of DTI-based muscle fiber tracking and optimal tracking parameters. Magn Reson Med 61: 467–472, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Heemskerk AM, Sinha TK, Wilson KJ, Ding Z, Damon BM. Repeatability of DTI-based skeletal muscle fiber tracking. NMR Biomed 23: 294–303, 2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Heemskerk AM, Strijkers GJ, Vilanova A, Drost MR, Nicolay K. Determination of mouse skeletal muscle architecture using three-dimensional diffusion tensor imaging. Magn Reson Med 53: 1333–1340, 2005 [DOI] [PubMed] [Google Scholar]
- 23.Hiblar T, Bolson E, Hubka M, Sheehan F, Kushmerick M. Three dimensional ultrasound analysis of fascicle orientation in human tibialis anterior muscle enables analysis of macroscopic torque at the cellular level. In: Molecular and Cellular Aspects of Muscle Contraction, edited by Sugi H. New York: Springer, 2003, p. 635–645 [DOI] [PubMed] [Google Scholar]
- 24. Hsu EW, Muzikant AL, Matulevicius SA, Penland RC, Henriquez CS. Magnetic resonance myocardial fiber-orientation mapping with direct histological correlation. Am J Physiol Heart Circ Physiol 274: H1627–H1634, 1998 [DOI] [PubMed] [Google Scholar]
- 25. Karampinos D, King K, Sutton B, Georgiadis J. Myofiber ellipticity as an explanation for transverse asymmetry of skeletal muscle diffusion MRI in vivo signal. Ann Biomed Eng 37: 2532–2546, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Kinugasa R, Shin D, Yamauchi J, Mishra C, Hodgson JA, Edgerton VR, Sinha S. Phase-contrast MRI reveals mechanical behavior of superficial and deep aponeuroses in human medial gastrocnemius during isometric contraction. J Appl Physiol 105: 1312–1320, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Koay CG, Chang LC, Carew JD, Pierpaoli C, Basser PJ. A unifying theoretical and algorithmic framework for least squares methods of estimation in diffusion tensor imaging. J Magn Reson 182: 115–125, 2006 [DOI] [PubMed] [Google Scholar]
- 28. Lansdown DA, Ding Z, Wadington M, Hornberger JL, Damon BM. Quantitative diffusion tensor MRI-based fiber tracking of human skeletal muscle. J Appl Physiol 103: 673–681, 2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Li W, Liu W, Zhong J, Yu X. Early manifestation of alteration in cardiac function in dystrophin deficient mdx mouse using 3D CMR tagging. J Cardiovasc Magn Reson 11: 40, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Lopata RGP, van Dijk JP, Pillen S, Nillesen MM, Maas H, Thijssen JM, Stegeman DF, de Korte CL. Dynamic imaging of skeletal muscle contraction in three orthogonal directions. J Appl Physiol 109: 906–915, 2010 [DOI] [PubMed] [Google Scholar]
- 31. Maas H, Baan GC, Huijing PA, Yucesoy CA, Koopman BH, Grootenboer HJ. The relative position of EDL muscle affects the length of sarcomeres within muscle fibers: experimental results and finite-element modeling. J Biomech Eng 125: 745–753, 2003 [DOI] [PubMed] [Google Scholar]
- 32. Maganaris CN, Baltzopoulos V. Predictability of in vivo changes in pennation angle of human tibialis anterior muscle from rest to maximum isometric dorsiflexion. Eur J Appl Physiol Occup Physiol 79: 294–297, 1999 [DOI] [PubMed] [Google Scholar]
- 33. Maganaris CN, Paul JP. Hysteresis measurements in intact human tendon. J Biomech 33: 1723–1727, 2000 [DOI] [PubMed] [Google Scholar]
- 34. Maganaris CN, Paul JP. Load-elongation characteristics of in vivo human tendon and aponeurosis. J Exp Biol 203: 751–756, 2000 [DOI] [PubMed] [Google Scholar]
- 35. Maguire MA, Weaver TW, Damon BM. Delayed blood reoxygenation following maximum voluntary contraction. Med Sci Sports Exerc 39: 257–267, 2007 [DOI] [PubMed] [Google Scholar]
- 36. Nyman JS, Roy A, Tyler JH, Acuna RL, Gayle HJ, Wang X. Age-related factors affecting the postyield energy dissipation of human cortical bone. J Orthop Res 25: 646–655, 2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Osman NF, Kerwin WS, McVeigh ER, Prince JL. Cardiac motion tracking using CINE harmonic phase (HARP) magnetic resonance imaging. Magn Reson Med 42: 1048–1060, 1999 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Pappas GP, Asakawa DS, Delp SL, Zajac FE, Drace JE. Nonuniform shortening in the biceps brachii during elbow flexion. J Appl Physiol 92: 2381–2389, 2002 [DOI] [PubMed] [Google Scholar]
- 39. Quinlan JG, Johnson SR, McKee MK, Lyden SP. Twitch and tetanus in mdx mouse muscle. Muscle Nerve 15: 837–842, 1992 [DOI] [PubMed] [Google Scholar]
- 40. Scollan DF, Holmes A, Winslow R, Forder J. Histological validation of myocardial microstructure obtained from diffusion tensor magnetic resonance imaging. Am J Physiol Heart Circ Physiol 275: H2308–H2318, 1998 [DOI] [PubMed] [Google Scholar]
- 41. Scollan DF, Holmes A, Zhang J, Winslow RL. Reconstruction of cardiac ventricular geometry and fiber orientation using magnetic resonance imaging. Ann Biomed Eng 28: 934–944, 2000 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Scott SH, Engstrom CM, Loeb GE. Morphometry of human thigh muscles. Determination of fascicle architecture by magnetic resonance imaging. J Anat 182: 249–257, 1993 [PMC free article] [PubMed] [Google Scholar]
- 43. Shin DD, Hodgson JA, Edgerton VR, Sinha S. In vivo intramuscular fascicle-aponeuroses dynamics of the human medial gastrocnemius during plantarflexion and dorsiflexion of the foot. J Appl Physiol 107: 1276–1284, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Sinha S, Hodgson JA, Finni T, Lai AM, Grinstead J, Edgerton VR. Muscle kinematics during isometric contraction: development of phase contrast and spin tag techniques to study healthy and atrophied muscles. J Magn Reson Imaging 20: 1008–1019, 2004 [DOI] [PubMed] [Google Scholar]
- 45. Trotter JA, Purslow PP. Functional morphology of the endomysium in series fibered muscles. J Morphol 212: 109–122, 1992 [DOI] [PubMed] [Google Scholar]
- 46. Ward SR, Eng CM, Smallwood LH, Lieber RL. Are current measurements of lower extremity muscle architecture accurate? Clin Orthop Relat Res 467: 1074–1082, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47. Wickiewicz TL, Roy RR, Powell PL, Edgerton VR. Muscle architecture of the human lower limb. Clin Orthop Relat Res: 275–283, 1983 [PubMed] [Google Scholar]
- 48. William DT, Christof H, Ray V. The effects of elevated compartment pressure on tibial arteriovenous flow and relationship of mechanical and biochemical characteristics of fascia to genesis of chronic anterior compartment syndrome. J Vasc Surg 21: 810–817, 1995 [DOI] [PubMed] [Google Scholar]
- 49. Wolf SL, Kim JH. Morphological analysis of the human tibialis anterior and medial gastrocnemius muscles. Acta Anat (Basel) 158: 287–295, 1997 [DOI] [PubMed] [Google Scholar]
- 50. Young AA, Axel L, Dougherty L, Bogen DK, Parenteau CS. Validation of tagging with MR imaging to estimate material deformation. Radiology 188: 101–108, 1993 [DOI] [PubMed] [Google Scholar]
- 51. Yucesoy CA, Koopman BH, Baan GC, Grootenboer HJ, Huijing PA. Effects of inter- and extramuscular myofascial force transmission on adjacent synergistic muscles: assessment by experiments and finite-element modeling. J Biomech 36: 1797–1811, 2003 [DOI] [PubMed] [Google Scholar]
- 52. Yucesoy CA, Koopman BH, Huijing PA, Grootenboer HJ. Three-dimensional finite element modeling of skeletal muscle using a two-domain approach: linked fiber-matrix mesh model. J Biomech 35: 1253–1262, 2002 [DOI] [PubMed] [Google Scholar]
- 53. Zajac FE. Muscle and tendon: properties, models, scaling, and application to biomechanics and motor control. Crit Rev Biomed Eng 17: 359–411, 1989 [PubMed] [Google Scholar]
- 54. Zerhouni EA, Parish DM, Rogers WJ, Yang A, Shapiro EP. Human heart: tagging with MR imaging—a method for noninvasive assessment of myocardial motion. Radiology 169: 59–63, 1988 [DOI] [PubMed] [Google Scholar]
- 55. Zhong X, Epstein FH, Spottiswoode BS, Helm PA, Blemker SS. Imaging two-dimensional displacements and strains in skeletal muscle during joint motion by cine DENSE MR. J Biomech 41: 532–540, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]