Effects of maturation and acidosis on the chaos-like complexity of the neural respiratory output in the isolated brainstem of the tadpole, Rana esculenta

Abstract

Human ventilation at rest exhibits mathematical chaos-like complexity that can be described as long-term unpredictability mediated (in whole or in part) by some low-dimensional nonlinear deterministic process. Although various physiological and pathological situations can affect respiratory complexity, the underlying mechanisms remain incompletely elucidated. If such chaos-like complexity is an intrinsic property of central respiratory generators, it should appear or increase when these structures mature or are stimulated. To test this hypothesis, we employed the isolated tadpole brainstem model [Rana (Pelophylax) esculenta] and recorded the neural respiratory output (buccal and lung rhythms) of pre- (n = 8) and postmetamorphic tadpoles (n = 8), at physiologic (7.8) and acidic pH (7.4). We analyzed the root mean square of the cranial nerve V or VII neurograms. Development and acidosis had no effect on buccal period. Lung frequency increased with development (P < 0.0001). It also increased with acidosis, but in postmetamorphic tadpoles only (P < 0.05). The noise-titration technique evidenced low-dimensional nonlinearities in all the postmetamorphic brainstems, at both pH. Chaos-like complexity, assessed through the noise limit, increased from pH 7.8 to pH 7.4 (P < 0.01). In contrast, linear models best fitted the ventilatory rhythm in all but one of the premetamorphic preparations at pH 7.8 (P < 0.005 vs. postmetamorphic) and in four at pH 7.4 (not significant vs. postmetamorphic). Therefore, in a lower vertebrate model, the brainstem respiratory central rhythm generator accounts for ventilatory chaos-like complexity, especially in the postmetamorphic stage and at low pH. According to the ventilatory generators homology theory, this may also be the case in mammals.

in humans, ventilatory flow is not a truly periodic phenomenon. Its variability from breath to breath exhibits chaos-like mathematical complexity (16, 17, 71). This means that the trajectory of ventilatory flow is nonlinear, bounded, and predictable in the short term but not in the long term. It is dependent on low-dimensional deterministic processes and hence, not entirely random. This variability has been extensively documented in humans and has a prognostic value in certain clinical settings. For instance, the loss of respiratory pattern variability is predictive of outcome in comatose patients (29) or of failure of weaning from mechanical ventilation in critically ill patients (70). Beyond that, changes in chaos-like ventilatory complexity have also been observed in human diseases. They can help detect patient-ventilator dysharmony (31, 40), contribute to predict the outcome of weaning from mechanical ventilation (13), and be used to adjust the level of continuous positive airway pressure in patients with the obstructive sleep apnea syndrome (35). This type of approach has also been proposed as a diagnostic tool to identify sleep apnea patients without resorting to overnight polysomnography (34) or to distinguish patients with panic disorder from normal individuals (72).

Characterizing ventilatory complexity is therefore of putative clinical interest. However, the underlying mechanisms are not completely understood, which makes data interpretation difficult.

By demonstrating the absence of discernible low-dimensional nonlinearities within the ventilatory flow signal recorded in passive-state patients receiving mechanical ventilation, Mangin et al. (31) provided a strong argument against the contribution of the mechanical properties of the respiratory system to ventilatory complexity. Vagal afferents may play a role (47–49) but suprapontine interferences with breathing control do not (46). Of interest, stimulating ventilation with carbon dioxide in humans increases the sensitivity of ventilatory flow to the initial conditions, while hypocapnia, considered to be associated with a reduced drive to breathe, decreases it as well as the complexity of the signal (17). This points to the intrinsic properties of the oscillators governing the automatic command of breathing as one of the most probable origins of ventilatory chaos-like complexity.

One way to challenge this idea is to study the respiratory neural output of an isolated brainstem preparation. The present study was conducted with this aim, using isolated superfused tadpole brainstem preparations (23, 59, 67). Amphibians display two breathing rhythms of which the relative prevalence changes during metamorphosis (4, 5, 51). Premetamorphic frog tadpoles are exclusively aquatic. They breathe by pumping water through their gills using rhythmic contractions of their mouth floor. Their lungs are first immature and then rarely ventilated. After metamorphosis, the gills degenerate. The adult animals breathe by propelling air into their lungs, again through buccal contractions (64). Between these lung breaths, smaller oscillations of the buccal floor persist, reminiscing gill ventilation (4, 5). The isolated superfused tadpole brainstem preparation (59, 67) generates ventilatory motor rhythms that can be recorded through electroneurography of cranial nerves and are similar to those characterized in vivo (22, 23, 33, 44, 45, 60). These motor rhythms consist almost entirely of lung and buccal bursts that are clearly visible on the neurograms from cranial nerves. The buccal and the lung oscillators, located in the brainstem, are coupled but physiologically and anatomically distinct (20, 52, 63, 66). The first governs gill or buccal ventilation, according to the developmental stage, while the other drives lung ventilation. Some consider the mammalian respiratory oscillators (parafacial respiratory group and Pre-Bötzinger complex) homologous to the amphibian gill/buccal and lung oscillators (63). The frog model however, has a major advantage on mammalian models to examine the interactions between several oscillators as the source of the complexity of breathing. Indeed, in this model, each respiratory nerve expresses the activity of the two breathing oscillators. It is therefore possible to study their respective role in the complexity of the signal on one single neurogram.

Mathematical and electronic (14, 27, 32) models predict that interactions between oscillators as well as pacemaker properties (41) can produce chaos. Furthermore, the in vitro brainstem slice preparation from neonatal rat can generate an aperiodic chaos-like rhythm, when it is sufficiently excited by high concentrations of extracellular K⁺ (8). With all of these elements in mind, we therefore hypothesized that 1) the ventilatory dynamics of the isolated tadpole brainstem would exhibit chaos-like complexity under certain circumstances; 2) it was more likely to do so at developmental stages known to involve both the buccal and the lung oscillator than at stages during which only the buccal generator is active; and 3) central chemosensitivity would have an influence on ventilatory chaos-like complexity. To test these hypotheses, we assessed the breathing dynamics of the isolated tadpole brainstem at two different developmental stages (pre- and postmetamorphic) and during acidic stimulation (pH 7.4 vs. pH 7.8).

MATERIALS AND METHODS

Ethical Approval

Experiments were carried on Rana (Pelophylax) esculenta tadpoles (European edible frog) of either sex obtained free of charge from a legally registered supplier (Centre Jean Rostand, Pouydesseaux, France). They were performed according to the French legislation on animal experimentation. The general protocol, including the techniques of anesthesia, was registered by the French Ministry for Agriculture. The experimenters held an official authorization to perform experimentations on amphibians and the experimental premises had been visited and authorized by the same administration. The institutional animal care committee (Comité Régional d'Ethique pour l'Expérimentation Animale, Ile-de-France, Paris, Comité 3) approved the specific protocols used in this study.

Animals

For at least 5 days before the experiments, the animals were housed at ambient temperature (∼20°C), in aquariums or aquaterrariums (depending on developmental stage) containing dechlorinated, aerated, and filtered water. Animals were then assigned to one of two groups of development, according to the staging of Taylor and Köllros (54), either premetamorphic (stages X–XIII, n = 8) or postmetamorphic (stages XXIV–XXV, n = 8). We chose such a division because of the dramatic change in breathing mode that differentiates these stages of development.

Superfused Isolated Brainstem Preparation

Tadpoles were weighed (1.00 g ± 0.47 g) and anaesthetized by placing them in water taken from their aquarium and containing tricaine methane sulphonate (1:10,000). Once unresponsive to pinches, the animals were decerebrated by a decapitation that removed the forebrain. The thoracic and abdominal organs were removed and the tail or the limbs (depending on the developmental stage) were cut. The remaining cranium and vertebral column were transferred into a dissection chamber. The dissection was performed under continuous flow-through superfusion (∼10 ml/min) with mock cerebrospinal fluid (CSF) equilibrated with ∼98%O₂ /2%CO₂ (in mM): 104 NaCl, 4 KCl, 1.4 MgCl2, 10 d-glucose, 25 NaHCO3, 2.4 CaCl2 (pH ∼7.8). The total duration of the dissection was 50–70 min. The preparation consisted of the isolated brainstem (caudal to cranial nerve CN III) and rostral spinal cord (transected caudal to spinal nerve SN V) with the choroid plexus, dura, and most of the ventral arachnoid removed. Experiments were then performed in a recirculating superfusion chamber, previously described (67) in which the recirculation mechanism was driven by gas (98% O₂/2% CO₂), which also equilibrated the superfusate. During experiments, the pH in the chamber was monitored and maintained either at 7.8 (normocapnic, physiological pH for these animals) or at 7.4 (hypercapnic, acidic pH for these animals) by adjusting the fractional concentration of CO₂ in the gas. The experiments were performed at room temperature (19.8°C- 22.5°C). Because of the much smaller size (∼10 times) of our animals compared with Lithobates (formerly R.) catesbeiana, the species for which the superfusion chamber was originally designed, we modified the recording chamber. We removed the original spacer and nets (circulating volume in the dish ∼10 ml) and coated the bottom with silicone elastomer (Sylgard 184; Dow Corning France, Lyon, France). This allowed us to pin the preparations ventral side up and to obtain stable recordings.

Electrophysiology

Motor rhythms corresponding to buccal and lung ventilation were recorded from the root of CN V or CN VII using glass suction electrodes. Action potentials were amplified (10,000 times) and filtered (100 Hz-1 kHz) using a high gain, differential AC amplifier (model 1700; A-M Systems, Everett, WA), digitized at 2,000 Hz (PowerLab, ADInstruments), and the root mean square (RMS) of the raw signal was numerically calculated using a moving window with a width of 100 ms (Chart 5.2, ADInstruments). The raw and RMS signals were archived as computer files for subsequent analysis.

Lung and gill or buccal bursts were identified, from the RMS signal, accordingly to previously published criteria (20, 22, 23, 60). In this study, we also chose to call “buccal ventilatory rhythm” the motor rhythm corresponding to gill ventilation in premetamorphic tadpoles. Briefly, buccal ventilatory bursts were defined as bursts of low amplitude and high frequency (20, 22, 23, 60). Lung bursts were defined as discharges of high amplitude (20, 22, 23, 60) and duration < 1 s (42). In this study, we required their amplitude to be at least 150% of that of the surrounding buccal bursts.

Experimental Protocol

The experimental protocol began after having washed out the preparation during 10 min with ∼100 ml of mock CSF at physiological pH, flowing through the recirculating chamber from an external tonometer, and after having waited for ∼30 min for rhythm stabilization. When stable rhythm was obtained, the pH of the recirculating mock CSF was set either at 7.8 or at 7.4. Nerve activities were recorded at each pH for 20–35 min.

Analysis of Ventilatory Rhythm and Burst-By-Burst Variability

The first 10 min of each recording were used to ensure stabilization of the rhythms and then discarded. Then, 5 min of RMS signal with the best identifiable rhythms of clear buccal and lung bursts and with a minimum number of discharges of an undeterminable kind, like, for example, the so called “complex discharges” (see Ref. 52) , were selected for analysis. If occasional lung bursts were seen in premetamorphic preparations, a second subsequent recording epoch of 5 min including those bursts was also kept for further analysis of complexity only (see below). In one case, there was an overlap of 1 min between the two epochs, and in the three other cases, there was an interval of 36 s to 3 min between the two epochs that were analyzed from the same recording.

The period of each buccal cycle, their amplitude (μV), measured as their height from baseline of the RMS signal, and their time to peak were determined using Chart 5.2 software (ADInstruments) and a specific routine developed with Matlab V.7.0.1 R14 (MathWorks, Natick, MA). Because lung bursts were exceptional in premetamorphic preparations and rare in some postmetamorphic tadpoles at pH 7.8 we did not calculate the period of the lung bursts and its coefficient of variation. Instead, we calculated an overall lung frequency by dividing the number of lung bursts by the duration of the recording. This duration was 5 min in postmetamorphic tadpoles. It was 9 to 10 min in premetamorphic preparations because we recorded two epochs of 5 min when we observed lung bursts. When no lung burst was seen (this was often the case in premetamorphic tadpoles), the lung frequency was considered equal to zero. The amplitude of the lung bursts was measured the same way as that of the buccal bursts.

Nonlinear Analysis and Assessment of Chaos-Like Complexity

The nonlinear analysis of the whole trajectory of the RMS signal was performed as previously described for human ventilatory flow [(16, 17, 31, 71), see discussion]. A detailed description of the methods is provided in Wysocki et al. (71). For each recording, the frequency content of the signal was described using a 1,024-point fast Fourier transform function (Hamming window, no overlap, zero values removed, Chart 5.2 software; ADInstruments). The range of maximal frequency (7.8–9.8 Hz) was the same in pre- and postmetamorphic preparations. The digitized files were then subsampled at 40 Hz (Dataplore software package; Datan, Teltow, Germany), a frequency always greater than the Nyquist frequency of the signal that was chosen like in previous human studies (71) to correspond to 4–5 times the maximal frequency.

A windowed spectral analysis was performed with the aim of identifying nonstationarity, as follows. Each recording was divided in three epochs of 100 s. Then, their power spectral densities and the one of the entire signal were computed, normalized to their mean to take into account the difference in the number of data points (Matlab, V.7.0.1 R14;, MathWorks) and compared by using the nonparametric Friedman test for repeated measures. A significant difference between two epochs was found in only one recording (post hoc Dunn's Multiple Comparison Test). This hint to nonstationarity in one unique recording was not considered as an issue for the analysis of chaos-like complexity (see below).

Detection and quantification of chaos-like complexity.

This was performed by applying the noise-titration method to the trajectory of the RMS signal (38, 71). This approach was chosen because of its robustness even in short and noisy time series (38). In our case, studying short signal epochs is a major advantage, because it helps alleviating the issue of nonstationarity. In brief, the noise-titration process begins with a nonlinearity detection step (2). Several nonlinear autoregressive series of the Volterra form are produced, with different degrees of nonlinearity (d) and embedding dimensions Kappa (K), to produce a family of linear and nonlinear polynomial autoregressive models. The models are then compared, and the null hypothesis (linearity) is tested against the alternate hypothesis (nonlinearity) using parametric (F-test) and nonparametric (Whitney-Mann U-test) statistics (2). The rejection of the null hypothesis means that a nonlinear model best describes the data (in other words, that the dynamics is nonlinear). Therefore, the titration process can start. White noise of incrementally increasing standard deviation is added to the time series until the null hypothesis can no longer be rejected. This defines a noise limit, which, when above zero, provides a quantitative estimate of the chaotic dynamics from autonomous (deterministic) systems. The technique, however, does not differentiate deterministic chaos from chaos-like variability induced by the interaction of noise and low-dimensional nonautonomous systems. We will thus call “chaos-like” the complexity defined by a positive noise limit (see discussion). When the noise limit is equal to zero or when no nonlinearity is detected, the presence of nonlinear complexity cannot be ascertained. In any case, variations of noise limit from one state of a system to another state can be interpreted as witnessing changes in the underlying processes. We performed the noise titration using a specific routine developed under Matlab V.6.5 R13 (MathWorks) according to a trial-and-error process, including the default testing of K values of 4 to 6 and of nonlinear degrees of 3 to 5, like in humans. In the absence of nonlinearity, other combinations of K and d values were tested (Table 1). We retained the highest value of noise limit for each condition.

Table 1.

Combinations of embedding dimensions Kappa (K) and degree of nonlinearity (d) tested for the assessment of chaos-like complexity with the noise titration method

K Value	Associated d Values
3	2–7
4	2–7
5	2–7
6	2–6
7	2–5
8	2–5

We also applied the more traditional surrogate data approach to the signals, as a supplementary measure (12). To do this, we first generated iterated amplitude adjusted Fourier-transformed surrogates (iAAFT) of the signals, with a specific routine developed with Matlab, V.7.0.1 R14 (MathWorks). This kind of surrogate data preserves both the amplitude distribution and the power spectrum of the original data, within a set tolerance (12). For each original recording, we generated 10 surrogate data series. Then, we calculated the approximate entropy (ApEn), a global index of irregularity and complexity (37), of each original signal and of its 10 surrogates. The “filter factor” r equaled to 0.2 times the standard deviation of the original time series and the embedding dimension m was 2 (see for example, Ref. 7). Finally, we conducted a statistical comparison between each original data series and their 10 surrogates, according to Burioka et al. (6). The method relies on the calculation of the sigma value defined by Theiler et al. (57). A sigma value > 2.26 indicates a significant difference and is in favor of the nonlinear nature of the signal.

Graphical assessment of signal trajectories.

Peak interval maps were used to assess qualitatively the trajectories of the signals. To draw these maps, we plotted the amplitude of each burst against the period to the following burst.

Statistical Analysis

For all criteria seen in the two developmental stages and the two pH values, effects of development stages and pH were assessed using ANOVAs with repeated measurements for pH. An interaction term was also systematically tested. Model validity was checked by visual inspection of the residual plots, and log transformation of criteria was applied when suggested by the plots. Log transformations were performed on pulmonary frequency and time to peak coefficient of variation. When interaction terms were found significant, the statistical analysis was completed by testing the pH effect in each group of developmental stage. Since pH data are paired, the tests performed at this stage were Wilcoxon signed-rank tests. Since lung bursts and nonlinear dynamics were absent in most premetamorphic tadpoles, we assessed the effect of pH on lung-burst amplitude and noise limit in postmetamorphic animals only, again using the Wilcoxon signed-rank test.

The frequency of chaotic dynamics of neural respiratory output was compared in pre- and in postmetamorphic preparations using the Fisher's exact test.

RESULTS

Buccal Rhythm

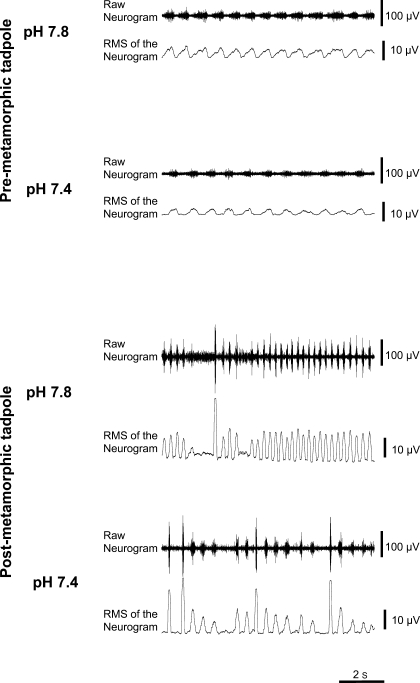
The motor rhythm corresponding to buccal ventilatory activity (22, 23, 60) was clearly visible in all preparations (Fig. 1).

Fig. 1.

Examples of recordings performed in the 7th cranial nerve of a premetamorphic (stage XIII) and of a postmetamorphic tadpole (stage XXIV). At each pH, the top trace shows the raw neurogram and the bottom trace its root mean square (RMS), obtained with a moving time constant of 100 ms. Bursts of lower amplitude correspond to gill or to buccal ventilatory rhythm and discharges of higher amplitude-to-lung ventilatory rhythm. The premetamorphic tadpole corresponds to preparation 7 in Table 2. Nonlinear complexity was detected, at pH 7.4 only, in the gill rhythm of which a sample is shown here, with an embedding dimension (K) of 8 and a degree of nonlinearity (d) of 4. The noise limit was 17%. In the case of this tadpole, the gill/buccal frequency decreased with pH. However, on average, pH variations had no significant effect on buccal period in premetarmorphic animals (see results and Fig. 2).

Buccal ventilatory rhythm period.

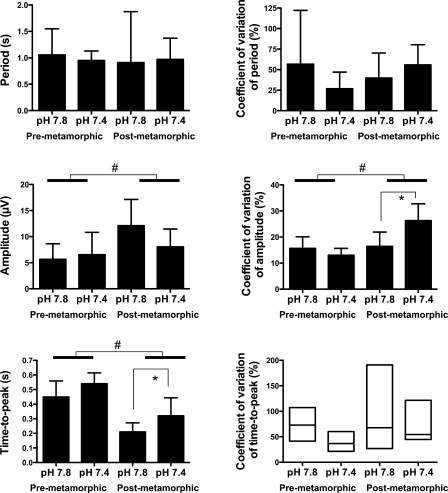
Neither the developmental stage (P = 0.77), nor the changes in pH (P = 0.92), nor their interaction (P = 0.70) had an effect on buccal period. Neither the developmental stage (P = 0.67), nor the pH (P = 0.63), nor their interaction (P = 0.12) affected the coefficient of variation of buccal period (Fig. 2).

Fig. 2.

Buccal rhythm, according to developmental stage and pH. Histograms show mean ± SD except for the coefficient of variation of time to peak where the median and the range are indicated. #Significant effect of developmental stage. *Significant effect of pH within groups of development.

Buccal rhythm amplitude.

The developmental stage had a significant effect on buccal-burst amplitude (P < 0.015). However, the pH (P = 0.28) and its interaction with development (P = 0.10) had no effect. The coefficient of variation of buccal amplitude was significantly affected by the developmental stage (P < 0.002) and its interaction with pH (P < 0.004) but not by pH alone (P = 0.059). It increased significantly in postmetamorphic animals only, at pH 7.4 compared with pH 7.8 (P < 0.01) (Fig. 2).

Time-to-peak of the buccal bursts.

The interaction of development and pH had no significant effect on the time to peak of the buccal bursts (P = 0.78). However, the time to peak shortened with development (P < 0.0001) and there was an effect of pH (P < 0.01). The time to peak of the buccal bursts was shorter at pH 7.8 than at pH 7.4, in postmetamorphic preparations only (P < 0.04). Neither the developmental stage (P = 0.07), nor the changes in pH (P = 0.058), nor their interaction (P = 0.06) had an effect on the coefficient of variation of the time to peak of the buccal bursts (Fig. 2).

Lung Rhythm

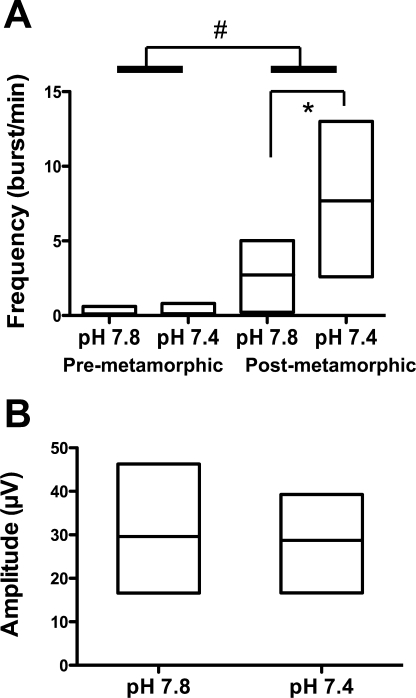
Lung rhythm was present in all postmetamorphic tadpoles (Figs. 1 and 3). Among eight premetamorphic preparations, only four displayed very rare lung discharges, two at pH 7.8 and two at pH 7.4 (Table 2). Lung frequency increased with development (P < 0.0001). The pH (P < 0.05) and its interaction with development (P < 0.05) also affected the lung frequency. The latter increased significantly at pH 7.4 compared with pH 7.8, in postmetamorphic tadpoles only (P < 0.05). In postmetamorphic animals, lung amplitude did not change with pH (P = 0.20).

Fig. 3.

Lung rhythm. A: median and range of lung burst frequency, according to developmental stage and pH. B: median and range of lung-burst amplitude in postmetamorphic tadpoles. #Significant effect of developmental stage. *Two-by-two significant differences within groups of development.

Table 2.

Detection of chaos-like complexity in premetamorphic tadpoles with the noise titration method

Preparation No.	Developmental Stage	pH	Presence of Lung Bursts	Highest Noise Limit of Buccal Ventilatory Rhythm Without Lung Bursts	Highest Noise Limit of Ventilatory Signal with Lung Bursts	K-d Combinations Having Detected Nonlinear Complexity
1	X	7.8	no	No nonlinearity detected
		7.4	yes
2	XIII	7.8	yes
		7.4	no
3	X	7.8	no
4	XII	7.8-7.4	no
5	XII	7.8-7.4	no
7	XIII	7.8	no
8	XIII	7.8	no
6	XII	7,8	yes	No nonlinearity	44%	7-4, 7-5, 8-3, 8-4, 8-5
		7.4	no	6%		8-4, 8-5
3	X	7.4	no	22%		8-3, 8-4, 8-5
7	XIII	7.4	yes	17%	36%	6-4, 6-5,7-4, 7-5, 8-4, 8-5
8	XIII	7.4	no	50%		8-3, 8-4, 8-5

Chaos-Like Complexity

Postmetamorphic preparations.

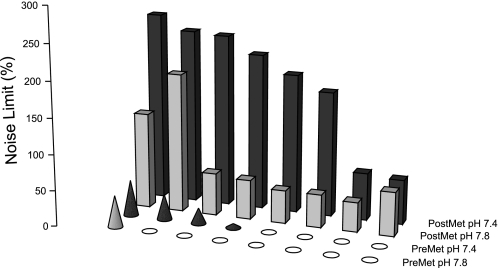
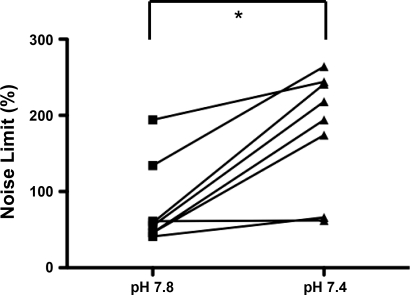
The dynamics of the signal were nonlinear, complex, and chaos-like in all postmetamorphic preparations, as ascertained by values of noise limit above zero (Fig. 4). Nonlinearity was always detected with the default values of K (4 to 6) and d (3 to 5). In all animals, the noise limit was higher at pH 7.4 than at pH 7.8 (P < 0.01, Fig. 5). The surrogate data analysis confirmed the nonlinear dynamics of all of the recordings obtained in postmetamorphic preparations, except in two recordings of two different preparations. One of these recording was performed at pH 7.8 and the other at pH 7.4. The peak-interval maps did not display any reproducible pattern (see an example in Fig. 6A).

Fig. 4.

Individual values of noise limit in recordings from premetamorphic (PreMet, cones) and postmetamorphic (PostMet, parallelepipeds) preparations. Values are shown in descending order, at pH 7.4. Light grey corresponds to a pH of 7.8 and dark grey to a pH of 7.4. Circles indicate that nonlinearities were not detected in the corresponding recording. At pH 7.8, nonlinearities were significantly less frequent in pre- than in postmetamorphic tadpoles. The noise limit, when present, was lower in the pre- than in the postmetamorphic preparations.

Fig. 5.

Individual values of noise limit (%) in postmetamorphic tadpoles. *Noise limit increased significantly when the pH decreased. Connected symbols indicate values from the same preparation.

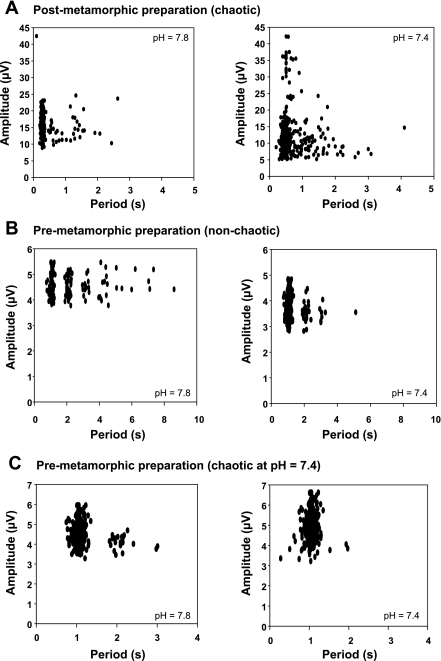
Fig. 6.

Examples of peak-interval maps in 3 preparations. The amplitude of each burst (y-axis) was plotted against the period to the following burst (x-axis). A: example of a postmetamorphic preparation. All the recordings performed in postmetamorphic animals exhibited nonlinear chaos-like complexity. B: example of a premetamorphic preparation. No nonliearities were detected in the signals at both pH. C: example of a premetamorphic preparation of which the dynamics of ventilatory output became nonlinear and chaos-like at low pH.

Premetamorphic preparations.

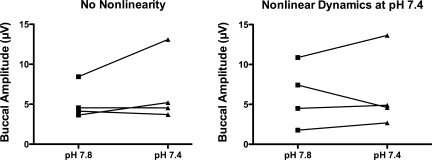
At pH 7.4 the noise titration of the buccal ventilatory rhythm yielded a positive value in four premetamorphic preparations (Table 2). The surrogate data analysis confirmed the nonlinear dynamics of the signals recorded in those preparations. One of these animals (no. 7 in Table 2) displayed eight lung bursts. The dynamics of the signal including those bursts had a higher noise limit than the recording containing only buccal ventilatory rhythm. We could not detect any nonlinearity in the four other animals. Thus, the proportion of chaos-like preparations in premetamorphic animals was not different from this proportion in postmetamorphic tadpoles (P > 0.05). Using the amplitude of the buccal bursts as an estimation of the signal-to-noise ratio, we could not detect any difference between the premetamorphic preparations with and without nonlinear signal (P = 1.00, Fig. 7).

Fig. 7.

Individual values of buccal-burst amplitudes in premetamorphic tadpoles in which no nonlinearity was detected (left) or in which ventilatory rhythm was nonlinear and chaos-like at pH 7.4 (right). Connected symbols indicate values from the same preparation. Taking the buccal amplitude as an estimation of the signal-to-noise ratio, no obvious increase in this ratio can be seen in the animals in which nonlinear dynamics was detected at pH 7.4 compared with those in which nonlinearities were not detected at this pH.

At pH 7.8, the noise titration yielded a positive value in only one recording from a premetamorphic animal that displayed two lung discharges (no. 6 in table 2). The highest noise limit was obtained with a K value of 8 and a degree of nonlinearity of 5. The surrogate data analysis confirmed the nonlinear dynamics of the signals recorded in this preparation. We did not detect any nonlinearity in the second recording from the same animal that displayed only a buccal rhythm. Of note, we did not detect any nonlinearity in all other premetamorphic preparations even if they displayed lung bursts. Therefore, at pH 7.8, ventilatory nonlinear complexity was significantly less frequent in premetamorphic than in postmetamorphic tadpoles (P < 0.005, Fig. 4).

In half of the recordings where no nonlinearities were detected by noise titration, the ApEn of the surrogate data was not significantly different from that of the original data set (Theiler's sigma below 2.26). In the other half, Theiler's sigma was marginally above 2.26, its overall value averaging 2.04 ± 0.71 (not significantly different from 2.26). In contrast, among the set of signals found to be nonlinear by noise titration, only two had a sigma value below 2.26, with an average of 10.74 ± 8.7 that was significantly higher than that found in the (linear) set.

The peak interval maps displayed a single cloud of dots in 12 recordings, nonlinear or not (see, for example, Fig. 6C, pH 7.4) and multiple clusters of dots in four non-nonlinear recordings (see 3 of these in Fig. 6, B and C).

DISCUSSION

This study shows that the ventilatory-related neural activity of the isolated superfused R. (Pelophylax) esculenta tadpole brainstem is best described by linear models in premetamorphic, i.e., immature, preparations when studied under physiologic pH conditions. This activity can become nonlinear and exhibit complexity with chaos-like features during development (postmetamorphic preparations) and/or chemostimulation. The intrinsic properties of the ventilatory central rhythm generator located in the brainstem are therefore sufficient to account for the complex nature of the ventilatory behavior, independently of peripheral afferents.

Validity of the R. (Pelophylax) Esculenta Tadpole Isolated Brainstem Model

To date, the amphibian isolated brainstem model validated for in vitro breathing control studies uses the American bullfrog Lithobates catesbeiana (see, for example Refs. 18, 23, 25, 26, 30, 33, 51, 55, 58, 61, 62). Because this species is considered noxious in Europe, we had to resort to the most common European edible frog, R. (Pelophylax) esculenta (same family, Ranidae., as Lithobates, formerly R. catesbeiana). Our preparations indeed displayed neural outputs very similar to those described in L. catesbeiana. The sensitivity of lung bursts to CO₂ in the postmetamorphic animals attested to the respiratory nature of the signal (55, 58, 61, 66). Nevertheless, the tadpoles of R. (Pelophylax) esculenta are about 10 times smaller than those of L. catesbeiana (1.00 g ± 0.47 g in the present study vs. e.g., 11.24 ± 1.81 g in Ref. 53), with correspondingly smaller nerve roots [diameter of cranial nerve - CN - VII 40–80 μ, vs. ∼200 μ in L. catesbeiana; spinal nerve (SN II, even smaller)]. This smaller size has methodological consequences. First, the duration of the dissections was long (50–70 min). This duration, added to the 10 min washout period at the beginning of the protocol, provided, however, a likely complete washout of the anesthetic, since the latter needs ∼45 min (24). Second, to obtain stable signals we had to modify the superfusion chamber (67) and to pin the organs ventral side up at the bottom of the chamber. This could have impaired the oxygenation of the brainstems. To assess this issue, we fixed seven premetamorphic and five postmetamorphic brainstems in ice-cold paraformaldehyde at the end of the recordings. The dorsoventral thickness of the brainstems at the level of the obex (maximal diameter), measured with a dissection microscope fitted with a calibrated scale, ranged from 0.74 to 0.98 mm. As a result, the deepest part of the brainstem was always < 500 μ from the oxygenated fluid. Although we did not assess cell viability, pH, CO₂, and O₂ gradients directly, available information (59, 67) indicates that a depth of 500 μ corresponds to a Po₂ > 100–150 Torr. Therefore, despite the technical adaptations of the experimental setup that were imposed on us by the size of our preparation, the brainstems remained probably well oxygenated. Third, the very small size of R. (Pelophylax) esculenta prevented us from safely applying suction electrodes to SN II. Consequently, we could not record a neural output purely reflecting the activity of the lung oscillator (22, 23, 55, 60). This could have led to an underestimation of the number of lung bursts, or to some degree of ambiguity in their identification.

Comparison with Available Data

This study provides the first data of this type in R. (Pelophylax) esculenta. Comparable data on changes in buccal and lung rhythms with development and pH were only obtained in L. catesbeiana. In this animal, lung frequency increases with CO₂ only at the postmetamorphic stages (55, 56, 58, 61, 66), but occasional lung bursts can occur in premetamorphic tadpoles (52, 55, 56, 61). The pH does not affect lung amplitude in L. catesbeiana (55, 61). We obtained the same results. Regarding the buccal rhythm, some authors found that its frequency and its amplitude increased with lowering the pH in premetamorphic tadpoles and that its amplitude only increased in postmetamorphic animals (61). Others found no systematic change in amplitude and reported a decrease in frequency with pH (55). In our study, the amplitude of the buccal bursts increased with development, but neither the period nor the amplitude of the buccal rhythm displayed any chemosensitivity. However, we found that development decreased the time to peak of the buccal bursts and that lowering the pH increased it at the postmetamorphic stage (Fig. 2). The latter result suggests a kind of chemosensitivity of the buccal generator that predominates on motor neuron recruitment. Our results are similar to those obtained in L. catesbeiana (55). In this latter species, the duration of the buccal bursts (duty cycle) decreased with development and increased when the preparations were exposed to hypercapnia and acetazolamide (55). Taken together and compared with previously published data obtained in L. catesbeiana, our results support the validity of the model of the isolated brainstem of R. (Pelophylax) esculenta.

To our knowledge, burst-by-burst variability in tadpoles has not been studied before our work. We did not assess the variability of the lung bursts because of their insufficient number in some postmetamorphic tadpoles at pH 7.8 and in all premetamorphic preparations. The variability of the buccal period did not change in our study but the coefficient of variation of buccal amplitude was significantly higher in postmetamorphic animals at pH 7.4. This greater variability may have been permitted by the higher intensity of complexity at this stage of development (see below).

Chaos-Like Complexity

Choice of methods.

Identifying nonlinear and chaotic dynamics within biological signals is difficult because of noise. In this study, we chose the noise-titration technique to keep consistency with our previous works (16, 17, 31, 71) and thus be able to meaningfully compare our findings among studies. The noise-titration technique has the ability to easily and reliably ascertain low-dimensional nonlinearity, which is the object of its first step (Volterra autoregressive algorithm, see materials and methods) (2, 28, 38). Its second step (the noise titration per se) provides a sufficient proof and quantification of deterministic chaos in time series from autonomous systems (38). This is not necessarily the case in nonautonomous systems, namely systems that are perturbed by time-varying drives, such as stochastic inputs (i.e., dynamic noise) (38). For example, the noise limit of a low-dimensional nonlinear system driven by dynamic noise can be positive (2, 9, 19). Some authors call “stochastic chaos” or “noise-induced chaos” dynamics from nonlinear systems of which the noise limit value becomes positive under the influence of stochastic noise (46, 69). Biological systems may belong to this latter kind of chaos since they are likely to be influenced by random noise (see discussions in Refs. 46, 69). Therefore, biological signals exhibiting positive noise limit values (9–11, 16, 17, 31, 39, 71, 74) such as ours may represent either purely deterministic chaos or noise-induced chaos. For the sake of rigor, we thus term “chaos-like” rather than only (deterministically) “chaotic” the signals exhibiting a positive noise limit. This does not detract from the interest of the noise titration. Indeed, this technique can reliably ascertain the low-dimensional nonlinear nature of short time series (2, 38), and changes in noise limit reflect changes in the chaos-like underlying state of the system, be the low-dimensional chaos entirely deterministic or partly stochastic. The capability of noise titration to detect chaos in short time series is furthermore useful for the detection of transient changes within long-term processes (69). In our case, studying short signal epochs is a major advantage, because it helps in alleviating the issue of nonstationarity. The ability of the noise-titration technique to detect transient changes was also useful to assess the impact of occasional lung bursts in premetamorphic preparations.

Inferring nonlinear dynamics in a noisy signal is also possible through the comparison of this signal statistically with an appropriate set of randomly generated “surrogate” data (12, 50). This approach suffers, however, from multiple caveats such as the choice of the method to generate the surrogates (28) or the choice of the statistical test to compare them to the original data [(12, 21, 50), see also detailed discussion in Ref. 71 and in Appendix 1 of Ref. 69]. Accordingly, in his 1999 article that reviewed the surrogate data method, Kugiumtzis (28) concluded “the Volterra polynomial fit turned out to be a useful diagnostic tool for detecting dynamic nonlinearity directly on the original data as well as verifying the performance of the surrogate data.” In fact, “the Volterra polynomial fit” is precisely the technique we used in the noise-titration process to analyze the original data in this study. Furthermore, the surrogate data approach only tests for nonlinearity and, in contrast to noise titration, does not provide any sort of complexity quantification. Nevertheless, this is a popular method, and we felt it interesting to compare the two approaches. In our study, the surrogate data analysis was generally consistent with the noise-titration approach. With the exception of two recordings performed in two distinct preparations at two different pH, a positive noise limit indicating nonlinearity was always associated with Theiler's sigma unambiguously above 2.26. In the premetamorphic animals, the surrogate data analysis concluded to nonlinearity more often that noise titration, with values of Theiler's sigma that could be slightly above 2.26 in spite of a nondetectable noise limit. These slight discrepancies however, do not call into question our general observation that nonlinearity in our preparations depended on maturation and on chemosensitivity. Of note, they are not unexpected because of the known propensity of the surrogate data approach to generate falsely positive results (28).

We performed nonlinear analysis on the whole trajectory of the RMS signal because we wanted to interpret the results in the perspective of human results pertaining to ventilatory flow (16, 17, 31, 71). Since it correlates well with the pressure produced by the respiratory muscles (44, 45), the integrated neurogram (which is similar to RMS) is indeed related to flow, as a function of resistance. Of note, the RMS signal is a nonlinear transformation of the raw neural signal. Since chaotic dynamics is invariant under any diffeomorphic transformation (see, for example, Ref. 43), the RMS of the electroneurogram is suitable to assess nonlinear complexity and chaos-like behaviors. Furthermore, the fact that all but one of the recordings performed in premetamorphic preparations did not display nonlinear dynamics at pH 7.8 and that only half of them were found to be nonlinear at pH 7.4 indicates that the RMS transformation of the signal was not sufficient to render it nonlinear and that the analysis of the RMS signal was suitable to reveal physiological changes. The comparison of the results of the surrogate data analysis in the recordings classified as linear or nonlinear with noise titration support this.

Source of respiratory chaos-like complexity.

Using the noise-titration technique, our study demonstrates that the dynamics of the respiratory neural output of isolated superfused brainstems of postmetamorphic tadpoles is nonlinear and chaos-like under physiological pH conditions. This means that the nonstimulated automatic command of breathing can suffice to produce nonlinear chaos-like complexity, even without any other input except chemosensitivity. In other words, our study suggests that nonlinear chaos-like complexity is a normal feature of breathing in mature animals. As a consequence, its absence (e.g., in an intact animal or a human being) could be an indicator of disease. Furthermore, hypercapnic stimulation increased the noise limit (Fig. 5). It should be taken as indicative of a change in the characteristics of ventilatory chaos-like complexity. Our results may seem to contrast with the reports of Sammon et al. (47–49) who assigned an essential role to vagal afferents in the production of breathing complexity. The contradiction may be only apparent, because anesthesia in the studies of Sammon et al. may have played an important role. Indeed, if ventilatory complexity depends on the degree of excitation of the respiratory central rhythm generators (6, 7, 17; this study), then anesthesia is bound to decrease it. This would emphasize the role of vagal afferents, and thus explain the major effects of vagotomy observed by Sammon et al. Of note, caution is necessary when comparing Sammon et al.'s studies with ours, because of major differences in the mathematical description of complexity. Further studies are necessary to clearly understand the contribution of vagal afferents to ventilatory complexity.

Developmental considerations.

In the present study, nonlinearity was not detected in premetamorphic tadpoles at physiological pH of 7.8, except in one recording epoch that contained two lung bursts. Methodologically speaking, the failure of noise titration do detect nonlinearities could be a spurious finding due to an elevated noise floor (38). However, we believe that nonlinearities were truly absent or of marginal intensity in these preparations. Indeed, in four of them the noise limit did become positive with CO₂ stimulation. Yet the amplitudes of the corresponding buccal bursts were roughly unchanged and the signal-to-noise ratio was not obviously different as can be seen in Figs. 1 and 7. The absence of nonlinear dynamics in premetamorphic preparations at a pH of 7.8 suggests that complexity within the neural output of the isolated superfused tadpole brainstem depends on both ontogeny and chemosensitivity. Of interest, the interaction between the buccal and the lung oscillators does not appear to be a necessary condition of chaos-like complexity (68). Indeed, nonlinearities were not detected in two preparations exhibiting lung bursts at a pH of 7.8. More importantly, a positive noise limit was occasionally detected in premetamorphic preparations exhibiting a buccal rhythm only, at a pH of 7.4 (Table 2). In these cases, the positive noise limit was found with higher values of the embedding dimension K (7–8) than in postmetamorphic tadpoles (Table 2). This indicates that the system was at the threshold of moving from randomness to possible “low-dimensional” chaos, and could speculatively be taken as an argument for a “maturation” process.

The interpretation of these results can only be very speculative. The fact that all postmetamorphic preparations displayed nonlinear complex chaos-like dynamics and only half of the premetamorphic preparations at acidic pH, suggests that the lung oscillator might be an important source of chaos-like complexity. This oscillator is precociously present but inhibited in premetamorphic tadpoles (52). It has also been shown that it stimulates the buccal oscillator, in postmetamorphic animals (66). One could thus hypothesize that the low pH stimulated the quiescent lung oscillator, which turned the linear buccal dynamics into nonlinear chaos-like dynamics.

In young premetamorphic and metamorphic tadpoles, the buccal rhythm depends on postsynaptic, chloride-mediated, fast inhibition. In contrast, the lung rhythm does not and is therefore assumed to depend on pace maker neurons (3, 20). Electronic models predict that the bursting pattern of such neurons can be chaotic and that as few as three ion channels (one for burst initiation and two for burst termination) would be sufficient, “without the need for any intrinsic or extrinsic stochastic influences or other complex intracellular processes” (41). Furthermore, the pre-Bötzinger complex that drives ventilation in neonatal rodents and contains pace maker neurons, produces also a chaos-like dynamic, when it is sufficiently exited by high concentrations of K⁺ (8). Taken altogether, these data suggest that the nonlinear chaos-like dynamics of ventilation in the tadpole might depend on the properties of pace maker neurons that would drive the lung oscillator.

Perspectives and Significance

This study indicates that the superfused isolated brainstem of the tadpole R. (Pelophylax) esculenta provides a suitable model to investigate the intricate mechanisms of the control of breathing and their ontogeny similar to the L. catesbeiana model. This being said, our results confirm that detecting and characterizing chaos-like complexity within a respiratory-related behavior can be useful to describe the properties and functioning of the respiratory central rhythm generators.

Additional work is necessary to better understand the implications of the information provided in this study. In this frame, a more graded approach of the relationships between both ventilatory rhythms and complexity may be interesting. It could rely on other analytical tools like structural analyses. The respective contribution of the buccal and the lung oscillators to the ventilatory chaos-like complexity in postmetamorphic animals could also be assessed through pharmacological manipulations. For instance, it is possible to pharmacologically silence one or the other of the oscillators, and thus to study their respective complexity independently of one another at a given maturation stage. It will also be necessary to confirm the present results in mammals. In this regard, it must be emphasized that the current tadpole data are likely to be relevant to mammalian respiration. Indeed, the latter also depends on two coupled oscillators, the parafacial respiratory group and the pre-Bötzinger complex, that are analogous to the amphibian oscillators (15). They probably all come from an ancestor common to all tetrapods (36, 65) and are thus most likely homologous (63). Furthermore, the present results gathered in tadpoles are very consistent with human data previously obtained by our group (17). It is therefore tempting to hypothesize that ventilatory chaos-like complexity took its origin in a distant common ancestor and provided some selective advantage. Accordingly, some degree of ventilatory complexity should characterize health, and a decreased ventilatory complexity could be a marker of respiratory diseases, as it is the case in cardiac failure (see, for example, Ref. 39).

For these reasons, it appears relevant to seek a better understanding of ventilatory chaos-like complexity in humans, in the perspective of a better assessment of breathing control. Furthermore, the developmental emergence of nonlinear chaos-like complexity reported here is consistent with previous studies having shown an ontogenetic increase in ventilatory complexity in mammals, through the use of approximate entropy (1, 73). This provides thus a strong incentive to assess the effects of development on ventilatory complexity. It could help in characterizing the maturation of the ventilatory control system and therefore provide clinically useful indications in situations where respiratory immaturity can present a threat like the dreaded apneas of premature human newborns.

GRANTS

This study was funded in part by a grant from Legs Poix of the Chancellerie des Universités de Paris France and in part by a grant from du Collège des Enseignants de Pneumologie, France. It was also supported by the Association pour le Développement et l'Organisation de la Recherche en Pneumologie, Paris, France and by a grant from Santé Environnement -Santé travail of the French Agence Nationale pour la Recherche (Grant ANR0003205, Transport et transfert via le système pulmonaire humain). Ziyad Samara was supported in part by a scholarship from the Société de Pneumologie de Langue Française and by a grant from the French Ministère des Affaires Etrangères. M.-N. Fiamma was supported by a grant from the Comite d'organisation de l'Assistance Respiratoire a Domicile d'Ile-de-France (CARDIF), Fontenay-aux-Roses, France. A. Ranohavimparany was supported by a grant from the Association Française du Syndrome d'Ondine (AFSO). C.-S. Poon was supported by National Institute of Health Grants HL-079503, HL-072849, HL-067966, and RC1-RR-028241.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).