Using computer simulations to determine the limitations of dynamic clamp stimuli applied at the soma in mimicking distributed conductance sources

Abstract

In previous studies we used the technique of dynamic clamp to study how temporal modulation of inhibitory and excitatory inputs control the frequency and precise timing of spikes in neurons of the deep cerebellar nuclei (DCN). Although this technique is now widely used, it is limited to interpreting conductance inputs as being location independent; i.e., all inputs that are biologically distributed across the dendritic tree are applied to the soma. We used computer simulations of a morphologically realistic model of DCN neurons to compare the effects of purely somatic vs. distributed dendritic inputs in this cell type. We applied the same conductance stimuli used in our published experiments to the model. To simulate variability in neuronal responses to repeated stimuli, we added a somatic white current noise to reproduce subthreshold fluctuations in the membrane potential. We were able to replicate our dynamic clamp results with respect to spike rates and spike precision for different patterns of background synaptic activity. We found only minor differences in the spike pattern generation between focal or distributed input in this cell type even when strong inhibitory or excitatory bursts were applied. However, the location dependence of dynamic clamp stimuli is likely to be different for each cell type examined, and the simulation approach developed in the present study will allow a careful assessment of location dependence in all cell types.

dynamic clamping is an increasingly widely used technique that allows the application of artificial conductances (Robinson and Kawai 1993; Sharp et al. 1993) to a neuron using whole cell methods. However, a major limitation of dynamic clamp is that the artificial conductances are focally applied only at the site of the electrode, usually the soma, and may not realistically represent the effects of distributed dendritic synapses (Prinz et al. 2004). Because of passive cable properties, synaptic potentials from distal dendritic sites are delayed and attenuated before reaching the soma (Rall 1967). On the other hand, local dendritic voltage-gated currents can interact with synaptic potentials to amplify synaptic input or even initiate action potentials (Johnston et al. 1996; London and Hausser 2005). Because many of these processes are nonlinear and depend on analytically nonsolvable systems of equations, computer simulations provide the only tool to systematically investigate the role of dendritic morphology and voltage-gated conductances in affecting synaptic responses and hence affecting the difference in responses for dynamic clamp stimuli applied at the soma and naturally distributed synaptic input.

In the present study, we have developed a computer simulation approach and a set of benchmarks to assess differences in responses between distributed synaptic input and the same input applied focally at the soma. To test this approach against real dynamic clamp data, we used deep cerebellar nucleus (DCN) neurons as a model system because we have extensive dynamic clamp data available (Gauck and Jaeger 2000, 2003) and have developed a morphologically realistic compartmental model with appropriate voltage-gated conductances to replicate current clamp data recorded in vitro (Steuber et al. 2011). Since an important aspect of dynamic clamp data is given in the precision of spike responses in the presence of stochastic voltage fluctuations, a noise source needs to be implemented in simulations replicating dynamic clamp data. Validating a simple somatic noise current to allow replication of dynamic clamp data provided the first step in developing the benchmarks described presently. We then applied the same background synaptic input used in our previous experimental studies to the model neuron and determined how the output spike pattern, spike timing precision, and spike rate differed for focalized and distributed input. In the case of our relatively electrotonically compact DCN neuron, distributing the same synaptic input patterns over the dendritic tree resulted in only minor differences in the resulting spike patterns. Our simulation approach and benchmark tests are applicable to any neural morphology, however, and a higher degree of deviation between focal and distributed input conditions is expected in larger cell types with prominent local dendritic processing. We have provided a set of simulation scripts on the ModelDB database (http://www.neuron.yale.edu/course/modeldb.html) that can easily be adapted to other cell types by importing morphology files and membrane conductance settings.

METHODS

Dynamic Clamp Experiments

The methods for performing dynamic clamp in DCN neurons have been described previously by Gauck et al. (2000, 2003). Briefly, 300-μm sagittal cerebellar slices were obtained from 14- to 17-day-old Sprague-Dawley rats and placed in a medium containing (in mM) 124 NaCl, 3 KCl, 1.2 KH₂PO₄, 26 NaHCO₃, 2 CaCl₂, 1.9 MgSO₄, and 20 glucose. Inhibitory and excitatory synapses were blocked with 100 μM 2-amino-5-phosphonovaleric acid (AP-5), 10 μM 6-cyano-7-nitroquinoxaline-2,3-dione (CNQX), and 40 μM picrotoxin. For comparison with simulation data, the recordings were corrected for a junction potential of 10 mV as calculated with JPCalc (Barry 1994) for our solutions containing 140 mM K-gluconate.

DCN Model

Our DCN model was developed in a previous study to closely match the membrane potential trajectory found during spontaneous pacemaking in brain slices as well as responses to positive and negative current injections (Steuber et al. 2011). We have used the identical model in the present study with the exception of added current noise to the soma as described below. Similarly, any compartmental model developed in the literature can be used to employ the same methods to compare different conductance locations for synaptic input (or, in fact, the location dependence of voltage-gated currents). We suggest that such modeling provides an important companion to all dynamic clamp studies.

Morphology, passive properties, and active conductances.

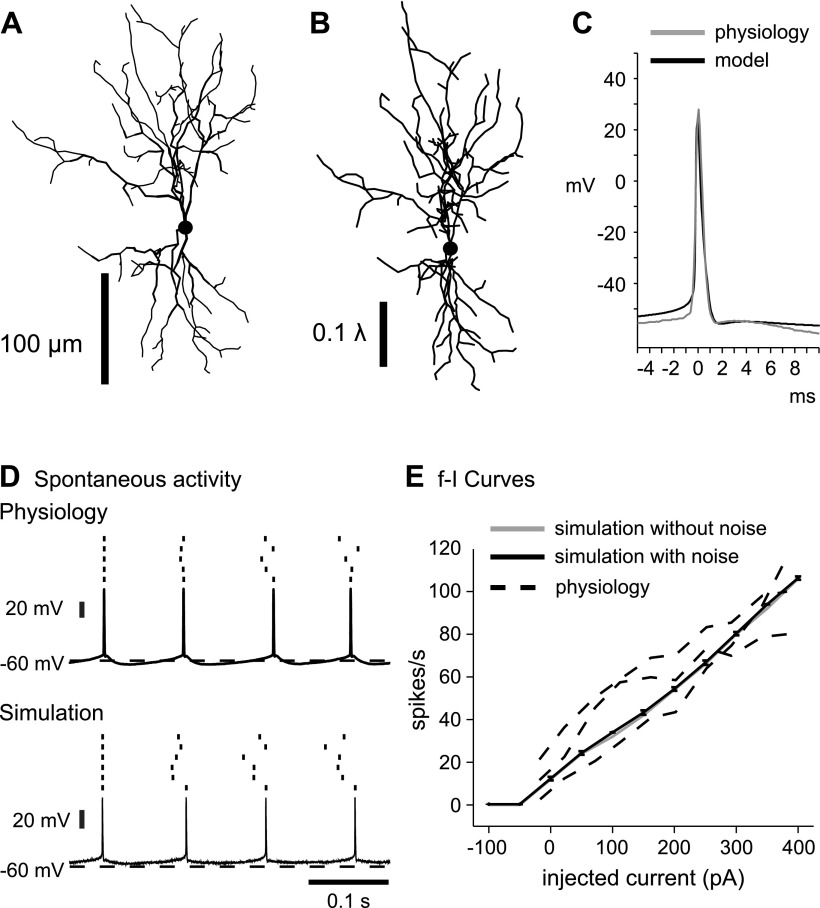
The DCN model morphology was derived from a Neurolucida reconstruction of a biocytin-labeled deep cerebellar neuron (Fig. 1A). In a previous study, a genetic algorithm was used to find passive model parameters that fit the neuron's voltage responses to positive and negative current injection in the presence of ion channel and synaptic blockers (Steuber et al. 2003). The resulting passive parameters were a uniform specific membrane resistance of 3.56 MΩ, axial resistance of 2.35 MΩ, and membrane capacitance of 0.0156 F/m². These parameters yield a total membrane resistance of 271 MΩ (inverse of summed membrane conductance for the soma and 485 dendritic compartments). The model neuron is relatively electrotonically compact with an average dendritic electrotonic distance from the soma of 0.2 λ and a maximum electrotonic distance of 0.53 λ from the soma to the most distal dendritic tip (Fig. 1B). A spike initiation zone was implemented by attaching a 30-compartment artificial axon containing an axon hillock and initial segments with increased sodium channel density following a published method (Shen et al. 1999). Simulations were run using a fixed time step of 0.01 ms.

Fig. 1.

Match of deep cerebellar nuclei (DCN) model neuron to physiological properties. A: morphological reconstruction of the DCN neuron used in model simulations. B: the same morphological reconstruction of the DCN neuron in A, redrawn to electrotonic scale. C and D: there is a good match in spike shape (C) and afterhyperpolarization properties (D) between a physiological slice recording and a sample simulation. E: spike frequency increases in response to current injection pulses similarly for the model neuron (solid) and 3 recorded neurons (dashed). Note that the addition of noise had virtually no effect on the frequency-intensity (f-I) curve of the model. Error bars for simulations with noise (n = 6) representing 1SD are plotted but due to their small size are mostly within the line width of the graph.

The model features a full complement of membrane channels based on conductances known to be present in DCN neurons (Aizenman and Linden 1999; Jahnsen 1986b; Llinas and Muhlethaler 1988; Raman et al. 2000) and implemented using the Hodgkin-Huxley formalism in GENESIS (Bower and Beeman 1997). They include a fast sodium current (NaF) that contains both a fast and slow inactivation component as shown by experiments in the DCN (Aman and Raman 2007; Raman et al. 2000), a mixture of fast Kv3 family (fKdr) and slow Kv2 family delayed rectifiers (sKdr) based on a family of tetraethylammonium-sensitive Kdr channels (Baranauskas et al. 1999, 2003), a tonic nonspecific cation current (TNC) to provide persistent inward current for tonic spiking (Raman et al. 2000), a high-voltage-activated (HVA) calcium current (Gauck et al. 2001; Molineux et al. 2006, 2008), and a low-voltage-activated T-type calcium current (CaT) that is implicated in fast rebound responses (Aizenman and Linden 1999; Llinas and Muhlethaler 1988; Molineux et al. 2006, 2008). Although several T-type channel isoforms are expressed in DCN neurons, only the Ca_V3.1 subtype is associated with strong rebound activity in DCN neurons (Molineux et al. 2006) and is included in our model. We have adapted the kinetics of an extensive CaT channel model previously developed for thalamocortical neurons (Destexhe et al. 1998). Calcium influx through the HVA calcium conductance is coupled to an intracellular calcium pool that is modeled as a diffusion shell with an exponential decay time constant of 70 ms. This long time constant results in accumulation of intracellular calcium as observed experimentally during fast spiking in DCN neurons (Muri and Knopfel 1994; Zheng and Raman 2009). The final membrane conductances in the model are a calcium-gated voltage-independent potassium current (SK) that underlies the medium afterhyperpolarization (AHP) (Aizenman and Linden 1999; Feng and Jaeger 2008; Jahnsen 1986a; Raman et al. 2000), a hyperpolarization activated (IH) current (Aizenman and Linden 1999; Jahnsen 1986a; Raman et al. 2000; Uusisaari et al. 2007), and a slowly inactivating persistent sodium current (NaP) (Jahnsen 1986b; Llinas and Muhlethaler 1988).

The density of active conductances in the model was variable among four major divisions of the model: axonal, somatic, proximal dendritic, and distal dendritic (Table 1). In particular, there were no NaF or Kdr conductances in the distal dendrites of the model, since there is no experimental evidence showing a dendritic location for these channels in the DCN. The SK conductance was also primarily somatic, to match the strong somatic medium afterhyperpolarization seen in recordings. Both the CaT and HCN conductances were distributed in a gradient with a higher density in the dendrites following experimental findings (Gauck et al. 2001; Raman et al. 2000). All channel kinetics were adjusted to a temperature of 32°C as used for the slice recordings by applying a Q10 value of 3.0 for all Hodgkin-Huxley rate constants. The density of each channel type in the model was manually adjusted until a good match of current-clamp responses with model traces was achieved. The spike shape and AHP trajectory of recordings were used as targets as well as spontaneous spike rate and frequency-intensity (f-I) curves. Detailed parameters for all channel kinetics used can be found in the Supplemental Material as well as in the simulation scripts available in the NeuronDB database (http://senselab.med.yale.edu/neurondb/default.asp). Steady-state voltage and calcium dependencies of activation and inactivation curves for the membrane conductances are provided in Supplemental Fig. S1. (Supplemental data for this article is available online at the Journal of Neurophysiology website.)

Table 1.

Channel conductance densities and CaHVA permeability for different compartment types

	Channel Conductance Density, S/m2								Permeability, ×10−8 m/s
	NaF	fKdr	sKdr	TNC	SK	CaT	NaP	IH	CaHVA
Soma	330	150	90	0.09	2	0.6	2	1.5	7.5
Proximal dendrite	33	45	27	0.018	0.6	0	0	0	5
Distal dendrite	0	0	0	0	0.6	0	0	0	5
Axon	495	300	270	0.12	0	0	0	0	0

Values are channel conductance densities for fast sodium current (NaF), fast Kv3 family (fKdr) and a slow Kv2 family delayed rectifier current (sKdr), tonic nonspecific cation current (TNC), calcium-gated voltage-independent potassium current (SK), low-voltage-activated T-type calcium current (CaT), slowly inactivating persistent sodium current (NaP), and hyperpolarization-activated current (IH) and permeability for high-voltage-activated calcium current (CaHVA) for the different compartment types. Axon refers to the conductance densities and CaHVA permeability in the axon hillock and initial segment.

Synaptic input.

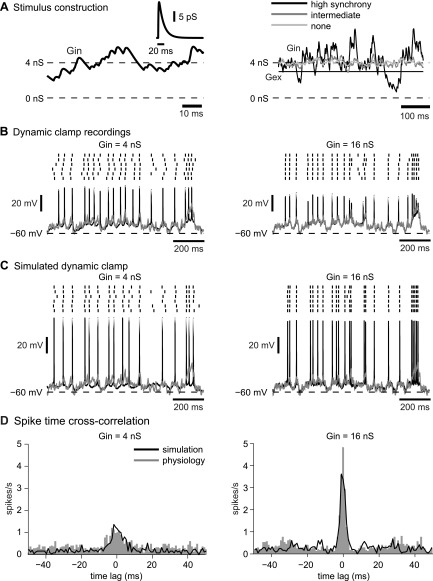
In this study, we utilized the synaptic kinetics used to construct the original dynamic clamp stimuli in Gauck et al. (2000), which were based on in vitro recordings (Anchisi et al. 2001). Although some synaptic kinetic parameters for dl-α-amino-3-hydroxy-5-methylisoxazole-propionic acid (AMPA) and GABA_A synapses onto DCN neurons have since been updated in the literature (Pugh and Raman 2006, 2008; Telgkamp et al. 2004), using the original model synapses allows us to exactly reproduce the experimental dynamic clamp input conductance waveforms. Inhibitory GABA_A-type Purkinje cell input was modeled as 400 presynaptic input elements and implemented as GENESIS “synchan” objects. The GENESIS “timetable” object was used to generate random distributions of synaptic events that activated the synapses at a mean rate of 35 Hz. The inhibitory synapses were modeled as dual-exponential functions with a rise time constant of 0.93 ms and a decay time constant of 13.6 ms. The sum of the inhibitory postsynaptic conductances from all 400 inhibitory synapses was used as the inhibitory conductance waveform (G_in) (see Fig. 3A, left). To isolate the effect of inhibition on spiking, the excitatory conductance (G_ex) was held at a constant level such that the ratio of total excitatory to mean inhibitory conductance was 3:4. We varied the level of synaptic strength by multiplying both the inhibitory and excitatory conductances by a gain factor. The default amount of conductance used (gain of 1) corresponded to a total mean G_in of 2 nS and a unitary conductance of 8.6 pS, and this level was increased up to 16-fold for a mean G_in of 32 nS (gain of 16). Three different levels of input synchronization were also implemented (see Fig. 3A, right). At the highest level of synchronization, the 400 inhibitory synapses were divided into 10 groups of 40 synchronized synapses. To simulate an intermediate level of synchronization, the 400 inhibitory synapses were divided into 100 groups of 4 synchronized synapses.

Fig. 3.

Match of dynamic clamp simulations to slice recordings. A: the dynamic clamp inhibitory conductance waveform (G_in) is the sum of 400 inhibitory input conductances over time. The timing of inputs is stochastic and composed of single inhibitory postsynaptic conductances with a double-exponential time course and a peak of 17.2 pS (inset), which results in a mean G_in of 4 nS. Inhibitory conductance waveforms for higher levels of synchronicity have larger transient fluctuations around the mean. Excitatory conductance (G_ex) is constant at a level of ¾ that of mean G_in. B: sample recordings of dynamic clamp voltage traces are shown for high input synchronization and 2 levels of inhibition. For a mean G_in of 16 nS, the subthreshold membrane potential (solid) closely follows the synaptic driving force (E_syn; shaded). C: voltage traces from the computer model with the exact same synaptic inputs applied to the soma, simulating dynamic clamp. D: there is a more prominent central peak in the spike-time cross-correlogram for a G_in of 16 nS than for a G_in of 4 nS, indicating greater spike-time precision at higher input gains. The spike-time cross-correlograms are very similar between the model (solid) and the experimental data (shaded). The percentages of spikes that were aligned within a window of ±1 ms for the sample neuron shown and the model, respectively, were 12 and 11.5% for a G_in of 4 nS and 42 and 38.7% for a G_in of 16 nS.

The maximal conductance of a single inhibitory synapse and the level of tonic excitatory conductance were originally chosen by Gauck et al. (2000) to yield in vivo spike frequencies in dynamic clamp. The average combined synaptic reversal potential (E_syn) was −40 mV. E_syn is the weighted average of the inhibitory (E_in) and excitatory reversal potentials (E_ex): E_syn = (E_ex·G_ex + E_in·G_in)/(G_ex + G_in). For dynamic clamp, the injected current can be formulated as I_inj = (G_ex + G_in)(E_syn − V_m) such that I_inj is zero when the membrane potential (V_m) equals Esyn. The reversal potentials of the excitatory and inhibitory synaptic conductances were initially set to 0 and −70 mV, respectively. Since the original recordings were not corrected for a junction potential of 10 mV during dynamic clamp, the reversal potentials of the synapses in the model were shifted downward by 10 mV. They were then further shifted by the difference in the mean value of the subthreshold membrane potential between the slice recordings (−49.4 ± 3.0 mV) and the model (−53.8 ± 1.83 mV). These values were calculated after a window of 3 ms before and after the peak of each action potential was removed. The final reversal potentials of the excitatory and inhibitory synapses in the simulations were set at −14.4 and −84.4 mV, respectively. The result of these manipulations was that the amplitude of total synaptic current generated in the model was comparable to the current injected by dynamic clamp in the experiments by Gauck et al. (2000) for a given input condition.

For simulations using synaptic excitation rather than tonic excitation, we used the synaptic input conditions presented by Gauck et al. (2003). A population of 100 excitatory mossy fiber synapses was modeled with three components: an AMPA component, a fast N-methyl-d-aspartate (NMDA) component, and a slow NMDA component. The rise and decay time constants were 0.5 and 7 ms for AMPA, 5 and 20.2 ms for fast NMDA, and 5 and 136.4 ms for slow NMDA. The fast unitary NMDA conductance had a peak value of 57% of the AMPA peak, and the slow unitary NMDA conductance had a peak value of 28% of the AMPA peak. The unitary peak conductance amplitude of the AMPA conductance was set to 58.5 pS so that the sum of all excitatory conductances still had a mean of 1.5 nS at a gain of 1 to maintain the 3:4 ratio of mean excitatory to inhibitory conductance. These synapses were activated at a mean rate of 20 Hz and used the shifted excitatory reversal potential described earlier.

Focalized vs. distributed synaptic input.

To simulate dynamic clamp, the synapses were focalized completely on the soma, which is the site of current injection with a somatic whole cell recording. The total synaptic current generated in the model is analogous to the current injected by the dynamic clamp. For the distributed input condition, the same number of inhibitory synapses was randomly distributed with 12% (48) on the soma, 37% (148) on the proximal dendrites, and 51% (204) on the distal dendrites to approximate experimentally observed input distributions (Palkovits et al. 1977). Since nearly all somatic synapses are inhibitory for DCN neurons, no excitation was placed on the soma for either the tonic or synaptic excitation input conditions (Chan-Palay 1977; De Zeeuw and Berrebi 1995; Palkovits et al. 1977). Tonic excitatory conductance was added to each proximal or distal dendritic compartment that contained an inhibitory synapse and scaled so that the total amount of excitatory conductance was the same for both the focalized and distributed input conditions. For synaptic excitation, the 100 excitatory synapses were placed on randomly chosen proximal and distal dendritic compartments. The total amount of inhibitory and excitatory synaptic conductance as well as the temporal input patterns were the same for both focalized and distributed input conditions.

Simulation of Noise

To simulate repeated trials of the dynamic clamp stimuli, noise was introduced to the model as a fluctuating somatic current injection. The noise was constructed as a white noise stimulus with a mean of 0 pA and a standard deviation of 200 pA. Since the noise had zero mean, its application did not change the net current that passed through the membrane over the course of synaptic input simulations. The level of noise was chosen to reproduce the amplitude of subthreshold fluctuations in membrane potential in the experimental recordings (Fig. 2B). This current was always applied somatically in the model for both focalized and distributed synaptic input conditions. Six waveforms of frozen noise were obtained by using different random seeds to result in six repeated runs with identical synaptic input conditions under varying noise conditions, as we had previously obtained in our recordings. In test simulations, we also applied current noise to the action potential initiation zone in the axon hillock and initial segment, which has a twofold increase in sodium channels compared with the soma (Steuber et al. 2011).

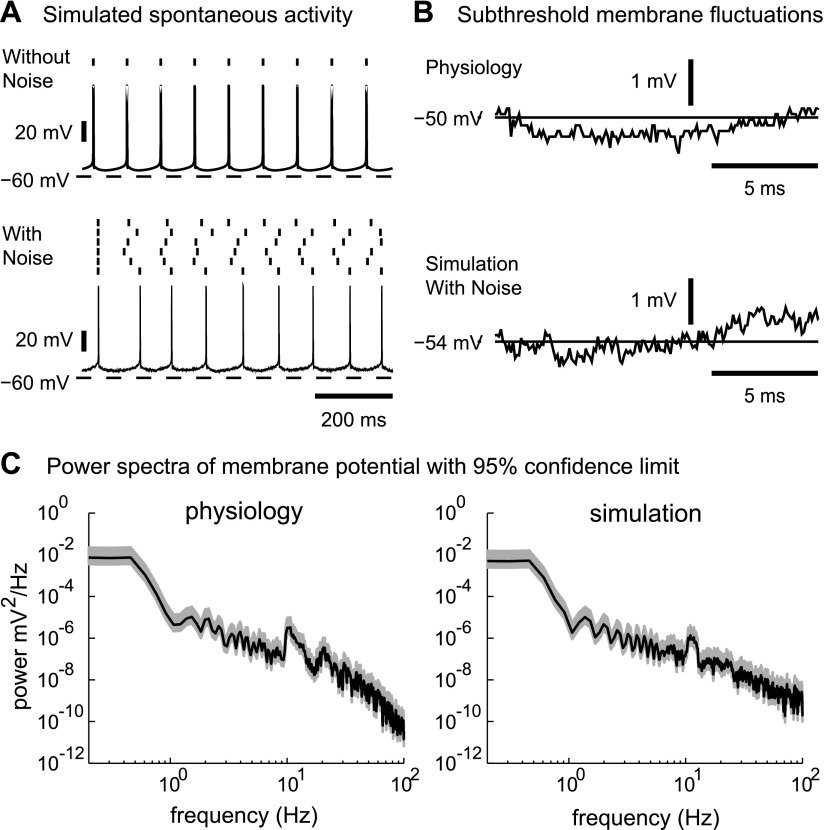
Fig. 2.

Effect of noise on spontaneous spiking and subthreshold voltage oscillations in the model. A: the model without noise spikes perfectly regularly (top). The effect of the additional white noise current introduces variability in spike timing that simulates variability of spontaneous spiking seen in vitro even in the presence of synaptic blockers (bottom). B: there is a good match in the amplitude of the subthreshold voltage fluctuations between a recorded neuron (top) and the simulation (bottom), further validating our noise model. C: the power spectra of the membrane potential also show a good match between recordings and simulations with noise. Spikes were removed before analysis (see methods). The shaded area indicates the 95% confidence level for the power spectral estimate.

Data Analysis

Simulation data were analyzed using MATLAB (The MathWorks, Natick, MA). Spike-time precision was calculated using the same method as Gauck et al. (2000) and is defined as the percentage of spikes that occur synchronously above chance level as computed by cross-correlation histograms with 1-ms binwidth. The cross-correlogram was calculated from pairwise comparison of spike trains obtained with successive stimulus applications. The raw correlogram was corrected for its dependency on spike frequency by computing the expected level of correlation from spike trains with shuffled interspike intervals and subtracting it from the raw correlogram. The power spectral density of the membrane potential was estimated using a multitaper method to reduce bias (Yaron-Jakoubovitch et al. 2008). A window of 3 ms before and after the peak of each spike was removed before the analysis. To analyze the input events responsible for spike generation, we computed the spike-triggered average (STA) of the excitatory and inhibitory input conductances in a window of ±150 ms around detected spike times. This technique is a reverse correlation method often used in neural electrophysiology to determine the optimal features of a time-varying stimulus that elicits a specific response by providing an estimate of a neuron's linear receptive field (Aguera y Arcas and Fairhall 2003; Bialek and Rieke 1992; de Boer and Kuyper 1968).

RESULTS

Spontaneous Spiking Properties of the Model With Added Noise and Comparison With Slice Recordings

In the absence of excitatory or inhibitory synaptic inputs, the model was able to reproduce the spontaneous spike waveforms and spike rates observed in DCN neurons in brain slices (Fig. 1, C and D). In fact, for each target measure such as spike height and width, spike afterdepolarization, spontaneous spike rate, and f-I curve, the model's performance was within the variability of the same measures observed in recordings. The model showed a spontaneous spike rate of 11.2 Hz both with and without added somatic current noise, since the applied noise current had a mean of 0 pA. The additional somatic noise current also did not significantly affect the model's spike rate increases in response to injected current pulses (Fig. 1E). The subthreshold membrane potential of the model was calculated after removal of spikes to be −53.8 mV without noise and −53.9 mV with noise (Fig. 2A). This compared well with a subthreshold membrane potential in experimental recordings of −49.4 mV (n = 33 neurons) after the 10-mV junction potential was removed (see methods). The added noise introduced small irregularities to the spontaneous firing pattern of the model [coefficient of variance (CV) = 0.143], which settled to nearly perfectly regular pacemaker activity in the absence of noise. The irregularity of spontaneous spiking in our experimental recordings was similar to the model with added noise (CV = 0.126, n = 9 neurons). This similarity served as an independent verification of the validity of adding noise in the form of somatic current injection, since our noise amplitude was originally chosen to match the level of subthreshold membrane potential fluctuations found in the experimental recordings (Fig. 2B). The power spectra of the voltage noise at the soma for the electrophysiology recordings and our simulations were very similar (Fig. 2C). Because noise affects spike timing predominantly through effects in the spike initiation zone, we examined the subthreshold noise trajectory in our simulated axon hillock and initial segment with a somatic noise source and compared this result with a direct application of the same noise to the axon hillock and the axon initial segment (Supplemental Fig. S2). The noise fluctuations in V_m were nearly indistinguishable in all cases, which can be explained by the electrotonically close proximity of the axon initial segment to the soma in the model.

Comparison Between Dynamic Clamp Experiments and Focalized Synaptic Inputs in the Model

To isolate the effect of Purkinje cell inhibition on the control of DCN spiking, excitation was held constant while inhibitory inputs were constructed from spike trains of 400 inhibitory presynaptic elements that generated inhibitory postsynaptic conductances in the model. This input pattern exactly matched our previous dynamic clamp input used in published experiments (Gauck et al. 2000; see methods).

In close parallel, in both the experiment (Fig. 3B) and the model (Fig. 3C), the subthreshold membrane potential was increasingly controlled by the trajectory of the synaptic input conductance when the average level of input was increased from 4 to 16 nS. As we previously described in our dynamic clamp studies (Gauck and Jaeger 2000, 2003), the subthreshold membrane potential was forced to follow the combined reversal potential of excitation and inhibition (E_syn) because any deviation from this trajectory leads to a sharp increase in synaptic driving force and a resulting corrective current. The magnitude of the central peak in the cross-correlogram between E_syn and the subthreshold membrane potential (spikes were removed using a window of ±3 ms around the spike time) increased smoothly from a value of 0.20 to 0.85 as the average level of input was increased from 1 to 32 nS (Supplemental Fig. S3). At a mean inhibitory input conductance of 4 nS, the activation of intrinsic currents of the neuron still results in substantial deviations of the subthreshold membrane potential from E_syn, most notably during activation of the postspike AHP currents. At an increased mean inhibitory conductance of 16 nS, the shunting effect of inhibition was increased such that in both the dynamic clamp data and the model, the spike AHPs were almost completely suppressed, and the subthreshold membrane potential converged onto E_syn (Supplemental Fig. S4). Spike alignment for repeated applications of the same synaptic conductance trajectory was apparent from the raster plots (Fig. 3, B and C). We quantified this spike alignment using a cross-correlation analysis, which showed an increasingly pronounced central peak for spike alignment between trials when the mean synaptic conductance level was increased (Fig. 3D). For all input conditions, the spike time cross-correlograms were very similar between the model and the experimental data. The percentage of spikes that were aligned within a window of ±1 ms for the sample neuron shown and the model, respectively, were 12 and 11.5% for a 4-nS mean inhibitory conductance and 42 and 38.7% for 16 nS. Therefore, the model provided a close match to our slice recordings with respect to the conductance amplitude needed to control spiking by somatic conductance application.

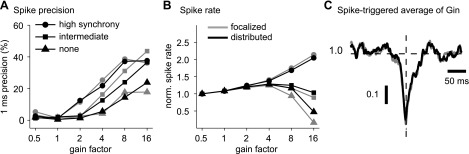
Synchronicity of spiking between Purkinje cells might provide an important coding feature in the cerebellum (De Schutter and Steuber 2009; Lang et al. 1999; Shin and De Schutter 2006; Wylie et al. 1995; Yamamoto et al. 2001), and therefore we had used partly synchronized inhibitory input patterns in our dynamic clamp study to determine the consequences of input synchronization. When our 400 inhibitory inputs were divided into 40 or 4 groups of synchronously firing subpopulations, the ensuing fluctuations in total inhibitory conductance were much larger and strong depolarizing shifts in E_syn were more frequent (Fig. 3A, right). This change in input conductance resulted in a similar increase in spike rate as well as spike precision in the model and the slice recordings (Fig. 4A). Another benchmark, the STA of input conductance, was computed for a duration of ±150 ms around the peak of the action potentials and normalized to a mean value of 1.0. This measure shows that a transient decrease in inhibition caused by brief pauses in Purkinje cell input served as a reliable trigger for spikes. Both the amplitude and the time course of the STA for inhibitory conductance were similar between the recording and the model (Fig. 4A, right). Both the recordings and the model also showed that at high input gains but low levels of synchronization, the spike rate precipitously dropped to near zero, although the mean conductance levels were identical with those at higher levels of synchronization that elicited much faster spike rates. This effect is of high physiological interest, because it suggests that DCN spiking may primarily be due to input fluctuations and that in the presence of completely random Purkinje cell inputs, DCN neurons would not spike due to a high steady-state GABA conductance. In contrast, in the presence of input fluctuations due to synchronous input populations, an increase in input level leads to an increase in output spike rate in recordings, an effect that was also matched by the model (Fig. 4A). Note that the balance of excitatory and inhibitory conductance and the trajectory of the combined reversal potential are identical at all input levels. Therefore, an increase in spike rate at higher input levels is due to the increase in synaptic current that occurs for the same driving force when the conductance is increased. Overall, the good matches observed between model responses and our previous dynamic clamp study indicate that the model and the recorded neurons responded reliably to the same features in inhibitory input conductance.

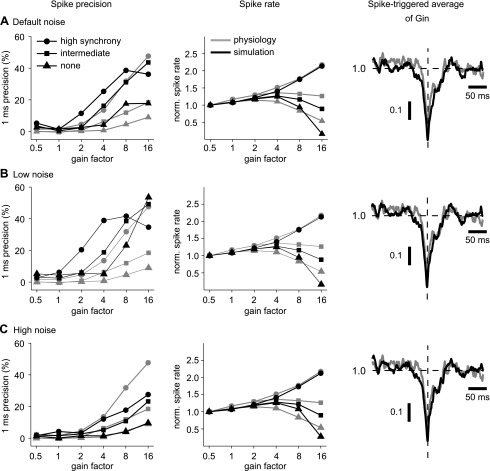
Fig. 4.

Spike-time precision and spike frequency for 3 different levels of noise in the model. A, left: spike-time precision increases with both input gain and synchronicity for recorded neurons (shaded) and the model (solid). The relationships between precision and gain are preserved in the model, although precision values are slightly higher. Middle: spike frequency increases with input gain at high input synchronicity but actually decreases for intermediate or no input synchronicity. Spike frequency is normalized by the value at a gain of 0.5. The mean spike frequencies at a gain of 0.5 for the model were 12.4 (high synchronicity), 12.7 (intermediate synchronicity), and 12.7 Hz (no synchronicity). The mean spike frequencies at a gain of 0.5 for the recordings were 10.0 (high input synchronicity), 9.0 (intermediate synchronicity), and 10.2 Hz (no synchronicity). Right: the spike-triggered average (STA) of inhibitory conductance (normalized to the mean conductance value) for high input synchronicity and a gain of 16 is similar for both the model and recorded neurons. The transient drop in STA conductance indicates that spikes were triggered by brief pauses in Purkinje cell input. B and C: the relationships between precision and output spike rate with input gain and synchronicity and the STA of inhibitory conductance are shown for additional levels of low noise (B) and high noise (C). For low noise, the mean spike frequencies at the gain of 0.5 were 12.4 (high input synchronicity), 12.6 (intermediate synchronicity), and 12.6 Hz (no synchronicity). For high noise, the mean spike frequencies at the gain of 0.5 were 12.4 (high input synchronicity), 12.7 (intermediate synchronicity), and 12.7 Hz (no synchronicity).

Spike precision of spontaneous activity in the model was highly dependent on the amplitude of the added noise. Although the level of noise was tuned only to replicate the amplitude of subthreshold voltage fluctuations, the model also reproduced comparable values of spike-time precision in spontaneous spiking. In addition, our simulations with dynamic clamp stimuli show that the model with this level of noise also replicated the spike timing precision benchmark measurement and its dependence on input gain and synchronicity as observed in recordings, although some deviations in the absolute values of precision existed at low and intermediate levels of synaptic gain (Fig. 4A). In additional simulations, we sought to address the question of what role the level of membrane noise plays in the control of spike timing precision by synaptic input. To address this question, we repeated the dynamic clamp simulations for two additional levels of noise, a high level of noise with a standard deviation of 720 pA (Fig. 4C) and a low level of noise with a standard deviation of 60 pA (Fig. 4B). As expected, for a low level of noise, the spike-time precision increased across all input conditions. This effect was especially pronounced in the absence of input synchronicity, where noise contributed most to spike timing variability. In contrast, a low level of noise did not result in a change in output spike rate or the STA of inhibitory conductance This independence of output spike rate and spike-triggered conductance average was also seen at a high level of applied noise current (Fig. 4C). The effect of a high noise level on spike timing precision was opposite to that of reduced noise, because the spike-time precision decreased for all combinations of input gain and synchronization. This actually resulted in an improved match between model and recordings for spike-time precision in the case of no or intermediate input synchronicity but a worse match for high input synchronicity. These observations suggest that our simplified simulation of noise as a purely somatic current may not fully reproduce the biological noise source in its effects on spike precision under different input conditions. However, the simulations using our default level of noise showed all qualitative dependencies of input conditions on spike precision seen in recordings as well as reasonable quantitative matches for all input conditions and was therefore fully sufficient to examine how distributing the same synaptic input patterns across dendrites may affect the control of spike output.

Comparison Between Focalized and Distributed Synaptic Inputs in the Model

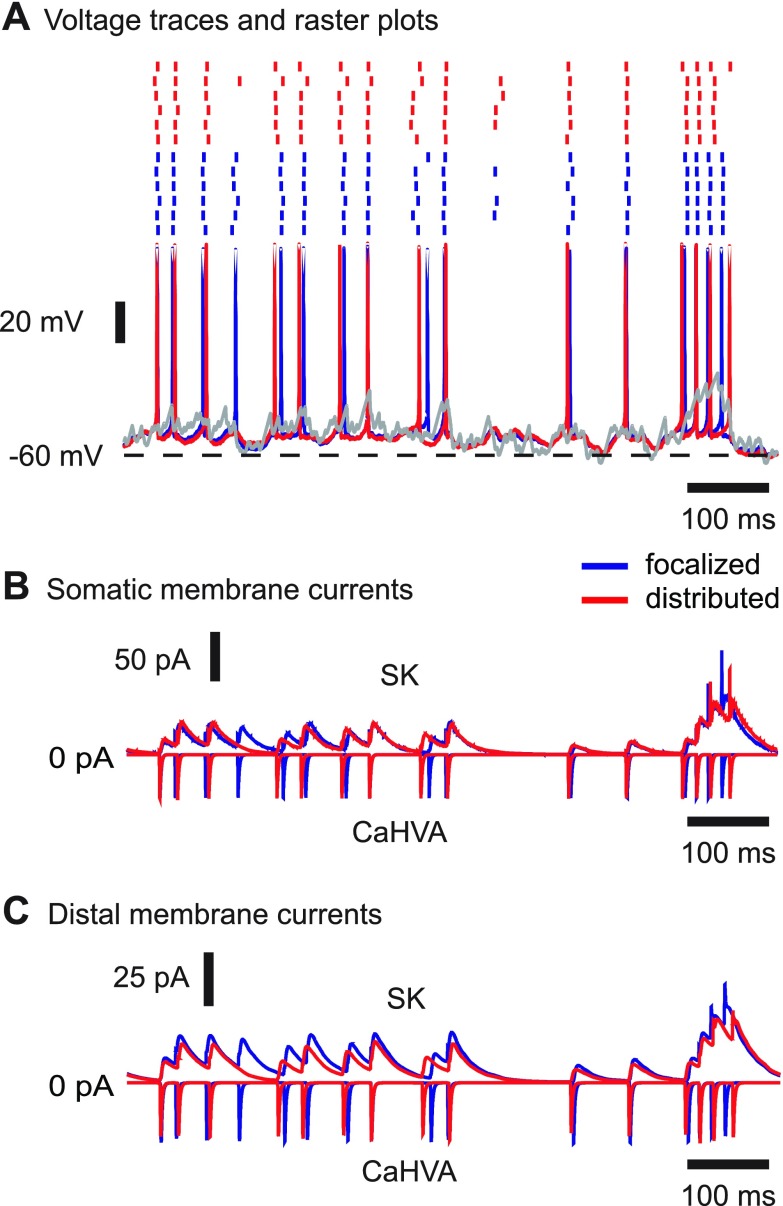
A major limitation of dynamic clamp is that the artificial conductances are focally applied only at the site of the electrode, in this case the soma, and may not realistically represent the effects of distributed dendritic synapses (Prinz et al. 2004). Distributed synaptic input was simulated by relocating synapses from the soma of the model neuron to dendritic compartments such that the summed synaptic conductance waveform remained the same. For high input synchronicity and a mean inhibitory input level of 16 nS, the mean subthreshold membrane potential was slightly more depolarized for focalized inputs (−53.3 mV) than for distributed inputs (−53.9 mV). Spike heights were also ∼3–4 mV shorter for focalized inputs, which is likely due to the increased local shunting of spike conductances when the input is focused at the soma. We found that the spike pattern induced with a simulated dynamic clamp at the soma in this model was very similar to the spike pattern induced with the same synaptic conductance patterns applied through a set of distributed dendritic synapses (Fig. 5A). Although the exact timing of individual spikes was slightly different for these two input conditions when the same pattern of frozen noise was applied to the soma, changes in spike rate due to depolarizing or hyperpolarizing transients in E_syn clearly matched.

Fig. 5.

Comparison of responses to focalized or distributed inputs in the model. A: the same set of synaptic inputs was delivered focally at the soma or distributed over the dendrites and resulted in very similar membrane voltage trajectories and spike patterns. B and C: the calcium-gated voltage-independent potassium (SK) and high-voltage-activated calcium currents (CaHVA) in the soma (B) and distal dendrites (C) are activated similarly by focalized or distributed dendritic input, despite the very different localization of inputs.

This similarity in the action of focal and distributed input can be explained by the relatively electrotonically compact structure of DCN neurons (Fig. 1B). In a passive morphology in which the large majority of dendritic surface is within 0.2 λ of the soma, little attenuation occurs in the dendrites for low-frequency voltage signals caused by synaptic inputs. We found that somatic membrane voltage fluctuated similarly for purely somatic or distributed dendritic inputs (Fig. 5A) and that dendritic voltage-gated currents were evoked in a very similar pattern in both input conditions (Fig. 5C). In the model, action potentials triggered the inward calcium HVA current, increasing the intracellular calcium concentration that drives SK channel activation. For both purely somatic or distributed synaptic input, these currents were evoked with similar time courses and amplitudes in the soma (Fig. 5B) and in the dendrites (Fig. 5C). The SK current dominates the intrinsic currents in the middle of interspike intervals and makes a particularly strong contribution to spacing between spikes (Feng and Jaeger 2008). Therefore, the similarity of the time course of this current in both the soma and the dendrites between focalized and distributed input conditions allows for closely matching spiking responses. The added noise in the model not only contributed to spike time jitter but also caused “extra” or “missing” spikes across trials. In our sample of brain slice recordings, although some spike times did occur with high reliability between neurons given the same stimulus, the variability in spike pattern was still quite high (Fig. 6). In fact, the spike patterns found for somatic or dendritic input conditions in the simulated neuron were much more closely aligned with each other than were different recorded neurons. We quantified the similarity in the spike pattern by using the same spike-time precision benchmark described above. The average 1-ms spike-time precision was computed from cross-correlations of all pairwise combinations of trials. Across the set of biological neurons, the proportion of shared precisely aligned spikes was 23.0 ± 5.2% compared with 40.1% between simulations using somatic vs. dendritic input (Table 2). Furthermore, the average 1-ms spike-time precision between pairwise combinations of all the experimental trials with the simulations was 22.3 ± 2.8%, indicating that the spike patterns that emerged from the simulations are within the variability of the set of responses elicited from the biological neurons. Note that the spike responses of neuron 4 in the experimental sample in particular very closely match the simulated responses.

Fig. 6.

The model shows a spike pattern response to focal somatic synaptic input similar to that of recorded neurons under dynamic clamp. Note the variability in output spike patterns between recorded neurons given the same stimulus. Data are shown for a mean G_in of 16 nS and high input synchronization.

Table 2.

Average 1-ms spike-time precision computed from cross-correlations of all pairwise combinations of trials

	Spike-Time Precision, %
	Neuron 1	Neuron 2	Neuron 3	Neuron 4	Focal	Distributed
Neuron 1	28.6	24.3	15.9	19.6	19.6	19.7
Neuron 2		34.9	31.2	22.7	19.6	20.9
Neuron 3			30.5	24.5	22.3	24.8
Neuron 4				35.3	25.0	26.6
Focal					38.7	40.1
Dist						37.2

Values are the 1-ms spike-time precision (%) computed from cross-correlations of all pairwise combinations of trials across the set of biological neurons and the neuron model with focalized or distributed synaptic input. Data are shown for a mean G_in of 16 nS and high input synchronization.

In addition to a very similar spike pattern, the focalized and distributed synaptic input simulations also resulted in a similar dependency of spike precision and rate on input conditions (Fig. 7). Overall, spike frequency in response to these stimuli was about 0.2 Hz lower for distributed inputs than for focalized inputs. This small difference in spike rate is probably due to the 0.6 mV more depolarized average V_m in the soma for focal input noted above. In addition, with distributed inputs, the model was slightly less sensitive to changes in input amplitude such that spike rates were not increased or decreased as much at different input levels. This is likely due to a decrease in synaptic shunting effects at the soma for distributed inputs. Nevertheless, the STA of inhibitory conductance matched closely for both input conditions (Fig. 7C), indicating that spikes were evoked by the same time course of disinhibition.

Fig. 7.

Spike-time precision and spike frequency for focalized or distributed inputs in the model. The relationship between spike precision (A) and spike frequency (B) with input gain and synchronicity was very similar for focalized inputs (shaded) and distributed inputs (solid). C: The STA of inhibitory conductance (normalized to the mean conductance value) for high input synchronicity and a gain of 16 showed that the same time course of disinhibition evokes spikes in both cases.

Response to Patterned Synaptic Input

The synaptic background input used in our dynamic clamp study was purely stochastic with a stationary mean rate, whereas DCN neurons in vivo are likely subject to strongly patterned synaptic input due to bursts and pauses in Purkinje cell and mossy fiber activity in vivo. Prolonged increases or decreases in the simple spike firing rate of Purkinje cells have been observed in response to both sensory stimulation (Loewenstein et al. 2005) and motor behavior (Medina and Lisberger 2008). Numerous studies have demonstrated correlations in simple and complex spike activity (Lang et al. 1999; Wylie et al. 1995; Yamamoto et al. 2001) that can be modulated by behavior (Heck et al. 2002, 2007; Shin et al. 2007) as well as correlated pauses in Purkinje cell firing that can mediate DCN activity (De Schutter and Steuber 2009; Shin and De Schutter 2006). This correlated activity produces sharp fluctuations in input to DCN neurons that can then be encoded with high reliability. Mossy fiber input to the DCN is less well understood, but its firing rate is known to be strongly modulated by movement with complex biphasic or triphasic activity patterns and high-frequency bursts that can last up to several hundreds of milliseconds (Rancz et al. 2007; van Kan et al. 1993).

To determine how strongly patterned synaptic input can shape the response of DCN neurons and whether the distributed input condition still resembles the focalized one, we added burst and pause features in addition to the background synaptic input in the model. We replaced the tonic level of excitation with mixed AMPA and NMDA synapses as in Gauck et al. (2003) and generated 10 different stimuli of random background synaptic activity with the same added frozen current noise. Inhibitory input was modeled with an input level of 16 nS and intermediate synchronicity, which resulted in moderate fluctuations of input conductance so that the additional bursts and pauses could stand out against the background activity. Excitatory input was also modeled with intermediate synchronicity with a gain such that mean excitatory conductance was 75% that of inhibitory conductance. For a 200-ms window of time, we imposed a burst or pause in inhibition or a burst in excitation. The mean firing rate of the model without an additional input burst or pause was 26.9 Hz for focalized inputs and 23.0 Hz for distributed inputs, which is similar to previously reported in vivo firing rates (Alvina et al. 2008; LeDoux et al. 1998). The mean subthreshold membrane potential was again slightly more depolarized for focalized inputs (−52.5 mV) than for distributed inputs (−53.3 mV). A summary of the firing rates resulting from inhibitory and excitatory bursts and pauses is presented in Table 3.

Table 3.

Average firing rate for patterned synaptic input

	Spike Rate, Hz
	Focalized	Distributed
Base model
Control (stochastic)	26.9	23.0
Inhibitory burst	1.0	1.5
Inhibitory pause	51.2	41.3
Excitatory burst (2×)	52.4	40.5
Excitatory burst (3×)	88.3	64.7
Model with stronger rebound currents
Control (stochastic)	29.7	25.3
Inhibitory burst	4.7	3.0
Inhibitory pause	55.4	44.3
Excitatory burst (2×)	56.1	43.7
Excitatory burst (3×)	90.9	68.1

Values are average spike rate during a burst or pause for patterned synaptic input.

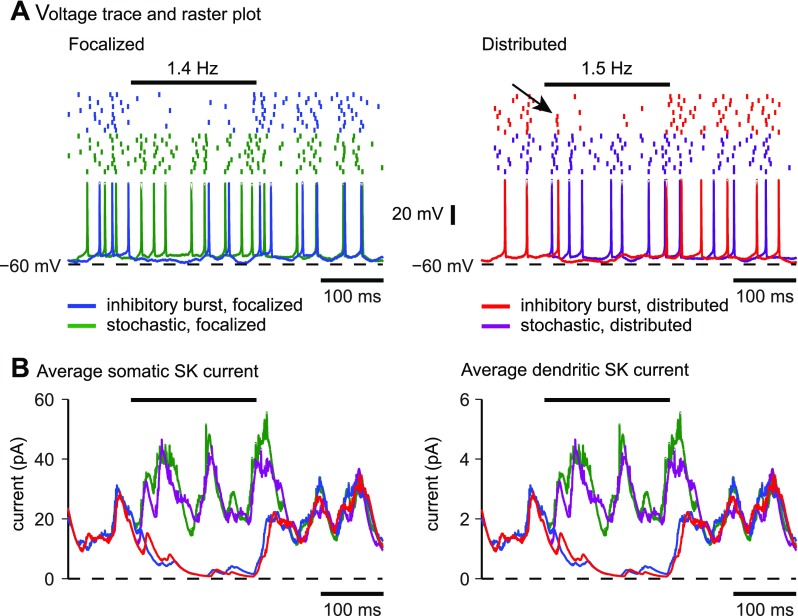
An inhibitory burst was modeled as a 200-ms-long doubling of the 35-Hz firing rate in one-half of the inhibitory synapses to 70 Hz, which was equivalent to an overall increase of 50% in the frequency of inhibitory inputs. An inhibitory input rate of 70 Hz is well within the range of reported Purkinje cell firing rates, which can reach rates of up to 100 Hz in vivo (Armstrong and Rawson 1979; Thach 1968). This simulated inhibitory burst was sufficient to cause a nearly complete cessation of spiking in the model for both focalized and distributed input (Fig. 8A). The membrane potential was slightly hyperpolarized during the inhibitory burst but did not go below −60 mV. Thus a pause in spiking was achieved without deep hyperpolarization and without an ensuing rebound, as was observed in the same model with much stronger inhibitory input bursts that hyperpolarize the membrane below −75 mV (Steuber et al. 2011). For distributed but not focalized inputs, a few spikes still occurred shortly after the start of the burst (Fig. 8A, arrow), indicating that the model was a little slower to hyperpolarize following the increase in inhibition. These spikes all occurred within the first 20 ms of the burst. The similarity in spiking between focalized and distributed inhibitory burst input was paralleled by a similar change in intrinsic currents during the burst. Regardless of input location, the inhibitory input burst resulted in a near complete cessation of SK current in both the soma (Fig. 8B, left) and the dendrites (Fig. 8B, right). It took an additional 50 ms after the end of the input burst before the SK current reapproached the control traces (Fig. 8B), again regardless of input location.

Fig. 8.

Response to an inhibitory input burst for focalized or distributed input in the model. The horizontal bar above the raster plots indicates the duration of the input burst. The mean firing rate in the control trials was 26.9 Hz for focalized inputs and 23.0 Hz for distributed input. Before the start of the input burst, spike times in the control and patterned trials were exactly the same. A: a 50% increase in the inhibitory input rate caused a nearly complete suppression of spiking to a 1.4-Hz spike rate for focalized input (left) and to a 1.5-Hz spike rate for distributed input (right). For distributed dendritic input, the onset of spike suppression was not as complete during the first 25 ms, and in some trials spikes were still present early during the inhibitory period (arrow). B: during the inhibitory burst, the magnitude of the SK current strongly decreased due to the absence of spikes but returned to the control trajectory when the burst ended. The pattern of SK activation was similar for both the focalized and distributed input conditions. The average SK current across different noise conditions is shown.

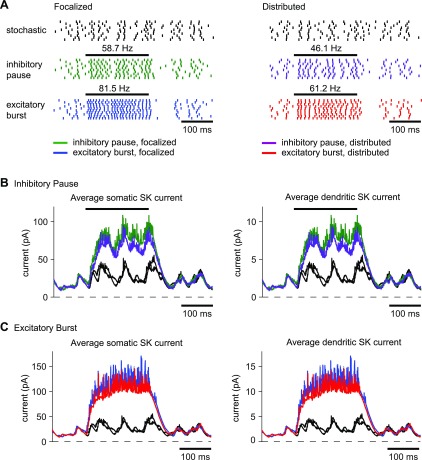
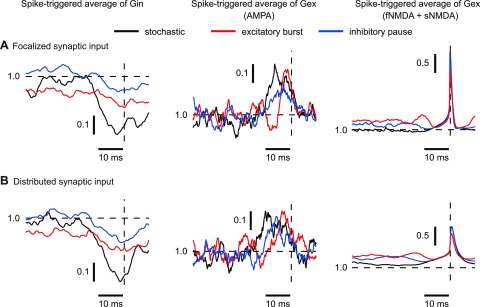
An inhibitory pause was modeled as a complete block of input from one-half of the inhibitory synapses, which reduced the overall firing rate of the population of inhibitory inputs by 50%. This resulted in an increase in firing rate in the model to 58.7 Hz for the focalized input and to 46.1 Hz for the distributed input (Fig. 9A), indicating that disinhibition is a highly effective condition to increase DCN spiking. The spike rate increase in the focalized input condition was noticeably higher, suggesting that the somatic location of the excitatory input when not compensated by inhibition was more effective in driving spiking than an identical pattern of distributed excitation. This difference was paralleled by a slightly higher increase in SK current activation for the focalized disinhibition over the distributed case in both the soma (Fig. 9B, left) and the dendrites (Fig. 9B, right). Nevertheless, the difference was relatively minor and does not invalidate the use of dynamic clamping in the exploration of stronger disinhibitory input events. The overall similarity in mechanism is also shown by STAs of the conductances (Fig. 10). For both focalized (Fig. 10A) and distributed input conditions (Fig. 10B), a pause in 50% of inhibitory inputs resulted in about a twofold decrease in the drop of inhibitory conductance before spike initiation. Note that the plotted conductance was normalized so that the drop in conductance before a spike depicts the relative decrease in spike-triggered conductance regardless of overall input rate. Therefore, the observed decrease in the STA drop indicates that under the condition of reduced inhibition the timing of spiking is less precisely controlled by inhibitory inputs. In addition, the average increase in AMPA excitation before spike triggering was also reduced (Fig. 10, middle), indicating that it was an overall decrease in the precise relationship between input conductance and spike timing rather than a shift of spike control to excitation that was caused by disinhibition.

Fig. 9.

Response to an inhibitory input pause or excitatory input burst for focalized or distributed input in the model. A: a 50% decrease in the inhibitory input rate approximately doubled the output spike rate of the model. This increase was slightly higher for focalized inputs, which is likely due to greater excitation on the soma in the focalized case. A 100% increase in the excitatory input rate had an effect similar to that of an inhibitory pause but drove the model to spike at even higher frequencies. B: during the inhibitory pause, the magnitude of the SK was larger due to increased spiking. C: the effect of an excitatory burst was similar to that of an inhibitory pause with the magnitude of the SK current driven even higher by the higher spike rate. The effect for both input conditions was somewhat stronger for focalized than for distributed inputs due to the higher achieved spike rate. In all cases, the SK current took about 60 ms to relax back to the control trajectory after the end of the input burst.

Fig. 10.

STAs of inhibitory and excitatory conductance (normalized to the mean conductance value) when purely stochastic synaptic input or patterned input was applied. The vertical dashed lines indicate the time of the spike. The STA was computed over all spikes for all trials during the 200-ms excitatory burst (focalized, 188 spikes; distributed, 145 spikes) or inhibitory pause (focalized, 129 spikes; distributed, 100 spikes). In the case of stochastic input, the spike rate was much lower, so the STA was computed over all spikes (focalized, 149 spikes; distributed, 123 spikes) in the 5-s-long control trial without input transient. All STAs were normalized to the average conductance for each trial (horizontal dashed line). A: in the focalized input condition, the STAs show that both excitation and inhibition could control spike timing when both synaptic excitation and inhibition were applied. There was a transient decrease in inhibition (G_in) and transient increase in dl-α-amino-3-hydroxy-5-methylisoxazole-propionic acid (AMPA) conductance preceding each spike. The N-methyl-d-aspartate (NMDA) conductance also increased preceding a spike, but its voltage dependence resulted in a steep conductance increase during action potentials. When an excitatory burst or inhibitory pause was applied, the signal in the STA for G_in decreased. The STA for AMPA conductance showed diminished amplitude during inhibitory pauses but a sharper increase during an excitatory burst. The STA for NMDA predominantly reflected the NMDA voltage dependence such that it was much increased during a spike. B: very similar STAs were observed when synaptic input was distributed over the dendritic tree. However, the voltage-dependent increase in NMDA conductance during a spike was decreased, because spike backpropagation into the dendrite was incomplete due to its fast time course, and as a result dendritic NMDA conductance did not show as strong an increase during spikes.

Although inhibitory Purkinje cell input is likely a dominant mechanism in controlling DCN activity, spike rate increases could also be caused by increased mossy fiber input. We simulated excitatory input bursts as a doubling of the original 20-Hz firing rate in one-half of the excitatory synapses, yielding an overall increases of 50% in the frequency of excitatory input. This input condition had a similar effect to the case of an inhibitory pause, although the amount of firing rate increase was somewhat larger. The increase to 81.5-Hz spiking for focalized input was again higher than the increase to 61.2 Hz for distributed input (Fig. 9A). This is consistent with the explanation that a purely somatic imbalance in excitation is somewhat more effective than the distributed case. The STAs of synaptic conductances for increased excitation also showed similarities to the case of decreased inhibition (Fig. 10). The drop in inhibition before a spike was decreased about 50% compared with control, suggesting less inhibition-locked spiking. In contrast, the absolute size of AMPA conductance increase before a spike was about 50% larger during excitatory bursts, although there was no increase in the relative increase in excitation normalized to the increased total excitatory conductance during an excitatory burst (Fig. 10). The similarity between GABA and AMPA transients related to spike initiation between focalized somatic and distributed dendritic input suggests that synaptic control of spiking is virtually unchanged between these conditions.

DISCUSSION

We developed a computer simulation approach to examine differences between focalized somatic or distributed dendritic synaptic input in a morphologically realistic compartmental model of a DCN neuron. Our approach allowed us to apply the exact same synaptic conductance patterns used previously in dynamic clamp studies to the computer model either only at the soma, to simulate dynamic clamping, or distributed throughout the dendritic tree, to simulate natural synaptic input in vivo. We found that the model was capable of reproducing not only responses obtained experimentally under current clamp but also responses to complex fluctuating inhibitory and excitatory conductances previously recorded with dynamic clamping (Gauck and Jaeger 2000). With additive white current noise applied to the soma, the model could also reproduce the millisecond precision in spike times between repeated trials of stimulation. We then developed a set of benchmark measurements that can be used to assess differences in synaptic responses to focalized or distributed synaptic input. These measurements include important variables such as spike rate, spike time precision, and spike-triggering conductances that are frequently used in analyzing dynamic clamp data (Chance et al. 2002; Fernandez and White 2010; Gauck and Jaeger 2003; Tateno and Robinson 2009).

In our DCN neuron model, there were only minor differences in spike pattern generation between focalized or distributed input in the model, even when strong inhibitory bursts and pauses or excitatory bursts were applied. The relationships between spike-time precision and spike frequency with different input levels and input synchronicity were also very similar. The lack of differences in responses to focalized or distributed synaptic inputs suggests that deep cerebellar nucleus neurons essentially do not rely on their morphology for input processing. Different cell types, and larger types of neurons in particular, will likely show more pronounced local dendritic processing and hence less similar results for focal somatic and distributed dendritic synaptic input.

Additive Somatic Current Noise Can Simulate Variability in a Neuron's Response to Repeated Presentations of the Same Stimulus

Variability in neuronal responses to repeated identical stimuli is partly due to subthreshold membrane voltage fluctuations, which underlie the phenomena of “spontaneous spikes” for subthreshold inputs and “missing” spikes for suprathreshold inputs (Schneidman et al. 1998). In fact, many dendritic computations occur within the subthreshold regime. In real neurons, these fluctuations can be caused by random changes between conducting and nonconducting states of voltage-gated ion channels (Hille 1992). In our neuron model, deterministic Hodgkin-Huxley-type equations were used to simulate homogeneous populations of channel types in each compartment rather than single channels, so subthreshold fluctuations due to channel noise were not observed. In our simulations as well as our published dynamic clamp experiments (Gauck and Jaeger 2000, 2003), there is no synaptic noise due to variability in the number of transmitter molecules, availability of receptors, or spontaneous release of vesicles, since we used deterministic input conductance waveforms. To reproduce subthreshold fluctuations in the membrane potential, we added a white current noise to the soma of the model and matched the amplitude of the voltage fluctuations observed in slice recordings by setting the standard deviation of the noise to a specific value.

In some cases, fluctuations in membrane voltage have been shown to be both activity and voltage dependent. For example, in a model of neurons in the entorhinal cortex, voltage-independent noise was unable to reproduce spike clustering that arises in a stochastic model due to enhanced responses to weak period stimuli in a form of stochastic resonance (White et al. 1998). However, in a study comparing single-compartment neuron models based on linearized approximations to the Hodgkin-Huxley equations with an additive white current noise or Monte Carlo simulations of Markov-scheme channel kinetics, the magnitude of computed voltage noise was within 0.1 mV for all voltage ranges tested with error being <8% for subthreshold voltages (Steinmetz et al. 2000). The good match we observed between spike variability in slice recordings and in the model using identical synaptic conductance patterns indicates that for DCN neurons, a voltage-independent somatic current noise adequately reflects the influence of channel noise on synaptic responses.

Computer Modeling in Conjunction With Dynamic Clamping Presents a Powerful Combined Approach to the Study of Synaptic Integration of In Vivo Synaptic Input Patterns

Our simulations support the premise that dynamic clamping presents a valid approach to probe DCN neurons for their function of synaptic integration with complex input patterns. The observed close match between somatic focalized and distributed synaptic input processing is likely due to the relatively electrotonically compact size of DCN neurons. Because the electrotonic distance for any dendritic input to the soma rarely exceeds 0.2 λ, little voltage attenuation between the site of synaptic input and the soma is taking place. Attenuation becomes more severe for strong dendritic input transients while the neuron is in a high-conductance state (Rall 1967; Lev-Tov et al. 1983), and consequently the largest departure between distributed dendritic and somatic input was observed in the case of intense AMPA excitatory input bursts.

Although our results show that a membrane conductance of electrotonically compact neurons may be applied equally well at the soma or in a distributed fashion, this similarity will likely break down for large cell types with extended dendrites such as cortical pyramidal neurons. In such cells, local dendritic processing such as amplification through dendritic voltage-gated sodium and calcium channels or regenerative events (Gasparini et al. 2004; Hanson et al. 2004) could not be adequately recreated with dynamic clamp inputs to the soma. The simulation scripts we used in this study are downloadable from the ModelDB database (http://www.neuron.yale.edu/course/modeldb.html) and can be adapted to other neural morphologies that are also freely downloadable from the same database. The stimulus designs and benchmark analysis methods developed in this study provide a general toolkit that will allow a detailed comparison between focal and distributed conductance distributions in all cell types for which detailed compartmental models are available. Because dynamic clamping is becoming more widely used in many cell types, such as cortical pyramidal neurons (Morita et al. 2008; Otte et al. 2010; Sceniak and Sabo 2010), hippocampal CA1 pyramidal neurons (Campanac et al. 2008; Fernandez and White 2010; Kerr and Capogna 2007; Prescott et al. 2006, 2008; Vervaeke et al. 2006), neurons of the rat entorhinal cortex (Fernandez and White 2008, 2009; Haas et al. 2010; Kispersky et al. 2010; Pervouchine et al. 2006), and midbrain dopaminergic neurons (Deister et al. 2009; Hahn et al. 2006; Lobb and Paladini 2010; Lobb et al. 2010), the modeling approach developed in the present study will likely result in valuable insights regarding the specific limitations in each neural morphology.

GRANTS

This work was supported by National Institute of Mental Health Grant R01-MH065634 and National Institute of Neurological Disorders and Stroke Grant R01-NS-067201 to D. Jaeger and National Science Foundation Integrative Graduate Education and Research Traineeship Fellowship DGE-0333411 to R. Lin.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).