Abstract
We used the framework of the uncontrolled manifold hypothesis to explore the relations between anticipatory synergy adjustments (ASAs) and anticipatory postural adjustments (APAs) during feedforward control of vertical posture. ASAs represent a drop in the index of a multimuscle-mode synergy stabilizing the coordinate of the center of pressure in preparation to an action. ASAs reflect early changes of an index of covariation among variables reflecting muscle activation, whereas APAs reflect early changes in muscle activation levels averaged across trials. The assumed purpose of ASAs is to modify stability of performance variables, whereas the purpose of APAs is to change magnitudes of those variables. We hypothesized that ASAs would be seen before APAs and that this finding would be consistent with regard to the muscle-mode composition defined on the basis of different tasks and phases of action. Subjects performed a voluntary body sway task and a quick, bilateral shoulder flexion task under self-paced and reaction time conditions. Surface muscle activity of 12 leg and trunk muscles was analyzed to identify sets of 4 muscle modes for each task and for different phases within the shoulder flexion task. Variance components in the muscle-mode space and indexes of multimuscle-mode synergy stabilizing shift of the center of pressure were computed. ASAs were seen ∼100–150 ms prior to the task initiation, before APAs. The results were consistent with respect to different sets of muscle modes defined over the two tasks and different shoulder flexion phases. We conclude that the preparation for a self-triggered postural perturbation is associated with two types of anticipatory adjustments, ASAs and APAs. They reflect different feedforward processes within the hypothetical hierarchical control scheme, resulting in changes in patterns of covariation of elemental variables and in their patterns averaged across trials, respectively. The results show that synergies quantified using dissimilar sets of muscle modes show similar feedforward changes in preparation to action.
Keywords: uncontrolled manifold hypothesis
during standing, the human body is inherently unstable because of the small support area, high center of mass, and multijoint design. Voluntary movements performed by a standing person contribute to problems of postural control by producing postural perturbations because of the mechanical coupling of the body segments. When a standing person performs a fast arm movement, changes in the activation of postural muscles are typically seen about 100 ms before movement initiation; these changes have been addressed as anticipatory postural adjustments (APAs; reviewed in Massion 1992). The role of APAs has been assumed to produce joint torques and forces that minimize perturbation of the vertical posture that would otherwise be associated with the movement (Bouisset and Zattara 1987; Massion 1992). Characteristics of the APAs have been shown to depend on a number of factors, including the magnitude and direction of the expected perturbation, magnitude of the intended movement, and features of the postural task, particularly postural stability (Aruin and Latash 1995, 1996; Aruin et al. 1998).
Recently, a phenomenon has been described with characteristics resembling those of APAs. This phenomenon is based on a definition of synergy as a neural organization of a redundant set of elements with the purpose to stabilize a value of a potentially important performance variable produced by the set (reviewed in Latash et al. 2007; Latash 2010). Quantitative analysis of synergies typically has been performed within the framework of the uncontrolled manifold (UCM) hypothesis (Scholz and Schoner 1999; reviewed in Latash et al. 2002, 2007). According to this hypothesis, a neural controller acts in a space of elemental variables, creates in that space a subspace (UCM) corresponding to a desired value of a performance variable, and then acts to limit variance of the elemental variables to that subspace. In more intuitive terms, variance within a set of elemental variables may be viewed as consisting of two components, “good” (VGOOD) and “bad” (VBAD) with respect to a performance variable. VGOOD has no effect on the magnitude of the performance variable, whereas VBAD affects that variable. A synergy stabilizing the performance variable may be operationally defined as VGOOD > VBAD (properly quantified). Note that the term “stabilized” in this context refers not to classic mechanical stability (as in “ability to return to a state after a transient perturbation”) but to reproducibility across repetitive trials (as in “performance of the athlete was stable over the year”). This use of “stabilization” is common in analysis of synergies (reviewed in Latash et al. 2007); it is related to its current use in analysis of dynamic stability (see Martin et al. 2009).
Studies of multifinger synergies stabilizing total force produced by a set of fingers showed that an index of synergy reflecting the normalized difference, (VGOOD − VBAD), dropped about 150 ms before the initiation of a quick force change by the subject (Olafsdottir et al. 2005; Shim et al. 2005). Later studies confirmed the existence of anticipatory synergy adjustments (ASAs) in a variety of multidigit and multijoint tasks associated with self-initiated perturbations (Degani et al. 2010; Kim et al. 2006; Shim et al. 2006). The purpose of ASAs has been assumed to attenuate synergies that would otherwise interfere with the planned quick change of the performance variable. We assume that ASAs reflect an important neural mechanism that is typical of a variety of tasks involving redundant sets of elements; this mechanism modifies stability of specific performance variables when a person plans to perform an action associated with a quick change in that performance variable.
ASAs were observed when subjects produced actions in a self-paced manner. When the same action was performed under the simple reaction time instruction, the synergy index drop was delayed until the action initiation (Olafsdottir et al. 2005). This observation resembles the behavior of APAs under the simple reaction time instruction: Changes in the activation of postural muscles shift in time toward the moment of focal movement initiation (De Wolf et al. 1998; Lee et al. 1987). There is one more similarity between the ASAs and APAs. Compared with younger persons, healthy elderly persons show a drop in the magnitude and a delay in the initiation of both ASAs and APAs (Olafsdottir et al. 2007; Woollacott et al. 1988).
These similarities between the two described phenomena of anticipatory motor control have led to the hypothesis that performance of a quick action by a standing person is associated with a sequence of events (Latash 2010). First, the multimuscle synergies stabilizing the coordinate of the center of pressure (COP, an important variable for postural control; Winter et al. 1998) are attenuated (ASAs). This process may or may not be associated with visible changes in patterns of muscle activation averaged across trials, since ASAs are defined by variance across trials. Next, changes in postural muscle activation levels take place, resulting, after an electromechanical delay, in shifts of mechanical variables such as the COP coordinate. The main purpose of this study has been to test this hypothesis.
The design of the study and the associated analyses are rather complicated. They are based on the idea of hierarchical control of posture. At the lower level of the hierarchy, postural muscles are organized into groups with activation levels scaling in parallel within each group. Such groups have been addressed as muscle synergies (d'Avella et al. 2003; Ivanenko et al. 2005, 2006; Ting and Macpherson 2005; Torres-Oviedo and Ting 2007; Torres-Oviedo et al. 2006) or muscle modes (M-modes; Danna-Dos-Santos et al. 2007; Klous et al. 2010; Krishnamoorthy et al. 2003a, 2003b). At the upper level of the hierarchy, the controller manipulates gains with which the M-modes are recruited (reviewed in Latash et al. 2007).
Several recent studies have shown that the composition of M-modes may change depending on the task and also at different times before and after a postural perturbation (Asaka et al. 2008; Krishnamoorthy et al. 2004; Robert and Latash 2008). Until now, there have been no attempts to compare synergy indexes computed for the same data set based on different sets of M-modes. In our study, we used several sets of M-modes defined based on a standard task (voluntary body sway; see Danna-Dos-Santos et al. 2007; Klous et al. 2010) and on data extracted from different time intervals with respect to the action initiation during the shoulder flexion task. The purpose of using different tasks was to test whether the results were consistent across the methods of M-mode identification.
We selected the task of quick bilateral shoulder movement as the focal task. This task was used in earlier studies of APAs (Aruin and Latash 1995; Bouisset and Zattara 1987). In our study, however, an important modification was made. The subjects performed the task from an initial posture corresponding to a relatively large COP shift backward (COPAP) compared with comfortable standing. The purpose of this modification was to obtain substantial levels of activation of postural muscles at the initial steady state to allow for the computation of the synergy index before movement and for quantification of the early shifts of this index (ASAs) if they were to happen.
We tested the following two hypotheses. First, action initiation will be associated with an early drop in the index of a multi-M-mode synergy stabilizing COPAP about 150 ms before movement initiation. These ASAs will be followed by APAs as reflected in changes in postural muscle activation levels seen in data averaged across trials. Second, the method of synergy index computation will yield similar results when the M-mode composition is defined based on data obtained during voluntary body sway or during certain phases within the quick bilateral shoulder movement task, as long as the M-mode sets are obtained from the same person.
METHODS
Subjects
Nine healthy subjects (5 males and 4 females; means ± SD: age 24 ± 6 yr, body mass 67 ± 9 kg, height 169 ± 9 cm) without any known neurological or muscular disorder participated in the experiment. All the subjects were right-handed based on their preferential hand use during daily activities such as writing and eating, and right-legged based on their preferred leg usage when kicking a ball. All the subjects gave informed consent based on the procedures approved by the Office for Research Protection of The Pennsylvania State University.
Apparatus
The equipment and setup are described in detail by Klous et al. (2010). A force platform (AMTI, OR-6) was used to record the horizontal component of the ground reaction force in the anterior-posterior direction (FX; resolution 0.677 μV/N), the vertical component of the ground reaction force (FZ; resolution 0.173 μV/N), and the moment of force around the frontal axis (MY; resolution 1.65 μV/Nm). In addition, a three-dimensional accelerometer (model 356B11, ICP Accelerometer; PCB Pizotronics, Depew, NY) was taped to the dorsal aspect of the subject's hand, just under the metacarpophalageal joint of the index finger. The y-axis of the accelerometer was directed along the required arm motion (see below). Surface muscle activity as measured by electromyogram (EMG) of the following muscles was recorded: tibialis anterior (TA), soleus (S), gastrocnemius medialis (GM), gastrocnemius lateralis (GL), biceps femoris (BF), semitendinosus (ST), vastus lateralis (VL), rectus femoris (RF), vastus medialis (VM), lumbar erector spinae (ES), latissimus dorsi (LD), and rectus abdominis (RA).
Procedures
In the initial position, subjects were standing barefoot on the force platform with their feet in parallel and the insides of the feet 15 cm apart (about hip width). This foot position was marked on the top of the platform and reproduced across trials.
The experiment consisted of 1) control trials, 2) voluntary body sway trials, and 3) shoulder flexion trials. A detailed description of the experimental procedures involved in both the control trials and the voluntary body sway trials can be found in Klous et al. (2010) and Danna-Dos-Santos et al. (2007). The control trials involved holding steadily a standard 5-kg load in front of the body with extended arms; the weight of the load acted downward in one trial and upward (using a set of pulleys) in the other trial. The subjects also performed three 30-s trials of continuous voluntary body sway in the anterior-posterior direction with the arms crossed on the chest with the fingertips placed on the shoulders. Before data collection, a period of familiarization with the task was given to each subject. On average, subjects performed two practice trials of 30 s each.
The shoulder flexion task was performed under reaction time (RT) and self-paced (SP) conditions (24 trials per condition). The order of these two conditions was balanced across subjects. In the initial position, subjects were leaning backward such that their COPAP matched a target set at the same value as the backward target during the sway task, i.e., at 60% of the maximal backward sway. The arms were supinated 90° so that the palms were oriented toward the body; they were hanging loosely by the sides of the subject's body. The subjects were required to make a fast, bilateral shoulder flexion movement over 90° so that the arms ended up being parallel to the floor. After the motion, the subjects were required to keep the arms in the final position and return the COPAP to the target position. This final position was then kept until the end of the trial. In the RT condition trials, the subjects were asked to perform the described motion as quickly as possible after an auditory signal. The auditory signal was turned on unexpectedly by the experimenter within a 2- to 4-s time window after the subject occupied the initial position and reported that he/she was ready. In the SP trials, the subjects were asked to perform the required motion in a self-paced manner at any time within a 10-s time window. The rest intervals between trials within a condition were 10 s. There were 3-min rest intervals between conditions to avoid fatigue. Before each condition, subjects were given three practice trials. The whole experiment lasted about 45 min, including setting up the data collection.
Data Processing
All signals were processed off-line using customized Matlab 7.6 software. FZ, FX, and MY were filtered with a 20-Hz low-pass, second-order, zero-lag Butterworth filter. Time-varying COPAP was calculated using the following equation:
| (1) |
where dz pertains to the distance from the surface to the platform origin (0.043 m). The displacement of COPAP was computed by subtracting the average COPAP coordinate during quiet stance from the COPAP coordinate in body sway trials and shoulder flexion trials.
EMG: voluntary body sway task.
The initiation and the end of each cycle were defined by two consecutive extreme anterior positions of COPAP. The duration of each cycle was time normalized to 100%. EMG data were rectified and filtered with a 50-Hz low-pass, second-order, zero-lag Butterworth filter. The rectified EMG signals were integrated over 1% time windows of the cycles (IEMGBS) where the number of cycles (n) could slightly vary. IEMG data were normalized (IEMGNORM_BS) using the method described in Krishnamoorthy et al. (2003a, 2003b) and Wang et al. (2005):
| (2) |
where IEMGQS is the average rectified EMG obtained during quiet stance trial integrated over a time window of the same duration as IEMGBS. IEMGREF is the average rectified EMG in the middle of the trial obtained during the two control trials when subjects held the 5-kg load that produced either downward or upward force (see Procedures), integrated over a time window of the same duration as for IEMGBS. For the ventral muscles (TA, VM, VL, RF, RA), the EMG integrals were computed when the load was producing an upward force on the bar. Conversely, for the dorsal muscles (S, GL, GM, BF, ST, ES, LD), the EMG integrals were computed when the load was producing a downward force.
EMG: shoulder flexion task.
The accelerometer signal was filtered with a 50-Hz, low-pass, second-order, zero-lag Butterworth filter and corrected for offset. Movement initiation was defined as the point in time at which the signal exceeded 1% of maximum acceleration. This value was confirmed by visual inspection and is referred to as time 0 (t0). Data in the range −500 (i.e., 500 ms before t0) to +500 ms (i.e., 500 ms after t0) were selected for further analysis.
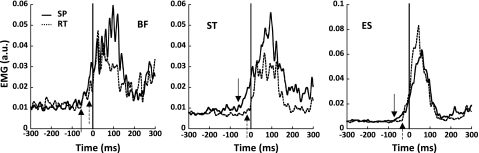
The APAs were determined by inspecting the rectified and filtered muscle activation patterns in the shoulder flexion averaged across trials. The EMG data for the BF, ST, and ES muscles showed clear APAs in all subjects with a clear difference in the activation patterns between the SP and RT conditions (Fig. 1).
Fig. 1.
Electromyographic (EMG) data averaged across trials for a representative subject (S6) for self-paced (SP; solid line) and reaction time conditions (RT; dashed line) for the biceps femoris (BF; left), semitendinosus (ST; middle), and erector spinae (ES; right) muscles. Vertical lines show the alignment time, time 0 (t0). Arrows (solid arrow for SP, dashed arrow for RT) represent the times when muscle activity exceeded the average ± 2.5 times the standard deviation (SD) calculated between 500 and 200 ms before t0. a.u., Arbitrary units.
To identify the initiation of APAs for EMG data, we defined tAPA-EMG as the instant in time when the average muscle activation level over trials differed by more than ±2.5 SD from the average value within the time interval {−500 ms; −200 ms} before t0. This criterion was selected based on a study by Küng et al. (2009) (also see De Wolf et al. 1998; Santos et al. 2010). During the {−500 ms; −200 ms} time interval, no APAs were expected to occur. The EMG signal of a muscle (BF, ST, ES) in which the earliest change was observed was taken as exhibiting tAPA.
The rectified and filtered EMG signals were integrated using a trapezoidal numerical integration with 10-ms time windows. IEMG shoulder flexion data were normalized (IEMGNORM_SF) as described for the body sway task using the equation
| (3) |
For further analysis, data for the shoulder flexion trials were divided into five phases, as follows: steady-state phase, {−500 ms; −200 ms}; transition phase, {−200 ms; −150 ms}; APA phase, {−150 ms; t0}; corrective postural adjustments (CPA) phase, {t0; 150 ms}; and voluntary posture stabilization phase, {150 ms; 500 ms}. The choice of these particular phases was based on the following considerations. APAs and ASAs were previously documented starting not earlier than 200 ms before action initiation (Massion 1992; Olafsdottir et al. 2005; Shim et al. 2005). Hence, we selected the time window of the steady-state phase from −500 to −200 ms. Most commonly, ASAs and APAs were reported to happen within 150 ms preceding action initiation. However, there are reports of earlier ASAs (Wang et al. 2006a, 2006b); hence, a time window between −200 and −150 ms was selected as a transition phase. The time window from −150 ms to t0 was selected as the APA phase. Short-latency CPAs have typically been described within a time window starting about 50 ms after a postural perturbation and lasting until the beginning of voluntary postural corrections, 150–200 ms after the perturbation (Diener et al. 1988; Santos et al. 2010). Therefore, we analyzed the data separately within the time intervals {t0; +150 ms} (CPA phase) and {+150 ms; +500 ms} (voluntary posture stabilization phase).
For each phase, we define sets of M-modes and Jacobian matrices, as described below. In results, we describe a subset of all possible analyses, focusing mostly on the steady-state and APA phases as potentially most relevant to the APAs and ASAs; the data within the transition phase showed similar results but with less consistency, likely due to the small size of that time window.
For the RT condition, to avoid a major distortion of results, we imposed rather strict rules to exclude the trials that were unusually quick or slow in reaction time. Specifically, the trials with reaction time <120 ms and >300 ms were excluded from further analysis. In addition, the two trials with the fastest and the two trials with the slowest reaction times for each subject were also excluded from further analyses. Combined, this led to a subsequent exclusion of ∼30% of RT trials (see results).
Defining M-modes.
The objective of this step of analysis was to identify groups of muscles (M-modes) that showed covaried levels of activation (IEMGNORM). These analyses were performed separately for the body sway task and for each of the five phases in the shoulder flexion task. M-modes were used as the elemental variables for further analysis of M-mode synergies. This step reduces the 12-dimensional muscle activation space to a 4-dimensional M-mode space. A detailed explanation of this procedure can be found in the Appendix. Briefly, principal component analysis (PCA) was applied to correlation matrices of IEMG data for each of the five phases, as well as for the body sway task. We opted to use correlation over covariance matrices based on the following considerations. Using covariance makes all variables (IEMGs) “equal”; we were not sure whether all muscles equally contributed to the task. If, for example, one muscle were absolute quiescent, using covariance matrix would inflate its noncontribution to the task and distort the variance picture. Using correlation matrices makes results more immune to such cases.
To ensure that each muscle was significantly loaded on at least one principal component (PC; loading value over ±0.5; see Hair et al. 1995) within each phase of the shoulder flexion task and within the body sway task, we chose to accept the first four PCs for PCA. Visual inspections of the scree plots confirmed the validity of this criterion. In particular, scree plots displayed an inflection point after the fourth PC; hence, PCs with a number higher than four accounted for similar fractions of the remaining variance per PC. The PCs were subjected to Varimax rotation with factor extraction. The factors (eigenvectors) will further be addressed as M-modes. Sets of 4 M-modes accounted for a percentage of variance in line with previous studies (Danna-Dos-Santos et al. 2007, 2009; Krishnamoorthy et al. 2003a, 2003b, 2004). This analysis resulted in six sets of M-modes: one for the body sway task and five for each of the phases in the shoulder flexion task. To calculate the magnitudes of the M-modes, the eigenvectors were multiplied with the IEMG data.
The M-modes were identified for the body sway task and for each of the five phases in the shoulder flexion task to examine the influence of M-mode composition on the synergy index. The M-mode magnitudes formed time functions. The time of APA initiation, tAPA-MODES, was determined for those variables for each of the subjects. The average value and SD over the steady-state phase from −500 ms to −200 ms before t0 were calculated for each of the four M-modes. Similarly to the computation based on EMGs, tAPA-Mode was defined at the instant in time when the M-mode magnitude differed from the average steady-state value by ±2.5 times the SD.
Defining the Jacobian matrix.
Linear relations were assumed between small changes in the magnitude of the M-modes and the change in the performance variable (ΔCOPAP). For the body sway task, multiple linear regression over all cycles (37 ± 6 cycles) was used to define the relations between and ΔCOPBS for each subject separately. For the shoulder flexion task, multiple regressions over all trials within a condition (SP or RT) (SP: 23 ± 1 cycles; RT: 18 ± 3 cycles) were performed for each of the five phases separately. Further details about the procedure to define the Jacobian matrix can be found in the Appendix.
Uncontrolled manifold analysis: computation of the synergy index.
The UCM hypothesis assumes that the controller manipulates a set of elemental variables and tries to limit their variance to a subspace corresponding to a desired value of a performance variable. Within the UCM analysis, the trial-to-trial variance in the space of elemental variables is divided into two components. The first component lies within a subspace (the UCM) where the selected performance variable does not change. The second component of the variance lies within the orthogonal complement to the UCM. Comparing the two components of the variance, normalized by the dimensionality of their respective subspaces, produces an index of variance that is compatible with stabilization of the selected performance variable.
In the current study, this analysis was only performed for the shoulder flexion task. M-mode magnitudes were the elemental variables, whereas COPAP was the performance variable. The analysis was performed six times using the six sets of M-modes and six Jacobian (J) matrices defined for each of the phases of the shoulder flexion task and for the body sway task. In the first step of the analysis, for each subject, the mean magnitude over the trials of each of the M-modes was subtracted from the vectors of the individual changes in the magnitudes of the M-modes (ΔM) for each trial and each time window. The null space of the Jacobian was then calculated as an approximation of the UCM. The demeaned vector (ΔMdemeaned) was projected onto the null space and its orthogonal complement. In the last step, the trial-to-trial variance in each of the two subspaces (VUCM and VORT), and the total variance (VTOT) normalized by the number of degrees of freedom was calculated. To quantify the relative amount of variance that is compatible with stabilization of the COPAP, we calculated ΔV as the index of synergy. A more detailed description can be found in the Appendix.
To define the time of ASA initiation, tASA, we calculated an average value and SD for the z-transformed values of ΔV (ΔVZ) for the period from −300 to −200 ms before t0 for each subject. The instant in time when the difference in ΔVZ (ΔΔVZ) exceeded 1 SD from the average value over the mentioned time interval was accepted as tASA. This criterion was also used in a previous study (SKM et al. 2010). The results were checked visually by observing ΔVZ time profiles at an optimal time resolution. This analysis was performed based on the six sets of M-modes and J matrices, separately resulting in six tASA values for each subject. Subsequently, an average tASA value across subjects was calculated. The data for two phases within the shoulder flexion task (steady-state and APA phases) and for the body sway data were used to test whether similar results were obtained across sets of M-modes and Jacobians.
The softer criterion for tASA was used because of its relatively slow changes. We also examined whether using the same criterion for determining tASA as the criteria used for tAPA-EMG and tAPA-Mode (2.5 SD away from the steady-state average value) would change any of the major conclusions of the study. No major differences in the results were found except for a modest increase in the P value for comparisons across the timing indexes (see results).
We now take this opportunity to further clarify our stand regarding the use of different criteria for determining the timing of various indexes (tASA, tAPA-EMG, and tAPA-MODES). The different variables were characterized by different steady-state variability, different rates of change, and different typical magnitudes of change. One more factor is presence or absence of spontaneous, relatively large-amplitude changes in the signals that could be rare (so they did not affect the SD by much) and were not timed to the task execution. All these factors forced us to try different criteria for different signals. Ultimately, the described set of criteria was selected as the one that led to results that could be confirmed by visual data observation (no missed starts and no false starts) in nearly all the trials.
Statistics
Data are means ± SE. We used Wilcoxon's signed-rank test to compare the number of co-contraction patterns observed during the body sway task and the shoulder flexion task (averaged across time intervals). The time of initiation of APAs calculated from EMG data (tAPA-EMG) was compared between SP and RT trials using a paired Student's t-test.
A two-way repeated-measures ANOVA with factors of condition (2 levels: RT and SP) and methods (3 levels: steady state, APA, and body sway) using a mixed linear model was performed to compare the time of initiation of APAs calculated based on M-modes (tAPA-MODES). To analyze the time profiles of the early changes in the synergy index, for each subject we computed ΔΔVZ values within the time interval between −250 ms before t0 and t0 with steps of 50 ms and applied a three-way repeated-measures ANOVA with factors of condition (2 levels), methods (3 levels), and time (6 levels).
To compare tAPA-EMG, tAPA-MODES, and tASA, we applied a two-way repeated-measures ANOVA with factors of condition (2 levels) and index (3 levels: tAPA-EMG, tAPA-MODES, and tASA) using a mixed linear model. Pairwise contrasts were used to explore significant effects. The level of significance was set at P < 0.05.
RESULTS
Reaction Time
All subjects were able to perform the quick bilateral shoulder flexion task under both the SP and RT conditions without losing balance. Overall, 60 of the 216 RT trials were excluded from further analyses based on RT values (see methods). The exclusion of a relatively large number of trials was due to the strict criteria imposed to avoid corruption of the results by inclusion of trials with unusually fast or slow RT. Across the accepted trials, the RT ranged from 155 to 256 ms with an average RT of 203 ms (SE: 11 ms).
EMG and COPAP patterns
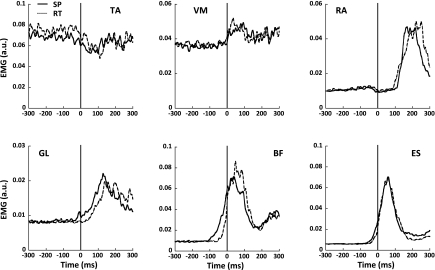
There were common features across the EMG and COPAP patterns across conditions. Figure 2 shows the rectified EMGs averaged across trials and subjects for selected muscles during the SP and RT conditions. Before the data were averaged, the trials were aligned by the first detectable change in the accelerometer signal that was inspected at optimal resolution. These particular muscles were selected because they showed clear APAs across the subjects.
Fig. 2.
EMG data averaged across trials and subjects for SP (solid line) and RT condition trials (dashed line) for selected muscles. Vertical line corresponds to t0. TA, tibialis anterior; VM, vastus medialis; RA, rectus abdominis; GL, gastrocnemius lateralis.
Since the subjects were instructed to lean backward before performing the bilateral shoulder flexion movement, nonzero EMG activity could be observed in ventral muscles before the movement initiation. Dorsal muscles (BF, ST, and ES) showed an increase in the activity just before the focal movement initiation starting −100 to −50 ms before t0; we refer to these transient EMG changes as APAs. The early activation of these muscles was sometimes followed by an EMG burst in ventral muscles, commonly in RA and VL, ∼100–150 ms after t0.
Changes in the background muscle activity before arm movement initiation occurred earlier in the SP condition than in the RT condition. In the SP condition, the earliest change in the background activity in BF, ST, and ES averaged across subjects was observed −77 ± 12 ms before t0; we refer to this time as tAPA-EMG-SP. In the RT condition, APAs occurred later; on average, −37 ± 8 ms before t0; this time is addressed as tAPA-EMG-RT. A paired t-test confirmed that APAs in the SP condition occurred earlier compared with the RT condition (tAPA-EMG-SP < tAPA-EMG-RT, t = −3.6, P < 0.05). Figure 3 shows the ΔCOPAP time pattern for the two conditions averaged across all accepted trials for a typical subject (left) and across all subjects (right).
Fig. 3.
Center of pressure displacement in the anterior-posterior direction (ΔCOPAP) for a representative subject (S6; left) and averaged across subjects (right) for SP (solid line) and RT conditions (dashed line). Vertical line corresponds to t0.
Identification of M-modes and Jacobians: Results of PCA and Multiple Regression
For each subject, the normalized integrated EMG indexes for all muscles were subjected to PCA with factor extraction to identify M-modes, eigenvectors in the muscle activation space. This procedure was performed for the body sway task, as well as for the data within each of the phases in the shoulder flexion task (see methods for details). In the SP condition, the total amount of variance across all subjects that the four PCs accounted for was, on average, 66.5 ± 1.3% for body sway, 55.5 ± 2.0% for the steady-state phase, 58.4 ± 1.4% for the transition phase, 58.9 ± 1.1% for the APA phase, 59 ± 1.8% for the CPA phase, and 56.7 ± 1.8% for the late posture stabilization phase. Similar values were observed for the RT condition. The percentage of explained variance in the current study is similar to that observed in previous studies (Danna-dos-Santos et al. 2007, 2009; Krishnamoorthy et al. 2003a, 2003b, 2004).
Table 1 shows an example of the loadings for all the muscles on the four factors for a representative subject for the body sway task and for the APA phase in the shoulder flexion task under the RT condition. The significant loadings (i.e., loadings with the absolute magnitude of at least 0.5; see Hair et al. 1995) are shown in bold type. The first M-mode composition in the sway task showed high loading values for the IEMG indexes of the dorsal muscles (“push-back” M-mode, Krishnamoorthy et al. 2003a). The second and third PCs showed high loading values for the IEMG indexes of the ventral muscles (“push-forward” M-modes). The fourth PC typically showed one or two muscles significantly loaded, and these muscles varied across subjects (“mixed” M-mode). A similar pattern was observed in previous studies (Danna-Dos-Santos et al. 2007; Krishnamoorthy et al. 2003a, 2003b). Such typical M-modes did not show co-contraction patterns. We define a co-contraction pattern within an M-mode as a pattern with significant loading coefficients on the same PC for two muscles with opposing actions (an agonist-antagonist pair) at a particular joint (i.e., ankle, knee, or hip). Such patterns were rare in the body sway task. In contrast, the different phases in the shoulder flexion task did show M-modes with co-contractions; an example can be seen in Table 1 for the ankle (M3-mode) and knee (M2-mode) flexors-extensors within a set of M-modes computed for the APA phase.
Table 1.
Results of the principal component analysis
| Sway |
APA |
|||||||
|---|---|---|---|---|---|---|---|---|
| Muscle | M1-mode | M2-mode | M3-mode | M4-mode | M1-mode | M2-mode | M3-mode | M4-mode |
| TA | 0.36 | −0.44 | 0.54 | −0.07 | −0.36 | −0.17 | −0.55 | −0.11 |
| S | −0.63 | 0.31 | −0.37 | 0.00 | −0.04 | −0.08 | −0.62 | −0.06 |
| GM | −0.83 | 0.26 | −0.23 | 0.06 | 0.29 | 0.11 | −0.83 | 0.12 |
| GL | −0.83 | 0.22 | −0.16 | 0.02 | 0.25 | 0.08 | −0.81 | 0.14 |
| VM | 0.05 | −0.43 | 0.63 | −0.14 | −0.44 | 0.53 | −0.03 | −0.01 |
| RF | 0.33 | −0.70 | 0.19 | 0.01 | −0.82 | 0.24 | 0.09 | 0.09 |
| VL | 0.28 | −0.79 | 0.08 | 0.00 | −0.83 | 0.07 | 0.08 | −0.02 |
| ST | −0.81 | 0.21 | −0.11 | 0.08 | −0.15 | 0.81 | 0.06 | 0.10 |
| BF | −0.73 | 0.30 | −0.22 | 0.05 | 0.32 | 0.75 | −0.14 | 0.37 |
| RA | 0.33 | 0.05 | 0.77 | 0.15 | −0.05 | 0.01 | 0.01 | −0.92 |
| ES | −0.67 | 0.08 | −0.15 | 0.42 | −0.05 | 0.73 | 0.11 | −0.31 |
| LD | −0.12 | −0.01 | 0.03 | 0.95 | 0.73 | 0.18 | −0.09 | 0.38 |
Data are for a representative subject (S11) for the body sway task and for the anticipatory postural adjustment (APA) phase under the reaction time condition in the shoulder flexion task: TA, tibialis anterior; S, soleus; GM, gastrocnemius medialis; GL, gastrocnemius lateralis; VM, vastus medialis; RF, rectus femoris; VL, vastus lateralis; ST, semitendinosus; BF, biceps femoris; RA, rectus abdominis; ES, erector spinae; LD, latissimus dorsi. Loadings over 0.5 are shown in bold.
Table 2 presents the number of co-contraction patterns across subjects observed at the ankle, knee, and hip joints during body sway and during the steady-state, APA, and CPA phases for both SP and RT conditions. The number of observed co-contraction patterns during the body sway task was significantly smaller than that averaged across the time intervals in the shoulder flexion task. This was confirmed with the Wilcoxon's signed-rank test (P < 0.05). Within the shoulder flexion task, the number of observed co-contraction patterns was the highest in the steady-state phase, decreased in the APA phase, and was lowest in the CPA phase. No significant differences were observed between the SP and RT conditions. Average values across the SP and RT conditions were compared across the phases. Wilcoxon's test revealed a significant difference between the steady-state and CPA phases (P < 0.05, with Bonferroni corrections).
Table 2.
Number of co-contraction patterns
| Ankle Joint |
Knee Joint |
Hip Joint |
Total |
|||||
|---|---|---|---|---|---|---|---|---|
| Interval | SP | RT | SP | RT | SP | RT | SP | RT |
| Steady state | 9 | 8 | 1 | 2 | 5 | 4 | 15 | 14 |
| APA | 6 | 8 | 1 | 2 | 2 | 2 | 9 | 12 |
| CPA | 4 | 3 | 1 | 3 | 1 | 2 | 6 | 8 |
| Body sway task | 0 | 1 | 4 | 5 | ||||
Data are the number of co-contraction patterns across subjects for 3 phases of the shoulder flexion task [steady state, APA, and corrective postural adjustment (CPA)], as well as for the body sway task, under the SP and RT conditions.
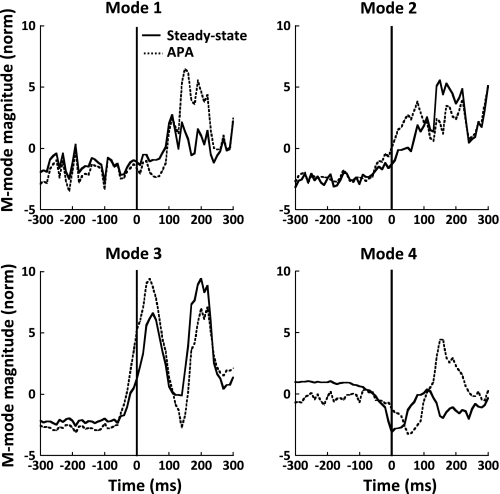
Figure 4 shows an example of the time profiles of the magnitudes of four M-modes calculated by using the loadings computed over the steady-state and APA phases in the shoulder flexion task under the SP condition and multiplied by the corresponding IEMG data for a representative subject. The M-mode magnitude time profiles show changes before t0; that is, they show APAs. Note the similar time profiles of the M-modes magnitudes defined using the data over different time intervals of the task. In general, despite the differences in the loading coefficients, the M-mode magnitude time profiles were similar for the sets defined using the EMG data in the body sway task and using the data over different phases in the shoulder flexion task.
Fig. 4.
Time profiles of the 4 M-mode magnitudes, shown for a typical subject (S1), when calculated with loadings from the steady-state phase (solid line) and the APA phase (dashed line) for the SP condition. Because no changes are expected before 300 ms prior to t0, data are only shown from −300 ms until +300 ms. norm, Normalized.
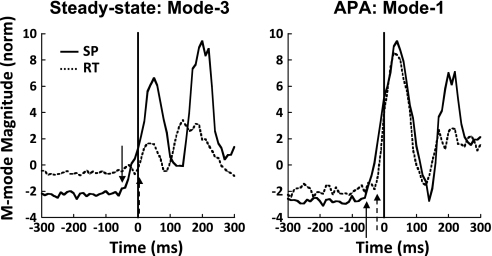
The timing of the earliest changes in the M-modes magnitudes in the shoulder flexion task showed a clear difference between the SP and RT conditions. Figure 5 shows the time profiles of the magnitudes of M-modes that showed the earliest change for the SP and RT condition trials for a representative subject. The M-mode magnitudes were calculated using the loadings defined over the data in the steady-state phase (left) and in the APA phase (right). For this particular subject, the earliest change in M-mode magnitude in the steady-state phase was found in M3, whereas the earliest change in M-mode magnitude in the APA phase was observed in M1. A change in the M-mode magnitude magnitudes in the SP condition (indicated by arrows in Fig. 5) can be seen approximately −50 ms before t0, earlier than in the RT condition (between −20 ms before t0 and t0).
Fig. 5.
Time profiles of 2 M-mode magnitudes, shown for a representative subject (S1), under the SP (solid line) and RT conditions (dashed line). Profiles show the magnitude of the M-mode that showed the earliest change from a set of M-modes defined using the data from the steady-state phase (Mode 3; left) and the APA phase (Mode 1; right) Arrows (solid arrow for SP, dashed arrow for RT) show the times when the M-mode magnitude started to change compared with the interval between −500 and −200 ms before t0.
Averaged across subjects, the time of the earliest observed change in M-modes magnitudes in the SP condition was −54 ± 15 and −58 ± 10 ms before t0 when the M-mode sets were defined based on data within the steady-state and the APA phases, respectively. In the RT condition, the earliest observed M-mode changes shifted toward t0: −11 ± 6 ms for the steady-state phase and −28 ± 5 ms for the APA phase. An ANOVA with repeated measures with factors condition (SP and RT) and method (body sway, steady-state, and APA) showed only a significant effect of condition [F(1,23.3) = 32.745, P < 0.001]. Hence, M-modes magnitude changes started earlier in the SP condition than in the RT condition without differences across the methods of M-mode identification. Because no differences between methods of M-mode identification were found, in further analysis (see Fig. 8) the time of APA initiation based on M-mode analysis, tAPA-MODES, was calculated by averaging the tAPA-MODES determined when three sets of M-modes were used: from the body sway task and from the steady-state and APA phases of the shoulder flexion task.
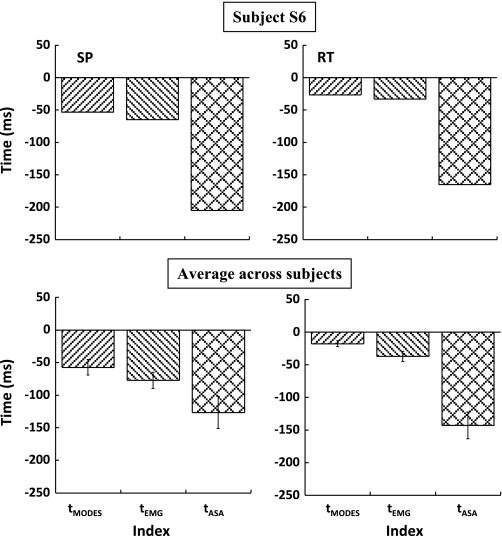
Fig. 8.
Times of the earliest changes in M-modes (tMODES), EMGs (tEMG), and synergy index (tASA) for a typical subject (S6; top) and averaged across the subjects (with SE bars; bottom) are shown for the SP (left) and RT conditions (right).
Linear relations between small changes in the magnitudes of the M-modes (ΔMi) and COPAP shifts (ΔCOPAP) were assumed and expressed using the Jacobian matrix (see methods). Multiple linear regression analysis was performed for each subject, each task, and each phase within the shoulder flexion task. The average amount of explained variance across subjects was 71% for the body sway task. It was significantly lower for the shoulder flexion task, ranging between 28 and 41% (on average, 34%). There were no differences between the SP and RT conditions. The number of M-modes that were significant predictors of COPAP shifts ranged between 24 and 32 (out of 36) for the shoulder flexion task, whereas for the body sway task, all M-modes were significant predictors.
Analysis of the COPAP Stabilizing Synergy
We used the framework of the UCM hypothesis to analyze covariation among the magnitudes of M-modes related to stabilization of the COPAP coordinate. Briefly, within the four-dimensional space of M-modes, the null space, null(J), of the Jacobian linking M-mode changes to COPAP shifts was computed. Since we identified several sets of M-modes and several Jacobians; this analysis was performed several times. Furthermore, the M-mode data for each time sample across trials were projected on the null(J), and the variance of these data was computed. This variance (VUCM) is compatible with a fixed COPAP location at that time. Variance within the orthogonal, complementary subspace was also computed (VORT); VORT led to COPAP shifts. Both VUCM and VORT were quantified per degree of freedom in the corresponding subspaces. An index of multi-M-mode synergy stabilizing the COPAP coordinate was computed as the normalized difference: ΔV = (VUCM − VORT)/VTOT. This analysis was performed for each condition and each subject separately. For more detail, see methods. Data from 24 trials performed under the SP condition and from 13–20 accepted trials performed under the RT condition were used to carry out this analysis for each subject.
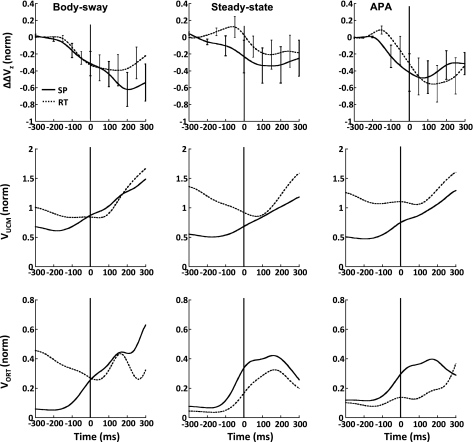
Figure 6 shows a typical example of the ΔV time profiles for the shoulder flexion task performed under the SP condition based on three sets of M-modes and Jacobians, four M-modes and the Jacobian per set, defined based on the body sway task data, and when the M-modes and the Jacobian were defined based on two time intervals within the shoulder flexion task, the steady-state and APA phases. Note the similar ΔV time profiles across the methods applied. All three methods show greater values in the steady-state phase preceding the movement initiation and a drop in ΔV within the interval t0 ± 150 ms. Note that ΔV values are positive for all three of the applied methods of M-mode and Jacobian identification. This may be interpreted as a multi-M-mode synergy stabilizing the COPAP coordinate.
Fig. 6.
An index of synergy (ΔV) for the SP condition for a representative subject (S1) was calculated for 3 sets of M-modes and Jacobians based on the body sway task (solid line) and on the steady-state (dashed line) and APA phases (dotted line) from the shoulder flexion task. Note the similar ΔV values and time profiles.
The two components of M-mode variance, VUCM and VORT, averaged across subjects, are shown in Fig. 7, middle and bottom. VUCM shows higher values than VORT for both the SP and RT conditions for different methods of M-mode and Jacobian identification. Both variance indexes show an increase before or about t0. The decrease in ΔV about the time of action initiation is mainly caused by the disproportionate increase in VORT.
Fig. 7.
Changes in the synergy index (ΔΔVZ: top), variance within the uncontrolled manifold (VUCM; middle), and variance orthogonal to the uncontrolled manifold (VORT; bottom) averaged across subjects were calculated using the 3 sets of M-modes and Jacobians from the body sway task (left) and from the steady-state (center) and APA phases (right) from the shoulder flexion task for the SP (solid line) and RT conditions (dashed line). SE bars across subjects are shown for selected times.
For statistical analysis, ΔV data were log-transformed, resulting in the index ΔVZ (see methods). In Fig. 7, top, the change in the z-transformed values of ΔV (ΔΔVZ) is shown for the SP and RT conditions averaged across subjects. For both conditions, ΔΔVZ decreased before t0, approximately within the interval {−150 ms; −100 ms} before t0. We refer to this early drop in ΔVZ as ASA. In the SP condition, a decrease in ΔVZ occurred earlier than in the RT condition; this difference was particularly obvious when the M-modes and the Jacobians were defined based on the data from the different time intervals within the shoulder flexion task.
To analyze possible differences in the timing of ASAs, ΔΔVZ data in the interval {−250 ms ; t0} were divided into five 50-ms time windows and compared using a repeated-measures ANOVA with the factors condition (SP and RT), method (body sway, steady state, and APA), and time (−250 ms, −200 ms, −150 ms, −100 ms, −50 ms, and t0). The ANOVA showed significant main effects of condition [F(1,124.929) = 11.8, P < 0.05] and time [F(5,186.306) = 5.13, P < 0.001] and no other effects. Pairwise comparisons revealed that ΔΔVZ was greater for −250, −200, and −150 ms than for −50 ms and t0 and that ΔΔVZ for −100 ms was greater than ΔΔVZ for t0. The effects of condition reflected smaller values for the SP compared with the RT condition.
Figure 8 depicts tASA, tAPA-MODES, and tAPA-EMG data for a typical subject (top) and data averaged across subjects (bottom) for the SP (left) and RT conditions (right). The drop in ΔV (i.e., tASA) was calculated by averaging the tASA determined when three sets of M-modes and Jacobian were used, from the body sway task and from the steady-state and APA phases of the shoulder flexion task. Under the RT condition, tASA occurred, on average, 143 ± 20 ms before task initiation. Thus tASA occurred earlier than tAPA-EMG (−37 ± 8 ms) and tAPA-MODES (−18 ± 5 ms). Similarly, in the SP condition, tASA occurred earlier than tAPA-EMG (−77 ± 12 ms) and tAPA-MODES (−57 ± 12 ms). An ANOVA with repeated measures with the factors condition (SP and RT) and index (tASA, tAPA-MODES, tAPA-EMG) revealed significant main effects of condition [F(1,24.493) = 4.54, P < 0.05] and index [F(2,37.830) = 19.99, P < 0.001]. Pairwise comparisons for the factor index showed that tASA was significantly smaller than both tAPA-MODES (P < 0.001) and tAPA-EMG (P < 0.001). The index × condition interaction approached significance (P = 0.06).
DISCUSSION
There are two main findings in this study. First, ASAs (Olafsdottir et al. 2005; Shim et al. 2005) were documented as changes in the index of covariation of muscle modes (M-modes) related to stabilization of COPAP. ASAs were seen about 100–150 ms before the initiation of the instructed voluntary action, fast shoulder flexion movement. They were initiated before any changes could be seen in EMG signals averaged across trials.
Second, analysis of M-mode covariation was performed several times, assuming different sets of M-modes and Jacobian matrices defined over different tasks (body sway and shoulder flexion) and over different time intervals within the shoulder flexion task. Despite the major differences in the M-mode sets (in particular, in the number of co-contraction patterns), indexes of M-mode covariation showed strikingly similar values and time profiles. This result indicates that synergies with similar characteristics can be built on dissimilar sets of M-modes (see also Danna-Dos-Santos et al. 2009).
Muscle Synergies in Postural Tasks
The notion of muscle synergy has been used in the field of movement studies for over 100 yr (Babinski 1899; Hughlings Jackson 1889). However, rarely has this notion been defined explicitly in a way that allows identification and quantification of synergies. Given the current surge in interest to synergies reflected, in particular, in several recent reviews on the topic (Grafton 2010; Latash et al. 2007; Latash 2008; Morasso et al. 2010; Ting and Chvatal 2010; Tresch and Jarc 2009), we want to clarify our stance on the issue.
We assume that the neural control of multimuscle redundant systems is based on a hierarchy with at least two levels. At the lower level of the hierarchy, muscles are united into groups such that a single variable can be used to produce parallel changes in the muscle activation levels within each group. Such groups have been documented in many recent studies and referred to as “synergies” (d'Avella et al. 2003; Ivanenko et al. 2005, 2006; Ting and Macpherson 2005; Torres-Oviedo et al. 2006; Torres-Oviedo and Ting 2007) or “M-modes” (Krishnamoorthy et al. 2003a, 2003b; Danna-Dos-Santos et al. 2007; Klous et al. 2010). The latter terms implies that such muscle groups form the basis (elemental variables) for synergies to be built upon; in that sense, it is similar to the notion of finger modes introduced to study multifinger synergies (Danion et al. 2003; Latash et al. 2001; Zatsiorsky et al. 1998). A variety of matrix factorization methods have been used to identify such muscle groups both across repetitive attempts at the same task and over consecutive time samples. Those methods involved principal component analysis, factor analysis, independent component analysis, and nonnegative matrix factorization. In one study, results of analysis using different methods were compared, and no clear advantage was shown for any one of them (Tresch et al. 2006).
At the upper level of the assumed hierarchy, a limited number of variables are manipulated corresponding to gains for the individual M-modes. We view this level as the one where covariation of variables is organized to produce task-specific stable behaviors (reviewed in Latash et al. 2002, 2007). We use the term “synergy” for such covaried adjustments of elemental variables that make most variance of elemental variables “good” in a sense that it does not affect a value (time profile) of an important performance variable. This definition links synergies to stability of performance and differs from the more commonly used one, “variables that show parallel scaling.”
On the basis of this definition, analysis of multi-M-mode synergies involves several important steps described in detail in methods. At the first step, the multidimensional space of muscle activations is reduced to a smaller dimensional set of eigenvectors (M-modes) using data pooled over a range of values of the potentially important variable (COPAP in our study). These data are also used to map small changes in the M-mode magnitudes on COPAP shifts, resulting in a Jacobian matrix. In our study, four M-modes were accepted, which is similar to three to five modes accepted in earlier studies of such tasks (Danna-Dos-Santos et al. 2007; Klous et al. 2010; Krishnamoorthy et al. 2003a, 2003b, 2004; Robert et al. 2008; Wang et al. 2006a).
There were two main types of M-modes identified at the first step. M-modes of the first type included significantly loaded activation indexes of either dorsal or ventral muscles (push-back and push-forward) as in most earlier studies (Danna-Dos-Santos et al. 2007; Krishnamoorthy et al. 2003a, 2003b; Wang et al. 2006a). M-modes of the second type involved dorsal-ventral muscle pairs significantly loaded with the same sign of the loading coefficients. Such M-modes were described earlier and termed “co-contraction modes” (Asaka et al. 2008; Krishnamoorthy et al. 2004; Robert and Latash 2008). In our experiments, the more common task (body sway) was associated with only a few cases of co-contraction modes. The number of such modes increased in the less usual shoulder flexion task, which was performed from an initial posture with the body leaning backward. This observation supports the earlier reports on more common occurrence of co-contraction M-modes in more challenging tasks (Asaka et al. 2008; Krishnamoorthy et al. 2004).
The initial nonneutral position could also contribute to the atypical behavior of the TA compared with earlier studies (e.g., Aruin and Latash 1995; Bouisset and Zattara 1990; Crenna and Frigo 1991). Since the subjects were leaning backward, TA showed a high activity level during the steady state. As a result, at the onset of focal movement, TA stayed active to secure this nonneutral posture (in contrast to the studies mentioned earlier and a modeling study by Ramos and Stark 1990, but in agreement with reports on APA reversals by Krishnamoorthy and Latash 2005). The TA then relaxes (50–100 ms after t0), and after the subject stabilizes the requested posture once again, the TA becomes active again.
The nonneutral initial posture could play a role in altering the typical APA patterns. In particular, we did not observe anticipatory activity in TA that is commonly described during similar tasks performed while standing upright (e.g., Aruin and Latash 1995). This could be related to the lower postural stability in the initial posture of our subjects. In particular, APAs are known to be reduced in conditions of low postural stability (Aruin et al. 1998; Nouillot et al. 1992). Therefore, we cannot discard a possibility that the specific patterns observed in our study were affected by the less stable initial posture and the necessity to maintain this active posture by the subjects. As mentioned earlier, we opted to use a posture with sufficient levels of muscle activation to enable computation of M-mode variance indexes. In a neutral posture, this would not be possible, since EMG signals are typically very low. We also emphasize that a typical EMG burst in TA is only one component of APAs. Other studies described multimuscle patterns of muscle activation during APAs that involved changes in the activity of both dorsal and ventral muscles (De Wolf et al. 1998; Slijper et al. 2002). Studies of APAs in below-the-knee amputees described COP shifts, although those persons were obviously unable to use lower leg muscles (Aruin et al. 1997; see also Rougier and Bergeau 2009). A major point of our approach is that the control of vertical posture is not muscle specific, it is muscle-group specific, and even this type of control is redundant.
A number of earlier studies emphasized similarities in the M-modes (they were addressed as “synergies”) across a variety of tasks (Ivanenko et al. 2004, 2005; Torres-Oviedo et al. 2006; Torres-Oviedo and Ting 2010). Our observations suggest that M-mode composition can show significant differences across tasks (Krishnamoorthy et al. 2004) and even across different time windows within a task (cf. Robert and Latash 2008). However, despite these differences, indexes of synergies computed on the basis of different sets of M-modes showed striking consistency in both magnitude and time patterns over the whole time of data analysis within the shoulder flexion task.
The synergy index computed in our study reflected the relative amounts of “good” and “bad” variance in the M-mode space. As such, it could be expected to be sensitive to the choice of the elemental variables (the eigenvectors). Nevertheless, when the same data were analyzed using different sets of M-modes, in steady state, the synergy index showed significantly positive values corresponding to VGOOD > VBAD, which is interpreted as a multi-M-mode synergy stabilizing the COPAP time profile. Furthermore, for all analyses, 100–150 ms before the action initiation, the synergy index started to decline (ASA). This decline reflected the faster growth of VBAD compared with VGOOD as the time of action initiation approached.
The similarity of the synergy index values computed on the basis of different sets of M-modes resembles results of an earlier study using upper body locomotor-like movements (Danna-Dos-Santos et al. 2009). In that study, multi-M-mode synergies stabilizing the moment of force about the longitudinal axis of the body were observed in subjects who showed different muscle organizations into M-modes. These results suggest that the redundancy in the muscle space allows the central nervous system to organize muscles into different sets of M-modes equally able to ensure stabilization of important mechanical variables at the higher level of the assumed hierarchy.
Two Aspects of Feedforward Control of Posture
The prevailing view on feedforward control of vertical posture has involved the generation of neural control signals based on predicted effects of one's own planned actions and/or expected changes in the environment on posture. A typical example of this mode of control is the APAs leading to changes in the patterns of muscle activation and mechanical variables in anticipation of a planned action (Belen'kii et al. 1967; reviewed in Massion 1992). The assumed role of such adjustments has been to generate forces and moments of force that would counteract the expected effects on posture. APAs have typically been studied using time patterns of EMG and mechanical variables averaged across repetitive attempts (Aruin and Latash 1995; Bouisset and Zattara 1990; Lee et al. 1987).
Within our theoretical framework, two types of feedforward adjustments can be identified: those reflected in time patterns of performance variables averaged across repetitive attempts (such as APAs) and those reflected in covariation patterns computed across repetitive attempts (ASAs). To explain this, one has to consider a model of motor synergies.
Both feedback-based (Latash et al. 2005; Todorov and Jordan 2002) and feedforward (Goodman and Latash 2006) models have been offered to account for synergic adjustments in elemental variables that stabilize certain features of performance. Recently, direct links between the equilibrium point (referent configuration) hypothesis (Feldman 1986; Feldman and Levin 1995) and the notion of synergies have also been proposed (Latash 2008, 2010; Latash et al. 2010; Martin et al. 2009). One of the mentioned models (Latash et al. 2005) is based on short-latency back-coupling loops within the central nervous system, somewhat similar to the well-known Renshaw cell system. Input into this system from a hierarchically higher controller consists of two groups of variables. One group (CV1) defines the overall pattern of performance, reflected in patterns averaged across trials, whereas the other group (CV2) specifies gains of the back-coupling projections and is reflected in indexes of covariation of elemental variables across trials (reviewed in Latash 2010). In general, the controller can change CV1 and/or CV2 in a feedforward fashion. Such changes in typical postural tasks are expected to result in APAs and ASAs, respectively.
Our experiments have shown that changes in CV2 can take place before changes in CV1 (similar conclusions based on studies of multifinger tasks have been reached by Kim et al. 2006; Olafsdottir et al. 2005). This was reflected in significantly earlier deviations of the synergy index, ASAs, compared with the earliest adjustments in such variables as individual muscle EMGs, and M-modes. These results allow us to conclude that feedforward control processes related to postural stabilization involve more than APAs; indeed, significantly earlier changes can be detected in patterns of covariation of elemental variables (M-modes). One could tentatively conclude that a reduction in the index of a COP-stabilizing synergy (ASA) is required to allow the muscles to make postural adjustments (APA) before movement initiation.
We emphasize that the covariation indexes in our study were computed across trials. Any trend in signals evident in the data averaged across trials is compatible with unchanged, increased, or decreased covariation across trials (both before EMG changes and during those changes). Indeed, earlier studies have shown no major changes in the index of covariation of M-modes while EMG signals varied strongly (for example, during voluntary body sway at different frequencies; Danna-Dos-Santos et al. 2007). Our current study shows an opposite result: changes in the index of M-mode covariation without changes in the EMG levels. The dissociation between average performance patterns and patterns of covariation of elemental variables (quantified with a synergy index) was shown previously in studies using multifinger tasks (Kim et al. 2006; Olafsdottir et al. 2005, 2007; Shim et al. 2005). This study is the first to demonstrate that changes in covariation of patterns of muscle activation can happen without changes in average levels of those patterns. These findings allow us to offer a hypothesis (to be further tested in future) that the patterns of the ΔV index are not consequences of processes tightly linked to EMG changes such as, for example, subthreshold depolarization of corresponding motoneuronal pools.
Comparison of the SP and RT trials showed one more qualitative difference between APAs and ASAs. Under the RT instruction, the onset of APAs shifted closer to the time of action initiation or was even seen after the action initiation (similar to earlier reports by Benvenuti et al. 1997; Bouisset and Zattara 1990; De Wolf et al. 1998; Lee et al. 1987). This was true for both estimates of the APA timing, using EMGs, and M-modes. In contrast, the timing of the ASA initiation was not different between the SP and RT conditions (in contrast to an earlier report on ASAs in multifinger force pulse production; Olafsdottir et al. 2005). This shows that the time pressure under the RT conditions did not change the average time at which the subjects started to adjust covariation patterns among the elemental variables. It is possible that CV2 adjustments start early, when an action has been planned but not initiated yet, and proceed slowly, resulting in significant shifts of the synergy index at 100–150 ms before action initiation. Since ASAs are defined using covariation patterns across multiple trials, some kind of averaging is unavoidable, and significant ASA shifts are seen at the same time under the two conditions.
To summarize, we have shown that preparation to a self-triggered postural perturbation is associated with two types of anticipatory adjustments, ASAs and APAs. ASAs and APAs reflect different feedforward processes within the hypothetical control scheme and result in changes in patterns of covariation of elemental performance variables and in their patterns averaged across trials, respectively. Studies of feedforward postural control should consider not only trends of performance variables but also changes in their stability as reflected by changes in the indexes of respective synergies.
GRANTS
The National Institutes of Health Grants NS-035032 and AG-018751 supported this study in part. P. Mikulic is grateful to The National Foundation for Science, Higher Education and Technological Development of the Republic of Croatia, for support for postdoctoral training at The Pennsylvania State University.
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the author(s).
ACKNOWLEDGMENTS
We appreciate helpful discussions with Dr. Alexander Aruin, and we thank PCB Piezotronics (Depew, NY) for donating the accelerometer.
APPENDIX
Defining M-modes
For the body sway task, the IEMGNORM_BS data formed a matrix with 12 columns, representing 12 muscles, and with the number of rows corresponding to 1% time windows of the cycles analyzed (i.e., 40 sway cycles give 4,000 rows). For the shoulder flexion task, the IEMGNORM_SF data were divided into the five phases described in EMG: shoulder flexion task [IEMGNORM_SF-PHASE(p), with p referring to the phase number]. IEMGNORM_SF-PHASE(p) data formed a matrix with 12 columns, representing 12 muscles, and with the number of rows corresponding to the number of time windows (each window 10 ms wide) within a particular phase multiplied by the number of trials analyzed (e.g., the APA phase of 150-ms duration over 24 trails gave 24 × 15 = 360 rows). The correlation matrices for the IEMGNORM_BS and IEMGNORM_SF-PHASE(p) were subjected to PCA using Matlab 7.6 software. The four PCs were subject to Varimax rotation with factor extraction. The factors (eigenvectors) were addressed as M-modes. Hence, this analysis resulted in six sets of M-modes: five for each of the phases in the shoulder flexion task, M-modeSF-PHASE(p) [12 × 4], and one for the body sway task, M-modeBS [12 × 4]. The M-mode magnitudes () were then obtained by multiplying the loadings of the M-modes with the IEMGNORM matrix using the following equations:
| (4) |
where and are calculated for each of the five phases (p). The number of data points depended on the size of the phases.
Defining the Jacobian matrix
Both the magnitudes of the M-modes and the COPAP were filtered with a 20-Hz, low-pass, second-order, zero-lag Butterworth filter before the changes between time windows were calculated. For the body sway task, multiple linear regression over all cycles was used to define the relations between [(N cycles × 100) × 4] and ΔCOPBS [(N cycles × 100) × 1] for each subject separately. Specifically, for each subject, and ΔCOPBS were computed over all cycles for each 1% of the cycle duration:
| (5) |
where k values are constants. The coefficients of the regression equations were arranged in a matrix that is a Jacobian matrix (J) reduced in this case to a 4 × 1 vector:
| (6) |
where T is the sign of transpose.
For the shoulder flexion task, multiple regressions over all trials within a condition (SP or RT) were performed for each of the five phases separately. For each subject, and ΔCOPSF-PHASE(p) were computed over all trials for each of the data points within a phase:
| (7) |
This analysis resulted in five Jacobian matrices for each of the phases of the shoulder flexion task:
| (8) |
Uncontrolled Manifold Analysis: Computation of the Synergy Index
For each subject, the mean magnitude over the trials of each of the M-modes () was calculated for each time window. This value was subtracted from the vectors of the individual changes in the magnitudes of the M-modes () for each trial for each time window. The residual mean-free vectors were calculated for each of the subjects:
| (9) |
where n is the number of dimensions in the M-mode space and d is the number of constraints.
The UCM subspace was approximated with the null space of the corresponding J. The null space of J is a set of all vector solutions x of a system of equations Jx = 0. The null space is spanned by basis vectors εi,SF-PHASE(p) and εi,SF-BS. The vector ΔM was resolved into its projection onto the UCM, fUCM, and the orthogonal subspace, fORT:
| (10a) |
and
| (10b) |
The trial-to-trial variance in each of the two subspaces (VUCM and VORT), as well as the total variance (VTOT) normalized by the number of degrees of freedom of the respective spaces, were calculated as
| (11a) |
and
| (11b) |
To quantify the relative amount of variance that is compatible with stabilization of COPAP, an index of synergy ΔV was calculated. The normalization of the index by the total amount of variance was carried out as described in earlier studies (Krishnamoorthy et al. 2003b; Robert et al. 2008) to facilitate comparison across subjects and conditions:
| (12) |
where all variance indexes are computed per degrees of freedom.
Because VUCM, VORT, and VTOT are computed per degrees of freedom, the index of synergy ΔV ranges between 1.33 (all variance is within the UCM) and −4 (all variance is in the orthogonal subspace). For further analyses, the ΔV values were transformed using a Fisher z-transformation (ΔVZ) adapted to the boundaries of ΔV:
| (13) |
REFERENCES
- Aruin AS, Forrest WR, Latash ML. Anticipatory postural adjustments in conditions of postural instability. Electroencephalogr Clin Neurophysiol 109: 350–359, 1998 [DOI] [PubMed] [Google Scholar]
- Aruin AS, Latash ML. Directional specificity of postural muscles in feed-forward postural reactions during fast voluntary arm movements. Exp Brain Res 103: 323–332, 1995 [DOI] [PubMed] [Google Scholar]
- Aruin AS, Latash ML. Anticipatory postural adjustments during self-initiated perturbations of different magnitude triggered by a standard motor action. Electroencephalogr Clin Neurophysiol 101: 497–503, 1996 [DOI] [PubMed] [Google Scholar]
- Aruin AS, Nicholas JJ, Latash ML. Anticipatory postural adjustments during standing in below the knee amputees. Clin Biomech (Bristol, Avon) 12: 52–59, 1997 [DOI] [PubMed] [Google Scholar]
- Asaka T, Wang Y, Fukushima J, Latash ML. Learning effects on muscle modes and multi-mode postural synergies. Exp Brain Res 184: 323–338, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Babinski F. De l'asynergie cerebelleuse. Rev Neurol 7: 806–816, 1899 [Google Scholar]
- Belen'kii VE, Gurfinkel VS, Pal'tsev EI. [Control elements of voluntary movements]. Biofizika 12: 135–141, 1967 [PubMed] [Google Scholar]
- Benvenuti F, Stanhope SJ, Thomas SL, Panzer VP, Hallett M. Flexibility of anticipatory postural adjustments revealed by self-paced and reaction-time arm movements. Brain Res 761: 59–70, 1997 [DOI] [PubMed] [Google Scholar]
- Bouisset S, Do MC. Posture, dynamic stability, and voluntary movement. Neurophysiol Clin 38: 345–362, 2008 [DOI] [PubMed] [Google Scholar]
- Bouisset S, Zattara M. Biomechanical study of the programming of anticipatory postural adjustments associated with voluntary movement. J Biomech 20: 735–742, 1987 [DOI] [PubMed] [Google Scholar]
- Bouisset S, Zattara M. Segmental movement as a perturbation to balance? Facts and concepts. In: Multiple Muscle Systems Biomechanics and Movement Organization, edited by Winters J, Woo S-Y. New York: Springer, 1990, p. 498– 735–506 [Google Scholar]
- Crenna P, Frigo C. A motor programme for the initiation of forward-oriented movements in humans. J Physiol 437: 635–653, 1991 [DOI] [PMC free article] [PubMed] [Google Scholar]
- d'Avella A, Saltiel P, Bizzi E. Combinations of muscle synergies in the construction of a natural motor behavior. Nat Neurosci 6: 300–308, 2003 [DOI] [PubMed] [Google Scholar]
- Danion F, Schoner G, Latash ML, Li S, Scholz JP, Zatsiorsky VM. A mode hypothesis for finger interaction during multi-finger force-production tasks. Biol Cybern 88: 91–98, 2003 [DOI] [PubMed] [Google Scholar]
- Danna-Dos-Santos A, Shapkova EY, Shapkova AL, Degani AM, Latash ML. Postural control during upper body locomotor-like movements: similar synergies based on dissimilar muscle modes. Exp Brain Res 193: 565–579, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Danna-Dos-Santos A, Slomka K, Zatsiorsky VM, Latash ML. Muscle modes and synergies during voluntary body sway. Exp Brain Res 179: 533–550, 2007 [DOI] [PubMed] [Google Scholar]
- De Wolf S, Slijper H, Latash ML. Anticipatory postural adjustments during self-paced and reaction-time movements. Exp Brain Res 121: 7–19, 1998 [DOI] [PubMed] [Google Scholar]
- Degani AM, Danna-Dos-Santos A, Robert T, Latash ML. Kinematic synergies during saccades involving whole-body rotation: a study based on the uncontrolled manifold hypothesis. Hum Mov Sci 29: 243–258, 2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Diener HC, Horak FB, Nashner LM. Influence of stimulus parameters on human postural responses. J Neurophysiol 59: 1888–1905, 1988 [DOI] [PubMed] [Google Scholar]
- Feldman AG. Once more on the equilibrium-point hypothesis (lambda model) for motor control. J Mot Behav 18: 17–54, 1986 [DOI] [PubMed] [Google Scholar]
- Feldman AG, Levin MF. The origin and use of positional frames of reference in motor control. Behav Brain Sci 18: 723–806, 1995 [Google Scholar]
- Goodman SR, Latash ML. Feed-forward control of a redundant motor system. Biol Cybern 95: 271–280, 2006 [DOI] [PubMed] [Google Scholar]
- Grafton ST. The cognitive neuroscience of prehension: recent developments. Exp Brain Res 2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hair JF, Anderson RE, Tatham RL, Black WC. Factor analysis. In: Multivariate Data Analysis, edited by Borkowski D. Englewood Cliffs, NJ: Prentice Hall, 1995, p. 364–404 [Google Scholar]
- Hughlings Jackson J. On the comparative study of the disease of the nervous system. Br Med J 17: 355–362, 1889 [Google Scholar]
- Ivanenko YP, Cappellini G, Dominici N, Poppele RE, Lacquaniti F. Coordination of locomotion with voluntary movements in humans. J Neurosci 25: 7238–7253, 2005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ivanenko YP, Poppele RE, Lacquaniti F. Five basic muscle activation patterns account for muscle activity during human locomotion. J Physiol 556: 267–282, 2004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ivanenko YP, Wright WG, Gurfinkel VS, Horak F, Cordo P. Interaction of involuntary post-contraction activity with locomotor movements. Exp Brain Res 169: 255–260, 2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim SW, Shim JK, Zatsiorsky VM, Latash ML. Anticipatory adjustments of multi-finger synergies in preparation for self-triggered perturbations. Exp Brain Res 174: 604–612, 2006 [DOI] [PubMed] [Google Scholar]
- Klous M, Danna-dos-Santos A, Latash ML. Multi-muscle synergies in a dual postural task: evidence for the principle of superposition. Exp Brain Res 202: 457–471, 2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krishnamoorthy V, Goodman S, Zatsiorsky V, Latash ML. Muscle synergies during shifts of the center of pressure by standing persons: identification of muscle modes. Biol Cybern 89: 152–161, 2003a [DOI] [PubMed] [Google Scholar]
- Krishnamoorthy V, Latash ML. Reversals of anticipatory postural adjustments during voluntary sway in humans. J Physiol 565: 675–684, 2005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krishnamoorthy V, Latash ML, Scholz JP, Zatsiorsky VM. Muscle synergies during shifts of the center of pressure by standing persons. Exp Brain Res 152: 281–292, 2003b [DOI] [PubMed] [Google Scholar]
- Krishnamoorthy V, Latash ML, Scholz JP, Zatsiorsky VM. Muscle modes during shifts of the center of pressure by standing persons: effect of instability and additional support. Exp Brain Res 157: 18–31, 2004 [DOI] [PubMed] [Google Scholar]
- Küng UM, Horlings CGC, Honegger F, Ullum JHJ. Incorporating voluntary unilateral knee flexion into balance corrections elicited by multi-directional perturbations to stance. Neuroscience 163: 466–481, 2009 [DOI] [PubMed] [Google Scholar]
- Latash ML. Evolution of motor control: from reflexes and motor programs to the equilibrium-point hypothesis. J Hum Kinet 19: 3–24, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Latash ML. Stages in learning motor synergies: a view based on the equilibrium-point hypothesis. Hum Mov Sci 29: 457–471, 2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Latash ML, Friedman J, Kim SW, Feldman AG, Zatsiorsky VM. Prehension synergies and control with referent hand configurations. Exp Brain Res 202: 213–229, 2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Latash ML, Scholz JF, Danion F, Schöner G. Structure of motor variability in marginally redundant multi-finger force production tasks. Exp Brain Res 141: 153–165, 2001 [DOI] [PubMed] [Google Scholar]
- Latash ML, Scholz JP, Schoner G. Motor control strategies revealed in the structure of motor variability. Exerc Sport Sci Rev 30: 26–31, 2002 [DOI] [PubMed] [Google Scholar]
- Latash ML, Scholz JP, Schoner G. Toward a new theory of motor synergies. Motor Control 11: 276–308, 2007 [DOI] [PubMed] [Google Scholar]
- Latash ML, Shim JK, Smilga AV, Zatsiorsky VM. A central back-coupling hypothesis on the organization of motor synergies: a physical metaphor and a neural model. Biol Cybern 92: 186–191, 2005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee WA, Buchanan TS, Rogers MW. Effects of arm acceleration and behavioral conditions on the organization of postural adjustments during arm flexion. Exp Brain Res 66: 257–270, 1987 [DOI] [PubMed] [Google Scholar]
- Martin V, Scholz JP, Schöner G. Redundancy, self-motion and motor control. Neural Comput 21:1371–1414, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Massion J. Movement, posture and equilibrium: interaction and coordination. Prog Neurobiol 38: 35–56, 1992 [DOI] [PubMed] [Google Scholar]
- Morasso P, Casadio M, Mohan V, Zenzeri J. A neural mechanism of synergy formation for whole body reaching. Biol Cybern 102: 45–55, 2010 [DOI] [PubMed] [Google Scholar]
- Nouillot P, Bouisset S, Do MC. Do fast voluntary movements necessitate anticipatory postural adjustments even if equilibrium is unstable? Neurosci Lett 147: 1–4, 1992 [DOI] [PubMed] [Google Scholar]
- Olafsdottir H, Yoshida N, Zatsiorsky VM, Latash ML. Anticipatory covariation of finger forces during self-paced and reaction time force production. Neurosci Lett 381: 92–96, 2005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olafsdottir H, Yoshida N, Zatsiorsky VM, Latash ML. Elderly show decreased adjustments of motor synergies in preparation to action. Clin Biomech (Bristol, Avon) 22: 44–51, 2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramos CF, Stark LW. Postural maintenance during movement: simulations of a two joint model. Biol Cybern 63: 363–375, 1990 [DOI] [PubMed] [Google Scholar]
- Robert T, Latash ML. Time evolution of the organization of multi-muscle postural responses to sudden changes in the external force applied at the trunk level. Neurosci Lett 438: 238–241, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robert T, Zatsiorsky VM, Latash ML. Multi-muscle synergies in an unusual postural task: quick shear force production. Exp Brain Res 187: 237–253, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rougier PR, Bergeau J. Biomechanical analysis of postural control of persons with transtibial or transfemoral amputation. Am J Phys Med Rehabil 88: 896–903, 2009 [DOI] [PubMed] [Google Scholar]
- Santos MJ, Kanekar N, Aruin AS. The role of anticipatory postural adjustments in compensatory control of posture: 1. Electromyographic analysis. J Electromyogr Kinesiol 20: 388–397, 2010 [DOI] [PubMed] [Google Scholar]
- Scholz JP, Schoner G. The uncontrolled manifold concept: identifying control variables for a functional task. Exp Brain Res 126: 289–306, 1999 [DOI] [PubMed] [Google Scholar]
- Shim JK, Olafsdottir H, Zatsiorsky VM, Latash ML. The emergence and disappearance of multi-digit synergies during force-production tasks. Exp Brain Res 164: 260–270, 2005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shim JK, Park J, Zatsiorsky VM, Latash ML. Adjustments of prehension synergies in response to self-triggered and experimenter-triggered load and torque perturbations. Exp Brain Res 175: 641–653, 2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- SKM V, Zatsiorsky VM, Latash ML. Variance components in discrete force production tasks. Exp Brain Res 205: 335–349, 2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Slijper H, Latash ML, Mordkoff JT. Anticipatory postural adjustments under simple and choice reaction time conditions. Brain Res 924: 184–197, 2002 [DOI] [PubMed] [Google Scholar]
- Ting LH, Chvatal SA. Decomposing muscle activity in motor tasks: methods and interpretation. In: Motor Control: Theories, Experiments, and Applications, edited by Danion F, Latash ML. New York: Oxford University Press, 2010 [Google Scholar]
- Ting LH, Macpherson JM. A limited set of muscle synergies for force control during a postural task. J Neurophysiol 93: 609–613, 2005 [DOI] [PubMed] [Google Scholar]
- Todorov E, Jordan MI. Optimal feedback control as a theory of motor coordination. Nat Neurosci 5: 1226–1235, 2002 [DOI] [PubMed] [Google Scholar]
- Torres-Oviedo G, Macpherson JM, Ting LH. Muscle synergy organization is robust across a variety of postural perturbations. J Neurophysiol 96: 1530–1546, 2006 [DOI] [PubMed] [Google Scholar]
- Torres-Oviedo G, Ting LH. Muscle synergies characterizing human postural responses. J Neurophysiol 98: 2144–2156, 2007 [DOI] [PubMed] [Google Scholar]
- Torres-Oviedo G, Ting LH. Subject-specific muscle synergies in human balance control are consistent across different biomechanical contexts. J Neurophysiol 103: 3084–3098, 2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tresch MC, Cheung VC, d'Avella A. Matrix factorization algorithms for the identification of muscle synergies: evaluation on simulated and experimental data sets. J Neurophysiol 95: 2199–2212, 2006 [DOI] [PubMed] [Google Scholar]
- Tresch MC, Jarc A. The case for and against muscle synergies. Curr Opin Neurobiol 19: 601–607, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Y, Asaka T, Zatsiorsky VM, Latash ML. Muscle synergies during voluntary body sway: combining across-trials and within-a-trial analyses. Exp Brain Res 174: 679–693, 2006a [DOI] [PubMed] [Google Scholar]
- Wang Y, Zatsiorsky VM, Latash ML. Muscle synergies involved in preparation to a step made under the self-paced and reaction time instructions. Clin Neurophysiol 117: 41–56, 2006b [DOI] [PubMed] [Google Scholar]
- Wang Y, Zatsiorsky VM, Latash ML. Muscle synergies involved in shifting the center of pressure while making a first step. Exp Brain Res 167: 196–210, 2005 [DOI] [PubMed] [Google Scholar]
- Winter DA, Patla AE, Prince F, Ishac M, Gielo-Perczak K. Stiffness control of balance in quiet standing. J Neurophysiol 80: 1211–1221, 1998 [DOI] [PubMed] [Google Scholar]
- Woollacott MH, von Hosten C, Rosblad B. Relation between muscle response onset and body segmental movements during postural perturbations in humans. Exp Brain Res 72: 593–604, 1988 [DOI] [PubMed] [Google Scholar]
- Zatsiorsky VM, Li ZM, Latash ML. Coordinated force production in multi-finger tasks: finger interaction and neural network modeling. Biol Cybern 79: 139–150, 1998 [DOI] [PubMed] [Google Scholar]