Unique characteristics of motor adaptation during walking in young children

Abstract

Children show precocious ability in the learning of languages; is this the case with motor learning? We used split-belt walking to probe motor adaptation (a form of motor learning) in children. Data from 27 children (ages 8–36 mo) were compared with those from 10 adults. Children walked with the treadmill belts at the same speed (tied belt), followed by walking with the belts moving at different speeds (split belt) for 8–10 min, followed again by tied-belt walking (postsplit). Initial asymmetries in temporal coordination (i.e., double support time) induced by split-belt walking were slowly reduced, with most children showing an aftereffect (i.e., asymmetry in the opposite direction to the initial) in the early postsplit period, indicative of learning. In contrast, asymmetries in spatial coordination (i.e., center of oscillation) persisted during split-belt walking and no aftereffect was seen. Step length, a measure of both spatial and temporal coordination, showed intermediate effects. The time course of learning in double support and step length was slower in children than in adults. Moreover, there was a significant negative correlation between the size of the initial asymmetry during early split-belt walking (called error) and the aftereffect for step length. Hence, children may have more difficulty learning when the errors are large. The findings further suggest that the mechanisms controlling temporal and spatial adaptation are different and mature at different times.

the ability to modify motor programs to sustained changes in the walking state must be very important for young children, since they learn to walk in varied environments amid enormous changes in body dimensions in the first few years of life. We know that transient sensory disturbances applied during supported stepping on the treadmill in young children result in functionally appropriate responses (Lam et al. 2003; Pang et al. 2003). For example, a touch to the dorsum of the foot during the swing phase causes the foot to be raised higher in that swing phase (Pang et al. 2003), similar to the stumbling corrective response observed in adult humans (Eng et al. 1994; Schillings et al. 1996). Repeated touch to the foot over consecutive steps causes the high-stepping to persist after the perturbation is removed (called an aftereffect), indicating that the children have modified their motor program to adapt to the new task (Pang et al. 2003). Spinal cats also show this form of learning (Hodgson et al. 1994).

Learning during walking can be more complex and take place over longer time scales than the high-stepping example described above. For example, walking on a split-belt treadmill with the two belts (1 for each leg) running at different speeds disrupts the left-right symmetry (henceforth referred to as “symmetry”) of walking. Both temporal symmetry (such as equal durations for comparable periods in the left and right walking cycle) and spatial symmetry (such as equal kinematic excursions of the left and right legs) are disrupted (Reisman et al. 2005). Symmetry can be restored with continued stepping on the split-belt treadmill for about 10 min. When the two belts are returned to the same speed after split-belt walking, the walking is asymmetric in a direction opposite to that seen initially (aftereffect), indicating the motor program for walking has been altered. Returning to symmetric walking with the belts at the same speed now requires unlearning. Young children make immediate modifications to their walking when on a split-belt treadmill (Yang et al. 2005), but the effects of sustained walking on the split-belt treadmill have not been studied.

In this study we refer to motor learning in response to a single session of walking on the split-belt treadmill as “motor adaptation” and adopt the definition of Martin et al. (1996). They state that three conditions must be satisfied: 1) there is no change in the movement form (e.g., normal walking and split-belt walking), 2) repetition is required to learn (e.g., continued walking for a few minutes), and 3) there is a significant aftereffect (defined above). For simplicity, “split-belt adaptation” refers to motor adaptation on the split-belt treadmill.

The importance of the cerebellum for split-belt adaptation is supported by the impairment of this adaptation in individuals with diffuse damage to the cerebellum (Morton and Bastian 2006) and in decerebrate cats with focal inhibition of nitric oxide activity in the vermis (Yanagihara and Kondo 1996). Cerebral structures are less essential for split-belt adaptation, since this adaptation is present in decerebrate cats (Yanagihara et al. 1993) and humans with cerebral stroke (Reisman et al. 2007). Moreover, only partial impairment results following extensive damage to the cerebral cortex [e.g., children with hemispherectomy (Choi et al. 2009)]. Split-belt adaptation is especially interesting to study in young children because the cerebellum is immature at birth and undergoes rapid maturation through the first year of life (Altman and Bayer 1997; Lavezzi et al. 2006; Rorke and Riggs 1969). We sought to determine when split-belt adaptation emerges in young children. Furthermore, adaptation of temporal and spatial symmetry during split-belt walking may be controlled by distinct neural regions (Malone and Bastian 2010), so we also investigated whether there are differences in the emergence and characteristics of temporal and spatial adaptation at this young age.

METHODS

Subjects.

Healthy, full-term children ages 6–36 mo were recruited through community parent/infant groups in Edmonton, Alberta, Canada. A parent provided written informed consent. All procedures were approved by the local Health Research Ethics Board.

Experimental procedures.

All children attended one to two testing sessions. Two sessions were included if the parent's schedule permitted (∼70% of the children). The first session (optional) was to familiarize the child with walking on the treadmill with belts at the same speed (tied-belt, speed 0.25–0.4 m/s) for ∼10–15 min. Pilot data indicated this practice reduced the variability of stepping in the subsequent testing session. The two sessions occurred within a week of each other. Testing sessions were 1–1.5 h in duration. Children were supported under the arms by a researcher over a custom-made split-belt treadmill (model INFSBT-FP; R. Gramlich and S. Graziano, University of Alberta). The researcher rested his/her forearms on a platform to minimize imposing movements on the children. Children were allowed to support as much of their own body weight as possible while avoiding hip and knee collapse during stepping. A piece of Plexiglas (15 cm high) between the two belts ensured that each leg stayed on its respective belt. All children were distracted with movies and toys in an effort to make the testing conditions (such as attention) as similar as possible across subjects of different ages.

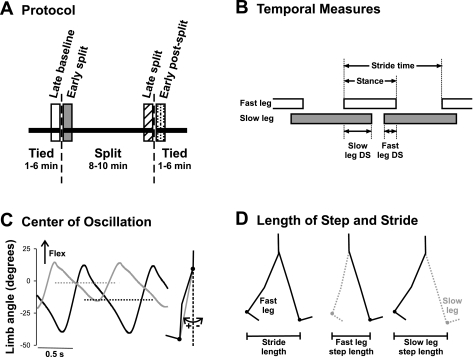
The protocol for the testing session (Fig. 1A) included periods of tied-belt walking, followed by split-belt walking and then tied-belt walking again. The belt speed for both tied-belt periods and the slow belt speed during split-belt walking was 0.25–0.35m/s. The slow belt speed was selected by trial and error to be the slowest speed at which regular walking steps could still be elicited. This allowed the belt speed ratio to be 2:1 for the majority of the subjects (n = 24) and 3:1 for 3 subjects, without inducing running in any of the subjects. The leg (left or right) on the fast belt was determined randomly for each child. Multiple trials were performed in each of the tied- and split-belt periods. Each trial was 1–3 min long, depending on the child's tolerance, with sitting breaks of about 1 min between trials. The total time spent in the tied- and split-belt periods was 1–6 and 8–10 min, respectively.

Fig. 1.

Methods. A: experimental protocol. Children walked on a split-belt treadmill with the belts at the same speed (tied), followed by the belts at different speeds (split), and finally again in the tied condition. Time periods of interest are late baseline (open bar), early split (shaded bar), late split (hatched bar), and early postsplit (stippled bar) at 40 steps for each period. B: temporal measures of walking are shown: stride time, stance time, and double support time. Open and shaded horizontal bars indicate the duration of the stance phase, and the space between the bars represents the duration of the swing phase. The duration of a stride includes a stance and a swing phase. Temporal coordination was quantified by double support times (i.e., time when both feet are in contact with the ground), shown for when the slow leg is trailing (slow DS) and when the fast leg is trailing (fast DS). C: center of oscillation is the mean limb angle over a stride. Limb angles of the fast (solid line) and slow (shaded line) legs are plotted for 1 child (35.2 mo) during early split. Dashed horizontal solid and shaded lines represent the mean limb angles for the fast and slow legs, respectively. Limb angle is the angle between the vertical and a vector connecting the hip and ankle markers (shaded line in inset at right). D: step length and stride length are illustrated. Step length, defined as the distance between the ankle markers of the 2 legs in the anteroposterior direction, was measured at the time of foot contact of the leading limb (i.e., instant in time illustrated at middle and right). The step lengths are named according to the leading leg, by convention. Stride length (left) is the distance traveled in the anteroposterior direction by the ankle marker of a single leg through the stance phase (i.e., foot contact to lift off, limb position shown for the 2 instances in time).

Instrumentation.

The motion was videotaped in the sagittal plane from the right side in all children (30 frames/s; Canon Elura 50) and also recorded in three dimensions (3-D) in eight children with the Optotrak system (Northern Digital, Waterloo, ON, Canada), which was acquired part way through the study. Reflective or infra-red emitting markers (as the case may be for the recording system) were placed at the midline of the trunk above the iliac crest, the greater trochanter, the lateral knee joint line, the lateral malleolus, and the head of the fifth metatarsal. This was done bilaterally when using infra-red markers and on the right leg (i.e., camera side) and left medial malleolus when using reflective markers. All children wore black leotards to enhance contrast. The video data were de-interlaced to 60 frames/s off-line, and the Optotrak system sampled at 100 Hz. Two force plates, one under each treadmill belt, recorded the vertical forces for each leg in all experiments.

Video, Optotrak, and analog signals were synchronized by a custom-made digital counter that generated a 5-V pulse (1 Hz) and advanced an LED display (resolution 10 ms) in view of the camera. In addition, an output pulse from the Optotrak indicated the timing of the first and last frame from that system. Force-plate signals were low-pass filtered at 30 Hz and analog-to-digital converted at 250 Hz (Axoscope; Molecular Devices, Foster City, CA).

Analysis.

The analysis was done for children who 1) completed the experiment (i.e., stepped on the treadmill for ≥1 min during both tied-belt periods and ≥8 min during the split-belt period) and 2) whose stepping was not too variable. Variability was estimated with the coefficient of variation (CV) for double support and step length, for both legs separately (i.e., 4 measures in total), in the first tied-belt period. If two of the four CVs were ≥50%, then the child was excluded, because variability could mask adaptation. A cutoff of ≥50% was chosen based on pilot data. The data from children with CVs ≥50% were sufficiently variable that the process of adaptation and the aftereffect could not be clearly seen. During split-belt walking, all children showed mostly 1:1 stepping (i.e., left-right alternation for every step). Occasional 2:1 steps were eliminated from the analysis because those steps would not have contributed to adaptation of 1:1 coordination.

Temporal and spatial measures that have been previously shown to change with split-belt walking were studied (Reisman et al. 2005). Temporal measures (e.g., stride time, percent time in stance, percent time in double support) were calculated from the times of foot contact and lift off, derived from the force-plate signals using a customized software program (MATLAB; The Mathworks, Natick, MA). The legs that stepped on the fast and slow treadmill belts during the split-belt period are always referred to as the fast and slow legs, respectively, even for the tied-belt period. Stride time is the time interval from foot contact of one leg to the subsequent foot contact of the same leg (see Fig. 1B). Stance time is the time interval when the foot is in contact with the ground and is expressed as a percentage of the stride time. For each stride, there are two periods of double support (i.e., both feet in contact with the ground). Fast double support is the time from foot contact of the slow leg to lift off of the fast leg; slow double support is the time from foot contact of the fast leg to lift off of the slow leg (see Fig. 1B). The peak force exerted during the stance phase by the fast and slow legs for every step was also calculated and is expressed as a percentage of the child's body weight.

Spatial measures included center of oscillation and stride length. Center of oscillation (Malone and Bastian 2010; Vasudevan et al. 2011) was obtained from the children recorded with the Optotrak system (n = 8), because this system provided bilateral kinematic data for the estimation of limb angle. The center of oscillation is the average limb angle in a stride (see Fig. 1C). Limb angle is the angle formed with respect to the vertical by a line joining the greater trochanter and lateral malleolus markers. The definition of stride length used has been modified for treadmill walking (Reisman et al. 2005) and refers to the distance traveled by the ankle marker in the anterior-posterior direction from foot contact to lift off of one leg (see Fig. 1D).

The final measure, step length, reflects both spatial and temporal components of coordination. Step length is the anterior-posterior distance between the ankle markers of the two legs at foot contact of the anterior leg (i.e., fast and slow step length is measured at fast and slow foot contact, respectively) (see Fig. 1D). In able-bodied adults, step length can be altered by changing the spatial coordination of the legs (i.e., shifting the center of oscillation of each leg) or the temporal coordination (i.e., changing the timing relationship of the legs) (Malone and Bastian 2010). Stride length and step length were obtained off-line using either an automatic marker tracking system (Peak Motus; Vicon, Los Angeles, CA), in the case of video recordings, or coordinates obtained from the Optotrak system.

To quantify symmetry, the above measures obtained from the left and right legs were combined. For stance time, stride length, and center of oscillation, symmetry was the measure from the fast leg minus the measure from the slow leg. Symmetry in double support and step length were further normalized as follows:

$$\text{Double}\hspace{0.17em}\text{support}\hspace{0.17em}\text{symmetry}=\frac{\text{fast}\hspace{0.17em}\text{leg}\hspace{0.17em}\text{DS}-\text{slow}\hspace{0.17em}\text{leg}\hspace{0.17em}\text{DS}}{\text{stride}\hspace{0.17em}\text{time}}\times 100\%$$

$$\text{Step}\hspace{0.17em}\text{length}\hspace{0.17em}\text{symmetry}=\frac{\text{fast}\hspace{0.17em}\text{SL}-\text{slow}\hspace{0.17em}\text{SL}}{\text{fast}\hspace{0.17em}\text{SL}+\text{slow}\hspace{0.17em}\text{SL}}$$

For each child, the symmetries in double support time and step length were estimated from the average of 40 steps from each of 1) late baseline, 2) early split, 3) late split, and 4) early postsplit (see Fig. 1A). Similar calculations were made for center of oscillation when available. The number of steps chosen for analysis ensured a power level of 0.8 for the comparison of the various time periods. Moreover, because of the very slow time course of adaptation, 40 steps captured the status of each of the time periods well (see Fig. 3).

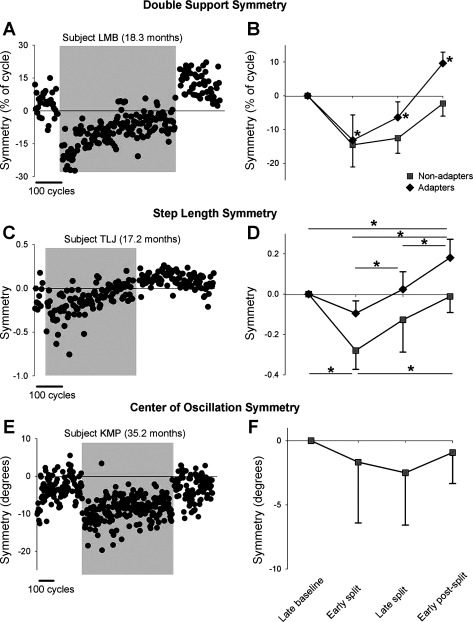
Fig. 3.

Symmetry of double support time, step length, and center of oscillation. A and C show data from single subjects who showed adaptation in double support and step length, respectively. E shows data from a single subject who did not show adaptation in center of oscillation. Data points represent means of 3 consecutive steps. Shaded region indicates the split-belt period. B, D, and F show group data for the adapters (solid diamonds) and nonadapters (solid squares) in measures of double support (n = 23 and 3, respectively), step length (n = 12 and 7, respectively), and center of oscillation (n = 0 and 7, respectively). Values are means ± SD, after the asymmetry in baseline was removed (see methods). In B: *P < 0.008, significantly different from other time periods, including baseline. In D: *P < 0.008, significant difference, with results for adapters and nonadapters shown at top and bottom of graph, respectively.

To study the time course of learning across subjects for the period of split-belt walking, we combined the steps of all children who showed adaptation to produce average plots of double support and step length symmetry. Before data were averaged across subjects, the mean symmetry of the last 40 steps in baseline walking was subtracted from each subject's measures to remove differences in asymmetry between subjects during baseline walking. Double support time and step length data from 10 healthy adults who participated in the same split-belt walking protocol are shown for comparison. These adults were also used in Vasudevan et al. (2011). The adults walked for 4 min with the belts tied [speed = leg length (m)/s], followed by 14 min of split-belt walking (2:1 speed differential) and 16 min of tied-belt walking. Adults also took rest breaks every 2 min and watched videos during walking. The average time-course plots were fitted with linear, single-exponential, and double-exponential functions, and the coefficients of determination (r²) were used to determine which function provided the best fit.

Statistics.

Mean values are reported with ±1 standard deviation (SD), and the level of significance for statistical tests was 0.05 unless otherwise noted. To determine whether a child had an asymmetry during the baseline period (i.e., a preexisting inequality in the temporal or spatial measures from the left and right sides), we used a paired t-test to compare double support, step length, and center of oscillation between the fast and slow legs. Fisher's exact test was used to compare the proportion of children with asymmetries in spatial (i.e., center of oscillation) and temporal measures (i.e., double support time). To induce adaptation, the split-belt treadmill must produce a significant change in the symmetry of the child's walking, which we call “error,” defined as a significant difference in the symmetry measures between late baseline and early split periods (1-way independent t-test). Children who did not show a significant error were not included in the analysis to avoid including children who did not have a chance to adapt because the error was too small. Similarly, the presence of adaptation (i.e., an aftereffect) was defined as a significant difference in symmetry between late baseline and early postsplit (1-way independent t-test). The proportions of children who showed adaptation in temporal and spatial measures were compared using Fisher's exact test.

The mean values for symmetry during the four time periods for each child were combined for group analysis. Nonparametric tests were used when the assumption of normality was not met (assessed with Shapiro-Wilk's test). To compare measures of stance time and stride length across time periods, we used a repeated-measures ANOVA with time period as the within-subjects factor. Since many children showed asymmetries in double support time, step length, and center of oscillation during baseline walking, the mean value in the late baseline period was subtracted from the mean values of the other three time periods for each child before the data were plotted. To examine how these three measures changed across time periods, we first divided children into two groups depending on whether or not they showed adaptation (i.e., significant aftereffect, described above). Children who showed adaptation (adapters) or did not show adaptation (nonadapters) were analyzed separately. The measures for each group were compared across time periods with a one-way repeated-measures ANOVA. Age, body weight supported when walking (i.e., average peak force exerted during each time period for each leg), and size of error (i.e., difference in symmetry between baseline and early split periods) were compared for the adapters and nonadapters with either an independent t-test or the Mann-Whitney U-test (when normality assumption was not met). Walking status (independent or not) was compared for the same two groups using Fisher's exact test. The size of the aftereffect (i.e., difference in symmetry values between baseline and early postsplit periods) was correlated with the size of the error and the size of the baseline asymmetry (i.e., difference in symmetry values between fast and slow legs during late baseline) using Pearson's correlation coefficient (r). Bonferroni's test was used for all post hoc analyses at P < 0.008.

RESULTS

Thirty-five of the 44 children tested completed all walking conditions of the experiment. All children tested between the ages of 6 and 8 mo (n = 5) were unable to complete the minimum of 8 min of split-belt walking and were not included. Of the 35 children who completed the experiment, 8 were excluded because of excessive variability in their walking (ages 8.7–14.2 mo, 4 males, 1 walking independently at time of testing), leaving 27 children (ages 8.5–35.2 mo, 15 males, 16 walking independently at time of testing) for analysis.

Stance time and stride length.

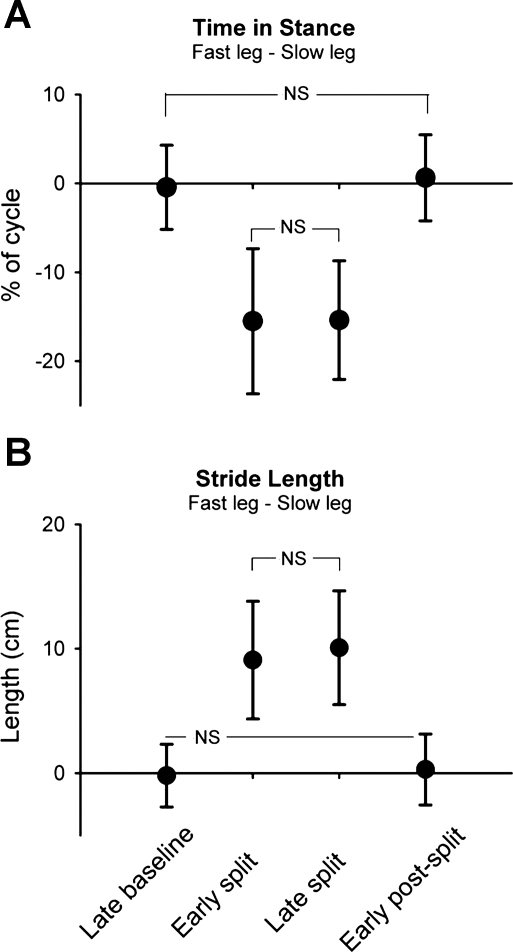
Consistent changes in stance time and stride length were seen across all children. On exposure to the split-belt treadmill, asymmetries in both measures occurred immediately. Stance time was shorter in the fast leg compared with the slow leg, whereas stride length (modified for treadmill walking, see methods) was longer in the fast leg compared with the slow leg. The asymmetries in stance time and stride length were maintained throughout split-belt walking. In early postsplit there was an immediate return to the baseline values for stance time and stride length (i.e., no aftereffect). Group data for the two measures are shown in Fig. 2.

Fig. 2.

Stance time and stride length. Group data (n = 27) are shown for time in stance (expressed as % of step cycle; A) and stride length (in cm; B). Data points represent mean values (from 40 steps) for each time period with error bars (SD). NS, not statistically significant. All other comparisons are significant (P < 0.008, Bonferroni).

Double support time.

On exposure to split-belt walking, all but 1 child showed a change in double support time of the 2 legs (i.e., significant error), so 26 children were included in the analysis. After the early split period, the children showed one of two outcomes for double support throughout the remainder of the experiment. The first group, called adapters, (n = 23, mean age = 15.7 ± 7.0 mo) showed a gradual return to symmetry by the end of the split-belt period. Moreover, a significant aftereffect was seen during the early postsplit period, with an asymmetry in the opposite direction from that seen in early split. An example of a single subject from this group is shown in Fig. 3A. The second group, called nonadapters, did not show a return to symmetry by the end of the split-belt period and did not show an aftereffect (n = 3, mean age = 11.2 ± 2.7 mo). Group data are shown in Fig. 3B.

Step length.

Unlike double support time, several children (8/27) did not show any change in their step length with initial exposure to split-belt walking (i.e., no error). Of the remaining 19 children, adaptation of step length was seen in 12 children (adapter group), all of whom also showed adaptation with respect to time in double support (mean age = 14.7 ± 3.8 mo). In these children, the error in step length symmetry seen in the early split period gradually diminished over the course of the split-belt period. An aftereffect in step length symmetry was seen during the early postsplit period in these children. Data from a single subject are shown in Fig. 3C. Seven children did not show any adaptation in step length (i.e., no aftereffect, nonadapter group) (mean age = 17.5 ± 10.2 mo). In some of these children the error in step length symmetry seen in the early split period was reduced with further split-belt walking, whereas in others the size of the error remained unchanged throughout split-belt walking. Group data are shown in Fig. 3D.

Center of oscillation.

Center of oscillation data was available for eight children, and most (7/8) showed a significant asymmetry (i.e., error) in the early split period. In two children, this error was reduced over the course of split-belt walking, but none of the children showed an aftereffect. Data from a single subject are shown in Fig. 3E, and group data are shown in Fig. 3F.

Emergence of temporal and spatial adaptation can occur at different times.

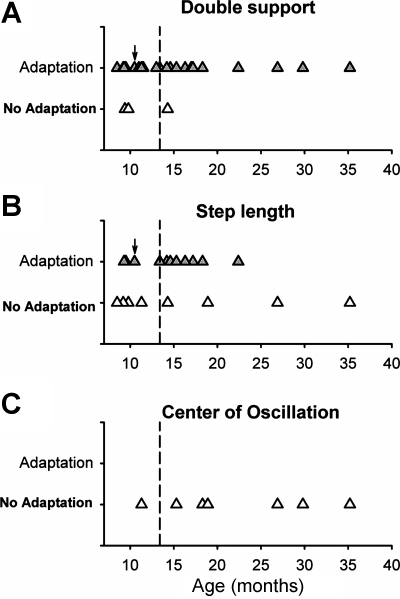
Only a few children did not show adaptation in double support (3/26), with ages ranging 9.4–14.3 mo (Fig. 4A). In contrast, more children did not show adaptation in step length (7/19), with ages ranging 8.5–35.2 mo (Fig. 4B). None of the children showed adaptation in center of oscillation (Fig. 4C), and this observation was significantly different from the proportion of children who showed adaptation in double support (P < 0.001, Fisher's exact test). Hence, emergence of adaptation in temporal (double support) and spatial symmetry (center of oscillation) did not occur at the same time for a child.

Fig. 4.

Emergence of adaptation: age at which adaptation in split-belt walking appears. The ages of those who showed adaptation (shaded triangles) and those who did not (open triangles) are shown for double support (A; n = 26), step length (B; n = 19), and center of oscillation (C; n = 7). Children who did not show an error in a measure on exposure to split-belt walking were not included in the plot for that measure. Emergence of adaptation in double support time, step length, and center of oscillation does not always occur at the same time. Children whose data are plotted to the right of the dashed vertical lines were independent walkers at the time of testing. Children whose data are plotted to the left of the dashed vertical lines were nonwalkers, with the exception of 1 child (indicated by arrow) who was an independent walker.

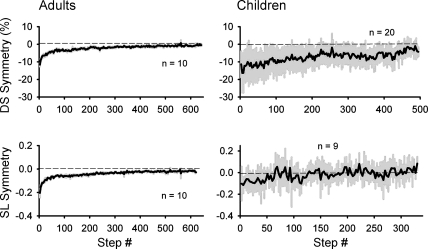
Time courses of adaptation.

The time courses of adaptation for both double support and step length symmetry in adults and children are shown in Fig. 5. The adult data is best fit with a double-exponential function (r² = 0.88 and 0.85 for double support and step length, respectively), whereas the data from the children is best fit with a straight line (r² = 0.64 and 0.36 for double support and step length, respectively). Hence, the time course of adaptation in the early split period (i.e., first 40 steps) is slower in the children than in the adults.

Fig. 5.

Time course of adaptation. Group data show means (solid line) across subjects for the period of split-belt walking. Double support symmetry (top) and step length symmetry (bottom) for both adults (left) and children (right) are shown, with 1SD represented by shading. Only adapters (i.e., those showing significant aftereffects) are included.

Differences between adapters and nonadapters.

For double support time, there was no difference between the adapters and nonadapters with respect to age, size of error, walking status or the amount of body weight supported during the time periods of early split, late split, and early postsplit (P > 0.05). Walking status is illustrated in Fig. 4, with the dashed vertical lines separating the independent walkers (right of dashed line) from the nonwalkers (left of dashed line, with one exception: 1 child in this grouping was an independent walker, indicated by a black arrow).

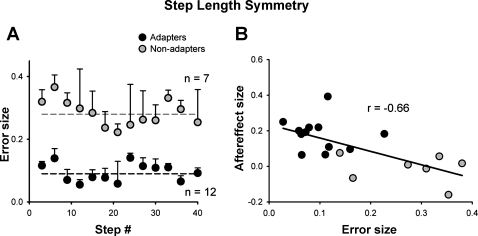
For step length, there was a significant difference in the error size between the two groups (P = 0.004). The adapters experienced significantly less error in step length during the early split period than the nonadapters (error in step length symmetry was 0.09 ± 0.06 and 0.28 ± 0.09, respectively, Fig. 6A). There was a negative correlation between the size of the error and the size of the aftereffect (r = −0.66, P = 0.002) (Fig. 6B). There was no difference between the adapters and nonadapters with respect to age, walking status, or the amount of body weight supported (P > 0.05).

Fig. 6.

Error size. A: error size in step length symmetry (difference between mean values for baseline and early split periods) plotted for the early split period. Each data point represents mean of 3 consecutive steps from n subjects, as indicated, with error bars (SD). Dashed horizontal solid and shaded lines represent the mean error experienced by the adapters and nonadapters, respectively, during the early split period. B: error size in step length symmetry vs. size of the aftereffect (difference between mean values for baseline and early postsplit periods). Each data point represents 1 child. Solid and shaded circles represent children who did and did not show adaptation in step length, respectively.

Asymmetry during baseline walking and the effect on split-belt adaptation.

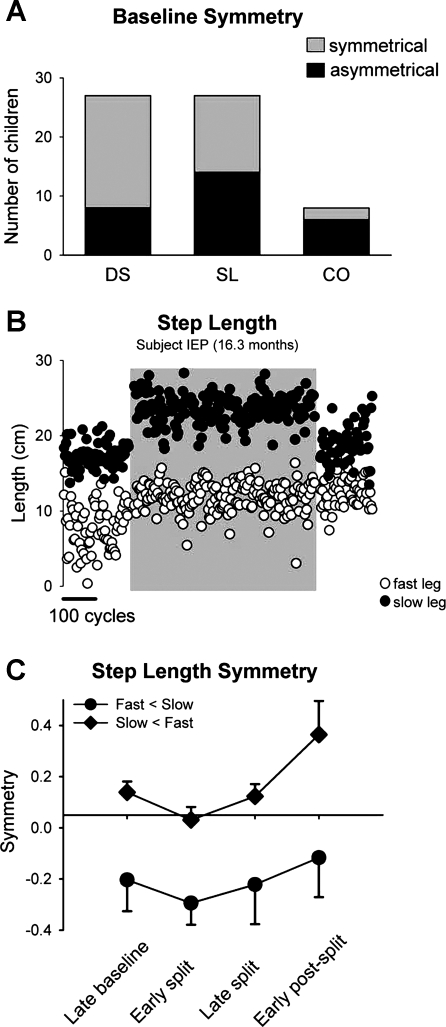
Not all children stepped symmetrically during the baseline period. More children were asymmetric in step length (14/27; mean age = 12.6 ± 4.7 mo) than in double support (8/27; mean age = 13.5 ± 5.1 mo) during baseline stepping (Fig. 7A). Six of the eight children for whom we have center-of-oscillation data were asymmetric in that measure (mean age = 23.4 ± 8.8 mo) (Fig. 7A). The proportion of children (i.e., 6/8) showing asymmetry in center of oscillation was significantly greater than the proportion showing asymmetry in double support time (i.e., 8/27, P = 0.039, Fisher's exact test). There was no correlation between the size of the baseline asymmetry and the size of the aftereffect for either double support time or step length. Hence, despite the presence of an asymmetry, the children were able to show adaptation.

Fig. 7.

Asymmetries. A: number of children that showed symmetrical (shaded bars) and asymmetrical (solid bars) walking with respect to double support (DS), step length (SL), and center of oscillation (CO). B: step length data from a single subject who showed an asymmetry during the baseline period (fast step length < slow step length). Open and solid circles represent the fast and slow step lengths (mean of 3 steps), respectively. Shaded region indicates the split-belt period. C: values are means ± SD of step length symmetry (mean late baseline values not subtracted) for children who 1) showed asymmetries in step length at baseline, 2) showed an error in step length symmetry during early split, and 3) showed adaptation (total of 5 children). Two children had fast < slow asymmetry (solid circles) (i.e., step length of the fast leg was shorter), and 3 children had slow < fast asymmetry (solid diamonds) (i.e., step length of the slow leg was shorter).

Split-belt walking caused either an increase or a decrease in the asymmetry of double support and step length compared with that seen in the baseline period. If the asymmetry was increased, the aftereffect caused the stepping to be more symmetric (an example from a single subject is shown in Fig. 7B; group data are shown in Fig. 7C, circles). In contrast, if the baseline asymmetry was reduced with split-belt walking, the children showed a greater asymmetry during early postsplit compared with baseline walking (Fig. 7C, diamonds). Similar findings have been reported in adults with stroke (Reisman et al. 2007) and children with hemispherectomy (Choi et al. 2009).

DISCUSSION

We have shown that most children ages 8.5–36 mo of age adapt to split-belt walking. This adaptation was demonstrated as a reduction in the error in double support and step length symmetry caused by split-belt walking and the presence of an aftereffect on the return to tied belt walking. A few children showed adaptation in double support time, but not step length; none showed the reverse. No children showed adaptation in the spatial measure, center of oscillation. In addition, baseline asymmetry was seen more often in step length and center of oscillation compared with double support, suggesting that the neural mechanisms controlling spatial symmetry are different from those controlling temporal symmetry, in agreement with studies of patient populations (Choi et al. 2009). Furthermore, the time courses of adaptation to both double support and step length during early split-belt walking were slower in children compared with adults, suggesting that the neural mechanisms for adaptation are either different or not functioning in the same way. In contrast to the gradual emergence of adaptation in double support and step length, all children, regardless of age, showed immediate changes in stance time and stride length similar to those seen in adults (Reisman et al. 2005), indicating early maturation of the neural mechanisms controlling these measures.

Neural mechanisms underlying split-belt walking and adaptation.

All children showed adultlike changes in measures of stride length and stance time during split-belt walking with no aftereffect during the early postsplit period (Reisman et al. 2005). Adults with diffuse cerebellar atrophy (Morton and Bastian 2006) and those with cerebral strokes (Reisman et al. 2007) also showed normal changes in these measures. Although time-dependent changes have not been reported for these two measures in spinal cats, it is clear that spinal cats can adjust their stance and swing phase durations to accommodate split-belt walking (Forssberg et al. 1980). The duration of the stance phase and the excursion of the limb (i.e., stride length) are regulated by movement-related afferent feedback that affects phase transitions (i.e., stance to swing, swing to stance). For example, sensory inputs related to hip position and ankle loading regulate phase durations and transitions during locomotion (reviewed in Pearson 2008; Rossignol et al. 2006). Together, the results suggest that neural substrates controlling stance time and stride length in split-belt walking are contained in parts of the nervous system that mature early, possibly the spinal cord.

Midline structures in the cerebellum may be especially important for split-belt adaptation, since cerebellar patients with gait and postural disturbances (functions controlled by midline cerebellar structures) were more impaired in split-belt adaptation than those with limb ataxia (functions controlled by intermediate and lateral cerebellar structures) (Morton and Bastian 2006). Experiments in decerebrate cats also showed that disruption of nitric oxide activity in the vermis impaired split-belt adaptation (Yanagihara and Kondo 1996). Interestingly, the midline cerebellar structures are earlier to mature than the lateral parts of the cerebellum, as seen from histology (Rorke and Riggs 1969; Yakovlev and Lecours 1967). Perhaps the midline cerebellar structures are not functionally mature in spite of the appearance of mature myelin. Alternatively, split-belt adaptation may also depend on intermediate or lateral regions of the cerebellum, which are later to mature. For example, spatial adaptation may involve cerebral-cerebellar interactions, whereas temporal adaptation may involve spinal cord-cerebellar interactions (Malone and Bastian 2010; Vasudevan et al. 2011), which could explain the different ages at which spatial and temporal adaptation appear.

Although the cerebellum is clearly important for split-belt adaptation, other neural structures cannot be discounted. For example, children with hemispherectomy show an impaired ability to adapt double support time but not step length, suggesting that the cerebrum may also play a role in temporal adaptation of split-belt walking (Choi et al. 2009). The basal ganglia are involved in many forms of motor learning, including motor adaptation (reviewed in Doyon et al. 2009), so its role in split-belt adaptation should be explored. The spinal cord may also have a role, since spinal animals are able to adapt their locomotor pattern in response to sustained force perturbations (Heng and de Leon 2007; Hodgson et al. 1994). Its role in split-belt adaptation remains to be determined.

Time course of adaptation in children is slower than adults.

Adaptation of double support time and step length was seen in many of the children. The time course of adaptation, however, was slower than adults. The adult data fit best with a double-exponential function, reflecting fast and slow components of adaptation (Smith et al. 2006). The time courses of the children were best fit to a straight line, perhaps suggesting their learning involves only the slow component. The children appear to have experienced a smaller initial error in step length symmetry and a more rapid return to symmetry compared with the adults (Fig. 5). This may have resulted from the method used to remove baseline asymmetry from the data (i.e., subtraction of mean baseline values, see methods), since the children had greater asymmetry and variability in their step lengths during baseline walking. Our data agree well with development of split-belt adaptation in older children, in that the adaptation of temporal coordination for children 3–5 yr old is best fit with a double-exponential function (i.e., similar to adults), whereas the adaptation of step length is best fit with a linear function (i.e., different from adults, whose data are fit with a double exponential) (Vasudevan et al. 2011). Hence, there is a continuum in the protracted development toward adultlike adaptation rates, and our data show the pattern of adaptation shortly after it emerges.

It is possible that the differences in adaptation observed between young children and adults could result from the children having less experience with walking. This hypothesis is difficult to test, because experience varies with maturation of the nervous system. We think experience may not be a large factor, however, because there were no differences between the adapters and nonadapters with respect to the proportion walking independently (i.e., with more experience than those not yet walking independently).

Mechanisms controlling spatial and temporal symmetry are likely different.

Most children showed adaptation in temporal symmetry (double support), but none showed adaptation in spatial symmetry (center of oscillation). In addition, the incidence of asymmetry during baseline stepping was significantly greater for center of oscillation than double support time. Together, these findings suggest that independent neural substrates and/or mechanisms are responsible for coordinating the temporal and spatial coordination of the legs and that these two substrates mature at different rates in humans. Choi et al. (2009) found that the spatial and temporal components of split-belt adaptation were affected differently by damage to the cerebral cortex. Children with hemispherectomy had difficulty adapting double support time and interlimb phasing (temporal measures), yet their ability to adapt step length did not differ from controls (Choi et al. 2009). Individuals with damage to the cerebellum showed some correction of double support asymmetry when walking on the split-belt treadmill but no improvement in step length symmetry (Morton and Bastian 2006). Furthermore, when able-bodied adults adapted to split-belt walking, their temporal and spatial coordination showed differing sensitivities to distraction level (Malone and Bastian 2010) and visual input (Torres-Oviedo and Bastian 2010). Hence, there is converging evidence that spatial and temporal symmetry are independent, and the neural substrates responsible are likely different.

Adaptation of step length not seen when initial errors are large.

Prediction error, i.e., the difference between the expected movement and the actual movement, is thought to drive motor adaptation (reviewed in Shadmehr et al. 2010). In our case, the initial asymmetry during the split-belt period, which we call error, is thought to approximate prediction error. The size of the prediction error also affects learning. For example, healthy adults have been shown to have greater and more enduring aftereffects when errors in eye or arm movements were introduced gradually, rather than abruptly (Kagerer et al. 1997; Klassen et al. 2005; Michel et al. 2007). The size of the initial error induced by split-belt walking may be another factor influencing the presence of adaptation in children. The error in step length induced by the split-belt treadmill during the early split period was significantly greater in the children who did not show adaptation compared with those who did. Since the children were slow to adapt step length (i.e., took >40 steps), the difference in error size between the adapters and nonadapters did not result from the adapters reducing the error within the first 40 split-belt steps (see Fig. 6A). A similar situation has been reported in patients with severe cerebellar damage who adapted to a novel reaching task when the asymmetry was presented gradually (i.e., small error) but not when the asymmetry was initially presented at full strength (i.e., large error) (Criscimagna-Hemminger et al. 2010). Like cerebellar patients, children may have greater difficulty learning from large errors. However, the relationship between error size and adaptation in children needs to be tested directly. We are currently exploring this in more detail.

Split-belt walking did not induce an error in step length in seven children, whereas only one child showed no error in double support time. Interestingly, children with hemispherectomy sometimes showed the opposite: no error in double support time but an error in step length (Choi et al. 2009). Since in each of these cases the children were more asymmetric during baseline walking in the parameter that showed no error (step length for our subjects, double support for the children with hemispherectomy), it may have resulted from a ceiling effect, in that the existing asymmetry was severe enough that the split-belt treadmill could not further exaggerate it (Choi et al. 2009). In our children who did not show an error, however, about the same number showed baseline asymmetries in both directions (i.e., fast leg step length longer and slow leg step length longer), so a ceiling effect alone cannot explain the lack of error in all cases.

Split-belt walking can temporarily correct baseline asymmetries in walking.

Some children showed baseline asymmetries in double support or step length that were corrected through split-belt walking. This phenomenon also has been reported in individuals with stroke (Reisman et al. 2007) and in children with hemispherectomy (Choi et al. 2009). If split-belt walking worsened the baseline asymmetry, the child's walking became more symmetrical in the early postsplit period (Fig. 7C). Thus we speculate that split-belt walking may prove a valuable therapy for correcting walking asymmetries in individuals with early childhood stroke.

GRANTS

This work was supported in part by the Natural Sciences and Engineering Foundation of Canada and the Canadian Institutes of Health Research (to J. F. Yang). K. E. Musselman was supported by scholarships from the Canadian Institutes of Health Research and the Alberta Heritage Foundation for Medical Research. E. V. L. Vasudevan was supported by National Institutes of Health (NIH) Grant F32NS63642. A. J. Bastian was supported by NIH Grant HD048741.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).