High-frequency, short-latency disinhibition bursting of midbrain dopaminergic neurons

Abstract

During reinforcement and sequence learning, dopaminergic neurons fire bursts of action potentials. Dopaminergic neurons in vivo receive strong background excitatory and inhibitory inputs, suggesting that one mechanism by which bursts may be produced is disinhibition. Unfortunately, these inputs are lost during slice preparation and are not precisely controlled during in vivo experiments. In the present study we show that dopaminergic neurons can be shifted into a balanced state in which constant synaptic N-methyl-d-aspartate (NMDA) and GABA_A conductances are mimicked either pharmacologically or using dynamic clamp. From this state, a disinhibition burst can be evoked by removing the background inhibitory conductance. We demonstrate three functional characteristics of network-based disinhibition that promote high-frequency, short-latency bursting in dopaminergic neurons. First, we found that increasing the total background NMDA and GABA_A synaptic conductances increased the intraburst firing frequency and reduced its latency. Second, we found that the disinhibition burst is sensitive to the proportion of background inhibitory input that is removed. In particular, we found that high-frequency, short-latency bursts were enhanced by increasing the degree of disinhibition. Third, the time course over which inhibition is removed had a large effect on the burst, namely, that synchronous removal of weak inhibitory inputs produces bursts of high intraburst frequency and shorter latency. Our results suggest that fast, more precisely timed bursts can be evoked by complete and synchronous disinhibition of dopaminergic neurons in a high-conductance state.

dopaminergic neurons fire bursts of action potentials during reward (Schultz 2002) and sequence learning (Jin and Costa 2010). One mechanism by which dopaminergic neurons subjected to background excitatory and inhibitory inputs can generate bursts is disinhibition (Lobb et al. 2010; Paladini et al. 1999b; Tepper et al. 1995). Dopaminergic neurons are bombarded by strong synaptic input from spontaneously active excitatory and inhibitory inputs in vivo (e.g., Grace and Bunney 1985). The effect of these tonic inputs on the activity of dopaminergic neurons is observed when N-methyl-d-aspartate (NMDA) or GABA_A receptor antagonists are applied in vivo (Brazhnik et al. 2008; Chergui et al. 1993; Overton and Clark 1992; Paladini and Tepper 1999). In addition, deafferented dopaminergic neurons recorded in slices do not exhibit the range of firing patterns observed in vivo (Grace and Bunney 1983, 1984a, 1984b; Llinas et al. 1984; Paladini et al. 1999a, 1999b).

Although disinhibition of dopaminergic neurons has been shown in vivo (Gale and Perkel 2010), a detailed study of disinhibition bursting in intact animals is hindered by the lack of experimental control of the network. We have recently shown that dynamic clamp (Robinson and Kawai 1993; Sharp et al. 1993) can be used to apply background synaptic conductances to a dopaminergic neuron recorded in slices and that bursts may be evoked with disinhibition (Lobb et al. 2010). In this study, we have utilized dynamic clamp to quantitatively investigate the functional characteristics of disinhibition bursts evoked by a disinhibitory pathway; for example, the striatum to substantia nigra pars reticulata (SNr) to substantia nigra pars compacta (SNc) pathway, or the striatopallidalnigral pathway.

Dopaminergic neurons were shifted into a high-chord conductance state either pharmacologically, with NMDA and GABA_A agonists, or by applying simultaneous NMDA/GABA_A conductance ramps using dynamic clamp. The high-chord conductance state is characterized by an increase in chord conductance without an increase in the slope conductance (see Lobb et al. 2010). In this state, intrinsically generated currents are not shunted and thus are capable of influencing the firing of dopaminergic neurons. Hence, the single spiking activity of dopaminergic neurons in the high-chord conductance state remains intact. We then showed that high-frequency, temporally precise disinhibition bursting produced from dopaminergic neurons in the high-chord conductance state depends on several characteristics of disinhibition: the total applied NMDA/GABA_A conductance, the degree of disinhibition, and the degree of synchrony in which the tonic inhibition is removed. Furthered by a quantitative anatomic discussion, our results show that fast, precisely timed bursts can be evoked by disinhibition of dopaminergic neurons in the high-chord conductance state.

MATERIALS AND METHODS

Slice preparation and recordings.

Experiments were carried out as previously described (Lobb et al. 2010). All experimental procedures were approved by the University of Texas at San Antonio Institutional Animal Care and Use Committee. Briefly, postnatal day (P)17–P28 Sprague-Dawley rats (Charles Rivers Laboratories) were anesthetized with isoflurane (3% in O₂) and decapitated, and the brains were rapidly removed and cooled. Horizontal slices (240 μm) were cut using a vibrating microtome (Microm HM 650V) in oxygenated, cold artificial cerebrospinal fluid (aCSF) and then transferred to an incubation chamber. The cutting aCSF contained (in mM) 110 choline-Cl, 2.5 KCl, 1.25 NaH₂PO₄, 7 MgCl₂, 0.5 CaCl₂, 10 dextrose, 25 NaHCO₃, 1.3 ascorbic acid, and 2.4 sodium pyruvate. The incubation chamber was filled with recording aCSF modified to include 4 mM MgCl₂ and 0.05 mM glutathione. The recording aCSF contained (in mM) 126 NaCl, 2.5 KCl, 1.25 NaH₂PO₄, 2 MgCl₂, 2 CaCl₂, 10 dextrose, 25 NaHCO₃, 1.3 ascorbic acid, and 2.4 sodium pyruvate.

A slice was then transferred to an intracellular recording rig and superfused with recording aCSF heated to 35°C with an inline heater at a rate of 2 ml/min. Presumed SNc neurons were visualized with a gradient contrast imaging system. SNc neurons were patched with a 4- to 10-MΩ micropipette containing (in mM) 138 K-gluconate, 10 HEPES, 2 MgCl₂, 0.2 EGTA, 0.0001 CaCl₂, 4 Na-ATP, and 0.4 Na-GTP. The internal solution was adjusted to a pH of 7.3, using 1 M KOH, and an osmolarity of 270–275 mOsm. Identified dopaminergic neurons exhibited a slow and pacemaker-like firing pattern (at a frequency of 1–4 Hz), an I_h-mediated voltage sag on passage of hyperpolarizing current, and a prominent spike afterhyperpolarization consistent with previous studies in our laboratory (Deister et al. 2009; Lobb et al. 2010). Recordings were acquired with a Multiclamp 700B and digitized (Instrutech) under command of the AxographX software program. Dynamic clamp experiments were conducted in whole cell mode as previously described (Deister et al. 2009; Lobb et al. 2010). All recordings were done with a balanced bridge in continuous current clamp (Bridge Mode) using a −6-mV junction potential correction. The equations used to calculate the applied current were

$$I_{\text{NMDA}}=-g_{\text{NMDA}}·\left\{1/\left[\left(1+\left(\left[\text{Mg}\right]/3.57\right)·e^{\left(-V_{\text{m}}·0.062\right)}\right)\right]\right\}·\left(V_{\text{m}}-E_{\text{NMDA}}\right)$$

$$I_{{\text{GABA}}_{\text{A}}}=-g_{{\text{GABA}}_{\text{A}}}·\left(V_{\text{m}}-E_{{\text{GABA}}_{\text{A}}}\right)$$

where Mg²⁺ concentration ([Mg]) = 1.5 mM and the reversal potential for NMDA (E_NMDA) = 0 mV. For dynamic clamp studies, E_GABAA was set to −60 mV to approximate the physiological reversal potential for GABA_A receptors (Gulácsi et al. 2003). For pharmacological studies, E_GABAA was set to −94 mV as determined by the chloride reversal potential with our solutions (Nernst, 35°C). Synaptic blockers were not used in these experiments because these afferents are removed during slice preparation.

Drugs.

Isoguvacine (40 μM) and NMDA (40 μM) were applied to the slice via superfusion. All drugs were purchased from Tocris.

Data analysis.

Action potentials were detected using a derivative threshold in AxographX (4–5 V/s). Spiking analysis was done using custom code in Mathematica 7 (Wolfram Research). Maximum intraburst frequency was determined as the reciprocal of the minimum interspike interval (ISI) for all spikes in the analysis window. Mean intraburst frequency was determined as the reciprocal of the mean intraburst ISI in that same window. The time window for analysis was determined by the removal and return of the GABA_A conductance. Frequency analysis for asynchronous disinhibition was performed only on the first second of the 2-s disinhibition window. The failure point for spiking in Fig. 1 was determined as the total applied conductance of the last spike during the conductance ramp. The failure point is therefore underestimated for the three cells that would have continued spiking with total conductance greater than 80 nS. Convolutions were also done in Mathematica 7. The GABA_A conductance waveform was modeled as

$$-g·\left[e^{\left(-t/{\tau }_{\text{rise}}\right)}-e^{\left(-t/{\tau }_{\text{decay}}\right)}\right],$$

where g is the single-channel conductance of the GABA_A receptor (30 pS), τ_rise is the rise time constant (0.1 ms), and τ_decay is the GABA_A deactivation time constant (6 ms). For the current-voltage relationships shown in Fig. 1DII, the holding potential was stepped from −60 mV to a command potential (−100 to −30 mV at increments of 10 mV) for 1 s. The average current amplitude in the latter 100 ms of the step was used to calculate the steady-state value.

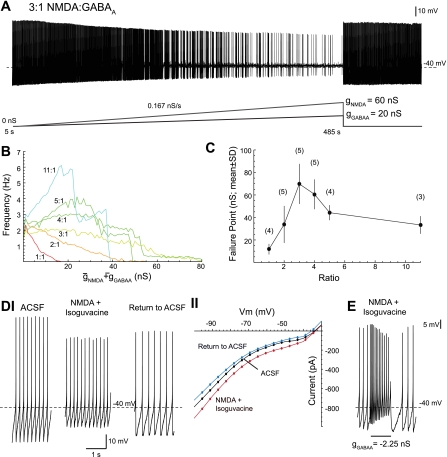
Fig. 1.

Dopaminergic neurons in a high-chord conductance state with N-methyl-d-aspartate (NMDA)/GABA_A receptor activation. A: concurrent NMDA and GABA_A conductance ramps were applied to a dopaminergic neuron in a whole cell recording. A fixed 3:1 NMDA-to-GABA_A ratio was maintained during the ramp. The ramp began at time t = 5 s and was completed at t = 485 s with a total conductance (g_NMDA + g_GABAA) of 80 nS. Spontaneous activity resumed after both conductances were removed. B: mean single spiking frequency during application of conductance ramps for a series of fixed NMDA-to-GABA_A conductance ratios (number of cells shown in C). C: the conductance at which single spiking failed during the conductance ramp (failure point) is plotted for the different NMDA-to-GABA_A conductance ratios. The numbers of cells for each ratio are shown in parenthesis. D: single spiking persisted after application of 40 μM NMDA and 40 μM isoguvacine (a GABA_A receptor agonist) (I). The steady-state current-voltage (I-V) curve of the dopaminergic neuron is shown (II) for control artificial cerebrospinal fluid (aCSF; black), after application of NMDA and isoguvacine (red), and postdrug aCSF (return to aCSF; blue). The shape of the I-V curve largely remained unchanged with drug application. E: the dopaminergic neuron in the pharmacologically induced high-chord conductance state could generate bursts of action potentials in response to subtraction of a GABA_A receptor conductance with the dynamic clamp (maximum burst frequency 19.4 Hz; mean burst frequency 13.4 Hz). Recordings in D and E are from the same cell.

Regression and statistics.

Exponential and Boltzmann functions were used to fit the data in Fig. 2C. The following formula was used for exponential fitting: y = a + b × e^(g_total/τ), where a and b are constants, g_total is the total applied conductance (g_total = g_NMDA + g_GABAA), and τ is the growth/decay time constant. The following formula was used for the Boltzmann function:

$$y=n_{\max }/\left[1+e^{-\left(g_{\text{total}}-v_{1/2}\right)/k}\right]$$

where n_max is the asymptotic maximum, v_1/2 is the half-maximal conductance, and k is the slope factor. Regression analysis was used to compare the curves' fit to maximum and mean burst frequency, latency to first spike, and latency to burst onset data (Lobb et al. 2010). This was implemented in SAS (SAS Institute). Except for mean frequency data, these data were well fit by exponentials, and thus a logarithmic transform was applied. For spike counts, a Boltzmann function was used. We used t-tests for statistical comparisons of fit parameters in both groups. Statistical tests to determine whether the slope of a fitted line was nonzero were also performed in Mathematica 7. For all other statistical tests, Prism (GraphPad Software) was used. All effects are means ± SE except those in Fig. 2C, which are means ± SD. In all experiments presented, the criterion for statistical significance was set at P < 0.05.

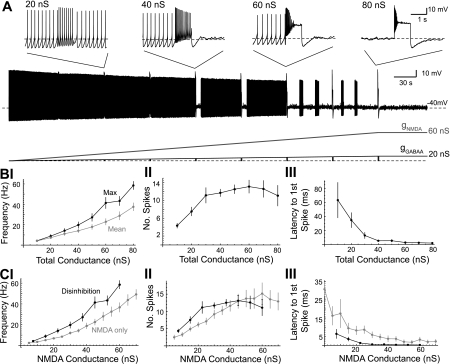
Fig. 2.

Disinhibition burst frequency increases as the total applied NMDA/GABA_A conductance increases. A: concurrent NMDA and GABA_A conductance ramps (3:1 ratio) were applied to a dopaminergic neuron in a representative example. As the total applied conductance reached 10, 20, ..., 80 nS, the GABA_A conductance was phasically set to zero for 1 s. Insets show the change in firing at total conductance of 20, 40, 60, and 80 nS. B: summary data for the maximum and mean frequency (I), number of spikes (II), and latency to the first spike (III) during the 1-s disinhibition window as a function of the total applied conductance (n = 9). Burst onset was defined as the latency of the first spike in the first interspike interval (ISI) of <80 ms (cells in which this criteria were not met were excluded from the mean calculation for that conductance). C: maximum firing frequency (I), number of spikes (II), and latency to first spike (III) for disinhibition bursts (solid) are shown along with bursts evoked from phasic NMDA receptor activation alone (shaded). The NMDA conductance of the disinhibition burst was 0.75 times the total applied conductance. NMDA-only bursts were evoked by a 1-s NMDA conductance step (5–70 nS, 5-nS increment) in a spontaneously firing dopaminergic neuron.

RESULTS

To consistently provide tonic excitatory and inhibitory inputs to the dopaminergic neuron so that disinhibition could be explored in a reliable way across cells, we applied concurrent NMDA and GABA_A conductance ramps, using the dynamic clamp technique, to the dopaminergic neuron. The total applied conductance was increased linearly from 0 to 80 nS in 480 s. The ratio of NMDA to GABA_A conductance was varied (1:1 to 11:1). An example in which a 60-nS NMDA ramp and a 20-nS GABA_A ramp are applied simultaneously is shown in Fig. 1A. The average single-spike firing rate during the NMDA/GABA_A ramps was plotted for different ratios (Fig. 1B). The total conductance (g_NMDA + g_GABAA) at which single spiking failed during the ramp (its failure point) is plotted in Fig. 1C. Dopaminergic neurons were best able to maintain a constant firing rate at a ratio between 3:1 and 4:1. (Fig. 1, B and C). These findings agree well with our previous results (Lobb et al. 2010) where the conductance ratio when manually tuned was 3.2:1 across cells. Therefore, a NMDA/GABA_A conductance ratio of 3:1 was chosen for subsequent experiments.

These results were not unique to background synaptic conductances activated from the dynamic clamp. Single spiking persisted after application of 40 μM NMDA and 40 μM isoguvacine (a GABA_A receptor agonist) to a spontaneously firing dopaminergic neuron (Fig. 1D). Application of NMDA and isoguvacine depolarized the cell (P < 0.05, paired t-test; average membrane potential in aCSF: −50.7 ± 1.0; NMDA/isoguvacine: −45.4 ± 1.8; n = 4). Drug application increased the chord conductance of the neuron while having little effect on its slope conductance (Fig. 1DII). This differs from the high-conductance state described by Destexhe et al. (2003) in which there is an increase in both the chord and slope conductances. Bursts could be evoked by subtraction of a GABA_A conductance with the dynamic clamp (e.g., −2.25 nS in Fig. 1E).

We found that single spiking was maintained better with NMDA/GABA_A but not AMPA/GABA_A conductances (data not shown; range of applied ratios was 1:11 to 11:1). Dopaminergic neurons were best able to maintain a constant firing rate for an AMPA/GABA_A conductance ratio of 1:3. The failure points at this 1:3 AMPA/GABA_A conductance ratio were significantly less than the failure points measured with the 3:1 NMDA/GABA_A ratio described above (P < 0.05, unpaired t-test; AMPA/GABA_A: 9.2 ± 1.5 nS; NMDA/GABA_A: 69 ± 7.9 nS; n = 5).

Using conductance ramps with a NMDA/GABA_A ratio of 3:1, we investigated how the frequency and timing of disinhibition bursts changed with the total applied conductance (Fig. 2). When the total conductance reached 10, 20, ..., 80 nS, g_GABAA was stepped to zero for 1 s to evoke disinhibition bursts (Fig. 2A; n = 6). The NMDA conductance continued its slow ramp during this period. In separate experiments, we applied ramps in which no disinhibition bursts were evoked until each of the target total conductances were reached (i.e., 10, 20, ..., 80 nS; n = 3 for each). Results were similar, and the data were pooled (n = 9). The maximum and mean frequency of spiking (Fig. 2BI) during the disinhibition window increased exponentially with the total applied conductance [maximum: R² = 0.92, τ (growth/decay constant) = 41 nS; mean: R² = 0.90, τ = 54 nS]. The number of spikes that occurred during the disinhibition window also increased with the total applied conductance (Fig. 2BII). These data were well fit by a Boltzmann function (R² = 0.89, n_max =12.4 spikes, v_1/2 = 15.4 nS, k = 7.7 nS). We also observed that the latency to spiking decreased with the total applied conductance. Specifically, the latency to the first spike evoked from disinhibition decreased exponentially with the total applied conductance (Fig. 2BIII; R² = 0.50, τ = 13 nS). The latency to the first spike occurring in the first ISI less than 80 ms (“burst onset”; Grace and Bunney 1984b) also decreased with the total applied conductance (R² = 0.60, τ = 58 nS).

The effects on spiking seen with increases in applied conductance may just be due to an increase in NMDA conductance. To test this, we applied 1-s NMDA square conductance pulses (5–70 nS with 5-nS increments) to spontaneously firing dopaminergic neurons (n = 9). These data were compared with the disinhibition data from Fig. 2B in Fig. 2C using regression analysis (see materials and methods; Lobb et al. 2010). The maximum and mean intraburst firing rates during disinhibition-induced bursts were significantly faster than the maximum and mean intraburst firing rates during application of NMDA alone (Fig. 2CI; P < 0.05; maximum: 10–60 nS; mean: 10–38 nS; regression analysis). Spike counts (Fig. 2CII) could not be transformed, so a linear regression could not be performed. However, Boltzmann functions fit to both curves revealed a significant difference in fit parameters between the number of action potentials per burst in the NMDA-alone or disinhibition-induced bursts (P < 0.05, t-test with pooled variance; v_1/2: NMDA alone = 23.5 nS, disinhibition = 11.6 nS; n_max: NMDA alone = 14.3 nS, disinhibition = 12.4 nS; k: NMDA alone = 10.9 nS, disinhibition = 5.80 nS). Both the latency to the first spike (Fig. 2CIII) and the latency to burst onset (data not shown) of disinhibition bursts were significantly shorter compared with NMDA-alone bursts (P < 0.05; 10–60 nS; regression analysis). These results suggest that increasing the total background NMDA/GABA_A conductances promotes high-frequency, short-latency bursts.

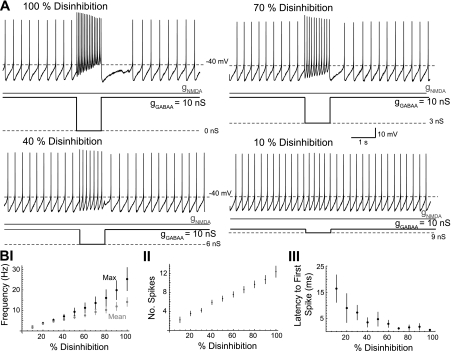
In the preceding experiments, the GABA_A conductance was set to zero during the disinhibition period. However, in vivo disinhibition may not be complete, but rather reduced to some nonzero level provided by the remaining inhibitory influences. Therefore, we investigated whether the degree of disinhibition achieved during the disinhibition period had an effect on disinhibition burst frequency. NMDA/GABA_A conductance ramps (3:1 ratio, 240 s) with a total maximal conductance of 40 nS (30-nS NMDA, 10-nS GABA_A) were applied to put the dopaminergic neuron in the high-chord conductance state. At 30-s intervals, g_GABAA was stepped for 1 s to a new value that ranged from 10 to 100% of the original g_GABAA (i.e., 1 to 10 nS). g_NMDA remained constant during those steps. This was done in an ascending (n = 6) or a random order (n = 3). Data were similar and therefore were pooled (n = 9). An example is shown in Fig. 3A. Lines fit (not shown) to burst frequencies (P < 0.05; slope of maximum burst frequency = 24 s⁻¹; slope of mean burst frequency = 13 s⁻¹) and the number of spikes (P < 0.05; slope = 11) had nonzero slopes and increased linearly with the degree of steady-state disinhibition (Fig. 3B, I and II; n = 9). The latency of burst onset did not change significantly with increased disinhibition (Fig. 3BIV; P > 0.05) due the large variability encountered (linear fit: R² = 0.0092). However, the latency to the first spike on disinhibition decreased and became less variable with the degree of steady-state disinhibition (Fig. 3BIII; P < 0.05; n = 9).

Fig. 3.

Burst frequency increases as the degree of disinhibition increases. A: concurrent NMDA and GABA_A conductance ramps (3:1 ratio; not shown) were applied to a dopaminergic neuron in a representative example. A total conductance of 40 nS (g_NMDA = 30 nS; g_GABAA = 10 nS) was reached at the end of the ramp and held steady. In 1-s windows, a proportion of g_GABAA was removed, causing a phasic increase in firing. B: summary data for the maximum (Max; solid) and mean (shaded) frequency of spikes (I), number of spikes (II), and latency to first spike (III) as a function of the proportion of g_GABAA removed (n = 9).

We next investigated the time course for the removal of a tonic inhibitory input on the frequency and temporal precision of disinhibition bursts in dopaminergic neurons. We assumed a tonic NMDA-mediated input (e.g., subthalamic nucleus, STN; Chergui et al. 2004) and a tonic GABA_A-mediated input (e.g., SNr; Paladini et al. 1999a; see materials and methods). Periodic, weak synaptic input will summate in time with an average steady-state conductance (g_ss) given by the equation (e.g., Wilson et al. 2004)

$$g_{\text{ss}}=\Delta g/\left\{1-e^{\left[-1/\left(\tau \text{Fn}\right)\right]}\right\}$$

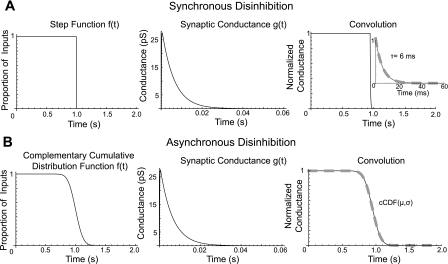
where Δg is the conductance increment per activated receptor [GABA_A: 30 pS (Guyon et al. 1999; Macdonald and Olsen 1994); NMDA: 50 pS (Edmonds et al. 1995)], τ is the deactivation time constant [GABA_A: 6 mS (Brancucci et al. 2004); NMDA: 43 ms (Schilström et al. 2006)], F is the firing frequency of the presynaptic neuron [rat SNr: 30 Hz (Celada et al. 1999; Deniau et al. 1978); rat STN: 5 Hz (Chergui et al. 2004)], and n is the number of postsynaptic receptors activated from activity in afferent nuclei. Thus the 30-nS NMDA and 10-nS GABA_A conductances used above correspond to the activation of 2,788 NMDA receptors and 1,849 GABA_A receptors. The overall time course for disinhibition differs depending on whether disinhibition is synchronous (Fig. 4A) or asynchronous (Fig. 4B). Complete and synchronous removal of inhibition causes the tonic inhibitory drive to decay according to the deactivation time constant for each GABA_A receptor. If the deactivation time constant for each of the 1,849 GABA_A receptors is the same, then the tonic inhibitory drive decays exponentially according to that deactivation time constant. This is illustrated in Fig. 4A as the convolution of a step function and a GABA_A conductance waveform with a 6-ms deactivation time constant. However, if removal of inhibition is asynchronous and occurs over a time course longer than the GABA_A deactivation time constant, then the time course of disinhibition follows the time course in which inhibition is removed (Fig. 4B). If the disinhibition activating process (i.e., the inhibitory nuclei which when activated causes disinhibition through a tonically active intermediary) is normally distributed, then the time course of disinhibition is well fit by the complementary cumulative distribution function. This function is described by the mean (μ) and standard deviation (σ) of the activating normal distribution

$$1-\left(1+\text{Erf}\left[\left(t-\mu \right)/\sigma \sqrt{2}\right]\right)/2,$$

where Erf is the error function and t is time.

Fig. 4.

Modeling the time course of disinhibition of substantia nigra pars compacta dopaminergic neurons. A source of tonically active inhibitory inputs was turned off synchronously (A) or asynchronously (B). This is represented by a step function (A, left) or the complementary cumulative distribution function [f(t) = cCDF (mean μ = 1.0 s, standard deviation σ = 100 ms)] (B, left). Each input is described by the conductance waveform g(t) (middle) with a deactivation time constant (τ) of 6 ms. The time course of disinhibition is determined by their convolution [f*g](t). Thus tonic inhibition decays according to the GABA_A deactivation time constant (A, synchronous) or the complementary cumulative distribution function (B, asynchronous). The time at which an individual GABA_A input in the asynchronous case is removed is taken from a normal distribution.

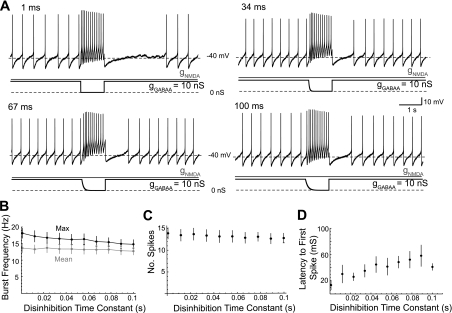
Disinhibition caused by synchronous removal of GABA_A receptor activation will occur with a time course that is approximated by the GABA_A deactivation time constant (Fig. 4A). The deactivation time constant of miniature inhibitory postsynaptic currents recorded in dopaminergic neurons is ∼6 ms (Brancucci et al. 2004). Desensitization may increase the deactivation time constant (Jones and Westbrook 1995); however, it is unclear how much desensitization of GABA_A receptors will occur on dopaminergic neurons in vivo in response to a tonic inhibitory input. To explore this, g_GABAA was removed with a simple exponential decay rather than stepwise (Fig. 5). NMDA/GABA_A conductance ramps (3:1 ratio, 40 nS total) were applied to dopaminergic neurons (as described in Fig. 1). At regular 30-s intervals, a 1-s disinhibition pulse was applied such that g_GABAA decayed to zero with a given time constant. The range of disinhibition time constants (τ_d) applied ranged from 1 to 100 ms and were given in a random order. A representative example is shown in Fig. 5A. Maximum burst frequency decreased as the disinhibition time constant (τ_d) increased (Fig. 5B; P < 0.05; slope = −30 s⁻²; n = 8). The mean frequency of the burst (Fig. 5B; P > 0.05; slope = −8 s⁻²; n = 8) and the number of spikes in the burst (Fig. 5C; P > 0.05; slope = −12 s⁻¹; n = 8) were unchanged. There was no difference between bursts evoked by stepwise disinhibition described previously and bursts evoked with an ∼6-ms τ_d [P > 0.05, unpaired t-test; maximum burst frequency for 5.4-ms τ_d: 16 ± 1.6 Hz (n = 8); stepwise: 22 ± 3 Hz (n = 18; data pooled from Fig. 2, 40 nS, and Fig. 3, 100% disinhibition); mean burst frequency for 5.4-ms τ_d: 13 ± 1.5 Hz (n = 8); stepwise: 14 ± 1.3 (n = 18)]. The latency to the first spike increased with the disinhibition time constant (Fig. 4D; P < 0.05; slope = 0.34; n = 8). The latency to the burst also increased with the disinhibition time constant (P < 0.05; slope = 1.6; n = 8).

Fig. 5.

Burst frequency decreases as the time constant of disinhibition increases. A: concurrent NMDA and GABA_A conductance ramps (3:1 ratio) were applied to a dopaminergic neuron in a representative example (as in Fig. 1). A total conductance of 40 nS (g_NMDA = 30 nS; g_GABAA = 10 nS) was achieved at the end of the ramp and maintained. In 1-s intervals, g_GABAA was removed according to a simple exponential decay, 10*e^(−t/τ_d). The disinhibition time constant (τ_d) was varied. B: unlike mean burst frequency (P > 0.05, n = 8), the maximum burst frequency showed a significantly nonzero slope across the range of τ_d values (P < 0.05, n = 8). C: the total number of spikes in the disinhibition window was not changed with different τ_d values (P < 0.05, n = 8). D: the latency to the initiation of the burst, defined as an ISI <80 ms, increased significantly with τ_d values (P < 0.05, n = 8).

Disinhibition caused by asynchronous removal of GABA_A receptor activation will occur with a time course that is approximated by the complementary cumulative distribution function, which is described by its mean and standard deviation (Fig. 4A). The mean will determine when the burst occurs, and thus a change in mean will shift the onset of the burst in time. The standard deviation will have a large effect on the shape and time course of the conductance decay. We then investigated what the effect the standard deviation of the complementary cumulative distribution function would have on the bursts produced by disinhibition (Fig. 6).

Fig. 6.

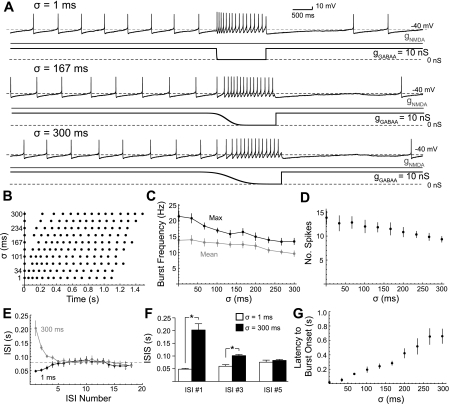
Disinhibition bursts change in frequency and shape with asynchronous removal of the GABA_A conductance. A: concurrent NMDA and GABA_A conductance ramps (3:1 ratio) were applied to a dopaminergic neuron in a representative example (as in Fig 1). A total conductance of 40 nS (g_NMDA = 30 nS; g_GABAA = 10 nS) was achieved at the end of the ramp and maintained. At 30-s intervals, g_GABAA was removed according to the complementary cumulative distribution function, which describes the asynchronous removal of a population of tonically activated GABA_A receptors. The standard deviation parameter of that function is described by σ. A raster plot of disinhibition spiking as sampled in A is shown in B. The maximum (solid) and mean frequency (shaded) of the burst (C) as well as the number of spikes in the burst (D) decreased significantly with increasing σ (P < 0.05, n = 6). E–G: the shape of the disinhibition bursts changed with increasing σ; changes in the ISI as the burst progressed in all 6 cells. With small σ (i.e., more synchronous g_GABAA removal), disinhibition bursts showed a progressive increase in the ISI of each spike in the burst (B and E, solid). With large σ (more asynchronous g_GABAA removal), disinhibition bursts showed a progressive decrease in the ISI of each spike in the burst (B and E, shaded). The first ISI <80 ms (dashed line in C) defines the onset of the burst. F: there was a significant increase in the ISI up to ISI #3 for σ = 1 ms compared with σ =300 ms (P < 0.05, n = 6). G: the latency at which the burst began increased with σ (P < 0.05, n = 6).

NMDA/GABA_A conductance ramps totaling 40 nS were applied to dopaminergic neurons as before. At 30-s intervals, g_GABAA was removed according to the complementary cumulative distribution function. The mean μ was fixed, but the standard deviation σ was varied between 1 and 300 ms in a random order. A representative example is shown in Fig. 6, A and B.

Varying σ had a significant effect on the frequency of the disinhibition burst. Maximum and mean burst frequency decreased linearly with σ (Fig. 6C; maximum burst frequency slope = −28 s⁻², P < 0.05; mean burst frequency slope = −15 s⁻², P < 0.05; n = 6). The slopes of lines fit to maximum and mean burst frequency were significantly different from one another (P < 0.05, t-test). The number of spikes in the disinhibition burst also decreased with increasing σ (Fig. 6D; P > 0.05; slope = 14 s⁻¹; n = 6).

Varying σ also affected the shape of the disinhibition burst. The ISIs of disinhibition bursts with a small σ (e.g., 1 ms) progressively increased during the burst (Fig. 6A, top, B, E). The ISIs of disinhibition bursts with large σ (e.g., 300 ms) progressively decreased until the middle of the burst, where the ISIs began to progressively increase (Fig. 6A, bottom, B, E). The difference in ISI between σ =1 and σ =300 ms persisted out to the third ISI in the sequence (Fig. 6F). Both the latency to first spike (P < 0.05; slope = 0.85; n = 6) and the latency to burst onset increased with σ (Fig. 6D; P < 0.05; slope = 1.82; n = 6).

To determine whether dopaminergic neurons responded differently to an exponential decay (τ_d; Fig. 5) or to a decay governed by the standard deviation of the complementary cumulative distribution function (σ; Fig. 6), the regression slopes calculated above for maximum and mean burst frequency, number of spikes elicited, latency to first spike, and latency to burst onset were compared. Only the latency to first spike was statistically significant (P < 0.05; unpaired t-tests with pooled variance). Regression analysis confirmed that the latency to first spike for disinhibition described by the complementary cumulative distribution function was significantly greater than disinhibition occurring with an exponential decay (P < 0.05; τ_d/σ ≥ 70 ms).

DISCUSSION

Dopaminergic neurons fire bursts of action potentials in response to salient stimuli (Horvitz et al. 1997; Redgrave et al. 1999; Schultz et al. 1997), when a greater than expected reward is received (Schultz et al. 1997), or during sequence learning (Jin and Costa 2010). Burst firing in midbrain dopaminergic neurons may be caused by phasic activation of AMPA or NMDA receptors (Blythe et al. 2009; Deister et al. 2009; Lobb et al. 2010; Zweifel et al. 2009). However, neither AMPA nor NMDA receptor activation may be well suited to produce bursts with high temporal precision due to the presence of a strong tonic GABAergic input in vivo (Brazhnik et al. 2008; Grace and Bunney 1985; Paladini and Tepper 1999) and A-type potassium channels (Liss et al. 2001). In addition, NMDA receptors activate slowly, with a rise time of 5–10 ms (e.g., Dalby and Mody 2003).

Bursts produced by disinhibition produce high-frequency bursting at short latencies (Lobb et al. 2010). Disinhibition bursts also require NMDA receptor activation; however, NMDA receptors are employed as a source of tonic excitation. It is possible that separate populations of dopaminergic neurons can evoke different types of bursts. Single dopaminergic neurons in the high-chord conductance state may also be able to employ both phasic AMPA or NMDA receptor activation and disinhibition to drive bursting. The capacity of a neuron to fire both phasic NMDA bursts and disinhibition bursts will depend largely on the number of NMDA receptors that are not activated by tonic inputs. If the majority of NMDA receptors are activated tonically, then it is less likely that the remaining inputs will generate the large NMDA conductance required to generate a burst. In these cases, it is more probable that a single dopaminergic neuron in the high-conductance state will fire bursts only by disinhibition. On the other hand, if there are sufficient numbers of NMDA receptors that are not activated by tonic inputs and that can overcome strong tonic inhibition (e.g., Grace and Bunney 1985), then it is possible that the neuron can generate both phasic NMDA bursts and disinhibition bursts.

Our results demonstrate three aspects of disinhibition that promote high-frequency bursts of short latency: 1) increased background conductances, 2) completeness of disinhibition, and 3) synchronous removal of tonic inhibition.

Increased background conductances.

The activity of dopaminergic neurons in vivo depends on the dopaminergic neuron's intrinsic pacemaking currents acting in tandem with tonic NMDA- and GABA_A-mediated synaptic currents. Our results suggest that a g_NMDA-to-g_GABAA ratio close to 3:1 will yield a state in which single spiking can be maintained with a minimal change in firing rate. We do not yet know the level of tonic inputs in vivo or the contributions of g_NMDA/g_GABAA to the total background synaptic conductance imposed by these inputs. At a 3:1 ratio, the effective reversal potential is depolarizing (see also Lobb et al. 2010). As g_total is increased during the ramp and the cell depolarizes, the increase in input resistance seen with NMDAR activation (Koch 1999) is lost and the intrinsic conductances are shunted. This explains why single spiking frequency falls off with increased g_total (Fig. 1B).

We found an increase in intraburst frequency and decrease in latency with increasing g_total. This can be partially accounted for by the increased NMDA receptor conductance at the moment of disinhibition (Fig. 2C). The remainder is probably due to increased inactivation of A-type potassium currents with depolarization (see Lobb et al. 2010). The pause in firing after the offset of disinhibition also increases with the total background synaptic conductance. This may due to the activation of a sodium pump as a result of sodium accumulation (Johnson et al. 1992).

Completeness of disinhibition.

Tonic GABAergic input onto SNc dopaminergic neurons arises predominately from afferents such as the globus pallidus (GP), endopeducular nucleus (EP), SNr, and rostral tegmental nucleus (reviewed in Jhou et al. 2009; Tepper and Lee 2007). The relative contribution of inhibition provided from each afferent structure is unknown. Our results show that the intraburst frequency and latency of bursting depend on the degree of disinhibition achieved.

Striatal projection neurons are often described as either direct or indirect pathway neurons projecting to the SNr and GP, respectively (e.g., Albin et al. 1989). However, axons of single striatal neurons in both the rat and monkey send collaterals to multiple axonal targets (Kawaguchi et al. 1990; Parent et al. 1995). Our results suggest that an important role of collateralization may be during disinhibition. For example, type IIa projection neurons in the rat project to the GP, EP, and SNr (Kawaguchi et al. 1990). Phasic activation of type IIa cells would remove three of the four sources of tonic inhibition described above and would thus be expected to produce greater disinhibition bursts in dopaminergic neurons than type I neurons, which only innervate the GP.

Synchronous vs. asynchronous disinhibition.

The frequency and latency of the burst depends on the time course of disinhibition. Synchronous removal causes the tonic GABA_A-mediated input to decay according to the deactivation time constant of the GABA_A receptor. Asynchronous removal of tonic GABA_A-mediated inputs by a Poisson process evolves according to the complementary cumulative distribution function (Fig. 4). The burst will be shifted in time according to the mean of the Gaussian distribution. The shape, frequency, and latency of the disinhibition burst are strongly affected by its standard deviation. The mean and the standard deviation are determined by the asynchronous generation of action potentials of medium spiny neurons (Stern et al. 1998) and differences in axonal transmission delays.

Implications for reward learning.

Many models of reinforcement learning encode reward-related learning through plastic changes at corticostriatal synapses (Houk et al. 1995; Pawlak and Kerr 2008; Wickens and Kotter 1995). The efficacy of these synapses is dependent on the relative timing of cortical to striatal spiking and phasic increases in dopamine. According to this hypothesis, synapses that contribute to the selection of the rewarded response undergo long-term potentiation (LTP), whereas synapses that did not contribute to selection undergo long-term depression (LTD). Thus the corticostriatal synapses encoding the stimulus or expect reward outcome during stimulus-response and action-outcome learning are strengthened (Horvitz 2009). Previous results have shown that LTP occurs on concurrent activation of presynaptic corticostriatal terminals and postsynaptic medium spiny neurons when paired with a phasic increase in dopamine (Thivierge et al. 2007; Wickens et al. 1996). If activation of medium spiny neurons generates a disinhibition burst in SNc dopaminergic neurons, then our results will show that a high-frequency burst will occur at short latencies. This is expected to produce greater changes in synaptic efficacy than if the dopamine signal were delayed.

The striatum may have a causal role in the generation of reward signaling of dopaminergic neurons. Phasic activation of both medium spiny neurons of the striatum and dopaminergic neurons increases according to reward prediction error (Oyama et al. 2010). One hypothesis is that the direct projection from the striatum to the SNc (Bolam and Smith 1990) may be important for the generation of an inhibitory reward prediction signal (Houk et al. 1995). However, this hypothesis predicts an inhibitory period during the delay between cue and reward. Fiorillo et al. (2003) have shown that there is a sustained increase in firing during the delay period. Furthermore, none of the medium spiny neurons sampled by Oyama et al. (2010) were phasically activated on trials in which reward was not received. Another hypothesis is that activation of striatum evokes disinhibition bursts in SNc cells. The striatonigral pathway is necessary for reward learning (Hikida et al. 2010). Striatal cells are phasically activated at the time of salient stimulus (e.g., Hikosaka et al. 1989a; Schulz et al. 2009; Sedgwick and Williams 1967), a reward-predicting cue (Cromwell and Schultz 2003; Oyama et al. 2010), or the time of reward (Hikosaka et al. 1989b; Oyama et al. 2010). Activation of these cells would inhibit neurons in the GP, EP, and SNr (e.g., Kimura et al. 1984; Shin and Sommer 2010). Similar results have been found in songbirds (Gale and Perkel 2010). Concurrent activation of the STN (Darbaky et al. 2005; Lardeux et al. 2009) or superior colliculus (Comoli et al. 2003) would further increase the frequency of the disinhibition burst, or reduce its latency.

Disinhibition is an effective mechanism for generating bursts in dopaminergic neurons. The temporal precision of the burst as well as its intraburst frequency is determined by specific characteristics of the disinhibitory process. We have demonstrated that high-frequency, precisely timed bursts can be generated by a complete and synchronous disinhibition of dopaminergic neurons in the high-chord conductance state. As a result, disinhibition bursts could act as a robust and scalable teaching signal to the striatum during reward and sequence learning.

GRANTS

This work was supported by National Institutes of Health Grants MH084494 (to C. J. Lobb), MH079276, and NS060658 (to C. A. Paladini).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).