On the Chemical Mechanism of Succinic Semialdehyde Dehydrogenase (GabD1) from Mycobacterium tuberculosis*

Abstract

Succinic semialdehyde dehydrogenases (SSADHs) are ubiquitous enzymes that catalyze the NAD(P)⁺-coupled oxidation of succinic semialdehyde (SSA) to succinate, the last step of the γ-aminobutyrate shunt. Mycobacterium tuberculosis encodes two paralogous SSADHs (gabD1 and gabD2). Here we describe the first mechanistic characterization of GabD1, using steady-state kinetics, pH-rate profiles, ¹H-NMR, and kinetic isotope effects. Our results confirmed SSA and NADP⁺ as substrates and demonstrated that a divalent metal, such as Mg²⁺, linearizes the time course. pH-rate studies failed to identify any ionizable groups with pKa between 5.5 and 10 involved in substrate binding or rate-limiting chemistry. Primary deuterium, solvent and multiple kinetic isotope effects revealed that nucleophilic addition to SSA is very fast, followed by a modestly rate-limiting hydride transfer and fast thioester hydrolysis. Proton inventory studies revealed that a single proton is associated with the solvent-sensitive rate-limiting step. Together, these results suggest that product dissociation and/or conformational changes linked to it are rate-limiting. Using structural information for the human homolog enzyme and ¹H-NMR, we further established that nucleophilic attack takes place at the Si face of SSA, generating a thiohemiacetal with S stereochemistry. Deuteride transfer to the Pro-R position in NADP⁺ generates the thioester intermediate and [4A-²H, 4B-¹H] NADPH. A chemical mechanism based on these data and the structural information available is proposed.

1. Introduction

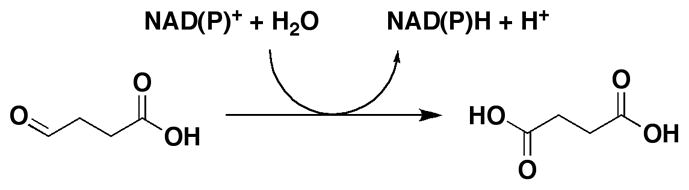
Succinic semialdehyde dehydrogenases (SSADHs) are ubiquitous enzymes that use NAD(P)⁺ and water to oxidize succinic semialdehyde (SSA) to succinate (Scheme 1). These enzymes differ from other succinic semialdehyde dehydrogenases that use CoA-SH as a nucleophile, generating succinyl-CoA instead of succinate [1]. In mammals, these enzymes are involved in the turnover of γ-aminobutyric acid (GABA), the last step of the GABA shunt (Scheme S1). GABA is directly formed from glutamate and is the chief inhibitory neurotransmitter in the central nervous system. Pharmacologic modulation of GABA levels in humans is a validated therapeutic strategy used for the treatment of some forms of anxiety and epilepsy [2]. The role of the GABA shunt in bacteria and plants is less understood. In these organisms, GABA has been associated with glutamate metabolism, anaplerosis, and/or in antioxidant defense. In plants, activity of the GABA shunt rapidly increases in response to stress. In Arabidopsis thaliana, a genetic knockout of the mitochondrial SSADH displayed drastic phenotypes such as altered growth, necrotic lesions on leaves and hypersensitivity to light, attributed to inability to cope with reactive oxygen damage [3].

Scheme 1.

SSADH (EC 1.2.1.16) enzymes are relatively poorly studied in comparison to other dehydrogenases, and with respect to kinetic and chemical mechanism. Nonetheless, SSADHs from A. thaliana, rat and human brains, Drosophila melanogaster and Escherichia coli, have been purified and partially characterized [4–7]. The A. thaliana SSADH has a MW of 53 kDa and exists as a tetramer in solution. Steady-state kinetic analysis indicated high specificity for SSA and NAD⁺ as substrates, with K_mSSA = 15 μM and K_mNAD+ = 130 μM [6]. Interestingly, ATP was shown to allosterically inhibit activity and affect NAD⁺ binding, suggesting regulation of enzyme’s activity by the energy status of the cell [7]. Rat brain SSADH displayed even lower K_mSSA (2.5 μM), absolute specificity for NAD⁺, and a compulsory kinetic ordered mechanism with NAD⁺ as the first substrate to bind to the enzyme and NADH the last product to dissociate [4]. ¹H-NMR studies indicate that SSA exists in solution as a 1:1 mixture of two forms, its aldehydic and gem-diol forms. Saturation transfer difference NMR experiments demonstrated that only the aldehydic form was competent to bind to the E. coli and D. melanogaster SSADHs [5].

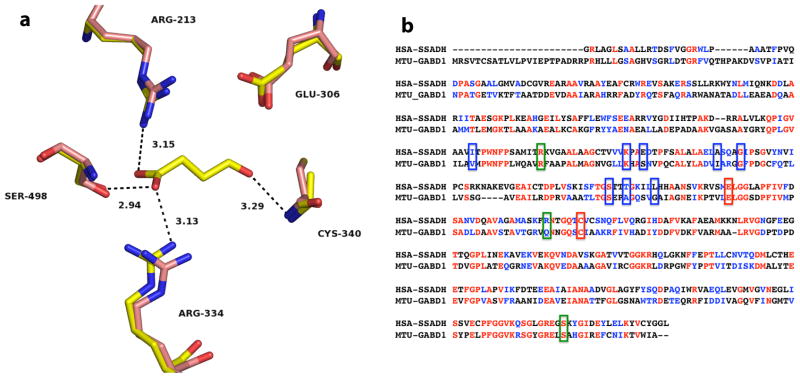
The three-dimensional structures of human and E. coli SSADHs (HsaSSADH and EcoSSADH, respectively) were also recently determined by X-ray crystallography [8,9]. The NAD⁺-utilizing HsaSSADH was shown to exist in both an oxidized and a reduced form, involving an intramolecular disulfide bond between the catalytic cysteine residue (Cys340) and an adjacent cysteine residue (Cys342), within a “catalytic loop”. The sensitivity of the catalytic thiol to oxidation and disulfide formation was interpreted to represent a potential redox switch. That is, once oxidized, the catalytic loop was proposed to close the active site, allowing NAD⁺ to bind only in a conformation that does not allow catalysis. Upon disulfide reduction, this same catalytic loop was proposed to reorient, allowing NAD⁺ to assume a productive conformation. Although the active sites of HsaSSADH and EcoSSADH are very similar, with identical orientation of most of the catalytic residues and an additional cysteine residue in the catalytic loop, the EcoSSADH was found to be sensitive to oxidation. However, this modification was not reversed by addition of DTT, as observed with the human homolog. In addition, size exclusion chromatography and crystallographic data demonstrated that the oligomerization state of HsaSSADH and EcoSSADH was tetrameric. As expected, the structures of the two SSADHs share a general fold of class 1 and class 2 aldehyde dehydrogenase (ALDH). As shown in Fig. 1a, HsaSSADH has only two residues optimally positioned for catalysis, Glu306 and Cys340. SSA is held in the active site mainly by its carboxylate, which interacts by hydrogen bonding and/or electrostatics with Arg213, Arg334 and Ser498. The ADP moiety of NAD⁺ is stabilized by several residues including a group of hydrophobic residues, Ile201, Ala 264, Gly268 and Leu292, which make a hydrophobic pocket for the adenine, Lys228, Glu231 and Thr288 stabilize the ribose, and the diphosphate hydrogen bonds with Ser285 and Thr288. The remaining piece of the NAD⁺ could not be properly modeled.

Fig. 1.

Active site of the human SSADH and primary sequence comparison with GabD1. (a) Active site of Cys340Ala mutant of human SSADH (yellow) in complex with SSA (PDB_ID 2W8Q), and the reduced form of the wild-type enzyme (pink) without SSA (PDB_ID 2W8O), at 2.4 Å and 3.4 Å resolution, respectively. Potential hydrogen bonds of SSADH with SSA are shown as dashed lines, with corresponding distances in Å. Image was generated using PyMol. (b) Alignment of human SSADH and M. tuberculosis GabD1. Amino acids highlighted in red are identical in both enzymes (31.5% identity) and amino acids highlighted in blue are strongly similar (20% strong similarity). Green boxes indicated residues involved in NAD⁺ binding, blue boxes indicate residues involved in SSA binding, and red boxes indicate residues that are involved in catalysis (Cys319 and Glu285, GabD1 numbering). Alignment was performed using ClustalW, with Blosum matrix, and the default parameters.

The human pathogen Mycobacterium tuberculosis has all predicted homologs of the GABA shunt enzymes, and two paralogous SSADHs, encoded by gabD1 (Rv0234c) and gabD2 (Rv1731) genes [10]. Both gene products were shown to catalyze oxidation of SSA to succinate, but substrate specificity was not studied further [11]. In M. tuberculosis, the most likely physiological route for production of SSA is through the GABA shunt enzymes glutamate decarboxylase and GABA transaminase. We recently showed that the Rv1248c-encoded 2-hydroxy-3-oxoadipate synthase does not generate SSA, and instead couples the decarboxylation of α-ketoglutarate to condensation with glyoxylate [12]. Interestingly, primary sequence analysis indicates that despite significant sequence identity and similarity, both GabD1 and GabD2 lack the commonly observed second cysteine residue (non-catalytic thiol) in the catalytic loop (Fig. 1b), responsible for disulfide formation in the human enzyme. This residue also appears to be conserved in several other SSADH homologs [8]. Lack of this second cysteine residue is predicted to drastically alter the properties of mycobacterial GabDs, especially the ones concerning the oxido-reduction of the catalytic thiol, and conformational changes linked to NAD(P)⁺ binding and chemistry. The proposed catalytic cysteine and glutamate residues are conserved (Cys319 and Glu285, GabD1 numbering). While gabD2 appears to be nonessential, based on transposon mutagenesis data, no knockout or transposon mutants of gabD1 have been described to date, implying that it might be essential for growth [13]. Moreover, no kinetic or mechanistic studies have been reported for either enzyme to establish their activity as SSADHs, rather than broad specificity ALDHs. The identity and role of mycobacterial GabDs in aldehyde detoxification, glutamate metabolism and energy generation, through production of succinate, thus remains undefined.

Here, we report the first mechanistic characterization of the M. tuberculosis succinic semialdehyde dehydrogenase 1 (GabD1) enzyme. We specifically characterize the substrate specificity of GabD1 and its chemical mechanism, including the stereochemical course of the reaction, using steady-state kinetics, pH-rate studies, ¹H-NMR spectroscopy, kinetic isotope effects.

2. Experimental procedures

2.1 Materials

All chemicals were obtained from Sigma, unless otherwise stated. Nickel-NTA resin was from Novagen. Chromatographic columns were purchased from GE. SSA solutions were prepared from commercially available SSA, titrated, and stored at −80 °C.

2.2 Trypsinolysis/LC-MS of GabD1

In order to identify whether or not GabD1 was able to react with SSA we performed mass measurements with GabD1 in the presence or absence of ligands. Reaction mixtures contained (1) 10 μM GabD1 in buffer A (50 mM KPi, 10 mM MgCl₂), (2) 10 μM GabD1 in buffer A containing 100 μM SSA and (3) 10 μM GabD1 in buffer A containing 100 μM SSA and 100 μM NADPH. Samples were trypsinized and peptides were separated and analyzed by LC-MS using an LTQ-Orbitrap (Rockefeller University’s Proteomics Resource Center).

2.3 Determination of Bound Ligands

Due to hysteresis observed with GabD1 (pronounced lag phase under steady-state conditions), we sought to test our enzyme preparation for heat-labile ligands, of which slow dissociation could cause the lag observed in the time-courses. 200 μL solution of 85 μM GabD1 was boiled for 5 min to denature protein and release potential small molecules. This solution was cleared by centrifugation followed by filtration on an YM10 filter (Millipore). Filtered supernatant was probed by UV-Vis spectroscopy and mass spectrometry for small molecules. For LC-MS analysis, sample was extracted with acetonitrile/methanol/water (2:2:1, v/v/v) and separated and analyzed using a Congent Silica Hydride Type C column using an Agilent 6220 accurate mass time-of-flight mass spectrometer, as described elsewhere [12].

2.4 Measurements of Enzymatic Activity

Enzymatic activity was measured by following the increase in absorbance at 340 nm resulting from the reduction of NADP⁺ (ε₃₄₀ = 6,220 M⁻¹ cm⁻¹). Samples were pre-equilibrated at 37°C and the reaction was initiated by addition of enzyme, typically 45 nM. Initial velocity was estimated from the initial linear portion of the time-courses. Unless stated otherwise, all experiments were performed in the presence of saturating concentrations of Mg²⁺ (10 mM MgCl₂). Viscosity experiments were carried out with 9% glycerol (w/v) as viscogen, as described elsewhere [14].

2.5 pH-rate Studies

The pH dependence of k_cat/K_NADP+ and k_cat were studied by varying the concentration of NADP⁺ at a fixed concentration of SSA (50 μM) and a fixed saturating concentration of Mg²⁺ (10 mM). The pH dependence of k_cat/K_SSA was studied by varying the concentration of SSA at a fixed saturating concentration of NADP⁺ (200 μM) and Mg²⁺ (10 mM). The following buffers were used at the indicated pH ranges: MES (pH 5.73–6.2), PIPES (pH 6.0), HEPES (pH 6.5–8.3), TAPS (pH 8.1–8.4), and CHES (pH 8.6–9.45), allowing overlap [15,16]. The pH values reported are the final ones, determined with the reaction mixtures after the initial rate was recorded, allowing correction for changes due to buffer dilution and pH changes caused by the added substrates, MgCl₂ and enzyme solutions.

2.6 Inactivation Studies with H₂O₂

The oxidation of GabD1 by H₂O₂ was studied by following the loss of enzymatic activity upon exposure to H₂O₂. 225 nM solution of GabD1 containing 1 mM H₂O₂ was incubated for up to 40 min, at 4°C. Aliquots were taken every 10 min and enzymatic activity was assayed. Reaction mixtures contained 100 mM HEPES pH 7.4, 10 mM MgCl₂, 100 μM SSA and 200 μM NADP⁺.

Stereochemistry of Hydride Transfer

To determine the stereospecificity of the hydride transfer catalyzed by GabD1 we used [²H]SSA and ¹H-NMR analysis of the reaction product, as described elsewhere [17]. In short, the reaction mixtures contained 50 mM KPi pH 7.4, 10 mM MgCl₂, 1 mM NADP⁺, 1 mM [²H]SSA, and 3 μM enzyme in D₂O. Reaction progress was followed by ¹H-NMR, as described below. Each spectrum averages 128 scans, obtained during 11 min.

2.7 Kinetic Isotope Effects

Kinetic isotope effects (KIEs) for the GabD1-catalyzed reaction were determined in 100 mM HEPES pH 7.4, at saturating concentrations of Mg²⁺. Primary deuterium KIEs on V and V/K were determined using [¹H]SSA and [²H]SSA, in the presence of saturating concentrations of NADP⁺, or at a fixed saturating concentration of [¹H]SSA and [²H]SSA and variable concentrations of NADP⁺. Solvent isotope effects (SIEs) on V and V/K were determined in 85% D₂O or 0% D₂O, using [¹H]SSA in the presence of saturating concentrations of NADP⁺, or at a fixed saturating concentration of [¹H]SSA and variable concentration of NADP⁺. Multiple KIEs on V and V/K were determined in D₂O using [¹H]SSA and [²H]SSA, in the presence of saturating concentrations of NADP⁺, or at a fixed saturating concentration of [¹H]SSA and [²H]SSA and variable concentration of NADP⁺.

2.8 Data Analysis

Data were fitted using the nonlinear, least-squares, curve-fitting programs of SigmaPlot 2000 for Windows, version 6.00. The quality of the fit to the equations used was confirmed by plotting the residuals of y versus x, and looking for nonrandom distribution, which indicates systematic error [18]. Errors were propagated as described in Skoog and West for indeterminate errors [19]. Saturation curve showing a non-zero Y intercept was fitted to eq.

$$v=v0+[VA/(A+K)]$$ (1)

where v0 is the velocity in the absence of activator, V is the maximal velocity, A is the concentration of activator, and K is the concentration of activator that gives half-maximal activation (K_act). Individual saturation curves showing linear substrate inhibition were fitted to

$$v=VA/[K+A+(A^2/K_i)]$$ (2)

where V is the maximal velocity, K is the Michaelis constant for substrate (K_m), A is the concentration of substrate, and K_i is the apparent inhibition constant for substrate A. Individual saturation curves displaying partial substrate inhibition were fitted to eq. 3, which is a general equation for nonhyperbolic kinetics

$$v=(aA+{bA}^2)/(1+cA+{dA}^2)$$ (3)

where a, b, c, and d are complex functions of rate constants and concentration of the nonvaried substrate and therefore have no physical meaning. Data plotted in the Lineweaver-Burke format was fitted to

$$1/v=(A+K)/VA$$ (4)

Individual saturation curves were fitted to eq. 5, which is the reciprocal of eq. 4

$$v=VA/(A+K)$$ (5)

Primary deuterium and solvent kinetic isotope effects were fitted to eqs. 6, 7, and 8 for isotope effects on V only, V/K only, or both V and V/K, respectively

$$v=VA/[K+A(1+F_i{E}_V)]$$ (6)

$$v=VA/[K(1+F_i{E}_{V/K})+A]$$ (7)

$$v=VA/[K(1+F_i{E}_{V/K})+A(1+F_i{E}_v)]$$ (8)

where F_i is the fraction of the isotopic label and E_V and E_V/K are the isotope effects minus one on V and V/K, respectively. Linear V_max proton inventory was fitted to

$$V_n=V_n[1-n+n(k_D/k_H)]$$ (9)

where n is the atom fraction of deuterium, V_n is the velocity in the solvent with the atom fraction of deuterium n, V₀ is the velocity in H₂O, and k_D/k_H is the isotope effect.

3. Results

3.1 General Properties of GabD1

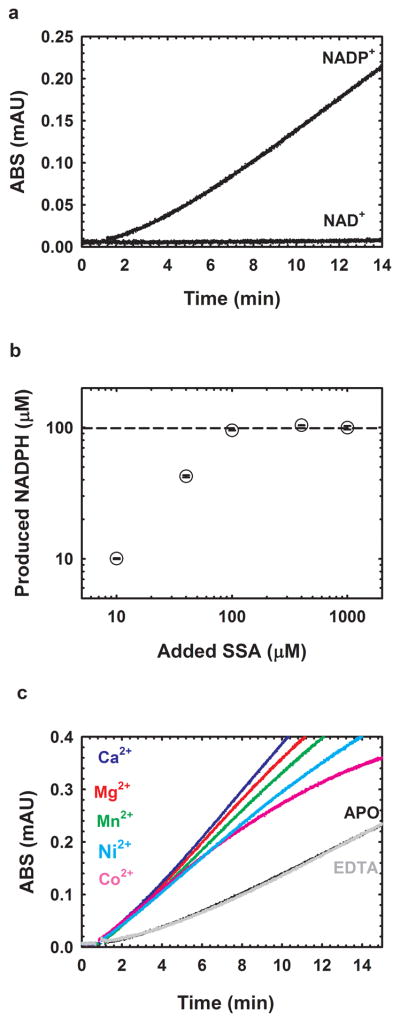
GabD1 progress is characterized by a pronounced lag which precedes steady-state velocity (Fig. 2a). Steady-state velocity does not decrease until nearly all substrates have been converted to products, indicating low K_m values for substrates and high K_i values for products. Although long incubations led to a modest utilization of NAD⁺ as substrate (Fig. 2a), NADP⁺ is the preferred substrate. Also, high concentrations of NAD⁺ led to visible precipitation, impeding further characterization. Of the aldehydes tested, only SSA served as a substrate (Table 1). Other aldehydes, such as formaldehyde, acetaldehyde and glutaraldehyde, were very poor substrates and, at high concentrations, caused visible precipitation of GabD1, precluding further characterization.

Fig. 2.

General properties of GabD1-catalyzed oxidation of SSA. (a) Time-course of the NADP⁺-dependent oxidation of SSA catalyzed by M. tuberculosis GabD1. (b) Stoichiometry of the GabD1-catalyzed oxidation of SSA. Reaction mixtures contained 100 mM HEPES pH 7.4, 10 mM MgCl₂, 100 μM NADP⁺, 90 nM GabD1 and SSA at 10, 40, 100, 400, 1000 μM. Reactions were followed for up to 30 min to assure that completion was reached. Reactions were performed in duplicates. Dashed line represents the maximum NADPH concentration that could be reached assuming a 1:1 stoichiometry. (c) Activation of GabD1 by divalent metals. In the absence of added divalent metals or in the presence of 1 mM EDTA the time course displays hysteresis (lag to achieve steady-state velocity). Addition of saturating concentrations of Mg²⁺, Mn²⁺, Ca²⁺, Co²⁺ and Ni²⁺ led to linearization of the time courses and a slight increase of the steady-state initial velocity.

TABLE 1.

Steady-State Kinetic Parameters for GabD1^a

variable ligand	fixed substrate concentration	[Mg2+] (mM)	kcat (s−1)b	Km (μM)b	kcat/K (M−1s−1)	Ki (μM)b	Eq. used
SSA	200 uM	-	1.9 ± 0.2	13.3 ± 2.6	(1.4 ± 0.2) × 105	62.8 ± 12	2
SSA	200 uM	10	4.7 ± 0.1	3.0 ± 0.2	(1.6 ± 0.1) × 106	NDc	3,4d
NADP+	50 uM	-	1.3 ± 0.1	61.3 ± 7.5	(2.1 ± 0.1) × 105	-	5
NADP+	50 uM	10	2.7 ± 0.1	9.2 ± 1.0	(2.9 ± 0.1) × 105	-	5

^aReactions performed at pH 7.5 and 37ºC.

^bValues are mean of two experiments ± standard error obtained upon fitting the data to the appropriate equation.

^cND = not determined.

^dNumbers displayed were derived from the fit of the uninhibited segment of the curve to eq. 3. Fit of the entire data to eq. 4 gave the following results: a = 0.78, b = 0.03, c = 0.03 and d = 0.02.

Pre-incubation of GabD1 with either substrate did not alter the time-course (data not shown). In addition, no change in the reaction rate was observed in the presence of CoA-SH and no succinyl-CoA was detected by spectrophotometry and liquid chromatography coupled to time-of-flight mass spectrometry (LC-MS) (data not shown), ruling out succinyl-CoA as product of GabD1. To probe if GabD1 contained a tightly bound, heat-unstable inhibitor, which could cause the observed lag in reaction progress, we performed UV-Vis spectroscopy and LC-MS analysis on the supernatant of heat-denatured GabD1 samples. No difference between buffer and GabD1 samples was observed, indicating that the lag observed was not caused by slow dissociation of a tightly bound inhibitor (data not shown).

To confirm the irreversibility of the reaction and proposed stoichiometry, we quantified the amount of NADPH in a mixture containing increasing concentrations of SSA but fixed quantity of NADP⁺ (100 μM). As seen in Fig. 2b, the amount of NADPH produced is identical to the initial concentration of SSA until 100 μM (concentration of NADP⁺ present). This confirms a 1:1 stoichiometry. These results also indicate that GabD1 catalyzed oxidation of SSA to succinate is irreversible under all experimental conditions tested.

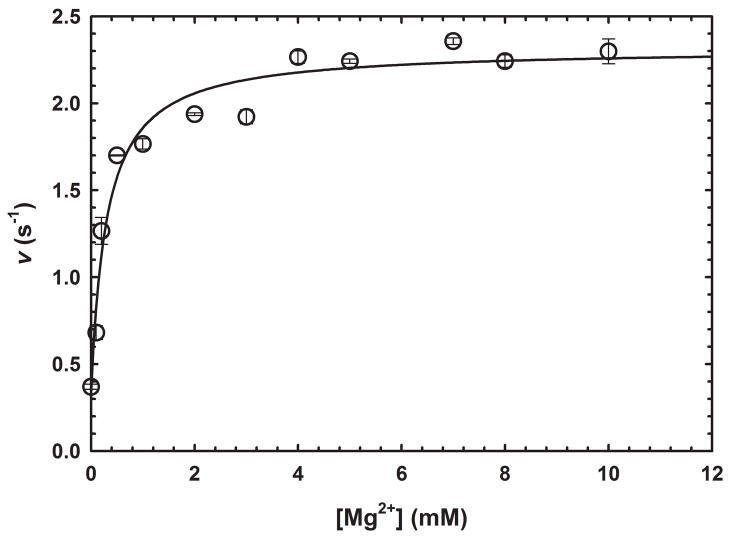
GabD1 is activated by divalent metals such as Ca²⁺, Mg²⁺, Mn²⁺, Co²⁺, and Ni²⁺ (Fig. 2c) but not Cd²⁺ or Zn²⁺ (data not shown). This divalent cation activation increased steady-state rates of GabD1 only modestly (2 to 3-fold) but linearized the time-course (Fig. 2c). By varying the concentration of Mg²⁺ at saturating substrates (200 μM NADP⁺ and 50 μM SSA), we observed a K_act Mg²⁺ value of 0.30 ± 0.07 mM. More detailed analysis, using Mg²⁺, revealed a 4-fold decrease in the K_m value for SSA and a 6-fold decrease in the K_m value for NADP⁺ (Table 1 and Fig. 3). Addition of an excess of divalent metal chelator (5 mM EDTA) did not alter the activity of GabD1 (Fig. 2c and data not shown), indicating an absence of loosely associated divalent metal in our enzyme preparation and reaction mixture. Prolonged pre-incubation of GabD1 with EDTA (4 hours) prior to activity measurement also did not alter the time course (data not shown), indicating a similar lack of slowly dissociating metal bound to our preparation of GabD1.

Fig. 3.

Activation of GabD1 by Mg²⁺. Effect of MgCl₂ on the initial velocity of GabD1. Symbols represent data from duplicates ± standard error, and solid lines represent the fit to eq 1. These results are representative of two independent experiments.

Mass spectrometry analysis of GabD1 in the absence and in the presence of SSA, and SSA:NADPH indicate that thiol addition to the aldehyde does not occur in the absence of NADP⁺ (data not shown). Trypsinolysis of solutions containing GabD1, GabD1:SSA, and GabD1:SSA:NADPH displayed identical peptide profiles showing that the catalytic cysteine residue was not modified in any of the above-mentioned conditions. These results are consistent with the requirement of ternary complex formation, prior to chemistry.

Attempts to oxidize the catalytic cysteine residue and inactivate GabD1 using H₂O₂ were unsuccessful. That is, we observed no significant loss of catalytic activity, after up to 40 min of incubation of GabD1 with 1 mM H₂O₂ at pH 7.4 (data not shown). This result thus indicates that either the thiol is protonated, in the free enzyme and therefore more protected from oxidation, or it is inaccessible to hydrogen peroxide.

3.2 Steady-State Kinetics

Initial velocities were determined by varying the concentration of one substrate at a fixed, saturating concentration of the co-substrate, and found to be proportional to the concentration of enzyme. Kinetic parameters obtained for SSA and NADP⁺, in the presence or absence of saturating Mg²⁺ are summarized in Table 1. Saturation curves for GabD1 with NADP⁺ followed Michaelis-Menten kinetics (Fig. 4 upper panel). In contrast, saturation curves for SSA displayed nonhyperbolic response, showing an intermediate plateau (Fig. 4 lower panel). In the absence of Mg²⁺, SSA reaction kinetics fitted well to a linear model of substrate inhibition, but at saturating Mg²⁺, could not be fitted to the same equation. In the presence of saturating Mg²⁺, substrate inhibition by SSA was observed to be only partial, i.e. velocity decreased to a non-zero value at saturating concentrations of SSA.

Fig. 4.

GabD1 steady-state kinetics. (a) Titration of GabD1 with NADP⁺ at constant SSA (50 μM), in the presence (closed circles) or absence (open circles) of Mg²⁺ (10 mM). Solid lines represent the fit to eq. 4. (b) Titration of GabD1 with SSA at constant NADP⁺ (200 μM), in the presence (closed circles) or absence (open circles) of Mg²⁺ (10 mM). Solid lines represent the fit to eq. 2 (open circles) and eq. 3 (solid circles). Open or closed symbols represent data from replicates ± standard error. These results are representative of two independent experiments.

3.3 pH-Rate Studies

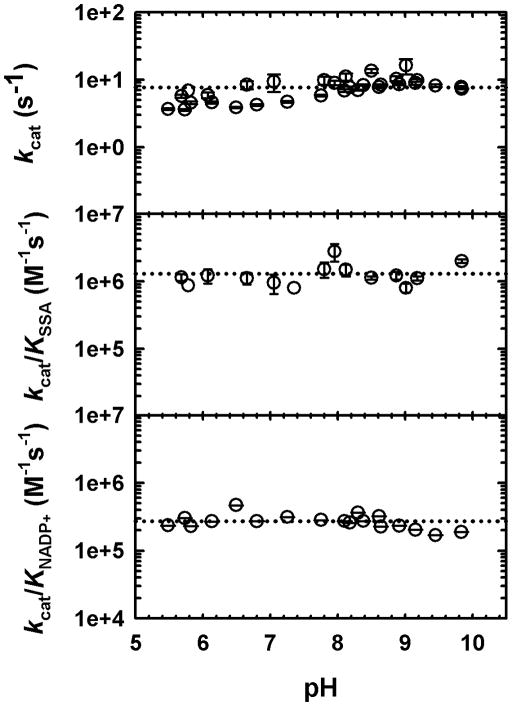
We employed pH-rate studies to probe the role of general acid-base chemistry on the reactions catalyzed by GabD1. Control experiments were performed to confirm GabD1’s stability at the limiting pH values used. GabD1 could not be assayed below pH 5.5, due to precipitation and loss of activity (data not shown). As shown in Fig. 5, no ionizable groups required for any rate-limiting chemistry, in the pH range of 5.5 to 10.0 could be detected. In addition, no ionizable groups required for substrate binding were similarly detected within this range. These results strongly suggest that the groups involved in substrate binding and chemistry have pKa values out of the range analyzed and/or that additional pH-dependent chemistry is not rate-limiting (see discussion).

Fig. 5.

pH dependence of GabD1 catalyzed NADP⁺-dependent oxidation of SSA. The k_cat and K_m values were determined at each pH by varying the concentration of one substrate at a fixed saturating concentration of the other substrate, and saturating concentrations of Mg²⁺. k_cat/K_m is the ratio of the values. Symbols are data and error bars represent the standard error. Dotted lines represent the average of the data and were added to aid visualization.

3.4 Primary Deuterium Kinetic Isotope Effects

To characterize the contribution of the hydride-transfer step to the rate of the GabD1-catalyzed reaction, we conducted primary deuterium kinetic isotope effects experiments, using [¹H]SSA or [²H]SSA, at pH 7.4 (Table 2). ^DV/K (1.8/1.5) were observed when SSA was varied, indicating modest contribution of hydride transfer to the catalytic rate of GabD1. The lack of a KIE on V/K_NADP+ under these conditions indicates that either NADP⁺ is a very sticky substrate or that the kinetic mechanism is steady-state ordered with NADP⁺ binding first. To differentiate between these two cases, we measured the ^DV/K_NADP+ at different concentration of SSA. At lower SSA concentrations, a normal KIE is observed, indicating that the kinetic mechanism is, in fact, random, and that NADP⁺ is a sticky substrate. Further analysis of the dependence of the co-substrate on the KIEs was not possible due to the complex kinetics and tight binding of the substrates. Lack of ^DV indicates that a step after the first irreversible step (hydrolysis), either product release or conformational change linked to product release, is also partially rate-limiting.

TABLE 2.

Primary Deuterium and Solvent Kinetic Isotope Effects for GabD1-catalyzed Reaction^a

parameter	solvent	KIEb
		1st exp.	2nd exp.
DV	H2O	1	1
DV/KSSA	H2O	1.8 ± 0.3	1.5 ± 0.2
DV/KNADP+	H2O	1	1
DV/KNADP+c	H2O	1.4 ± 0.2	-
D2OV	H2O/D2O	2.4 ±0.1	2.4 ± 0.1
D2OV/KSSA	H2O/D2O	1	1
D2OV/KNADP+	H2O/D2O	2.9 ± 0.9	2.8 ± 0.8
D2OV[2H]	H2O/D2O	2.2 ± 0.1	2.5 ± 0.2
D2OV/K([2H]SSA)	H2O/D2O	1	1
D2OV/KNADP+ [2H]	H2O/D2O	1.4 ± 0.4	1.6 ± 0.4
DV	D2O	1	1
DV/KSSA	D2O	1	1
DV/KNADP+	D2O	0.6 ± 0.1	0.6 ± 0.1

^aExperiments performed at pH 7.4 and 37°C, in the presence of 10 mM MgCl₂. SSA was kept at 50 μM when NADP⁺ was varied, and NADP⁺ was kept at 200 μM when SSA was varied.

^bValue ± standard error obtained upon fitting the data to the appropriate equation. For solvent isotope effects experiments were performed in 100% H₂O or 85% D₂O.

^cSSA concentration was kept at 25 μM.

3.5 Solvent Kinetic Isotope Effects

SIEs were employed to study the reaction catalyzed by GabD1 at pH 7.4 (Table 2 and Figs. S1 and S2). Normal SIEs of ^D2OV (2.4–2.5) and ^D2OV/K (2.9–2.8) were observed when NADP⁺ was varied, while no ^D2OV/K was observed when SSA was varied. These results suggest that a solvent-sensitive step is significantly rate-limiting for the reaction catalyzed by GabD1. As both ^D2OV and ^D2OV/K are seen, it is likely that these effects reflect isomerization of free enzyme to a form that allows NADP⁺ binding. Control experiments confirmed that these results are not explained by increased solvent viscosity². Although it appears that SSA does not show a ^D2OV/K isotope effect, the low K_m value for this substrate and its complex kinetics make this result unreliable. To determine the number of protons transferred during the solvent isotope-sensitive step, ^D2OV proton inventory experiments were carried out. As seen in Fig. S2, the linear correlation of the ^D2OV with the atom fraction of D₂O indicates a single proton transfer during this solvent isotope-sensitive step.

3.6 Multiple Isotope Effects

To determine the relative timing of the steps associated with the primary deuterium KIEs and SIEs, multiple isotope effects were employed (Table 2). The use of [²H]SSA in the SIEs caused only a decrease in the ^D2OV/K_NADP+ (Table 2 and Fig. S1). This decrease in the ^D2OV/K_NADP+ associated with deuteration of SSA indicates that hydride transfer and proton transfer occur in separate steps (reviewed in [20]). The lack of change in the ^D2OV value (as well as in the ^DV_D2O value) indicates that an enzyme isomerization rather than a chemical step is rate-limiting.

Looking at the variation of the primary deuterium KIE as a function of deuterated solvent, we observed that the ^DV/K_SSA becomes unity in D₂O, while ^DV/K_NADP+ goes from unity in H₂O to ca. 0.6 in D₂O. These results are similarly consistent with two separate steps, one giving rise to the primary deuterium KIE and another giving rise to the SIE. The large ^DV/K_NADP+ observed in D₂O is most likely an equilibrium isotope effect observed as a KIE (see discussion below).

3.7 Stereochemistry of hydride transfer

¹H-NMR was used to probe the stereospecificity of GabD1. Incubation of GabD1 with NADP⁺, [²H]SSA, and Mg²⁺ led to stereospecific transfer of the deuteride from [²H]SSA to the pro-R position of NADP⁺ generating [4A-²H, 4B-¹H] NADPH (Fig. 6). This result indicates that GabD1 displays A-type stereospecificity.

Fig. 6.

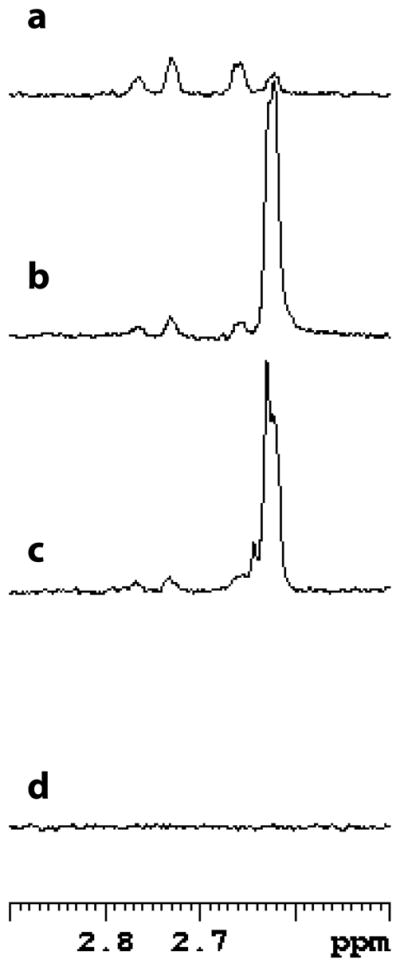
GabD1-catalyzed production of [4A-²H, 4B-¹H] NADPH. Spectral region of interest of the spectra of NADPH and reaction mixtures. The assay mixture contained, in a final volume of 0.6 mL (ca. 65% D₂O), 1 mM [²H]SSA (~ 95% ²H), 1 mM NADP⁺, 10 mM Mg²⁺, and 100 μg GabD1 in 50 mM KPi buffer pH 7.4. (a) Spectrum of 200 μM NADPH, with both methylene protons, (b) spectrum of the reaction after 25 min, (c) spectrum of the reaction after 15 min, and (d) spectrum of 200 μM NADP⁺. The chemical shift of the 4A proton is 2.76 ppm and the 4B proton is 2.64 ppm. Each spectrum is the average of 128 scans.

4. Discussion

4.1 General properties of GabD1

Our studies establish GabD1 as a bona fide succinic semialdehyde dehydrogenase, with narrow substrate specificity for the aldehyde substrate, as reported for SSADHs from other sources [4–7]. In addition, GabD1 was found to use NADP⁺, but not NAD⁺, as the preferred hydride acceptor. Our data further refute a role for CoA as a third substrate, generating succinyl-CoA instead of succinate. Like SSADH from A. thaliana and rat brain, GabD1 also exhibits substrate inhibition by SSA [4,6]. For the Mg²⁺-activated enzyme, the K_m values for SSA and NADP⁺ are 3 μM and 9 μM, respectively. These values are significantly lower than the K_m values measured for A. thaliana SSADH which uses NAD⁺ as oxidant. Wheat grain SSADH has a K_mSSA value of 7.4 μM and the K_mNAD+ is 200 μM. Rat brain SSADH also displayed a low K_mSSA, 2.5 μM, and the K_mNAD+ value was 30 μM. Although it is clear that the high affinity for SSA is a common trait in SSADHs, the K_m values for NAD(P)⁺ appear to vary more. Based on the k_cat/K_m values obtained, in the 10⁵–10⁶ M⁻¹ s⁻¹ range, SSA and NADP⁺ are likely the physiological substrates for GabD1.

Interestingly, Mtb’s GabD1 is naturally resistant to oxidation by H₂O₂. This feature distinguishes it from both HsaSSADH and EcoSSADH. In HsaSSADH, oxidation of the catalytic cysteine occurs, but can be easily reversed by treatment with DTT. Mutation of the noncatalytic cysteine residue to alanine in the HsaSSADH caused greater sensitivity to oxidation, and abolished rescue by DTT [8]. EcoSSADH is also oxidized by H₂O₂, but this oxidation cannot be reversed by DTT treatment. Consistent with an already maximal effect, mutation of the noncatalytic cysteine residue does not cause any further changes in the oxidation profile of EcoSSADH [9]. From these results, it is clear that sensitivity to oxidation of the catalytic thiol in SSADHs is a complex phenomenon, dependent on other active-site residues in addition to the catalytic and noncatalytic cysteine residues. The striking resilience of GabD1 to oxidation/inactivation could be due to the selection pressure imposed by the human host, Mtb’s sole reservoir, in which Mtb is constantly challenged with reactive oxygen and nitrogen intermediates [21].

We also discovered that Mtb’s GabD1 is the first SSADH subject to activation by a divalent metal, such as Mg²⁺. Our results indicate that GabD1 hysteresis is caused by the lack of a divalent metal activator, rather than a tightly bound inhibitor or product, like observed for M. tuberculosis LpdA with NADP⁺ [22], E. coli MurA with UDP-N-acetylmuramic acid [23] or rabbit liver 10-formyltetrahydrofolate dehydrogenase with tetrahydropteroylpentaglutamate [24]. Some eukaryotic type 1 and type 2 ALDHs have been reported to be activated by Mg²⁺, such as a cytosolic ALDH from Saccharomyces cerevisiae [25], horse liver ALDH [26–28], and human liver and mitochondrial ALDH [29–31], all of which have broad substrate specificity for the aldehyde substrates and utilize NAD⁺ as co-substrate. The activation of these ALDHs seems to be similar to the activation observed with GabD1, in terms of magnitude of the effect. It appears that divalent cation affects very little the V_max of ALDHs and this is also true for GabD1. In contrast to what was observed with type 1 and type 2 ALDHs, the effect of Mg²⁺ on GabD1 is limited to the linearization of the time course, with only modest changes in affinity for substrates. The fact that Ca²⁺ can replace Mg²⁺ is intriguing, as Ca²⁺ is considerably bigger than Mg²⁺. Determination of the divalent metal binding site by mutagenesis and crystallographic studies is essential for the further understanding of the metal activation. However, it seems logical to conclude that it is not a catalytic cofactor, as the reaction proceeds nearly at the same rate in the absence of divalent metals.

4.2 Chemical mechanism of GabD1

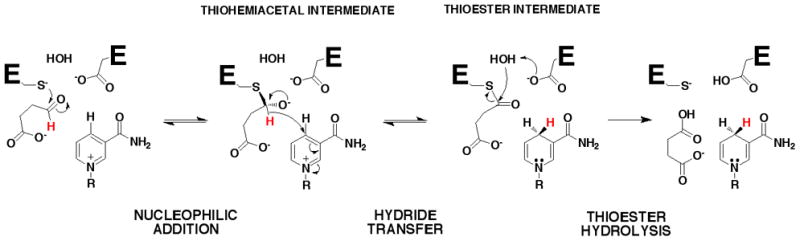
The reaction catalyzed by GabD1 can be separated into three distinct chemical steps (Scheme 2), each of which involves a covalent enzyme-intermediate. In the first step, thiol/thiolate addition to SSA generates a thiohemiacetal intermediate. Second, hydride transfer to NADP⁺ generates a thioester intermediate and NADPH. Third, hydrolysis of the thioester intermediate regenerates free enzyme and succinate. To characterize the chemical mechanism and the model proposed, we conducted pH-rate and kinetic isotope effects studies.

Scheme 2.

The lack of significant pH dependence of the steady-state kinetic parameters of the GabD1-catalyzed reaction is quite unusual for a dehydrogenase. That is, we observed no ionizable groups in GabD1’s k_cat pH-rate profile within the pH range of 5.5 to 10.0. This result is unexpected because the reactions in question generally require (i) a general base for activation of the water molecule that will hydrolyze the thioester intermediate, (ii) a general acid to catalyze the hydride transfer step and (iii) another general base to deprotonate the active site thiol. Ionizable groups observed in the k_cat pH-rate profile are typically important for conversion of enzyme-substrate to enzyme-product complexes, potential isomerizations and product release. However, ionizable groups involved with these steps will not be seen in the k_cat pH-rate profiles if binding occurs only when all ionizable groups are in the correct protonation state when they fall outside the range analyzed, or when a conformational change is rate-limiting [15]. Although unusual, a similar pH-dependence of k_cat, from pH 5.5 to 9.5, was reported for A. suum NAD⁺-dependent malic dehydrogenase-catalyzed oxidative decarboxylation of malate [32]. In the case of GabD1, it seems rational to suggest that the carboxylate from Glu285 cannot be seen, as its pK_a value is probably below 5. The absence of a pK_a corresponding to the thiol from Cys319 is probably caused by an altered pK_a, which should be out of the range tested.

The lack of detectable ionizable groups on the k_cat/K_SSA and k_cat/K_NADP+ versus pH plots can be more easily explained by the nature of the residues involved in binding. The pH dependence of the k_cat/K parameter reports on free substrate and on the free enzyme form with which it combines. As can be seen in Fig. 1, GabD1 uses two Arg residues and one Gln to bind SSA. In addition, backbone amide nitrogen from Cys340 lies within hydrogen bonding distance of SSA’s carbonyl oxygen, in the structure of the HsaSSADH. None of these residues have pK_a values in the range tested, and therefore these groups would not be identified in our analysis. SSA’s carboxylate should not be seen as well, as its pKa must be ~ 4.7, as judged by structurally similar analogs, butanoic acid and 4-hydroxybutanoic acid, which have pKa ~ 4.8 and 4.72, respectively. The same is true for the k_cat/K_NADP+, all residues predicted to bind NADP⁺, should not appear in the pH range analyzed. Therefore, the lack of change observed in the k_cat/K pH-rate profiles for GabD1 are more likely due to the absence of ionizable groups in either binding or rate limiting steps, within the pH range tested. Based on theory reviewed elsewhere [20,33–36], assuming limiting cases for slow isotope-sensitive chemical steps and that the rule of the geometric mean³ still applies, four conclusions can be drawn from our results. (1) The small but significant ^DV/K_SSA and the unity ^DV obtained in H₂O indicate that a step after and including the first irreversible step (most likely hydrolysis of the thioester intermediate) partially limits the overall reaction and a step from binding of the substrate SSA up to the hydrolysis of the enzyme-thioester intermediate is partially rate-limiting. Conformational changes could lead to these slow steps, as demonstrated for malic enzyme [37], where at pH 7 NADPH dissociation is fully rate-limiting.

Based on the normal isotope effect, its magnitude and chemistry in question, it seems logical to assign it to the hydride transfer step. This result contrasts with formate dehydrogenase, where hydride transfer is fully rate-limiting and the primary deuterium KIE observed equals the intrinsic KIE for hydride transfer [38]. (2) Large normal solvent isotope effects, of different magnitude, were observed on ^D2OV and ^D2OV/K_NADP+, indicating that a solvent-sensitive step is partially rate-limiting for GabD1. Because these effects are observed in both V and V/K, it is likely that they are reporting on an isomerization of free enzyme. The inequality of ^D2OV and ^D2OV/K_NADP+ indicates that the associated commitment factors are not negligible. Furthermore, the linearity of our proton inventory experiment denotes that a single proton is in motion during the solvent-sensitive step (isomerization of free enzyme). (3) When the primary deuterium KIE is performed in D₂O the ^DV/K_SSA decreases to unity, consistent with hydride transfer and the solvent sensitive step being localized in a different segment within the reaction. Surprisingly, an inverse ^DV/K_NADP+ is now observed when the reaction is carried out in D₂O. Possible explanations for this result are discussed below. (4) By performing SIEs using [²H]SSA we also observed a decrease in the ^D2OV/K_NADP+ value, but no change was observed on ^D2OV. Decrease in SIE in this case is fully consistent with the idea that the steps giving rise to the primary deuterium KIE and the SIE are different. The decrease in the magnitude of the observed SIE when [²H]SSA was present is considerably lower than the decrease in the magnitude of the primary KIEs observed when the reaction was performed in D₂O, suggesting that the solvent-sensitive step is more rate-limiting than hydride transfer. Finally, the lack of change in ^D2OV with [²H]SSA indicates that the solvent sensitive step is not a chemical step, but most likely a conformational change. Based on these results we conclude that a conformational change of the free enzyme limits the rate of GabD1-catalyzed reaction, while hydride transfer contributes to the steady-state rate only modestly.

Inverse primary deuterium and solvent kinetic isotope effects have been observed during multiple isotope effects experiments with other dehydrogenases, which do not use cysteine residues or metals for chemistry. This is the case for two other mycobacterial enzymes, enoyl-ACP reductase (InhA) and 3-oxoacyl-ACP reductase (MabA) [39,40]. Conformational changes were suggested as potential cause for these inverse isotope effects, and conformational changes have been described to exist in both, InhA and MabA active sites [41,42]. A similar explanation, which is fully consistent with the chemistry proposed for GabD1 and the inverse primary deuterium KIE observed is offered. Thiol addition to SSA is fast under normal conditions, while enzyme isomerization prior to substrate binding is considerably more rate-limiting for GabD1. Based on this sequence, it seems logical to propose that the primary deuterium KIE observed in D₂O is caused by an increase in the barrier to isomerization of free enzyme to its catalytic form (decrease in the steady-state turnover), which in turn, manifests as an equilibrium isotope effect (EIE) on the thiol addition step. An EIE is an isotope effect on the equilibrium constant of a chemical step, as oppose to on its rate. In other words, the decrease in the levels of catalytic competent form of GabD1 in D₂O may increase the frequency with which the catalytic thiol attacks SSA, as well as the reverse reaction, where the thiohemiacetal breaks down into free thiol and SSA. Although it would be tempting to propose that this EIE (^DV/K_NADP+ = 0.6) is reporting on the hydride transfer itself, EIE have been measured for hydride transfer from thiohemiacetal to NAD⁺, and these EIEs are normal and of small magnitude [43]. Based on these observations, we interpret this inverse primary deuterium KIE in D₂O (^DV/K_NADP+ = 0.6) as representing an EIE, which is caused by the ionization of the thiol happening prior its attack on SSA (which could have a limiting value of ca. 0.5)⁴. Finally, further evidence for conformational changes prior to or linked to NADP(H) binding come from a variety of studies in other aldehyde dehydrogenases. Marchal and Branlant demonstrated that NADP⁺ binding to glyceraldehyde 3-phosphate dehydrogenase causes a 2.4 pK units shift in the pK_app of the catalytic cysteine, simultaneous with changes in the protein fluorescence, indicating that small changes in conformation of the enzyme upon NADP⁺ binding exist [44]. Mitochondrial aldehyde dehydrogenase is another good example where different bound conformations of NAD⁺/NADH and isomerizations of these molecules within the enzyme were extensively characterized by X-ray crystallography, NMR and fluorescence studies [45–47].

To define the stereochemical course of the reaction catalyzed by GabD1, we employed ¹H-NMR and analysis of the structural data available for the human homolog. First, analysis of the structure of the human homolog indicates that prior to thiolate addition to SSA, the catalytic cysteine residue has to undergo a rotation around its Cβ, to allow the proper positioning of its thiolate for nucleophilic attack. As it can be seen on Fig. 7, in the apo structure the Cys340’s thiolate is pointing away from SSA, blocking access and correct positioning for nucleophilic attack. A rotation of ca. of 106 º would allow its proper positioning, parallel to SSA, 2.4 A apart from SSA’s C4. Also, this conformation would position the Cys340’s thiolate directly below the carboxylate from Glu306, at a distance of 2.7 Å, which could also contribute to its activation and/or protection from oxidizing agents. Review of the literature indicates that at least one other aldehyde dehydrogenase was shown to display this conformational change [48]. Cobessi et al. observed an identical conformational change with the catalytic cysteine residue in apo and NADP⁺-bound structures of Streptococcus mutants NADP⁺-dependent glyceraldehyde 3-phosphate dehydrogenase [48]. At this stage, we cannot assign the precise role of this conformational change in the mechanism of GabD1, but it must be required prior to the first chemical step. Therefore, it is tempting to propose that the reorientation of the catalytic cysteine is the cause of the EIE described above. By looking at the relative orientation of the catalytic cysteine residue, after its rotation, and SSA we can conclude that GabD1 generates a thiohemiacetal intermediate with (S) stereochemistry (Fig. 7 and Scheme 2). The hydride from the thiohemiacetal intermediate is then transferred to the R face of NADP⁺ (pro-R position) generating the enzyme-bound thioester. Pro-R (type A) specificity has been demonstrated for rat liver ALDH [17], among others.

Fig. 7.

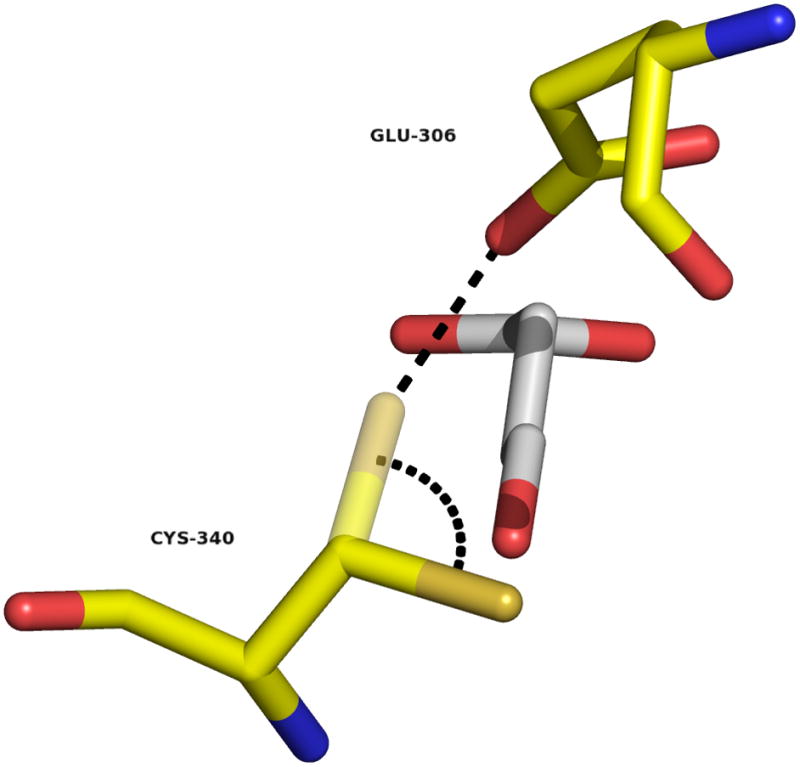
Conformational change require for the initial chemical step. Superimposition of SSA (from the C340A mutant structure) on the structure of HsaSSADH, reduced form. Cys340 thiol/thiolate is shown in two conformations, one pointing away of the substrate (obtained in the absence of SSA) and the other, after 106º rotation, parallel to SSA, shown in semi-transparent (modeled). This rotation would allow the proper positioning of the thiol/thiolate to attack on the Si-face of SSA at C4 position. The distance between C4 and the thiol/thiolate is within 2.4 Å. Furthermore, the catalytic thiol/thiolate would be positioned 2.7 Å of the oxygen from Glu306’s carboxylate, allowing its proper position and/or activation (show as dashed black line). Image was generated using PyMol.

The overall chemical mechanism of GabD1 (Scheme 2) derived from these results consists of the nucleophilic addition of the Cys319 thiolate on the Si-face of the carbonyl of SSA generating a (S)-thiohemiacetal intermediate. Collapse of this tetrahedral intermediate leads to hydride transfer to the Reface of NADP⁺, followed by hydrolysis of the thioester intermediate, regenerating the active site thiolate.

4.3 Kinetic mechanism of GabD1

Although the goals of these studies were not to characterize the kinetic mechanism of GabD1, several lines of evidence point to non-rapid random equilibrium kinetics. First, the partial substrate inhibition observed indicates that some degree of randomness is present, as shown for yeast alcohol dehydrogenase [49]. Second, the plateau observed when SSA is varied is typical of enzymes that display non-rapid equilibrium random kinetic mechanism, where there is a preferred path to the central complex [50,51]. This type of mechanism has been assigned to E. coli tRNA nucleotidyltransferase [52], gentamycin acetyltransferase [53], E. coli phosphofructokinase [54], and M. tuberculosis α–isopropylmalate synthase [55]. Third, the inequality of the KIEs on V and V/K values for both substrates in all conditions tested strongly suggests that the forward commitment factors are not zero, ruling out a rapid equilibrium kinetic mechanisms. Fourth, the changes observed for ^DV/K for both substrates depending on the solvent (H₂O or D₂O) are more easily explained by changes in the commitment factors for the substrates, as oppose to a change in the order of addition of the substrates, in a strictly sequential ordered mechanism. Fifth, at lower SSA concentration, a primary deuterium KIE is observed for NADP⁺, indicating that indeed the mechanism is random, and the lack of ^DV/K_NADP+ at higher concentrations of SSA is due to the apparent increase of the forward commitment for NADP⁺.

Together, our results suggest that GabD1 follows a nonrapid equilibrium random kinetic mechanism with a preferred pathway for the ternary complex, shown in Scheme S2. For GabD1, the preferred pathway most likely starts and ends with NADP⁺ binding and NADPH dissociating, respectively. Isomerization of free enzyme (E′) to a form (E) that allows productive substrate binding is also shown.

Abbreviations

SSADH

Succinic semialdehyde dehydrogenase

SSA

succinic semialdehyde

CoA-SH

coenzyme A

GABA

γ-aminobutyric acid

NMR

nuclear magnetic resonance

IPTG

isopropyl β–D-1-thiogalactopyranoside

TEA

triethanolamine

HEPES

4-(2-hydroxyethyl)-1-piperazine ethanesulfonic acid

GabD1

M. tuberculosis SSADH1

MES

2-(N-morpholino)ethanesulfonic acid

CHES

2-(N-cyclohexylamino)ethanesulfonic acid

TAPS

N-tris[hydroxymethyl]methyl-2-aminopropanesulfonic acid

PIPES

piperazine-N-N′-bis[2-ethanesulfonic acid]

CAPS

3-(cyclohexylamino)propanesulfonic acid

KIE

kinetic isotope effect

SIE

solvent kinetic isotope effect

EIE

equilibrium isotope effect