Standing on the Shoulders of Giants: Improving Medical Image Segmentation via Bias Correction

Abstract

We propose a simple strategy to improve automatic medical image segmentation. The key idea is that without deep understanding of a segmentation method, we can still improve its performance by directly calibrating its results with respect to manual segmentation. We formulate the calibration process as a bias correction problem, which is addressed by machine learning using training data. We apply this methodology on three segmentation problems/methods and show significant improvements for all of them.

1 Introduction

Automatic image segmentation plays an important role in medical applications. Due to the limitations of the imaging process and the difficulty of transferring manual segmentation protocols into algorithms, automatic segmentation is challenging. We show that without deeply understanding the limitations of an existing segmentation method, one easy/straightforward way to make improvements is through a calibration process to directly transfer its results closer to manual segmentations. To this end, we propose to use machine learning techniques to correct segmentation errors.

From a theoretical perspective, the segmentation errors produced by a segmentation algorithm can be categorized into two classes: 1) random errors and 2) consistent bias. The random errors are caused by random effects, e.g. imaging noises or random anatomical variations. They can be reduced by averaging techniques such as multi-atlas based segmentation. In this paper, we focus on addressing the other type of errors, consistent bias³. Bias are systematic errors mostly caused by mistranslating manual segmentation protocols into the criteria followed by the automatic segmentation method. By definition, bias occurs consistently across different segmentation trials when certain conditions are met. For example, a manual segmentation protocol may assign a specific label to a voxel if and only if a certain criterion, e.g. the voxels next to it all have low intensities, is met. However, because of the translation error an automatic method may follow a slightly different criterion, e.g. the average intensity of its neighbors is low. In this example, the automatic segmentation method makes errors whenever a voxel’s neighbors have a low average intensity but have at least one bright voxel.

Since bias occurs consistently, it is feasible to detect and correct them. Although it may be difficult to figure out the exact cause behind each bias, it is relatively easy to capture the patterns that are strongly correlated to the bias. Hence, one can detect bias via capturing the correlated patterns. For example, the example above demonstrates a simple bias whose correlated appearance pattern, i.e. a voxel’s neighbors have a low average intensity but have at least one bright voxel, can be learned using training images. In reality, the bias may appear in more complex and less intuitive patterns. Although it may be difficult for the human to identify such bias, most machine learning techniques are capable of providing satisfactory solutions.

In related work, Morra et al [3] use machine learning to directly learn how to perform segmentation. During training, they use intermediate classification results to improve the classifier’s performance. The main difference with our method is that they do not use any other segmentation methods and train the classifier from scratch. By contrast, our contribution lies in proposing the idea of improving the performance of existing segmentation algorithms relative to a specific manual segmentation protocol via learning-based bias correction. Our approach takes full advantage of other segmentation algorithms to simplify learning. To validate our method, we apply it to three segmentation problems/methods and show significant improvements for all of them.

2 Learning-based explicit bias correction (EBC)

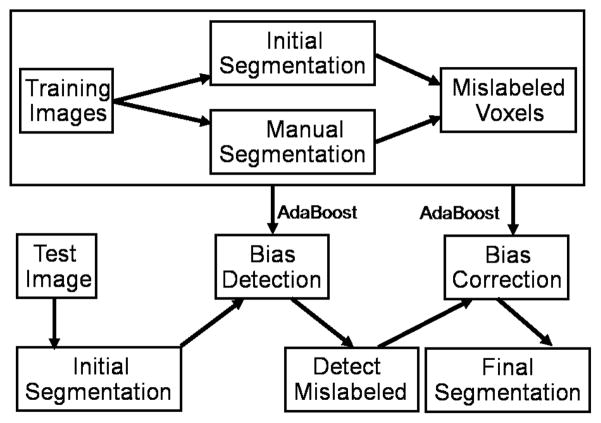
To improve segmentation results produced by a segmentation method, we propose a two-step procedure for bias correction (see Fig. 1): 1) bias detection that finds the mislabeled voxels produced by the host segmentation method and 2) bias correction that corrects the mislabeled voxels found by bias detection.

Fig. 1.

Flow chart of our explicit bias correction approach.

2.1 Bias detection as a binary classification problem

Given a segmentation produced by a host segmentation method, our goal is to identify mislabeled voxels. With manual segmentations, it is straightforward to formulate the bias detection problem as a binary classification problem. For each label we train one classifier using all voxels assigned to this label to separate correctly labeled voxels from mislabeled.

To train classifiers, we use AdaBoost [2]. For effective learning, abundant informative features are crucial. The simplest feature is the raw image appearance, i.e. pixel-wise intensities. For more discriminative representations, textures are often used as well. One common approach to construct texture features is to use an over-complete description for each voxel and its neighborhood by convolving the image with a filter bank. In our experiment, for more efficiency we use the following features. We denote A^ΔX(i) = I(X_i + ΔX) − Ī to be the appearance feature for voxel i with coordinate X_i at the relative location ΔX. I is intensity. To compensate for different intensity ranges, we normalize the intensities by the average intensity of the region of interest (ROI), Ī. To train a bias detection classifier for a label, the ROI contains all voxels assigned to the label by the host method (see experiments). More robust features with scale and rotation invariance can be used as well. Since the brain image data used in our experiments all have similar scales and orientations, we use these simple features.

Low level texture features can capture image related bias, e.g. the host segmentation method always makes errors when a certain appearance pattern occurs. To capture non-image related bias, e.g. the host method always shifts the segmentation a few voxels, we include the segmentation produced by the host segmentation method for learning. We denote these features by L^ΔX(i) = s(X_i + ΔX), where s is the segmentation produced by the host method.

To include spatial information, we use the coordinate feature S_X(i) = X_i − X̄, where X̄ are the average coordinates of the ROI. To enhance the spatial correlation, we include the joint feature obtained by multiplying spatial features with appearance and label features, i.e. A^ΔX(i)S_X(i) and L^ΔX(i)S_X(i). Overall, we use ~ 1000 features in all experiments.

For each feature, a weak classifier is constructed using a simple threshold. AdaBoost combines these weak classifiers into a single strong classifier.

2.2 Learning-based bias correction

Bias detection outputs candidate mislabeled voxels. We need to reassign labels to them. Again, we use a learning-based method. Given mislabeled voxels in the initial segmentations, applying the same learning algorithm with the same features used for bias detection we train a binary classifier for each label to separate it from others. To assign a new label to a candidate mislabeled voxel detected by bias detection, we re-evaluate the voxel by each bias correction classifier and assign the label whose corresponding classifier gives the strongest response to the voxel. Since bias correction is only for detected candidate mislabeled voxels, the computational cost is much lower than re-evaluating the whole image when the host segmentation method can produce accurate results.

2.3 Variants of the learning algorithm

In our method, we explicitly perform bias detection and bias correction. This strategy is efficient because for bias correction only the potentially mislabeled voxels need to be relabeled. One variant of our bias correction method is that we skip the bias detection step and directly perform bias correction on the initial segmentation. Instead of only using mislabeled voxels, we use all voxels in ROI for training. We call this method implicit bias correction (IBC). Note that IBC has higher computational complexity for both training and testing. IBC is closely related to [3], where instead of segmentation results produced by other segmentation methods the segmentation labels produced by the learning algorithm itself are included in the learning process.

One way to view the segmentation feature produced by other host segmentation methods is that like the low level texture filters any host segmentation method can be considered as a high level, task specific filter. If the host segmentation method works reasonably well, i.e. better than random guesses, the produced segmentation provides useful information for the segmentation task. To demonstrate the usefulness of host segmentation methods for learning, we compare with a variant of IBC that each classifier is learned without using segmentation results produced by any other segmentation methods. We call this variant the direct learning (DL) approach. So given training images and their manual segmentations, we train one classifier for each label to separate voxels belonging to this label from other voxels. The features used for DL, is only image and spatial features. For IBC and DL, the ROI is the whole segmentation produced by the host method plus some dilation. Dilation is necessary only when the background label needs to be corrected (see experiments for examples).

3 Experiments

We apply our methods to three segmentation problems. The problems are image registration based hippocampal segmentation, whole brain extraction using BET [7] and brain tissue segmentation using FAST [8].

3.1 Hippocampal segmentation

The hippocampus plays an important role in memory function [6]. Macroscopic changes in brain anatomy, detected and quantified by magnetic resonance imaging (MRI), consistently have been shown to be highly predictive of AD pathology and highly sensitive to AD progression [5]. Compared to clinical measures and neuropsychological testing, MRI-derived biomarkers require an order of magnitude smaller cohort size to detect disease-related changes over time. Accordingly, automatic hippocampus segmentation from MR images has been widely studied e.g. [1, 3, 4]. In this section, we test our methods with one semi-automatic hippocampal segmentation method [4].

We use the data in the Alzheimer’s Disease Neuroimaging Initiative (ADNI, www.loni.ucla.edu/ADNI). Our study is conducted using only 3 T MRI and only includes data from mild cognitive impairment (MCI) patients and controls. Overall, the data set contains 139 images. The image has 1.22 × 1.03 mm in plane resolution and 0.99 mm slice thickness. For cross validation evaluation, 70 subjects are randomly selected for training, and the remaining 69 for testing. The reported results are the average of 10 cross-validation experiments.

A landmark-guided atlas-based segmentation method [4] is applied to segment the hippocampi for each image. This method is designed to minimize user efforts while maximizing the benefit of human input to the algorithm. It requires a user to approximately label six key landmarks of the hippocampus through a user-interface. The partial labeling is combined with image similarity terms to guide volumetric diffeomorphic normalization between an individual brain and an unbiased template, with fully labeled hippocampi. It is shown that such simple human interactions help increase minimum performance levels relative to fully-automatic segmentation algorithms and provides high inter-rater reliability.

Whole hippocampal segmentation is a binary segmentation problem (we do experiemnts on left side and right side separately). Once the mislabeled voxels are identified we can fix them by simply switching their labels and vice versa. Hence, for the binary segmentation problem EBC is equivalent to IBC.

Since the results produced by [4] are accurate, we define the ROI for bias correction to be the initially segmented hippocampi plus one voxel dilation. On average, this ROI includes 99.5% hippocampal voxels. By contrast, the ROI obtained from the initial segmentation plus two voxel dilation covers 99.9% hippocampal voxels but also includes significantly more irrelevant voxels, which increases the chances for our bias correction to make mistakes. Since DL does not use the results produced by [4], DL should take the whole image as ROI. However, for direct comparison with our methods, we apply the same ROI for DL. Since the ROI excludes significant non-hippocampus distracters, using ROI simplifies the learning problem. Hence, in this experiment DL partially benefits from the results produced by [4].

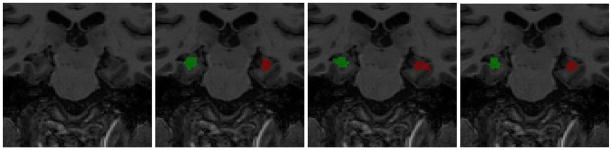
On average, each hippocampus contains 1603 voxels. [4] produces 465 mislabeled voxels. Note that the errors include hippocampal voxels mislabeled as background and background voxels mislabeled as hippocampi. Our bias correction method achieved 35.7% fewer errors (299 mislabeled voxels). Using the larger ROI, i.e. initial segmented hippocampi plus two voxel dilation, results in slightly worse results of 305 mislabeled voxels. By contrast, DL produces worse segmentations with 523 mislabeled voxels. Fig. 2 shows example segmentation results. In terms of average Dice overlaps, [4], DL and IBC/EBC resulted in 0.862, 0.832 and 0.903 respectively.

Fig. 2.

Hippocampal segmentation. Left to right: original image, manual segmentation, segmentation produced by [4], after bias correction.

3.2 Brain extraction/segmentation in MR images

In this section, we test brain segmentation. The data set contains 18 T1-weighted MR brain images and their manual segmentations, which are available at the Internet Brain Segmentation Repository (IBSR). The manual segmentation contains labels for gray and white matter and ventricles. These images have been positionally normalized into the Talairach space (rotation only) and have been preprocessed by intensity inhomogeneity correction routines. These images have the same slice thickness of 1.5 mm with three in plane resolutions: eight have 0.94 × 0.94 mm; six have 1.0 × 1.0 mm; four have 0.84 × 0.84 mm.

Using this data, we test two methods: the Brain Extraction Tool (BET) [7], and the FMRIB’s Automated Segmentation Tool (FAST) [8]. For cross validation evaluation, 9 subjects are randomly selected for training, and the remaining 9 for testing. The results are the average of 10 cross-validation experiments.

Brain extraction

The BET algorithm is applied with the default parameter setting to segment the images into brain and non-brain regions. Again, for this binary segmentation problem EBC is equivalent to IBC. Since the BET algorithm is relatively accurate and most segmentation errors are mislabeling background voxels as brain tissues, we define a ROI for bias correction by performing a one-voxel dilation of the BET result, similar to how the ROI was defined in the binary hippocampus segmentation experiment. On average, this ROI covers 99.3% manually labeled brain. DL still partially benefits from BET’s results by using the same ROI.

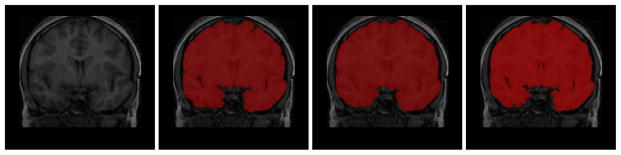
On average, each brain contains 9.7 × 10⁵ voxels. BET produces 1.1 × 10⁵ mislabeled voxels. Our bias correction method achieved 29% fewer errors (8.0 × 10⁴ mislabeled voxels). By contrast, DL produces worse segmentations with 9.1 × 10⁴ mislabeled voxels. In terms of average Dice overlaps, BET, DL and IBC/EBC resulted in 0.948, 0.956 and 0.961 respectively.

Brain tissue segmentation

In this experiment, the FAST [8] algorithm is applied for segmenting gray matter, white matter and cerebrospinal fluid (CSF) for all 18 subjects used in the previous experiment. To apply FAST, the binary brain segmentation is assumed to be provided.

Since the manual segmentation in IBSR merges CSF outside ventricles into gray matter (see Fig. 4), the CSF produced by FAST that overlaps gray matter in manual segmentation is also considered correct. For quantitative evaluations, we merge the CSF into gray matter for both manual and automatic segmentation and compare the consistency of white matter and merged gray matter. See Fig. 4 for segmentation examples.

Fig. 4.

Brain tissue segmentation. left to right: original image, manual, initial segmentation produced by FAST, after bias correction by IBC, and EBC.

Out of the average brain volume, 9.7 × 10⁵ voxels, the FAST algorithm produces 8.9 × 10⁴ mislabeled voxels. For EBC, the bias detection step achieved the precision( $\frac{\#\text{of}\text{correct}\text{detection}}{\#\text{of}\text{detection}}$) of 92% with the recall( $\frac{\#\text{of}\text{correct}\text{detection}}{\#\text{of}\text{true}\text{bias}}$) of 84%. The bias correction step correctly classified 91% of the detected mislabeled voxels. Overall, EBC achieved 21% fewer errors (7.0 × 10⁴ mislabeled voxels). IBC achieved 17% fewer errors (7.4 × 10⁴ mislabeled voxels). Note that EBC outperforms IBC with even fewer computational costs. By contrast, DL produces worse segmentations with 8.1 × 10⁴ mislabeled voxels. Table 1 reports the average Dice overlaps. Like in the previous experiments, our bias correction methods outperformed DL and the host segmentation method.

Table 1.

Brain tissue segmentation results in Dice overlap.

method	FAST(Dice)	DL(Dice)	IBC(Dice)	EBC(Dice)
gray	0.936	0.944	0.948	0.951
white	0.862	0.891	0.899	0.905

4 Discussion

Combining segmentations/methods has been proven to be a good strategy to improve performance. One can view our bias correction as a combining method that integrates a pure machine learning based segmentation method with the host segmentation method. One main difference from previous combining methods is that the machine learning method can automatically adapt itself through training to optimally combine with the host segmentation method. As demonstrated in our experiments, as long as the machine learning algorithm uses complementary information to the host segmentation methods the combined results consistently outperform the host segmentation methods and the machine learning method when applied separately. The information integration interpretation also suggests that using the same machine learning algorithm used in bias correction to improve the results produced by our bias correction may not give as much improvement because of the significant information overlap. However, a learning method using different features or learning models may still help.

Fig. 3.

Brain extraction. Left to right: original image, manual brain extraction, initial brain extraction by BET, after bias correction.