Influences of Source - Item Contingency and Schematic Knowledge on Source Monitoring: Tests of the Probability-Matching Account

Abstract

The authors investigated conditions under which judgments in source-monitoring tasks are influenced by prior schematic knowledge. According to a probability-matching account of source guessing (Spaniol & Bayen, 2002), when people do not remember the source of information, they match source guessing probabilities to the perceived contingency between sources and item types. When they do not have a representation of a contingency, they base their guesses on prior schematic knowledge. The authors provide support for this account in two experiments with sources presenting information that was expected for one source and somewhat unexpected for another. Schema-relevant information about the sources was provided at the time of encoding. When contingency perception was impeded by dividing attention, participants showed schema-based guessing (Experiment 1). Manipulating source - item contingency also affected guessing (Experiment 2). When this contingency was schema-inconsistent, it superseded schema-based expectations and led to schema-inconsistent guessing.

How we interpret, understand and use information is often influenced by the source from which we believe the information originated. For example, we might trust our doctor's health advice but not our hairdresser's (for good reasons). Thus, remembering the source of information is an important aspect of human memory functioning. In a typical source-monitoring paradigm, participants are presented with items of information that originate from one of two or more sources (e.g., speakers, presentation modalities, backgrounds etc.). In a subsequent memory test, participants judge whether test items originated from Source A, Source B (etc.), or are new. According to Johnson's theoretical framework of source monitoring (Johnson, Hashtroudi, & Lindsay, 1993), there are two general types of information that people use to attribute their memories to a source. One type of information consists of episodic contextual features that are encoded in memory. We may, for example, remember perceptual details, such as the sound of the voice that told us something. The second type of information involves general knowledge, schemas, stereotypes, beliefs, and plausibility. For example, one might reason “Sam was the only person there who would have said this sort of thing, so he must have said it” (Johnson et al., 1993, p. 4).

In recent years, a number of empirical studies found evidence that prior knowledge may influence source judgments (Bayen, Nakamura, Dupuis, & Yang, 2000; Cook, Marsh, & Hicks, 2003; Dodson, Darragh, & Williams, 2008; Ehrenberg & Klauer, 2005; Hicks & Cockman, 2003; Klauer & Ehrenberg, 2005; Marsh, Cook, & Hicks, 2006; Mather, Johnson, & DeLeonardis, 1999; Sherman & Bessenoff, 1999; Spaniol & Bayen, 2002). In these studies, items originated from sources for which they were either expected (e.g., a doctor talking about a surgery) or less expected (e.g., a doctor talking about a court trial). Generally, source identification performance was better for items that originated from a source for which they were expected than for items that originated from a source for which they were somewhat unexpected. For example, participants were more likely to attribute masculine items to a male source rather than to a female source independent of the item's actual origin (Marsh et al., 2006).

Johnson's framework does not specify the cognitive mechanisms through which prior knowledge influences source judgments. Bayen et al. (2000) proposed a guessing hypothesis stating that people who cannot remember the source of information will make a guess that is biased by prior knowledge. They found support for this hypothesis in two experiments. In one of them, two male faces, “Tom” and “Jim”, presented sentence statements that were either expected of a doctor or were expected of a lawyer. In addition, both sources presented statements that were equally expected for both professional groups. Immediately preceding the source-monitoring test, it was revealed to the participants that Jim was a doctor and Tom was a lawyer. At test, participants showed better source-identification performance for expected-doctor statements stemming from the doctor source and expected-lawyer statements stemming from the lawyer source, while performance was equal across the two sources for equally expected statements. By analyzing the data with the two-high-threshold multinomial model of source monitoring (Bayen, Murnane, & Erdfelder, 1996), the authors showed that this schema-consistent bias in source attributions resulted from biased source guessing rather than from better source memory for statements that were presented by the expected source. That is, for example, when participants did not remember the source of an expected-lawyer statement, they were more likely to guess that it originated from the lawyer rather than the doctor.

Hicks and Cockman (2003) used the doctor-lawyer materials from Bayen et al. (2000), but their study additionally included an experimental group for which the professional information about the two sources was already provided during the study phase. That is, at the time of encoding, participants knew that the source named Jim was a doctor and the source named Tom was a lawyer. We will further refer to this group in which the schema-relevant information was provided at the time of encoding as the encoding condition. In this group, source identification performance did not differ for items originating from an expected source in comparison to items originating from a somewhat unexpected source. Thus, while providing the professional information after encoding of the statements yielded a schema-consistent bias on schema-expected statements (in replication of Bayen et al., 2000), this was not the case if the professional information was already known at encoding. These results were supported by Sherman and Bessenoff (1999) and by Cook et al. (2003). However, several studies contradict these findings and report a schema-bias on source identification even though the schema information was provided at encoding (Bayen et al., 2000, Experiment 1; Ehrenberg & Klauer, 2005; Klauer & Ehrenberg, 2005; Mather et al., 1999).

The purpose of the current study was to shed further light on the circumstances under which prior knowledge influences performance in source-monitoring tasks. We suggest that the probability-matching account of guessing bias in source monitoring (Spaniol & Bayen, 2002) provides an explanation for ostensible inconsistencies in results. Therefore, we will first discuss the nature of guessing bias in source monitoring and then differences in the studies mentioned above that may, in light of the probability-matching account, help explain apparent inconsistencies in results.

Guessing bias in source monitoring

Guessing bias in source monitoring is typically measured with multinomial processing tree (MPT) models, stochastic models that allow us to disentangle different cognitive processes or states underlying task performance. The first such model for source monitoring was introduced by Batchelder and Riefer in 1990. Since then, this modeling approach has been further developed to accommodate variations in source-monitoring task paradigms (e.g., Bayen et al., 1996; Klauer & Wegener, 1998; Meiser & Bröder, 2002; Riefer, Hu, & Batchelder, 1994). In the present study, we used the two high-threshold MPT model of source monitoring by Bayen et al. (1996). This model is illustrated in Figure A1 and further described in Appendix A. The model parameter most relevant for our current study is the guessing or response-bias parameter g, which is part of all MPT models designed for the source-monitoring paradigm. This parameter measures the probability of answering a particular source if the source in a source-monitoring task is not remembered.

Wegener (2000) determined two influences on guessing in source monitoring. One of these influences is based on prior knowledge in the form of stereotypes and schemas that evoke certain expectations about which source is more likely to be associated with a certain item. We refer to this type of guessing as schema-based. The other influence is contingency-based and depends on the perceived contingency between sources and items in a particular episode, such as the presentation phase of an experiment. For example, in an experiment by Ehrenberg and Klauer (2005) one source was predominantly paired with negative items, while the other source was predominantly paired with positive items. When participants later did not remember the source of a particular test item, they more likely guessed that a negative item originated from the “negative” source, and a positive item originated from the “positive” source. A priori, participants knew nothing about the person sources, thus they could not apply any prior knowledge. The guessing bias matched the source - item contingencies employed in the experiment. That is, participants were more likely to attribute negative statements to the “negative” person source and positive statements to the “positive” statement source. Furthermore, Klauer and Meiser (2000) demonstrated that source-guessing can reflect perceived contingencies despite a given actual zero-contingency in the study list. They used Hamilton and Gifford's (1976) illusory-correlation paradigm in which a negative bias occurs towards the group for which less information is available overall. Klauer and Meiser showed that source-guessing probabilities reflected the perceived illusory correlation (as also measured by trait ratings and frequency judgments) and not the actual zero-contingency. This result has been replicated in several other studies (e.g., Meiser, 2003, 2006). The idea that there are multiple influences on source guessing is also proposed by Batchelder and Batchelder (2008), who state that participants will try to optimize their performance in an experiment by drawing onto “metacognitive knowledge (…) along with knowledge and beliefs acquired from other experimental and extra experimental sources” (p. 237). The idea that there are schema-based and contingency-based influences on guessing bias has also been expressed by Spaniol and Bayen (2002) in their probability-matching account of source guessing bias in source monitoring. This account focuses on the interaction of these two influences and will be discussed in turn.

The probability-matching account of guessing bias in source monitoring Probability matching is a robust phenomenon observed in human choice behavior (e.g., Estes & Straughan, 1954; Rubinstein, 1959; Siegel, 1959). For example, when faced with the task to predict which one of two lights will flash, humans will match their response probabilities to the actual probabilities with which the light flashed across previous trials. Probability matching is not only observed in humans, but in various kinds of animals including pigeons and bees (Bullock & Bitterman, 1962; Niv, Joel, Meilijson, & Ruppin, 2002). Given the robustness of the phenomenon, it is no surprise that people also have been shown to engage in probability matching in simple old-new item recognition tasks (e.g., Buchner, Erdfelder, & Vaterrodt-Plünnecke, 1995; Healy & Kubovy, 1978; Ratcliff, Sheu, & Gronlund, 1992; Van Zandt, 2000). That is, in such tasks, respondents match their response bias to the perceived ratio of old to new test items. The probability-matching account of guessing bias in source monitoring, introduced by Spaniol and Bayen (2002), is an extension of these findings and states that when people do not remember the source of an item and have to guess the source, they match their guessing bias to their perceived contingency of sources and certain types of items in the study list. For example, if participants in an experiment believe that 70% of the positive statements were made by the source named Jim, and 30% of the positive statements by the source named Tom, then when they do not remember the source of a positive statement, they will guess with a probability of about .7 that the statement originated from Jim. Furthermore, in some situations, participants have pre-experimental schema-based expectations about the source from which a certain type of item should originate. That is, in some situations there are two types of probability that source-response probabilities may be matched to, namely 1) perceived source-item contingencies in a particular episode such as the presentation phase of an experiment, and 2) schema-based source-item contingencies. According to the probability-matching account of source guessing, if and only if participants do not have a representation of the contingencies in the study list, will they use these schema-based probabilities in their probability matching. However, if they do have a representation of contingencies in the study list, they will match probabilities according to this perceived contingency. That is, the perceived contingency in the study list supersedes schema-based probabilities in the probability-matching process. As a consequence, participants' guessing probability does not necessarily reflect their schema-based expectations. In fact, according to the probability-matching account, guessing probabilities only reflects schema-based expectations if the perceived contingency is in line with these expectations (and thus the two cannot be distinguished) or if participants do not have a representation of contingencies in the study list.

Contingency-based guessing can be investigated independently of schema-based guessing with material about which participants have no prior knowledge (Ehrenberg & Klauer, 2005; Klauer & Meiser, 2000; Klauer & Wegener, 1998). By contrast, it is not possible to investigate the schema-based influence in isolation, because there always is an actual contingency of source and item type in the experiment. Thus, to understand why some of the studies showed schema-biased source identifications when the schema information was provided at encoding and some did not, one must take into account the role of the contingency-based influence: Did the perceived contingency in the particular study list agree with the schematic expectations or contradict them? In most studies in which schema-relevant information was provided at encoding and that report no schema-based guessing bias, there was a zero contingency in the study list (e.g., Hicks & Cockman, 2003, Experiment 1). That is, each source was paired with each item type equally often. This zero contingency contradicts schema-based expectations. If participants notice this zero contingency, then probability matching should lead to a guessing probability of .5 for each source. Thus, a possible explanation for the absence of a schema-based bias in Hicks and Cockman's encoding condition is that the actual zero contingency counteracted the schema-based expectations. The participants showed a contingency-based response pattern which was not consistent with the schema. Two studies that provided the schema at encoding included an actual schema-consistent contingency (Mather et al., 1999; Klauer & Ehrenberg, 2005). That is, there were more expected than somewhat unexpected source–item pairings in the study list. In Mather et al. (1999), for example, a Democrat source made three times as many expected-Democrat statements than expected-Republican statements. Both studies report a schema-consistent bias in source identification. In these studies, the contingency concurs with schema-based expectations, and thus responses based on contingency are indistinguishable from responses based on schemas. Therefore, a response pattern appears in these studies that is consistent with schema-based responding.

Overview of the Experiments

Although the probability-matching account has been introduced a few years ago (Spaniol & Bayen, 2002) and there are several findings that are compatible with it, to date this account has not been put to systematic test. The purpose of the present research was to test the two core assumptions of the probability-matching account, namely that 1) when people have no representation of encountered contingencies, they will default to schema-based guessing (Experiment 1) and that 2) perceived contingency affects guessing in source monitoring and supersedes effects of schematic knowledge (Experiment 2). We focused on the encoding condition where the schema-relevant information about the two sources is already provided at encoding since this is the condition that has produced the most inconsistent results. We propose that Hicks and Cockman (2003) did not find a schema influence on source identification in their encoding condition in the doctor-lawyer scenario because their participants noticed the actual zero-contingency of sources and item types and thus did not rely on their schemas. By taking into account the role of perceived contingency, we created experimental conditions in which the schema-relevant information was provided at encoding and still a predictable bias resulted. In Experiment 1, we impeded contingency perception by dividing attention, resulting in schema-based guessing bias. In Experiment 2, we manipulated (perceived) contingencies resulting in contingency-based guessing bias that superseded the influence of schemas.

Experiment 1

The purpose of Experiment 1 was to test one core assumption of the probability-matching account, namely the assumption that if people do not have a representation of the contingency in the study list, they default to a guessing bias that reflects the schema-based expectations. That is, they will attribute most of the schema-expected statements to the source for which these statements are expected based on schematic knowledge. In this experiment, all participants knew the sources' professions at encoding and were in a zero-contingency condition. That is, schema-expected statements were presented by the doctor or the lawyer with equal likelihood. According to Hicks and Cockman (2003), people do not rely on their schematic knowledge if the schema-relevant information is provided at encoding. However, according to the probability-matching account, reliance on schematic knowledge occurs if participants do not have a representation of the source – item contingency in the study list independent of when the schema-relevant information is provided. Therefore, we aimed to prevent contingency detection in half of our participants by dividing their attention at encoding. In the divided-attention condition, participants performed a random-number-generation task during the study phase. A prior study by Klauer and Ehrenberg (2005) investigated the effects of cognitive load on contingency detection in an extended version of the regular source-monitoring paradigm including groups (categories) of speakers as sources. While load at encoding had little impact on contingency detection in conditions with a non-zero contingency, it seemed to disrupt the detection of a zero contingency. The probability-matching account would predict that people default to their schema-based contingencies in this condition. Indeed, participants in this particular condition in the Klauer and Ehrenberg study estimated the source – item contingency to be somewhat schema-consistent (even though it was actually zero) and also showed a schema-consistent source guessing bias. The objective of the present study was to replicate these findings within the doctor-lawyer paradigm and to demonstrate the effects of load on the source guessing parameter g of the 2HT MPT model of source monitoring. Based on Klauer and Ehrenberg's results we expected that dividing attention at encoding would prevent (zero-) contingency detection and based on the probability-matching account we predicted that therefore a schema-consistent guessing bias would occur in the divided-attention condition. That is, in contrast to Hicks and Cockman, we expected reliance on schematic knowledge in this condition even though the schema-relevant information was provided. For participants whose attention was not divided at encoding the results should replicate those of Hicks and Cockman (2003). That is, participants should not show a schema-based bias. Thus, we expected source guessing parameter g to deviate significantly from .5 in the divided-attention condition but not in the full-attention condition. Due to this schema-consistent guessing bias we expected to find better source identification for schema-consistent than for schema-inconsistent source - item pairings in the divided-attention condition but not in the full-attention condition where source-identification was not expected to differ for the two sources. This analysis of source-identification performance in addition to multinomial modeling extends the study by Klauer and Ehrenberg.

Method

Participants

Forty-eight native English speakers (36 females, 12 males) participated in this experiment. The participants were between the ages of 18 and 27 years, were recruited from introductory psychology courses at the University of North Carolina at Chapel Hill and received course credit for their participation.

Design

The design was a 3 × 2 × 2 mixed factorial with expectancy of statements (expected-doctor, expected-lawyer, equally expected) and source of statements (doctor vs. lawyer) as within-subjects factors, and attention at encoding (full vs. divided attention) as a between-subjects factor. Participants were randomly assigned to the full or divided attention condition.

Materials

The sources used in this experiment were taken from Bayen et al. (2000, Experiment 2) and were two black-and-white pictures of male faces. The statements were also taken from Bayen et al. (Appendix C). However, in order to keep source memory from floor level in the divided-attention condition, we presented only 72 statements during the study phase. By comparison, Bayen et al. (2000) presented 96 statements. These statements are listed in the left column of Appendix C of Bayen et al. (2000). For the present experiment, 72 of these statements were presented in the study phase; the remaining 24 statements served as distractors in the source memory test. The 96 statements were randomly divided into four groups that contained eight statements of each statement type (expected doctor, expected lawyer, equally expected). Three of those four groups served as the target items in the study list and the statements of the fourth group served as distractors in the source memory test. Four different versions of the memory test were constructed such that each statement group served as the distractors in one of the test versions and as target statements in all other test versions. The four test versions were completely counterbalanced across participants.

Procedure

The procedures were similar to those used by Bayen et al. (2000, Experiment 2). An important difference, however, was that Bayen et al. (2000) did not reveal the profession of the two sources to the participants until shortly before the memory test, whereas in the present experiment, we revealed the profession of the sources before the encoding phase. That is, our participants were run under conditions similar to those in the encoding condition of Hicks and Cockman (2003, Experiment 1).

At the beginning of the experiment, each participant signed a consent form and was seated in a computer booth. Participants were informed that they would see the faces of two people, a doctor and a lawyer, accompanied by a sentence “spoken” by the doctor or the lawyer. Participants were instructed to read the sentences carefully because their memory for the sentences would later be tested. Participants were not told at this point that source memory would also be tested. The 72 statements were then presented one at a time below the picture and the label of the source “speaking” each statement. Presentation time was six seconds per item. The source pictures were labeled with their names and respective profession in capital letters, that is, TOM=DOCTOR or JIM=LAWYER. The source label was followed by a colon indicating that this source “spoke” the sentence. The statements were presented in 24-point font size and the source labels in 45-point font size. A random half of the statements in each of the three expectancy groups was presented by one source, and the other half was presented by the other source. Hence there was a zero contingency between sources and item types. The order of statement presentations was randomized by participant, and the sources alternated randomly. Four additional equally-expected statements were presented first, as a primacy buffer. Each source presented two of these. They later served as practice items in the source-monitoring test.

In the divided-attention condition, participants generated a random number between one and nine every two seconds during the entire study phase and said it out loud. Performance was monitored by an experimenter and recorded on tape. All participants in the divided-attention condition were run individually. To help them keep with the pace, every two seconds a tone sounded (similar to a metronome). Participants received detailed instructions about the concept of randomness. That is, they were instructed to imagine they were drawing these numbers blindly out of a hat, simply reading them off and then putting them back into the hat. They were instructed to avoid familiar sequences (e.g., 1, 2, 3), repetition of sequences (e.g., always saying 7 after 4) and to use all numbers equally often. The importance of generating a number for every tone they heard was stressed and instructions were given to try to get back into the pace as soon as possible if they missed a tone. They then practiced random number generation for one minute. At the end of the study phase, before receiving instructions for the memory test, participants were instructed to stop generating the random numbers, and the tone sequence was turned off. Participants' performance on the number generation task performed during the study phase was screened for poor performance characterized by regular (1, 2, 3, 4, 5, …) or repetitive (1, 6, 3, 1, 6, 3, …) number strings and long pauses. No participant showed poor performance on the number generation task and thus no exclusions were made. Participants in the full-attention condition did not perform a secondary task during the study phase.

After study, the instructions for the source-monitoring test were presented on the screen. Participants were informed that they would now see sentences and were asked to judge whether each sentence had been presented by the doctor, by the lawyer, or by neither of them. Ninety-six test statements appeared on the screen, one at a time. Seventy-two of the test trials included target items, and 24 included distractor items. The ninety-six test trials were preceded by four practice trials in which the primacy-buffer items were used. During the test, both source pictures appeared side by side on the screen. Below each picture, the source label was printed in capital letters, that is, DOCTOR or LAWYER. Below these labels appeared the option NEITHER in the center of the screen. Participants gave responses by hitting color-coded keys on the computer-keyboard. Each response option was shown on the screen in the same color as the key. The “D” key was marked with a green sticker, “K” with a yellow sticker, and the space bar with a red sticker. Assignment of the “D” and “K” keys to the two sources was counterbalanced across participants, and completely crossed with memory test version. The space bar always represented the response option “NEITHER”. The response keys were located directly below the corresponding response options and were marked in the same color. Responses were self-paced. Participants did not receive error feedback. After a response was made, the next test item immediately appeared on the screen.

Results and Discussion

We first report analyses with an empirical measure of source identification and then analyses based on the MPT model of source monitoring. We used an alpha level of .05 for all statistical tests.

Analyses based on an empirical measure of source identification

We used the single-source conditional source identification measure (CSIM) as our empirical measure of source identification performance (Murnane & Bayen, 1996). This measure is calculated by dividing the number of items from a particular source that were attributed to the correct source by the number of items from this same source that were attributed to either of the two sources. For Sources Doctor and Lawyer, respectively, CSIM is thus calculated as follows.

$${\text{CSIM}}_{\mathrm{D}}=Y_{\text{DD}}/(Y_{\mathrm{D}\mathrm{D}}+Y_{\text{DL}})$$ (Equation 1)

$${\text{CSIM}}_{\mathrm{L}}=Y_{\text{LL}}/(Y_{\text{LL}}+Y_{\text{LD}})$$ (Equation 2),

where Y_ij indicates the frequency of responding Source j to items originating from Source i. Index D indicates Doctor, and Index L indicates Lawyer.

These measures of source identification are independent of item memory under most circumstances (Murnane & Bayen, 1996), but are influenced by guessing bias in addition to source memory. Figure 1 shows CSIM as a function of attention condition, statement expectancy, and source. A repeated-measures ANOVA was performed on CSIM with statement expectancy (expected-doctor, expected-lawyer, equally expected) and source (doctor vs. lawyer) as within-subjects factors, and attention at encoding (full vs. divided) as a between-subjects factor. Expectancy yielded a significant main effect, F(2, 92) = 7.84, MS_e = .02. As in Bayen et al. (2000, Experiment 2), source-identification performance was better for equally expected statements (M = .71) than for expected-doctor statements (M = .65), t(47) = 2.92, d = 0.85, and for expected-lawyer statements (M = .63), t(47) = 3.95, d = 1.15. The interaction of expectancy and source was significant, F(2, 92) = 6.96, MS_e = .11, but it was qualified by a significant three-way-interaction of attention at encoding, expectancy, and source, F(2,92) = 5.76, MS_e = .11. Separate repeated measures analyses with expectancy and source as within-subjects factors for each of the two attention conditions were performed to further investigate this interaction. The interaction of source and expectancy was significant in the divided-attention condition, F(2, 46) = 8.49, MS_e = .16, but not in the full-attention condition, F(2, 46) < 1. Simple main-effects analyses on the two-way interaction in the divided-attention condition revealed that CSIM was significantly higher for expected-doctor statements that were presented by the doctor (M = .70) as opposed to the lawyer (M = .40), F(1, 23) =6.81, MS_e = .16. Similarly, CSIM was significantly higher for expected-lawyer statements that were presented by the lawyer (M = .70) as opposed to the doctor (M = .35), F(1,23) = 12.03, MS_e = .12. CSIM did not significantly differ as a function of source for equally expected statements (M = .64 for the doctor source and M = .55 for the lawyer source). That is, as expected, participants in the divided attention condition showed the typical schema-consistent source-identification pattern, while participants in the full-attention condition did not.

Figure 1.

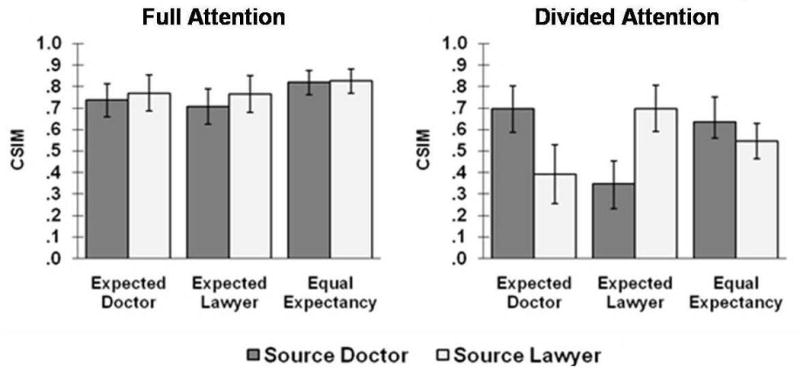
Experiment 1. Conditional source identification measure (CSIM) for statements as a function of expectancy and source in the full-attention and divided-attention conditions. Error bars indicate 95% confidence intervals.

According to Bayen et al.'s (2000) guessing hypothesis, differences in CSIM as a function of source and statement expectancy are due to a response or guessing bias when the participant does not remember the source. CSIM is independent of item memory under most circumstances (Murnane & Bayen, 1996). However, it measures a mixture of source memory and source guessing. We, therefore, used a formal model of source monitoring to disentangle source memory and guessing.

MPT-model based analyses

The 2HT MPT model of source monitoring provides separate and independent parameters of item memory, source memory, and guessing or response biases. Thus, this model enables us to test the hypotheses regarding participants' guessing. We hypothesized that the divided-attention group would show schema-consistent source guessing bias, while the full-attention group would not.

The model and its parameters are described in Appendix A. We performed all parameter estimations, goodness-of-fit tests, and significance tests with the HMMTree computer program by Stahl and Klauer (2007). As a goodness-of-fit measure, we used the log-likelihood ratio statistic, G², which is asymptotically chi-square distributed (Hu & Batchelder, 1994). The data we analyzed with the model were the frequencies of responses (“doctor”, “lawyer”, or “neither”) to different item types (expected-doctor, expected-lawyer, equally expected) stemming from different sources (presented by the doctor, presented by the lawyer, or new) as listed in Appendix B. Goodness-of-fit tests yielded that the most parsimonious of the identifiable submodels (for a listing see, Bayen et al., 1996), namely Model 4 (which Bayen et al., 2000, also used), provided a good fit to the data, G²(6) = 5.75 for the full-attention group, and 10.65 for the divided-attention group). Model 4 assumes the following: (1) Item recognition is equal for statements presented by the doctor, statements presented by the lawyer, and new statements (D₁ = D₂ = D₃). (2) Source memory is equal for statements presented by the doctor and for statements presented by the lawyer (d₁ = d₂). Thus, Model 4 has four free parameters: Parameter D (item recognition); Parameter d (source memory); Parameter b (probability of guessing that an item is old); and Parameter g (probability of guessing that an item was presented by the doctor). Table 1 presents a list of all parameter estimates with 95% confidence intervals.

Table 1. Parameter Estimates, Confidence Intervals, and G² Goodness-of-Fit Values for the Four-parameter Two-high Threshold MPT Model of Source Monitoring under Different Conditions of Expectancy and Attention in Experiment 1.

Item Expectancy	D	d	g	b	G2(6)
	Full Attention				5.75
Expected Doctor	.66 (.60-.72)	.62 (.51-.72)	.48 (.41-.56)	.40 (.30-.49)
Expected Lawyer	.57 (.51-.63)	.60 (.48-.72)	.42 (.35-.50)	.35 (.27-.43)
Equal Expectancy	.83 (.80-.86)	.67 (.59-.73)	.47 (.38-.57)	.09 (.00-.19)
	Divided Attention				10.65
Expected Doctor	.24 (.16-.32)	.32 (.05-.60)	.72 (.68-.77)	.57 (.52-.62)
Expected Lawyer	.15 (.07-.24)	.17 (.00-.56)	.29 (.24-.34)	.56 (.52-.61)
Equal Expectancy	.35 (.28-.43)	.26 (.07-.44)	.57 (.51-.62)	.41 (.35-.47)

Note. These are probability estimates that can range from 0 to 1. D = probability of item recognition; d = probability of remembering the source; g = probability of guessing that an item was presented by the doctor (estimates higher than the chance level of .5 indicate guessing bias towards doctor; estimates lower than .5 indicate guessing bias towards lawyer); b = probability of guessing that an item is old (chance level is .5). 95% confidence intervals are in parentheses. G²(6) values lower than 12.59 indicate a good fit of the model to the data.

The parameter of greatest interest to us is the guessing parameter g. It reflects the probability of guessing that a statement was presented by the doctor in cases where the source is not remembered. The complementary probability 1-g is the probability of guessing that a statement was presented by the lawyer. Figure 2 presents the guessing probabilities as a function of statement expectancy for the two attention groups. These probabilities are conditional on not remembering the source. Parameter g can assume any value between 0 and 1 independent of the value of other parameters including Parameter d (with the exception that g cannot be estimated if item and source memory are both 1). Thus, d provides a measure of source memory independent of source guessing, while g provides a measure of source guessing independent of the level of source memory. If schematic knowledge influences source guessing, g will significantly differ from .5. In case of a schema-consistent bias, participants who do not remember the source of a statement will guess with a probability larger than .5 that the statement originated from the expected source. By contrast, in case of a schema-inconsistent bias, participants who forgot the source of a statement will guess with a probability larger than .5 that the statement originated from the somewhat unexpected source. We tested whether guessing parameter g differed from .5 by setting this parameter equal to .5 and testing whether this constraint significantly decreased model fit. With one degree of freedom, G² values above 3.84 are significant.

Figure 2.

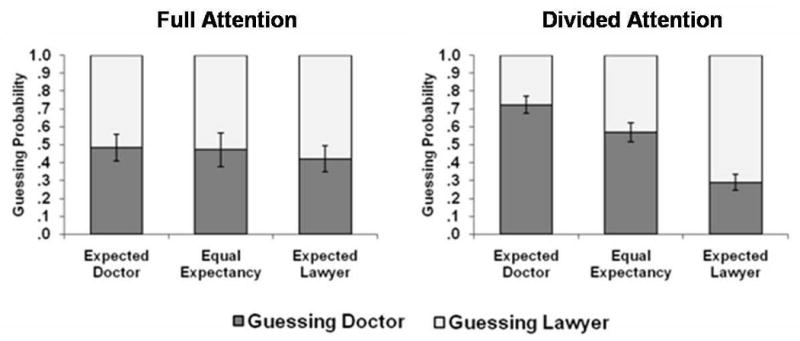
Experiment 1. Guessing probability as a function of statement expectancy in the full-attention and divided-attention conditions. Error bars indicate 95% confidence intervals.

In the divided-attention condition, model parameter g (guessing “doctor”) was significantly above .5 for expected-doctor statements, g = .72, G²(1) = 81.08, and significantly below .5 for expected-lawyer statements, g = .29, G²(1) = 76.74. For equally expected statements, g was significantly above .5, g = .57, G²(1) = 6.1. This bias towards guessing doctor for equally expected statements was significantly less strong than for expected-doctor statements, G²(1) = 17.25.

In the full-attention condition, g did not significantly differ from .5 for expected-doctor statements, g = .48, G²(1) = 0.2, nor for equally-expected statements, g = .48, G²(1) = 0.34, but was significantly below .5 for expected-lawyer statements, g = .42, G²(1) = 4.31. That is, participants were a little more likely to attribute expected-lawyer statements to the lawyer source when they could not remember the source than to the doctor source. This slight schema-consistent guessing bias for expected-lawyer statements in the full-attention condition was unexpected, but, as predicted, it was significantly less strong (g = 0.42) than in the divided-attention condition (g = 0.29), G²(1) = 9.06.

Thus, participants whose attention had been divided at test showed a strong schema-consistent guessing bias in their source attributions, while guessing in the full attention condition showed hardly any deviations from the actual zero contingency. To summarize, CSIM results for the full attention condition replicated Hicks and Cockman (2003, Experiment 1), as expected. No effects of schemas on CSIM emerged. According to the probability-matching account, participants in this condition matched guessing probabilities to the perceived zero contingency in the study list. This was confirmed via MBT analyses that showed that participants in the full attention condition guessed either source with a probability close to .5. In the divided attention condition, we sought to disrupt the perception of the zero contingency during encoding via a secondary task. CSIM results for this condition showed the pattern that is expected when schemas exert their influence on source monitoring. In line with the probability-matching account, when the perception of contingency in the study list was disrupted, participants used schema-based contingencies in their guessing. This was confirmed in the MBT-model based analyses, which showed a strong bias to guess in favor of the source for which statements were expected based on schemas. Results of this experiment thus support the probability-matching account.

As expected, the divided-attention manipulation also resulted in lower item and source memory compared to the full-attention condition (compare parameter estimates for D and d between conditions in Table 1)¹. This was necessary in order to prevent contingency detection in the divided-attention condition. If memory for item-source pairings is very good, participants will inevitably have a good representation of the contingencies in the study list.²

The finding of lower item recognition and source memory along with a strong schema bias is consistent with prior findings. Hicks and Cockman (2003) reported that in their study, item and source memory was higher in the encoding condition compared to the retrieval condition and only in the latter a schema bias occurred. However, the authors did not provide a compelling explanation for this apparent dependency of schema bias on memory level. The probability-matching account does provide an explanation for the observed dependency. Good memory for source-item pairings implies a good representation of the source-item contingency (cf. Spaniol & Bayen, 2002) and thus reduces schema reliance. Of course, if the source-item contingency is not zero, then g would still be expected to deviate from .5 to match this contingency, even if memory is high. This is demonstrated in the following experiment. Importantly, in this experiment all participants had full -attention at encoding, and (to anticipate) we demonstrate biased source guessing, although the memory level is comparable to that in the encoding condition of Hicks and Cockman's Experiment 1.

Experiment 2

The purpose of Experiment 2 was to test another core assumption of the probability-matching account, namely that guessing probabilities reflect the source - item contingency in the study list, when participants are able to perceive the contingency. Hicks and Cockman (2003, Experiment 1) demonstrated that when there was a zero contingency in the study list (i.e., the two professional groups present equal numbers of doctor-expected and lawyer-expected statements), there was no effect of schemas on source identification. In the full-attention condition of Experiment 1, we replicated this finding and demonstrated that it is caused by participants' matching of source-guessing probabilities to the true zero-contingency in the study list. The purpose of Experiment 2 was to demonstrate that when participants notice true positive or negative source - item contingencies in the study list, they will match their guessing probabilities to these contingencies as well. We thus manipulated the true source - item contingency in the study list to test the probability-matching account. All participants devoted full attention to the study list and professional information about the sources were given before study, so that the true source – statement contingencies should be noticeable to participants.

In one condition of this experiment, statements appeared more often with the source from which they were expected than with the source from which they were somewhat unexpected (e.g., the doctor presented mostly expected-doctor statements), while in another condition, statements appeared more often with the source from which they were somewhat unexpected than with the source from which they were expected (e.g., the doctor presented mostly expected-lawyer statements). According to the probability-matching account of source guessing, we expected participants' guessing bias to reflect these contingencies. Specifically, in the schema-consistent contingency condition, we expected participants to show a guessing pattern in accord with schema-based expectations. In the schema-inconsistent contingency condition, by contrast, we expected participants to show a guessing pattern that contradicts schema-based expectations. On the performance level (as measured by CSIM), these different guessing patterns should result in a performance advantage for schema-consistent pairings in the schema-consistent contingency condition and a performance disadvantage for schema-consistent pairings in the schema-inconsistent contingency condition. The performance advantage for schema-consistent pairings has been demonstrated before in a similar study by Mather et al. (1999) with schema-relevant information provided at encoding and true schema-consistent contingency in the study list. Thus our schema-consistent contingency condition replicates this study but also extends it by demonstrating that the performance advantage can be traced back to a guessing bias and not to alternative explanations such as better source memory for schema-consistent pairings. In addition, we included a zero-contingency condition as the comparison condition for the consistent- and inconsistent-contingency conditions. To our knowledge, this study would be the first to demonstrate three different directions of bias in source monitoring (schema-consistent bias, no bias, schema-inconsistent bias) in one experiment.

To test the assumption of the probability-matching account that people match guessing probabilities to perceived contingencies, we additionally assessed participants' contingency perception via a contingency-judgment task administered after the source-monitoring test. In the contingency-judgment task, we asked participants to estimate the percentage of statements of each expectancy type that had been presented by the doctor versus the lawyer.

Method

Participants

Seventy-two native English speakers between 18 and 30 years of age participated in this experiment. Some of them were students who received partial course credit. The other participants were university employees recruited via a mass e-mailing and received payment. One participant classified as “new” all four expected-doctor test items that had been presented by the doctor in his experimental condition. We replaced this participant, because with a value of zero in the denominator, CSIM is not defined (see Equation 1).

Design

The design was a 3 × 2 × 3 mixed factorial with expectancy of statements (expected-doctor, expected-lawyer, equally expected) and source of statements (doctor vs. lawyer) as within-subjects factors and contingency between statement type and source (zero contingency, schema-consistent contingency, schema-inconsistent contingency) as a between-subjects factor. Depending on the contingency condition, the doctor and lawyer sources presented different percentages of each statement type. In the zero-contingency condition, doctor and lawyer each presented half of the expected-doctor statements and half of the expected-lawyer statements (as in Experiment 1). In the schema-consistent contingency condition, the doctor source presented 75% of the expected-doctor statements and 25% of the expected-lawyer statements. Conversely, the lawyer presented 75% of the expected-lawyer statements, and 25% of the expected-doctor statements. Thus, in this condition, most of the source - statement pairings were consistent with schema-based expectations. In the schema-inconsistent contingency condition, the proportions were reversed. That is, the doctor presented 25% of the expected-doctor statements and 75% of the expected-lawyer statements, while the lawyer presented 75% of the expected-doctor statements and only 25% of the expected-lawyer statements. Thus, in this condition, most of the source - statement pairings were inconsistent with schema-based expectations. In all three contingency conditions, each source presented one half of the equally expected statements.

Materials and Procedure

The sources were the same as in Experiment 1. The procedures were similar to those in Experiment 1 with the important difference that participants were randomly assigned to one of the three contingency conditions described above. Another difference was that the study list included 96 items and was thus longer than the one used in Experiment 1. The statements we used in the study and test lists of Experiment 2 were those used in Bayen et al. (2000) and published in Appendix C of that article. The list in this Appendix includes two versions of each statement of a total of 96 statements, a target and a distractor version. The two versions of each statement are identical with the exception of one word or phrase that alters the meaning of the statement (e.g., “Do you have any food allergies?” versus “Do you have any drug allergies?”). We presented the target version of each statement listed in Bayen et al. (2000) during the study phase. One third of the 96 statements in the study list were expected for the doctor, one third were expected for the lawyer, and one third were equally expected for both professions. The assignment of statements to sources in the study phase was randomized by participants within each condition. At test, for each source a random half of the statements of each statement type were tested in their study version, while the other half of the statements were tested in the distractor version. We used the highly similar targets and distractors to avoid ceiling effects in item recognition.

Immediately after the source monitoring test, participants' contingency perception was assessed via a brief questionnaire that appeared on the computer screen. They were asked to judge what percentage of the expected-doctor, expected-lawyer, and equally expected statements (in this order) had been presented by each source. (e.g., TOM=DOCTOR spoke __% of the doctor-expected sentences). The participants were asked to round to the nearest whole number. Responses were self-paced. Once participants had entered their estimate for one source on one statement type, the computer program automatically filled in the estimate for the other source on this statement type so that both estimates added up to 100%. The participant could then decide to log this response by pressing a key, or to change the response before logging it. Whether the first estimate was given for TOM=DOCTOR or JIM=LAWYER was counterbalanced for expected-doctor and expected-lawyer statements, and randomized for equally expected items. Error feedback was not provided, but the program was designed such that only values between 0 and 100 could be entered.

Results and Discussion

Again, we performed analyses using CSIM as well as MPT model based analyses.

Analyses based on an empirical measures of source identification

Figure 3 shows CSIM as a function of statement expectancy and source for the three contingency conditions. We performed a repeated measures ANOVA on CSIM with statement expectancy (expected-doctor, expected-lawyer, equally expected) and source (doctor vs. lawyer) as within-subject factors, and contingency condition (schema-consistent vs. schema-inconsistent vs. zero contingency) as a between-subjects factor. Expectancy yielded a significant main effect, F(2,138) = 10.44, MS_e = .04. As in Experiment 1 and in Bayen et al. (2000), source identification was better for equally expected statements than for expected-doctor statements, F(1, 69) = 11.84, MS_e = .05, and for expected-lawyer statements, F(1,69) = 20.12, MS_e = .04. More importantly, the interaction of expectancy, source, and contingency was significant, F(4,138) = 20.14, MS_e = .08. To further investigate this three-way interaction, we performed separate repeated measures ANOVAs with expectancy and source as within-subject factors for each of the three contingency conditions. There was a significant interaction of expectancy and source in the schema-consistent condition, F(2,46) = 31.95, MS_e = .06, and in the schema-inconsistent condition, F(2,46) = 10.88, MS_e = .12, but not in the zero-contingency condition, F(2,46) = 1.35, MS_e = .05. We performed simple main-effects analyses on the two-way interaction in the schema-consistent and schema-inconsistent conditions. In the schema-consistent condition, CSIM was significantly higher for expected-doctor statements that were presented by the doctor as opposed to the lawyer, F(1, 23) = 19.59, MS_e = .07. Similarly, CSIM was significantly higher for expected-lawyer statements that were presented by the lawyer as opposed to the doctor, F(1,23) = 35.37, MS_e = .07. CSIM did not significantly differ as a function of source for equally expected statements. In the schema-inconsistent condition, we found the opposite pattern. CSIM was significantly higher for expected-doctor statements that were presented by the lawyer as opposed to the doctor, F(1,23) = 10.19, MS_e = .14. For expected-lawyer statements, CSIM was significantly higher for those originating from the doctor as opposed to the lawyer, F(1,23) = 12.89, MS_e = .09. Again, CSIM did not differ between sources for equally expected statements. Thus, source identification was better for expected than somewhat unexpected statements in the schema-consistent condition, while it was better for somewhat unexpected than expected statements in the schema-inconsistent condition. That is, participants' biases were in accord with the actual contingencies during study.

Figure 3.

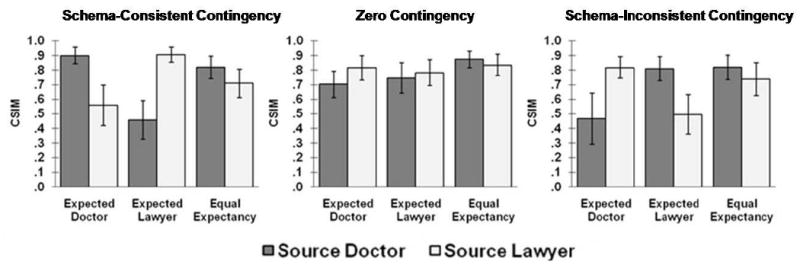
Experiment 2. Conditional source identification measure (CSIM) for statements as a function of expectancy and source in the schema-consistent contingency condition, zero-contingency condition, and schema-inconsistent contingency condition. Error bars indicate 95% confidence intervals.

MPT model-based analyses

We performed MPT model-based analyses to determine the degree of guessing that participants showed for the different statement types in the different contingency conditions. These analyses were based on the response frequencies listed in Appendix C. Again, we used Submodel 4 of the 2 HT MPT model of source monitoring which fit the data from all three experimental groups, all G²(6) ≤ 7.49. Table 2 presents all parameter estimates with 95% confidence intervals. Recall that a good fit of Model 4 indicates that source memory does not differ for items that are expected for their source and for items that are unexpected for their source (e.g., source memory is not better for the doctor as opposed to the lawyer on expected-doctor statements).

Table 2. Parameter Estimates, Confidence Intervals, and G² Goodness-of-Fit Values for the Four-Parameter Two-high Threshold MPT Model of Source Monitoring Under Different Conditions of Expectancy and Source - Item Contingency in Experiment 2.

Item Expectancy	D	d	g	b	G2(6)
	Schema-Consistent Contingency Condition				5.48
Expected Doctor	.33 (.26-.40)	.98 (.67-1.00)	.79 (.73-.83)	.52 (.47-.57)
Expected Lawyer	.35 (.28-.42)	.72 (.46-.99)	.18 (.13-.23)	.45 (.40-.50)
Equal Expectancy	.59 (.53-.65)	.71 (.58-.85)	.57 (.49-.65)	.41 (.34-.48)
	Zero Contingency Condition				7.48
Expected Doctor	.38 (.32-.45)	.99 (.77-1.00)	.45 (.39-.52)	.54 (.49-.59)
Expected Lawyer	.41 (.34-.47)	.97 (.76-1.00)	.45 (.39-.52)	.53 (.47-.58)
Equal Expectancy	.64 (.58-.69)	.93 (.81-1.00)	.56 (.48-.64)	.58 (.50-.64)
	Schema-Inconsistent Contingency Condition				4.51
Expected Doctor	.35 (.28-.41)	.66 (.37-.95)	.24 (.19-.28)	.61 (.56-.66)
Expected Lawyer	.33 (.26-.39)	.59 (.30-.87)	.78 (.73-.83)	.53 (.48-.58)
Equal Expectancy	.59 (.48-.64)	.81 (.68-.95)	.56 (.49-.64)	.53 (.46-.60)

Notes. These are probability estimates that can range from 0 to 1. D = probability of item recognition; d = probability of remembering the source memory; g = probability of guessing that an item was presented by the doctor (estimates higher than the chance level of .5 indicate guessing bias towards doctor; estimates lower than .5 indicate guessing bias towards lawyer); b = probability of guessing that an item is old (chance level is .5). 95% confidence intervals are in parentheses. G²(6) values lower than 12.59 indicate a good fit of the model to the data.

Figure 4 shows the guessing probabilities g as a function of statement-expectancy for the three contingency conditions: schema-consistent contingency, zero contingency, and schema-inconsistent contingency, respectively. In the schema-consistent contingency condition, model parameter g (for guessing “doctor”) was significantly above .5 for expected-doctor statements, g = .79, G²(1) = 78.01, significantly below .5 for expected-lawyer statements, g = .18, G²(1) = 85.13, and did not differ significantly from .5 for equally expected statements, g = .57, G²(1) = 3.19. That is, when participants in the schema-consistent contingency condition did not remember the source, they were more likely to guess towards the source for which the statements were expected. In the zero-contingency condition, parameter g did not significantly differ from .5 for any statement type, all G²(1) < 1.95. That is, in this condition, participants were not more likely to attribute a specific statement type to a particular source when they did not remember the source. For the schema-inconsistent contingency condition, model parameter g was significantly below .5 for expected-doctor statements, g = .24, G²(1) = 78.28, significantly above .5 for expected-lawyer statements, g = .78, G²(1) = 86.57, and not significantly different from .5 for equally expected statements, g = .56, G²(1) = 2.51. That is, participants in this condition were more likely to guess towards the source for which the statements were somewhat unexpected.

Figure 4.

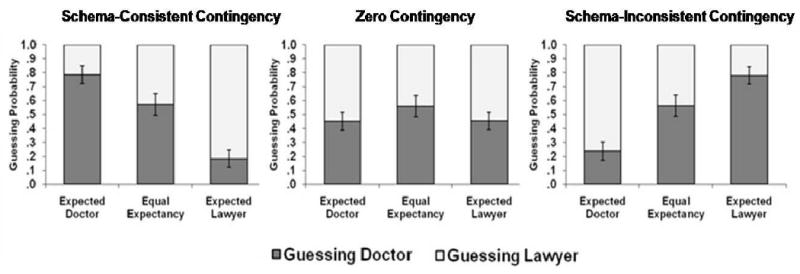
Experiment 2. Guessing probability as a function of statement expectancy in the schema-consistent contingency condition, zero-contingency condition, and schema-inconsistent contingency condition. Error bars indicate 95% confidence intervals.

Contingency Judgments

Next, we analyzed the source - statement contingency judgments. Participants had estimated the percentage of each of the three statement types that each source presented. From these estimates, we calculated the estimated percentage of schema-consistent and schema-inconsistent source - statement pairings. For each participant, the estimated percentage of schema-consistent pairings is the mean of the estimated percentage of the expected-doctor statements presented by the doctor and the estimated percentage of the expected-lawyer statements presented by the lawyer. Correspondingly, for each participant, the estimated percentage of schema-inconsistent pairings is the mean of the estimated percentage of the expected-lawyer statements presented by the doctor and the estimated percentage of the expected-doctor statements presented by the lawyer. Since these two estimated percentages always add up to 100%, we will only report results based on the estimated percentage of schema-consistent pairings below.

We conducted a univariate ANOVA on the estimated percentage of schema-consistent pairings with contingency condition (schema-consistent contingency, zero contingency, schema-inconsistent contingency) as the independent variable. The effect of contingency condition was significant, F(2,69) = 14.0, MS_e = 195.19. Post-hoc tests using Tukey HSD revealed that participants in the schema-consistent contingency condition indicated a higher percentage of schema-consistent pairings (M = 62.1%, SD = 13.3) than those in the zero-contingency condition (M = 51.9%, SD = 11.6). Participants in the schema-inconsistent contingency condition indicated a lower percentage of schema-consistent pairings (M = 40.8%, SD = 16.5) than those in the zero-contingency condition. One-sample t tests showed that in the schema-consistent contingency condition, the estimated percentage of schema-consistent pairings was significantly higher than 50%, t(23) = 4.46, d = 1.86, whereas it was significantly lower than 50% in the schema-inconsistent condition, t(23) = -2.73, d = 1.14. In the zero-contingency condition, this percentage did not differ from 50%. Thus, participants were able to perceive the true direction of the contingency in their experimental condition. The percentage estimates, however, were not as extreme as the actual percentages that were 75% of schema-consistent pairings in the schema-consistent contingency condition and 25% of schema-consistent pairings in the schema-inconsistent condition.

Next, we analyzed contingency estimates for statements that were equally expected for both sources. In these analyses, we used the estimated percentage of equally expected statements presented by the doctor as the dependent variable. Since the percentage estimates for the two sources add up to 100%, using lawyer estimates would have yielded equivalent results. For equally expected statements, a univariate ANOVA yielded no significant effect of contingency condition on percentage estimates. This result was expected, because for equally expected statements, the true contingency (50% presented by each source) did not differ between contingency conditions. Simple t tests revealed that these percentage estimates did not differ from the actual value of 50% in any of the contingency conditions.

The results of this experiment support the probability-matching account of guessing bias in source monitoring. By varying the contingencies of sources and statement types, we demonstrated that participants matched their guessing probabilities to the given contingency in the experiment. Most remarkably, our analyses demonstrated that a strong schema-inconsistent contingency (ratio of 1:3 for expected to somewhat unexpected pairings) led to guessing bias that contradicted schema-based expectations. The contingency condition differences in source-guessing bias were paralleled by differences in contingency judgments as expected by the probability-matching account.

General Discussion

Effects of schematic knowledge on source monitoring have been shown in most published experiments (e.g., Bayen et al., 2000; Marsh et al., 2006; Mather et al., 1999), but not in all (Hicks & Cockman, 2003). While there is agreement that schemas affect source monitoring if the schema-relevant information is not provided until the time of retrieval (e.g., Bayen et al., 2000; Hicks & Cockman, 2003), there is disagreement as to whether the effect can be found if the schema-relevant information is provided at the time of encoding (Bayen et al., 2000, Experiment 1; Hicks & Cockman, 2003; Mather et al., 1999).

We propose that the probability-matching account of source guessing (Spaniol & Bayen, 2002) can resolve apparent inconsistencies in effects of schema-based knowledge on source monitoring. According to this account, participants will base their source-guessing probabilities on schematic expectations only if they do not have a representation of the actual source - item contingency in a study list. Whenever they do have a representation of the actual contingency, they will match their source guessing probabilities to this contingency rather than to schematic expectations. That is, a schema bias in source monitoring will only occur if (1) participants do not have a representation of the source-item contingency or (2) if the source-item contingency is consistent with schematic expectations.

In Experiment 1, we tested the first condition under which a schema-bias occurs. When participants had schematic information about the sources during encoding and their attention was undivided, their source guessing was not biased by schematic knowledge (replicating Hicks & Cockman, 2003). This finding indicates that participants were able to detect the actual source-item contingency in this condition. When attention was divided at encoding, however, a schema bias did occur. Presumably, dividing attention hindered participants' processing of the source-item contingency, and thus they defaulted to their schema-based expectations.

Experiment 2 further demonstrated that participants will match the actual source-item contingency in the study list when possible even if it opposed schematic expectations. Again, schematic information about sources was provided at the time of encoding and participants' attention was undivided, supporting contingency detection (as demonstrated in contingency estimates). Participants' source guessing reflected the actual source-item contingency in the study list which was manipulated to be either schema-consistent, zero, or schema-inconsistent. Source-guessing probability estimates based on aggregated response frequencies closely matched the actual source-item contingencies in the respective conditions (see Figure 4). For example, in the schema-inconsistent contingency condition of this experiment, the average probability of guessing doctor, g, was .24 for expected-doctor statements. This probability very closely matched the proportions in the study list, where the doctor presented 25% of the expected-doctor statements. It is evident from the conditions with a zero contingency or a schema-inconsistent contingency that participants' contingency representation superseded schematic expectations. A schema bias in source identification still occurred when the actual contingency was consistent with schematic expectations.

Alternative Accounts of Schema-Bias in Source Monitoring

Memory-based explanations of schema-effects on source monitoring would predict better memory for schema-inconsistent as opposed to schema-consistent source - item pairings (e.g., Brewer & Treyens, 1981; Graesser & Nakamura, 1982). While this account is in line with the source-identification pattern of the schema-inconsistent contingency condition of Experiment 2, it cannot explain that there was no difference in source-identification performance or better identification for schema-consistent pairs in our other conditions as well as in previous studies (e.g., Bayen et al., 2000; Hicks & Cockman, 2003). In addition, the model-based analyses revealed that there was no difference in source-memory for schema-consistent versus schema-inconsistent source – item pairings (i.e., d₁ = d₂ in all analyses). Rather, any biases in source monitoring (whether schema-consistent or schema-inconsistent) stemmed from source-guessing biases.

Another alternative account of our results would be the well-established finding that stereotype application is greater when mental resources are low such as under divided attention (e.g., Devine, 1989). This account would predict the reliance on schematic knowledge in the divided attention condition of Experiment 1. However, this account makes no predictions regarding the biasing effects of the contingency manipulations in Experiment 2 where attention was undivided. Overall, only the probability-matching account can account for all of the present findings.

Reconciling Previous Findings

Considering participants' ability to detect and use source-item contingencies for source guessing potentially explains inconsistent findings reported in the literature. In particular, we believe that contingency detection is a core concept in explaining why schemas consistently influence source monitoring if schema-relevant information is not provided until the time of retrieval. Experiment 2 shows that participants were very able to detect the source – item contingency when schematic information was provided at encoding and attention was undivided. There is ample evidence in the schema literature that the availability of schemas during encoding improves the accuracy of memory reports (Alba & Hasher, 1983; Bransford & Johnson, 1972). With the aid of schematic information, participants in an encoding condition can easily form a representation of the source – item contingency in the study list. On the other hand, if schema-relevant information was not provided until retrieval it is likely more difficult for participants to encode the source – item associations and to form a contingency representation. Lacking a contingency representation, these participants will default to schema-based guessing as suggested by the probability-matching account. This is supported by the finding that memory for source – item associations is better in an encoding than in a retrieval condition (Hicks & Cockman, 2003). In addition, Dodson et al. (2008) showed that participants in a retrieval condition were susceptible to contingency information provided before the test. When providing information about the profession of the sources before retrieval, the investigators also told the participants that the doctor had actually presented more expected-lawyer statements and vice versa. Participants then showed a schema-inconsistent bias. This receptiveness to contingency information provided by the experimenter supports the assumption that participants in the retrieval condition do not form a contingency representation on their own.

The Process of Probability-Matching

In the present experiments, we demonstrated that people are inclined to match experimental source - item contingencies whenever possible. Probability matching is a frequently observed phenomenon in human and animal behavior and can be adaptive for survival (e.g., Niv et al., 2002). It seems highly adaptive that source guessing can be both schema- and contingency-based and that experimental contingencies have priority. This hierarchy allows people to use specific information (the episodic contingencies) when available, but leaves them with at least some information (schematic knowledge) when specific information is not available.

These considerations imply that people's reliance on experimental contingencies should be specific to the sources encountered in an episode and should not extend to other sources (e.g., other doctors and lawyers). Such behavior would be in line with the well-established process of subtyping in which people often engage upon encountering an individual that diverges from what is expected for its social category (e.g., Kunda & Oleson, 1995; Richards & Hewstone, 2001). That is, people can categorize a deviant individual as a special instance and use this specific knowledge for just this member without changing their beliefs about the whole group. Similarly, people can learn that the sources in an experiment are special cases without any changes to their general world knowledge. Thus, upon encountering other members of a category, people can still resort to their general knowledge. Future research should address how specific people's use of experimental contingencies is. In addition, future research might also address the question if people are possibly more likely to adopt schema-opposing contingencies in an experimental setting as opposed to a more realistic setting. This willingness might vary with the strength of the schema or stereotype.

Another important question is if the process of matching experimental and schema-based probabilities is rather conscious-controlled or unconscious-automatic. We are not aware of any studies addressing this question directly. Bröder, Noethen, Schütz, and Bay (2007) argue that participants only use explicit but not implicit knowledge in source guessing. In their studies, participants were assumed to have implicitly learned a hidden item-source contingency but their source-guessing behavior did not reflect this contingency. However, the authors did not show that participants had indeed formed implicit knowledge of the hidden contingency (see Hendrickx, DeHouwer, Baeyens, Eelen, & VanAvermaet, 1997, for problems with the hidden covariation paradigm). Furthermore, even if knowledge underlying source guessing is explicit this does not necessarily imply that the use of this knowledge to guide source guessing is conscious and controlled (cf. Meiser et al., 2007). At this stage, we therefore believe that both the reliance on schematic knowledge as well as on experimental contingencies can be conscious-controlled or unconscious-automatic.

In Experiment 2, we assessed explicit knowledge of experimental contingencies. Contingency estimates were slightly biased in the expected direction but were much less biased than the observed source-guessing biases. There might be problems with our contingency measure such as participants' avoidance of extreme ratings or misunderstanding of probabilities (e.g., Gigerenzer & Hoffrage, 1995). Alternatively, this finding could indicate that participants are not fully aware of their contingency-based biases. It is well known from research on implicit learning that people can sometimes perfectly learn a rule without being able to verbalize it (e.g., Reber 1989) and a similar process might underlie the matching of experimental contingencies in source guessing. Future studies should try to examine the use of experimental contingencies (and schematic knowledge) in source guessing more directly, for example by having participants verbalize their source-attribution decision at test as well as looking at the time course of probability matching at test (Spaniol & Bayen, 2002).

Findings on the effects of divided attention on source guessing can speak to this question as well. Divided attention at test should disrupt the matching of experimental contingencies if it is conscious-controlled but not if it is unconscious-automatic. In the current study, we focused on encoding conditions and used divided attention to disrupt contingency detection. However, two published studies examine the effects of divided attention at retrieval on source guessing (Klauer & Ehrenberg, 2005; Sherman & Bessenoff, 1999). Both studies provided schematic information about the sources at encoding. When attention was undivided at encoding and test, participants showed no schema bias; their source attributions were in line with the zero contingency of sources and item types. If attention was divided at test, participants still guessed according to the actual zero contingency in the study by Klauer and Ehrenberg but showed a schema bias in the study by Sherman and Bessenoff. The latter finding suggests that there may be some retrieval conditions under which reliance on contingency knowledge is disrupted possibly because it requires mental resources. Differences in the divided attention manipulation (random number generation vs. maintaining a number) might be responsible for the inconsistent findings.

Recently, Dodson et al. (2008) demonstrated that false but expectancy-consistent source attributions are often accompanied by vivid memories reflected in participants' “remember” judgments for these attributions. This finding led Dodson et al. to formulate a retrieval expectancy account according to which stereotypes and other expectations (e.g., those based on experimental contingencies) at the time of retrieval interact with memory traces for information and thereby lead to the false (or illusory) recollection of expectation-consistent information. They challenge the idea that participants strategically guess a source based on their expectations. This idea is in line with a possible unconscious use of contingencies in source guessing. However, the underlying mechanism suggested by Dodson et al. claims that such illusory recollections only occur if there is a preexisting memory trace. In the model that fitted all data from the experiments presented here, source-guessing bias is the same for old items (whether recognized or not) and distracter items (i.e., a = g). That is, the bias in source attributions does not seem to differ for items with a preexisting memory trace (old recognized items) and those without a memory trace (new items and old unrecognized items). Therefore it seems unlikely that the process leading to false schema-based source attributions differs for items that have a memory trace and those that do not. Rather as suggested by Bayen et al. (2000) schema- or contingency-based expectations at test influence source guessing processes for any type of item (old or new) that is believed to be old but for which no source is remembered; however, this source guessing is not necessarily conscious and strategic hence high confidence misattributions are possible.

In sum, we believe that the dominance of experimental contingencies over schematic expectations helps to flexibly adapt human behavior to maximize correct source attributions in a specific situation. It is currently unclear if the use of such contingency knowledge is rather unconscious-automatic or conscious-controlled. Future research should attempt to address this question more directly.

A Framework for Future Research

Overall, our research suggests the importance of considering participants' ability to detect and use the source-item contingency in the study list in addition to other expectations participants bring into the experiment from outside sources (i.e., general world knowledge) to understand biases in source monitoring. According to the probability-matching account, experimental contingencies supersede schematic expectations. This assumption limits the conditions under which a schema bias occurs to those where the source-item contingency cannot be detected and those where the source-item contingency can be detected and is consistent with schematic expectations.

By embedding schema reliance in source monitoring in the well-established phenomenon of probability matching we have advanced our understanding of schema reliance in source monitoring. Johnson et al. (1993) proposed that schematic knowledge may play a role in source monitoring. Then Bayen et al. (2000) provided empirical support for this idea and localized the source of a schema bias in inferential source-guessing processes rather than memory-based mechanisms. Finally, Hicks and Cockman (2003) demonstrated that this reliance on schematic knowledge varied depending on encoding conditions. Now, the probability-matching account specifies conditions under which people do and do not rely on schematic knowledge.

The probability-matching account can account for our own findings as well as those reported by other research groups and allows us to reconcile apparent inconsistencies in results. Next steps will be to establish a better understanding of encoding and retrieval conditions under which experimental contingencies can be matched as well as an examination if such probability-matching in source guessing is rather a conscious-controlled or an unconscious-automatic process. We propose the probability-matching account as a guiding framework for the further exploration of effects of schematic knowledge on source monitoring.

Appendix A: The Two-High Threshold MPT Model of Source Monitoring

For a detailed discussion of MBT models, see Batchelder and Riefer (1999). Figure A1 illustrates the two-high threshold MPT model of source monitoring presented by Bayen, Murnane, and Erdfelder (1996). For a more detailed description of this model and its experimental validation, please refer to this article. The first tree in this figure represents test trials with items that had been presented by the doctor at study. With probability D₁, participants recognize such items as old items. With conditional probability d₁, participants remember that the item originated from the doctor; with probability 1-d₁, they do not, in which case they must guess the source of the item. With probability g participants guess “doctor”, and with the complementary probability 1-g, they guess “lawyer”. When items are not recognized as old (with probability 1-D₁), participants guess, with probability b, that they are old, and with probability 1-b that they are new. If they guess that the item is old, then they further guess, with probability g, that the item was presented by the doctor, with probability 1-g, that it was presented by the lawyer. 1-b is the probability of guessing that an unrecognized item is new.

The second processing tree in Figure A1 illustrates the processing of items that originated from the lawyer source. Index 2 indicates item-recognition and source-memory parameters for items that had been presented by the lawyer at study, whereas Index 1 indicates item-recognition and source-memory parameters for items that had been presented by the doctor at study. The third tree shows the processing involved in responding to new items. With probability D₃, participants know that such items are new; with probability 1-D₃ they do not. In the latter case, they guess that the items are old or new and from which source they originated.

The model as shown in Figure A1 is not mathematically identifiable because it has more free parameters than there are degrees of freedom in the data. Identifiable submodels are constructed by imposing equality constraints on parameters. All possible submodels are shown in Bayen et al. (1996, p. 202). Submodel 4 with four free parameters (D₁ = D₂ = D₃, d₁ = d₂, b, g) fit all data sets reported in this article. With the help of the HMMTree computer program (Stahl & Klauer, 2008), we obtained parameter estimates using a combination of an EM algorithm and the conjugate-gradient method for maximum-likelihood parameter estimation.

Figure A1.

Two-high-threshold MPT Model of Source Monitoring. D₁ = probability of recognizing an item that had been presented by the doctor; D₂ = probability of recognizing an item that had been presented by the lawyer; D₃ = probability of knowing that a distractor item is new; d₁ = probability of remembering the source of an item that had been presented by the doctor; d₂ = probability of remembering the source of an item that had been presented by the lawyer; b = probability of guessing that an unrecognized item is old; g = probability of guessing that an item had been presented by the doctor. Adapted from “Source discrimination, item detection, and multinomial models of source monitoring” by U. J. Bayen, K. Murnane, and E. Erdfelder, 1996, Journal of Experimental Psychology: Learning, Memory, and Cognition, 22, p. 202.

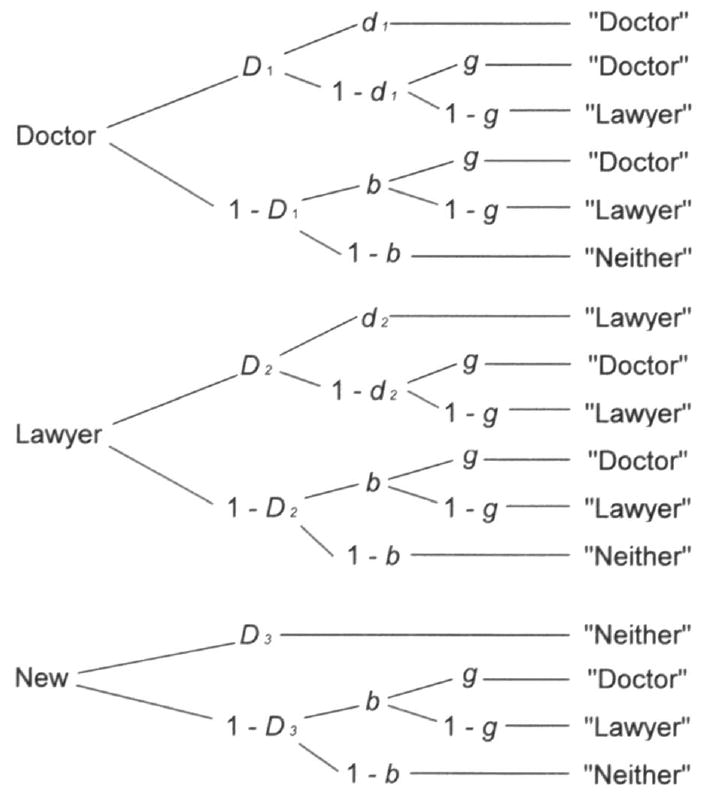
Appendix B: Raw Data from Experiment 1

Frequencies of “D” (“Doctor”), “L” (“Lawyer”), and “N” (“Neither”) Responses to Items that had been Presented by the Doctor, Items that had been Presented by the Lawyer, and New Items under Different Conditions of Expectancy and Attention in Experiment 1.

	Item Expectancy
	Expected Doctor			Expected Lawyer			Equal Expectancy
Source	“D”	“L”	“N”	“D”	“L”	“N”	“D”	“L”	“N”
	Full Attention
Doctor	167	60	61	148	60	80	198	45	45
Lawyer	52	179	57	49	158	81	41	203	44
New	16	10	166	8	21	163	1	2	189
	Divided Attention
Doctor	141	55	92	61	127	100	110	68	110
Lawyer	120	72	96	50	124	114	85	94	109
New	70	14	108	24	67	101	33	18	141

Appendix C: Raw Data from Experiment 2

Frequencies of “D” (“Doctor”), “L” (“Lawyer”), and “N” (“Neither”) Responses to Items that had been Presented by the Doctor, Items that had been Presented by the Lawyer, and New Items under Different Conditions of Expectancy and Source - item Contingency in Experiment 2.

	Item Expectancy
	Expected Doctor			Expected Lawyer			Equal Expectancy
Source	“D”	“L”	“N”	“D”	“L”	“N”	“D”	“L”	“N”
	Schema-Consistent Contingency
Doctor	169	20	99	28	31	37	116	25	51
Lawyer	30	40	26	18	170	100	40	110	42
New	104	30	250	24	89	271	35	30	319
	Zero Contingency
Doctor	101	41	50	104	30	58	145	21	26
Lawyer	23	111	58	32	111	49	27	132	33
New	64	63	257	51	69	264	44	36	304
	Schema-Inconsistent Contingency
Doctor	34	39	23	159	35	94	132	28	32
Lawyer	34	178	76	36	32	28	34	116	42
New	37	115	232	112	25	247	46	36	302