Modularity in the mammalian dentition: Mice and monkeys share a common dental genetic architecture

Abstract

The concept of modularity provides a useful tool for exploring the relationship between genotype and phenotype. Here, we use quantitative genetics to identify modularity within the mammalian dentition, connecting the genetics of organogenesis to the genetics of population-level variation for a phenotype well represented in the fossil record.

We estimated the correlations between dental traits due to the shared additive effects of genes (pleiotropy) and compared the pleiotropic relationships among homologous traits in two evolutionary distant taxa – mice and baboons. We find that in both mice and baboons, who shared a common ancestor >60 Ma, incisor size variation is genetically independent of molar size variation. Furthermore, baboon premolars show independent genetic variation from incisors, suggesting that a modular architecture separates incisors from these posterior teeth as well. Such genetic independence between modules provides an explanation for the extensive diversity of incisor size variation seen throughout mammalian evolution--variation uncorrelated with equivalent levels of postcanine tooth size variation. The modularity identified here is supported by the odontogenic homeobox code proposed for the patterning of the rodent dentition. The baboon postcanine pattern of incomplete pleiotropy is also consistent with predictions from the morphogenetic field model.

Introduction

Developmental genetics can provide insights for how the information stored within the genome may be translated into the phenotype during early ontogeny. Evolutionary biologists have incorporated some of these insights into paleontology, with tremendous success at higher taxonomic levels, such as the origins of body plans (e.g., Raff. ‘96) and the fin-limb transition (e.g., Davis et al, 2007). However, given that much of evolution is characterized by smaller scale variation, it is logical to consider whether those genes involved in making an organ are the same that influence minor variation in the ultimate phenotype (Hlusko, 2004). Selection typically operates at this population level. Therefore, making a connection between developmental genetic mechanisms and normal population-level variation is essential for bringing an “evo-devo” approach to most of vertebrate evolution.

Quantitative genetic analyses can be used to make this phenotype-genotype connection, as they enable the investigation of the genetics of normal adult phenotypic variation, working back towards the genome. Our goal is to link these two approaches—quantitative and developmental genetics—together to form a more complete understanding of the relationship between genotype and phenotype, and ultimately, to incorporate this knowledge into our understanding of phenotypic evolution as evidenced in the fossil record (Hlusko, 2004).

Since antiquity biologists have recognized the importance of the size and shape of an animal’s teeth (e.g., Aristotle’s On the Generation of Animals, Book V, Chapter 8). Given the dentition’s fundamental role in procuring and processing food and in social interactions with conspecifics, the dentition has evolved to be one of the most informative parts of the skeleton for inferring evolutionary relationships and adaptations. Because teeth are largely inorganic, they also survive well in the fossil record—for many extinct vertebrates, all we know of them is what their teeth looked like. Considerable advances have also been made in identification and functional analyses of the genes necessary to make and pattern the dentition (Jernvall and Thesleff, 2000; Tucker and Sharpe, 2004). Consequently, the dentition is an important organ system for developmental biologists, neontologists, and paleontologists alike, making it an ideal system for an integrated developmental, genetic, and paleontological approach (Jernvall and Jung, 2000; Hlusko, 2004). Here, we report on the first comparative quantitative genetic analysis of dental variation in two mammalian taxa: mouse and baboon.

Background

In 1939 Butler proposed the morphogenetic field theory which became the foundation for most morphologists’ understanding of dental variation. In this model, primordial teeth are pluripotent, and tooth type is determined by extrinsic factors (“morphogens”). An alternative was later proposed, the clone model (Osborn, ‘78) in which tooth type is intrinsically determined. Neither of these hypotheses relied on actual knowledge of genetics, but rather posed speculative hypotheses that were difficult to test, but tested nonetheless via adult phenotypic variation yielding inconclusive results (e.g., Dahlberg, ‘45; Van Valen, ‘61; Henderson and Greene, ‘75; Lombardi, ‘75).

Advances in developmental genetics over the last 20 years have dramatically improved our understanding of tooth organogenesis and patterning (Tucker and Sharpe, 2004). This research has primarily focused on the mouse model, as has much of mammalian developmental genetics. We now know that the dentition is patterned quite early during development, by mouse embryonic day 11. At this stage, the oral cavity has started to form in a layer of epithelial cells oral to neural crest derived mesenchyme. Patterning information for the dental arcade appears to be regulated by this epithelial layer, called the dental lamina. Once the epithelium invaginates into the mesenchyme at mouse embryonic day 13, control of tooth type shifts to the surrounding mesenchymal cells. By mouse embryonic day 14 the primary signaling for continued tooth formation has returned to the epithelium, but now is centered within a mass of non-proliferating cells that form the enamel knot, a known signaling center (Jernvall et al, ‘94).

The genetic mechanism formally proposed for how genes determine tooth type during the dental lamina stage is the odontogenic homeobox code (Thomas and Sharpe, ‘98). This model suggests that bone morphogenetic proteins (BMP) and fibroblast growth factor (FGF) proteins in the epithelium induce and inhibit expression of 8 homeobox genes in various permutations, with specific combinations resulting in a particular tooth type. For example, Msx1, Msx2, Lhx6, and Lhx7 are expressed in presumptive incisor tissue and Dlx1, Dlx2, Barx1, Lhx6, and Lhx7 are expressed in presumptive molar tissue. The molecular evidence for this derives from experiments on mice, and as such, the odontogenic code is only proposed for determining the reduced dentition (incisors and molars) of rodents (but see McCollum and Sharpe, 2001). Since a recent study by Munne et al (2010) suggests that this odeontogenic homeobox code may be based on a misinterpretation of gene knock-out morphology, the genetic patterning mechanism for the dental arcade remains speculative.

Developmental genetics more generally shows that organisms have morphological and developmental modularity that results from modules at the genomic level, such as gene families, and from modules in embryogenesis (Raff, ‘96; Carroll et al, 2005). This modularity is critical since it enables an organism to be “evolvable” (Wagner and Altenberg, ‘96; Scholsser and Wagner, 2004; Draghi and Wagner, 2009). This modularity has been defined more specifically as “a genotype-phenotypic map in which there are a few pleiotropic effects among characters serving different functions, with pleiotropic effects falling mainly among characters that are part of a single functional complex” (Wagner and Altenberg, ‘96: 967). Considerable research has demonstrated modularity within the vertebrate limb (Wagner and Vargas, 2008, Reno et al, 2008; Shubin et al, ‘97; Shubin, 2002; Davis et al, 2007) and the skull (Richtsmeier et al, ‘84; Kohn et al, ‘93; Cheverud, ‘96; Ackermann and Cheverud, 2002; Marroig et al, 2004; Roseman, 2004; Marroig and Cheverud, 2005; Wolf et al, 2005; Ackermann, 2007; Hallgrimsson et al, 2007; Mitteroecker and Bookstein, 2008; Sherwood et al, 2008), for example.

Although the dentition is in a sense its own module, given the hierarchical nature of its development (Bateson, 1894; Stock, 2001), in this paper we focus on modularity within the dentition. This is the level of modularity often thought to be represented by characters in paleontological analyses, especially those at the sub-family level or below (Hlusko, 2004).

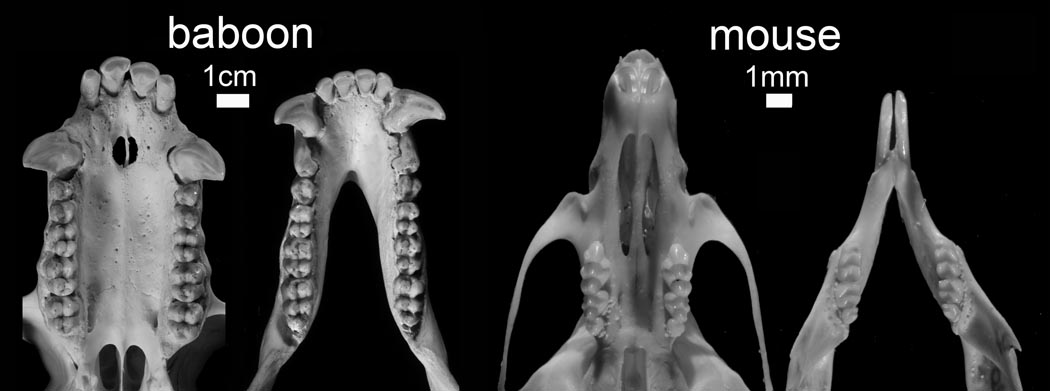
The modularity reported here is defined by the genetic architecture of mammalian population-level dental variation. We employ two animal models (Fig. 1). The first is the baboon because this primate has a relatively generalized mammalian dental pattern in that it is dyphyodont with incisors, canines, premolars and molars. The second is the mouse, as this taxon provided the source for most of the developmental genetics research to date despite its highly derived and reduced dentition (mice are monophyodont with only incisors and molars).

FIGURE 1.

Photograph of mouse and baboon maxillae and mandibles. Baboons have a more evolutionarily primitive dental formula (diphyodont: 2 incisors, 1 canine, 2 premolars, 3 molars) compared to the highly derived and reduced mouse dentition (monophyodont: 1 incisor, 3 molars).

Using quantitative genetic analyses in pedigreed populations, we detected and estimated additive genetic correlations between linear measurements of tooth size for teeth along the maxillary and mandibular dental arcades of these two taxa. These additive genetic correlations were compiled into matrices, each matrix characterizing the contribution of pleiotropy to the genetic architecture underlying observed patterns of covariation in tooth size measurements. Our results demonstrate significant similarity between mouse and baboon dental genetic architectures, a common pattern of modularity that may result from a conserved mammalian genetic patterning mechanism.

Materials and Methods

BABOON POPULATION

For 630 baboons we measured mesiodistal length and buccolingual widths of all incisors, premolars, and molars (maxillary and mandibular). These animals are part of a captive, pedigreed breeding colony of Papio hamadryas (as defined in Jolly, ‘93) housed at the Southwest National Primate Research Center (SNPRC) in San Antonio, Texas. The colony is maintained in pedigrees with all mating opportunities controlled. Age and sex (as well as other life history and health data) are known for all individuals.

Genetic management of the colony was started over 30 years ago and allows for data collection from non-inbred animals. All non-founder animals in this study resulted from matings that were random with respect to dental, skeletal, and developmental phenotype. The female-to-male sex ratio is approximately 2:1. The animals from which data were collected are distributed across eleven extended pedigrees that are 3–5 generations deep. The mean number of animals with data per pedigree was 44, and these individuals typically occupied the lower two or three generations of each pedigree. All pedigree data management and preparation was facilitated through use of the computer package PEDSYS (Dyke, ‘96).

The Institutional Animal Care and Use Committee, in accordance with the established guidelines (National Research Council, '96), approved all procedures related to the treatment of the baboons during the conduct of this study.

MOUSE POPULATION

We measured mesiodistal length and buccolingual width of all teeth (1 incisor and 3 molars for each dental quadrant, maxillary and mandibular) of 207 mice that are part of a large pedigreed colony made by R.D.S. between 1977 and 1992, currently housed at the University of California at Berkeley’s Museum of Vertebrate Zoology.

The colony was established in 1977 with either mice wild-caught by R.D.S., or outbred mice from another lab that established their colony with wild-caught animals. For example, Mus cervicolor popaeus founders were from the pedigreed breeding colony established and maintained by the National Cancer Institute (Escot et al, ‘86). We restrict our analyses to animals that are first-generation from these founders in order to minimize the chances of inbreeding. As such, all mice used in this study are from litters born between 1977 and 1981. Pedigrees were reconstructed from breeding records, enabling ascertainment of age at death and sex, as well as familial relationships. Seven taxa are represented (Table 1). No in-bred laboratory strains were used in this study.

Table 1.

Taxonomic composition and pedigree structure of mouse population

Taxon	Mating pairs	Litters	Offspring	Total
Mus caroli	5	8	31	41
M. cervicolor cervicolor	6	13	42	54
M. c. popaeus	3	8	35	41
M. cookii	4	11	40	48
M. musculus	2	3	17	21
M. domesticus brevirostris	2	3	5	9
M. d. praetextus	1	1	1	3
M. pahari	2	5	11	15
M. spretus	1	1	1	3
Mus total				235

Two of four subgenera within Mus (Nowak, ‘91) are represented: 15 are Coelomys (shrew mice: M. pahari), and 220 are Mus (house and rice field mice: M. caroli, M. cervicolor cervicolor, M. c. popaeus, M. cookii, M. musculus, M. domesticus brevirostris, M. d. praetextes, M. spretus). Our taxonomy follows Sage et al. (’93) and Prager et al. (’93). Each taxon has 1–6 pure mating pairs and 1–13 litters from these pairs (Table 1). There are no hybrids included in the analysis, only offspring from conspecific (or con-subspecific) matings. Although our sample represents non-inbred populations, the taxonomic structure makes it less than ideal for these analyses. By including parent/offspring sets from multiple taxa we artificially inflate the degree of correlation, as interspecific differences will increase the appearance of intra-familial resemblance. Therefore, analyses of this population are prone to overestimate correlations. Our results need to be interpreted with this caveat in mind.

In total, pedigree data for 235 mice were used to reconstruct the pedigrees, 207 with phenotype data. The female to male ratio is approximately 1:1. Mice were maintained and sacrificed under protocols approved by the Office of Laboratory Animal Care, University of California Berkeley.

PHENOTYPIC DATA

All dental measurements from the baboons were collected from casts, as described in detail elsewhere (Hlusko et al, 2002). Linear measurements for the baboons were collected with calipers for the incisors and premolars, and from digital photographs for the molars, following a protocol described elsewhere (Hlusko et al, 2002). Measurements were taken from photographs for the molars because of the need for a protocol that avoided the problem of the gumline obscuring the maximum buccolingual width of the crown – maximum width was standardized as 1 mm below the maximum depth of the occlusal surface. The shape of the other teeth makes caliper measurements more reliable than the two-dimensional representations of photographs. All dental data from the mice were collected from digital photographs using the software program Image Pro Plus©. Because mouse teeth are very small, they are more easily measured with digital photographs that can be magnified. Definitions of length and widths follow standard odontological methods (e.g., Hillson, ‘86).

Abbreviations: I = incisor, P = premolar, M = molar; number following first letter indicates tooth position; ll = labiolingual width of the incisor; md = mesiodistal length of the incisor; l = mesiodistal length (the longest mesiodistal axis of the premolar or molar), w = maximum buccolingual width of the premolar (not necessarily perpendicular to the mesiodistal length); mw = maximum buccolingual width of the molar through the mesial-most pair of cusps (not necessarily perpendicular to the mesiodistal length); dw = maximum buccolingual width of the molar through the distal cusp pair on baboons, and the second cusp pair for mice (not necessarily perpendicular to the mesiodistal length).

ANALYTICAL METHODS

Quantitative genetic analyses test the hypothesis that environmental, or rather non-genetic factors alone can account for the phenotypic similarities seen among family members. A significant heritability estimate and significant genetic correlation indicate that environmental effects by themselves cannot account for, respectively, the pattern of phenotypic variation and covariation between phenotypes seen in a population of related individuals; that is, the degree of interrelatedness – and, hence, genetic similarity – contributes to observed phenotypic similarities.

Our statistical genetic analyses were performed using a maximum likelihood based variance decomposition approach implemented in the computer package SOLAR (Almasy and Blangero, ‘98). Accordingly, the phenotypic covariance for each trait within a pedigree in this study is modeled as $\mathrm{\Omega }=2\mathrm{\Phi }{\sigma }_G^2+I{\sigma }_E^2,$, where Φ is a matrix of kinship coefficients for all relative pairs in a pedigree, ${\sigma }_G^2$ is the additive genetic variance, I is an identity matrix (composed of ones along the diagonal and zeros for all off diagonal elements), and ${\sigma }_E^2$ is the environmental variance. Because the components of the phenotypic variance are additive, such that σ²_P = σ²_G + σ²_E, we estimated heritability, or the proportion of the phenotypic variance attributable to additive genetic effects, as h² = σ²_G / σ²_P. Identifying such additive genetic effects are essential to evolutionary theory, as only phenotypic variation that is inherited will respond to selective pressure. Phenotypic variance attributable to non-genetic factors is estimated as e² = 1 – h². The mean effects of sex and age were included in the analyses when they had a significant influence on the phenotypic variance (age serves as a proxy for wear in these analyses).

Using extensions to univariate genetic analysis that encompass the multivariate state (Hopper and Mathews, ‘82; Lange and Boehnke, ‘83; Boehnke et al, ‘87), we follow an approach described in detail elsewhere (Mahaney et al, ‘95) to model the multivariate phenotype of an individual as a linear function of the measurements on the individual's traits, the means of these traits in the population, the covariates and their regression coefficients, plus the additive genetic values and random environmental deviations. From this model, we obtained the phenotypic variance-covariance matrix from which we partitioned the additive genetic and random environmental variance-covariance matrices, given the relationships (kinship coefficients) observed in the pedigree. From these two variance-covariance matrices, we estimated the additive genetic correlation, ρ_G, and the environmental correlation, ρ_E, between trait pairs. Respectively, these correlations are estimates of the additive effects of shared genes (i.e., pleiotropy) and shared environmental (i.e., unmeasured and nongenetic) factors on the variance in a trait.

The genetic and environmental components of the phenotypic correlation matrix are additive, like those of the corresponding variance-covariance matrix, so we use the maximum likelihood estimates of the additive genetic and environmental correlations to obtain the total phenotypic correlation between two traits, ρ_P, as

$${\rho }_P=\sqrt{h_1^2}\sqrt{h_2^2}{\rho }_G+\sqrt{(1-h_1^2)}\sqrt{(1-h_2^2)}{\rho }_E.$$

We conducted bivariate quantitative genetic analyses of trait pairs using multivariate extensions to the basic variance decomposition methods implemented in SOLAR (Almasy and Blangero 1998). We used this approach to obtain simultaneous maximum likelihood estimates of the phenotypic means (μ), phenotypic standard deviations (σ), heritabilities (h²), and the mean effects of covariates on all traits, and the genetic and environmental correlations between them.

Significance of the maximum likelihood estimates for heritability and other parameters is assessed by means of likelihood ratio tests. Twice the difference of the maximum likelihoods of a general model (in which all parameters are estimated) and a restricted model (in which the value of a parameter to be tested is held constant at some value, usually zero) are compared. This difference is distributed asymptotically approximately as either a ½:½ mixture of χ² and a point mass at zero, for tests of parameters like h² for which a value of zero in a restricted model is at a boundary of the parameter space, or as a χ² variate for tests of covariates for which zero is not a boundary value (Hopper and Mathews, ‘82). In both cases degrees of freedom is equal to the difference in the number of estimated parameters in the two models (Boehnke et al, ‘87). However, in tests of parameters like h², whose values may be fixed at a boundary of their parameter space in the null model, the appropriate significance level is obtained by halving the P-value (Boehnke et al, ‘87).

For bivariate models in which genetic correlations are found to be significantly greater than zero, additional tests are performed to compare the likelihood of a model in which the value of the genetic correlation is fixed at 1 or 0 to that of the unrestricted model in which the value of the genetic correlation is estimated. A significant difference between the likelihoods of the restricted and polygenic models suggests incomplete pleiotropy, i.e., not all of the additive genetic variance in the two traits is due to the effects of the same gene or genes.

Genetic correlations between traits can result from either pleiotropy or gametic phase disequilibrium (Lynch and Walsh, ‘98). The degree of gametic phase disequilibrium (or linkage disequilibrium, LD) is a function of a population’s genetic history and demography: e.g., it will be lower in outbred populations with many unrelated founders as recombination exerts its effects each generation, higher in populations undergoing rapid expansion from a small number of founders and those resulting from recent admixture. Given a conducive set of population characteristics, the likelihood of genetic correlation between two traits being due to LD is higher for simple traits, with monogenic (or nearly so) inheritance. However, if variation in a pair of traits is attributable to the effects of multiple alleles at multiple loci, LD is not likely to be a major contributor to the genetic correlation (Lande, ‘80; Lynch and Walsh, ‘98). Therefore, we are cautiously confident that significant additive genetic correlations estimated in our analyses on pairs of complex, multifactorial dental measures from our non-inbred, extended baboon and mouse pedigrees are primarily indicative of pleiotropy rather than LD. Ongoing and planned whole genome screens and LD analyses will help confirm this.

Results

The last 50 years of quantitative genetics have repeatedly shown that dental phenotypes tend to have the highest heritability estimates reported for the skeleton (Rizk et al, 2008), indicating that dental variation is largely influenced by genetic variation, although non-genetic affects can be significant. This is not surprising given that the size and shape of teeth are unaltered after eruption, save for wear and breakage, unlike the rest of the mammalian skeleton that continues to remodel over the animal’s lifespan.

As expected, the tooth size variation reported here is highly heritable for both baboons and mice, and as such, highly susceptible to selective pressures (see Table 2a and b for residual h² estimates). These tables report the residual heritability (h²) estimate after the affects of the covariates (c²) are removed (i.e., sex and age). The remaining variance is attributed to non-genetic effects (e²) such as measurement error, environmental influences, and/or unaccounted for covariates.

Table 2a.

Polygenic models for individual baboon tooth measurements¹

	Trait	Mean	Var	n	Kurtosis	Total h2	p-value	Total c2	Total e2	Residual h2 ± SE
Baboon Right Maxillary	I1ll	9.07	1.08	473	−0.3274	0.49	<0.0001	0.194	0.32	0.605±0.12
	I1md	9.51	0.55	480	0.4816	0.51	<0.0001	0.125	0.37	0.578±0.11
	I2ll	7.98	1.09	463	0.5029	0.51	<0.0001	0.204	0.28	0.642±0.11
	I2md	7.05	0.91	474	0.5982	0.52	<0.0001	0.141	0.33	0.611±0.11
	P3l	6.71	0.31	276	−0.1182	0.25	0.006	0.201	0.55	0.316±0.15
	P3w	7.82	0.44	317	0.7641	0.43	<0.0001	0.346	0.22	0.659±0.20
	P4l	7.63	0.27	400	0.4849	0.48	<0.0001	0.295	0.23	0.680±0.12
	P4w	8.51	0.38	430	0.0152	0.37	<0.0001	0.368	0.26	0.591±0.12
	M1l	10.68	0.40	471	0.2626	0.44	<0.0001	0.336	0.23	0.659±0.11
	M1mw	8.38	0.30	438	0.7627	0.55	<0.0001	0.184	0.27	0.672±0.14
	M1dw	7.87	0.29	439	0.4530	0.62	<0.0001	0.190	0.19	0.763±0.16
	M2l	12.47	0.69	531	1.4037	0.46	<0.0001	0.425	0.12	0.798±0.11
	M2mw	9.88	0.47	530	0.5056	0.39	<0.0001	0.291	0.32	0.544±0.12
	M2dw	8.85	0.40	517	0.5223	0.37	<0.0001	0.305	0.32	0.533±0.13
	M3l	12.62	0.83	243	2.2095	0.14	0.06	0.429	0.43	0.241±0.19
	M3mw	9.97	0.75	444	0.9430	0.35	<0.0001	0.381	0.27	0.562±0.13
	M3dw	8.50	0.56	286	0.0408	0.22	0.021	0.345	0.44	0.331±0.19
Baboon Right Mandibular	Trait	Mean	Var	n	Kurtosis	Total h2	p-value	Total c2	Total e2	Residual h2 ± SE
	I1ll	8.82	1.46	474	0.6858	0.53	<0.0001	0.099	0.37	0.589±0.12
	I1md	6.79	0.30	465	0.6396	0.55	<0.0001	0.053	0.40	0.581±0.11
	I2ll	8.30	1.66	468	0.4795	0.28	<0.0001	0.189	0.54	0.340±0.11
	I2md	5.67	0.35	463	−0.1269	0.26	<0.0001	0.116	0.62	0.293±0.10
	P3l	11.46	13.08	162	5.1955	0.30	0.06	0.365	0.33	0.473±0.41
	P3w	5.58	0.42	274	0.1837	0.22	0.0003	0.513	0.27	0.442±0.16
	P4l	8.45	0.46	409	0.1038	0.39	<0.0001	0.413	0.19	0.672±0.10
	P4w	6.99	0.32	368	0.2922	0.56	<0.0001	0.234	0.21	0.729±0.14
	M1l	10.47	0.30	362	0.7650	0.59	<0.0001	0.360	0.05	0.927±0.14
	M1mw	7.33	0.25	326	0.1957	0.56	<0.0001	0.226	0.22	0.722±0.15
	M1dw	7.36	0.26	334	0.4025	0.67	<0.0001	0.146	0.18	0.781±0.16
	M2l	12.36	0.62	490	0.7256	0.49	<0.0001	0.444	0.06	0.886±0.10
	M2mw	9.22	0.45	501	0.5369	0.53	<0.0001	0.305	0.17	0.760±0.10
	M2dw	8.61	0.38	475	0.3637	0.43	<0.0001	0.309	0.26	0.622±0.12
	M3l	15.28	1.60	232	2.2398	0.40	0.0004	0.449	0.15	0.722±0.22
	M3mw	9.68	0.62	483	0.0916	0.49	<0.0001	0.394	0.11	0.811±0.11
	M3dw	8.68	0.51	463	0.2065	0.38	<0.0001	0.391	0.23	0.630±0.11
	Trait	Mean	Var	n	Kurtosis	Total h2	p-value	Total c2	Total e2	Residual h2 ± SE
Baboon Left Maxillary	I1ll	8.96	1.06	469	0.5843	0.37	<0.0001	0.176	0.46	0.446±0.11
	I1md	9.58	0.48	471	0.0452	0.55	<0.0001	0.156	0.29	0.654±0.10
	I2ll	7.12	0.60	481	0.3304	0.54	<0.0001	0.099	0.36	0.595±0.12
	I2md	5.62	0.48	471	0.3270	0.36	<0.0001	0.212	0.43	0.452±0.11
	P3l	6.69	0.34	287	−0.1619	0.20	0.017	0.148	0.65	0.236±0.14
	P3w	7.75	0.41	323	0.5493	0.18	0.004	0.388	0.43	0.292±0.14
	P4l	7.65	0.28	418	0.5649	0.34	<0.0001	0.285	0.37	0.478±0.10
	P4w	8.52	0.37	454	−0.0675	0.42	<0.0001	0.303	0.27	0.608±0.12
	M1l	10.66	0.37	470	−0.1161	0.47	<0.0001	0.379	0.15	0.751±0.12
	M1mw	8.38	0.30	458	0.5261	0.56	<0.0001	0.221	0.22	0.722±0.11
	M1dw	7.89	0.27	454	0.3962	0.62	<0.0001	0.206	0.17	0.786±0.12
	M2l	12.55	0.69	539	0.6799	0.44	<0.0001	0.479	0.08	0.847±0.10
	M2mw	9.90	0.45	539	0.7125	0.49	<0.0001	0.276	0.23	0.676±0.11
	M2dw	8.92	0.39	530	0.2218	0.39	<0.0001	0.302	0.31	0.557±0.11
	M3l	12.49	0.87	234	0.8855	0.13	0.07	0.432	0.44	0.231±0.19
	M3mw	9.98	0.61	440	0.3233	0.15	0.002	0.373	0.48	0.234±0.11
	M3dw	8.52	0.51	271	0.0973	0.16	0.01	0.411	0.43	0.271±0.16
Baboon Left Mandibular	Trait	Mean	Var	n	Kurtosis	Total h2	p-value	Total c2	Total e2	Residual h2 ± SE
	I1ll	8.62	1.38	467	0.1537	0.49	<0.0001	0.125	0.39	0.560±0.12
	I1md	6.80	0.27	456	−0.0292	0.60	<0.0001	0.095	0.30	0.668±0.11
	I2ll	8.16	1.40	468	0.3457	0.30	<0.0001	0.224	0.48	0.386±0.11
	I2md	5.62	0.48	457	0.3326	0.25	<0.0001	0.087	0.66	0.277±0.10
	P3l	11.18	14.57	134	10.076	0.32	0.055	0.273	0.41	0.440±0.32
	P3w	5.59	0.43	274	0.3597	0.21	0.0003	0.468	0.32	0.403±0.16
	P4l	8.49	0.44	389	1.0291	0.29	<0.0001	0.435	0.28	0.511±0.12
	P4w	7.03	0.33	366	0.2336	0.49	<0.0001	0.183	0.33	0.598±0.14
	M1l	10.47	0.33	357	0.0992	0.61	<0.0001	0.284	0.11	0.848±0.13
	M1mw	7.32	0.28	336	−0.2091	0.42	<0.0001	0.215	0.36	0.539±0.16
	M1dw	7.32	0.26	342	1.2749	0.24	0.053	0.186	0.57	0.289±0.19
	M2l	12.31	0.66	485	1.2870	0.32	<0.0001	0.489	0.19	0.628±0.11
	M2mw	9.22	0.49	480	0.8268	0.30	<0.0001	0.362	0.34	0.464±0.11
	M2dw	8.60	0.46	490	0.3373	0.31	<0.0001	0.341	0.35	0.469±0.12
	M3l	15.20	1.58	336	0.5854	0.25	0.0005	0.404	0.35	0.415±0.16
	M3mw	9.62	0.63	500	0.5294	0.27	<0.0001	0.384	0.34	0.441±0.10
	M3dw	8.62	0.48	470	0.3896	0.26	<0.0001	0.343	0.40	0.392±0.10

¹Total c² = amount of phenotypic variance attributable to covariates. Total h² = (Residual h²)(1-Total c²). Total e² = [1 – (Total c² + Total h²)]; All data are presented in mm but were analyzed as multiples of 10 to raise the variance above 1.0.

Table 2b.

Polygenic models for individual mouse tooth measurements ¹

	Trait	Mean	Stdv	n	Kurtosis	Total h2	p−value	Total c2	Total e2	Residual h2 ± SE
Mouse Right Maxillary	I1ll	0.16	0.02	199	2.07	0.366	<0.0001	none	0.634	0.366±0.09
	M1l	2.18	0.20	207	−0.58	0.765	<0.0001	none	0.235	0.765±0.06
	M1mw	1.16	0.09	207	−0.37	0.910	<0.0001	none	0.090	0.910±0.05
	M1dw	1.19	0.10	207	−0.99	0.991	<0.0001	none	0.009	0.991±0.03
	M2l	1.29	0.13	207	−0.94	0.942	<0.0001	none	0.058	0.942±0.03
	M2mw	0.56	0.06	207	0.18	0.758	<0.0001	none	0.242	0.758±0.09
	M2dw	0.98	0.09	206	−0.63	0.906	<0.0001	none	0.094	0.906±0.04
	M3l	0.70	0.08	201	−0.34	0.784	<0.0001	none	0.216	0.784±0.06
	M3mw	0.66	0.07	201	−0.32	0.878	<0.0001	none	0.122	0.878±0.06
Mouse Left Maxillary	M1l	2.18	0.21	207	−0.67	0.817	<0.0001	none	0.183	0.817±0.06
	M1mw	1.15	0.08	207	−0.54	0.811	<0.0001	none	0.189	0.811±0.06
	M1dw	1.18	0.09	207	−0.99	0.939	<0.0001	none	0.061	0.939±0.04
	M2l	1.30	0.127	207	−1.00	0.952	<0.0001	none	0.048	0.952±0.03
	M2mw	0.56	0.06	207	−0.51	0.696	<0.0001	none	0.304	0.696±0.07
	M2dw	0.98	0.08	206	−0.65	0.866	<0.0001	none	0.134	0.866±0.05
	M3l	0.71	0.08	202	12.6	0.739	<0.0001	none	0.261	0.739±0.07
	M3mw	0.67	0.07	202	18.8	0.731	<0.0001	none	0.269	0.731±0.08
Mouse Right Mandibular	I1ll*	0.09	0.02	197	92.7	0.372	<0.0001	none	0.628	0.372±0.09
	I1md	0.05	0.01	197	0.01	0.174	0.0087	none	0.826	0.174±0.09
	M1l	1.62	0.13	204	−0.95	0.984	<0.0001	none	0.016	0.984±0.08
	M1mw	0.67	0.06	204	0.07	0.729	<0.0001	0.009	0.262	0.736±0.08
	M1dw	0.91	0.07	204	−0.73	0.988	<0.0001	none	0.012	0.988±0.30
	M2l	1.01	0.09	203	−0.59	0.757	<0.0001	0.035	0.208	0.784±0.04
	M2mw	0.95	0.09	203	−0.55	0.886	<0.0001	none	0.114	0.886±0.05
	M2dw	0.89	0.10	203	−0.86	0.876	<0.0001	0.042	0.082	0.914±0.04
	M3l	0.72	0.10	197	−0.06	0.698	<0.0001	none	0.302	0.698±0.08
Mouse Left Mandibular	M1l	1.61	0.13	204	−0.87	0.980	<0.0001	none	0.020	0.980±0.03
	M1mw	0.67	0.06	204	0.27	0.690	<0.0001	none	0.310	0.690±0.10
	M1dw	0.91	0.07	204	−0.91	0.892	<0.0001	none	0.108	0.892±0.05
	M2l	1.00	0.09	203	−0.81	0.744	<0.0001	none	0.256	0.744±0.06
	M2mw	0.95	0.09	203	0.87	0.827	<0.0001	none	0.173	0.827±0.05
	M2dw	0.89	0.10	203	−0.91	0.932	<0.0001	none	0.068	0.932±0.04
	M3l	0.71	0.10	195	−0.50	0.695	<0.0001	none	0.305	0.695±0.08

¹Total c² = amount of phenotypic variance attributable to covariates. Total h² = (Residual h²)(1-Total c²). Total e² = [1 – (Total c² + Total h²)];

^*phenotype was also analyzed after being I-normalized to reduce kurtosis; I-normalized h²_r estimate was 0.314±0.08 (p < 0.0001; kurtosis −0.23). All data are presented in mm but were multiplied by 100 for the genetic analyses to raise the variance above 1.0.

All but 5 of the 68 baboon tooth measurements yield significant heritabilities (p<0.05), with an average residual heritability of 0.56 and an average total heritability of 0.40. Covariate effects (primarily sex) contribute, on average, 28% to the total phenotypic variance. Non-genetic effects average 32%.

All of the mouse tooth measurements returned significant heritability estimates (p<0.01). The incisor residual heritabilities are lower (average is 0.30) than are those estimated for the molars (average is 0.84). Covariates were found to account for little to no amount of the total phenotypic variance. Non-genetic effects average account for about 16% of the total phenotypic variance.

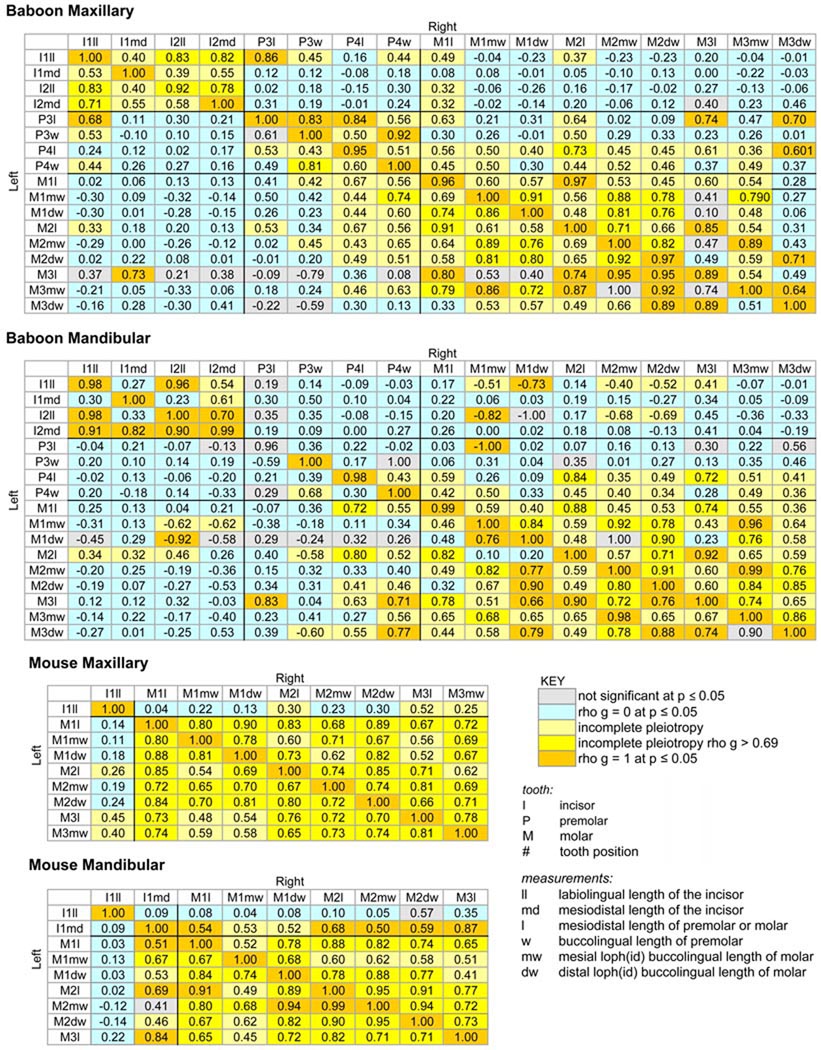
These residual heritability estimates were then used to construct patterns of genetic interrelatedness (correlations), i.e., that aspect of the genetic architecture that is of significance to evolutionary studies (Lande, ‘79; Schluter, 2000), shown as correlation matrices in Figure 2 and reported in detail in Table 3. Genetic correlations were estimated for all possible pair-wise comparisons, even though some of these were based on insignificant heritability estimates. As such, some of the values that populate the matrix, especially those indicated in gray, should be considered tentative at best. The genetic correlation estimates were compared to models in which the correlation was constrained to zero and one. The two far-right columns in Table 3 indicate the probability that the estimated genetic correlation is significantly different from one of these constrained models. Estimates that are significantly different from both one and zero are interpreted to indicate incomplete pleiotropy (see discussion in the Analytical Methods section).

FIGURE 2.

Matrices showing estimated genetic correlations between tooth size measurement pairs for pedigreed baboon and mouse populations described in the main text. All estimates are statistically significant at p ≤ 0.05 unless shaded gray (see key). Specific probabilities and other parameter estimates are reported in Table 3.

Table 3.

Bivariate statistical genetic analyses: Maximum-likelihood estimates of genetic and environmental correlations¹

Baboon Right Maxillary
		Correlations (MLEs)		Significance of Correlations P(Hypothesis)
Phenotype pair	N	ρG	ρE	ρG =0	| ρG |=1
I1ll v I1md	473	0.397	0.206	0.016	<0.0000001
I1ll v I2ll	444	0.831	0.340	<0.0000001	0.000016
I1ll v I2md	455	0.820	−0.065	<0.0000001	0.002
I1ll v P3l	206	0.857	−0.247	0.003	0.32
I1ll v P3w	248	0.448	0.039	0.027	0.0004
I1ll v P4l	309	0.156	0.344	0.31	<0.0000001
I1ll v P4w	325	0.438	0.011	0.008	0.0000003
I1ll v M1l	380	0.488	−0.035	0.002	<0.0000001
I1ll v M1mw	368	−0.04	−0.101	0.83	0.0000003
I1ll v M1dw	369	−0.227	0.015	0.21	0.0000003
I1ll v M2l	429	0.366	0.161	0.018	<0.0000001
I1ll v M2mw	427	−0.233	0.052	0.19	0.0000004
I1ll v M2dw	418	−0.232	0.078	0.20	0.0000006
I1ll v M3l	119	0.198	0.467	0.50	0.032
I1ll v M3mw	353	−0.035	0.162	0.85	0.0000001
I1ll v M3dw	201	0.011	−0.018	0.97	0.020
I1md v I2ll	452	0.391	−0.233	0.017	0.0000002
I1md v I2md	463	0.549	0.001	0.0008	0.000006
I1md v P3l	207	0.118	0.222	0.64	0.007
I1md v P3w	253	0.116	0.320	0.54	0.000003
I1md v P4l	315	−0.083	0.308	0.62	0.0000005
I1md v P4w	331	0.178	0.255	0.30	<0.0000001
I1md v M1l	384	0.080	0.361	0.63	<0.0000001
I1md v M1mw	372	0.082	0.317	0.65	<0.0000001
I1md v M1dw	373	−0.014	0.192	0.94	0.0000004
I1md v M2l	436	0.049	0.486	0.75	<0.0000001
I1md v M2mw	434	−0.102	0.294	0.56	0.0000001
I1md v M2dw	425	0.128	0.116	0.47	<0.0000001
I1md v M3l	123	−0.001	0.532	0.99	0.04
I1md v M3mw	358	−0.224	0.321	0.23	0.000004
I1md v M3dw	205	−0.029	0.148	0.902	0.015
I2ll v I2md	462	0.779	−0.070	<0.0000001	0.000009
I2ll v P3l	205	0.017	0.115	0.95	0.007
I2ll v P3w	249	0.179	0.130	0.33	0.000001
I2ll v P4l	310	−0.152	0.698	0.30	<0.0000001
I2ll v P4w	324	0.299	−0.036	0.08	<0.0000001
I2ll v M1l	368	0.318	−0.201	0.03	<0.0000001
I2ll v M1mw	358	−0.056	−0.381	0.74	<0.0000001
I2ll v M1dw	358	−0.256	−0.182	0.12	0.0000002
I2ll v M2l	421	0.162	0.357	0.28	<0.0000001
I2ll v M2mw	418	−0.166	−0.026	0.33	0.0000002
I2ll v M2dw	409	−0.019	−0.095	1	<0.0000001
I2ll v M3l	121	0.266	0.110	0.31	0.043
I2ll v M3mw	343	−0.125	0.230	0.50	0.000001
I2ll v M3dw	203	−0.060	−0.014	0.81	0.020
I2md v P3l	208	0.312	0.133	0.19	0.012
I2md v P3w	253	0.191	0.158	0.29	0.000003
I2md v P4l	314	−0.009	0.571	0.95	<0.00000001
I2md v P4w	330	0.238	0.044	0.16	<0.00000001
I2md v M1l	377	0.322	0.062	0.03	<0.00000001
I2md v M1mw	367	−0.015	−0.058	0.93	0.0000002
I2md v M1dw	367	−0.136	0.055	0.41	0.0000001
I2md v M2l	430	0.202	0.208	0.17	<0.00000001
I2md v M2mw	428	−0.061	−0.062	0.71	0.0000001
I2md v M2dw	419	0.119	−0.125	0.49	0.0000001
I2md v M3l	122	0.400	0.261	0.142	0.052
I2md v M3mw	351	0.231	−0.105	0.183	<0.0000001
I2md v M3dw	204	0.460	−0.185	0.046	0.033
P3l v P3w	243	0.833	0.016	0.004	0.20
P3l v P4l	259	0.837	0.088	0.0002	0.193
P3l v P4w	256	0.561	0.064	0.02	0.02
P3l v M1l	212	0.631	0.093	0.014	0.038
P3l v M1mw	198	0.213	0.437	0.47	0.003
P3l v M1dw	198	0.309	0.233	0.305	0.013
P3l v M2l	246	0.636	0.300	0.004	0.016
P3l v M2mw	244	0.016	0.428	0.953	0.005
P3l v M2dw	237	0.091	0.480	0.77	0.017
P3l v M3l	81	0.740	0.170	0.03	0.13
P3l v M3mw	212	0.472	0.130	0.094	0.005
P3l v M3dw	146	0.703	0.142	0.024	0.063
P3w v P4l	311	0.495	0.213	0.003	0.0000003
P3w v P4w	309	0.915	0.090	<0.000001	0.144
P3w v M1l	255	0.299	0.561	0.126	0.000001
P3w v M1mw	240	0.263	0.343	0.212	0.0000003
P3w v M1dw	240	−0.009	0.764	0.967	0.000001
P3w v M2l	297	0.503	0.300	0.003	0.0000008
P3w v M2mw	293	0.293	0.320	0.136	0.0000006
P3w v M2dw	287	0.333	0.236	0.113	0.000003
P3w v M3l	103	0.227	0.217	0.461	0.026
P3w v M3mw	251	0.256	0.112	0.213	0.000006
P3w v M3dw	166	0.010	0.319	0.97	0.02
P4l v P4w	383	0.511	0.195	0.0006	<0.00000001
P4l v M1l	318	0.560	0.166	0.0003	0.0000001
P4l v M1mw	303	0.499	−0.196	0.002	<0.00000001
P4l v M1dw	304	0.402	0.114	0.024	0.0000007
P4l v M2l	375	0.725	0.369	<0.0000001	<0.00000001
P4l v M2mw	371	0.454	0.184	0.003	<0.00000001
P4l v M2dw	362	0.451	0.197	0.005	<0.00000001
P4l v M3l	138	0.614	0.221	0.002	0.005
P4l v M3mw	315	0.359	0.131	0.024	<0.0000001
P4l v M3dw	209	0.601	0.116	0.006	0.049
P4w v M1l	332	0.448	0.247	0.007	<0.00000001
P4w v M1mw	317	0.500	0.277	0.005	0.0000001
P4w v M1dw	317	0.302	0.392	0.104	<0.00000001
P4w v M2l	389	0.436	0.383	0.007	<0.00000001
P4w v M2mw	384	0.515	0.195	0.003	0.0000001
P4w v M2dw	375	0.460	0.106	0.013	0.0000005
P4w v M3l	143	0.374	0.201	0.189	0.012
P4w v M3mw	325	0.488	−0.023	0.007	0.00001
P4w v M3dw	213	0.374	0.229	0.18	0.039
M1l v M1mw	435	0.599	0.310	0.0003	<0.0000001
M1l v M1dw	437	0.565	0.061	0.0008	0.0000004
M1l v M2l	439	0.972	0.055	<0.0000001	0.33
M1l v M2mw	437	0.526	0.047	0.002	0.000006
M1l v M2dw	425	0.453	0.214	0.009	<0.0000001
M1l v M3l	137	0.601	0.418	0.021	0.043
M1l v M3mw	362	0.544	0.079	0.002	0.00002
M1l v M3dw	225	0.281	0.209	0.211	0.009
M1mw v M1dw	432	0.914	0.676	<0.000001	0.0005
M1mw v M2l	426	0.564	0.003	0.0003	0.0000002
M1mw v M2mw	425	0.878	0.388	<0.000001	0.004
M1mw v M2dw	414	0.781	0.275	<0.00001	0.0006
M1mw v M3l	133	0.414	0.151	0.19	0.06
M1mw v M3mw	347	0.789	0.007	<0.00001	0.005
M1mw v M3dw	213	0.269	0.383	0.316	0.014
M1dw v M2l	426	0.482	−0.065	0.002	0.0000008
M1dw v M2mw	426	0.806	0.218	<0.00001	0.0005
M1dw v M2dw	414	0.763	0.278	<0.00001	0.000009
M1dw v M3l	131	0.103	0.205	0.77	0.049
M1dw v M3mw	349	0.482	0.168	0.015	0.00006
M1dw v M3dw	213	0.056	0.703	0.83	0.004
M2l v M2mw	525	0.714	0.240	<0.00001	0.000009
M2l v M2dw	513	0.658	0.267	0.00002	0.0000001
M2l v M3l	167	0.854	0.548	0.003	0.28
M2l v M3mw	424	0.538	0.219	0.002	0.00004
M2l v M3dw	260	0.309	0.357	0.13	0.005
M2mw v M2dw	516	0.820	0.744	<0.00001	<0.0000001
M2mw v M3l	165	0.472	0.337	0.14	0.08
M2mw v M3mw	422	0.891	0.273	<0.000001	0.08
M2mw v M3dw	258	0.431	0.507	0.13	0.03
M2dw v M3l	164	0.492	0.341	0.09	0.03
M2dw v M3mw	418	0.589	0.367	0.002	0.000002
M2dw v M3dw	255	0.709	0.557	0.009	0.054
M3l v M3mw	168	0.535	0.749	0.023	0.003
M3l v M3dw	133	0.486	0.607	0.17	0.004
M3mw v M3dw	275	0.643	0.699	0.04	0.047

Baboon Left Maxillary
		Correlations (MLEs)		Significance of Correlations P(Hypothesis)
Phenotype pair	N	ρG	ρE	ρG =0	| ρG |=1
I1ll v I1md	469	0.529	0.178	0.0007	<0.0000001
I1ll v I2ll	447	0.828	0.366	<0.000001	0.0015
I1ll v I2md	456	0.711	−0.069	0.0001	0.004
I1ll v P3l	211	0.678	−0.159	0.034	0.21
I1ll v P3w	255	0.527	−0.075	0.038	0.023
I1ll v P4l	322	0.235	0.161	0.191	<0.0000001
I1ll v P4w	339	0.441	−0.133	0.018	0.00003
I1ll v M1l	382	0.021	0.343	0.909	<0.0000001
I1ll v M1mw	377	−0.295	0.168	0.11	0.0000002
I1ll v M1dw	374	−0.304	0.225	0.089	0.0000002
I1ll v M2l	428	0.330	0.126	0.027	<0.0000001
I1ll v M2mw	429	−0.292	0.183	0.121	0.000004
I1ll v M2dw	424	0.019	−0.098	0.92	<0.0000001
I1ll v M3l	165	0.373	0.078	0.23	0.07
I1ll v M3mw	343	−0.209	0.147	0.42	0.008
I1ll v M3dw	193	−0.159	0.255	0.56	0.012
I1md v I2ll	448	0.401	−0.131	0.011	<0.0000001
I1md v I2md	457	0.550	0.144	0.0015	0.00006
I1md v P3l	211	0.108	0.256	0.68	0.026
I1md v P3w	255	−0.099	0.346	0.635	0.0001
I1md v P4l	323	0.115	0.363	0.484	<0.0000001
I1md v P4w	341	0.264	0.112	0.089	<0.0000001
I1md v M1l	384	0.063	0.531	0.669	<0.0000001
I1md v M1mw	379	0.087	0.279	0.57	<0.0000001
I1md v M1dw	376	0.014	0.399	0.92	<0.0000001
I1md v M2l	430	0.178	0.481	0.17	<0.0000001
I1md v M2mw	431	0.003	0.439	0.98	<0.0000001
I1md v M2dw	426	0.224	0.163	0.144	<0.0000001
I1md v M3l	165	0.732	−0.110	0.019	0.283
I1md v M3mw	344	0.045	0.076	0.83	0.0016
I1md v M3dw	194	0.282	0.118	0.194	0.008
I2ll v I2md	462	0.582	0.009	0.0015	0.0005
I2ll v P3l	211	0.302	0.015	0.31	0.038
I2ll v P3w	251	0.100	0.084	0.69	0.0002
I2ll v P4l	319	0.020	0.336	0.907	<0.0000001
I2ll v P4w	335	0.273	−0.087	0.135	<0.0000001
I2ll v M1l	374	0.125	−0.015	0.484	<0.0000001
I2ll v M1mw	369	−0.323	0.234	0.075	<0.0000001
I2ll v M1dw	366	−0.277	0.313	0.114	<0.0000001
I2ll v M2l	422	0.199	0.156	0.17	<0.0000001
I2ll v M2mw	423	−0.256	0.195	0.156	0.0000002
I2ll v M2dw	418	0.082	−0.057	0.65	<0.0000001
I2ll v M3l	164	0.208	0.002	0.47	0.054
I2ll v M3mw	336	−0.330	0.194	0.17	0.015
I2ll v M3dw	191	−0.296	0.426	0.23	0.012
I2md v P3l	215	0.205	0.219	0.52	0.049
I2md v P3w	258	0.150	0.150	0.54	0.0002
I2md v P4l	327	0.171	0.209	0.36	<0.000001
I2md v P4w	344	0.162	0.071	0.40	<0.000001
I2md v M1l	382	0.133	0.209	0.49	<0.000001
I2md v M1mw	376	−0.144	0.184	0.467	<0.000001
I2md v M1dw	373	−0.145	0.163	0.45	<0.000001
I2md v M2l	430	0.130	0.405	0.413	<0.000001
I2md v M2mw	431	−0.116	0.281	0.536	<0.000001
I2md v M2dw	426	0.010	0.251	0.958	<0.000001
I2md v M3l	167	0.384	0.078	0.28	0.12
I2md v M3mw	344	0.063	0.068	0.81	0.002
I2md v M3dw	195	0.409	0.125	0.111	0.010
P3l v P3w	248	0.614	0.315	0.058	0.062
P3l v P4l	263	0.530	0.254	0.036	0.0099
P3l v P4w	262	0.493	0.261	0.052	0.017
P3l v M1l	224	0.407	0.263	0.13	0.019
P3l v M1mw	215	0.497	0.195	0.05	0.007
P3l v M1dw	211	0.255	0.238	0.38	0.017
P3l v M2l	259	0.534	0.271	0.020	0.019
P3l v M2mw	257	0.015	0.427	0.95	0.006
P3l v M2dw	253	−0.010	0.443	0.97	0.008
P3l v M3l	133	−0.094	0.570	0.84	0.09
P3l v M3mw	214	0.181	0.310	0.62	0.005
P3l v M3dw	143	−0.222	0.394	0.71	0.18
P3w v P4l	314	0.434	0.405	0.041	0.0001
P3w v P4w	319	0.812	0.486	<0.00001	0.009
P3w v M1l	268	0.423	0.392	0.04	0.00004
P3w v M1mw	262	0.423	0.466	0.06	0.0003
P3w v M1dw	258	0.229	0.597	0.29	<0.0001
P3w v M2l	308	0.338	0.453	0.07	0.00001
P3w v M2mw	304	0.448	0.347	0.03	0.00001
P3w v M2dw	301	0.198	0.420	0.35	0.00001
P3w v M3l	146	−0.789	0.553	0.058	0.345
P3w v M3mw	252	0.237	0.291	0.44	0.002
P3w v M3dw	153	−0.584	0.483	0.16	0.19
P4l v P4w	405	0.603	0.282	0.0001	<0.0000001
P4l v M1l	339	0.667	0.288	0.00004	0.000005
P4l v M1mw	328	0.437	0.257	0.013	<0.0000001
P4l v M1dw	323	0.441	0.356	0.009	<0.0000001
P4l v M2l	396	0.668	0.450	<0.000001	<0.0000001
P4l v M2mw	392	0.431	0.134	0.011	<0.0000001
P4l v M2dw	388	0.488	0.030	0.003	<0.0000001
P4l v M3l	189	0.355	0.442	0.184	0.031
P4l v M3mw	321	0.462	0.107	0.028	0.0004
P4l v M3dw	195	0.297	0.335	0.24	0.004
P4w v M1l	358	0.558	0.086	0.0005	<0.0000001
P4w v M1mw	348	0.736	0.057	<0.000001	<0.000001
P4w v M1dw	343	0.600	0.193	0.00009	<0.0000001
P4w v M2l	416	0.560	0.109	0.00009	<0.0000001
P4w v M2mw	412	0.652	0.128	0.00003	<0.0000001
P4w v M2dw	407	0.508	0.242	0.002	<0.0000001
P4w v M3l	194	0.078	0.301	0.836	0.095
P4w v M3mw	337	0.626	0.264	0.003	0.0007
P4w v M3dw	203	0.126	0.426	0.69	0.009
M1l v M1mw	454	0.692	0.066	<0.00001	<0.000001
M1l v M1dw	450	0.742	−0.199	<0.000001	0.00003
M1l v M2l	455	0.913	0.072	<0.000001	0.043
M1l v M2mw	454	0.644	−0.002	0.000019	0.0000005
M1l v M2dw	447	0.575	0.135	0.0002	<0.000001
M1l v M3l	188	0.803	0.345	0.0004	0.053
M1l v M3mw	368	0.794	0.140	0.00005	0.015
M1l v M3dw	224	0.334	0.186	0.156	0.002
M1mw v M1dw	447	0.856	0.749	<0.000001	<0.000001
M1mw v M2l	444	0.613	−0.085	<0.00001	<0.000001
M1mw v M2mw	444	0.887	0.276	<0.000001	0.00012
M1mw v M2dw	437	0.813	0.242	<0.000001	0.0002
M1mw v M3l	182	0.528	0.216	0.082	0.092
M1mw v M3mw	359	0.860	0.246	<0.00001	0.049
M1mw v M3dw	216	0.528	0.093	0.024	0.019
M1dw v M2l	440	0.576	−0.203	0.00002	<0.000001
M1dw v M2mw	440	0.758	0.296	<0.000001	<0.000001
M1dw v M2dw	434	0.803	0.406	<0.000001	<0.000001
M1dw v M3l	179	0.397	0.412	0.221	0.062
M1dw v M3mw	354	0.721	0.281	0.0004	0.003
M1dw v M3dw	212	0.571	0.183	0.011	0.013
M2l v M2mw	530	0.687	0.111	<0.000001	<0.000001
M2l v M2dw	522	0.649	0.159	<0.000001	<0.000001
M2l v M3l	225	0.743	0.388	0.0007	0.085
M2l v M3mw	427	0.868	0.055	<0.000001	0.068
M2l v M3dw	259	0.490	0.158	0.007	0.0008
M2mw v M2dw	528	0.916	0.532	<0.000001	0.0013
M2mw v M3l	224	0.951	−0.026	0.0006	0.42
M2mw v M3mw	422	1.00	0.373	nc	<0.000001
M2mw v M3dw	257	0.663	0.210	0.0013	0.008
M2dw v M3l	222	0.947	0.086	0.001	0.41
M2dw v M3mw	421	0.917	0.292	<0.00001	0.12
M2dw v M3dw	256	0.889	0.263	0.00003	0.158
M3l v M3mw	218	0.743	0.492	0.054	0.159
M3l v M3dw	158	0.885	0.433	0.015	0.286
M3mw v M3dw	268	0.511	0.702	0.224	0.012

Baboon Right Mandibular
		Correlations (MLEs)		Significance of Correlations P(Hypothesis)
Phenotype pair	N	ρG	ρE	ρG =0	| ρG |=1
I1ll v I1md	456	0.273	0.310	0.116	<0.000001
I1ll v I2ll	427	0.959	0.626	<0.000001	0.19
I1ll v I2md	435	0.539	0.129	0.033	0.019
I1ll v P3l	120	0.186	0.623	0.66	0.34
I1ll v P3w	203	0.140	−0.148	0.62	0.009
I1ll v P4l	302	−0.093	0.292	0.59	<0.0000001
I1ll v P4w	295	−0.026	0.102	0.88	<0.0000001
I1ll v M1l	288	0.174	0.233	0.325	<0.0000001
I1ll v M1mw	273	−0.510	0.065	0.006	0.000006
I1ll v M1dw	282	−0.730	0.480	0.0002	0.046
I1ll v M2l	388	0.140	0.222	0.388	<0.0000001
I1ll v M2mw	381	−0.395	0.185	0.014	0.0000001
I1ll v M2dw	376	−0.522	0.189	0.004	0.00002
I1ll v M3l	167	0.412	−0.333	0.040	0.002
I1ll v M3mw	372	−0.070	−0.134	0.67	<0.0000001
I1ll v M3dw	354	−0.006	−0.046	0.97	<0.0000001
I1md v I2ll	433	0.226	0.148	0.263	0.0001
I1md v I2md	444	0.612	0.502	0.006	0.003
I1md v P3l	123	0.297	−1.00	0.066	0.024
I1md v P3w	208	0.497	−0.298	0.045	0.026
I1md v P4l	308	0.095	0.336	0.583	<0.0000001
I1md v P4w	302	0.043	0.343	0.795	<0.0000001
I1md v M1l	294	0.219	0.422	0.195	<0.0000001
I1md v M1mw	279	0.057	0.150	0.764	0.0000001
I1md v M1dw	288	0.025	0.279	0.89	0.000004
I1md v M2l	397	0.188	0.586	0.214	<0.0000001
I1md v M2mw	390	0.153	0.184	0.34	<0.0000001
I1md v M2dw	384	−0.273	0.440	0.138	0.00001
I1md v M3l	170	0.338	−0.364	0.066	0.0002
I1md v M3mw	379	0.053	0.076	0.74	<0.0000001
I1md v M3dw	360	−0.092	0.288	0.60	<0.0000001
I2ll v I2md	451	0.698	0.086	0.019	0.128
I2ll v P3l	124	0.353	0.827	0.238	0.110
I2ll v P3w	206	0.352	−0.334	0.272	0.026
I2ll v P4l	307	−0.083	0.148	0.67	0.00004
I2ll v P4w	296	−0.146	0.268	0.457	0.00008
I2ll v M1l	281	0.199	0.270	0.33	0.00004
I2ll v M1mw	267	−0.824	0.197	0.0002	0.116
I2ll v M1dw	275	−1.00	0.418	nc	0.00002
I2ll v M2l	385	0.167	0.297	0.373	0.00004
I2ll v M2mw	378	−0.678	0.307	0.0008	0.033
I2ll v M2dw	373	−0.691	0.303	0.001	0.020
I2ll v M3l	167	0.453	−0.159	0.048	0.002
I2ll v M3mw	371	−0.360	0.138	0.083	0.002
I2ll v M3dw	357	−0.326	0.150	0.136	0.0008
I2md v P3l	126	0.186	1.00	0.588	0.011
I2md v P3w	210	0.090	−0.167	0.86	0.005
I2md v P4l	311	−0.000	0.194	0.99	0.0002
I2md v P4w	300	0.268	0.194	0.22	0.0003
I2md v M1l	291	0.258	0.130	0.27	0.0002
I2md v M1mw	277	0.000	0.187	1.00	0.0003
I2md v M1dw	285	0.021	0.204	0.94	0.0003
I2md v M2l	395	0.175	0.503	0.395	0.0002
I2md v M2mw	389	0.080	0.326	0.72	0.0002
I2md v M2dw	383	−0.131	0.215	0.583	0.0006
I2md v M3l	169	0.413	−0.097	0.13	0.007
I2md v M3mw	378	0.035	−0.007	0.875	0.0002
I2md v M3dw	362	−0.187	0.214	0.439	0.0008
P3l v P3w	167	−0.364	1.00	0.26	0.007
P3l v P4l	160	0.215	1.00	0.224	<0.000001
P3l v P4w	147	−0.021	−1.00	0.90	<0.000001
P3l v M1l	114	0.032	−1.00	0.775	0.025
P3l v M1mw	103	−1.00	0.570	nc	0.86
P3l v M1dw	104	0.019	1.00	0.933	0.0003
P3l v M2l	147	0.068	−1.00	0.64	0.001
P3l v M2mw	144	0.155	−1.00	0.38	0.008
P3l v M2dw	142	0.128	−1.00	0.535	0.007
P3l v M3l	79	0.301	−1.00	0.172	0.162
P3l v M3mw	149	0.215	−1.00	0.283	0.026
P3l v M3dw	144	0.555	−1.00	0.048	0.045
P3w v P4l	255	0.171	0.175	0.520	0.031
P3w v P4w	244	1.00	0.420	nc	<0.000001
P3w v M1l	174	0.061	0.663	0.85	0.033
P3w v M1mw	160	0.313	0.590	0.363	0.030
P3w v M1dw	161	0.045	0.558	0.898	0.021
P3w v M2l	233	0.355	0.298	0.249	0.046
P3w v M2mw	229	0.010	0.789	0.972	0.018
P3w v M2dw	222	0.269	0.387	0.361	0.020
P3w v M3l	108	0.127	−0.120	0.656	0.026
P3w v M3mw	238	0.350	0.318	0.230	0.025
P3w v M3dw	225	0.458	0.133	0.102	0.029
P4l v P4w	357	0.429	−0.040	0.007	<0.000001
P4l v M1l	242	0.585	0.179	0.00009	<0.000001
P4l v M1mw	225	0.256	0.295	0.161	<0.000001
P4l v M1dw	231	0.092	0.706	0.621	<0.000001
P4l v M2l	337	0.839	−0.085	<0.000001	0.0003
P4l v M2mw	332	0.352	0.290	0.015	<0.000001
P4l v M2dw	324	0.488	0.234	0.002	<0.000001
P4l v M3l	161	0.720	−0.466	<0.00001	0.009
P4l v M3mw	334	0.508	−0.008	0.0004	<0.000001
P4l v M3dw	319	0.409	0.262	0.009	<0.000001
P4w v M1l	238	0.423	0.071	0.010	<0.000001
P4w v M1mw	217	0.496	0.246	0.004	<0.000001
P4w v M1dw	225	0.325	0.363	0.09	0.00001
P4w v M2l	334	0.449	0.091	0.003	<0.000001
P4w v M2mw	328	0.400	0.360	0.008	<0.000001
P4w v M2dw	323	0.340	0.350	0.037	<0.000001
P4w v M3l	163	0.283	−1.00	0.162	0.0006
P4w v M3mw	338	0.488	−0.207	0.001	<0.000001
P4w v M3dw	322	0.364	0.034	0.034	<0.000001
M1l v M1mw	321	0.586	−0.195	0.0007	<0.0000001
M1l v M1dw	330	0.403	0.471	0.03	0.000003
M1l v M2l	342	0.876	−0.365	<0.0000001	0.0003
M1l v M2mw	336	0.445	−0.078	0.002	<0.0000001
M1l v M2dw	329	0.525	−0.368	0.0009	<0.0000001
M1l v M3l	144	0.744	−1.00	<0.0000001	0.02
M1l v M3mw	309	0.547	−0.240	0.0002	<0.0000001
M1l v M3dw	296	0.358	0.196	0.03	<0.0000001
M1mw v M1dw	314	0.842	0.750	0.00005	0.0003
M1mw v M2l	319	0.587	−0.461	0.00004	<0.000001
M1mw v M2mw	313	0.920	0.177	<0.000001	0.039
M1mw v M2dw	306	0.778	0.208	<0.000001	0.000001
M1mw v M3l	132	0.434	−1.00	0.004	0.00002
M1mw v M3mw	288	0.964	0.011	<0.000001	0.211
M1mw v M3dw	277	0.641	0.134	0.0002	0.00006
M1dw v M2l	327	0.478	−0.155	0.001	<0.0000001
M1dw v M2mw	321	1.00	0.124	nc	<0.000001
M1dw v M2dw	313	0.903	0.233	<0.0000001	0.022
M1dw v M3l	137	0.227	−0.254	0.28	0.0001
M1dw v M3mw	295	0.755	0.194	0.00001	0.014
M1dw v M3dw	284	0.583	0.298	0.0005	0.00007
M2l v M2mw	480	0.566	0.397	<0.0001	<0.000001
M2l v M2dw	474	0.706	−0.098	<0.000001	<0.000001
M2l v M3l	207	0.920	−0.249	<0.000001	0.109
M2l v M3mw	437	0.650	−0.049	<0.000001	<0.000001
M2l v M3dw	417	0.590	0.036	0.00002	<0.000001
M2mw v M2dw	466	0.905	0.536	<0.000001	<0.000001
M2mw v M3l	200	0.595	−1.00	<0.00001	0.00007
M2mw v M3mw	427	0.985	0.016	<0.000001	0.203
M2mw v M3dw	408	0.762	0.153	<0.00001	0.0001
M2mw v M3l	198	0.601	−1.00	<0.00001	0.0004
M2dw v M3mw	424	0.844	0.160	<0.000001	<0.000001
M2dw v M3dw	405	0.850	0.264	<0.000001	0.0008
M3l v M3mw	227	0.739	−1.00	<0.000001	0.0001
M3l v M3dw	226	0.654	−1.00	<0.000001	0.00001
M3mw v M3dw	459	0.859	0.534	<0.000001	0.00004

Baboon Left Mandibular
		Correlations (MLEs)		Significance of Correlations P(Hypothesis)
Phenotype pair	N	ρG	ρE	ρG =0	| ρG |=1
I1ll v I1md	449	0.301	0.225	0.077	0.0000001
I1ll v I2ll	424	0.979	0.438	<0.000001	0.239
I1ll v I2md	430	0.907	0.025	<0.00001	0.159
I1ll v P3l	109	−0.044	1.00	0.884	0.0196
I1ll v P3w	196	0.199	−0.068	0.494	0.013
I1ll v P4l	280	−0.016	0.059	0.935	<0.000001
I1ll v P4w	278	0.202	−0.106	0.326	0.00004
I1ll v M1l	288	0.251	0.073	0.142	<0.000001
I1ll v M1mw	280	−0.309	−0.032	0.133	0.0001
I1ll v M1dw	276	−0.453	0.034	0.123	0.116
I1ll v M2l	375	0.336	−0.318	0.032	<0.000001
I1ll v M2mw	375	−0.201	−0.075	0.259	<0.000001
I1ll v M2dw	367	0.192	−0.047	0.127	0.0000068
I1ll v M3l	248	0.117	0.002	0.583	0.0016
I1ll v M3mw	373	−0.137	−0.016	0.494	0.0000058
I1ll v M3dw	350	−0.266	0.030	0.177	0.00001
I1md v I2ll	426	0.333	0.155	0.071	0.000006
I1md v I2md	434	0.824	0.321	0.00028	0.081
I1md v P3l	111	0.207	1.00	0.505	<0.000001
I1md v P3w	199	0.102	0.253	0.705	0.005
I1md v P4l	284	0.128	0.167	0.514	<0.000001
I1md v P4w	281	−0.175	0.251	0.443	0.003
I1md v M1l	289	0.127	0.734	0.443	<0.000001
I1md v M1mw	281	0.130	0.260	0.522	0.00006
I1md v M1dw	277	0.289	0.0695	0.269	0.035
I1md v M2l	378	0.324	0.285	0.039	<0.000001
I1md v M2mw	377	0.252	0.276	0.154	<0.000001
I1md v M2dw	370	0.068	0.263	0.732	<0.000001
I1md v M3l	249	0.122	0.020	0.547	0.00069
I1md v M3mw	376	0.2199	0.088	0.297	0.0000053
I1md v M3dw	353	0.010	0.152	0.96	0.0000046
I2ll v I2md	448	0.897	0.067	0.00003	0.178
I2ll v P3l	108	−0.069	1.00	0.796	0.021
I2ll v P3w	197	0.144	0.122	0.659	0.018
I2ll v P4l	284	−0.061	0.173	0.773	0.0000017
I2ll v P4w	282	0.144	0.153	0.518	0.000008
I2ll v M1l	284	0.045	0.527	0.806	0.0000001
I2ll v M1mw	276	−0.616	0.080	0.013	0.023
I2ll v M1dw	271	−0.921	0.141	0.0099	0.422
I2ll v M2l	373	0.464	−0.147	0.004	0.0000004
I2ll v M2mw	372	−0.187	−0.087	0.358	0.0000186
I2ll v M2dw	365	−0.266	−0.055	0.231	0.0002
I2ll v M3l	248	0.317	−0.081	0.164	0.0017
I2ll v M3mw	374	−0.165	0.069	0.469	0.00035
I2ll v M3dw	350	−0.246	0.017	0.274	0.0003
I2md v P3l	110	−0.134	1.00	0.756	0.052
I2md v P3w	200	0.185	0.121	0.612	0.008
I2md v P4l	289	−0.203	0.207	0.466	0.002
I2md v P4w	286	−0.332	0.163	0.264	0.006
I2md v M1l	290	0.207	0.231	0.432	0.0015
I2md v M1mw	282	−0.616	0.135	0.032	0.033
I2md v M1dw	277	−0.579	0.056	0.119	0.130
I2md v M2l	378	0.260	0.097	0.275	0.0007
I2md v M2mw	377	−0.356	0.010	0.191	0.007
I2md v M2dw	370	−0.527	0.037	0.086	0.039
I2md v M3l	251	−0.034	0.073	0.911	0.0003
I2md v M3mw	379	−0.398	−0.010	0.207	0.011
I2md v M3dw	355	0.528	−0.099	0.532	0.0162
P3l v P3w	135	−0.593	−1.00	0.368	0.007
P3l v P4l	135	0.206	1.00	0.425	0.0000001
P3l v P4w	127	0.292	−1.00	0.363	0.205
P3l v M1l	91	−0.068	−1.00	0.751	<0.0000001
P3l v M1mw	90	−0.378	−1.00	0.27	0.00005
P3l v M1dw	88	0.285	−0.900	0.449	0.125
P3l v M2l	125	0.396	1.00	0.097	<0.0000001
P3l v M2mw	123	0.151	−1.00	0.475	0.004
P3l v M2dw	119	0.341	−1.00	0.169	0.020
P3l v M3l	80	0.829	−1.00	0.013	0.237
P3l v M3mw	126	0.231	1.00	0.380	0.00006
P3l v M3dw	118	0.391	−1.00	0.259	0.013
P3w v P4l	246	0.392	0.045	0.177	0.013
P3w v P4w	233	0.676	0.581	0.015	0.007
P3w v M1l	164	0.361	0.519	0.211	0.019
P3w v M1mw	163	−0.181	−0.428	0.564	0.005
P3w v M1dw	159	−0.237	0.364	0.581	0.109
P3w v M2l	229	−0.581	−0.091	0.016	0.008
P3w v M2mw	225	0.320	0.362	0.220	0.004
P3w v M2dw	220	0.308	0.323	0.252	0.002
P3w v M3l	153	0.044	−0.126	0.902	0.003
P3w v M3mw	230	0.414	0.186	0.141	0.002
P3w v M3dw	213	−0.599	0.083	0.022	0.008
P4l v P4w	328	0.303	0.314	0.191	0.000076
P4l v M1l	222	0.724	0.123	0.00005	0.0002
P4l v M1mw	217	0.114	0.312	0.629	0.00003
P4l v M1dw	210	0.321	0.324	0.315	0.065
P4l v M2l	313	0.801	−0.027	<0.000001	0.0005
P4l v M2mw	309	0.334	0.454	0.104	<0.000001
P4l v M2dw	303	0.408	0.325	0.044	0.0000001
P4l v M3l	219	0.626	−0.024	0.005	0.001
P4l v M3mw	322	0.267	0.270	0.215	0.0000003
P4l v M3dw	301	0.554	0.052	0.004	0.00001
P4w v M1l	216	0.553	0.264	0.005	0.0008
P4w v M1mw	214	0.339	0.397	0.168	0.00004
P4w v M1dw	205	0.264	0.356	0.470	0.087
P4w v M2l	304	0.519	0.062	0.005	0.00003
P4w v M2mw	300	0.395	0.257	0.056	0.00001
P4w v M2dw	294	0.456	0.003	0.041	0.0007
P4w v M3l	218	0.706	−0.462	0.006	0.056
P4w v M3mw	317	0.557	0.126	0.012	<0.0001
P4w v M3dw	299	0.771	−0.315	0.0003	0.060
M1l v M1mw	330	0.463	0.574	0.023	0.00007
M1l v M1dw	323	0.484	0.593	0.071	0.034
M1l v M2l	327	0.818	0.073	<0.0000001	0.0005
M1l v M2mw	326	0.487	0.268	0.004	<0.0000001
M1l v M2dw	321	0.319	0.553	0.091	0.0000001
M1l v M3l	206	0.777	−1.00	<0.0000001	0.035
M1l v M3mw	309	0.649	−0.216	0.0001	0.00002
M1l v M3dw	291	0.436	0.161	0.020	0.00004
M1mw v M1dw	320	0.760	0.902	0.008	0.099
M1mw v M2l	321	0.102	0.516	0.58	0.00001
M1mw v M2mw	320	0.820	0.442	<0.00001	0.024
M1mw v M2dw	316	0.673	0.455	0.0005	0.0007
M1mw v M3l	199	0.506	0.062	0.04	0.007
M1mw v M3mw	303	0.684	0.334	0.0007	0.002
M1mw v M3dw	286	0.575	0.277	0.007	0.0015
M1dw v M2l	314	0.199	0.438	0.44	0.029
M1dw v M2mw	313	0.770	0.468	0.0008	0.061
M1dw v M2dw	308	0.899	0.456	0.00005	0.193
M1dw v M3l	195	0.663	0.153	0.040	0.056
M1dw v M3mw	294	0.652	0.274	0.014	0.031
M1dw v M3dw	279	0.790	0.225	0.002	0.13
M2l v M2mw	479	0.587	0.544	0.0002	<0.0000001
M2l v M2dw	471	0.491	0.575	0.004	<0.0000001
M2l v M3l	291	0.902	0.034	<0.00001	0.157
M2l v M3mw	440	0.651	0.020	0.0001	0.00001
M2l v M3dw	415	0.494	0.198	0.009	0.00003
M2mw v M2dw	468	0.798	0.761	<0.00001	0.0000002
M2mw v M3l	289	0.715	−0.190	0.0007	0.016
M2mw v M3mw	436	0.976	0.230	<0.0000001	0.329
M2mw v M3dw	412	0.780	0.224	0.00005	0.011
M2dw v M3l	287	0.761	−0.190	0.002	0.059
M2dw v M3mw	429	0.654	0.379	0.0019	0.0004
M2dw v M3dw	407	0.876	0.327	0.00001	0.054
M3l v M3mw	320	0.674	0.294	0.013	0.029
M3l v M3dw	314	0.738	0.235	0.006	0.049
M3mw v M3dw	451	0.897	0.847	nc	nc

Mouse Right Maxillary
		Correlations (MLEs)		Significance of Correlations P(Hypothesis)
Phenotype pair	N	ρG	ρE	ρG =0	| ρG |=1
I1ll v M1l	207	0.043	0.590	0.768	<0.0001
I1ll v M1mw	207	0.215	−0.193	0.15	<0.0001
I1ll v M1dw	207	0.127	−0.161	0.33	<0.0001
I1ll v M2l	207	0.296	−0.842	0.019	<0.0001
I1ll v M2mw	207	0.227	−0.005	0.206	<0.0001
I1ll v M2dw	207	0.304	−0.576	0.03	<0.0001
I1ll v M3l	207	0.518	−0.535	<0.001	<0.0001
I1ll v M3mw	207	0.252	−0.279	<0.01	<0.05
M1l v M1mw	207	0.797	−0.291	<0.0001	<0.0001
M1l v M1dw	207	0.895	−0.572	<0.0001	<0.0001
M1l v M2l	207	0.834	−0.798	<0.0001	<0.0001
M1l v M2mw	207	0.683	−0.220	<0.0001	<0.0001
M1l v M2dw	207	0.886	−1.000	<0.0001	<0.01
M1l v M3l	207	0.667	−0.850	<0.0001	<0.0001
M1l v M3mw	207	0.716	−0.563	<0.0001	<0.0001
M1mw v M1dw	207	0.783	0.438	<0.0001	<0.0001
M1mw v M2l	207	0.603	−0.148	<0.0001	<0.0001
M1mw v M2mw	207	0.707	−0.270	<0.0001	<0.0001
M1mw v M2dw	207	0.666	−0.252	<0.0001	<0.0001
M1mw v M3l	207	0.563	−0.343	<0.0001	<0.0001
M1mw v M3mw	207	0.690	−0.721	<0.0001	<0.0001
M1dw v M2l	207	0.732	−1.000	<0.0001	<0.0001
M1dw v M2mw	207	0.624	−0.278	<0.0001	<0.0001
M1dw v M2dw	207	0.821	−0.938	<0.0001	<0.0001
M1dw v M3l	207	0.524	−0.911	<0.0001	<0.0001
M1dw v M3mw	207	0.671	−1.000	<0.0001	<0.0001
M2l v M2mw	207	0.735	−0.621	<0.0001	<0.0001
M2l v M2dw	207	0.854	0.207	<0.0001	<0.0001
M2l v M3l	207	0.711	0.221	<0.0001	<0.0001
M2l v M3mw	207	0.619	0.119	<0.0001	<0.0001
M2mw v M2dw	207	0.742	0.054	<0.0001	<0.0001
M2mw v M3l	207	0.806	−0.325	<0.0001	<0.001
M2mw v M3mw	207	0.692	−0.456	<0.0001	<0.0001
M2dw v M3l	206	0.660	0.147	<0.0001	<0.0001
M2dw v M3mw	206	0.711	−0.166	<0.0001	<0.0001
M3l v M3mw	201	0.782	0.515	<0.0001	<0.0001

Mouse Left Maxillary
		Correlations (MLEs)		Significance of Correlations P(Hypothesis)
Phenotype pair	N	ρG	ρE	ρG =0	| ρG |=1
I1ll v M1l	207	0.137	0.427	0.346	<0.0001
I1ll v M1mw	207	0.110	0.053	0.488	<0.0001
I1ll v M1dw	207	0.176	−0.135	0.199	<0.0001
I1ll v M2l	207	0.262	−0.880	0.044	<0.0001
I1ll v M2mw	207	0.187	0.145	0.257	<0.0001
I1ll v M2dw	207	0.238	−0.261	0.097	<0.0001
I1ll v M3l	207	0.446	−0.472	0.003	<0.0001
I1ll v M3mw	207	0.404	−0.416	0.009	<0.0001
M1l v M1mw	207	0.801	−0.183	<0.0001	<0.0001
M1l v M1dw	207	0.878	−0.438	<0.0001	<0.0001
M1l v M2l	207	0.852	−0.961	<0.0001	<0.0001
M1l v M2mw	207	0.716	−0.302	<0.0001	<0.0001
M1l v M2dw	207	0.839	−0.500	<0.0001	<0.001
M1l v M3l	207	0.729	−0.410	<0.0001	<0.0001
M1l v M3mw	207	0.739	−0.398	<0.0001	<0.01
M1mw v M1dw	207	0.808	0.363	<0.0001	<0.0001
M1mw v M2l	207	0.538	−0.137	<0.0001	<0.0001
M1mw v M2mw	207	0.652	−0.199	<0.0001	<0.0001
M1mw v M2dw	207	0.700	−0.414	<0.0001	<0.0001
M1mw v M3l	207	0.484	−0.063	<0.001	<0.0001
M1mw v M3mw	207	0.588	−0.089	<0.0001	<0.0001
M1dw v M2l	207	0.692	−0.451	<0.0001	<0.0001
M1dw v M2mw	207	0.704	−0.525	<0.0001	<0.0001
M1dw v M2dw	207	0.808	−0.477	<0.0001	<0.0001
M1dw v M3l	207	0.537	−0.046	<0.0001	<0.0001
M1dw v M3mw	207	0.578	−0.072	<0.0001	<0.0001
M2l v M2mw	207	0.671	−0.159	<0.0001	<0.0001
M2l v M2dw	207	0.795	0.268	<0.0001	<0.0001
M2l v M3l	207	0.762	0.256	<0.0001	<0.0001
M2l v M3mw	207	0.651	0.373	<0.0001	<0.0001
M2mw v M2dw	207	0.720	0.141	<0.0001	<0.0001
M2mw v M3l	207	0.721	−0.009	<0.0001	<0.0001
M2mw v M3mw	207	0.728	−0.094	<0.0001	<0.0001
M2dw v M3l	206	0.695	0.075	<0.0001	<0.0001
M2dw v M3mw	206	0.741	0.192	<0.0001	<0.0001
M3l v M3mw	202	0.808	0.689	<0.0001	<0.0001

Mouse Right Mandible
		Correlations (MLEs)		Significance of Correlations P(Hypothesis)
Phenotype pair	N	ρG	ρE	ρG =0	| ρG |=1
I1ll v I1md	197	0.088	0.886	0.707	<0.0001
I1ll v M1l	204	0.079	0.228	0.571	<0.0001
I1ll v M1mw	204	0.038	0.125	0.851	<0.0001
I1ll v M1dw	204	0.079	−1.000	0.564	<0.0001
I1ll v M2l	204	0.095	−0.522	0.505	<0.0001
I1ll v M2mw	204	0.048	−0.368	0.742	<0.0001
I1ll v M2dw	204	0.574	0.522	nc	nc
I1ll v M3l	204	0.349	−0.554	0.030	<0.0001
I1md v M1l	204	0.538	0.325	0.003	0.074
I1md v M1mw	204	0.533	0.112	0.016	0.023
I1md v M1dw	204	0.521	−1.000	0.0012	0.008
I1md v M2l	204	0.675	−0.523	<0.001	0.072
I1md v M2mw	204	0.503	−0.183	0.008	0.042
I1md v M2dw	204	0.593	−0.408	0.001	0.075
I1md v M3l	204	0.870	−0.519	<0.0001	0.218
M1l v M1mw	204	0.524	0.441	<0.0001	<0.0001
M1l v M1dw	204	0.778	−1.000	<0.0001	<0.0001
M1l v M2l	204	0.876	−0.732	<0.0001	<0.01
M1l v M2mw	204	0.819	−0.554	<0.0001	<0.0001
M1l v M2dw	204	0.741	−1.00	<0.0001	<0.0001
M1l v M3l	204	0.645	−1.00	<0.0001	<0.0001
M1mw v M1dw	204	0.675	0.528	<0.0001	<0.0001
M1mw v M2l	204	0.599	−0.074	<0.0001	<0.0001
M1mw v M2mw	204	0.623	0.115	<0.0001	<0.0001
M1mw v M2dw	204	0.582	−0.017	<0.0001	<0.0001
M1mw v M3l	204	0.509	−0.404	<0.001	<0.0001
M1dw v M2l	204	0.782	−0.128	<0.0001	<0.0001
M1dw v M2mw	204	0.884	−0.522	<0.0001	<0.0001
M1dw v M2dw	204	0.767	−0.431	<0.0001	<0.0001
M1dw v M3l	204	0.409	1.000	<0.001	<0.0001
M2l v M2mw	203	0.947	0.036	<0.0001	<0.01
M2l v M2dw	203	0.907	−0.058	<0.0001	<0.01
M2l v M3l	203	0.768	0.188	<0.0001	<0.01
M2mw v M2dw	203	0.942	−0.008	<0.0001	<0.01
M2mw v M3l	203	0.719	−0.026	<0.0001	<0.0001
M2dw v M3l	203	0.729	0.268	<0.0001	<0.0001

Mouse Left Mandible
		Correlations (MLEs)		Significance of Correlations P(Hypothesis)
Phenotype pair	N	ρG	ρE	ρG =0	| ρG |=1
I1ll v M1l	204	0.027	1.000	0.844	<0.0001
I1ll v M1mw	204	0.126	−0.138	0.548	<0.0001
I1ll v M1dw	204	0.034	−0.271	0.817	<0.0001
I1ll v M2l	204	0.018	−0.491	0.906	<0.0001
I1ll v M2mw	204	−0.123	−0.150	0.416	<0.0001
I1ll v M2dw	204	−0.140	0.063	0.350	<0.0001
I1ll v M3l	204	0.220	−0.421	0.215	<0.0001
I1md v M1l	204	0.510	1.000	0.004	0.050
I1md v M1mw	204	0.665	−0.179	0.001	0.009
I1md v M1dw	204	0.534	−0.094	0.003	0.03
I1md v M2l	204	0.693	−0.531	0.0003	0.09
I1md v M2mw	204	0.405	−0.005	0.07	0.10
I1md v M2dw	204	0.455	−0.124	0.017	0.05
I1md v M3l	204	0.840	−0.541	<0.0001	0.12
M1l v M1mw	204	0.671	−0.608	<0.0001	<0.0001
M1l v M1dw	204	0.843	−0.560	<0.0001	<0.0001
M1l v M2l	204	0.905	−1.000	<0.0001	0.036
M1l v M2mw	204	0.803	−0.388	<0.0001	<0.0001
M1l v M2dw	204	0.671	−1.000	<0.0001	<0.0001
M1l v M3l	204	0.647	−1.000	<0.0001	<0.001
M1mw v M1dw	204	0.735	0.525	<0.0001	<0.0001
M1mw v M2l	204	0.492	0.398	<0.001	<0.0001
M1mw v M2mw	204	0.678	−0.140	<0.0001	<0.0001
M1mw v M2dw	204	0.621	−0.139	<0.0001	<0.0001
M1mw v M3l	204	0.447	−0.008	0.005	<0.0001
M1dw v M2l	204	0.886	−0.091	<0.0001	<0.01
M1dw v M2mw	204	0.937	−0.050	<0.0001	0.011
M1dw v M2dw	204	0.824	−0.434	<0.0001	<0.0001
M1dw v M3l	204	0.715	−0.306	<0.0001	<0.001
M2l v M2mw	203	0.989	−0.145	<0.0001	0.34
M2l v M2dw	203	0.897	−0.372	<0.0001	<0.01
M2l v M3l	203	0.823	0.099	<0.0001	<0.01
M2mw v M2dw	203	0.950	−0.264	<0.0001	<0.01
M2mw v M3l	203	0.710	0.004	<0.0001	<0.0001
M2dw v M3l	203	0.710	0.100	<0.0001	<0.0001

¹MLE: maximum likelihood estimate; P(Hypothesis): probability of the hypothesis (indicated in columns below) being true given the available pedigreed data; nc = not computable.

For the baboon population, of the 208 incisor:post-canine analyses (maxillary and mandibular), only 26 return significant (p≤0.05) genetic correlations (12 in the maxilla and 14 in the mandible).

In contrast, all of the maxillary incisor:incisor comparisons yield significant genetic correlations, 14 of 16 maxillary premolar:premolar analyses returned significant genetic correlations, as did 65 of 81 maxillary molar:molar comparisons. Approximately half of the 72 maxillary premolar:molar analyses returned significant genetic correlations.

For the mandible, the mesiodistal breadth of the central incisor is not significantly correlated with the labiolingual breadth of the lateral incisor, although all other mandibular incisor:incisor correlations are insignificantly different from one. The premolar:premolar analyses return fewer positive genetic correlations than found for the maxilla, although we note that the mandibular premolar sample sizes are much smaller (e.g., 150 versus 250). Twenty-nine of the premolar:molar correlations are significantly greater than zero, approximately 40% compared to the approximately 50% for the maxilla. Seventy-four of the 81 molar:molar analyses returned significant genetic correlations, even more than were seen for the maxilla.

The handful of genetic correlations noted between the mandibular incisors and molars suggest that the genetic relationship is inverse, as they returned negative correlations. This would indicate that when the incisors are smaller, the first and second molars are larger. Given that these results are not identical on the right and left sides, and are interspersed with insignificant analyses, this possible pattern needs to be explored in more detail as the evolutionary implications could be quite interesting and important.

In the mouse population, the labiolingual diameter of the mandibular incisors yields no significant genetic correlation with the molars while the mesiodistal diameter of the mandibular incisor is significantly correlated with the molars. For the maxillary incisors, the labiolingual diameter has no genetic correlation with the first molars (as seen in the mandible), and incomplete pleiotropy with the mesiodistal length of the second molars and both length and width of the third molars.

The mouse molar:molar analyses yield a more consistent pattern of high genetic correlations compared to the baboons, but we are hesitant to place emphasis on this distinction given that the mouse pedigree structure will tend to overestimate genetic correlations. While mouse molars do develop almost simultaneously, in contrast to the sequential formation of baboon molars (and this might result in a higher degree of integration), we do not feel that our analyses are robust enough to indicate that this difference is biologically significant at this point in time.

Discussion

In recent years, quantitative genetic methods have been most commonly employed to identify genomic loci that significantly influence phenotypic variation, and often within a medical framework (e.g., lipoprotein metabolism in baboons: Rainwater et al, 2009; MC4R influence on energy expenditure and appetite in children: Cole et al, 2010), but sometimes include other phenotypes (e.g., dog coat color variation: Cadieu et al, 2009; an adaptive allele for deer mouse coloration: Linnen et al, 2009). Quantitative genetics has also been recruited to explore phenotypic response to natural selection (e.g., Boag, ’83), or lack thereof (e.g., Kruuk et al, 2002), sexual selection (e.g., Lande and Kirkpatrick, ’88), selection in the laboratory (e.g., Beldade et al, 2002), adaptive radiations (Schluter, 2000), and complex fitness surfaces (e.g., Blows et al, 2003).

In contrast to these foci, our research uses quantitative genetics to understand how genes influence morphological variation with the specific goal of improving our ability to interpret evolutionary processes from the fossil record. As such, we use a quantitative genetic approach to recast skeletal variation in terms of the underlying pattern of genetic correlations between traits. Our objective has been to detect and exploit genetic correlations -- indicative of additive genetic pleiotropy or shared additive genetic effects between trait pairs. We then use these genetic correlations to infer patterns of morphological integration (similar to Hallgrimsson et al, 2007; for example see Hlusko et al, 2004a, b; Hlusko and Mahaney, 2009; Koh et al, 2010) rather than for identifying specific genomic loci or quantifying selection, as is more typically done.

Our results are the first quantitative genetic evidence for modularity within the mammalian dental arcade and the first evidence of a shared dental genetic architecture across mammals broadly. Developmental studies have shown that mammalian tooth organogenesis relies on many of the same genes, for example Shh expression in mouse (Vaahtokari et al, ‘96), vole (Keränen et al, ‘98), shrew (Yamanaka et al, 2007), ferret (Järvinen et al, 2009), and opossum (Moustakas et al, 2009). However, little is known about how these developmental genes are expressed similarly or differentially across the dental arcade in various mammals (but see Moustakas et al, 2009, for recent results in opossum compared to mouse).

Mice and monkeys last shared a genetic common ancestor ~ 69 million years ago (Eizirik et al, 2001) and extant mice have highly derived dentitions compared to those early mammals, in part by having large continuously growing incisors. As such, genetic independence of the incisors may be expected in extant mice. It is therefore intriguing that incisor size variation is genetically independent from the size variation in the postcanine dentition in both mice and baboons. This similarity predicts that dental variation is controlled in a similar way in other mammalian orders.

Other biologists have shown that the genetic architecture has a significant influence on how, and how quickly a species responds to selective pressure (Lande, ‘79; Schluter, 2000; Beldade et al, 2002). If similar genes or sets of genes influence size variation across the entire dental arcade, we would expect to see more concomitant change in incisor and molar size, as selection for or against change in one region of the arcade would simultaneously affect the other region. However, modularity (Wagner and Altenberg, ‘96; Schlosser and Wagner, 2004) in the dentition, or rather, a level of genetic independence between various regions along the tooth row as we have identified here, would facilitate evolvability in size disparity because each module could respond independently to different selective pressures.

For example, in mammals independent anterior and posterior dental modules would facilitate responses to the different selective pressures that act on the incisors in contrast to the molars (e.g., grooming or food procurement versus food mastication, respectively). This genetic modularity may either have facilitated or been the result of the very different selective pressures and functional constraints experienced by the anterior and posterior dentitions.

A survey of mammalian dental evolution provides strong morphological evidence for the pervasiveness of such a modular genetic architecture. Repeatedly, and in numerous lineages, incisors have undergone tremendous diversification in both size and shape (Wortman 1886), although we focus on size here. In some lineages, incisors have reduced in size tremendously (i.e., felids; manatees – only males have one incisors; and robust Australopithecus hominid species), or have been lost completely (i.e., all extant xenarthrans – armadillos, tree sloths, and anteaters; cervid and bovid maxillae). In other lineages, they have developed highly specialized functions, such as the elongated mandibular tooth combs used by lemurs for grooming (coupled with extreme size reduction in the maxillary incisors), the long spear-like incisors of “shrew” opossums (Caenolestidae, Marsupialia), the continuously growing incisors used for gnawing in several lineages (e.g., aye-ayes within the Primates, mice to porcupines in the Rodentia), the tusks/incisors of hippopotamus and dugongs, the very large tusks/incisors of elephants used for rooting and uprooting trees, and perhaps the most extreme case, the ~3 m long spiraled tusk/incisor in the Arctic Ocean narwhal (Monodon monoceros) thought to be used for breaking ice, weaponry, or possibly even echolocation (Nowak, ‘91). The eutherian mammalian fossil record yields even more variation than is seen in the extant taxa noted above (Rose, 2006). In virtually all of these taxa, the postcanine dentition may vary significantly in shape, but the size variance is not as extreme as in the incisors.

This pattern of dental size diversity is even seen in the earliest mammals in the late Cretaceous. For example, Zalambdalestes had long procumbent mandibular incisors in contrast to the shorter peg-like incisors of Malestes and even shorter Asioryctes, all of which sit outside the placental clade (Wible et al, 2007). Therefore, based on phenotypic data from extant and fossil mammals, and the results from our quantitative genetic analyses of dental variation in mice and baboons, we hypothesize that a genetic independence between incisor and postcanine size variation is symplesiomorphic to eutherian mammals, and perhaps to mammals more generally.

One clear difference between mouse and baboon genetic correlation matrices is the significant genetic correlation between the mesiodistal width of the mouse mandibular incisor and molar size, where baboons have no genetic correlation. Although one might propose multiple explanatory scenarios consistent with these two data points, they are inadequate for identifying an evolutionary trend, much less confirming one. Additional populations need to be studied to identify the evolutionary polarity of this pattern.

We also note that the baboon results suggest that there may be an inverse genetic relationship (genetic correlation) between the mandibular incisors and the mandibular first and/or second molars. While these results are not consistent, and are interspersed with some insignificant results, if further analyses bolster this pattern the evolutionary implications are interesting. Several primate lineages show a simultaneous reduction in the incisor region and expansion of the molar region (for example, in the robust Australopithecus species of hominids and the Theropithecus brumpti lineage of cercopithecoids).

From a developmental perspective, the odontogenic code (Thomas and Sharpe, ‘98) is clearly compatible with these results, as it could be interpreted to predict a certain degree of independence between the incisor and molar regions. However, for the post-canine pattern seen in baboons, this pattern of incomplete pleiotropy may better fit with a morphogenetic gradient, or reaction-diffusion mechanism (Jernvall, 2000; Kangas et al, 2004).

While the field (Butler, ’39) and clone (Osborn, ’78) models for tooth development have received a significant amount of attention historically, it is important to keep in mind that these models were developed primarily on phenotypic data and that hypothesis testing was rarely conclusive (see references cited previously). Our current understanding of tooth development suggests that neither is likely to be entirely right or wrong (as also suggested by the hybrid Cooperative Genetic Integration model proposed by Mitsiadis and Smith, 2006). As we continue to improve our understanding of tooth organogenesis from developmental studies and patterns of genetic correlation from quantitative genetic analyses, we are better off reconstructing tooth patterning mechanisms without these speculative models constraining our interpretation of the actual genetic data.

Here we demonstrated that quantitative genetic analyses provide a useful tool for linking developmental genetics of tooth organogenesis with studies of morphological variation in the adult dentition by employing the concept of modularity. As more pedigreed populations are developed for other taxa, this may prove to be a powerful and common approach through which we can bridge the gap between genotype and phenotype and better understand how this relationship has evolved through time as documented in the fossil record.