Development of Adherence Metrics for Caloric Restriction Interventions

Abstract

Background

Objective measures are needed to quantify dietary adherence during caloric restriction (CR) while participants are free-living. One method to monitor adherence is to compare observed weight loss to the expected weight loss during a prescribed level of CR. Normograms (graphs) of expected weight loss can be created from mathematical modeling of weight change to a given level of CR, conditional on the individual's set of baseline characteristics. These normograms can then be used by counselors to help the participant adhere to their caloric target.

Purpose

(1) To develop models of weight loss over a year of caloric restriction given demographics (age and sex), and well defined measurements of of Body Mass Index, total daily energy expenditure (TDEE) and %CR. (2) To utilize these models to develop normograms given level of caloric restriction, and measures of these variables.

Methods

Seventy-seven individuals completing a 6-12 month CR intervention (CALERIE) had body weight and body composition measured frequently. Energy intake (and %CR) was estimated from TDEE (by doubly labeled water) and body composition (by DXA) at baseline and months 1, 3, 6 and 12. Body weight was modeled to determine the predictors and distribution of the expected trajectory of percent weight change over 12 months of caloric restriction.

Results

As expected, CR was related to change in body weight. Controlling for time-varying measures, initially simple models of the functional form indicated that the trajectory of percent weight change was predicted by a non-linear function of initial age, TDEE, %CR, and sex. Using these estimates, normograms for the weight change expected during a 25%CR were developed. Our model estimates that the mean weight loss (% change from baseline weight) for an individual adherent to a 25% CR regimen is -10.9±6.3% for females and -13.9±6.4% for men after 12 months.

Limitations

There are several limitations. Sample sizes are small (n=77), and, by design, the protocols, including prescribed CR, for the interventions differed by site, and not all subjects completed a year of follow-up. In addition, the inclusion of subjects by age and initial BMI was constricted so that these results may no generalize to other older, obese subjects.

Conclusions

The trajectory of percent weight change during CR interventions in the presence of well measured covariates can be modeled using simple non-linear functions, and is related level of CR, the percent change in TDEE, gender, and age. Displayed on a normogram, individually tailored trajectories can be used by counselors and participants to monitor weight loss and adherence to a CR regimen.

It is difficult to determine adherence to dietary interventions in free-living individuals. Inter-individual weight change in response to calorie restriction (CR) is highly variable at a given point in time, as well as over time. This variability is likely due to individual differences in physiology and genetics(1) and, importantly, individual differences in adherence to the prescribed dietary intervention (2). However, change in body weight during CR is one easily measured and often used marker of adherence to the prescribed intervention (3-5). In animal experiments, food intake can be controlled precisely and the effect of dietary manipulations on body weight and other endpoints can be objectively measured and modeled. In free-living humans, however, where the level of adherence and hence CR cannot be controlled precisely, the observed changes in body weight are less well characterized. While investigators can enhance adherence with strategies such as controlled feeding under supervised conditions (6, 7), this is not feasible in large long-term outpatient studies.

A common strategy to assess adherence to a prescribed CR diet in an outpatient setting is to estimate daily energy intake from 7-day food diaries or 24-hour dietary recall. These self-report methods, however, have questionable validity (8). For example, doubly labeled water studies have demonstrated that people under-report energy intake when using self-report methods to measure energy intake (9, 10).

Combining assessments of energy expenditure (i.e., doubly labeled water) and changes in body composition (i.e., fat mass and fat-free mass) by dual x-ray absorptiometry (DXA) provides a more sophisticated determination of energy intake during CR (11). Validation of this method against 24–hour energy expenditure measured in a metabolic chamber indicated that this technique provides a good assessment of energy expenditure. Nevertheless, because changes in body energy stores are small and difficult to accurately quantify with DXA in the short-term (within 1 month), energy intake and hence adherence, can only be accurately determined over longer periods of negative energy balance (i.e., across months). Doubly labeled water studies are expensive, however, and not readily available in clinical settings. Body weight change is a widely acceptable metric for quantifying adherence to CR programs and body weight can easily and accurately be obtained by study subjects, clinicians and investigators. The Comprehensive Assessment of the Long-term Effect of Reducing Intake of Energy (CALERIE) is performing the first clinical studies examining the effects of CR on biomarkers of aging and longevity in non-obese human beings. Three clinical sites are involved in this research program; Washington University in St. Louis, MO, Tufts University in Boston, MA and Pennington Biomedical Research Center in Baton Rouge, LA; the Duke Clinical Research Institute, in Durham, NC, serves as the Coordinating Center. Phase 1 of the program was conceived as site-specific, short-term, pilot studies (12-14) to address specific design issues. These studies were of relatively short duration (6-12 months) and varied in amount of CR prescribed. In each study however, CR was prescribed on an individual basis as a percent reduction in energy intake measured by 4 weeks of energy expenditure by doubly labeled water during weight maintenance. Using the longitudinal weight change and adherence data (calculated %CR from doubly labeled water and DXA) from the CALERIE Phase 1 studies, our goal was to develop prediction equations to model percent weight change over time.

The Phase 2 study of CALERIE is in progress and designed as a single-protocol, multi-center, randomized controlled trial (15). An important goal of this analysis, therefore, is to establish boundaries for the expected percent change in body weight during a 25% CR to implement during our Phase 2 study. Moreover, the equations and methodology we developed might prove useful in other settings such as the prescription of CR diets for the treatment of obesity. The weight change normograms or graphs allow investigators to monitor individual adherence in real time and to counsel participants to better achieve their prescribed calorie target.

Methods

Subjects

Eligible subjects (Age: 20-60 years) were generally healthy (BMI: 23.5 - 29.9 kg/m²) and not engaged in regular exercise. Only subjects randomized to CR interventions without an exercise prescription were included in these analyses. Therefore, subjects randomized to control groups (Pennington: 2, Washington U: 1) or exercise groups (Pennington: 1, Washington U: 1) were omitted from these analyses. The CR prescriptions and duration of intervention differed by site; 20% CR for 12 months at Washington U, 10% and 30% CR for 12 months at Tufts, and 25% CR for 6 months at Pennington. In addition, the CR interventions at Tufts included a comparison of two types of diets (i.e., high and low-glycemic index), as described previously (12). Local Institutional Review Boards approved the site-specific studies and informed consent was obtained from each participant before enrollment. In total, 79 subjects were randomized, while 77 provided information on the covariates the outcomes measures.

Body Weight

Metabolic weight was determined by the mean of two consecutive measurements obtained in the morning following a 12 hour fast and morning void and corrected for the weight of a hospital gown.

Body Composition

Whole body percent body fat was measured using DXA (Hologics QDR 4500A, Bedford, MA) at Pennington and Washington U and air displacement plethysmography (BOD POD^®, Life Measurement, Inc. Concord, CA) at Tufts. Fat mass (FM) and fat-free mass (FFM) were calculated from percent body fat and metabolic body weight.

Total Daily Energy Expenditure (TDEE)

TDEE was measured over 14-days by doubly labeled water (DLW). Two consecutive measures were conducted at baseline and single measures at months 3, 6, 9, and 12 of the CR interventions. Briefly, subjects provided 2 pre-dose urine samples, and then received an oral dose of DLW containing 2.0 g 10% H₂¹⁸O and 0.12 g 99.9% ²H₂O per kg of estimated total body water. Post-dose urine samples were collected at 1.5, 3, 4.5 and 6 hours on the day of dosing (the 1.5 and 3 hour samples were discarded). On days 7 and 14 after dosing, subjects provided 2 more timed urine samples. Each sample was analyzed for ¹⁸O and ²H abundance by isotope ratio mass spectrometry at a central laboratory (16). The isotopic enrichments of the post-dose urine samples were compared with the pre-dose samples to calculate elimination rates of deuterium and oxygen-18 (k_H and k_O, respectively) using linear regression, and initial isotope dilution spaces were calculated by extrapolation to time zero. CO₂ production rate (rCO₂) was calculated using the equations of Schoeller et al. (17) as modified by Racette et al (18). Total daily energy expenditure was calculated by multiplying rCO₂ by the energy equivalent of CO₂; RQ was estimated to be 0.86, corresponding to a diet containing 55% carbohydrate, 30% fat, and 15% protein. Percent TDEE was computed by comparing the follow-up TDEE to the baseline TDEE.

Percent Calorie Restriction (%CR)

To estimate adherence, we calculated %CR from total daily energy expenditure (measured by DLW) and changes in body composition (measured by DXA or BodPod) at several time points (months 1, 3, 6, and 12) during the intervention (19). The energy contents for fat and fat-free mass loss were assumed to be 9.3 and 1.1 kcal/g, respectively.

Development of Weight Change Normograms

To develop normograms, as described below, a two-step analysis was utilized.

1. Modeling the functional form of weight change

First, we estimated the functional form of percent weight change during CR, controlling for time-varying effects (estimated %CR and TDEE) as well as time invariant effects (sex, age, and BMI). Second, to provide boundaries of adherence (similar to normograms in psychological experiments) for CR interventions (e.g., Phase 2 of the CALERIE trial), we modeled body weight against %CR as measured in CALERIE subjects, standardizing to a constant level of CR. To accomplish this, percent weight change during the intervention period was calculated for each subject and the functional form of the curve was estimated across individuals controlling for study duration, %CR, and %TDEE. Our objective was to estimate a single, simple monotonically decreasing curve which fit the observed data over the period of study. Models were estimated using non-linear repeated measures regression as implemented in SAS NLMIXED. The general form of the equation (with all terms) is:

$$\%\text{Wt}\text{.Change}=\alpha 0i+a{\text{1iTime}}_{it}^{\gamma }+\sum _{\text{j}=1}^5\left(\beta {\text{jX}}_{\mathit{\text{jit}}}+\beta {\text{j}\ast \text{X}}_{\mathit{\text{jit}}}{\ast \text{Time}}_{it}^{\gamma j}\right)+\varepsilon \text{it}$$ (1)

where the subscript i represents an individual participant i, (i=1 to N), at time t, (t=0 to 365 days). The ‘baseline’ weight was calculated several days before the initiation of CR, thus requiring the subject specific random intercept, α_0i which allows for the small individual changes in weight occurring in the time between the measurement of TDEE and the initiation of CR. It is expected to approximate 0. α_1i is a random slope parameter for each subject measuring the trajectory of % weight change, X_j is a measurefor each of the 5 covariates of interest (j=1,5), respectively, %CR, % of Baseline TDEE, sex, age, and BMI, and β_j and β_j* represent regression coefficients for respectively the main time varying impact on weight change for covariate j. Notice that the fixed-effect parameter, γ is a power of time and thereby determines the shape of the curve. Each covariate and %CR is allowed a separatepower (γ) indicating the process of change over time. The estimated individual change parameter, α_1i, for an individual is a random variable used in follow-up analyses described below.

Through the modeling process, terms were included or excluded depending on their contribution to the explanatory power and statistical significance. Initially simple models included only time, the exponents of time, and %CR, while subsequent models incorporated main and time varying effects for demographic variables,TDEE, and incorporated powers of time beyond linear time. Percent CR and relative TDEE were entered into the equation as time dependent covariates with the value corresponding to the most proximal outcome, %weight change being predicted. Measures of likelihood and fit (by Bayes Information Criteria, BIC) were compared for the various models and ultimately a final model was derived, deleting non-significant variables (p≥0.05). For the final model, we determined the relationship of the model estimates to demographic characteristics (sex and age), baseline adiposity (BMI), and %CR prescribed. As a final step, as a check of fit, a sensitivity analysis was performed comparing the fitted and observed lines and the residuals were compared to the fitted line.

2. Prediction of weight change for 25% CR

Using the relationship between the change in weight over time and calculated %CR at 1 year in CALERIE Phase 1, a prediction equation was derived, setting the intercept, α_0i, to 0, and the values of the covariates to common values. The estimate α_i assumed a 25% CR, (the level of CR prescribed in CALERIE Phase 2) for each of the models. Since α_i was a random effect, and hence had a distribution, as a second step, we assessed the distribution of these expected changes, fixing all covariates to common values. Finally, at pre-determined percentile values (80, 50 and 10%) from this expected change, a normogram for boundaries of expected change was developed for use in CALERIE Phase 2.

Results

Study subjects

Seventy-seven subjects (out of a total of 152 enrolled at the three study sites) met the criteria for inclusion in this analysis. The study cohort was an average 39.7±9.5 years, non-obese (BMI 27.7±1.7 kg/m²) and 68% female. Baseline demographic and body composition characteristics by study site are shown in Table 1. Aside from the subjects being older by design at Washington University, the subjects did not differ with respect to BMI or sex distribution.

Table 1. Baseline characteristics of the study cohort.

	Washington U	Pennington	Tufts
	20% CR	25% CR	30% CR	10% CR
N	19	12	34	12
Age (yrs)	55.4 ± 3.6	39.5 ± 5.3	34.8 ± 5.5	34.9 ± 5.5
% Female	63.2	50.0	76.5	66.7
Weight (kg)	78.7 ± 9.7	81.1 ± 11.3	79.2 ± 10.6	83.7 ± 10.0
BMI (kg/m2)	27.1 ± 2.4	27.9 ± 1.3	27.6 ± 1.6	28.6 ± 1.6
% White Race	89.5	58.3	85.3	75

Values represent mean (SD) or percentage of subjects.

Weight change and CR

The distribution of observed weight changes with CR across the 3 study sites is shown in Figure 1. As expected with these studies, there was some variability in the percent weight change over time and while there was a general loss of weight throughout the intervention, a few subjects gained weight during the course of the trial, particularly, after about six months.

Figure 1. Observed trajectories of Weight Change.

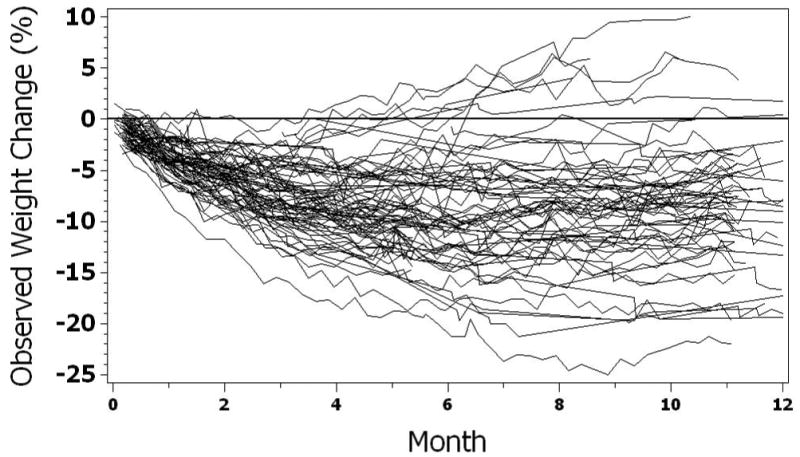
Actual percent change in weight in all subjects assigned to caloric restriction in CALERIE 1. The CR prescriptions and duration differed by site; 25% CR for 6 months at Pennington, 10% and 30% CR for 12 months at Tufts, and 20% CR for 12 months at Washington U.

1. Parameterization of weight change

A comparison of the estimates of increasingly parameterized models is shown in Table 2. With only time (days) and %CR included in the model (Table 2, Model 2), weight change occurred by a value close to the square root of time (γ₁=0.40). However, the impact of %CR over time (days) was closer to linear (Model 3, (γ=0.85). We note that a power of time for time (days)*%CR interaction was more predictive than linear time (comparison of BICs, Model 2 vs. Model 3), but the exponential value differed between time (days) and the time (days)*%CR interaction parameters (comparison of BICs, Model 3 vs. 3a). In the full models, there were interactions between the covariates, sex, TDEE and age with time, indicating, as expected, that the change over time varied for these covariates. Baseline BMI did BMI impact the percent change in weight. When we tested if the time effect impact of the covariates was (a) different from that of %CR and (b) from each other (model 4a), we found that the time-varying effect was different for TDEE, BMI, age and gender relative to %CR (λ=.81 for %CR, λ=1.65 for a common power for the remaining 4 covariates, change in -2LL=16,df=1, p<0.05), but, the powers were not different from one another among the 4 covariates (data not shown). When non-significant terms were eliminated, the BICs were substantively worse for the reduced model (model 5) relative to the full model (model 4a) (10644 vs. 10622), while the difference in log-likelihoods (10541-10580=39, df=4 p<0.05) indicates possible mediation(20) by one or more of the deleted variables. Therefore, the full model (Model 4a) was retained. This model included each of the 5 covariates as main effects, time covariate*(days) interaction, and a time (days)*%CR interaction with a separate power of time for %CR and a common power for the remaining covariates. In this model, lower relative levels of %TDEE change from baseline, males, and older subjects had higher estimated percentage weight loss. It is important to note that both %CR and %TDEE were related to %change in weight. Percent CR and %TDEE change from baseline are, of course, correlated (r=-0.32 across all observations), but, not so correlated as to create estimation problems due to multi-colinearity.

Table 2. Parameter Estimates for Models of Weight Change under CR over the course of 1 year.

%Weight Change= α₀ + α₁(Days) ^γ1 + β₁(%CR) + β₂(%CR^*Days ^γ2) + β₃(%TDEE) + β₄(%TDEE^*Days ^γ) + β₅(Age) + β₆(Age^*Days ^γ) + β₇(Female) + β₈(Female^*Days ^γ) + β₉(BMI) + β₁₀(BMI^*Days ^γ)

Parameter	Model 0	Model 1	Model 2	Model 3	Model 3a	Model 4: Full Model	Table 4a: Full Model2	Model 5: Reduced Model
Intercept (α0)		3.61 ***	1.42 ***	1.42***	1.13***	0.75***	0.45*	0.94***
Days (α1)	-1.02 ***	-3.67 ***	-1.39 ***	-1.38***	-1.20***	-1.15***	-0.96***	-1.18***
Power Days (γ1)	0.41 ***	0.22 ***	0.40 ***	0.40***	0.42***	0. 43***	0.46***	0.43***
%CR (β1)			-0.0028	0.016***	0.14***	0. 021*	0.024**	0.016*
%CR*Days (β2)			-0.0013***	-0.0030***	-0.044***	-0.0031***	-0.0036***	-0.0033***
Power %CR (γ2)				0.85***	0.42***	0.84***	0.81***	0.82***
%TDEE (β3)						0.038***	0.038
%TDEE*Days(β4)						-0.00012**	-0.0000034*	-0.00000070**
Age (β5)						0.017*	0.0062
Age*Days (β6)						-0.0013***	-0.000020*	-0.000070
Female (β7)						0.28	0.41*	0.41*
Female*Days (β8)						0.0044*	0.00016*	0.00044
BMI (β9)						0.044	0.050
BMI*Days (β10)						0.00057	0.0000064
Power (γ)							1.65***	1.46***
-2LL1	12754	12349	10814	10803	10941	10557	10541	10580
BIC2	12771	12363	10852	10846	10980	10634	10622	10644

Model 0 = uncontrolled, no intercept

Model 1 = uncontrolled, intercept

Model 2 = Controlling for CR and %CR*time (days)

Model 3 = Controlling for CR and %CR*time (days) ^γ1, separate powers for %CR*time (days) ^γ and time (days) ^γ.

Model 3a = Controlling for CR and %CR*time (days) ^γ, common power (γ) for %CR*time (days) ^γ and time (days) ^γ

Model 4 = Full model, controlling for %CR, %TDEE, Age, BMI, & Sex

Model 4a=Full model, controlling for %CR, %TDEE, Age, BMI, & Sex, separate powers for days, CR, and the 5 covariates.

Model 5 = Reduced model, removing non-significant covariates from Model 4a.

Age centered at 38 years, BMI centered at 28 Kg/M², % TDEE centered at 92% of baseline.

^*p<0.05

^**p<0.01

^***p<0.001

¹LL, Log Likelihood

²BIC, Bayes Information Criterion

Using the parameters listed in Model 4a (Table 2), the predicted weight loss for males and females at twenty-five percent CR over the course of a year is shown in Figure 2, controlling for average age, initial BMI, and %TDEE change from baseline observed in the sample.

Figure 2 a&b.

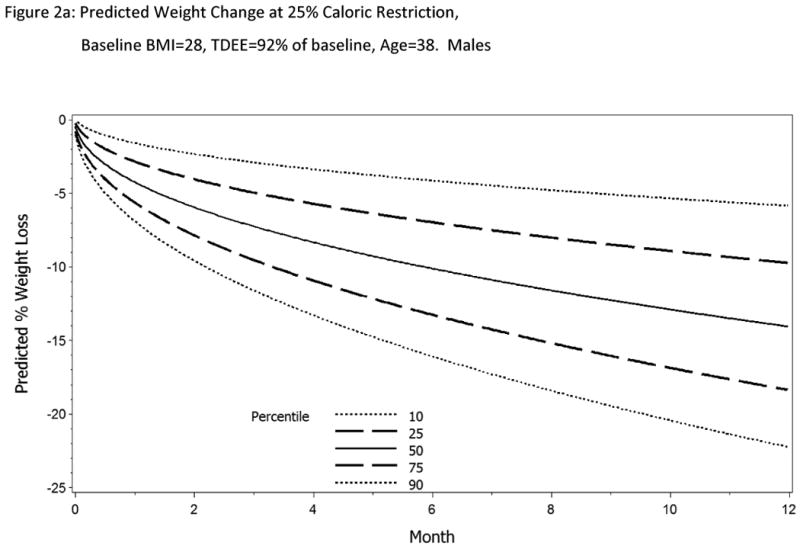
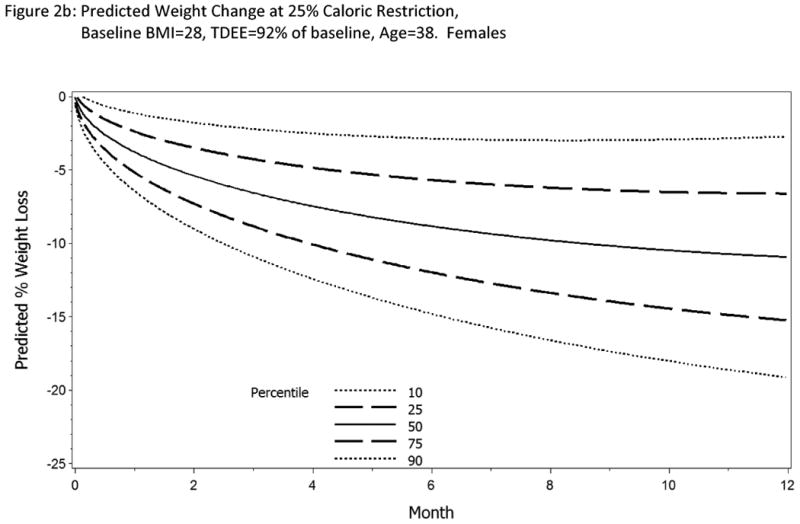
Predicted change in body weight with 25% CR for 12 months. Parameter estimates were calculated from Model 4a for a female and male subjects age 38y, BMI=28 kg/m² and TDEE change 92% from baseline. If the subject is adherent to the intervention, on average, we expect the body weight change to follow the 50^th percentile line (solid line). Also shown on the normogram is the expected trajectory for weight change at the 90^th and 10^th percentiles (long dashed lines) and 75^th and 25^th percentiles (short dashed lines). Investigators have the flexibility to set their own boundaries of adherence.

2. Estimation of bias in a monotonically decreasing model

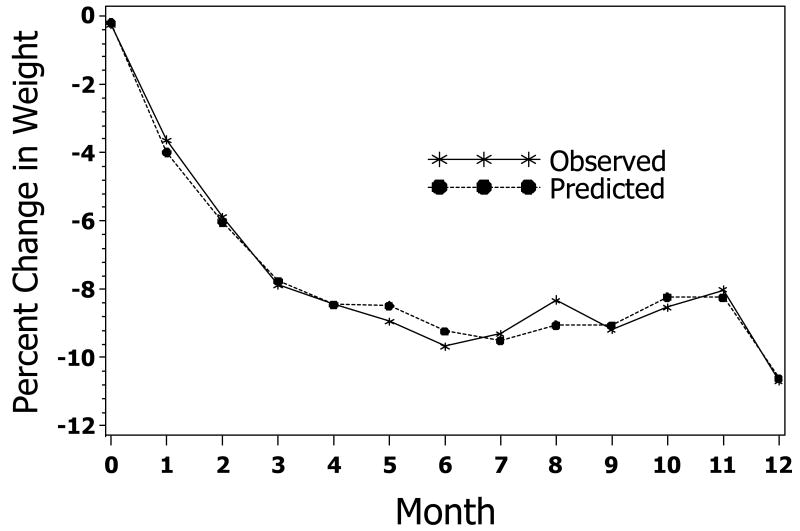
The upswing in weight after several months of study observed in many participants in Figure 1 could lead to bias in a single-parameter model of weight loss in which monotonicity is assumed. Figure 3 shows the observed and predicted marginal means during a 12 month period compared to the estimated average change in weight (i.e., across all subjects and time points) derived from the parameter values (i.e. controlling for %CR, sex, baseline BMI, %TDEE change, and age) in Model 4a. As observed in the comparison of these marginal means, no systematic bias was discerned. Throughout the 12 months, the bias is slight, indicating that the observed upswing in weights in Figure 1 was due to a change in %CR and %TDEE change from baseline.

Figure 3. Assessment of Bias. Marginal Mean values Observed vs. Predicted change.

Comparison of Observed and Predicted Weight Change. Predicted values were calculated from Model 4 parameters given the individual trajectory, intercept, sex, age, BMI, and time varying %CR and %TDEE.

3. Prediction of a range of weight change for 25% CR

The expected bounds for weight change for 25 %CR over 12 months was determined using regression parameters from Model 4a and the estimated variance in the random slope parameter, α₁. The slope parameters were adjusted to a fixed value of 25% CR with the covariates set to their mean values. The expected distribution of the adjusted predicted scores are shown in Figure 3, assuming the random variable, α₁, was distributed normally. As expected, after adjustment, the variability of these predicted values decreases. The expected percent changes in weight at 30, 90, 180 and 360 days are shown in Table 3 for females.

Table 3. Distribution of predicted percent weight change to a 25%CR diet at 30, 90, 180 and 360 days.

Females
	Percentile
Day	90th	75th	50th ± Std Dev	25th	10th
30	-1.1	-2.3	-3.7 ± 2.0	-5.1	-6.3
90	-2.2	-4.2	-6.5 ± 3.3	-8.7	-10.8
180	-2.8	-5.6	-8.8 ± 4.4	-11.9	-14.7
360	-2.7	-6.6	-10.9 ± 6.3	-15.2	-19.0
Males
	Percentile
Day	90th	75th	50th ± Std Dev	25th	10th
30	-1.5	-2.8	-4.1 ± 2.1	-5.5	-6.7
90	-2.9	-4.9	-7.2 ± 3.3	-9.4	-11.5
180	-4.1	-6.9	-10.0 ± 4.6	-13.1	-15.9
360	-5.8	-9.7	-13.9 ± 6.4	-18.2	-22.1

^*Determined from parameter estimates derived in Model 4a (table 2) where % weight change is adjusted for a 25% CR, constant 92% TDEE change from baseline, age=38, and baseline BMI=28.

Normograms: Using the regression parameters from Model 4a, normograms of expected weight loss in response to a 25% CR are developed for each individual subject according to their individual covariates. These normograms can be used by participants and interventionists to follow the expected course of weight change relative to study expectations, which in this case is a 25% CR. For pedagogy, we created a normogram of expected change in body weight with CR for three subjects from CALERIE Phase 1 using their individual covariate values (Figure 4); Subject 1: 25% CR (Figure 4A), Subject 2: 30% CR (Figure 4B), and Subject 3: 20% CR (Figure 4C), assuming they had been prescribed a 25% CR diet. As shown, the actual percent weight change for subjects one and three (Figure 4A and 4C) remained within the designated boundaries (10^th and 80^th percentile) throughout the course of the intervention. For subject two (Figure 4B) however, the percent change in body weight followed a trajectory consistent with the 80^th percentile line. If an adherence criterion for weight change more than the 80^th percentile were adopted in a study, counselors could implement various behavioral strategies to bring this subject back into adherence with the CR intervention. In addition, these figures also indicate that, early on, the first subject may have been losing weight at too fast a pace. A warning could also be issued to bring this subject back into compliance as well, or, the weight change monitored very carefully. Finally, we note, that since falling below a BMI of 18.5 is considered as a serious adverse event in the Phase 2 trial, the corresponding weight value for each subject could be included to serve as a reminder for the interventionist.

Figure 4.

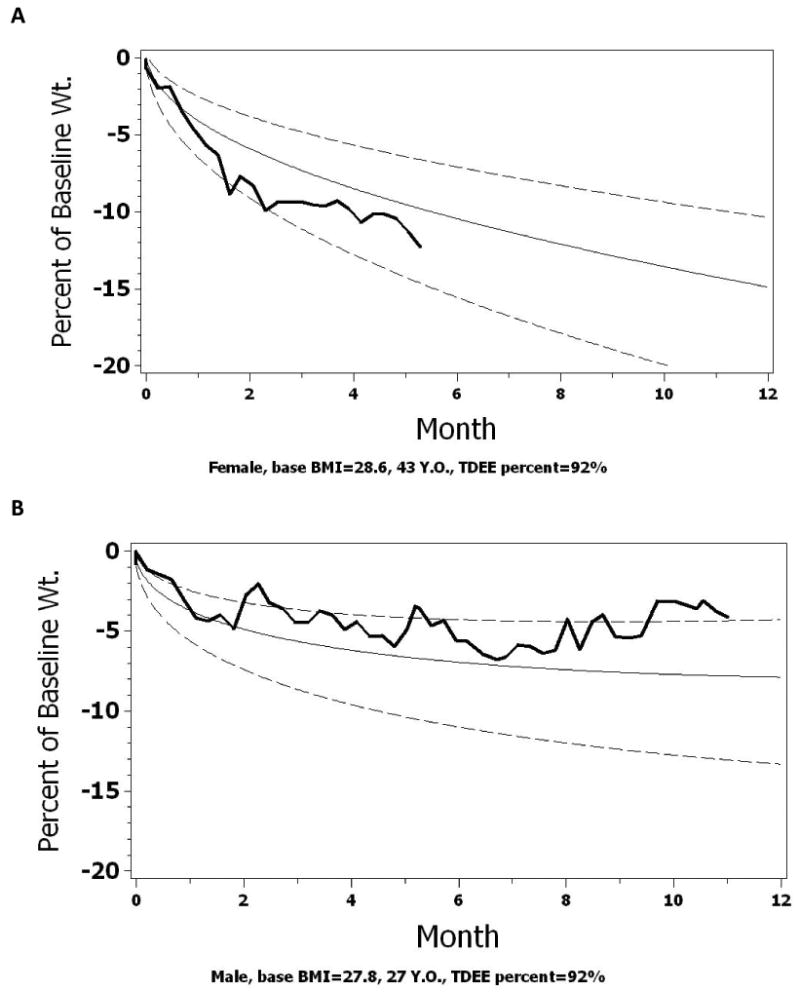
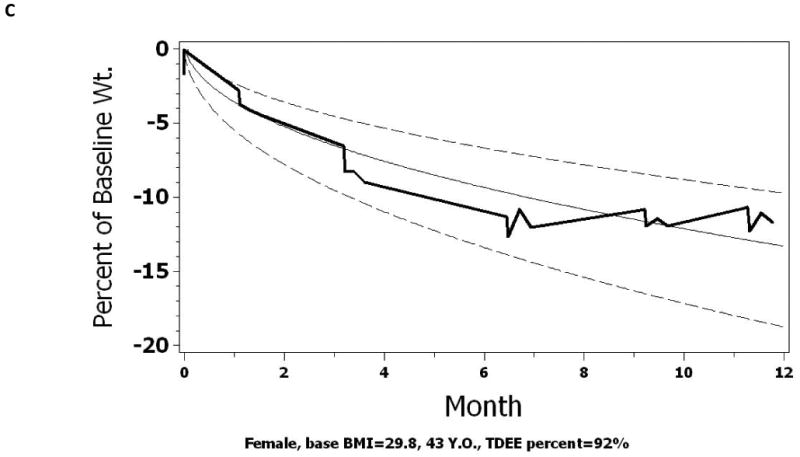
Normograms of expected and observed weight loss for 3 actual subjects from CALERIE Phase 1. Figure 4a shows the weight change of a 43y female with a starting BMI of 28.6 kg/m². Figure 4b shows the weight change of a 27y male with a starting BMI of 27.8 kg/m². Figure 4c shows the weight change of a 53y female with a starting BMI of 29.8 kg/m². The actual percent change in body weight is plotted as the solid dark line. A normogram of the expected trajectory of weight change is shown with the 50^th percentile line (solid line). In CALERIE 2, we set an upper adherence bound at the 10^th percentile and a lower adherence bound at the 80^th percentile (dashed lines).

Discussion

A challenge during CR and weight loss is determining if the variability in weight change is owed to inter-individual differences in physiological responses or simply due intra-individual differences in adherence. Weight changes in 77 participants enrolled in the Phase I CALERIE trial were compiled to develop prediction models for weight change at a given level of CR. Using these prediction models, we have shown that investigators can develop a normogram of expected weight changes tailored to a given individual. We propose that these normograms can be adopted for use in ‘real time’ during a CR intervention to track the progress and adherence of an individual following a CR prescription.

Previous investigators have shown that body weight is a good proxy for adherence during studies of CR (3-5). While a comprehensive mathematical model has been recently developed to predict changes in body weight, body composition and energy expenditure in response to CR (5), it is important to note that this model, while comprehensive was derived from group estimates and therefore has limited application to individual subjects.

This analysis describes the methods applied to develop a simple set of weight curves for CR interventions. Using weight change in the clinic from CALERIE Phase 1, we have demonstrated important demographic and energy related predictors of the observed weight change, and have developed a subject specific normogram which would allow an interventionist and subject to chart the course of weight loss against expectation (and hence adherence to a 25% CR intervention).

Several additional points should be made. First, the functional form of the curve used to estimate the curves may be unfamiliar to many, but was necessitated by the requirement of extrapolating to one (or more) year(s) from existing data. By design, some subjects in phase 1 provided data of only 6 months in duration. The estimated curve had to demonstrate an initial faster rate of weight loss, and continue to provide likely values over the period of interest. In CALERIE Phase 1, there was a great deal of variability in weight change between subjects, likely due to differences in adherence as well as prescribed CR. Weight increases in the latter part of the intervention may be explained by study fatigue and a commensurate reduction in adherence (with a commensurate reduction in estimated %CR and %TDEE), as well as by increased metabolic efficiency that would reduce the rate of weight loss and result in eventual weight stabilization. If we utilized only the 6 month weight observations, a simpler, monotonically decreasing, single parameter exponential estimate would have adequately fit the data.

In the development of the normogram for subsequent studies (including CALERIE Phase 2), interim CR measurements (from doubly labeled water and body composition) will be available for an individual but not considered. Utilization of these interim points into the analytic structure might have increased the precision of the estimates, and, perhaps allowed for adaptation of group averages to incorporate individual differences. This method however, was rejected because: (1) such calculations at these interim points would have led to distinct break in the smooth curves at the points of the interim points (3 months, 6 months, 9 months), (2) in order to be useful, the data would have had to be available in real time, which was not planned in the data management flow, and (3) if updated data in Phase 2 was used to update projections, the delivery of the intervention might differ for subjects enrolled in the early and late parts of the trial.

There are numerous limitations to the finding reported here. The sample sizes are small. The subjects come from 3 different sites and sampled with differing inclusion/exclusion criteria (most notably age) and were studied under several different protocols, including length of time on study (by design, one site had subjects on study for 6 months, while, in the other 2 sites, subjects were followed for a year) and, there were slight differences in the timing of TDEE measurements varied by site. There was great variability in subject characteristics, subject adherence, the level of CR prescribed, and the CR interventions between study sites. Most notably, expected level of %CR varied by site, increasing the heterogeneity of the observed weight curves and the resulting estimates. These factors necessitated statistical control to predict weight loss curves at 25% CR. The estimates reported here utilized statistical adjustment to control these factors, but this control likely resulted in larger estimates of variability than would have been observed had a uniform protocol for a given CR been employed. While the model we employed indicated that adjusting for factors contributing to heterogeneity of weight loss was precise (the correlation between calculated %CR and the change in weight parameter was -0.79), there were minimal subjects with which to investigate non-linearities in this relationship and sensitivity analyses based on demographic and medical variables. Our small sample size and reliance on statistical adjustment must temper the reliance on these curves to define ‘adherence’. Indeed, for this and the reasons below, the projections shown in our model stop at one year, the limits of the Phase 1 data used to define the curves. Ultimately, whether these estimates can be extended to, for example, more obese subjects, to other protocols for obtaining a given %CR, or older subjects will require validation in future studies.

Second, an important application of these predicted weight curves is in longer CR interventions or interventions with prescribed energy deficits different from 25% from baseline energy requirements. For example, CALERIE Phase 2 involves a 2-year intervention, and assessing adherence beyond the first year is critical. If a more common functional form (e.g., quadratic) were employed to develop the two year projections, then the observed upswing in weight at the end of the phase 1 study would result in an estimated large increase in weight at the end of a two-year intervention, due to the upswing in the final months in the observed results being extrapolated over the two-year period. The cost of the use of the exponential estimate is that inspection of the observed and predicted data across a large number of individuals shows that the expected weight loss is overestimated in the very initial days (two weeks) and, while the function slows as time increases, it is continually decreasing and does not asymptote. Thus, the values for the normogram are probably less useful during the first two weeks of the intervention, and extrapolation beyond the limits of the observed data is risky. Also, it should be noted that while these normograms may be useful for predicting under-adherence to a prescribed CR regimen, the actual degree of under-adherence cannot be inferred by the observed distance from the expected mean projection for a given CR level. Further, estimation of the curves require fixing the %CR, but also an estimate of expected %TDEE which will be obtained for the individual. While the curves can be updated as future information becomes available, updates of TDEE requires expensive and intensive measures not available to all researchers and clinicians.

The normograms developed have been extended to 1 year of a 2 year trial, the limits of the data in Phase 1. In any setting, projection of results beyond the observed data is always problematic, but the problem is acute in this setting. In Phase 1, many subjects gained weight in the final months of the 1 year trial, possibly due to ‘study creep’ or physiologic adaptation leading to increased weight even in the presence of constant caloric restriction. Thus, three viable projections are possible – (1) the model proposed here (based on an exponential and linear function of time) would posit increased weight loss (albeit at a slower power pace) in the second year, (2) one might posit a constant weight in the second year, and (3) if the upswing observed in the final months in Phase I continued into the second year, weight would return to pre-intervention levels at the end of the second year, even in the presence of true 25% CR.

Finally, the calculations here were developed for a generally young, normal weight population. While the methodology is straightforward, further analysis will be necessary to assess if the functional form and distribution of weight loss is applicable as a measure of adherence in the treatment of obesity.