An Entropy Model for Artificial Grammar Learning

Abstract

A model is proposed to characterize the type of knowledge acquired in artificial grammar learning (AGL). In particular, Shannon entropy is employed to compute the complexity of different test items in an AGL task, relative to the training items. According to this model, the more predictable a test item is from the training items, the more likely it is that this item should be selected as compatible with the training items. The predictions of the entropy model are explored in relation to the results from several previous AGL datasets and compared to other AGL measures. This particular approach in AGL resonates well with similar models in categorization and reasoning which also postulate that cognitive processing is geared towards the reduction of entropy.

Introduction

Shannon entropy is one of the most standard ways of quantifying uncertainty in making a selection. For example, imagine you have a bag of blue and red marble balls and you are trying to predict whether the next ball you will pick is red or blue. If there are nine red balls and only one blue ball in the bag, you are likely to be fairly certain that the one you select will be red. If, on the other hand, there are five reds and five blues, you would have no idea whether to expect a red or a blue one in a selection. In this second situation there is more uncertainty than in the first one; that is, the outcome of the selection process is less predictable. Shannon entropy is quantified using the equation $\text{Entropy=}-{\displaystyle {\sum }_{i=1}^N{p}_i{\log }_2}{p}_i$, where the index i labels the different possibilities in a situation (in the above example, selecting either a red or a blue ball), and p_i refers to the probability of occurrence of each of these possibilities. On the whole, entropy is higher when there are many, equiprobable, possibilities.

Entropy is routinely employed in thermodynamics in physics, as a way of quantifying how “disorderly” a system is and, also, it is one of the key constructs in information theory, as it provides a measure of regularity in information. Why should psychologists care about entropy? A short answer is because psychologists are interested in probability and entropy is a way of quantifying uncertainty in probability (a longer answer will be provided in the final section, once some promising results have been shown). This work explores a model for artificial grammar learning (AGL) based on entropy. AGL is a widely employed paradigm for the study of learning processes. It involves asking participants to (usually passively) observe a set of stimuli in a training phase. Subsequently, in a test phase they have to decide which new stimuli are compatible with the ones in training; no corrective feedback is typically provided. AGL is an important experimental task because it has been used to debate just about every theory of learning which has been prominent in the last few decades, from associative learning (e.g., Perruchet and Pacteau, 1990) to connectionist models (e.g., Cleeremans and McClelland, 1991; Dienes, 1992) to exemplar similarity (e.g., Vokey and Brooks, 1994) to concrete rules (e.g., Dulany et al., 1984) to abstract rules (Reber and Allen, 1978). So, in proposing a new theory of (or approach for) learning, doing so in the context of AGL, allows a researcher to concretely appreciate the theory's distinctive features relative to several other theories.

At a broad level, the present model of AGL is based on what we can call the Information Premise: In processing new information, the cognitive system prefers choices that allow for the greatest reduction in entropy (note that entropy means uncertainty in this context and the two terms will be used interchangeably throughout the paper). In other words, we suggest that the objective of the cognitive system is to represent the world with information that is as certain as possible (cf. Anderson, 1991). The meaning of “preference” is restricted to choices relevant to the task at hand, for example, in terms of establishing some type of conclusion on the basis of given premises. Work in reasoning by Oaksford and Chater (1994) and categorization by Pothos and Chater (2002) can both be interpreted as applications of the Information Premise (further discussion of this work is reserved until later).

The way the Information Premise is applied to AGL is as follows. Suppose that test items are encoded without any regard of the information collected during training, as novel instances. In such a case, in perceiving a test stimulus there is no information about its structure, in the sense that all possible arrangements of symbols are equally likely. This option involves a lot of uncertainty. Conversely, suppose we parse test stimuli by taking into account structural constraints which have been identified in training. In this case, some symbol arrangements would be recognized as more likely than others, and so processing different test stimuli would involve less uncertainty. The Information Premise suggests that the cognitive system will consider a test item as more compatible with the training ones, if it can be specified with less uncertainty on the basis of information from training. In other words, it is suggested that AGL performance can be accurately described by considering the extent to which new instances can be encoded, or parsed, on the basis of old ones (cf. Pothos and Wolff, 2006).

The structure of the paper is as follows. I will first consider the AGL learning experimental task in a little more detail and the proposals which have been put forward to explain human behavior in the task. I will then formally apply the Information Premise in AGL to develop an entropy model for AGL and will discuss its relation to other theoretical proposals. Finally, a range of analyses will be employed to illustrate the model's properties.

Artificial grammar learning

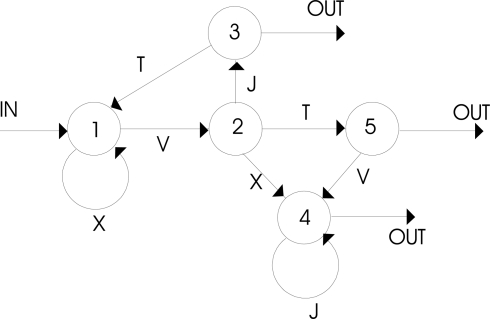
An artificial grammar, or a finite state language, is a set of rules to distinguish legal, or grammatical (G), arrangements of symbols, from illegal, or ungrammatical (NG) ones (for a review see Pothos, 2007). The rules used to construct the G items for a given AGL experiment are best illustrated using the pictorial representation of Figure 1. This is the simplest representation for an artificial grammar, or a finite state language. The circles with the numbers are the states of the grammar. Every time a transition is made between states, the symbol corresponding to this transition is added (in Figure 1 these symbols are letters), until a transition is made to one of the OUT states. Since not all transitions are possible, the G stimuli are usually only a small subset of the possible strings that can be created using the same set of symbols. Note, that a researcher is not restricted to creating letter strings using a finite state language; the letters corresponding to the different transitions in Figure 1 can be replaced by arbitrary symbols (for AGL with stimuli other than letter strings see Altmann et al., 1995; Whittlesea and Wright, 1997; Pothos and Bailey, 2000; Pothos et al., 2006).

Figure 1.

This is the grammar used in Knowlton and Squire (1996, Exp. 1), as well as in Pothos and Bailey (2000), whose results are analyzed in this work. From Pothos and Bailey (2000), published by APA. Reprinted with permission.

In a typical AGL experiment, participants are first presented with a subset of the G stimuli and they are simply told to observe them. Subsequently, in test, they are told that all the stimuli they saw in the first part were consistent with a particular set of rules and that they are about to see a set of new stimuli that either comply or violate these rules; their task would be to identify the stimuli that comply to the rules. A robust finding is that participants can identify with above chance accuracy the test G items from the NG ones. Note that this is far from a trivial observation, since, for all we know, participants might just as well have been inclined to select as grammatical the NG items in test. Also, another robust finding is that participants often have difficulty articulating the knowledge on the basis of which they made their item selections in test (Tunney and Shanks, 2003; Dienes and Scott, 2005; Tunney, 2005; Scott and Dienes, 2008).

The utility of AGL for the study of generalization can be primarily seen in two ways. Firstly, there has been a very long tradition of similar experiments, so that possible confoundings and the type of manipulations that may affect performance are relatively well understood (e.g., see Redington and Chater, 1996 or Tunney and Altmann, 1999). In this way, the likelihood of artifactual findings or invalid interpretation of results are reduced. Secondly, performance on an AGL task is potentially compatible with several different learning processes, involving rules, similarity, fragment information, and so forth (see below). By using sensitive enough statistical procedures, one can investigate in AGL the relative importance and interaction of several different hypotheses for learning (Johnstone and Shanks, 1999; Pothos and Bailey, 2000; Lotz et al., 2009). In point of fact, there are very few experimental paradigms that allow the simultaneous investigation of such a diverse range of possible hypotheses as are applicable in AGL.

Standard hypotheses for AGL

The original claim by Reber (e.g., Reber and Allen, 1978) has been that during training subjects acquired an abstract representation of the rule system underlying the G items and that on the basis of this knowledge they were able to identify with above chance accuracy the G stimuli in the test part. In fact, this proposal has been entirely abandoned, including by its own proponent (in Reber, 1993). However, more realistic rule accounts of AGL have been put forward. For example, Dulany et al. (1984, 1985) suggested that participants acquire “correlated grammars”, that is approximations of the underlying grammar, which may, however, include inaccurate rules. Such correlated grammars have been interpreted as basically a collection of explicit tests of which items are legal or not (cf. Ashby et al., 1998).

Other accounts have invoked similarity as the driving force in grammaticality decisions. For instance, Brooks and Vokey have suggested that an item would be as likely to be endorsed as G if it is actually G, as when it is more similar to the training items, with similarity operationalized in terms of ease of transformation (Brooks and Vokey, 1991; Vokey and Brooks, 1992; cf. Hahn et al., 2003). Pothos and Bailey (2000) employed an alternative exemplar similarity approach, by applying an exemplar categorization model in AGL (Nosofsky's generalized context model; e.g., Nosofsky, 1988a,b). An alternative approach is to suggest that it is not the entire exemplar which affects perceptions of similarity in AGL, but rather the pattern of repeating elements (i.e., the identical symbols in a sequence). Such a hypothesis appears very plausible, and has seen particularly supported in the context of transfer AGL experiments (Altmann et al., 1995; Tunney and Altmann, 1999).

Associative learning theory can be applied in AGL through the examination of the structures that can develop if the learning process involves associations between elementary symbols. Perruchet and Pacteau (1990; also Perruchet et al., 1992; Perruchet, 1994) argued that the knowledge acquired in an AGL experiment is best characterized in terms of the pairs (bigrams) or triplets (trigrams) of letters learned during training. This view was later extended by Knowlton and Squire (1994, 1996; see also Meulemans and Van der Linden, 1997, and Servan-Schreiber and Anderson, 1990), who computed various measures of fragment (i.e., bigrams or trigrams) overlap between test and training items. Finally, there have been several successful connectionist models of AGL (e.g., Cleeremans and McClelland, 1991; Dienes, 1992).

How mutually exclusive are the models presented above? With careful theoretical work, not to mention very precise stimulus construction, it can be argued that ultimately the above models do involve distinct hypotheses about AGL, corresponding to (broadly) rules, exemplar similarity, or fragment overlap (the latter can be interpreted in terms of feature-based similarity or associative learning; Pothos, 2007). In practice, there is considerable overlap between the predictions from different models, even though it is possible to create stimulus sets which reflect (approximately) orthogonal influences of two or more performance factors. To briefly review some relevant results, Vokey and Brooks (1992) reported independent influences of grammaticality and exemplar similarity on participants’ performance and Knowlton and Squire (1994, 1996) found independent influences of grammaticality and fragment overlap. Regression analysis investigations by Johnstone and Shanks (1999) and Pothos and Bailey (2000) further confirmed that most AGL hypotheses all appear to be valid, to some extent, but that there is also considerable overlap between the corresponding predictions.

How much should we be concerned by the overlap between the predictions of different AGL models? Overall, the degree of overlap between different theoretical constructs is a hotly debated issue (Pothos, 2005a). For example, some investigators consider connectionist and rules proposals of linguistic processing as mutually exclusive (e.g., Marcus et al., 1995). Other researchers, by contrast, have considered such proposals as potentially compatible, but from different viewpoints (cf. Marr, 1982; Dienes, 1992). For example, a connectionist model would be more about an explanation of the mechanistic processes involved in language, while the rules would be more about the representations formed and the relevant operations on these representations. In such a case, overlap between the connectionist and the rules model would simply affect our perception of how both models ought to be interpreted.

In this vein, in developing an entropy model for AGL, we can consider how much we a priori require this model to lead to distinct performance predictions from alternative models of AGL. Fundamentally, an entropy model of AGL and its reliance on the Information Premise involve hypotheses about AGL regarding the extent to which the cognitive system processes efficiently the available statistical structure in a set of observed stimuli (Chater, 1996, 1999). It is a trivial statement to point out that the cognitive system must involve processes which take advantage of the rich statistical regularity in our environment. Indeed, some psychologists have explored the extent to which the structure of the environment determines cognitive function (Shepard, 1992). Equally, most cognitive models can be seen as hypotheses of exactly how the cognitive system processes environmental structure. So, what is special about Shannon entropy?

The point about Shannon entropy is that this is a generic, or theory neutral, measure of statistical structure. In other words, it is a measure of structure in information, but which does not involve a particular hypothesis of what is the form of this structure. And here is the nub of the problem. One hypothesis is that the cognitive system may be set up to process information in terms of looking for rules or learning whole exemplars. Presumably, if the cognitive system does adopt such a strategy, it must be adaptive across the range of learning problems the cognitive system typically encounters, even though it may be informationally inefficient in any particular single learning problem (which could correspond to AGL). Indeed, there have been several proposals for learning involving multiple systems, such that each system is tuned to a particular type of problem (e.g., Ashby et al., 1998; Maddox et al., 2004; Sun et al., 2005). The converse hypothesis would be that the cognitive system may always be biased to simply pursue the informationally most efficient strategy in a learning situation and, as it happens, this strategy will correlate to a greater or lesser extent with (say) strategies based on rules or similarity in particular situations. Note that in AGL, and as is the case with all tasks of inductive inference, there are no correct or wrong answers, so that at best we can only say that a particular learning strategy is adaptive or maladaptive (i.e., we cannot label a learning strategy as “correct”).

So, ultimately, the theoretical question relates to what is the fundamental way of understanding human learning, whether we should aim to do so in terms of learning systems based on similarity/rules/associations or whether we should look to the Information Premise and corresponding entropy-based models. However, at a more practical and immediately relevant level, we do not know at this point how much the various existing AGL hypotheses (e.g., chunking models) are informationally efficient. This is an open and interesting issue and addressing it is one of the objectives of the present research.

An entropy model for AGL

We have discussed at length the possible relation of entropy minimization with other AGL accounts, such as rules and similarity. A slight complication is that there is no single best way to provide an entropy-based model. Alternative schemes can differ in terms of their assumptions regarding the elementary units involved in learning, which in turn affects the entropy computations. The main assumption in this work concerns how stimuli are processed. Following the work of Perruchet and Pacteau (1990) and Knowlton and Squire (1994), it is assumed that stimuli are processed primarily in terms of their bigrams and trigrams, so that participants’ knowledge is basically limited to bigrams and trigrams (including information about anchor positions). The reason why such an assumption is useful here is that it allows a straightforward scheme for computing the entropy of a particular test item, relative to the training items. After we have described the entropy model of AGL, we will briefly consider some alternative related approaches in AGL, so as to evaluate the present proposal.

At a broad level, in AGL in the test phase decisions can be thought of as judgments of compatibility: That is, participants are told that some test items are “compatible” with the training items, and that their task is to identify which are these. Entropy can provide a principled formal way to quantify compatibility: It is suggested that each test item is given a complexity measure according to how “specifiable” it is from training items. This complexity measure is computed by dividing the item into parts, and seeing how “determinable” the continuation from each of these parts is on the basis of information from training. Such a scheme is consistent with Miller's (1958) early work on quantifying the redundancy in strings of letters (in fact, his pioneering experiment was the predecessor to the very first AGL experiment ever, that of Reber, 1967). It is also similar in principle to simple recurrent network models of AGL, whereby the objective is to predict the next symbol in a sequence (e.g., Boucher and Dienes, 2003), although note that the entropy measure quantifies the ease of prediction, without regard of the actual fragments which are high or low frequency. We next describe in detail the present proposal.

First, each test string is broken down into all constituent bigrams and trigrams, including the anchors (that is, the beginning and end points). Letting symbols “b” and “e” stand for the beginning and the end of a string, test string MSV would be broken into the bigrams (bM, MS, SV, Ve) and into the trigrams (bMS, MSV, SVe). Note that we are assuming that a string of symbols (this is the traditional form of AGL stimuli) is processed from left to right. In situations in which it cannot be assumed that strings are read from left to right, one would expect the entropy model of AGL to do less well (this is something which will be assessed directly later on). These bigrams and trigrams will be less or more familiar on the basis of the information observed during the training phase. In standard fragment hypotheses for AGL, fragment familiarity is typically quantified as frequency, so that a fragment would be more familiar if it has been observed with a higher frequency in training. Here, we do something different: following Miller (1958), in observing a particular sequence of symbols, we ask how much uncertainty is there in recognizing this sequence as familiar from training. The Information Premise suggests that the less the uncertainty, the greater the ease with which a test item will be recognized, and so the greater the likelihood that it will be considered G.

As an example, let's say that a participant is exposed to strings XXX, XXX, YYY in training and XYZ in test. In encoding the test item, the first bigram eX has been observed at least once in training, so we can ask how familiar it is. Using the equation for Shannon entropy, $\text{Entropy=}-{\displaystyle {\sum }_{i=1}^N{p}_i{\log }_2}{p}_i,$ S(eX) = −Σp_i log₂ p_i = −2/3 log₂2/3 − 1/3 log₂1/3 = 0.92, since the continuation from the first symbol can be either an X with a probability of 2/3 or a Y with a probability of 1/3. In other words, S(eX) refers to the uncertainty in recognizing a particular continuation from symbol e, as familiar on the basis of the information from the training phase. The less the uncertainty, the greater the determinism in continuing from one symbol in a particular way (i.e., one can identify a particular continuation amongst alternatives more easily). To illustrate, if instead of XXX, XXX, YYY, we had an equal number of XXX's and YYY's, there would be a greater uncertainty in discriminating between possible continuations from e, and S(eX) = 1. But, say we had 99 XXX's and only one YYY, then there would be a greatly reduced uncertainty, S(eX) = 0.08. In such a case, we would readily recognize as familiar a bigram eX, even if we occasionally expect the odd eY. Indeed, if there have been 99 eX's and only one eY, it might be the case that the exception is as memorable as the rule, leading to an interesting prediction from the entropy model.

Note that this scheme implies that S(eX) = S(eY), for the above training and test items. In other words, if someone is trained with 99 X's and only one Y, according to the entropy approach, this means that both eX and eY continuations are less complex/easier to parse, and so they would be considered equally familiar. This assumption is less counterintuitive than it seems: If there have been 99 X's and only one Y in training, then this means that eY continuations are simply much less likely, so that the rare occurrences of eY would have a very small impact on performance (a subtlety arises if in test the ratio of eX's to eY's changes from training to test, however, this issue is beyond the scope of the present work). This example highlights the fact that the entropy computations reflect the uncertainty in continuing from a symbol (in a familiar way), neither the frequency of a bigram nor the conditional probability of a second symbol given the first one. Thus, the entropy model of AGL is a departure from standard intuitions regarding how to quantify the distributional information from training in an AGL task.

So, when faced with a familiar bigram in a test item, the model examines the uncertainty in having one particular continuation from the first symbol to the second, based on the statistics of the training set. But what happens when the bigram had not been observed in training? In such a case, the distributional information from training cannot help. Accordingly, we suggest that the corresponding entropy is computed by assuming that all possible continuations from the first symbol to the second are equiprobable. Continuing with the above example, once we have computed S(eX), we subsequently need to compute S(XY), S(YZ), and S(Ze). But, bigram XY has never been observed in training and so the information from training cannot reduce the uncertainty regarding possible continuations from symbol X. In such a case, I suggest that S(XY) = {−1/4 log₂ 1/4}·4 = 2. Note that we are assuming that any symbol can have four possible and equiprobable continuations, X, Y, Z, and e. An alternative possibility would be to compute S(XY) for an unfamiliar bigram XY in terms of the base probabilities of symbols X and Y. However, there is no evidence in AGL that such base probabilities play a role in performance. Moreover, such an approach would have difficulty when it comes to symbols in test which have never been encountered in training. Having said this, it certainly appears worthwhile in future work to explore alternative schemes for computing the entropy of unseen items.

More formally, we can express the entropy model for AGL in the following way: regarding a bigram S_iS_k which has been observed in training,

$$\begin{array}{c}{S}_{\text{bigram}}=(S_i{S}_k)=-{\displaystyle {\sum }_{l=1}^N\frac{\text{frequency\hspace{0.17em}}{S}_i{S}_l}{\text{number of all bigrams with\hspace{0.17em}}{S}_i\text{\hspace{0.17em}first}}}\\ \times \hspace{0.17em}{\log }_2\frac{\text{frequency\hspace{0.17em}}{S}_i{S}_l}{\text{number of all bigrams with\hspace{0.17em}}{S}_i\text{\hspace{0.17em}first}},\end{array}$$

where N is simply the number of distinct symbols including the end symbol, e. If bigram S_iS_k has not been observed in training, then

$$S_{\text{bigram}}(S_i{S}_k)=-{\displaystyle {\sum }_{l=1}^N\frac{1}{N}{\log }_2\frac{1}{N}}.$$

Note that we have used the index “bigram” for the above entropy calculations. A very similar scheme is possible for longer item fragments. In this work we consider entropy measures for bigrams and trigrams. Regarding the latter, the question is, given a particular bigram, how much uncertainty is there in determining the next symbol. More specifically, if in test we encounter a trigram XYZ that has been observed in training, the entropy for determining Z given the bigram XY can be computed by considering all possible trigrams such that XY are the first two symbols. If the trigram had not been observed in training, then, given bigram XY, all we can say regarding the following symbol is that all symbols are equiprobable. Extending this scheme to four-grams is not viable given existing AGL designs: there are too many distinct four-grams and trigrams to make the scheme meaningful.

We have so far considered the entropy for continuing from a single symbol or a bigram. How can this entropy lead to a measure for the overall entropy of a test item? Note that, given the latter, we would want to assume that the less the overall entropy associated with a string, the more familiar the string would be, given the statistical information from training, and so the more likely the string would be to be endorsed as grammatical. In general, a string would have a lower overall entropy if it is made up from such symbols (and bigrams) such that there is very low uncertainty in how they should be continued. We explore two possible ways for combining individual symbol (and bigram) entropies. According to a summative approach, the overall bigram entropy of a test item would be the sum of all entropies for continuing from individual symbols and the overall trigram entropy would the sum of all entropies for continuing from individual bigrams. Note immediately that this summative approach predicts that longer items would be more likely to be associated with a higher entropy. It is in fact true that there is an association between item length and grammaticality endorsement (e.g., Pothos and Bailey, 2000). This summative approach is also normatively more correct, if one interprets entropy as the number of binary questions required to identify a particular element. However, it is possible that participants are more influenced by individual particularly surprising or particularly familiar bigrams (or trigrams; cf. Dulany et al., 1984). Accordingly, it is worth exploring an averaging approach as well, according to which the overall bigram entropy of an item is the average of all the entropies for continuing from individual symbols and the overall trigram entropy of an item is the average of all the entropies for continuing from individual bigrams. Such an averaging approach is broadly consistent with other AGL proposals based on fragmentary information. For example, both Knowlton and Squire (1994, 1996) and Meulemans and van der Linden (1997) proposed their well-known measures of associative strength as averages of the corresponding bigrams or trigrams.

In sum, the entropy measures for AGL are about quantifying the expected difficulty of a continuation, either from a symbol or a bigram, given what has been observed in training. If for a particular test item, it is easy to guess all continuations from individual symbols or bigrams, then the overall (summative or average) entropy of the item will be low and the item should be more likely to be selected as grammatical – this is an application of the Information Premise in AGL. Note that in the above there is no claim regarding the actual cognitive process via which these computations are carried out; rather, it is suggested that psychological judgments of compatibility are made in a way that is consistent with the above computations (in other words, the model is a representation model, but not a process one; e.g., cf. van der Helm and Leeuwenberg, 1996). The proposed entropy measures are clearly different from standard measures of chunk strength, since, according to the latter, the higher the frequency of a bigram, the higher its corresponding chunk strength. By contrast, the entropy measures take into account not just the absolute frequency of a bigram or trigram, but critically the number of competing alternative options. The entropy measures are distinct from simple probabilistic measures as well. Suppose, for example, that a participant sees in training items XY, XY, XZ. Then P(Y|X) = 2/3 and P(Z|X) = 1/3. But, suppose now that the participant sees four XYs, one XZ, and one XQ. Then, it is still the case that P(Y|X) = 2/3, but now we also have and P(Z|X) = 1/6, P(Q|X) = 1/6. So, according to a conditional probability approach, the continuation Y from item X would be equally salient, regardless of the information in the other training items. By contrast, the bigram entropy in the first case would be 0.92 and in the second case 1.25. In other words, according to the entropy model for AGL, the salience of a bigram does not depend only on its frequency but also on the overall context of what other relevant bigrams have been observed as well.

Related proposals

The idea of using entropy to understand AGL performance is not new. Jamieson and Mewhort (2005) examined the overall redundancy of a particular finite state language. They did this by considering −Σp_ij log₂ p_ij, in which p_ij denotes the probability of symbol j following symbol i in a sequence. Clearly, the fewer the equiprobable “branches” in a finite state language, the lower this particular entropy measure and, so, the more redundant the corresponding finite state language. Jamieson and Mewhort (2005) computed a redundancy index for a finite state language by comparing its redundancy with the redundancy of an equivalent but entirely unconstrained finite state language. Jamieson and Mewhort's redundancy index is based on the same computation for entropy as that in Miller (1958) and the present proposal. However, while the present proposal aims to derive an entropy measure for individual test items in an AGL task, Jamieson and Mewhort wanted to determine the overall redundancy of a grammar. A priori, for Jamieson and Mewhort's measure to be psychologically relevant, participants must have acquired enough knowledge of the finite state language after being exposed to the training items, for the entropy computations for the entire grammar to be accurate. This seems unlikely and, indeed, Jamieson and Mewhort's analyses did not support the redundancy index. Instead, they found support for what they called a measure of “local redundancy”, computed as the number of alternative sequences which can be generated by re-arranging the symbols of a particular test sequence. This alternative measure is based on straightforward combinatorics, rather than a formal definition of redundancy (through entropy) as such. But, in any case, Jamieson and Mewhort's research provides some important boundary conditions on how entropy can be used in understanding AGL performance.

Poletiek and van Schijndel (2009) examined what they called the statistical coverage of a grammar, the idea being that different items will provide more information about the underlying finite state language than other items. Their basis for understanding AGL performance was a measure of the probability for a test item, which was computed in terms of the probabilities of the transitions in the finite state language which would be required to produce the item. With the additional assumption that all transitions are equiprobable, this measure predicts that in general longer items would be less probable than shorter items. This is no doubt an interesting measure but, as with the case of Jamieson and Mewhort's (2005) redundancy measure, it does assume that the underlying finite state grammar is psychologically relevant. In other work by the same group, van den Bos and Poletiek (2008) computed a measure called dependency length, which can be broadly understood as the number of symbols required before the current symbol in a test item can be determined. Overall, the work of Poletiek et al. highlights the fact that in attempting to specify a psychological measure of complexity, there are several choices other than entropy.

Note that one of the key assumptions in the present model concerns how to code for entirely novel sequences. But this issue does not come up at all in the proposals of Jamieson and Mewhort (2005), Miller (1958), and Poletiek and van Schijndel (2009). In the former models, an overall measure for the redundancy of the grammar is computed, partly on the basis of the number of sequences which can be generated by a grammar in relation to the total number of possible sequences. In the latter proposal, statistical coverage is computed as a property of training exemplars together, so the issue of unseen sequences does not affect the calculations.

Most related to the current proposal is previous work by Pothos and Bailey (1999). These investigators computed an entropy measure for each test item by taking into account the uncertainty of continuing the item in a standard forward (left to right) and reverse direction. For example, the entropy of test item ABCD would be a function (sum or average) of S(eA), S(eAB), S(eABC), and S(eABCD) in the forward direction, where the S measures are computed by taking into account the uncertainty in determining the particular continuation. Despite encouraging results, there is an important a priori problem with this proposal. It assumes that participants can take into account information regarding all previous symbols in trying to predict the next symbol in a sequence. Such an assumption seems to go against empirical observation. In AGL, the current evidence suggests that at most participants learn up to trigram information (see Pothos, 2007, for an overview). Moreover, when participants do learn information about larger fragments, this is typically achieved only after an extensive amount of training (Cleeremans and McClelland, 1991). Note that this issue concerns the largest fragment participants can learn about starting from individual symbols and does not preclude a mode of learning based on the processing of entire exemplars (as has been clearly demonstrated in AGL; for example, Vokey and Brooks, 1994).

Materials and Methods

Other measures

Most measures of AGL performance are based on some aspect of the statistical information available in training or the underlying grammar and, so, as pointed out, it is hardly surprising that they often correlate in practice (e.g., Johnstone and Shanks, 1999; Pothos and Bailey, 2000). Moreover, it has been argued above that in principle the entropy model can lead to predictions distinct from models based on, say, bigram or trigram frequency, but it is of course an empirical issue as to how much overlap there is in specific cases of empirical importance. To better understand the properties of the entropy model, we can examine it in relation to a few prominent measures for what is learned in AGL.

First, I considered the grammaticality of the test items, that is whether they are G or NG, according to the rules of the underlying finite state grammar. While most investigators today reject a hypothesis for AGL based on knowledge of the underlying grammar, grammaticality is still employed as a convenient index of AGL performance. Moreover, there are alternative hypotheses for what is learned in AGL based on rules, which involve more realistic assumptions about psychological representation (e.g., Dulany et al., 1984).

The second measure to be included was the global associative strength one of Knowlton and Squire (1994, 1996). This is a measure with a solid theoretical motivation (either as feature overlap or in terms of basic associative learning processes) and it has been explored in several AGL studies (e.g., Higham, 1997; Meulemans and van der Linden, 1997; Johnstone and Shanks, 1999; Pothos and Bailey, 2000; Lotz et al., 2009). Each test item has a global associative strength value, which is the average of the associative strength of all its bigrams and trigrams. The associative strength of a bigram or trigram is simply the average frequency with which it has been observed in training. For example, in computing the anchor associative chunk strength of string MSXVVR, we need to consider how frequently the following chunks appeared in training: MS, MSX, VR, VVR. A third measure, related to global associative strength, is anchor associative strength (e.g., see Knowlton and Squire, 1994, or Meulemans and van der Linden, 1997). The anchor associative chunk strength of a test item is computed in the same way as the global chunk strength, but taking into account only the bigrams and trigrams in the anchor positions of a string (the beginning and end of a string). The theoretical motivation for the anchor measure relates to the empirical finding that anchor chunks tend to be more salient to participants. For example, participants are more likely to identify NG strings if they violate the rules of the underlying finite state language in the anchor position (e.g., Reber and Allen, 1978).

Fourth, the edit distance of each test item was computed. The edit distance between two items is the number of changes that need to occur in one item so that it becomes identical to the other item. Specifically, edit distance was defined as the number of insertions and deletions that are required to map one item to another, such that substitutions were considered as an insertion and a deletion. Brooks and Vokey (1991) first employed edit distance in the study of AGL and since then it has been considered a measure of whole exemplar similarity, that is, a measure of how much the classification of a test item is influenced by its similarity to entire training instances (see Hahn et al., 2003, for a general model of similarity based on transformations). Thus, edit distance is aligned to exemplar theories of categorization (e.g., Nosofsky, 1988a) and represents a way to understand similarity in AGL that is alternative to chunk strength (for a discussion see Pothos, 2007). However, Brooks and Vokey (1991) computed the edit distance of each test item relative to a single training item (the one most similar to the test item). So, in a sense, Brooks and Vokey employed a “nearest neighbor” version of exemplar theory. Psychologically, there is not really any evidence for such nearest neighbor exemplar processes (unless one considers very extreme values of the sensitivity parameter in the generalized context model; Nosofsky, 1988a,b, but such situations have not been researched in any detail). Accordingly, and following Pothos and Bailey (2000), we adopted the more standard approach of calculating an edit distance value for each test item as the average edit distance between the test item and all training items.

The last, and least interesting, performance measure to be included in the analyses is the length of the items. For example, it is possible that smaller items are better remembered, so that it is easier for participants to decide whether they are G or NG in the test phase. Length has not really been examined in detail in the AGL literature, although some of the better-motivated models do actually covary quite a lot with length (e.g., Poletiek and van Schijndel, 2009). A theoretical interpretation of AGL competence on the basis of length as such is, of course, uninteresting, although if length can account for variance in grammaticality selections, then maybe alternative explanations for AGL performance ought to be pursued (possibly based more explicitly on memory processes).

Grammars

The possible equivalence (or not) between different putative measures of AGL performance is usually meaningfully defined only in the context of particular finite state languages (there may be trivial cases whereby one measure is a simple transformation of another, so that they would always covary regardless of the grammar). In this work, I consider the grammars (and particular sets of training, test items) employed by Reber and Allen (1978) and Knowlton and Squire (1996, Exp. 1). The Reber and Allen (1978) study is one of the early pioneering AGL studies and the corresponding grammar has been a focal point for much of the subsequent debate about what is learned in AGL (e.g., see Dulany et al., 1984; Perruchet and Pacteau, 1990; Redington and Chater, 1996). Reber and Allen's (1978) grammar involves 20 training items and 50 test items, 25 of which are G and 25 NG. An interesting aspect of this stimulus set is that the NG items were created so as to reflect different kinds of violations (e.g., a violation in the first position vs. a deep violation vs. legal strings spelt backwards). Also, the test G items were not all unique (as has become standard in later AGL studies), rather five items were repeated from training (this was done so as to examine whether performance on novel G items was as good as with repeated G ones). However, the Reber and Allen grammar only manipulated grammaticality – the test items were not balanced with respect to any other performance measure. This, indeed, has been a starting point for considerable debate in AGL, as other researchers argued that it was not grammaticality as such that allowed the successful discrimination between G and NG sequences in test, but rather some other performance factors, such as similarity. Speaking of which, Knowlton and Squire (1994, 1996) provided the most principled approach to modeling fragment overlap in AGL. In their 1996 study, they created a grammar (shown in Figure 1), which carefully balanced grammaticality against global chunk strength (though note that the Knowlton and Squire materials as reported in their paper actually have typos; see, e.g., Pothos and Bailey, 2000). Specifically, the training set of Knowlton and Squire (1996, Exp. 1) consisted of 23 training items and 32 unique test items. There were 16 G test items and 16 NG. Importantly, the average global chunk strength of the G items was equated to that of the NG items (this equivalence was established in terms of non-significant t-tests). Thus, Knowlton and Squire could examine independently the putative influence of grammaticality and chunk strength in participants’ performance. They reported effects for both, a result broadly replicated in subsequent research. Finally, it is worth noting that since the work of Knowlton and Squire (and that of Vokey and Brooks, 1991) with stimulus sets balancing different performance factors, researchers have developed automated computational procedures for creating such stimulus sets (e.g., Bailey and Pothos, 2008). Overall, the Reber and Allen (1978) and Knowlton and Squire (1996, Exp. 1) grammars are probably not the most sophisticated grammars a researcher could use today. However, they are “standard” in the sense that they have been employed in several studies and researchers fairly familiar with their properties.

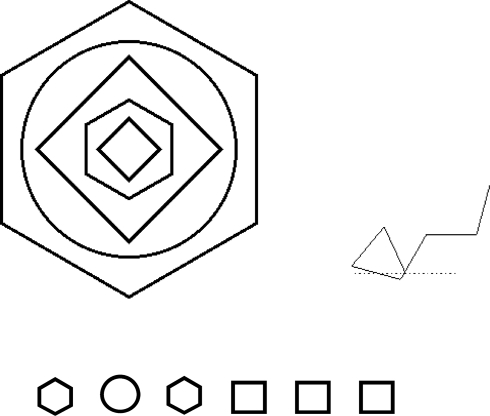
The particular datasets which will be analyzed are those of Pothos et al. (2006) and Pothos and Bailey (2000). Pothos et al. (2006) used the Reber and Allen (1978) grammar and manipulated stimulus format so that in one condition stimuli appeared as letter strings (as is standard), in another condition as sequences of cities which corresponded to the routes of an airline company, and in a final condition stimuli were embedded arrangements of shapes (the first symbol in a sequence corresponded to the inner-most shape and subsequent symbols enclosed all previous ones; Figure 2). The manipulation of stimulus format was employed to examine the extent to which AGL is about learning at the symbolic level or whether stimulus format affects learning processes. From this and other research it appears that stimulus format does affect learning to some extent, although it has not been possible to make this intuition more precise (see also, e.g., Altmann et al., 1995; Whittlesea and Wright, 1997). Also, Pothos et al. (2006) included a transfer manipulation, so that in three conditions the same symbols were used to specify both training and test stimuli, but in three additional conditions the symbols were changed after test.

Figure 2.

Examples of the types of stimuli used in Pothos et al. (2006).

Pothos and Bailey (2000) employed the Knowlton and Squire (1996, Exp. 1; see also Figure 1) grammar and also provided a manipulation of stimulus format. In one condition Pothos and Bailey employed embedded arrangements of shapes analogous to those of Pothos et al. (2006). In another condition, the stimuli were made of the same shapes, but now sequentially arranged. In the third condition stimuli were arrangements of line segments. In that condition each symbol (that is, each transition in the underlying finite state language) corresponded to an angle relative to the previous symbol. This means that the same symbol could result to adding line segments at different angles to the horizontal, depending on which other lines have preceded the current one (Figure 3). The lines stimuli in particular challenge any model which is sensitive only to the underlying symbolic structure of the stimuli, regardless of the particular format of the stimuli.

Figure 3.

Examples of the types of stimuli used in Pothos and Bailey (2000).

Preliminary considerations

We adopted the simple strategy of examining correlations between the entropy measures and the other predictors of AGL performance and between the entropy measures and grammaticality endorsements in the nine conditions of Pothos et al. (2006) and Pothos and Bailey (2000). The grammaticality endorsement of a test item is the probability with which is selected as grammatical. The prediction regarding the entropy measures is that grammaticality endorsements should correlate negatively with the entropy measures, in the simple sense that the more specifiable a test item is from the training items, the more it should be perceived to be compatible with the test items, and hence as G (note, though, that one cannot formulate an a priori prediction as to whether the bigram or the trigram version of the entropy measures will work better and likewise for the summative and averaging versions). Modeling grammaticality endorsements presents a sensitive test of any AGL model since there are (number of items minus one) degrees of freedom, while the model restricts only one degree of freedom.

Before presenting the results, it is worth bearing in mind both the possible sources of error in the application of the entropy model for AGL and its inherent limitations. First, the model's predictions are based only on the symbolic-level regularity of the AGL stimuli. How much of AGL performance can we understand by considering regularity only at the symbolic level? Note that all the AGL proposals which were reviewed above make no allowances for differences in stimulus format. As said above, it is unlikely that stimulus format does not affect AGL performance at all, even though attempts to quantify any corresponding effects have had limited success (e.g., Pothos et al., 2006). Second, some learning is bound to take place in the test phase of an AGL experiment as well. AGL research has identified situations where participants given only the test phase of an AGL experiment, perform in similar ways to participants given both the test and the training phases. In an ideal situation, we would be modeling grammaticality endorsements in test after all variability due to learning that can take place in test has been eliminated. However, it has not been possible to corresponding procedures. Third, grammaticality endorsements are noisy. In this work, we adopt the simplifying procedure of considering the average endorsement rate for each test item across participants (within conditions). Traditionally, in AGL work the dependent variable of interest has been overall grammaticality accuracy. Power analyses with such a variable indicate that population samples of between 15 and 30 participants to be adequate (e.g., Pothos, 2005b). However, investigations on grammaticality endorsements have been less frequent (Pothos and Bailey, 2000; Johnstone and Shanks, 1999; Lotz et al., 2009) and corresponding power analyses have not been conducted.

Results and Discussion

In Table 1 we show how the four entropy measures correlated with average grammaticality endorsements in the nine AGL conditions of Pothos et al. (2006) and Pothos and Bailey (2000). Negative correlations are in the expected direction, in the sense that greater complexity is associated with a lower endorsement rate for the corresponding item. One may get the impression that different entropy measures work better in different situations. However, in the absence of clear theoretical reasons as to why different measures should perform better in different cases, we should be careful before drawing any conclusions. In order to appreciate the qualitative pattern of results, I summed the correlations between the entropy measures and grammaticality endorsements for the no transfer and transfer conditions separately. These sums have no statistical meaning, they are just a convenient descriptive way to talk about the results. Regarding the no transfer results, the average trigram entropy performed best (sum: −2.83), followed by the average bigram entropy (sum: −1.9), followed by the summed trigram entropy (−1.7), with the summed bigram entropy being last (sum: 0.69). In fact, the pattern for the transfer results was identical.

Table 1.

The correlation of the four entropy measures for AGL, and the other AGL performance measures considered in this work, with average grammaticality endorsements for the test items in the nine AGL conditions of Pothos et al. (2006) and Pothos and Bailey (2000). Note that there were 50 test items in the Pothos et al. (2006) conditions and 32 in the Pothos and Bailey (2000) ones.

	Overall model	Summed bigrament	Summed trigrament	Average bigrament	Average trigrament	Grammaticality	Global Ch. Str.	Anchor Ch. Str.	Edit distance	Length
Pothos et al. (2006)
Letter strings	F(9,40) = 6.21 p < 0.0005	0.15	−0.46**	−0.61**	−0.61**	0.71**	0.48**	0.57**	−0.32*	0.07
Embedded shapes	F(9,40) = 6.30 p < 0.0005	0.09	−0.26	−0.25	−0.47**	0.52**	0.36*	0.63**	−0.36*	0.26
Sequences of cities	F(9,40) = 10.0 p < 0.0005	0.19	−0.61**	−0.69**	−0.67**	0.76**	0.37**	0.58**	−0.22	−0.10
TRANSFER
Letter strings	F(9,40) = 1.14 p = 0.36	0.24	−0.00	−0.08	−0.08	0.15	−0.07	0.12	−0.06	0.09
Embedded shapes	F(9.40) = 2.17 p = 0.045	0.23	0.25	0.01	0.04	0.04	−0.06	0.05	−0.03	0.34
Sequences of cities	F(9.40) = 2.84 p = 0.011	0.27	−0.29*	−0.17	−0.27	0.23	−0.16	0.11	0.06	−0.09
Pothos and Bailey (2000)
Embedded shapes	F(9,21) = 2.61 p = 0.034	0.42*	0.17	−0.05	−0.37*	0.31	0.27	0.30	0.07	0.47**
Lines	F(9,21) = 2.17 p = 0.069	−0.18	−0.43*	−0.28	−0.51**	0.28	0.43*	0.47**	−0.29	−0.10
Sequences of shapes	F(9,21) = 3.17 p = 0.014	0.02	−0.11	−0.02	−0.20	0.41*	0.37*	0.25	−0.35	0.05

Note: An ‘*’ flags a correlation significant at the 0.05 level and a ‘**’ flags one significant at the 0.01 level. Italic entries simply indicate the highest and next highest correlations with grammaticality endorsements in a particular condition (for the entropy measures, we highlighted only correlations which are in the expected direction). The ‘overall model’ column shows the F test for a regression model to predict grammaticality endorsements on the basis of all AGL performance measures entered concurrently.

A few immediate conclusions are possible. First, it appears that average trigram entropy is a fair model of AGL performance. In five out of six no transfer conditions, there was a significant correlation between average trigram entropy and grammaticality endorsements. Though note that the correlations between the entropy measures and grammaticality endorsements did not exceed 0.69. At the very least, this suggests that the entropy model in its current form is incomplete. One obvious limitation is that it assumes entropy computations are noiseless and that they lead to a criterion for item endorsement which is likewise noiseless. Future extensions without these assumptions, and possibly incorporating some kind of diffusion decision process (e.g., Pleskac and Busemeyer, in press), appear promising. Also, regarding the transfer conditions, the correlations were not significant, even though they were in the right direction. Second, for both bigram and trigram entropies, the average version was associated with higher correlations with performance than the corresponding summed version. This finding indicates that participants are not sensitive to the overall complexity in parsing a test item, but rather to the average complexity of all bigrams/trigrams in the test item.

Third, the entropy measures work a lot better in the no transfer condition, regardless of stimulus type, as opposed to the transfer conditions. Now, strictly speaking, the entropy measures do not quite apply in the transfer case (at least not in a sensible way) since all the symbols are different. Of course, in applying the entropy measures in the transfer case we follow the fairly standard assumption that participants’ performance is driven either by abstract symbolic versions of the actual stimuli (e.g., Vokey and Brooks, 1991) or that there is some kind of mapping between the symbols employed in training and test (e.g., Redington and Chater, 1996; see also Tunney and Altmann, 2001). But, the correlations between the entropy measures and grammaticality endorsements in the transfer conditions show that, in such conditions, participants are not sensitive to the uncertainty regarding either bigram or trigram continuations in test items.

To appreciate why the entropy model fails in the transfer case, it is useful to consider approaches which have been successful in accounting for transfer results. One such approach involves postulating a sensitivity to the repetition structure in each stimulus. For example, adjacent repetition structure concerns the number of immediately consecutive identical elements (cf. Mathews and Roussel, 1997) and global repetition structure concerns the number of identical elements in an item (Vokey and Brooks, 1994). Such measures have been shown to account for some variance in AGL experiments in both no transfer and transfer conditions (Tunney and Altmann, 1999, 2001; Scott and Dienes, 2008). There is a strong intuition as to why such repetition measures work in the transfer AGL paradigm: they depend on patterns of identity, irrespective of particular symbols. Observe that the entropy model should be blind to repetition structure, as it is only sensitive to the number of alternative continuations from one symbol to the next, irrespective of whether these continuations involve identical symbols or not. To conclude with this issue, a repetition structure approach has some obvious strengths especially when it comes to transfer experiments. Though note, it is currently difficult to unequivocally conclude that such an approach is superior to alternative ones (and indeed, e.g., Scott and Dienes, 2008, did not examine the relation of the repetition structure indices with the other measures of AGL performance they considered).

Table 1 also compares the correlations between grammaticality endorsements and the entropy measures with the correlations involving the other AGL measures. Note that we could not compare the performance measures with multiple regression analyses for two reasons. First, because of the large number of predictors, we would likely end up with saturated models, so that there would be reduced evidence that the standardized beta coefficients are significantly different from zero. Second, the different predictors correlate highly with each other (see Table 2) and a situation of colinearity would further reduce confidence in the relative size of the beta coefficients. Overall, the only AGL performance measure which appears clearly superior to the entropy ones is grammaticality. This is an interesting finding, not least because grammaticality attempts to model AGL performance on the basis of a simple binary distinction between G and NG items. Grammaticality works best with the Pothos et al.’s (2006) results, but these results were obtained using the Reber and Allen (1978) materials. As these materials were put together specifically with a view to examine Reber's early rules hypothesis, one might speculate that the materials are particularly favorable to this hypothesis. Theoretically, as noted, the grammaticality measure is probably better aligned with rules hypotheses in AGL, such as that of Dulany et al.’s (1984), rather than the early one by Reber (cf. Reber, 1993).

Table 2.

The correlations of the entropy measures and the other measures of AGL performance for the Reber and Allen (1978) training, test stimulus sets and for the Knowlton and Squire (1996, Exp. 1) training, test stimulus sets.

	Summed		Average
	Bigram entropy	Trigram entropy	Bigram entropy	Trigram entropy
Grammaticality	0.15/0	−0.67**/−0.33	−0.68**/−0.54**	−0.80**/−0.70**
Global Ch. Str.	0.06/−0.32	−0.38*/−0.53*	−0.39**/−0.07	−0.67**/−0.43*
Anchor Ch. Str.	−0.04/0.25	−0.54**/0.03	−0.43**/0.06	−0.65**/−0.23
Edit distance	0.19/0.51**	0.37**/0.54**	0.16/0.02	0.22/0.17
Length	0.12/0.96**	0.52**/0.74**	0.09/0.06	−0.11/−0.01

Note: Each cell of the table shows the correlation between an entropy measure and a standard AGL measure for the Reber and Allen grammar (first number) and the corresponding correlation for the Knowlton and Squire grammar (second number). Correlations which are significant at the 0.05 level are flagged with an ‘*’ and correlations which are significant at the 0.01 level are flagged with an ‘**’.

The correlations between the four entropy measures and the other measures for AGL performance are shown in Table 2. The most important conclusion from this table is that the entropy measures display a rich pattern of relationships with the existing measures of AGL performance. As discussed, this is desirable in the sense that all the AGL measures are based on some kind of statistical information from training (even grammaticality, since the underlying finite state grammar can be seen as a particular representation of regularity in the training items), so that it would have been puzzling to fail to observe a rich pattern of correlations. A less reassuring, but expected, conclusion is that the results somewhat differ between the Reber and Allen (1978) grammar and the Knowlton and Squire (1996, Exp. 1) one. For example, edit distance and length both correlate with the bigram summed entropy measure for the Knowlton and Squire grammar, but this is not the case for the Reber and Allen one. It is interesting to note that summed trigram entropy correlates, on average, most highly with the other performance measures, but this was not the measure which correlated most highly with participant performance. Thus, it is not the case that the best entropy measure is the one which simply covaries the most with existing measures. A final observation is that edit distance and length correlated, on average, more so with the summed entropy measures, compared to the average ones. One can see why this is the case, by considering that edit distance computations are likely to depend on length (the longer the two items that are compared, the more, on average, the expected number of changes required to convert one into the other), as is the case with the summed entropy measures.

Concluding comments

Entropy appears to provide a very promising approach for understanding AGL performance. There were entropy measures which correlated highly with average grammaticality endorsements across nine AGL conditions, with two different grammars (and training/test stimulus sets). Note that the AGL results analyzed in this work involve both the standard procedure of presenting stimuli as letter strings, but also procedures in which the underlying symbolic structure of the stimuli would be less salient (such as embedded arrangements of shapes or sequences of line segments). The success of the entropy model to (partly) account for grammaticality endorsements in such conditions further supports the notion that human learning may be biased to process regularity at a more abstract level, independent of particular stimulus characteristics (as noted, it still debated as to exactly how independent of stimulus properties human learning is).

In employing Shannon entropy to understand AGL performance, the underlying proposal about human learning is that people are sensitive to the regularity of information in the environment, in the specific sense that there is more regularity when there are fewer options to select from and these options are associated with either very high or very low probability. Put differently, most models of AGL (and cognitive processes in general) assume that the cognitive system exploits regularity in its environment in a particular way. An entropy approach is about quantifying regularity in a particular way. The advantage of adopting entropy, and the more general Information Premise from which specific models are developed, is that this is a very general framework for understanding uncertainty which, in turn, means that it can be applied in diverse areas. So, the key advantage of an entropy approach is its generality. At face value, Shannon entropy may seem a rather unlikely candidate for a unifying explanatory principle for diverse cognitive processes. However, this initial impression is misleading—we next consider an entropy model of categorization and an entropy model of reasoning behavior.

In categorization, work by Pothos and Chater (2002) has a straightforward interpretation in terms of the Information Premise. In their work it has been assumed that the instances in our experience are encoded in terms of similarity information; that is, for each object we encode the similarity information of this object with all other objects. Pothos and Chater suggested that the objective of categorization would be to describe this similarity information in a more compact and efficient way. In other words, categories were seen as a means of simplifying the description of the similarity structure of a set of items as much as possible. The particular model Pothos and Chater investigated was framed around the notion of Minimum Description Length (Rissanen, 1978), so that its predictions required the computation of various codelengths (e.g., the codelength for the similarity structure of the stimuli with and without categories). However, the codelengths in the model simply reflected the uncertainty in determining the corresponding information, so that they were computed as entropies. According to Pothos and Chater's (2002) model, the preferred classification for a set of items is the one that minimizes the uncertainty in predicting the similarity relations between a set of stimuli, which is a direct application of the Information Premise.

Perhaps a formal link between AGL and categorization is not so surprising; after all, AGL can be seen as a special case of a categorization task, and previous research has already been taken advantage of such a possible equivalence (cf. the exemplar models of AGL;Brooks and Vokey, 1991; Vokey and Brooks, 1994; Pothos and Bailey, 2000). However, a link with reasoning would certainly be less intuitive. At a broad level, AGL does involve some kind of a decision making process, in the sense that different test items are selected as G or NG. But this type of decision cannot be intuitively reconciled with the more traditional processes of deductive reasoning, whereby starting from a set of premises people come up with one or more conclusions. An impressive demonstration of the relevance of the Information Premise in the Wason Selection Task (e.g., Wason and Johnson-Laird, 1972) was provided by Oaksford and Chater (1994). The Wason selection task is a simple reasoning problem in which people are asked to examine whether a conditional rule is true or false, by making selections among a set of cards (the cards are labeled with one clause of the conditional and contain hidden information about the other clause of the conditional). Oaksford and Chater (1994) suggested that people select these cards that minimize the expected uncertainty in deciding whether the rule is true or not; uncertainty was quantified using the exact same notion of Shannon entropy that we used in this research, so that their model reflects another application of the Information Premise.

How compelling are the above equivalences? Clearly, there are several different ways in which the Information Premise can be translated to a specific model to describe a cognitive process. While the Information Premise asserts that all models reflect minimization of uncertainty, the exact mathematical specification of uncertainty in different situations is certainly not set in stone. However, the merit of the above discussion is seen in that, although there can be several different applications of the Information Premise for the same cognitive problem, such alternatives still need to share a similar foundation (a specific use of probabilities, quantifying uncertainty in a certain way, etc.), that would make them much more similar, as a class of models, compared to others.

Researchers have been exploring the potential of Shannon entropy for psychological models for several decades (for earlier attempts see, e.g., Miller, 1958; Garner, 1974). In trying to develop entropy models of cognitive processes as diverse as categorization, learning, and reasoning, the aim is to provide a theoretical framework to formally explore the relations between such cognitive processes. In other words, whether (e.g.) learning, categorization, and reasoning are different facets of the same cognitive process, or not, is clearly an empirical issue. Shannon entropy simply provides a theoretical medium for investigating their putative equivalence.

Cognitive research based on Shannon entropy has two important limitations, one theoretical and the other empirical. First, on the theoretical front, entropy models work best in situations where there is a choice amongst different alternatives, such that each alternative can be assigned a probability value. However, entropy models are less able to handle situations in which complex representational issues arise. For example, researchers have demonstrated that in certain situations similarity judgments may violate the metric axioms, such as symmetry. How could an entropy approach explain that the psychological similarity between items A and B may lead to one value, but the similarity between items B and A to another? Overall, the mathematics of entropy do not provide us with many tools for understanding representation and corresponding options tend to be somewhat limited (cf. Pothos and Chater, 2002). By contrast, the mathematics of quantum theory, for example, is the most general mathematical framework for assigning probabilities to subspaces. It has been used extremely successfully in physics for 100 years or so and it has recently started being introduced in psychology as well (Atmanspacher et al., 2004; Khrennikov, 2004; Busemeyer et al., 2006, 2009; Pothos and Busemeyer, 2009).

On the empirical front, entropy models can, at best, inform researchers as to what is the relevant computational principle regarding different aspects of cognition. They cannot as such help determine whether the underlying brain systems are the same or not. For example, suppose that after extensive research it is concluded that both learning processes (as exemplified by AGL experiments) and reasoning processes (in specific tasks such as the Wason selection task) can both be understood in terms of Shannon entropy models. Such a conclusion would mean, for example, that human behavior in learning and reasoning can be predicted in the same way. But it is still possible that the underlying brain systems are separate and even modular. Neuroscience methods appear particularly well-suited for questions relating to the single vs. multiple systems debate (e.g., Ashby et al., 1998; for an interesting discussion see Plunkett and Bandelow, 2006). In AGL there have been several neuroscience investigations in the last couple of years (mostly fMRI), however, differences in methodology have so far prevented the emergence of a confident conclusion (e.g., Fletcher et al., 1999; Skosnik et al., 2002; Lieberman et al., 2004; Smith and McDowall, 2006; Pothos and Wood, 2009).

In sum, the results reported in this paper corroborate the view that the application of entropy approaches in AGL can be very promising. It has been shown that a “minimalist” application of entropy ideas led to a very good description of AGL results across a range of conditions and to entropy models which related very well to alternative AGL models. Future work should attempt to provide more direct experimental tests of this entropy approach to AGL and finer investigations of the computational properties of the corresponding models.

Conflict of Interest Statement

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.