A UNIFIED FRAMEWORK FOR ESTIMATING DIFFUSION TENSORS OF ANY ORDER WITH SYMMETRIC POSITIVE-DEFINITE CONSTRAINTS

Abstract

Cartesian tensors of various orders have been employed for either modeling the diffusivity or the orientation distribution function in Diffusion-Weighted MRI datasets. In both cases, the estimated tensors have to be positive-definite since they model positive-valued functions. In this paper we present a novel unified framework for estimating positive-definite tensors of any order, in contrast to the existing methods in literature, which are either order-specific or fail to handle the positive-definite property. The proposed framework employs a homogeneous polynomial parametrization that covers the full space of any order positive-definite tensors and explicitly imposes the positive-definite constraint on the estimated tensors. We show that this parametrization leads to a linear system that is solved using the non-negative least squares technique. The framework is demonstrated using synthetic and real data from an excised rat hippocampus.

1. INTRODUCTION

Symmetric positive-definite (SPD) tensors of order-2 have been used in modeling the diffusivity function in the so called Diffusion Tensor MR Images (DT-MRI) [1]. The diffusion tensor can be estimated from a given Diffusion-Weighted (DW) MRI dataset by using the Stejskal-Tanner signal attenuation model:

$$S/S_0=e^{-bd(\mathbf{g})}$$ (1)

where d(g) is the diffusivity function and S/S₀ is the observed signal attenuation associated with the diffusion sensitizing magnetic gradient orientation g and the diffusion weighting b.

Higher even-order tensors (e.g. 4^th and 6^th) generalize the 2^nd-order tensors and have the ability to approximate multi-lobed functions [2] such as the kurtosis of diffusion [3]. Recently several methods have been proposed for estimating 4^th-order tensors with positive-definite constraints [4, 5] as well as for processing high-order tensor fields [6, 7].

One of the advantages of Cartesian tensor basis over spherical harmonic basis is that the local maxima of a higher-order tensor can be easily computed [8, 9]. This property has been used for computing the fiber orientations from a given orientation distribution function.

Although, high-order tensors have been employed in most of the aforementioned methods due to their simple polynomial form and their ability to model multi-lobed spherical functions, there are no existing methods for imposing positivity constraints in tensors of any order higher than 2 and 4. It has been shown that tensors of orders 6 and 8 can approximate complex fiber structures such as 3-fiber crossings, by overcoming the limitations of 4^th-order tensors [2]. Furthermore, the need for positivity constraints is essential especially in the case where the tensors approximate positive-valued physical quantities such as diffusion or displacement probability [4].

In this paper, we present a novel method for imposing the positivity constraints on high-order symmetric tensors. In our framework, we express any symmetric positive-definite tensor as a sum of squares of lower-order polynomials. This parametrization can be approximated by a convex combination of predefined homogeneous polynomials, and we show that the accuracy of the approximation can be easily adjusted to a desired level. We evaluate 2^nd, 4^th, and 6^th-order tensors computed by the proposed framework using synthetic data. Furthermore, we quantitatively compare our method with another existing technique for estimating diffusion tensors of order-6. Finally, the proposed method is demonstrated using real DW-MRI data from an isolated rat hippocampus.

The main contribution of the work presented here is a unified framework for estimating symmetric positive-definite tensors of any even order. To the best of our knowledge this is the first method in literature for imposing positivity constraints on any order symmetric tensor. The other significant contribution of this paper is a novel parametrization of tensors, which covers the full space of positive-definite high-order tensors.

2. DIFFUSION TENSORS OF EVEN ORDERS

The diffusivity function d(g) in Eq. 1 can be approximated by a Cartesian tensor as follows [2]:

$$d(\mathbf{g})=\sum _{i=1}^3\sum _{j=1}^3\cdots \sum _{k=1}^3\sum _{l=1}^3{g}_i{g}_j\cdots g_k{g}_l{D}_{i,j,\cdots ,k,l}$$ (2)

where g_i is the i^th component of the 3-dimensional unit vector g, and D_{i,j,···,k,l} are the tensor coefficients. The number of indices (or equivalently the number of sums in Eq. 2) is equal to the order of the tensor. When approximating the diffusivity function, we are interested in tensors of even orders with full symmetry. In this case, those tensor coefficients which correspond to the same monomial $g_1^a{g}_2^b{g}_3^c$ are equal to each other. For instance the coefficients D_1,1,1,2, D_1,1,2,1, D_1,2,1,1, D_2,1,1,1 of a 4^th-order symmetric tensor correspond to the monomial $g_1^3{g}_2$ and therefore are equal to each other.

Another property of the diffusivity is that d(g) is a positive-valued function ∀g ∈ S₂. There are various ways for re-parameterizing Eq. 2, so that it explicitly represents positive-definite tensors of orders 2 or 4. In the following sections we present a novel unified way of parameterizing positive-definite tensors of any (even) order. The proposed method covers the full tensor space and is not order specific.

3. PARAMETRIZATION OF POSITIVE TENSORS

Any positive-definite polynomial can be written as a sum of squares of lower order polynomials [10, 11]. In our particular case, any positive-definite K^th-order homogeneous polynomial in 3 variables can be written as a sum of squares of K/2^th-order homogeneous polynomials p(g₁, g₂, g₃; c), where c is a vector that contains the polynomial coefficients.

$$d(\mathbf{g})=\sum _{j=1}^{M}p{(g_1,g_2,g_3;{\mathbf{c}}_j)}^2$$ (3)

The number of terms in the summation of Eq. 3 is bounded by the number of unique monomials in a K/2^th-order homogeneous polynomial in 3 variables, i.e. $M\le \frac{(2+K/2)!}{2(K/2)!}$. For instance, 2^nd-order tensors can be written as a sum of M ≤ 3 squares of order-1 polynomials, which parametrization corresponds to the rank-1 decomposition of symmetric matrices. Similarly, 4^th-order tensors can be written as a sum of M ≤ 6 squares of order-2 polynomials. This agrees with Hilbert’s theorem on ternary quartics [4] according to which M = 3 terms are enough in Eq. 3. In the cases of 6^th and 8^th order tensors the upper bounds are ≤ 10 and ≤ 15 respectively.

The parametrization in Eq. 3 covers the full space of positive-definite homogeneous polynomials of any order. The unknown parameters are the coefficients of the polynomials p(.) whose number is bounded by $\frac{1}{8}{\left(\frac{(2+K/2)!}{(K/2)!}\right)}^2+\frac{(2+K/2)!}{4(K/2)!}$, i.e. 6, 21, and 55 coefficients for K = 2, 4, and 6 respectively.

4. TENSOR ESTIMATION FROM DW-MRI

Given a data set of DW-MRI signal attenuations S_i/S₀ associated with magnetic gradient orientations g_i and diffusion weighting b-values b_i, i = 1, ···, N, we can estimate the co-efficients of a K^th-order positive-definite diffusion tensor by minimizing the following energy function with respect to the unknown polynomial coefficients

$$E=\sum _{i=1}^N{\left(S_i/S_0-e^{-b_{i}d({\mathbf{g}}_i)}\right)}^2$$ (4)

where d(g) is given by Eq. 3.

The energy in Eq. 4 can be minimized by reformulating Eq. 3 in the form of a spherical convolution:

$$d(\mathbf{g})={\int }_{S_{\frac{(2+K/2)!}{2(K/2)!}-1}}\lambda (\mathbf{c})p{(g_1,g_2,g_3;\mathbf{c})}^{2}d\mathbf{c}$$ (5)

where λ(c) is a non-negative real function. Note that Eq. 5 is the continuous generalization of Eq. 3, and it also covers the full space of K^th-order positive-definite tensors. By substituting d(g) in Eq. 4 with Eq. 5, we can now estimate a diffusion tensor by minimizing Eq. 4 with respect to the unknown function λ(c). The value of this function can be approximated for a given set of M′ unit vectors c₁, ···, c_M′ by discretizing the integration over the sphere in Eq. 5 as follows:

$$d(\mathbf{g})=\sum _{j=1}^{M^{\prime }}{\lambda }_{j}p{(g_1,g_2,g_3;{\mathbf{c}}_j)}^2$$ (6)

where λ_j are non-negative real numbers. The parametrization in Eq. 6 approximates the space of K^th-order positive-definite tensors and the approximation accuracy depends on how well the set of vectors c_j sample the space of unit vectors c. By constructing a large enough set of well sampled vectors c_j, one can achieve any desired level of accuracy.

5. IMPLEMENTATION DETAILS

5.1. High SNR case

In the case of high signal-to-noise ratio (SNR) in the acquired data, the positive-definite tensors can be estimated by minimizing a log-linear version of Eq. 4, which can be efficiently achieved by solving a linear system with non-negative constraints. The constructed linear system is Px = y, where P is a N × M′ matrix with P_i,j = −b_ip(g_i; c_j)², y is a N-dimensional vector with y_i = log(S_i/S₀), and x is a vector that contains the unknown coefficients λ_j.

Here we should note that the size of matrix P does not depend on the order K of the estimated tensor; however, the elements of matrix P change with K, since their value is related to a K/2^th-order homogeneous polynomial. Furthermore, the rank of P is equal to the number of unique coefficients in a K^th-order tensor, i.e. $\mathit{rank}(\mathbf{P})\le \frac{(2+K)!}{2(K)!}$, which is equal to 6, 15, and 28 for K = 2, 4, and 6 respectively. This is related to the fact that P can be decomposed into the form P = GC, where G is of size N × rank(P) and contains only monomials constructed from the elements of the vectors g_i, and C is of size rank(P) × M′ and contains only monomials constructed from the elements of the vectors c_j.

Due to the need for estimating non-negative λ_j, the above linear system can be stably solved using NNLS (non-negative least squares) [12]. The obtained solution contains at most rank(P) non-zero elements, which are as many as the unknown tensor coefficients. We can easily compute the tensor coefficients by Cx, which multiplication produces a vector that contains the unique coefficients of a K^th-order tensor.

5.2. Low SNR case

In the case of low SNR, log-linearizing Eq. 4 may lead to inaccurately estimated tensor coefficients due to the inappropriate noise model assumed when using the logarithm of the signal values. Instead, one should minimize Eq. 4 by employing any non-linear functional minimization method. The function d(g) in Eq. 4 can be parametrized by either Eq. 3 or Eq. 6. In the first case, the minimization of Eq. 4 should be performed with respect to the polynomial coefficients c_j by using the Levenberg-Marquardt algorithm, as it was shown in [4] for estimating 4^th-order tensors.

If we employ the parametrization in Eq. 6, the minimization of Eq. 4 should be performed with respect to λ_j. The gradient of the energy can be easily computed by ∂E/∂x = 2P^Tdiag(exp(Px))[exp(Px) − exp(y)], where P, x, and y are defined similarly as in Sec. 5.1, and diag(x) denotes a square diagonal matrix whose diagonal elements are given by the vector x. The gradient can be used by any gradient-based energy minimization method for minimizing Eq. 4. The algorithm can be initialized by setting x to the solution of the linear system that was discussed in Sec. 5.1. Additionally, at each iteration of the minimization algorithm the negative values in the solution vector x should be forced to zero in order to guarantee that the estimated tensors are positive-definite.

5.3. Constructing sets of polynomials

In our experiments we constructed sets of polynomial coefficients c_j by first creating a set of 3D unit vectors v_i, i = 1, ···, L using tessellations of the icosahedron on the unit sphere. Then, for the case of K^th-order tensors we computed the homogeneous polynomials p(g) = Π_{k=1: K/2}(g^T v_ik), where i_k = 1, ···, L. The coefficients of these polynomials were stacked together in the form of a vector c_j for each polynomial. In the case of K = 2, 4, and 6, this procedure produces L, L²/2 + L/2, and L³/6 + L²/2 + L/3 unique co-efficient vectors respectively. From our experiments we have seen that the sets of vectors constructed by this procedure lead to parameterizations in the form of Eq. 6 that accurately approximate the space of K^th-order positive definite tensors.

6. EXPERIMENTAL RESULTS

We constructed a dataset of positive-definite tensors by first generating random vectors in 3, 6, and 10 dimensions, and then using them in Eq. 3 as coefficients of homogeneous polynomials. This process created 2^nd, 4^th and 6^th-order tensors and was repeated for 1000 times for each order case.

In order to investigate how many vectors c_j are necessary in Eq. 6 for our algorithm to produce accurate tensor fitting results, we evaluated Eq. 1 for N = 81 unit vectors g₁ ··· g₈₁ using the synthetic dataset of tensors. This produced 81 samples S₁/S₀ ··· S₈₁/S₀ for each tensor in the dataset. Then we reconstructed the original tensors by applying our framework (Sec. 5.1) to the obtained set of samples using various resolutions M′. Table 1 reports the number of polynomials that were required in Eq. 6 in order to reconstruct accurately the tensors. The table also reports the fitting errors computed by $\frac{{\sum }_{i=1}^N\mid d_{\mathit{truth}}({\mathbf{g}}_i)-d({\mathbf{g}}_i)\mid }{{\sum }_{i=1}^N\mid d_{\mathit{truth}}({\mathbf{g}}_i)\mid }$ and the running time per tensor using an Intel Pentium Dual CPU at 1.60 GHz and 1GB RAM. The results demonstrate that our method estimates accurately and efficiently positive-definite tensors of any order.

Table 1.

Order of tensor vs. the number of required polynom.

Order of Tensor	Polynomials	Fit. error	Run. Time
K=2	M′=321	0.00	0.7 ms
K=4	M′=900	0.01	12 ms
K=6	M′=3000	0.02	130 ms

In order to demonstrate the necessity for estimating tensors with positivity constraints we compared our method with an existing one that computes tensor without imposing the positive definite property [2]. In this experiment we added various levels of Riccian noise to the previously described synthetic dataset S₁/S₀ ··· S₈₁/S₀ that correspond to the synthesized set of 6^th-order tensors. The noisy datasets were given as input to: a) the algorithm in Sec. 5.1 (using M′ = 3000) and b) the method in [2], which is the only existing technique in literature for estimating 6^th-order tensors. In both cases, the computed 6^th-order tensors were compared to the ground truth tensors using the previously defined fitting error metric. Figure 1 shows a comparison of the fitting errors obtained for various levels of noise in the data. The results conclusively demonstrate that those tensors that were estimated using positivity constraints approximated the data significantly better, motivating the use of our method.

Fig. 1.

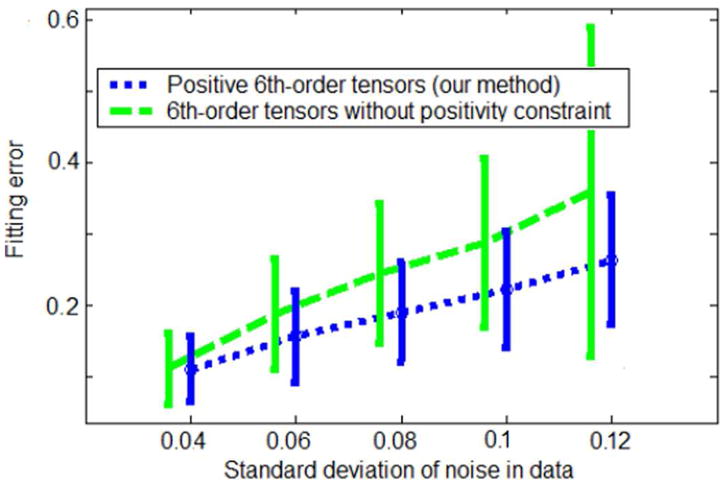
Comparison of the proposed method with the technique in [2] for various levels of Riccian noise in the data.

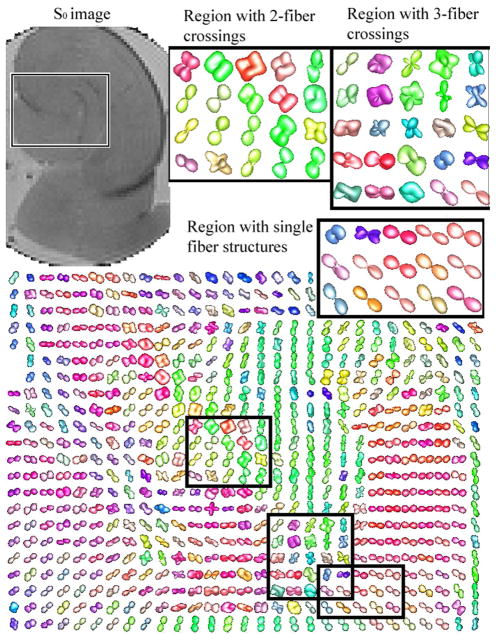
Finally, in order to illustrate the performance of our framework on real data sets, we applied the method in Sec. 5.2 to a DW-MRI data set from an excised rat hippocampus (shown in Fig. 2). The data set contained 46 images acquired using a pulsed gradient spin echo pulse sequence, with 45 different diffusion gradients and approximate b value of 1250s/mm². Figure 2 shows the computed 6^th-order diffusion tensor field. The highlighted regions of interest demonstrate the variability of the estimated structures. At each voxel, the fiber orientations can be estimated from the peaks of the displacement probability, which can be computed from the diffusion tensors as it was shown in [4].

Fig. 2.

DW-MRI dataset from an isolated rat hippocampus. The S₀ image is shown on the top left. The 6^th-order diffusion tensors estimated by the proposed method are shown as a field of spherical functions. One of the depicted regions of interest contains tensors that model 3-fiber structures, which can not be reconstructed by 2^nd or 4^th-order tensors.

7. CONCLUSIONS

Symmetric positive-definite tensors have been used in various applications. Although there are existing methods for imposing positivity constraints on the estimated tensors of order 2 and 4, none of these techniques can be easily extended to higher orders. In this paper we presented a framework for estimating SPD tensors of any order and we used our technique for approximating the diffusivity function from given DW-MR images. The formulation leads to a linear system which can be efficiently solved. Finally, we presented evaluations of our method using synthetic and real DW-MRI datasets.