Short-Range Mechanical Properties of Skeletal and Cardiac Muscles

Abstract

Striated muscles are disproportionately stiff for small movements. This facet of their behavior can be demonstrated by measuring the force produced when the muscle is stretched more than about 1% of its initial length. When this is done, it can be seen that force rises rapidly during the initial phases of the movement and much less rapidly during the latter stages of the stretch. Experiments performed using chemically permeabilized skeletal and cardiac muscles show that the initial stiffness of the preparations increases in proportion with isometric force as the free Ca²⁺ concentration in the bathing solution is raised from a minimal to a saturating value. This is strong evidence that the short-range mechanical properties of activated muscle result from stretching myosin cross-bridges that are attached between the thick and thin filaments. Relaxed intact muscles also exhibit short-range mechanical properties but the molecular mechanisms underlying this behavior are less clear. This chapter summarizes some of the interesting features of short-range mechanical properties in different types of muscle preparation, describes some of the likely underlying mechanisms and discusses the potential physiological significance of the behavior.

1 Introduction

When a skeletal or cardiac muscle is stretched further than ~1% of its initial length, force rises more quickly at the beginning of the movement than it does thereafter. This behavior has been recognized since at least 1924 (Liddell and Sherrington 1924) and is a general property of both relaxed and activated living striated muscle. The mechanical non-linearity is also evident when chemically permeabilized skeletal and cardiac muscle preparations are stretched in Ca²⁺-activating solutions but is much less obvious when the permeabilized samples are immersed in solutions with nanomolar free Ca²⁺ concentrations. The initial phase of the non-linear force response has a complex velocity-dependence but is traditionally regarded as a predominantly elastic effect (force proportional to length) as opposed to a predominantly viscous phenomenon (force proportional to stretch velocity).

Two of the most influential papers describing the non-linear behavior were written by D.K. Hill (1968) and Rack and Westbury (1974). Hill used relaxed frog muscles in his experiments and attributed the non-linear force response produced by the relaxed tissue to its “Short Range Elastic Component” (SREC). Rack and Westbury measured the non-linearity in tetanized cat soleus and lateral gastrocne-mius muscles and attributed it to the “short range stiffness” of the activated tissue. This chapter will discuss the mechanical properties of both relaxed and activated muscles. The initial phase of the non-linear force response observed in both types of tissue will be referred to in general terms as a short-range mechanical property. The goals of the chapter are to summarize the basic features of the non-linear force response in different types of muscle preparation, consider some of the likely underlying mechanisms and finally discuss the potential physiological significance of the behavior.

2 Short-Range Mechanical Properties are a General Feature of Muscle

To the Author’s knowledge, short-range mechanical properties have been observed in every type of muscle preparation that has been tested. He personally, for example, has published experimental records of short-range properties obtained using living frog fibers (Campbell and Lakie 1998), chemically permeabilized mammalian fast skeletal muscle fibers (Campbell and Moss 2000), chemically permeabilized mammalian slow skeletal muscle fibers (Campbell and Moss 2002) and chemically permeabilized mammalian cardiac muscle (Campbell et al. 2003). Figure 7 shows an unpublished experimental record obtained in his laboratory that demonstrates short-range mechanical behavior in an electrically-stimulated rat cardiac trabecula.

Fig. 7.

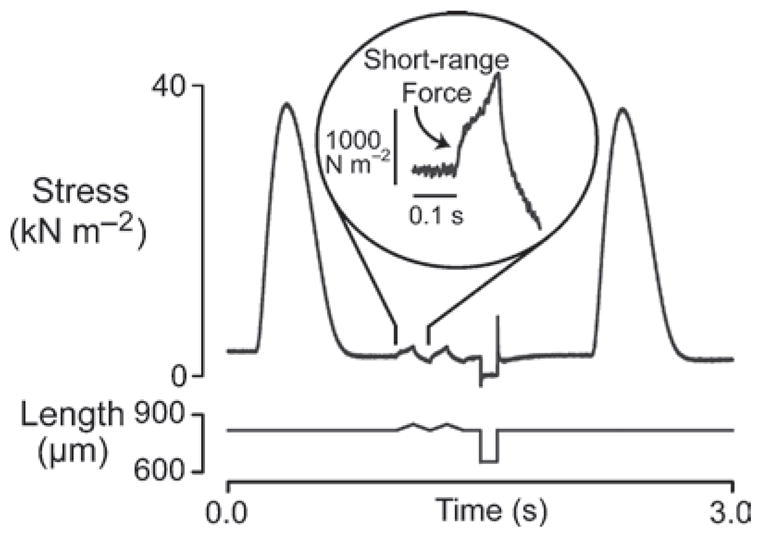
Intact rat trabecula. Two triangular length changes were imposed during the 2 s interval between electrically-excited twitch contractions. The relaxed trabecula exhibited a clear short-range force response. The experiment was performed at 22°C (unpublished records)

Short-range properties have also been measured in smooth muscle preparations. The experimental records published by Gunst (1983) and Meiss (1987), for example, were obtained using canine airway and rabbit mesotubarium superius and overian ligament smooth muscles, and with the exception of the relatively slow time-scale, appear very similar to those measured using striated muscles. It therefore seems possible that the molecular mechanism(s) underlying short-range molecular properties are similar in all muscle types but the behavior in smooth muscle will not be considered further in this work.

One of the many interesting features of short-range mechanical properties is that they are relatively easy to observe in experiments performed on human subjects. Lakie et al. (1984), for example, demonstrated that relaxed fore-arm muscles were disproportionately stiff for small movements. Loram et al. (2007) have recently used ultrasound measurements to show that the short-range stiffness of relaxed human calf muscles resides within the muscle fibers themselves. The short-range stiffness cannot therefore be attributed to non-linear mechanical properties of tendons.

A particularly interesting study was published by Axelson and Hagbarth in 2001. Their measurements showed that the short-range mechanical properties of the fore-arm muscles influenced wrist movements in healthy humans. More importantly, at least for those who are interested in how people control their own movements, the experimental results suggested that the central nervous system “… takes account of and compensates for the … short-range stiffness of the muscles antagonistic to the prime movers.” (Axelson and Hagbarth 2001).

3 Molecular Mechanism

3.1 Evidence Supporting a Cross-Bridge Mechanism

Short-range force responses are elicited when a muscle is stretched from any length in its normal operating range. The short-range properties are therefore not defined by the overall length of the muscle but rather self-reset whenever the muscle is held at a fixed length (Campbell and Lakie 1998). This, in itself, suggests that that the short-range mechanical properties of muscle are unlikely to reflect the behavior of a non-linear elastic component in parallel with the contractile apparatus but more quantitative information can be obtained from experiments performed using chemically permeabilized muscle preparations. These studies are particularly enlightening because they allow the short-range properties to be measured in muscles that are differentially activated in solutions with distinct free Ca²⁺ concentrations.

3.2 Calcium Dependence

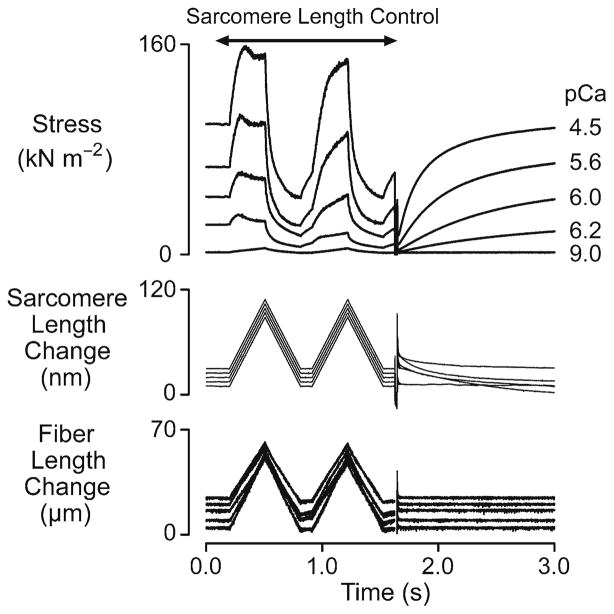
Figure 1 shows force, sarcomere and fiber length records obtained using a single chemically permeabilized rat soleus fiber immersed in solutions with different free Ca²⁺ concentrations. The records were obtained using a computer-controlled negative feedback system (SLControl: Campbell and Moss 2003) to ensure that the sarcomere length change (measured using laser diffraction) in the center of the muscle fiber was the same at every level of Ca²⁺-activation. This approach was designed to reduce potential artifacts that could have arisen due to Ca²⁺-dependent compliance in the ends of the fiber preparation.

Fig. 1.

Ca²⁺ dependence. Superposed experimental records for a chemically permeabilized rat soleus muscle fiber subjected to paired ramp stretches and releases (0.03 l₀, ±0.12 l₀⁻¹, where l₀ is the length of the relaxed muscle fiber at a mean sarcomere length of ~2.60 μm) followed by a large shortening/re-stretch perturbation (0.2 l₀, 20 ms duration) in solutions with different free Ca²⁺ concentrations. The sarcomere and fiber length records are offset vertically from each other for clarity. The sarcomere and fiber length signals are ‘clipped’ during the large shortening/re-stretch perturbation in this figure so that the quality of the sarcomere length control during the ramp stretch/shortening cycles can be assessed (reproduced with permission from Campbell and Moss 2002)

It is clear from Fig. 1 that the magnitude of the short-range response increased when the fiber was developing high levels of active force. More detailed analysis demonstrated that the stiffness of the initial phase of the response (defined in this example as the slope of a regression line fitted to the first 25 ms of an xy-plot of force against sarcomere length) increased in proportion with the steady-state isometric force (Campbell and Moss 2002). This result is consistent with the hypothesis that the initial phase of the tension response results from stretching cross-bridges bound between the actin and myosin filaments if complications due to thick and thin filament compliance (Huxley et al. 1994; Wakabayashi et al. 1994) are ignored.

3.3 Myosin ATP-ase Inhibitors

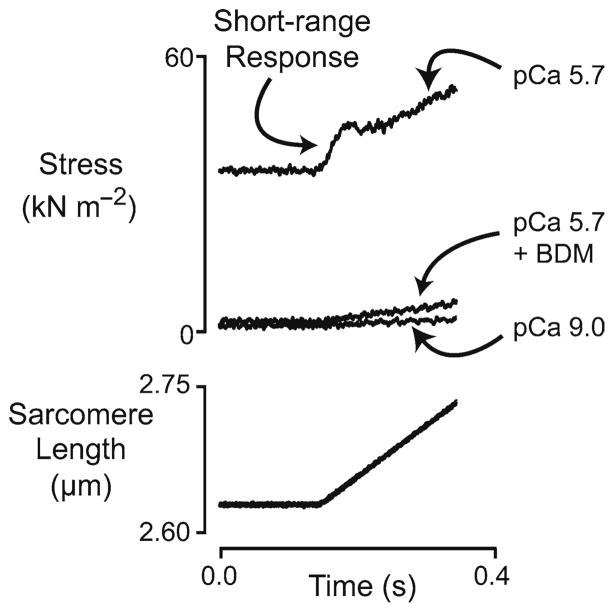
Further support for the cross-bridge basis for short-range mechanical properties comes from experiments using myosin ATP-ase inhibitors. Figure 2 shows short-range tension responses of a murine diaphragm fiber immersed in solutions with pCa (=−log₁₀[Ca²⁺]) 9.0, pCa 5.7, and pCa 5.7 + 16 mM 2,3-butanedione-2-monoxime (BDM). Force increased approximately linearly throughout the movement when the fiber was stretched in pCa 9.0 solution (minimal Ca²⁺-concentration) but there was a clear short-range force response when the trial was repeated using pCa 5.7 solution. When BDM was added to the pCa 5.7 solution, steady-state isometric force was reduced from its initial value of ~45% of the maximal isometric value measured in saturating pCa 4.5 solution to a level very near that measured in pCa 9.0 solution. The short-range force response to the linear stretch was also eliminated.

Fig. 2.

Short-range response of a single murine diaphragm fiber. Superposed force and sarcomere length records for a chemically permeabilized murine diaphragm fiber subjected to a single ramp stretch (0.04 l₀, 0.20 l₀⁻¹) imposed under sarcomere length control in three different experimental solutions. The fiber developed a steady-state isometric force equal to ~0.44 of the maximum isometric value measured in pCa 4.5 solution when it was immersed in the pCa 5.7 solution lacking BDM. Experiments were performed at 15°C (unpublished records)

These records suggest that the short-range force response can only be observed in a muscle in which the myosin cross-bridges are actively cycling. Additional measurements performed in the Author’s laboratory show that another myosin ATP-ase inhibitor, blebbistatin, also reduces the short-range force response of activated muscle fibers in a concentration-dependent manner (Mitov and Campbell unpublished data). (The magnitude of the reduction observed in these measurements also depended on the time that the muscle was incubated with blebbistatin (Farman et al. 2008)). This adds further support to the idea that the initial phase of the short-range response represents the stretch of myosin heads that are bound to the thin filament.

4 Dependence on Mechanical History

Up until this point, this chapter has only discussed the non-linear force response measured during a single ramp stretch. However, one of the most intriguing features of the short-range mechanical properties of muscle is the fact that they depend on the history of movement. The effect is clearly seen in Fig. 1. The tension response to the second lengthening movement is different from that measured during the first movement in every activating solution.

This behavior was demonstrated by Denny-Brown in 1929 in experiments in which one end of a cat limb muscle was freed from the skeleton and connected to the ceiling via a length of wire. The force response was then measured as the muscle was stretched by lowering the operating table (mounted on an oil-filled piston) towards the floor. Denny-Brown noted the short-range force response measured in the experiments and commented that it “lessens … upon rapid repetition of the stretch but recovers with rest at a stationary length” (Denny-Brown 1929).

A very similar effect, demonstrated using more modern technology, is shown in Fig. 3. The two upper panels show superposed force and sarcomere length change records for a sub-maximally activated chemically permeabilized rat soleus muscle fiber subjected to two identical length changes separated by different inter-stretch intervals in different trials. The graph in the bottom panel shows the relative prevailing force at the beginning of the second movement and the relative short-range stiffness during the second stretch as functions of the time interval between the two movements. Both parameters recover towards unity with a time-course that can be modeled as an exponential recovery process (Campbell and Moss 2002).

Fig. 3.

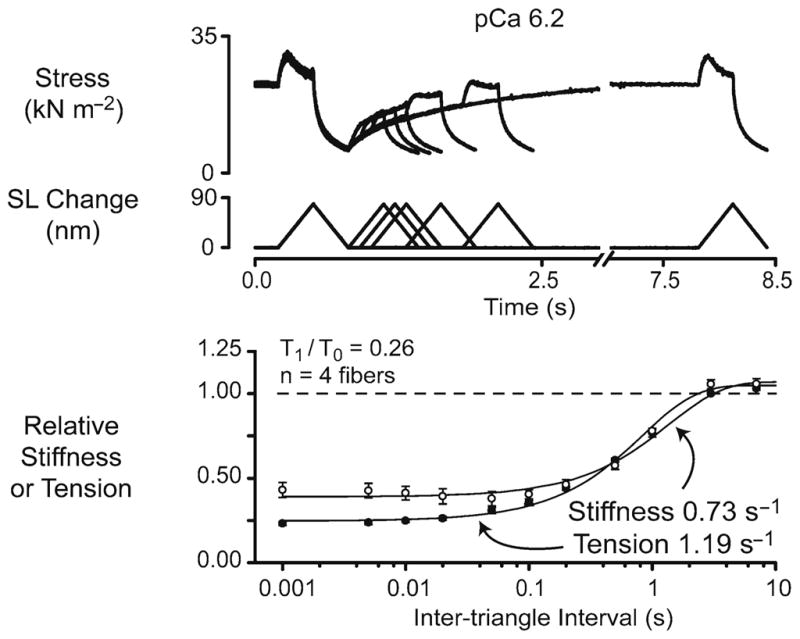
Recovery time-courses of relative stiffness and relative tension. The top two panels show superposed force and sarcomere length records for a single chemically permeabilized rat soleus fiber subjected to paired ramp stretch/shortening cycles separated by time intervals ranging from 1 ms to 7 s. The fiber was immersed in pCa 6.2 solution and developed a steady-state isometric force equal to ~0.26 of the maximum value measured in pCa 4.5 solution throughout the duration of the experiment. The bottom panel shows the relative initial stiffness and the relative prevailing tension measured at the beginning of the second length change plotted as functions of the time interval between the two stretch/shortening cycles. The continuous lines are best-fits of the form y = [a – b.exp(–c.Δt)] where a and b are constants greater than or equal to zero and t is the time interval between the length changes. The labels show the calculated values of the rate constant c for the recovery time-courses of relative stiffness and relative tension. Experiments were performed at 15°C (reproduced with permission from Campbell and Moss 2002)

The temporary reduction in muscle stiffness that follows movement in a relaxed intact muscle was attributed to a thixotropic effect by Buchthal and Kaiser (1951). The term thixotropy is still used in the biomedical literature (for example, Bianco et al. 2007) but it is not clear that different researchers always use the term in the same way. Another problem is that thixotropy in the more general contact of rheology (the study of the flow of matter) means a “decrease in the apparent viscosity under shear stress, followed by a gradual recovery when the stress is removed.” (Harris 1977). The distinction between a thixotropic and a shear-thinning effect therefore seems to be rather arbitrary, perhaps depending in a poorly-defined manner on the time-scale of the observation (Blair 1969).

The term thixotropy also has the unfortunate consequence of implying that the history-dependence of the short-range mechanical properties reflects non-linear viscous effects. This is probably not the case because short-range mechanical properties do not scale linearly with the stretch velocity (Hill 1968; Rack and Westbury 1974). The Author has suggested that muscle’s thixotropic behavior would be more accurately described as history-dependent stiffness (Campbell and Moss 2000) but he is not aware of a single word that describes this type of effect.

4.1 Recovery Rate

The fact that the short-range mechanical properties of a muscle depend on its history of movement seems to have been acknowledged for relaxed tissue before it was formally recognized in activated preparations. A particularly interesting set of experiments was performed by Herbst (1976). He used paired length changes similar to those shown in Fig. 3 to measure the recovery time-course of short-range mechanical properties in relaxed frog muscles and suggested that the asymptotic recovery reflected redevelopment of a population of bound cross-bridges that were perturbed by the first movement.

If myosin heads cycled only between a single detached and a single attached state, the rate of stiffness recovery following an imposed perturbation would, in the simplest kinetic models, be equal to the rate of tension recovery (Brenner 1988). The results published by Campbell and Moss in 2002 show that, at least in chemically permeabilized rat soleus fibers, the real behavior is more complicated. The rate of stiffness recovery in these measurements did vary with the level of Ca²⁺-activation but it was always lower than the rate of tension recovery between the two length changes and k_tr, the rate of tension recovery following a much larger mechanical perturbation (Brenner 1988). Although these results seem at first to argue against Herbst’s cross-bridge theory, computer simulations presented by Campbell and Moss (2002) showed that stiffness and tension can recover at different rates if myosin heads can be bound to the thin filament in more than one state. It is also now known that filament compliance effects will affect the measured rate of tension recovery (Campbell 2006).

5 The ‘Range’ of the Short-Range Response

An experimenter who wishes to demonstrate the existence of the short-range mechanical properties of muscle has to stretch their preparation far enough to observe a reduction in the rate of rise of force during the movement. The length change required to elicit the reduction is a key experimental parameter because it defines the ‘range’ of the short-range response. The parameter also provides important information about the potential underlying mechanisms. If, for example, the observed range was 100 nm half-sarcomere⁻¹ (many times the physical size of an S1 myosin head), it is unlikely that the biphasic force response observed experimentally could reflect the stretch and subsequent cyclic reformation of actin-myosin links.

5.1 Difficulty of Analysis

Although there is now no doubt that the length change required to demonstrate the short-range response is not greater than the distance that actin-myosin links could be stretched, it is difficult to be substantially more precise. One of the issues is that the range of the response varies with the experimental conditions so that it is impossible to come up with a single definitive value (Campbell and Holbrook 2006; Stienen et al. 1992). A more subtle point is that the transition between the ‘short’ and ‘long’ range portions of the force response often occurs as a gradual change in the measured force gradient rather than abruptly at a well-defined instant in time. Consequently it is difficult to envisage a method that can identify a single value for the range without at least some element of uncertainty.

Different researchers have used different techniques to calculate the experimental parameter. For example, Getz et al. (1998) defined L_c, the ‘critical strain’ of chemically permeabilized rabbit psoas fibers, as the length change at the first time point during the stretch at which the first derivative of force with respect to time was about 7.7 nm half-sarcomere⁻¹ and became zero. Their results showed that L_c independent of the stretch velocity for stretch speeds varying from 0.5 to 3.0 in tetanized muscle lengths per second. Lombardi and Piazzesi (1990) measured l_p frog fibers as the “lengthening necessary to attain the peak of force”. They obtained a value of ~15 nm half-sarcomere⁻¹ for stretch velocities of ~0.4 muscle lengths per second and ~11 nm half-sarcomere⁻¹ for stretch velocities of ~1.0 muscle lengths per second. Previous measurements (for example, Edman et al. 1981) performed without sarcomere length control have produced slightly larger values for the ‘range’ which suggests that experimental estimates of the parameter can be compromised by series compliance in the ends of the muscle preparation.

As noted above, even when experiments are (as in the case of Getz et al. and Lombardi et al.) confined to maximally activated fibers, there is probably not a single best method for measuring the range of the initial phase. Getz et al. could not values for stretch velocities less than or equal to 0.5 muscle lengths per calculate L_c second, for example, because the first derivative of force with respect to length did not drop below zero. Lombardi et al.’s method (noting the length change at the peak of force) would not have worked for the experimental records obtained by Getz et al. where (unlike the case with frog fibers) force continued to rise (albeit at a slower rate) beyond the first phase.

The situation is even more difficult when the experiments involve fibers activated in solutions with different free Ca²⁺-concentrations. In Fig. 2, for example, it seems clear that the fiber exhibits a short-range response in the pCa 5.7 condition (without BDM) and not when it is immersed in the pCa 9.0 solution. At some point between these conditions, there must be a Ca²⁺-concentration which is ‘just sufficient’ to elicit a short-range response. Is there a way of unambiguously defining the threshold level?

One such technique was described in a recent publication by Mitov et al. (2009) that summarized measurements of short-range mechanical properties in chemically permeabilized rat myocardial preparations. The authors in this case assumed that the slower rise in force beyond the short-range response was a linearly increasing tension resulting from the increased strain in passive mechanical components such as titin, collagen and elastin molecules. The authors estimated the stiffness of these structures from the rate of rise of force during the latter stages of the movement and used this parameter to deduce the force due to non-cross-bridge components at different time-points in the lengthening response. The force due to attached cross-bridges was then estimated at each time-point in the record by subtracting the calculated passive mechanical response from the experimental force signal.

These procedures allowed short-range responses to be detected using automated computer programs. A short-range response was defined as having occurred when the peak value in the force due to the attached cross-bridges exceeded a threshold level defined as the root mean square of the random noise in the measured force signal multiplied by a constant factor. When an event was detected, the ‘elastic limit’ of the short-range response was accordingly defined as the length change required to produce the peak cross-bridge force.

The main advantage of this technique was that it provided an unambiguous way of defining whether experimental records obtained in a wide range of experimental conditions exhibited short-range responses or not. It could also be implemented to run in automated computer programs without requiring continual user intervention. This allowed many hundreds of records to be processed in a very efficient manner. Visual inspection of selected traces showed that the calculated elastic limit values were generally slightly smaller than the ‘critical strain’ equivalents defined in the manner of Getz et al. as the length change at the time-point at which the first derivative of force with respect to time fell to zero.

Several other techniques have also been used to analyze short-range force responses. Stienen et al. (1992), for example, estimated the transition point between the ‘short’ and the ‘long’ range portions of the force response of rabbit psoas fibers using piece-wise linear regression (Vieth 1989). This technique is probably about as good as any when the force transition is very gradual but would underestimate the force at the end of the first phase in records where the first derivative of force is transiently negative. This Author, and probably many others preceding him, has published records (Campbell and Lakie 1998; Campbell and Moss 2000) in which the transition point was simply identified ‘by eye’.

In this Author’s opinion, ‘fitting by eye’, while not easy to implement as a computer algorithm, is probably not much worse at identifying plausible transition points than techniques that are considerably more mathematically sophisticated. The simple fact is that it is not easy to develop a single algorithm that all researchers will agree identifies the most appropriate transition point in every type of mechanical record showing a short-range response.

6 Velocity-Dependence

One of the reasons that so many researchers have tried to identify a single transition point at the end of the short-range response is that investigating how the point varies with the velocity of the imposed stretch can provide insights into the underlying biophysical mechanism(s). For example, the fact that the short-range force did not increase linearly with stretch velocity when Getz et al. (1998) stretched psoas fibers at rates ranging from 0.5 to 3.0 muscle lengths per second indicates that viscous drag of the myofilaments (a force that would be directly proportional to stretch velocity) was probably not important in these experiments.

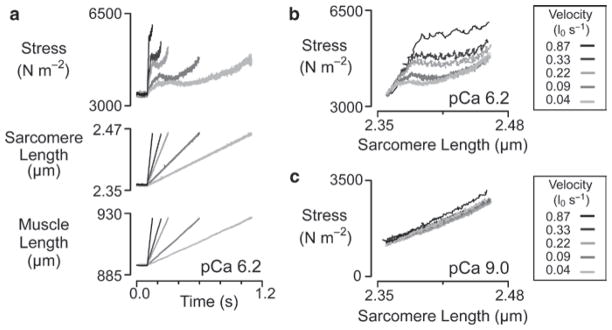
There are however conditions in which the short-range response does vary with the velocity of the imposed stretch. One example from the Author’s previous work is shown in Fig. 4. Panel a in this diagram shows records of force, sarcomere length and preparation length for a sample of canine myocardium developing ~3% of its maximal isometric force and stretched at five different velocities ranging from 0.04 to 0.87 muscle lengths per second. The magnitude of the short-range force response is clearly increased in the faster stretches. An interesting feature of these records is that the short-range force peaks at an earlier time in each record as the stretch velocity increases. This is important information because it implies that the short-range response, even at this low level of activation, cannot be attributed to passive visco-elastic components unless the relaxation time of the visco-elastic mechanism is itself influenced by stretch velocity.

Fig. 4.

Velocity dependence. Experimental records for a chemically permeabilized sample of s⁻¹. canine myocardium subjected to ramp stretches with velocities ranging from 0.04 to 0.87 l₀ Panel (a) shows experimental records plotted against time. Panels (b and c) show force records plotted against sarcomere length. Panels (a and b) show records obtained when the preparation was immersed in pCa 6.2 solution and developing ~0.03 of its maximal Ca²⁺-activated tension. Panel (c) shows the response of the same preparation when it was immersed in pCa 9.0 solution with minimal free Ca²⁺. Experiments were performed at 15°C (reproduced with permission from Campbell et al. 2003)

Plotting the records from panel a on different axes reveals more information. When force records are plotted not against time but against sarcomere length, as in panel b, the initial phases of the force records for the different stretch velocities now superpose. This analysis indicates that the faster stretch velocities do not produce greater force changes by producing a greater force increment per unit length change, but rather by stretching the muscle further along a fixed force/length trajectory before the transition to a slower rate of rise of force occurs.

This behavior is not consistent with simple visco-elastic mechanisms but could be explained by a cross-bridge mechanism if in these experiments fast stretches displaced attached myosin heads further before they detached than slow stretches. This mechanism would still be consistent with Getz et al.’s measurement of a critical strain in rabbit psoas fibers that was insensitive to stretch velocities for movements faster than 0.5 muscle lengths per second if there is a physical limit to the distance that an actin-myosin bond can be extended before it breaks. Forced detachment might, for example, occur when the strain energy stored in the actin-myosin link exceeds the binding strength of the actin-myosin interface.

Before leaving the discussion of velocity-dependence it is interesting to note that while many current-day experiments are carried out using very fast stretches (much faster than those encountered by a muscle in vivo), some of the earlier measurements were performed using very slow length changes. Hill (1968) measured short-range force responses in relaxed frog fibers using stretch velocities down to 1 × 10⁻⁵ muscle lengths per second. (This corresponds to a stretch that takes more than an hour to lengthen a muscle by 4%). It seems exceptionally unlikely that the short-range responses measured in this type of experiment are due to pure viscous components (elements that produce a force directly proportional to the stretch velocity) unless the viscosity ‘disappears’ during contraction (Ford et al. 1977). Any viscous resistance that was large enough to be detected in relaxed muscles during ultra-slow stretches and persisted during a contraction would drastically impede the muscle during normal physiological movements.

7 Second Component

Although this chapter focuses on the first phase of the non-linear tension response to an imposed stretch, the second phase of the response is also worthy of attention. This Author’s view of the “Second Component” (Campbell and Lakie 1995) has been heavily influenced by a model developed by Haugen and Sten-Knudsen (1981) to help analyze short-range force responses measured in relaxed frog muscle fibers stretched from different initial sarcomere lengths.

Haugen and Sten-Knudsen hypothesized that the gradual increase in force that occurred in their records after the short-range response resulted from the extension of a passive linear spring (Haugen and Sten-Knudsen 1981). This spring (the Parallel Elastic Component) was arranged in parallel with the “Short Range Elastic Component” which, in Haugen and Sten-Knuden’s work on relaxed muscle fibers, reflected the mechanical contribution from a relatively small number of myosin heads that continued to cycle between attached and detached states under resting conditions. The mean strain in the cross-bridge links was hypothesized to increase during interfilamentary movements so that the Short-Range Elastic Component produced a force that rose to a constant level during the initial stages of the length change and was maintained at that force plateau throughout the remainder of the stretch. The experimentally measured force response was the arithmetic sum of the Parallel and Short-Range Elastic Components at each time-point in the record.

The Author has since used this simple framework in several of his own publications (Campbell and Lakie 1998; Campbell and Moss 2000, 2002; Mitov et al. 2009). One of the advantages of the approach is that it is readily applicable to experimental data obtained using chemically permeabilized preparations. Mechanical responses obtained using muscles immersed in solutions with different free Ca²⁺-concentrations can be simulated simply by varying the number of cycling myosin heads in the “cross-bridge component” (a more general form of Haugen and Sten-Knudsen’s Short Range Elastic Component). The stiffness of the Parallel Elastic Component in a given sample can be estimated by fitting a (potentially non-linear) mathematical function to the latter stages of the measured force response. This should be appropriate for any cross-bridge mechanism because it can be shown mathematically that the force due to a fixed population of cycling cross-bridges eventually reaches a steady-state level during an imposed movement, irrespective of the number of bound states and/or the strain-dependence of the actin-myosin kinetics (Campbell and Moss 2000).

Although Haugen and Sten-Knudsen (1981) did not specify which proteins were likely to contribute to the Parallel Elastic Component, it now seems likely that the major contribution in single skeletal muscle fibers comes from titin molecules (Granzier and Labeit 2002). (Note that although these molecules are arranged in series between the actin and myosin filaments, they act as if they are mechanically in parallel with force-generating cross-bridges as long as minor complications due to actin and myosin filament extensibility (Huxley et al. 1994; Wakabayashi et al. 1994) are ignored.) In multicellular cardiac muscle samples, there are probably additional contributions from extracellular collagen components and intracellular tubulin and intermediate filaments (Granzier and Irving 1995).

All of the molecular components that can contribute to the Parallel Elastic Component were initially thought to have mechanical properties that are independent of the prevailing free Ca²⁺-concentration. It is therefore interesting to note that there are some experiments that suggest that the stiffness of the Parallel Elastic Component increases with the free Ca²⁺-concentration. One of these is shown in Fig. 2. The pCa 5.7 + BDM condition is an experimental situation in which the muscle fiber is immersed in a solution with a free Ca²⁺-concentration that is sufficient to activate significant cross-bridge cycling but in which the myosin ATP-ase activity is inhibited by BDM. There are two separate indications that the myosin inhibition is almost complete. First, the isometric force is reduced to a value very near that measured in the pCa 9.0 condition. Second, there is no obvious short-range response in the experimental record.

The interesting result demonstrated here is that the stiffness of the muscle (proportional to the slope of the force response) is increased relative to that measured in pCa 9.0 solution in the pCa 5.7 solution containing BDM. This would be the expected result if the Parallel Elastic Component had a stiffness that increased with the free Ca²⁺-concentration. Control experiments (not shown) demonstrated that BDM did not change the stiffness of the diaphragm muscle fiber when it was immersed in pCa 9.0 solution.

In a skeletal muscle fiber, the Parallel Elastic Component probably consists primarily of titin molecules, so the simplest interpretation is that titin molecules have Ca²⁺-dependent mechanical properties. Experiments performed by Fujita et al. (2004) using bovine atrial tissue also suggest that some titin isoforms have a stiffness that increases with the free Ca²⁺ concentration but the effect shown in Fig. 2 seems to be quite a lot larger than that described in their experiments. Similar effects were observed by Bagni et al. (2002, 2004) in frog muscle fibers subjected to very fast (~40 muscle lengths per second) ramp stretches. They suggested that there was a “static stiffness component” which had an elastic modulus which increased with the free Ca²⁺ concentration but was positioned “outside the cross-bridges”. The molecular identity of the ‘static’ structure remains unclear but there is no evidence to suggest that it is not titin.

Other published short-range force responses support the conjecture that titin molecules may exhibit Ca²⁺-dependent mechanical properties but the evidence from these measurements is less direct. Campbell and Moss measured short-range force responses in rabbit psoas (2000) and rat soleus (2002) muscles fibers. They then tried to fit their experimental records using a mathematical model consisting of a fixed population of cycling cross-bridges arranged in parallel with a non-linear elastic spring. In both cases, the best-fit to the force responses measured in fibers immersed in maximally-activating pCa 4.5 solution was obtained with a parallel elastic stiffness that was ~3 times greater than that measured in the same fibers when they were immersed in pCa 9.0 solutions. One interpretation of these findings is clearly that titin filaments have a stiffness that depends on the free Ca²⁺-concentration.

Although this remains a genuine possibility, computer simulations currently being developed by the Author suggest a potential alternative explanation. Work presented in abstract form at the 2009 Biophysical Society meeting (Campbell 2009) shows that the slope of the force response during the Second Component is increased at high levels of Ca²⁺-activation if adjacent half-sarcomeres contain different numbers of myosin heads. This is because the half-sarcomeres with fewer than average bound cross-bridges can only bear the force generated by half-sarcom-eres with a greater than average number of bound cross-bridges by continually ‘creeping’ towards longer lengths. This leads to dynamic inter-half-sarcomere interactions and an apparent Second Component stiffness that is greater than that of the Parallel Elastic Component in any one half-sarcomere (Morgan 1990).

A similar effect might explain why muscle stiffness is apparently increased in the pCa 5.7 + BDM condition shown in Fig. 2. It could be that the BDM reduces cross-bridge cycling in most half-sarcomeres but leaves a small number of units (perhaps in the ends of the preparation) where a few half-sarcomeres continue to develop force. This could create a situation in which sarcomere length heterogeneities developed during an imposed stretch which lead to over-estimates of the real stiffness of the Parallel Elastic Component. Simulations to test this hypothesis are currently underway.

8 Relaxed Muscle

Although there seems little doubt that short-range mechanical properties measured in activated muscle fibers primarily reflect the effects of interfilamentary movement on populations of cycling cross-bridges, the situation in relaxed muscle fibers is more controversial (Bianco et al. 2007; Campbell and Lakie 2008; Kellermayer et al. 2008; Mutungi and Ranatunga 2000; Proske and Morgan 1999; Proske et al. 1993). There is good evidence to support Hill’s conjecture (1968) that a small number of cross-bridges (of order 1% of the number involved in a maximal isometric contraction) continue to cycle in a relaxed frog muscle but new results increase the probability that short-range mechanical properties could reflect other mechanisms. For example, elegant experiments performed using optical tweezers by Bianco et al. (2007) show that fragments of the PEVK domain of titin molecules can bind to F-actin. If these interactions occur in vivo as well as in vitro, they probably exhibit all of the features required to produce a short-range response (Campbell and Lakie 2008).

It is possible of course that short-range mechanical properties can reflect more than one molecular mechanism. Some of the discrepancies in the existing literature might be resolved, for example, if the non-linear force response in relaxed frog fibers reflects actin-titin interactions while the behavior in mammalian muscle results from a small number of cycling cross-bridges. The converse situation is also possible. Finally, both mechanisms (cycling cross-bridges and actin-titin interactions) and potentially additional molecular effects could contribute simultaneously to the observed behavior.

The idea that cross-bridges underlie the short-range mechanical properties of relaxed muscles has been questioned for many different reasons since Hill’s original paper (1968). For example, Sandow (1970) was quite critical of Hill’s cross-bridge hypothesis because the stiffness of the short-range response remained fairly constant when the muscle was subjected to small stretches imposed in separate trials from starting sarcomere lengths estimated as ranging from 2.0 to 3.0 μm. Sandow argued that filament overlap would have decreased by ~40% over this experimental range and a short-range response due to bound cross-bridges should have shown a proportional change. Given the fact that all of Hill’s experiments were performed using whole amphibian muscles, there must now be some doubt as to whether or not the sarcomere length was the same in all regions in all the fibers in his preparations. Moreover, Hill did not correct his experimental results for the expected increase in Parallel Elastic Component stiffness at long sarcomere lengths. This could have masked a potential reduction in the stiffness of the short-range response at longer overall muscle lengths.

When Haugen and Sten-Knudsen (1981) repeated Hill’s experiments using single frog fibers (to improve the measurements of sarcomere length) and their Parallel Elastic Component framework (to correct for length-dependent stiffness of passive structures) they showed that the stiffness of the Short Range Elastic Component extrapolated to zero at a sarcomere length near 3.7 μm – the point at which thick and thin filaments no longer overlapped. However, as often seems to be the case with short-range mechanical properties, Haugen and Sten-Knuden’s results were not as simple to interpret as they might have hoped. The experimental data showed that the Short Range Elastic Component stiffness actually peaked at a sarcomere length of 3.0 μm rather than at full filament overlap. With the benefit of hindsight, this might reflect an effect of sarcomere length heterogeneity (Morgan 1990) but Haugen and Sten-Knudsen proposed that the increased stiffness of the short-range response at a sarcomere length of 3.0 μm could result from length dependent activation of their isolated frog fibers (Endo 1973). Both of these effects seem to be genuine possibilities. For example, the idea that the contractile apparatus in frog fibers can be activated by stretch is supported by the Feng effect – the increase in metabolic rate observed when a resting frog muscle is stretched to more than ~120% of its normal in vivo length (Feng 1932).

The sequence of experiments described above is an interesting example of the sort of difficulties that researchers have encountered when they have set out to measure short-range mechanical properties in relaxed muscles. The results have rarely been clear-cut and it often seems that researchers end up trying to compare results obtained in separate labs using different experimental preparations under dissimilar experimental conditions. For example, it is not completely clear that the very slight discontinuity observed when chemically permeabilized rat soleus fibers are stretched in pCa 9.0 solution (Campbell and Moss 2002) results from exactly the same mechanism as the Short Range Elastic Component response observed in relaxed intact frog fibers. The biochemical environments around the myofilaments in the two preparations are probably quite different which may emphasize distinct molecular mechanisms.

In this Author’s view (Campbell and Lakie 2008), the balance of evidence still suggests that at least a portion of the short-range mechanical properties of relaxed muscles is due to a small proportion of cross-bridges that continue to cycle in the resting tissue. Put simply, the contractile apparatus may not completely switch off when the muscle relaxes (Campbell and Lakie 1998).

The best evidence to support this view probably comes from experiments performed using chemically permeabilized muscle fibers. All of the experimental results obtained to date show that the stiffness of the short-range response increases linearly with isometric force as the free Ca²⁺ concentration in the bathing solution is raised from minimal to saturating values (Campbell and Moss 2000, 2002; Campbell et al. 2003). This is the expected result if the short-range response reflects the displacement of attached cross-bridges and complications due to filament compliance (which are probably quite small at very low levels of Ca²⁺-activation) are ignored. As shown, for example, in Fig. 2, chemicals that inhibit myosin ATP-ase also reduce the stiffness of the short-range response in permeabilized fibers though it must be mentioned that in relaxed intact muscle fibers, BDM appears have no effect (Mutungi and Ranatunga 1996). The interpretation of mechanical records will also become more complicated if additional experiments support a recently hypothesized interaction between myosin binding protein-C and actin filaments (Harris et al. 2009).

9 Cardiac Muscle

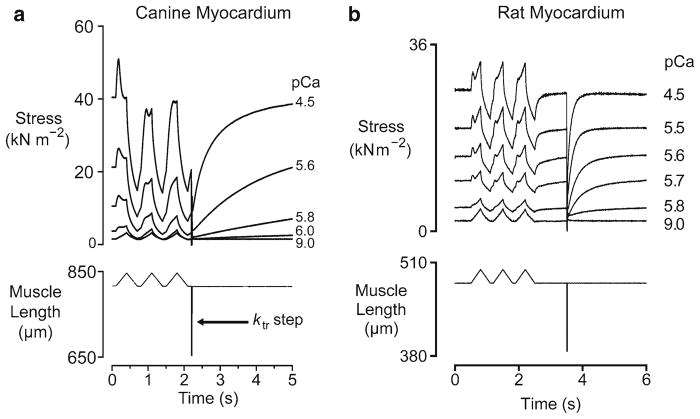
Figure 5 shows the force responses that were measured when chemically permeabilized multicellular myocardial preparations were subjected to three paired ramp stretches and releases followed by a rapid shortening/re-stretch perturbation. Trials were performed at different levels of Ca²⁺-activation and superposed. The records in panel a were obtained using canine myocardial samples (Campbell et al. 2003). The records in panel b were obtained using rat preparations (Mitov et al. 2009).

Fig. 5.

Mechanical properties of different types of myocardium. Panel (a) shows superposed force and muscle length records for a sample of chemically permeabilized canine myocardium subjected to repeated stretch/shortening cycles in solutions with different free Ca²⁺ concentrations. Panel (b) shows very similar experiments performed using samples of chemically permeabilized rat myocardium. Both sets of records were obtained at 15°C (panel a reproduced with permission from Campbell et al. 2003; panel b reproduced with permission from Mitov et al. 2009)

Although there are some features of the force records that look quite different in the two muscle types, it is the Author’s view that both sets of data can be explained by the same general mechanism. As described in several of the earlier sections, the force response can be decomposed into two separate signals: (a) a force representing the passive mechanical properties of the preparation and (b) a force representing the mechanical effects of a variable number of cycling cross-bridges. When described in this manner, it becomes obvious that the records from the different preparations look different because of two significant molecular effects. First, the Parallel Elastic Component is stiffer in the rat myocardium than it is in the canine samples. This probably reflects increased expression of the shorter, stiffer N2B titin isoform in the rodent samples (Wu et al. 2000). Second, the cross-bridges cycle more quickly in the rat myocardium than they do in the canine myocardium. This is consistent with the different rates of tension recovery measured in the two preparations. The k_tr values (Brenner 1988) in maximally- activating pCa 4.5 solution were about 1.3 s⁻¹ and 11.2 s⁻¹ for the canine and rat preparations respectively.

The reason that the rate of cross-bridge cycling makes such a big difference to the qualitative appearance of the records was explained by Hill (1968). He pointed out that if cross-bridge heads are attaching to the thin filament very quickly, any myosin head that is detached as a result of the imposed movement will be rapidly replaced by a new actin-myosin bond. The force response to a ramp stretch will therefore consist of a sustained, elevated, force plateau because the mean actin-myosin bond length will be stretched (relative to the isometric value) because of the sustained interfilamentary movement. If, on the other hand, cross-bridges are attaching quite slowly, not all the myosin heads that are detached by the imposed movement will be replaced. The force response to a ramp stretch will therefore consist of a large transient followed by a decline to a new steady-state level. This level will be substantially lower than the steady-state isometric force if the increase in mean cross-bridge strain is not sufficient to compensate for the reduction in the number of attached cross-bridges.

Another consequence of the different myosin cycling rates is that the mechanical properties of the two preparations have different recovery time-courses. In the canine samples, the responses to the second stretch are very different to those measured during the first stretch at every level of Ca²⁺-activation. This is because the cross-bridge populations were significantly perturbed by the first movement and have not had time to recover to their steady-state profiles in the time interval between the stretches. This contrasts with the behavior seen in the rodent samples where the faster cross-bridge cycling means that the measured forces are very similar for all three stretches, irrespective of the free Ca²⁺ concentration in the bathing solution.

9.1 Myosin Heavy Chain Effects

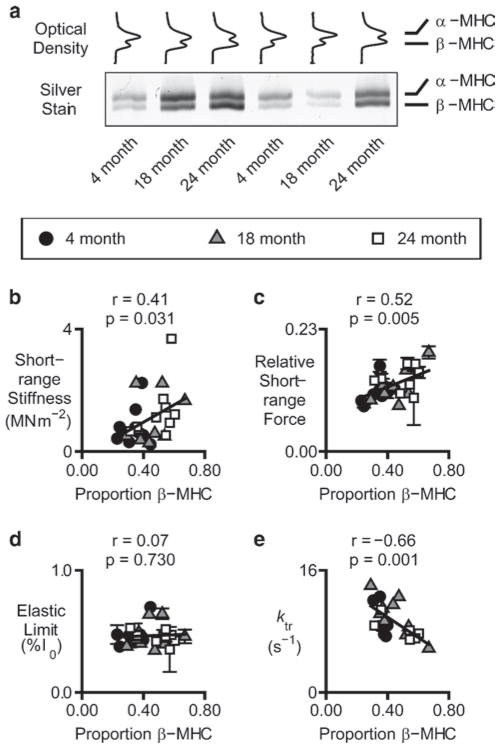
Rats express two cardiac myosin heavy chains and the proportion of the total myosin occurring as the slower β-isoform increases with age (for example Carnes et al. 2004). Figure 6 shows the results of experiments in which myocardial samples were isolated from Fischer 344 rats of different ages and subjected to experimental trials similar to those shown in Fig. 5. When the mechanical experiments were completed, the individual preparations (approximately three or four cells in size) were collected, processed, and analyzed by gel electrophoresis (Tikunov et al. 2001).

Fig. 6.

Myosin heavy chain effects. Panel (a) shows optical density profiles and a representative gel showing electrophoretic separation of the α and β myosin heavy chain isoforms in samples of chemically permeabilized rat myocardium that had been previously used for mechanical experiments. Panels (b–e) show various mechanical properties plotted as functions of the relative β myosin heavy chain content in the different experimental preparations. The initial stiffness and the maximum force produced during the short-range response increased linearly with the relative β myosin heavy chain content (reproduced with permission from Mitov et al. 2009)

Figure 6a shows representative optical density profiles obtained from the SDS-PAGE gels. Figure 6b–d show selected parameters calculated from the measured force responses plotted against the proportion of slow β-myosin heavy chain in the experimental preparations. The initial stiffness of the muscle and the relative force produced during the short-range response both correlated with the proportional β-myosin heavy chain content. This was a particularly exciting result when it was published in 2009 because, to the Author’s knowledge, it was the first time that the short-range mechanical properties of cardiac muscle had been directly associated with the differential expression of gene products.

10 Physiological Significance

It is possible that the short-range mechanical properties that seem to be a feature of all types of muscle are an inevitable consequence of using cross-bridges (thought of in this context as short elastic springs arranged in linear arrays) to generate force. It is also possible that this arrangement confers important advantages that mean that cross-bridges are a more effective way of powering animal movements than alternative mechanisms, for example flagellar whips.

It has been argued, for example, that short-range mechanical properties may help to stabilize sarcomere lengths in a working muscle and therefore may play an important role in minimizing sarcomere length inhomogeneity (Allinger et al. 1996). This theory is controversial (Zahalak 1997) but preliminary simulations currently under development by the Author support the general idea (Campbell 2009).

10.1 Skeletal Muscle

Campbell and Lakie (1998) pointed out that if short-range mechanical properties in relaxed muscles reflect a low level of persistent cross-bridge cycling, this would have significant metabolic implications. Muscle accounts for about 40% of an adult human’s weight. If the tissue is not completely deactivated when it relaxes, cycling myosin heads will continue to use ATP and to produce heat. The sheer amount of muscle in the body means that this could add up to a significant energy expenditure. Indeed, A.V. Hill, extrapolating from data obtained using isolated frog muscles, suggested that relaxed muscle might account for as much as 25% of the basal metabolic rate in humans (Hill 1965). Small variations in the magnitude of this resting activity might explain why some individuals have higher basal metabolic rates than others.

Irrespective of the molecular mechanism underlying short-range mechanical properties in relaxed muscle, the fact that they are history-dependent means that the neuromuscular control system has to allow for them if it is to control movements with precision. It is particularly interesting, for example, to learn that the integrated surface electromyogram signals recorded from the agonist muscles are different in repeated movements when healthy humans are asked to track a repeating signal (Axelson and Hagbarth 2003).

10.2 Cardiac Muscle

The stiffness of myocardium is important because it influences the amount of blood that enters into the ventricles during diastole. When the chambers are compliant, blood enters through the atrio-ventricular valves with little hindrance and the chambers distend fully at normal filling pressures. Conversely, when the walls are stiff, pressure rises sharply when blood enters and adequate ventricular filling is prevented. This can lead to a condition known as diastolic dysfunction (Zile et al. 2004).

The experimental records shown in Fig. 5 show that short-range mechanical properties clearly affect the stiffness of cardiac muscle. Whether these measurements obtained using chemically permeabilized samples are directly relevant to in vivo function has sometimes been regarded as less clear. The free Ca²⁺-concentration required to significantly augment the passive myocardial stiffness in the chemically permeabilized canine preparations was pCa 6.2 (630 nM) (Campbell et al. 2003). This is substantially higher than the basal free Ca²⁺-concentration (75–200 nM) normally assumed for working hearts (Bers 1991). The Ca²⁺-threshold for significant stiffness augmentation in chemically permeabilized rat myocardium is probably higher still (Mitov et al. 2009).

It has been argued (Campbell et al. 2003; Mitov et al. 2009) that it is not the precise threshold for Ca²⁺-activation that matters in these experiments but rather the relative level of Ca²⁺-activated force that the tissue is developing when the short-range mechanical properties become significant. This is because there is evidence to suggest that the tension-pCa relationship in cardiac muscle is significantly left-shifted in intact cardiac muscle compared to that measured in permeabilized preparations (Gao et al. 1994). Nevertheless, it would be interesting to see whether intact cardiac muscle exhibits short-range mechanical properties during the diastolic interval.

The necessary experiments are technically difficult because it is not easy to rule out the possibility that the mechanical measurements are compromised by series compliance artifacts. However, preliminary measurements obtained in the Author’s laboratory with twitching rat trabeculae (Fig. 7) show a clear short-range elastic response to an imposed rat stretch. This result suggests that there may be sufficient myosin heads bound to actin filaments in relaxed intact cardiac muscle to influence ventricular filling. Data obtained with single intact murine myocytes presented in abstract form at the 2009 Biophysical Society Annual Meeting by King et al. (2009) support a similar conclusion.