Male-female differences in the association between incident hip fracture and proximal femoral strength: A finite element analysis study

Abstract

Hip fracture risk is usually evaluated using dual energy x-ray absorptiometry (DXA) or quantitative computed tomography (QCT) which provide surrogate measures for proximal femoral strength. However, proximal femoral strength can best be estimated explicitly by combining QCT with finite element (FE) analysis. To evaluate this technique for predicting hip fracture in older men and women, we performed a nested age- and sex-matched case-control study in the Age Gene/Environment Susceptibility (AGES) Reykjavik cohort. Baseline (pre-fracture) QCT scans of 5500 subjects were obtained. During 4–7 years follow-up, 51 men and 77 women sustained hip fractures. Ninety-seven men and 152 women were randomly selected as age- and sex-matched controls. FE-strength of the left hip of each subject for stance (F_Stance) and posterolateral fall (F_Fall) loading, and total femur areal bone mineral density (aBMD) were computed from the QCT data. F_Stance and F_Fall in incident hip fracture subjects were 13%–25% less than in control subjects (p≤0.006) after controlling for demographic parameters. The difference between FE strengths of fracture and control subjects was disproportionately greater in men (stance, 22%; fall, 25%) than in women (stance, 13%; fall, 18%) (p≤0.033), considering that F_Stance and F_Fall in fracture subjects were greater in men than in women (p<0.001). For men, F_Stance was associated with hip fracture after accounting for aBMD (p=0.013). These data indicate that F_Stance provides information about fracture risk that is beyond that provided by aBMD (p=0.013). These findings support further exploration of possible sex differences in the predictors of hip fracture and of sex-specific strategies for using FE analysis to manage osteoporosis.

Introduction

Hip fracture is one of the most serious consequences of osteoporosis, leading to significant reductions in mobility, independence, and quality of life, and in some cases, increased mortality [1] [2]. In the United States alone, over 2 million osteoporotic fractures occurred in 2005 at a cost of $17 billion, with hip fracture accounting for 14% of the total incident fractures, and 72% of the total cost [2]. Because of the rapid increase in the mean age of the population of the United States and other industrialized countries, the incidence of hip fracture is expected to rise significantly. This underscores the importance of developing and validating techniques to estimate hip fracture risk, to better understand the etiology of hip fracture, and to evaluate the effects of risk-reducing interventions.

The risk of hip fracture fundamentally depends on two factors: (1) the proximal femoral structural strength, defined as the minimum force on the femoral head that would be required to break the proximal femur, is also called the hip bone strength or the hip fracture load; and (2) the probability of encountering a situation in which the force applied to the proximal femur exceeds the proximal femoral structural strength. The strength of the proximal femur depends strongly on the three-dimensional (3-D) geometry of the bone and the 3-D distribution of the material properties within the bone (e.g. elastic modulus and yield strength at each point) as well as the direction and location of the applied force. For example, the proximal femur can withstand the great forces on the hip during ambulation and other routine activities. However, if a force of the same magnitude were applied to the proximal femur during a fall onto the greater trochanter, this force would far exceed the hip bone strength and a fracture would occur. For falls, the probability of encountering an applied force that exceeds the hip bone strength and results in a fracture is related to multiple factors, among them the probability of falling in any given direction, the height from which the fall occurred, the ability to use the arm to break the fall, the compliance of the surface upon which the subject might fall, and the soft tissue thickness over the greater trochanter.

Hip fracture risk is often evaluated using non-invasive imaging techniques such as dual energy x-ray absorptiometry (DXA) and volumetric quantitative computed tomography (QCT), providing surrogate measures of bone strength. Both DXA and volumetric QCT measure bone mineral content and bone mineral density (BMD) in specific anatomic regions of the hip, such as the femoral neck or trochanter. However, DXA provides a single, combined measure of cortical and trabecular areal BMD (aBMD), whereas volumetric QCT provides separate 3-D measures for cortical and trabecular bone. Although these technologies are commonly used to evaluate hip fracture risk [3], DXA and QCT-derived BMD explain only 56%–72% and 47%–87% of the variance in proximal femoral strength, respectively [4–5]. Thus, we may be able to improve the assessment of hip fracture risk by implementing more robust techniques for evaluating proximal femoral strength.

Previous literature has demonstrated that proximal femoral strength can best be estimated by combining QCT imaging, which provides the bone geometry and density at each point in the bone, with a structural engineering technique called finite element (FE) analysis [4, 6–7]. In essence, this numerical technique subdivides a structure into many smaller parts (finite elements) which, together, explicitly represent the complex material heterogeneity and 3-D bone geometry as a mathematical model. Force or displacement is then mathematically applied to represent a specific loading condition (e.g. single-limb stance or a particular type of fall onto the greater trochanter). When the model is analyzed, stress and strain throughout the structure are computed and used in conjunction with material failure criteria to estimate the strength of the proximal femur under the particular loading condition. The strength of the proximal femur as measured on cadaveric femora under single-limb stance loading is more strongly predicted by QCT-based patient-specific FE modeling (r²=0.77 to 0.96 [4, 6–7]) than by aBMD from DXA [4]. Studies of cadaveric femora under loading from a fall onto the greater trochanter have shown similar trends [8–11].

Although FE models can strongly predict actual, measured hip bone strength, there is limited experience in using this technique to predict hip fracture in vivo. In a recent prospective study of hip fracture in a large multicenter cohort of older men, Orwoll et al. showed that FE-computed hip bone strength for loading due to a sideways fall onto the lateral aspect of the greater trochanter and, to a lesser extent, estimated fall impact force divided by lateral fall hip bone strength were strongly associated with incident fracture [12]. However, this study only included men and it only evaluated hip strength for a sideways fall. Thus, in the present study, we have evaluated FE-computed hip bone strength for loading similar to that during single-limb stance (F_Stance) and a fall onto the posterolateral aspect of the greater trochanter (F_Fall) in older male and female hip fracture and control subjects. The objectives were (1) to determine if F_Stance and F_Fall are associated with hip fracture, (2) to determine if these associations differ for men and women, and (3) to determine if F_Stance and F_Fall continue to be associated with hip fracture after accounting for aBMD computed from the same QCT images.

Methods

Subjects

This was a nested age- and sex-matched case-control study from the Age Gene/Environment Susceptibility (AGES) Reykjavik cohort [13]. The AGES-Reykjavik study is an ongoing population-based study of men and women nested in the Reykjavik Study [14–15], and both phases of this study have been described in detail. Baseline CT scans of 5500 subjects from this cohort who had no metal implants at the level of the hip, but who were otherwise not screened for medical history or medications, were obtained between 2002 and 2006, along with subject age, height, weight and history of medications that may induce changes in BMD (e.g. hormone replacement therapy, bisphosphonates or glucocorticoids). Subjects then were followed for 4 to 7 years, through November 15, 2009. Subjects with hip fractures during this period, but without documented hip fracture prior to baseline, were identified through the AGES-Reykjavik Fracture Registry for inclusion in this study [16]. Approximately two sex- and age-matched control subjects for each hip fracture subject were randomly selected. Informed consent was obtained from all participants in the study, which was approved (VSN 00-063) by the National Bioethics Committee in Iceland as well as the Institutional Review Board of the Intramural Research Program of the National Institute on Aging.

Imaging

CT measurements were performed in the hip using a 4-detector CT system (Sensation 4, Siemens Medical Systems, Erlangen, Germany). The scans extended from 35 mm inferior to the inferior aspect of the lesser trochanter of the left hip to 10 mm superior to the superior aspect of the left femoral head. To calibrate CT Hounsfield units to equivalent bone mineral concentration, all subjects were positioned supine on top of a calibration phantom (Image Analysis, Columbia, KY, USA), which extended from superior to the L1 vertebral body to the mid-femoral shaft. The phantom contained calibration cells of 0, 75 and 150 mg/cm³ equivalent concentration of calcium hydroxyapatite. A helical study of the hip (120 kVp, 140 mAs, 1-mm slice thickness, pitch = 1, coarsened to 3-mm slice thickness) encompassed the proximal femur from a point 1 cm superior to the acetabulum to a point 3–5 mm inferior to the lesser trochanter.

Finite Element Modeling

From the baseline (pre-fracture) QCT data, we computed the strength of the left hip of each subject in the fracture and control groups using our FE modeling method [6, 8, 17–18]. The models included the entire imaged portion of the proximal femurs. Two loading conditions were studied, one representing single-limb stance loading [6, 17–18], and the second simulating loading from a fall onto the posterolateral aspect of the greater trochanter [8, 18].

For single-limb stance loading, heterogeneous nonlinear properties were used to describe the nonlinear stress-strain relationship for each 3-mm cube of bone that was represented by a finite element [17–20]. The FE-computed bone strength under stance loading was defined as the maximum force on the femoral head. Nonlinear modeling was necessary for the stance loading condition because linear models did not provide adequate precision for predicting fracture loads under this type of loading [6, 8]. In contrast, linear models were used for fall loading because they provided good precision [8]. These fall loading models employed the same linearly elastic material properties as for stance loading. The fracture load for the fall loading condition was defined as the force on the femoral head at the onset of fracture, i.e. the point at which local failure begins within the proximal femur. The fracture loads computed using this FE modeling method and these particular stance and posterolateral fall loading conditions have been validated previously via mechanical testing of cadaveric specimens (stance, r²=0.93 [6]; fall, r²=0.90 [8]).

Areal Bone Mineral Density

The baseline QCT data for the left hip of each subject in the fracture and control groups were also used to compute the aBMD in a region of interest comparable to the total femur region of DXA that is used clinically to evaluate osteoporotic hip fracture risk. To evaluate the reliability of this aBMD measure as a surrogate for DXA-measured aBMD, an ancillary study was performed on 132 women age 62–81 years (mean±SD: 74.4±3.4 years). DXA scans (Lunar Prodigy, GE Medical Systems, Milwaukee, WI) of the proximal femur were performed, and total femoral aBMD from these scans (DXA_aBMD) was compared with that computed from the QCT data (QCT_aBMD) using simple linear regression between these two measures.

Statistical Analysis

The data for men and women were first analyzed separately (R http://www.r-project.org/) using descriptive statistics, and Student's t-tests were used to compare the demographic data, F_Stance, F_Fall and aBMD in the hip fracture and age- and sex-matched control groups. To test for sex differences and to identify the most important determinants of fracture risk, the data for men and women were analyzed together in a single model and multiple regression analysis was performed with each of the bone assessment measures serving as the dependent variable. We did not evaluate additional dependent variables, such as an estimated factor of safety (proximal femur strength divided by the applied force) for each loading condition because we found previously (in unpublished work) that parameters normalized by body weight, height or combinations thereof did not affect the findings. Fracture status (yes or no) and demographic parameters, age, height, weight, and sex were considered as candidate independent variables. Interactions between fracture status and the demographic parameters were also considered. We started with an inclusive model containing the pre-mentioned variables. In refining the model, variables/interactions were tested one at a time and retained only if they were significant at the alpha=0.1 level. If an interaction was retained, the individual variables making up that interaction were also retained, regardless of alpha level, so that the regression would not be forced through zero for those variables. However, results are only reported as significant for p<0.05. Regression diagnostics, including residual plots and calculation of Cook's distance, leverage and DFFITS, were performed to identify data points with a disproportionate influence on the regression results. To determine if F_Stance or F_Fall were related to fracture status after accounting for BMD, this procedure was repeated while including as independent variables aBMD and the interactions of aBMD with gender and fracture status. This procedure was then repeated in multiple regression analyses applied separately to men and women. In all of these analyses, F_Stance, F_Fall, aBMD, age, height, and weight were standardized by subtracting the mean and dividing by the standard deviation (SD) of the pooled data. No corrections were made for multiple comparisons. However, because only a single outcome was studied, multiple comparisons only occurred in the context of the search for the optimal predictive set of variables. The final p-values should therefore be interpreted in this context. Finally, the regression models for men and women together were reanalyzed after adding a dichotomous variable to account for subject use of medications that could affect BMD (although we could not evaluate the effects of specific medications due to small sub-group sample sizes). Significance of the medication yes/no variable would indicate that these medications influenced the study results.

Results

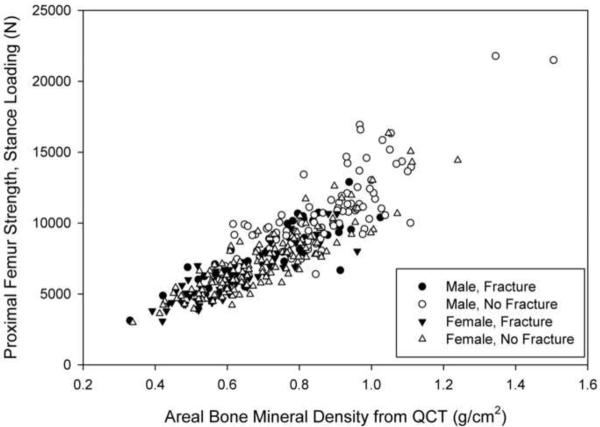
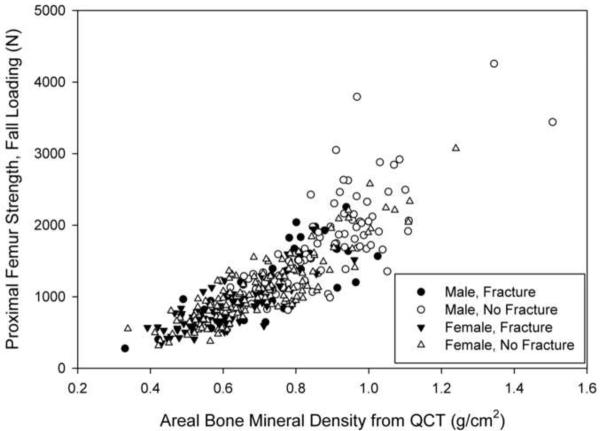
Fifty-one men and 77 women suffered hip fractures during the follow-up period (Figure 1). Ninety-seven men and 152 women were selected as control subjects (Figure 1). Eleven men (21.6%) and 40 women (51.9%) with fractures, and 28 men (28.9%) and 78 women (51.3%) without fractures had taken medications than can affect BMD. Within each sex, the fracture and control groups were not significantly different with respect to age, height, and weight at the time of the CT scan (Table 1). However, F_Stance, F_Fall and aBMD were significantly lower in each fracture group than in the respective control group (p<0.001) (Table 1; Figures 2a and 2b).

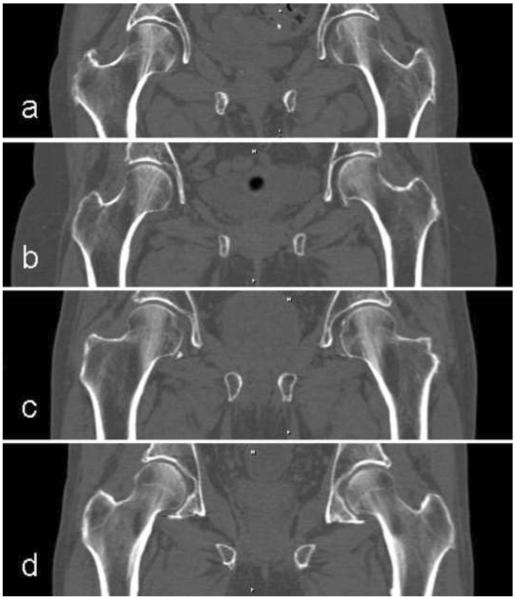
Figure 1.

Baseline CT scan images reconstructed in the mid-coronal plane for (a) female fracture, (b) female control, (c) male fracture and (d) male control subjects. Subjects had approximately average aBMD for their group.

Table 1.

Descriptive statistics for subjects with incident hip fracture and the age- and sex-matched controls (approximately two per subject). Statistical significance of differences between cases and controls was established using Student's t-test.

Sex	Measure	Controls					Cases					P
		Na	Min	Max	Mean	SD	Na	Min	Max	Mean	SD
Male	age (years)	97	70	90	79.6	5.2	51	71	93	80.0	5.6	0.66
	height (cm)	97	162.4	190.5	174.9	6.6	50	159.2	187.1	174.6	5.9	0.74
	weight (kg)	97	52.4	135.0	82.6	14.8	51	50.3	114.0	79.1	13.9	0.16
	aBMD (g/cm2)	97	0.511	1.505	0.867	0.155	51	0.330	1.025	0.720	0.147	<0.001
	FFall (N)	94	638	4257	1692	671	45	276	2254	1226	476	<0.001
	FStance (N)	94	4772	21,784	10,587	2949	45	3123	12,898	8081	2011	<0.001
Female	age (years)	152	67	92	79.3	5.7	77	67	93	79.5	5.9	0.75
	height (cm)	151	139.3	173.0	159.2	5.6	75	145.1	173.4	159.6	6.1	0.64
	weight (kg)	151	37.2	112.0	68.3	13.7	75	39.2	111.2	64.5	15.1	0.057
	aBMD (g/cm2)	152	0.338	1.239	0.696	0.156	76	0.392	0.961	0.605	0.121	<0.001
	FFall (N)	145	314	3071	1088	476	71	353	1945	844	333	<0.001
	FStance (N)	145	2978	16,330	7221	2347	71	3085	10,675	6028	1586	<0.001

^aDifferences in the number of data points for each measure within each group are due to missing data and/or CT scans that were inadequate for performing finite element analysis.

Figure 2.

Finite element-computed hip bone strength for loading during single-limb stance (a) and from a fall onto the posterolateral aspect of the greater trochanter (b) versus areal bone mineral density (aBMD) computed from QCT for male (filled symbols) and female (open symbols) fracture (circles) and control (squares) subjects. These data have not been adjusted for covariates, so this graph does not reflect the results of the regression analysis. Omitting the two points with greatest aBMD and strength in (a) did not significantly change the regression results.

When data from men and women were evaluated together using multiple regression analysis that controlled for demographic variables and interactions (Table 2), FE strength in incident hip fracture subjects was greater in men than in women (p<0.001) and was 13% to 25% less than in controls for both loading conditions (p≤0.006). There was a significant interaction between sex and fracture status for both loading conditions (stance, p=0.004; fall, p=0.033; Table 2), indicating that the difference between FE strengths of fracture and control subjects in men (stance, 0.822 SD or 22%; fall, 0.721 SD or 25%) was greater than that in women (stance, 0.337 SD or 13%; fall, 0.323 SD or 18%). Regression diagnostics revealed no data points that disproportionately influenced these regression results (Figure 2a). Including aBMD in the regression analyses for men and women together revealed a significant interaction between fracture status and sex only for stance loading (p=0.014), indicting that, after accounting for aBMD, F_Stance was 6.9% lower in male fracture subjects (Sex=1) compared with controls. However, there was no statistically significant difference between fracture and non-fracture female subjects (Sex=0) after accounting for aBMD (Table 2; coefficient for Fracture Status = −0.034, p=0.61). Controlling for medications that could affect BMD revealed no significant effect of this parameter on the study results, both without controlling for aBMD (Stance, p=0.17; Fall, p=0.51) and with controlling for aBMD (Stance, p=0.38; Fall, p=0.53). When data for men and women were evaluated separately and aBMD was included in the regression model, an interaction between fracture status and aBMD (p=0.013) emerged in men (Table 3) but not in women (Table 4). This finding indicates that, in men, for each 1 SD increase in aBMD, the difference between F_Stance of fracture and control subjects increased by 0.275 SD or 8.6%, after accounting for aBMD.

Table 2.

Multiple linear regression results for data from men and women combined, including coefficients of standardized variables, standard errors in parentheses, and p-values in italics. F_Stance, F_Fall, aBMD, age, height, and weight were standardized by subtracting the mean and dividing by the standard deviation of the pooled data.^a Fx=Fracture Status=1 for fracture subjects, 0 for control subjects. Sex = 1 for men, 0 for women. NA=Not applicable (variable was not part of the analysis). “–” indicates that the variable was not included in the model because the p-value would have been greater than 0.10.

Dependent Variable	Regression Coefficients for Standardized Variables (Standard Error) p value											R2
	Fx	Sex	Age	Weight	Height	aBMD	Fx:Age	Fx:aBMD	Fx:Sex	Sex:aBMD	Intercept
Without Adjustment for aBMD
FStance	−0.337 (0.104)	0.667 (0.143)	−0.186 (0.050)	0.320 (0.049)	0.137 (0.074)	NA	0.135 (0.079)	NA	−0.485 (0.165)	NA	−0.092 (0.073)	0.51
	0.001	<0.001	<0.001	<0.001	0.063		0.090		0.004		0.21
FFall	−0.323 (0.117)	0.748 (0.114)	−0.119 (0.044)	0.308 (0.049)	–	NA	–	NA	−0.398 (0.185)	NA	−0.137 (0.068)	0.37
	0.006	<0.001	0.007	<0.001					0.033		0.044
With Adjustment for aBMD
FStance	−0.034 (0.065)	0.182 (0.085)	–	0.067 (0.032)	0.120 (0.044)	0.738 (0.030)	–	–	−0.253 (0.102)	–	−0.037 (0.044)	0.81
	0.61	0.033		0.037	0.006	<0.001			0.014		0.40
FFall	–	0.130 (0.061)	–	–	–	0.749 (0.039)	–	–	–	0.164 (0.059)	−0.092 (0.036)	0.76
		0.033				<0.001				0.005	0.012

^aMeans and standard deviations for each variable (mean±SD): F_Stance=7982±2887 N; F_Fall=1216±596 N; aBMD=0.725±0.174 g/cm²; age=79.5±5.6 years; height=165.4±9.7 cm; weight=72.7±16.0 kg

Table 3.

Multiple linear regression results for men, including coefficients of standardized variables, standard errors in parentheses, and p-values in italics. F_Stance, F_Fall, aBMD, age, height, and weight were standardized by subtracting the mean and dividing by the standard deviation of the pooled data.^a Fx=Fracture Status=1 for fracture subjects, 0 for control subjects. Sex = 1 for men, 0 for women. NA=Not applicable (variable was not part of the analysis). “–” indicates that the variable was not included in the model because the p-value would have been greater than 0.10.

Dependent Variable	Regression Coefficients for Standardized Variables (Standard Error) p value								R2
	Fx	Age	Weight	Height	aBMD	Fx:Age	Fx:aBMD	Intercept
Without Adjustment for aBMD
FStance	−0.805 (0.155)	–	0.412 (0.079)	–	NA	–	NA	0.649 (0.100)	0.30
	<0.001		<0.001					<0.001
FFall	−0.736 (0.181)	–	0.312 (0.092)	–	NA	–	NA	0.607 (0.117)	0.18
	<0.001		<0.001					<0.001
With Adjustment for aBMD
FStance	−0.161 (0.108)	–	0.175 (0.052)	–	0.854 (0.063)	–	−0.275 (0.110)	0.102 (0.076)	0.73
	0.14		0.001		<0.001		0.013	0.18
FFall	−0.007 (0.130)	–	–	–	0.977 (0.073)	–	−0.249 (0.132)	0.007 (0.089)	0.67
	0.96				<0.001		0.060	0.94

^aMeans and standard deviations for each variable (mean±SD): F_Stance=7982±2887 N; F_Fall=1216±596 N; aBMD=0.725±0.174 g/cm²; age=79.5±5.6 years; height= 165.4±9.7 cm; weight=72.7±16.0 kg

Table 4.

Multiple linear regression results for women, including coefficients of standardized variables, standard errors in parentheses, and p-values in italics. F_Stance, F_Fall, aBMD, age, height, and weight were standardized by subtracting the mean and dividing by the standard deviation of the pooled data.^a Fx=Fracture Status=1 for fracture subjects, 0 for control subjects. Sex = 1 for men, 0 for women. NA=Not applicable (variable was not part of the analysis). “–” indicates that the variable was not included in the model because the p-value would have been greater than 0.10.

Dependent Variable	Regression Coefficients for Standardized Variables (Standard Error) p value								R2
	Fx	Age	Weight	Height	aBMD	Fx:Age	Fx:aBMD	Intercept
Without Adjustment for aBMD
FStance	−0.334 (0.087)	−0.244 (0.052)	0.318 (0.051)	0.135 (0.081)	NA	0.176 (0.083)	NA	−0.098 (0.070)	0.39
	<0.001	<0.001	<0.001	0.097		0.034		0.16
FFall	−0.317 (0.093)	−0.170 (0.044)	0.312 (0.050)	–	NA	–	NA	−0.139 (0.055)	0.30
	<0.001	<0.001	<0.001					0.012
With Adjustment for aBMD
FStance	−0.123 (0.067)	–	–	0.119 (0.043)	0.769 (0.346)	–	−0.132 (0.069)	−0.050 (0.040)	0.79
	0.067			0.006	<0.001		0.059	0.21
FFall	−0.109 (0.070)	–	–	–	0.776 (0.035)	–	−0.136 (0.072)	−0.077 (0.032)	0.76
	0.12				<0.001		0.061	0.015

^aMeans and standard deviations for each variable (mean±SD): F_Stance=7982±2887 N; F_Fall=1216±596 N; aBMD=0.725±0.174 g/cm²; age=79.5±5.6 years; height=165.4±9.7 cm; weight=72.7±16.0 kg

In the ancillary study comparing aBMD from QCT with that from DXA, a strong linear relationship between these two measures was confirmed (DXA_aBMD (g/cm²) = 0.924 × QCT_aBMD (g/cm²) + 0.137, r=0.935, standard error of the estimate (SEE)=0.046 g/cm²). However, aBMD from QCT was lower on average than that from DXA, with aBMD from QCT ranging from 0.496 g/cm² to 1.193 g/cm² (mean±SD: 0.805±0.134 g/cm²), and aBMD from DXA ranging from 0.605 g/cm² to 1.258 g/cm² (mean±SD: 0.884±0.134). The SEE for the regression equation, also known as the standard deviation of the residuals, was 0.047 g/cm², or 5.3% of the mean, indicating the precision with which DXA aBMD can be estimated from QCT aBMD.

Discussion

Our study is the first to examine associations of FE-computed proximal femoral strength with fracture in both men and women. We found that reduced FE strength is powerfully associated with incident hip fracture. In univariate comparisons for stance and fall loading, respectively, FE strength in fracture subjects was 31% and 38% lower in men and 20% and 29% lower in women compared with age- and sex-matched controls. The strength of this association persisted even after controlling for demographic variables (age, weight and/or height). In men, but not in women, we observed that the association of incident hip fracture risk with F_Stance remained after controlling for aBMD, supporting the rationale for our study that F_Stance accounts for characteristics of the proximal femur that cannot be captured by density measurements, such as bone geometry and the complex 3-D distribution of material properties within the structure.

Our most novel and important finding is that the association of FE strength with hip fracture differs for men and women, as shown by the statistical interaction between fracture and sex for both loading conditions (Table 2, regressions without adjustment for aBMD). These models showed that incident hip fracture is associated with a greater decrement in FE strength in men than in women, even after controlling for age, height and weight. This finding is consistent with the proposition that, on average, elderly women, who have considerably lower bone strength than men of comparable age (Table 1), may also have lower factors of safety, thereby making women more likely to fracture if they experience a fall. For example, consider the average peak impact force from a posterolateral fall onto a 13-cm-thick mattress, 2500 N, which was measured on four women and four men [21]. Based on energy considerations, the peak impact force from a lateral fall onto the greater trochanter increases in proportion to the square-root of the product of the subject's height and mass [22]. By applying this relationship to a fall onto the posterolateral aspect of the hip (and neglecting differences in soft-tissue thickness), adjusted peak impact forces for average male and female subjects can be estimated at 2714 N and 2353 N, respectively (see Tables 1 and 2 for the mean height and weight for each group and for all subjects pooled). Further, from the data in Table 1, the average factors of safety for fall loading can be computed as 0.62 and 0.45 (1692/2714 and 1226/2714) for male control and fracture subjects, respectively, and 0.46 and 0.36 (1088/2353 and 844/2353) for female control and fracture subjects, respectively. Keeping in mind the limitations of these calculations, e.g. we do not know the peak impact force on the bone itself, we can conclude that, on average, the factors of safety for women without a hip fracture are considerably lower than those of their male counterparts. This finding indicates that, even after accounting for the lower force of impact in women, who are both lighter and shorter than men, women are more likely than men of the same age to sustain a hip fracture if they experience a fall onto the posterolateral aspect of the proximal femur. A corollary to this result is that the greater factors of safety for men without hip fractures and the greater difference between factors of safety for men with and without hip fractures indicates that the variation of FE strength may be a more important determinant of fracture risk in men, while other risk factors may be more important in women. Further, in men, the interaction between fracture status and aBMD indicates that, as aBMD increases, the difference between FE strength of fracture and non-fracture subjects becomes greater (Table 3, F_Stance, with adjustment for aBMD). Therefore, FE analysis may be a more powerful discriminatory tool for assessing hip fracture risk in men who appear to have adequate aBMD. These findings point to the need to explore sex-specific or even aBMD-specific strategies for implementation of FE analysis as a fracture risk assessment tool. Due to the limited size of the present study, these important results should be examined further in a larger investigation.

The observed sex differences in the association between FE strength and incident hip fracture support further exploration of sex differences in risk factors that are not captured by bone strength assessment techniques and suggest that examination of risk factors for falls may be more critical for women than for men. Such risk factors include the propensity for falling and for falling in a particular direction, and the extent of soft tissue coverage over the greater trochanter [3, 12]. Numerous factors can affect the risk of falling, including age, use of specific medications, physical activity, muscle strength and quality, and others [3, 23–24]. Thus, there is great potential for finding additional important risk factors for hip fracture that are independent of bone structure and that may be particularly useful in women as well as in men with low aBMD.

Our results for men are consistent with those found by Orwoll et al. in a prospective multicenter study of 3549 men, including 40 hip fracture and 210 randomly selected, unmatched control subjects [12]. After adjustment for age, body mass index (BMI) and study site, they found that hip bone strength in a lateral fall condition was a strong predictor of hip fracture even after controlling for aBMD. However, this study differed substantially from ours with respect to study design and methodology. The previous work evaluated a sample of volunteers of mean age 74 years in a multicenter study, but the present study employed a random sample of older subjects, with a mean age of 80 years, who were from specific birth cohorts and who were living in Reykjavik as adults. Although the control subjects of both studies were randomly selected from the cohort, those of the former study were unmatched, while those from the present study were age- and sex- matched. Despite these differences, our mean QCT-derived aBMD values for the control and fracture groups were 99% and 102%, respectively, of the mean DXA aBMD values reported by Orwoll et al., after adjusting our QCT aBMD data via the linear regression equation from our ancillary study. With respect to methodology, the FE modeling techniques of these two studies employed different material properties, failure theories, definitions of hip bone strength, and loading conditions (lateral fall loading previously versus posterolateral fall and stance loading in the present work). Consequently, our mean hip bone strengths for posterolateral fall loading in men were about 28%(control) and 32% (fracture) of the lateral fall loading strengths reported by Orwoll et al. However, for additional perspective, our mean strengths for posterolateral loading in the male and female control groups were also 46% and 40% of those for lateral fall loading in men and women, respectively, in a study of age-dependence of hip bone strength, after adjusting to age 74 years [25]. The sizeable differences in hip bone strengths for the two studies that used the same modeling technique and loading conditions likely reflect differences in the study population but also point to potentially great sensitivity of results to a variety of factors. Thus, the extent to which differences in FE methodology, study design and subject populations influence fracture risk assessment is a question that remains to be answered.

Although this study was not powered to compare the regression equations for the two loading conditions statistically, our results suggest that hip fracture may be more strongly associated with F_Stance than F_Fall. From an engineering and statistical standpoint, the FE loading condition that is most strongly associated with hip fracture should be the loading condition in vivo that most frequently results in hip fracture. Thus, given that most hip fractures occur from falls [1], the better performance of F_Stance compared with F_Fall, particularly in men, where F_Stance was associated with fracture even after controlling for aBMD, is somewhat puzzling, although admittedly, this trend could be simply a numerical artifact of the small number of subjects. The stance and fall analyses for each subject modeled the same distribution of material properties within the proximal femur, and both types of analyses were validated for predicting fracture loads in cadaveric femora, with similar correlations between measured and predicted fracture loads (stance, r²=0.93 [6]; fall, r²=0.90 [8]). Even so, a number of factors could explain this finding. For example, due to methodological differences, the cadaveric femora, CT scans and loading conditions used in the validation study may not have been representative of the femora, CT scans and loading conditions in this in vivo study. Alternatively, the stronger results for F_Stance compared with F_Fall may be due to the unique challenges of defining consistent fall loading conditions, given that anatomical features can vary dramatically between subjects. Finally, the weaker findings for F_Fall compared with those for F_Stance may indicate that this posterolateral fall loading condition does not capture the greater fracture risk attributable to loading from a fall and that further investigations of loading conditions is warranted. The combination of our FE analytical technique and the design of the AGES-Reykjavik Study, with the relatively large number of fractures, will allow us to design future studies to examine the effect of the modeled fall direction and other aspects of fall biomechanics on the assessment of hip fracture risk.

Although our study has several important strengths, such as the prospective design, the inclusion of both men and women, and the investigation of two different loading conditions, it also has some limitations. These include a relatively small sample size, particularly for men, which limited our ability to explore some potential sex differences in more detail, a limited age range, limited ability to evaluate the effect of medications, and insufficient statistical power to include prior fractures as a covariate. Our Caucasian cohort limited our ability to extrapolate our findings to other racial groups. Further, due to the more time-intensive nature of the FE analysis, we could not carry out the calculation in the whole cohort, and thus were constrained to a nested case-control design which precluded a logistic regression approach (due to potential differences in fracture prevalence in the study group compared to the whole cohort). Our study results also may have been stronger if we had evaluated the fractured hip instead of the left hip irrespective of the side of fracture. The left-right difference in hip strength in lateral fall loading has been shown to vary randomly, with a mean absolute value of 17±12%, ranging from 0.3% to 57% [26], which is not trivial compared with the 20% to 38% difference in strength associated with fracture. We also used aBMD from QCT instead of aBMD from DXA in our study. However, we showed that total femur aBMD measures from QCT and DXA are strongly linearly related, which implies that our regression results would apply to aBMD from DXA, with the caveat that the intercepts and coefficients of aBMD (and its interactions) would need to be modified to reflect the linear relationship between these two aBMD measures. Finally, subject-specific FE analysis of the hip has technical limitations, such as the use of isotropic material properties and the distortion energy failure theory (von Mises criterion), that have been discussed in detail previously [6, 8, 17, 27]. Despite these limitations, our FE modeling method accounts for more than 90% of the variability in proximal femoral strength [6, 8, 17]. Therefore, given that low hip bone strength is just one component of fracture risk, which does not account for a multitude of variables (e.g. the probabilities of experiencing a fall and a specific impact force and direction), use of more sophisticated models for computing bone strength is unlikely to improve assessment of hip fracture risk.

In conclusion, men and women who had incident hip fractures had lower FE-predicted fracture loads for single-limb stance loading and for loading due to a fall onto the posterolateral aspect of the greater trochanter than did age- and sex-matched control subjects. For men, F_Stance continued to be associated with incident hip fracture even after accounting for aBMD. The association of FE strength with incident fracture differed in men and women, supporting additional exploration of sex-specific differences in strategies for using FE analysis to manage osteoporosis. Larger sample sizes should be studied to further examine these findings and possible sex differences in the predictors of hip fracture.

Abbreviations

FE

finite element

F_Stance

finite element analysis-computed proximal femoral strength for loading similar to that during single-limb stance

F_Fall

finite element analysis-computed proximal femoral strength for loading representing a fall onto the posterolateral aspect of the greater trochanter