A model of host response to a multi-stage pathogen

Abstract

We model the immune surveillance of a pathogen which passes through n immunologically distinct stages. The biological parameters of this system induce a partial order on the stages, and this, in turn, determines which stages will be subject to immune regulation. This corresponds to the system's unique asymptotically stable fixed point.

1 Introduction

Pathogens that traverse different stages during their life cycle or during an infection process have been studied since the late nineteenth century. The most prominent genus is Plasmodium, causer of Malaria, a pathology first described by Hippocrates in the fourth century BC, which is still a major public health problem in many continents (Greenwood et al. 2005). Other important examples are Trypanosoma (Tyler and Engman 2001) and Epstein-Barr virus (EBV) which is a member of the family of herpes viruses. Indeed, it seems likely that this entire family uses multiple stages (Thorley-Lawson et al. 2008). Our focus is on Epstein-Barr virus, which is known to cycle through at least four different stages during infection within the human body (Thorley-Lawson 2001). (For a quick sketch of EBV biology, see Sect. 9). One remarkable characteristic of infections with many of such pathogens is life-long persistent infection (Hochberg et al. 2004b; Thorley-Lawson et al. 2008; Khan et al. 1996; Greenwood et al. 2005; Tyler and Engman 2001).

Our main goal in this article is to study the properties of the immune response to such a pathogen using mathematical modeling. Mathematical approaches to studying host–pathogen interactions have steadily increased in the last four decades. For entry into the corresponding body of literature, we recommend (Nowak and May 2000; Perelson and Nelson 1999) and (Wodarz 2007). What to include in such a mathematical model depends not only on the host and pathogen in question, but also the taste and purpose of the modeler. Thus, models vary in scope and complexity. A simple model might include uninfected tissue, infected tissue and an immune response. More complex models can involve such factors as the details of T-cell activation, competing immune responses to multiple epitopes and the mutation, selection and consequent evolution of the pathogen. Much of this literature is driven by the urgent need to understand the host–pathogen dynamics of HIV infection. (A Pubmed search on the terms “HIV” and “mathematical model” produces close to 400 hits.) Our model is motivated by the broad outlines of EBV biology which it both simplifies and generalizes.

In the mathematical model we propose herein, the pathogen traverses a cycle of immunologically distinct stages during infection of the host. On the pathogen side, our model includes the natural proliferation or decay of the pathogen population at each stage, the rate at which each stage is lost to produce (or become) the next stage and any gain factor involved in this process. (For example, one lytically infected cell may produce ∼ 10⁴ free virions.) On the host side, it includes a distinct immune response to each stage, proliferation of this response due to encounter with the pathogen, the ability of this response to kill or disable the pathogen, and the decay of the response in the absence of the pathogen. Omitted from this model is the supply of uninfected tissue which supports the cycle of infected stages. This omission is only likely to be important when this supply is a limiting factor. This could happen when the immune response is weak or non-existent, as when a naive host is first exposed or in the case of an immunosuppressed host. As a consequence, this model may be more realistic in describing the long-term behavior of persistent infection when this is not tissue-limited.

We will see that when the host and pathogen stand in this relation to each other, there is a unique stable accommodation between them. This appears in the model as the unique biologically meaningful asymptotically stable fixed point. In particular, it determines exactly which stages will fall under immune regulation and determines the levels of pathogen population and host response at which this mutual accommodation occurs.

In Sect. 2 we will present the model's equations and the range of parameter values under consideration. We will start by considering parameter values such that the pathogen must traverse all stages in order to establish infection. In particular, no stage is capable of proliferating and establishing infection independent of the others. In addition, we will restrict our attention to generic values of the parameters and will exclude certain parameter sets of measure zero.

The central topic of this article will be the analysis of the steady state behavior of our model. To this end, we start by calculating necessary and sufficient conditions for the pathogen to establish infection. We view this both in terms of the basic reproductive constant, R₀, and in terms of the linear stability analysis of the uninfected equilibrium at which all stages of the pathogen as well as their corresponding immune responses become extinct.

We continue the steady state analysis by determining further fixed points of the model's equations. As we will see, for generic parameter values, this system has exactly 2ⁿ fixed points, (where n is the number of stages), depending on which stages are regulated by the immune response. In general, not all of these are biologically relevant since a given pattern of regulated and unregulated stages can give negative population levels at steady state. We give a criterion for detecting the biologically meaningful ones.

If the pathogen is able to establish infection, (R₀ > 1), the parameters induce a partial order on the pathogen's stages. We say stage j starves stage k (in symbol j ≻ k) if immune regulation at stage j deprives stage k of sufficient population to support immune regulation. A stage k is called starvable if there is another stage j such that j ≻ k. If no such j exists, k is called unstarvable. One of our main results is the fact that, generically, the system has a unique asymptotically stable fixed point, namely, the one at which all unstarvable stages are regulated and all starvable stages are unregulated.

The portrait we have just drawn holds for generic values of the parameter set. It turns out that there are highly non-generic parameter sets for which the system becomes a Lotka–Volterra predator–prey system. While mathematically interesting, this is unlikely to occur in nature. The condition that the parameters must obey has co-dimension n – 1. In particular, such parameters form a set of measure zero.

Finally, we show how to generalize the previous results to the case where the pathogen has individual stages which are capable of establishing infection independently of the remaining stages.

This article is organized as follows: In Sect. 2, we introduce the model and discuss its parameters. In Sect. 3, we examine the basic properties of the system's fixed points. In Sects. 4–6 we embark on the detailed analytical study of the model's equilibrium behavior. One of the main tools used is the partial order on stages, defined in Sect. 5. In Sect. 7, we present the highly non-generic Lotka–Volterra scenario. Finally, in Sect. 8 we consider self-establishing stages. We close in Sect. 9 by discussing some of the model assumptions and consequences for the characteristics of the immune response to a multi-stage pathogen. To provide a more concrete contrast between the model and reality, we focus on EBV infection biology.

2 Formulation of the model

We model the interaction between a host and a pathogen which traverses n ∈ ℕ, n > 1 different stages during its life-cycle. We treat these stages as immunologically distinct, that is, the host produces a separate immune response to each of them. Our model is given by

$$\begin{array}{c}{\dot{S}}_j=F_j(S,T)=r_{j-1}{f}_{j-1}{S}_{j-1}-a_j{S}_j-f_j{S}_j-p_j{S}_j{T}_j\hfill \\ {\dot{T}}_j=G_j(S,T)=c_j{S}_j{T}_j-b{T}_j.\hfill \end{array}$$ (*)

The subscripts are taken modulo n. We use S_j and T_j for the pathogen population and immune response¹ at each stage. These are assumed non-negative. The parameters represent the following processes:

• a_j is the decay rate of stage S_j. If a_j is negative, this stage proliferates.

• f_j is the rate at which stage S_j is lost to become (or produce) stage S_j+1.

• r_j is an amplification factor in the process by which stage S_j becomes (or produces) stage S_j+1. For example, the loss of one lytically infected cell may produce r_j ≈ 10⁴ free virus.

• p_j represents the efficacy of the immune response T_j in killing infected stage S_j.

• c_j is the antigenicity of stage S_j, i.e., its efficacy in inducing proliferation of immune response T_j.

• b is the natural death rate of the response T_j. We assume it is the same for all stages.

We will refer collectively to a choice of values for these parameters as θ. We will assume that with the possible exception of a_j, all of these are positive. In Sects. 3 through 7, we will assume that a_j + f_j > 0. Thus, while some stages may proliferate, none does this as fast as it is consumed in producing the next stage. In Sect. 8, we will lift this assumption and generalize our results to the case in which there are self-establishing stages. We will also assume that the values of these parameters are generic. Accordingly, at several places we will disregard certain sets of parameters which have measure zero (See Eqs. (3) and (4)).

The model's equations can be simplified by using the following change of coordinates

$$\begin{array}{c}{\overline{S}}_j=c_j{S}_j\\ {\overline{T}}_j=p_j{T}_j\end{array}$$

which produces the equations

$$\begin{array}{cc}{\dot{\overline{S}}}_j\hfill & ={\overline{F}}_j(\overline{S},\overline{T})={\overline{r}}_{j-1}{f}_{j-1}{\overline{S}}_{j-1}-a_j{\overline{S}}_j-f_j{\overline{S}}_j-{\overline{S}}_j{\overline{T}}_j\hfill \\ {\dot{\overline{T}}}_j\hfill & ={\overline{G}}_j(\overline{S},\overline{T})={\overline{S}}_j{\overline{T}}_j-b{\overline{T}}_j\hfill \\ {\overline{r}}_j\hfill & =\frac{c_{j+1}}{c_j}{r}_j\hfill \end{array}$$ (**)

We will henceforth assume our equations are in this form and omit the bars. When we refer to a fixed point, we will mean a fixed point of system (**). The notations $(S_0^{\ast },\dots ,S_{n-1}^{\ast },T_0^{\ast },\dots ,T_{n-1}^{\ast })$ or (S*, T*) will refer to such a fixed point. We will say that a point is biologically meaningful if its components are non-negative.

We will adopt the following notational conventions. Sets such as [j, k] and [j, k) are to be taken cyclically. That is to say, if j < k, then [j, k] = {j,…, k}, while if j > k, [j, k] = {j,…, n – 1, 0,…, k}. We take [j, j) to be the empty set so that any product taken over [j, j) is one. We abuse notation by taking [0, n) = {0,…,n – 1}.

3 First properties of the fixed points

The fixed points are defined by the system of polynomial equations

$${\dot{S}}_j=F_j(S^{\ast },T^{\ast })=r_{j-1}{f}_{j-1}{S}_{j-1}^{\ast }-S_j^{\ast }(a_j+f_j+T_j^{\ast })=0$$ (1)

$${\dot{T}}_j=G_j(S^{\ast },T^{\ast })=(S_j^{\ast }-b)T_j^{\ast }=0$$ (2)

where j = 0,…, n – 1 and indices outside the interval [0, n – 1] are understood modulo n.

In this section, we give formulas that determine the population values at fixed points of system (**). We will see that if stage k is unregulated, $S_j^{\ast }$ is determined as a “follow-on” population from the previous stage. This gives rise to “follow-on factors” (defined below) which will play a key role in this paper. This, in turn, will lead us to the notion of generic parameter values, and we will see that for generic parameter values, system (**) has exactly 2ⁿ fixed points.

This section is organized as a series of observations. These follow from easy computations which we omit when they would clutter rather than clarify.

We start by defining these follow-on factors

$$\begin{array}{cc}\hfill M_j& ≔\frac{r_j{f}_j}{a_{j+1}+f_{j+1}}\hfill \\ \hfill M_{\mathit{\text{jk}}}& ≔\prod _{\ell \in [j,k)}{M}_{\ell }\hfill \\ \hfill R_0& ≔\prod _{j\in [0,n)}{M}_j.\hfill \end{array}$$

which we will use throughout this article. We will take M_jj to be the empty product. Given a fixed point (S*, T*), if $T_j^{\ast }\ne 0$, we will say that j is regulated. Otherwise j is unregulated. We define

$$\begin{array}{c}\hfill \text{Reg}(S^{\ast },T^{\ast })=\{j\mid T_j^{\ast }\ne 0\}\\ \hfill \text{Unreg}(S^{\ast },T^{\ast })=\{j\mid T_j^{\ast }=0\}\end{array}$$

1. If there is a j such that $S_j^{\ast }=0$, then (S*, T*) = (0, 0). By (1) if $S_j^{\ast }=0$, then $S_{j-1}^{\ast }=0$. By (2) if $S_j^{\ast }=0$, then $T_j^{\ast }=0$. Continuing in this way $S_j^{\ast }=T_j^{\ast }=0$ for all j ∈ [0, n).

2. If j ∈ Reg(S*, T*), then $S_j^{\ast }=b$.

3. If j ∈ Unreg(S*, T*), then $T_j^{\ast }=0$.

4. If j + 1 ∈ Unreg(S*, T*), then $S_{j+1}^{\ast }=S_j^{\ast }{M}_j$. This follows quickly from (1).

5. If [j + 1, k] ⊂ Unreg(S*, T*), then $S_k^{\ast }=S_j^{\ast }{M}_{\mathit{\text{jk}}}$. This follows by induction on the previous observation.

6. If j ∈ Reg(S*, T*) and [j + 1, k] ⊂ Unreg(S*, T*), then $S_k^{\ast }={\mathit{\text{bM}}}_{\mathit{\text{jk}}}$.

7. If R₀ ≠ 1, and (S*, T*) ≠ (0, 0), then Reg(S*, T*) ≠ ∅. To see this, notice that by our first observation, we must have $S_j^{\ast }\ne 0$ for all j ∈ [0, n). But if Reg(S*, T*) = ∅, we must have $S_0^{\ast }=R_0{S}_0^{\ast }$.

   Before proceeding, two points are worth considering. The first is that we have just introduced our first condition for a generic parameter set θ, that is,

   $$R_0=\prod _{j\in [0,n)}{M}_j\ne 1$$ (3)

   The second is that the S population at an unregulated stage depends on follow-on constants and the previous regulated stage. Observation 7 guarantees that at a nontrivial fixed point, there always is such a stage. Accordingly, given k, we will define h_k to be this stage, that is, h_k is the unique stage such that h_k ∈ Reg(S*, T*) and [h_k + 1, k) ⊂ Unreg(S*, T*). As we will see, this notation is also useful in the case k ∈ Reg(S*, T*).

8. If j ∈ Reg(S*, T*), then $T_j^{\ast }=\frac{r_{j-1}{f}_{j-1}}{b}{S}_{j-1}^{\ast }-(a_j+f_j)$. This follows from (1).

9. If j ∈Reg(S*, T*), then $T_j^{\ast }=r_{j-1}{f}_{j-1}{M}_{h_{j}j-1}-(a_j+f_j)$. This follows from the fact that $S_{j-1}^{\ast }=S_{h_j}^{\ast }{M}_{h_{j}j-1}$ and $S_{h_j}^{\ast }=b$.

10. $T_j^{\ast }>0$ if and only if M_hjj > 1.

This latter will be important in Sect. 5 and leads to our second genericity requirement. We take

$$M_{\mathit{\text{jk}}}\ne 1\text{for}j\ne k.$$ (4)

This may seem overly broad since we have only used M_jk ≠ 1 for j, k ∈ Reg(S*, T*), with j = h_k. However, we wish to avoid making the genericity of θ depend on the fixed point in question. The sets in question are all of co-dimension 1 and hence have measure 0.

We have now arrived at the place where all of the populations are determined by the parameters and the pattern of regulation. We record these as follows:

$$S_j^{\ast }=b\text{and}{T}_j^{\ast }=r_{j-1}{f}_{j-1}{M}_{h_{j}j-1}-(a_j+f_j)\forall j\in \text{Reg}(S^{\ast },T^{\ast })$$ (5)

$$S_j^{\ast }=b{M}_{h_{j}j}\text{and}{T}_j^{\ast }=0\forall j\in \text{Unreg}(S^{\ast },T^{\ast })$$ (6)

We are now prepared to show that for generic parameters, (**) has exactly 2ⁿ fixed points. We will show that for an arbitrary set R ⊂ [0, n), there is exactly one fixed point (S*, T*) with Reg(S*,T*) = R. If R = ∅, we have seen that (S*, T*) = (0,0). Under the assumption that R ≠ ∅, $S_j^{\ast }$ and $T_j^{\ast }$ are determined for j ∈ R by (5). Observe that if θ is generic, then the T-values determined by (5) are non-zero, so that Reg(S*, T*) = R as required. Since the population values for j ∉ R are now determined by (6), we see that there is exactly one fixed point for each R ⊂ [0, n) as required.

In general, not all of these non-vanishing fixed points (defined by (5) and (6) under the genericity assumptions) are biologically relevant, since a given pattern of regulated and unregulated stages can give T_j < 0 for one or more values of j. We will call non-vanishing fixed points (i.e., different from the uninfected equilibrium (0, 0)) infected equilibria. Infected equilibria with the property $T_j^{\ast }\ge 0\forall$ j = 0, …, n – 1 ( $S_j^{\ast }>0\forall$ j = 0, …, n – 1 follows from the assumed positivity of parameters) are called biologically meaningful infected equilibria.

4 Establishing infection: stability of the uninfected equilibrium

We start by deriving the expression for the basic reproductive number R₀ already revealed above [see (3)]. Our first genericity assumption (3) allows us to eliminate the case R₀ = l. We will then show that the remaining dichotomy R₀ < 1 or R₀ > 1 determines whether the pathogen is able to establish infection. We give two proofs here. The first uses the interpretation of the parameters as describing the life-cycle of the pathogen. The second is based on the analysis of eigenvalues of the Jacobian at the uninfected fixed point. These two approaches correspond roughly to R₀ and r₀. For an excellent discussion of these, see (Heffernan et al. 2005).

Given θ and an arbitrary biologically meaningful point (S, T) = (S₀,…, S_n–1, T₀,…, T_n–1), we define

$$\begin{array}{cc}\hfill {\stackrel{\sim }{M}}_j& =\frac{r_j{f}_j}{a_{j+1}+f_{j+1}+T_{j+1}}\hfill \\ \hfill \stackrel{\sim }{R}& =\prod _{j=0}^{n-1}{\stackrel{\sim }{M}}_j\hfill \end{array}$$

Note that at a fixed point (S*, T*), M̃_j = M_j for j ∈ Unreg(S*, T*).

Proposition 1

1. The basic reproductive number of the system is R₀.

2. The reproductive number at an arbitrary biologically meaningful point (S, T) is R̃.

3. The overall reproductive number of the pathogen in the presence of any (non-negative) immune response is less than its basic reproductive number in the absence of an immune response.

4. If R₀ < 1, the pathogen fails to establish infection and the uninfected fixed point (0, 0) is a global attractor.

5. At an infected fixed point, the reproductive number is exactly 1. Thus, at an infected fixed point we have ∏_j∈[0,n) M̃_j = 1.

Proof

To see that R₀ is the basic reproductive constant of this system, consider the behavior of stage S₀ when the naive host encounters one unit of this stage. The average lifespan at this stage is 1/(a₀ + f₀). During the course of that lifespan, it produces r₀ f₀/(a₀ + f₀) units of stage S₁. This, in turn produces (r₁ f₁/(a₁ + f₁))(r₀ f₀/(a₀ + f₀)) units of stage S₂. Continuing in this way, we see that the original introduction of a unit of S₀ results in ${\prod }_{j=0}^{n-1}(r_j{f}_j(a_j+f_j))={\prod }_{j=0}^{n-1}{M}_j=R_0$ units of S₀.

To see that the basic reproductive number at an arbitrary point (S, T) is ∏_j∈[0,n) M̃_j, observe that in the presence of an immune response, the average lifespan of stage S_j is 1/(a_j + f_j +T_j). The result now follows as before. The third and fourth statements now follow immediately, while the final statement follows from observing that at a fixed point the pathogen exactly reproduces itself and therefore has basic reproductive number 1.

We now examine R₀ from a slightly different perspective.

Proposition 2

If R₀ < 1, the eigenvalues of the Jacobian matrix of system (**) evaluated at (S, T) = (0, 0) have negative real part and, consequently, the uninfected fixed point is asymptotically stable. On the other hand, if R₀ > 1, at least one eigenvalue of the Jacobian has positive real part and thus, the uninfected equilibrium is unstable.

Proof

The characteristic polynomial P of J(S, T) is given by the following expression.

$$P(\lambda )={(-1)}^n\prod _{j=0}^{n-1}\left((S_j-{\sigma }_j-\lambda )(b+\lambda )-S_j(-(a_j+f_j)+b)\right)-\prod _{j=0}^{n-1}\left({\rho }_j(b+\lambda -S_{j+1})\right)$$

where we use the notation ρ_j = r_j f_j and σ_j = a_j + f_j + T_j. (See Theorem 5 of the Appendix for the details on how these expressions were derived.) Evaluating these at (S*, T*) = (0, 0) gives

$$P(\lambda )={(-1)}^n{(b+\lambda )}^n\left(\prod _{j=0}^{n-1}(a_j+f_j+\lambda )-\prod _{k=0}^{n-1}{r}_k{f}_k\right).$$

Thus, the eigenvalues of J (0, 0) are given by the n-fold root λ = −b and the zeros of the polynomial $R(\lambda )≔\text{∏}_{j=0}^{n-1}(a_j+f_j+\lambda )-\text{∏}_{k=0}^{n-1}{r}_k{f}_k$. By our assumptions, all coefficients of R are positive except for $\text{∏}_{j=0}^{n-1}(a_j+f_j)-\text{∏}_{k=0}^{n-1}{r}_k{f}_k$, which is positive if and only if

$$R_0=\frac{\text{∏}_{k=0}^{n-1}{r}_k{f}_k}{\text{∏}_{j=0}^{n-1}(a_j+f_j)}<1$$

By Routh's criterion (reviewed in Barnett and Šiljak 1977), if R₀ > 1, at least one root of R (and therefore of the characteristic polynomial P) has positive real part. Therefore, the equilibrium point (S, T) = (0, 0) becomes unstable for R₀ > 1.

We now wish to see that if R₀ < 1, all roots of P have strictly negative real part implying that the equilibrium point (S, T) = (0, 0) is (locally) asymptotically stable.

To see this, consider the polynomials

$$Q(\lambda )≔\prod _{j=0}^{n-1}(a_j+f_j+\lambda )$$

and

$$E(\lambda )≔-\prod _{j=0}^{n-1}{r}_j{f}_j.$$

Thus, R = Q + E, and we can interpret R as a perturbation of Q by E. By our assumptions, the real parts of all roots of Q are strictly negative, in other words, Q is strictly Hurwitz². Here the question arises as to how big the perturbation E can be, so that R remains strictly Hurwitz. By Corollary 4 in (Lin et al. 1989), this will occur if³

$$\underset{\omega \ge 0}{max}\left|\frac{E(i\omega )}{Q(i\omega )}\right|<1$$

where i is the imaginary unit. We have

$$\begin{array}{ll}|E(i\omega )/Q(i\omega )|& =\left|\left(-\prod _{j=0}^{n-1}{r}_j{f}_j\right)/\left(\prod _{j=0}^{n-1}(a_j+f_j+i\omega )\right)\right|\\ & =\sqrt{{\left(\prod _{j=0}^{n-1}{r}_j{f}_j\right)}^2/\left(\prod _{j=0}^{n-1}(a_j+f_j+i\omega )(a_j+f_j-i\omega )\right)}\\ & =\sqrt{{\left(\prod _{j=0}^{n-1}{r}_j{f}_j\right)}^2/\left(\prod _{j=0}^{n-1}({(a_j+f_j)}^2+{\omega }^2)\right)}\end{array}$$

It is now clear that this achieves its maximum, namely R₀, at ω = 0. In particular, R₀ < 1 implies that all eigenvalues of the Jacobian have negative real part and the uninfected fixed point is asymptotically stable.

5 Starvation: a partial order on the stages

In this section, we introduce a relation j ≻ k which we read as j starves k. This relation depends only on θ. We will show that this relation limits which patterns of regulation can appear in a biologically meaningful fixed point, and will show that j ≻ k is a strict partial order, provided R₀ > 1.

Definition 1

We will say stage j starves stage k and write j ≻ k if M_jk < 1.

The following proposition explains our use of the term starves.

Proposition 3

Let the set of parameters θ be generic. Furthermore, let (S*, T*) be a biologically meaningful infected equilibrium (in particular, Reg(S*, T*) ≠ ∅) and let j, k ∈ [0, n) such that j ≠ k. If j ≻ k, then j ∈ Reg(S*, T*) implies k ∈ Unreg(S*, T*).

Proof

Suppose j ∈ Reg(S*, T*) and assume to the contrary that k ∈ Reg(S*, T*). Let m ∈ ℕ₀ be the number of regulated stages between j and k. That is, suppose [j + 1, k) ∩ Reg(S*, T*) = {j₁, …, j_m} and suppose these are ordered so that (cyclically) j = j₀ ≤ j₁ ≤ j₂ ≤ ⋯ ≤ j_m < j_m+1 = k. Since (S*, T*) is biologically meaningful and θ is generic, $T_j^{\ast }>0$ for j ∈ Reg(S*, T*). By observation 10 of Sect. 3, we have M_jsjs+1 > 1 for s = 0, …, m. But this gives

$$M_{\mathit{\text{jk}}}=\prod _{s=0}^m{M}_{j_s{j}_{s+1}}>1,$$

contradicting the assumption that j ≻ k.

This result can be biologically interpreted as follows: If j ≻ k, regulation at stage S_j starves stage S_k of sufficient population to support regulation.

Proposition 4

Let θ be such that R₀ > 1. Then ≻ is a strict partial order.

Proof

We must show that ≻ is transitive, anti-reflexive and asymmetric. Suppose j ≻ k and k ≻ ℓ. If k ∈ [j, ℓ] then

$$(M_j\dots M_{k-1})(M_k\dots M_{\ell -1})=M_j\dots M_{\ell -1}.$$

Since each of the quantities on the left are less than one, so is their product as required. On the other hand, if ℓ ∈ [j, k], then

$$\begin{array}{ll}(M_j\dots M_{k-1})(M_k\dots M_{\ell -1})& =M_j\dots M_{j-1}{M}_j\dots M_{\ell -1}\\ & =R_0{M}_j\dots M_{\ell -1}<1\end{array}$$

Since R₀ > 1,

$$M_j\dots M_{\ell -1}<1,$$

as required.

To see that ≻ is asymmetric, note that R₀ can be written as

$$R_0=M_0\dots M_{n-1}=(M_j\dots M_{k-1})(M_k\dots M_{j-1})$$

Thus, R₀ > 1 and j ≻ k imply 1 < M_k … M_j−1 contradicting k ≻ j.

Finally, to see that ≻ is anti-reflexive, note that by definition M_jj = 1.

Definition 2

We will say that S_j is unstarvable if j is ≻ -maximal. Otherwise S_j is starvable. We will refer to the set of indices of unstarvable respectively starvable stages as Str(θ) respectively Unstr(θ).

Remark 1

Note that if θ is such that no two stages are comparable, then ≻ is empty and every stage is ≻ -maximal, so Unstr(θ) = [0, n). In particular, Unstr(θ) ≠ ∅ ∀ θ.

6 Stability of infected equilibria

In this section, we consider biologically meaningful infected fixed points. In particular, we can assume R₀ > 1. We will show that for generic θ there is exactly one asymptotically stable biologically meaningful fixed point. We give two characterizations of this fixed point, one in terms of pathogen populations and one in terms of immune response.

Definition 3

Let (S*, T*) be an infected fixed point. We will say that the pathogen populations are moderated at (S*, T*) (or simply that (S*, T*) is moderated) if $S_j^{\ast }<b$ for j ∈ Unreg(S*, T*). We will say that the immune response is saturated at (S*, T*) (or simply that (S*, T*) is saturated) if Reg(S*, T*) = Unstr(θ).

Remark 2

Given a fixed point (S*, T*), $S_j^{\ast }=b$ for j ∈ Reg(S*, T*). Thus at a moderated fixed point, at no stage is the pathogen population greater than the regulated population.

Proposition 5

Let the set of parameters θ be generic. Furthermore, let (S*, T*) be a biologically meaningful infected fixed point. Then the pathogen populations are moderated at (S*, T*) if and only if the immune response is saturated at (S*, T*).

Proof

We start by proving that saturation implies moderation. Suppose (S*, T*) is saturated, and suppose θ is generic. If Unreg(S*, T*) = ∅, the claim holds vacuously. So suppose k ∈ Unreg(S*, T*). We then have k ∈ Str(θ). Let j be ≻-maximal such that j ≻ k. If [j + 1, k) ⊆ Unreg(S*, T *), we are done, for then $S_k^{\ast }=S_j^{\ast }{M}_{\mathit{\text{jk}}}={\mathit{\text{bM}}}_{\mathit{\text{jk}}}<b$. On the other hand if [j + 1, k)∩Reg(S*, T*) ≠ ∅, choose m ∈ [j + 1, k)∩Reg(S*, T*) so that [m + 1, k) ⊂ Unreg(S*, T*). Since M_jk = M_jmM_mk < 1, we must either have M_mk < 1 forcing $S_k^{\ast }<b$, or we have M_jm < 1. But the latter is impossible since m ∈ Reg(S*, T*) and hence m ∈ Unstr(θ). Hence (S*, T*) is moderated as required.

Now we show the converse. Suppose (S*, T*) is moderated. We then have

$$\begin{array}{r}\text{Reg}(S^{\ast },T^{\ast })=\{j\mid S_j^{\ast }=b\}\\ \text{Unreg}(S^{\ast },T^{\ast })=\{j\mid S_j^{\ast }<b\}\end{array}$$

We claim that Unreg(S*, T*) ⊆ Str(θ). If Unreg(S*, T*) = ∅, this holds vacuously. Now assume Unreg(S*, T*) ≠ ∅ and let k ∈ Unreg(S*, T*). Choose j ∈ Reg (S*, T*) such that [j +1, k] ⊂ Unreg(S*, T*). Then $S_k^{\ast }=S_j^{\ast }{M}_{\mathit{\text{jk}}}={\mathit{\text{bM}}}_{\mathit{\text{jk}}}<b$ proving j ≻ k as required.

We claim that Reg(S*, T*) ⊆ Unstr(θ). Suppose to the contrary that k ∈ Reg(S*, T*) ∩ Str(θ). Then there is j ∈ Unstr(θ) such that j ≻ k. Since Unreg(S*, T*) ⊂ Str(θ), we must have j ∈ Reg(S*, T*). But if j ∈ Reg(S*, T*) and j ≻ k, then, by Proposition 3, k ∈ Unreg(S*, T*) contradicting k ∈ Reg(S*, T*).

Since Unreg(S*, T*) ⊆ Str(θ) and Reg(S*, T*) ⊆ Unstr(θ) and Str(θ), Unstr(θ) as well as Reg(S*, T*), Unreg(S*, T*) are partitions of [0, n), we have Unreg(S*, T*) = Str(θ) and Reg(S*, T*) = Unstr(θ) proving that (S*, T*) is saturated as required.

We now justify the use of the term “saturated”.

Theorem 1

Let the set of parameters θ be generic. Furthermore, suppose (S*, T*) is a biologically meaningful infected fixed point and assume (S*, T*) is not saturated. Then there is a j ∈ [0, n) so that $T_j^{\ast }=0$ and for any neighborhood U of (S*, T*), there is a biologically meaningful point x ∈ U so that Ṫ_j∣_x > 0. In particular, (S*, T*) is unstable.

Proof

Since (S*, T*) is not saturated, by Proposition 5, it is not moderated. Furthermore, Unreg(S*, T*) ≠ ∅. Were Unreg(S*, T*) = ∅, then the fixed point would be completely regulated (Reg(S*, T*) = [0, n)) and such a fixed point is always saturated. To see this, assume that (S*, T*) is not saturated. Since Unreg(S*, T*) = ∅, this assumption is equivalent to Str(θ) ≠ ∅. Thus, there is a k ∈ Str(θ) which is dominated by another stage j, in other words, j ≻ k. But j ∈ Reg(S*, T*) and therefore, by Proposition 3, k ∈ Unreg(S*, T*), a contradiction.

Summarizing, there is j ∈ Unreg(S*, T*) so that $S_j^{\ast }>b$. Let e_Tj be the unit vector in the T_j direction. Recall that $\frac{\partial G_j}{T_j}(S^{\ast },T^{\ast })=(S_j^{\ast }-b)$. Thus, for any sufficiently small δ > 0, we have Ṫ_j∣_F+δeTj > 0. This implies that arbitrarily close to (S*, T*), there are orbits which move away from (S*, T*).

Remark 3

One can think of (S*, T*) as a state of a “micro-ecology” in which T_j plays the role of a species which is capable of invading.

Theorem 2

Let (S*, T*) be a biologically meaningful infected fixed point. Assume that not all T_j are equal. If (S*, T*) is moderated then (S*, T*) is a local asymptotically stable equilibrium. In particular, the eigenvalues of the Jacobian matrix J(S*, T*) have strictly negative real part.

Proof

For brevity, we will use the notations ℛ = Reg(S*, T*), 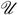= Unreg(S*, T*), ρ_j = r_jf_j and ${\sigma }_j=a_j+f_j+T_j^{\ast }$ (thus, σ_j = a_j + f_j for all j ∈ Unreg(S*, T*)). The characteristic polynomial of J(S*, T*) is given by

$$P(\lambda )=\pm \prod _{j=0}^{n-1}\left((S_j^{\ast }-{\sigma }_j-\lambda )(b+\lambda )-S_j^{\ast }(-(a_j+f_j)+b)\right)-\prod _{j=1}^n\left({\rho }_{j-1}(b+\lambda -S_j^{\ast })\right)$$

By grouping the factors containing regulated resp. unregulated stages we obtain

$$P(\lambda )=\pm \prod _{j\in ℛ}\left({\lambda }^2+{\sigma }_j\lambda +T_j^{\ast }b\right)\times \prod _{j\in \mathcal{\text{U}}}\left({\lambda }^2+(a_j+f_j+b-S_j^{\ast })\lambda +(a_j+f_j)(b-S_j^{\ast })\right)-{\lambda }^{\left|ℛ\right|}\prod _{j\in ℛ}({\rho }_{j-1})\prod _{j\in \mathcal{\text{U}}}\left({\rho }_{j-1}(\lambda +b-S_j^{\ast })\right)$$

As in Sect. 4, we consider the polynomials

$$\begin{array}{ll}Q(\lambda )& ≔\pm \prod _{j\in ℛ}\left({\lambda }^2+{\sigma }_j\lambda +T_j^{\ast }b\right)\times \prod _{j\in \mathcal{\text{U}}}\left({\lambda }^2+(a_j+f_j+b-S_j^{\ast })\lambda +(a_j+f_j)(b-S_j^{\ast })\right)\\ E(\lambda )& ≔-{\lambda }^{\left|ℛ\right|}\prod _{j\in ℛ}({\rho }_{j-1})\prod _{j\in \mathcal{\text{U}}}\left({\rho }_{j-1}(\lambda +b-S_j^{\ast })\right).\end{array}$$ (7)

Thus, P = Q + E, and we can interpret P as a perturbation of Q by E. By our assumptions on the parameters, by the positivity of all $T_j^{\ast }$ for j ∈ ℛ, and by the assumption $S_j^{\ast }<b$ for all j ∈ 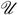, Q is strictly Hurwitz (this is also correct in the case 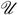= ∅). Here the question arises as to how big the perturbation E can be, so that P remains strictly Hurwitz. By Corollary 4 in (Lin et al. 1989), the strict Hurwitz property is preserved if max (|E(iω)/Q(iω)|) < 1. ⁴ We have

$$\begin{array}{ll}|E(i\omega )/Q(i\omega )|& =\frac{\left|{(i\omega )}^{\left|ℛ\right|}\text{∏}_{j\in ℛ}({\rho }_{j-1})\text{∏}_{j\in \mathcal{\text{U}}}({\rho }_{j-1}(i\omega +b-S_j^{\ast }))\right|}{\left|\text{∏}_{j\in ℛ}\left({(i\omega )}^2+i{\sigma }_j\omega +T_j^{\ast }b\right)\text{∏}_{j\in \mathcal{\text{U}}}\left({(i\omega )}^2+i(a_j+f_j+b-S_j^{\ast })\omega +(a_j+f_j)(b-S_j^{\ast })\right)\right|}\\ & =\frac{{\omega }^{\left|ℛ\right|}\text{∏}_{j=0}^{n-1}({\rho }_j)\text{∏}_{j\in \mathcal{\text{U}}}\sqrt{{\omega }^2+{(b-S_j^{\ast })}^2}}{\text{∏}_{j\in ℛ}\sqrt{{\left(T_j^{\ast }b-{\omega }^2\right)}^2+{\sigma }_j^2{\omega }^2}\text{∏}_{j\in \mathcal{\text{U}}}\sqrt{{\left((a_j+f_j)(b-S_j^{\ast })-{\omega }^2\right)}^2+{(a_j+f_j+b-S_j^{\ast })}^2{\omega }^2}}\\ & =\frac{{\omega }^{\left|ℛ\right|}\text{∏}_{j=0}^{n-1}({\rho }_j)\text{∏}_{j\in \mathcal{\text{U}}}\sqrt{{\omega }^2+{(b-S_j^{\ast })}^2}}{\text{∏}_{j\in ℛ}\omega \sqrt{{\left(T_j^{\ast }b-{\omega }^2\right)}^2/{\omega }^2+{\sigma }_j^2}\text{∏}_{j\in \mathcal{\text{U}}}\sqrt{({(b-S_j^{\ast })}^2+{\omega }^2)({(a_j+f_j)}^2+{\omega }^2)}}\\ & =\frac{\text{∏}_{j=0}^{n-1}({\rho }_j)}{\text{∏}_{j\in ℛ}\sqrt{{\left(T_j^{\ast }b-{\omega }^2\right)}^2/{\omega }^2+{\sigma }_j^2}\text{∏}_{j\in \mathcal{\text{U}}}\sqrt{{(a_j+f_j)}^2+{\omega }^2}}\end{array}$$

Each of the functions $h_j(\omega )≔{(T_j^{\ast }b-{\omega }^2)}^2/{\omega }^2$, j ∈ ℛ has a global minimum on (0, ∞) at $\omega =\sqrt{T_j^{\ast }b}>0$ whereas the function g(ω) ≔ (a_j + f_j)² + ω² has a global minimum on [0, ∞) at ω = 0. Therefore, we can conclude that for max_ω≥0 |E(iω)/Q(iω)|, if existent, it must hold

$$\underset{\omega \ge 0}{max}|E(i\omega )/Q(i\omega )|<\frac{\text{∏}_{j=0}^{n-1}({\rho }_j)}{\text{∏}_{j\in ℛ}({\sigma }_j)\text{∏}_{j\in \mathcal{\text{U}}}(a_j+f_j)}$$

This is also correct in the case 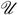= ∅, in which

$$|E(i\omega )/Q(i\omega )|=\prod _{j=0}^{n-1}({\rho }_j)/\prod _{j\in ℛ}\sqrt{{(T_j^{\ast }b-{\omega }^2)}^2/{\omega }^2+{\sigma }_j^2}\text{and}\prod _{j\in \mathcal{\text{U}}}(a_j+f_j)=1.$$

The strict inequality arises from the fact that not all $T_j^{\ast }$ are equal (and consequently not all $\sqrt{T_j^{\ast }b}$ are equal) and thus, the functions h_j(ω) do not achieve their minima simultaneously. By 5. in Proposition 1, it follows max_ω≥0 |E(iω)/Q(iω)| < 1 and the claim follows by Corollary 4 in (Lin et al. 1989).

Corollary 1

Let the set of parameters θ be generic. Furthermore, let (S*, T*) be a biologically meaningful infected fixed point. Assume that not all T_j are equal. Then (S*, T*) is locally asymptotically stable if and only if (S*, T*) is moderated.

Proof

The claim follows immediately from Proposition 5 and Theorems 1 and 2.

The previous Corollary can be restated as follows.

Theorem 3

Let the set of parameters θ be generic. Furthermore, let (S*, T*) be a biologically meaningful infected fixed point. Then (S*, T*) is locally asymptotically stable if and only if (S*, T*) is saturated.

Proof

Under the assumption that θ is generic, (S*, T*) is saturated if and only if it is moderated. Note that for a generic parameter set θ, the $T_j^{\ast }$ are not all equal as this occurs only on a subset of parameters of co-dimension n – 1.

Remark 4

We have introduced a third requirement for θ to be generic, namely that $T_j^{\ast }$ are not all equal. As we will see below, this is equivalent to the requirement that r_j−1f_j−1 − (a_j + f_j) is not independent of j.

Definition 4

Let (S*, T*) be a fixed point. If Reg(S*, T*) = [0, n), we will say that (S*, T*) is completely regulated.

Remark 5

If (S*, T*) is completely regulated, it follows that (S*, T*) is infected. It is also vacuously moderated. If θ is generic and (S*, T*) biologically meaningful, it is also saturated (see the Proof of Theorem 1). On the other hand, if θ is generic and such that no two stages are comparable, then the completely regulated (not necessarily biologically meaningful) fixed point is saturated (cf. Remark 1).

Corollary 2

Let (S*, T*) be the completely regulated biologically meaningful fixed point. Suppose that the $T_j^{\ast }$ are not all equal. Then (S*, T*) is locally asymptotically stable and the eigenvalues of the Jacobian matrix J(S*, T*) have strictly negative real part.

Proof

Since (S*, T*) is completely regulated, (S*, T*) is moderated.

Remark 6

Note that if we drop the assumption that not all the $T_j^{\ast }$ are equal, we are forced into the case $T_j^{\ast }=\tau$ for all j ∈ [0, n) for some τ ∈ ℝ⁺ and consequently Unreg(S*, T*) = ∅. In this case,

$$\underset{\omega \ge 0}{max}|E(i\omega )/Q(i\omega )|=\underset{\omega \ge 0}{max}\left(\frac{\text{∏}_{j=0}^{n-1}\left(p_j\right)}{\text{∏}_{j=0}^{n-1}\sqrt{{(\tau b-{\omega }^2)}^2/{\omega }^2+s_j^2}}\right)=\frac{\text{∏}_{j=0}^{n-1}\left(p_j\right)}{\text{∏}_{j=0}^{n-1}(a_j+f_j+T_j^{\ast })}$$

and by Proposition 1, max_ω≥0 |E(iω)/Q(iω)| = 1. Corollary 4 in (Lin et al. 1989) and the continuity of the eigenvalues on the entries of a matrix let us conclude that Re(λ_k) ≤ 0 for all roots λ_k of the characteristic polynomial P. In this very non-generic case, linearization of the right hand side of (**) does not yield a stability statement for (S*, T*). In the next subsection we will study this case in more detail.

7 An embedded Lotka–Volterra system

For certain highly non-generic sets of parameters, this system contains an embedded Lotka–Volterra predator–prey system. Recall that this system is given by

$$\begin{array}{l}\dot{x}=(\alpha -y)x\\ \dot{y}=(x-\beta )y\end{array}$$

where α, β ∈ ℝ⁺ are positive parameters and x and y are non-negative. (See, e.g., Hirsch and Smale 1974). We will use the notation Δ_S × Δ_T to denote points (S₀,…, S_n−1, T₀,…, T_n−1) where the values S_j and T_j are independent of j, that is, points satisfying S₀ = S₁ = ⋯ = S_n−1 and T₀ = T₁ = ⋯ = T_n−1.

Theorem 4

Suppose (S*, T*) is the completely regulated infected fixed point of (**). Then the following are equivalent:

1. $T_j^{\ast }$ is independent of j.

2. (S*, T*) ∈ Δ_S × Δ_T.

3. The expression r_j−1f_j−1 − (a_j + f_j) is positive and independent of j.

4. Δ_S × Δ_T is invariant and the dynamics of the system restricted to Δ_S × Δ_T is the Lotka-Volterra system.

5. There is an embedded Lotka-Volterra system.

6. The Jacobian of the system has a pair of pure imaginary eigenvalues.

Proof

1. ⇒ 2.: We have $T_j^{\ast }\ne 0$ for 0 ≤ j < n, so $S_j^{\ast }=b$ for 0 ≤ j < n.

2. ⇒ 3.: Recall that

$$T_j^{\ast }=\frac{r_{j-1}{f}_{j-1}}{b}{S}_{j-1}^{\ast }-(a_j+f_j).$$

Since $S_j^{\ast }=b$ for 0 ≤ j < n and $T_j^{\ast }$ is independent of j, the result follows.

3.⇒ 4.: We take S_j = x, T_j = y on Δ_S × Δ_T, r_j−1f_j−1 − (a_j + f_j) = α and b = β. We then have

$$\begin{array}{ll}{\dot{S}}_j& =r_{j-1}{f}_{j-1}{S}_{j-1}-(a_j+f_j+T_j)S_j\\ & =(\alpha -y)x\\ {\dot{T}}_j& =(S_j-b)T_j\\ & =(x-\beta )y\end{array}$$

Since the right-hand sides are independent of j, we may replace the left-hand sides with the derivatives of x and y giving the Lotka–Volterra equations.

4. immediately implies 5.

6. now follows from the well-known dynamics of the Lotka-Volterra equations.

It remains to prove that 6. implies 1. This follows from Corollary 2.

Remark 7

The Lotka–Volterra dynamics take place on an embedded 2-plane. Corollary 2 says that the eigenvalues of the Jacobian have non-positive real parts.

This implies that there is no exponential departure from the fixed point orthogonal to the Lotka-Volterra plane. We conjecture that the pure imaginary eigenvalues of the Lotka-Volterra dynamics are the only ones with non-negative real part. If this conjecture is correct, the Lotka-Volterra plane is an attractor in a neighborhood of the fixed point. This conjecture is consistent with the results of numerical investigations.

8 Self-establishing stages

In this section we show how to modify Definition 1 to generalize Theorems 1, 2 and 3 in the case where there exists a j ∈ [0, n) such that a_j + f_j < 0.

In previous sections, we have assumed that a_j + f_j > 0 for all j ∈ [0, n). The assumption that a_j > 0 says that stage j decays rather than proliferates. If a_j < 0 and a_j + f_j > 0, then stage j proliferates, but does so more slowly than it is lost to stage j + 1. Accordingly, no stage is able to establish itself independently of the other stages. We now lift this assumption and allow stages j such that a_j + f_j < 0. Such a stage proliferates faster than it differentiates and is thus able to establish itself independently of the remaining stages. We call such a stage self-establishing. Given a set of parameters θ, we will refer to the set of indices of self-establishing stages as SE(θ).

Since f_j and r_j are positive for all j, a self-establishing stage also establishes infection at all other stages. The converse is also true. Suppose a naive is infected with a small amount of S_j > 0 where j ∉ SE(θ). Suppose also that k ∈ SE(θ) with [j + 1, k) ∩ SE(θ) = ∅. Given that S_j > 0 for t = 0, (**) ensures that S_k > 0 for any sufficiently small t. S_k then proceeds to proliferate.

As our fourth and last genericity assumption, we assume a_j + f_j ≠ 0∀ j ∈ [0, n). We take SE(θ) = {j ∣a_j + f_j < 0}. In this section, we take it as a standing assumption that SE(θ) ≠ ∅.

Proposition 6

Let θ be a set of parameters. Furthermore, let (S*, T*) be a biologically meaningful infected fixed point. If j ∈ SE(θ), then j ∈ Reg(S*, T*).

Proof

If, on the contrary, $T_j^{\ast }=0$, it follows that ${\dot{S}}_j>0$, contradicting the assumption that (S*, T*) is a fixed point.

It should be clear that any self-establishing stage cannot be starved of sufficient population to support regulation.

Definition 5

We say that j starves k and write j ≻ if M_jk < 1 and [j + 1, k] ∩ SE(θ) = ∅.

Note that this reduces to the previous definition when SE(θ) is empty.

Proposition 7

Let θ be such that R₀ > 1. Then the relation ≻ is a strict partial order.

Proof

Let SE(θ) consist of j₁ < j₂ < ⋯ < j_m. These decompose [0, n) into U₁,…,U_m+1 where U_ℓ = [j_ℓ, j_ℓ+1) for ℓ = 1,…, m and U_m+1 = [j_m, j₁). We order each of these segments according to the reverse of the order induced by the cyclic order of [0, n). That is, for ℓ = 1,…, m, U_ℓ is ordered $j_{\ell }\stackrel{\ast }{>}{j}_{\ell }+1\stackrel{\ast }{>}\dots \stackrel{\ast }{>}{j}_{\ell +1}-1$, while U_m+1 is ordered $j_m\stackrel{\ast }{>}\dots \stackrel{\ast }{>}n-1\stackrel{\ast }{>}0\stackrel{\ast }{>}\dots \stackrel{\ast }{>}{j}_1-1$. Notice that if j ≻ k then j and k lie in the same U_ℓ and $j\stackrel{\ast }{>}k$. It is easy to see that this makes ≻ a strict partial order.

We define Str(θ), Unstr(θ), saturated and moderated as before. The statement of Proposition 3 as well as the equivalence of moderation and saturation (Proposition 5) and their necessity for stability (Theorem 1) can be proved analogously, where the result of Proposition 6 plays an important role.

In order to prove sufficiency in the presence of self-establishing stages, we need the following lemma.

Lemma 1

Let the set of parameters θ be generic. Furthermore, let (S*, T*) be a biologically meaningful infected fixed point. Then

1. $S_j^{\ast }>0$ for j ∈ [0, n).

2. ${\sigma }_j=a_j+f_j+T_j^{\ast }>0$ for j ∈ [0, n).

Proof

Since (S*, T*) is infected and biologically meaningful, there is j so that $S_j^{\ast }>0$. Hence, by Eq. (1) $r_j{f}_j{S}_j^{\ast }>0$, which in turn requires $-(a_{j+1}+f_{j+1}+T_{j+1}^{\ast })S_{j+1}^{\ast }<0$. This requires $S_{j+1}^{\ast }\ne 0$, and since (S*, T*) is biologically meaningful, $S_{j+1}^{\ast }>0$. This, in turn, requires ${\sigma }_{j+1}=a_{j+1}+f_{j+1}+T_{j+1}^{\ast }>0$. Continuing in this way extends this to all j ∈ [0, n).

The proof of Theorem 2 depends on Eq. 7, and we now revisit this in the case of a saturated fixed point with self-establishing stages. To see that Q(λ) is Hurwitz, we must check that its coefficients are positive. For the product taken over regulated stages, we note that σ_j and $T_j^{\ast }b$ are both positive. We turn to the product taken over unregulated stages. As we have seen, an unregulated stage cannot be self-establishing. In particular, at any unregulated stage, a_j + f_j is positive and we proceed as before. Theorem 3 and Corollary 2 now follow as before.

9 Discussion

In this paper, we have considered an ODE model (**) of the interactions between a host and a pathogen which uses a cycle of antigenically distinct stages to establish and maintain infection. We were able to give a simple expression for R₀ which determines whether the pathogen is able to establish infection. If R₀ < 1, exposure to the pathogen, even in large quantities, will not succeed in infecting the host since the pathogen dies faster than it can replace itself. Indeed, the host will clear the pathogen even in the absence of an immune response.

If R₀ > 1, then the pathogen is capable of infecting the host, and in this model, an immune response is necessary to control the infection.⁵ In this case, the absence of an immune response leads to unbounded expansion of the pathogen population and presumably, the host's death.

The question then arises, when an immunocompetent host is infected with an infectively competent pathogen (i.e., R₀ > 1), can they arrive at a stable equilibrium? If so, what are the balancing populations for pathogen population and host response? In terms of the model, this question translates to asking which of the model's equilibria are stable and under what conditions. A key ingredient towards answering this question was the ability to distinguish the different stages of the pathogen in terms of the net yield with which they are generated. We were able to formalize this distinction using a binary relation j ≻ k, which turns out to be a partial order if R₀ > 1 (see Sect. 5).

Assuming the pathogen can establish infection, the concepts of starvable and unstarvable stages restrict the possible patterns of regulation. The starvation relation j ≻ k is based on comparison of the rate at which stage j produces stage k with the rate at which stage k is lost to death and differentiation. This determines the ability of stage j to replenish the population at stage k. When this downstream yield is smaller than the regulated population b, it is insufficient to support regulation. In this way, if j ≻ k and j is regulated, then regulation of stage k vanishes. In this sense, the immune regulation of unstarvable stages is sufficient to immunologically control the starvable stages. At steady state, immune regulation is only required against those stages that are produced with relatively higher yield and the equilibrium becomes moderated (see Sect. 6). Accordingly, there is a unique biologically meaningful infected equilibrium, namely, the one at which all unstarvable stages are regulated and all starvable stages are unregulated.

If the parameters of the system allow for the existence of a biologically meaningful completely regulated fixed point, the model predicts that this will be the (only) stable equilibrium under the premise that the pathogen can establish infection (Corollary 2). According to Eq. 5, the completely regulated fixed point satisfies $S_j^{\ast }=b$ and $T_j^{\ast }=r_{j-1}{f}_{j-1}-(a_j+f_j)$, j = 0, …, n − 1 The inequalities $T_j^{\ast }>0$ imply that the amplification factors r_j are big enough for every stage to be replenished at a higher rate than the sum a_j + f_j of its own decay and transformation rate. Our model predicts that a pathogen which produces every stage with such an effectivity can only be immunologically controlled with a fine tuned immune response against every stage the pathogen cycles through.

Having clarified the properties of equilibria, it is pertinent to keep in mind that these are local properties of the model. We were unable to perform a global analysis of the dynamics (see for instance, Prüss et al. 2008). That is, we cannot give an account of trajectories along which the system might approach such a steady state configuration, the basins of attraction of attracting fixed points, nor can we eliminate the possibility that the system exhibits limiting cycles or other attractors. Our naive expectation is that the unique biologically meaningful infected equilibrium acts as a global attractor in the case where the host possesses an immunocompetent response to every stage.

Our methods for establishing the uniqueness and existence of the unique stable fixed point have very distinct flavors. The arguments for uniqueness have clear biological interpretations. In particular, the starvation relation, j ≻ k of Sect. 5 considers the maximal rate at which stage j can produce stage k with the rate at which stage k is lost to stage k + 1 and in turn compares these to the minimum population necessary to support immune regulation. Likewise, Theorem 1 describes the ability of an immune response to invade and therefore alter a given equilibrium.

Our methods for establishing existence have a very different character. Here we have turned to the eigenvalues of the system's Jacobian matrix and these have lead us to the roots of its characteristic polynomial. These sorts of computations can offer many challenges which have been the subject of intense study for the last five decades within the control and systems theory community. Many of the resulting techniques focus on the sorts of perturbations that can be applied to a strictly Hurwitz polynomial without losing the Hurwitz property. We predict that as biological models continue to grow in complexity, mathematical biologists will increasingly turn to these analytic tools. For entry into this topic we recommend the bibliographies (McNamee 1993, 2002).

Having stated the general predictions that can be derived from our model, we would like to elaborate on the model's features, properties and predictions within the biological framework of chronic EBV infection. It was indeed human EBV pathology what inspired the basic structure of our model. To this end, we provide a brief overview of what is known about EBV infection in humans.

EBV is a highly successful pathogen which infects over 90% of the adult human population (Thorley-Lawson 2001). It is horizontally transmitted via saliva (Hoagland 1955) and is tropic to the epithelium of the oropharynx and B-cells. It infects naive B-cells and causes them to become activated B-blasts. These enter the germinal centers of Waldeyer's ring where they are ultimately transformed into latently infected quiescent memory B-cells. These circulate in the peripheral blood where they rarely express viral proteins and are therefore invisible to the immune system (Hochberg et al. 2004a). Upon return to Waldeyer's ring, some of these are triggered to start producing virus (Laichalk and Thorley-Lawson 2005). These lytically infected B-cells ultimately burst, producing free virus which may be transmitted horizontally or may reinfect additional naive B-cells, thus completing the cycle (Thorley-Lawson and Gross 2004). The epithelium of the oropharynx appears to play a role in amplifying virus for transmission (Hadinoto et al. 2009). The host mounts T-cell responses against the blast, germinal center and lytic stages, and an antibody response against the free virus. The normal course of acute infectious mononucleosis involves an acute phase during which latently infected memory B-cells can become as much as 50% of the memory B-cells in the peripheral circulation (Hochberg et al. 2004b). Immune response is also high during the acute phase. This resolves to a chronic phase of persistent low-level infection (Hochberg et al. 2004b; Khan et al. 1996).

This suggests that a mathematical model of EBV infection might include the following infected populations: activated B-blasts, infected germinal center B-cells, quiescent infected memory B-cells and lytically infected B-cells. These latter can be subdivided into stages exhibiting distinct antigenic profiles, namely immediate early, early and late antigens. Due to its short life span one might choose to omit free virus from such a model. In short, it is not at all obvious what would be the “right” number of stages to include in an EBV model, and this has motivated our choice to study a model which is entirely general as to the number of stages.

We have chosen to omit the supply of uninfected tissue from our model for the sake of symmetry. We would argue that this does not affect the validity of the model unless a significant fraction of the uninfected tissue is lost to infection. To see this, consider a modification of the model to take this into account. Let us use S_n to model uninfected tissue, let us take S_n−1 to model free virus⁶, and let the rate of new infection be proportional to their product. We then have

$$\begin{array}{cc}\hfill {\dot{S}}_{n-1}& =r_{n-2}{f}_{n-2}{S}_{n-2}-(a_{n-1}+\beta S_n+T_{n-1})S_{n-1}\hfill \\ \hfill {\dot{S}}_n& =\lambda -(a_n+r_n\beta S_{n-1})S_n\hfill \\ \hfill {\dot{S}}_0& =r_n\beta S_n{S}_{n-1}-(a_0+f_0+T_0)S_0\hfill \end{array}$$

(Compare Eq. 3.1 of Nowak and May 2000). If S_n is relatively constant, then S_n can be eliminated from the model and we can take f_n−1 = βS_n and r_n−1 f_n−1 = r_nβS_n.

While acute phase EBV infection shows infected cells occupying a large portion of peripheral memory, it seems unlikely that it consumes a large portion of the uninfected naive B-cells supplied to Waldeyer's ring (Hochberg et al. 2004a; Souza et al. 2005). Accordingly, it seems unlikely that this will be an obstruction to application of this model.

Our primary purpose in developing this model is to cast light on the long-term persistence of EBV infection. Here we can surely treat the supply of uninfected tissue as nearly constant.

Biologists will be interested in solutions to (*) rather than (**). The follow-on factors are unchanged. The analogs of Eqs. 5 and 6 are

$$\begin{array}{r}{S}_j^{\ast }=\frac{b}{c_j}\text{and}{T}_j^{\ast }=\frac{1}{p_j}\left(\frac{c_j}{c_{h_{j-1}}}{r}_{j-1}{f}_{j-1}{M}_{h_{j}j-1}-(a_j+f_j)\right)\forall j\in \text{Reg}(S^{\ast },T^{\ast })\\ S_j^{\ast }=\frac{b}{c_{h_j}}{M}_{h_{j}j}\text{and}{T}_j^{\ast }=0\forall j\in \text{Unreg}(S^{\ast },T^{\ast })\end{array}$$

The starvation relation is now j ≻ k if $M_{\mathit{\text{jk}}}<\frac{c_j}{c_k}$.

People show different patterns of infection and immune response to EBV. Under 10% of the adult population is EBV negative. Given that over 90% of the adult population is EBV positive (Thorley-Lawson 2001; Rickinson and Kieff 2001), it is clear that most of the EBV negative population has had repeated exposure to EBV. Since these people show no EBV-specific antibodies (Henle and Henle 1979), it seems clear that they are negative due to the virus's inability to establish infection rather than the immune system's ability to clear it. This shows that R₀ is a host–pathogen property, not simply a property of the pathogen.

Chronically infected people show very stable levels of infected memory B-cells in the peripheral blood (Khan et al. 1996). This is an indication that we are dealing with a stable fixed point of the host–pathogen system. However, the level of infected memory B-cells varies from person to person (Khan et al. 1996) as does the pattern of immune response. To the best of our knowledge, there is always a humoral response to the free virus. Beyond that, we have seen the individuals who exhibit T-cell responses to both the blast and germinal center stages and to the lytic stages and individuals who only exhibit detectable T-cell response to the lytic stages (Thomas Greenough, 2009, personal communication). The latter patterns could arise from a gap in the available T-cell repertory. We think it is at least as likely that the starvation relationship varies due to population variation in θ. Empirical determination of these parameters is work in progress.

It is instructive to consider the variation levels of latently infected memory B-cells. To the best of our knowledge, this compartment is never regulated (Hochberg et al. 2004b). Due to the very low levels of viral protein expression, this stage has a very low overall antigenicity as compared to any other stage. Taking S_latent to be latently infected memory B-cells, we see that a low value for c_latent compared to other stages implies starvability since we then have $M_{j\text{latent}}<\frac{c_j}{c_{\text{latent}}}$.

The expression $S_j^{\ast }=\frac{b}{c_j}$, shows that the size of regulated populations depends on factors governing immune response, not on the flow of cells into that population. In particular, we can expect the size of the lytically infected B-cell population to show little or no correlation with the size of the latently infected memory B-cell population, while it might well be a correlate with immune factors such as HLA types.

The question arises whether to expect a correlation between $T_{\text{lytic}}^{\ast }$ and $S_{\text{latent}}^{\ast }$. Here the picture is not clear as the model's predictions depend on the reasons for the variation in $S_{\text{latent}}^{\ast }$. If high values of $S_{\text{latent}}^{\ast }$ are due to a high rate flow into this compartment from the infected germinal center population, then we would expect a positive correlation between $T_{\text{lytic}}^{\ast }$ and $S_{\text{latent}}^{\ast }$. If, on the other hand, high values of $S_{\text{latent}}^{\ast }$ are due to low rate of flow from the latently infected memory B-cell compartment into the lytically infected population, then we would expect a negative correlation between $T_{\text{lytic}}^{\ast }$ and $S_{\text{latent}}^{\ast }$.

In a different vein, from the point of view of the treatment of chronic infections, the characteristics of the immune response revealed by our model, in particular, the possibility of unregulated stages, give rise to speculation on the possible targets of such a treatment. Which stages would be most suitable drug targets, regulated or unregulated ones?

Finally, we would like to say a few words about some mathematical questions raised by this model. Our stability results are all local. We would conjecture that the unique asymptotically stable biologically meaningful infected fixed point is a global attractor for the positive orthant. This would follow from the existence of an appropriate Lyapunov function. However, we have not yet managed to find one.

We also conjecture that in the Lotka–Volterra case, the 2-plane that carries the Lotka–Volterra dynamics is an attractor, at least in a neighborhood of the fixed point. Our numerical investigations to date support this conjecture.

There are a number of generalizations of this model which deserve investigation. These include the supply of uninfected tissue, and immune cross-reactivity in which an immune response might target multiple stages.

One interesting generalization concerns the situation in which each stage may be regulated by an immune response to more than one epitope and in which each of these epitopes occurs in multiple variants. This question is addressed for single-stage pathogens in (Nowak et al. 1995). Indeed Nowak suggested (Martin A. Nowak, 2009, personal communication) that we examine this question for multi-stage pathogens and we have preliminary results in the case where only one stage exhibits this phenotype.

Appendix

Derivation of an expression for the characteristic polynomial of J (S, J)

Theorem 5

The characteristic polynomial of the Jacobian J (S, T) of system (**) is given by

$$P(\lambda )={(-1)}^n\prod _{j=0}^{n-1}\left((S_j-{\sigma }_j-\lambda )(b+\lambda )-S_j(-(a_j+f_j)+b)\right)-\prod _{j=0}^{n-1}({\rho }_j(b+\lambda -S_{j+1})).$$

Proof

The partial derivatives of the system are given by

$$\begin{array}{ccc}\frac{\partial F_k}{\partial S_j}=\{\hfill & r_{k-1}{f}_{k-1}\hfill & \text{if}j=k-1\hfill \\ -a_k-f_k-T_k\hfill & \text{if}j=k\hfill \\ 0\hfill & \text{otherwise}\hfill \\ \frac{\partial F_k}{\partial T_j}=\{\hfill & -S_k\hfill & \text{if}j=k\hfill \\ 0\hfill & \text{otherwise}\hfill \\ \frac{\partial G_k}{\partial S_j}=\{\hfill & T_k\hfill & \text{if}j=k\hfill \\ 0\hfill & \text{otherwise}\hfill \\ \frac{\partial G_k}{\partial T_j}=\{\hfill & S_k-b\hfill & \text{if}j=k\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}$$

Thus, we have

$$J(S,T)=\left(\begin{array}{cc}A& B\\ C& D\end{array}\right)$$

where A, B, C and D are the following n × n matrices

$$\begin{array}{l}A=\left(\begin{array}{lllll}\hfill -{\sigma }_0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill {\rho }_{n-1}\hfill \\ \hfill {\rho }_0\hfill & \hfill -{\sigma }_1\hfill & \hfill \ddots \hfill & & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \ddots \hfill & \hfill \ddots \hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill ⋮\hfill & & \hfill \ddots \hfill & \hfill \ddots \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill {\rho }_{n-2}\hfill & \hfill -{\sigma }_{n-1}\hfill \end{array}\right)\\ B=\left(\begin{array}{llll}\hfill -S_0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \ddots \hfill & & \hfill 0\hfill \\ \hfill ⋮\hfill & & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill -S_{n-1}\hfill \end{array}\right)\\ C=\left(\begin{array}{llll}\hfill T_0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \ddots \hfill & & \hfill 0\hfill \\ \hfill ⋮\hfill & & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill T_{n-1}\hfill \end{array}\right)\\ D=\left(\begin{array}{llll}\hfill S_0-b\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \ddots \hfill & & \hfill 0\hfill \\ \hfill ⋮\hfill & & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill S_{n-1}-b\hfill \end{array}\right)\end{array}$$

using the notation ρ_j = r_j f_j and σ_j = a_j + f_j + T_j. It is well known that a similarity transform does not modify the eigenvalues of a matrix. The similarity transform we use consists of the following operations: The first n columns of J (S, T) are transformed to

$$\left(\begin{array}{c}A\prime \\ C\prime \end{array}\right)=\left(\begin{array}{c}A\\ C\end{array}\right)-\left(\begin{array}{c}B\\ D\end{array}\right)$$

The resulting matrix

$$\left(\begin{array}{cc}A\prime & B\\ C\prime & D\end{array}\right)$$

undergoes the following row transformation

$$(\begin{array}{c}C″D\prime \end{array})=(C\prime D)+(A\prime B)$$

The resulting matrix

$$\left(\begin{array}{cc}A\prime & B\\ C″& D\prime \end{array}\right)$$

then undergoes the following column permutations

$$\left(\begin{array}{cc}B& A\prime \\ D\prime & C″\end{array}\right)$$

followed by row permutations

$$\left(\begin{array}{cc}D\prime & C″\\ B& A\prime \end{array}\right)$$

The similar matrix obtained satisfies

$$\begin{array}{l}A\prime =\left(\begin{array}{lllll}\hfill S_0-{\sigma }_0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill {\rho }_{n-1}\hfill \\ \hfill {\rho }_0\hfill & \hfill S_1-{\sigma }_1\hfill & \hfill \ddots \hfill & & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \ddots \hfill & \hfill \ddots \hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill ⋮\hfill & & \hfill \ddots \hfill & \hfill \ddots \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill {\rho }_{n-2}\hfill & \hfill S_{n-1}-{\sigma }_{n-1}\hfill \end{array}\right)\hfill \\ C″=\left(\begin{array}{lllll}\hfill T_0-{\sigma }_0+b\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill {\rho }_{n-1}\hfill \\ \hfill {\rho }_0\hfill & \hfill S_1-{\sigma }_1+b\hfill & \hfill \ddots \hfill & & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \ddots \hfill & \hfill \ddots \hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill ⋮\hfill & & \hfill \ddots \hfill & \hfill \ddots \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill {\rho }_{n-2}\hfill & \hfill T_{n-1}-{\sigma }_{n-1}+b\hfill \end{array}\right)\hfill \\ D\prime =\left(\begin{array}{llll}\hfill -b\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \ddots \hfill & & \hfill 0\hfill \\ \hfill ⋮\hfill & & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill -b\hfill \end{array}\right)\hfill \end{array}$$

Now we look at the eigenvalue equations of the transformed matrix

$$\left(\begin{array}{cc}\stackrel{\sim }{D\prime }& C″\\ B& \stackrel{\sim }{A\prime }\end{array}\right)≔\left(\begin{array}{cc}D\prime & C″\\ B& A\prime \end{array}\right)-\lambda I$$

where I is the 2n × 2n unity matrix. If we assume λ ≠ −b, the matrix

$$\stackrel{\sim }{D\prime }=\left(\begin{array}{llll}\hfill -(b+\lambda )\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \ddots \hfill & & \hfill 0\hfill \\ \hfill ⋮\hfill & & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill -(b+\lambda )\hfill \end{array}\right)$$

is invertible and we can use a well known formula for the determinant of block-partitioned matrices

$$\begin{array}{l}Q(\lambda )≔det\left(\begin{array}{cc}\stackrel{\sim }{D}\prime & C″\\ B& \stackrel{\sim }{A}\prime \end{array}\right)=det(\stackrel{\sim }{D}\prime )det(\stackrel{\sim }{A\prime }-B{\stackrel{\sim }{D\prime }}^{-1}C″)\\ ={(-1)}^n{(b+\lambda )}^n\\ \times det\left(\begin{array}{cccc}\hfill S_0-{\sigma }_0-\lambda -S_0\frac{(T_0-{\sigma }_0+b)}{b+\lambda }\hfill & \hfill 0\cdots & \hfill 0\hfill & \hfill {\rho }_{n-1}-\frac{S_0{\rho }_{n-1}}{b+\lambda }\hfill \\ \hfill {\rho }_0-\frac{S_1{\rho }_0}{b+\lambda }\hfill & \hfill \ddots \ddots & & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \ddots \ddots & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill ⋮\hfill & \hfill \ddots & \hfill \ddots \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \cdots 0& \hfill {\rho }_{n-2}-\frac{S_{n-1}{\rho }_{n-2}}{b+\lambda }\hfill & \hfill S_{n-1}-{\sigma }_{n-1}-\lambda -S_{n-1}\frac{(T_{n-1}-{\sigma }_{n-1}+b)}{b+\lambda }\hfill \end{array}\right)\end{array}$$

Laplace's theorem applied to the last column of the matrix yields for λ ∈ ℂ\{−b}

$$Q(\lambda )={(-1)}^n\left(\prod _{j=0}^{n-1}\left((S_j-{\sigma }_j-\lambda )(b+\lambda )-S_j(-(a_j+f_j)+b)\right)+{(-1)}^{n+1}\prod _{j=0}^{n-1}\left({\rho }_j(b+\lambda -S_{j+1})\right)\right)$$

Summarizing, we have obtained an expression Q(λ) that is equal to the characteristic polynomial P(λ) of J(S, T) for all λ ∈ ℂ\{−b}. If we drop the requirement λ ∈ ℂ\{−b}, Q is a polynomial on ℂ and thus a holomorphic function on ℂ. As a consequence, we have two holomorphic functions Q : ℂ → ℂ and P : ℂ → ℂ that are identical on the connected open subset ℂ\{−b}. By the well-known identity theorem for holomorphic functions, Q = P must hold.