Stabilization of the total force in multi-finger pressing tasks studied with the ‘inverse piano’ technique

Abstract

When one finger changes its force, other fingers of the hand can show unintended force changes in the same direction (enslaving) and in the opposite direction (error compensation). We tested a hypothesis that externally imposed changes in finger force predominantly lead to error compensation effects in other fingers thus stabilizing the total force. A novel device, the “inverse piano”, was used to impose controlled displacements to one of the fingers over different magnitudes and at different rates. Subjects (n =10) pressed with four fingers at a constant force level and then one of the fingers was unexpectedly raised. The subjects were instructed not to interfere with possible changes in the finger forces. Raising a finger caused an increase in its force and a drop in the force of the other three fingers. Overall, total force showed a small increase. Larger force drops were seen in neighbors of the raised finger (proximity effect). The results show that multi-finger force stabilizing synergies dominate during involuntary reactions to externally imposed finger force changes. Within the referent configuration hypothesis, the data suggest that the instruction “not to interfere” leads to adjustments of the referent coordinates of all the individual fingers.

Introduction

One of the central problems in motor control is the problem of motor redundancy (Bernstein 1967; Turvey 1990). This problem emerges when the number of variables at a selected level of analysis is higher than the number of constraints defined by the task such that an infinite number of solutions are possible. Recently, this problem has been addressed using the concept of a synergy as a neural organization of elemental variables that stabilizes a required value (or time profile) of a potentially important performance variable by co-varying adjustments of the elemental variables (Gelfand and Latash 1998; reviewed in Latash et al. 2002, 2007). A method of quantitative analysis of synergies has been developed within the framework of the uncontrolled manifold hypothesis (UCM hypothesis, Schöner 1995; Scholz and Schöner 1999). The UCM hypothesis assumes that the controller acts in a space of elemental variables, creates in that space a sub-space (UCM) corresponding to a desired value of a selected performance variable, and then tries to limit variability of the elemental variables within the UCM.

This general framework has been used to study multi-digit synergies in prehensile and pressing tasks (reviewed in Zatsiorsky and Latash 2008; Latash and Zatsiorsky 2009). Most of these studies (for a notable exception see Scholz et al. 2003) used analysis of co-variation of elemental variables (typically, forces and moments of force produced by individual digits) across trials to quantify synergies stabilizing such variables as the total force and total moment of force applied to an external object. In these analyses, elemental variables were measured at similar phases of actions across repetitive trials (or cycles, in cyclic tasks, Friedman et al. 2009) and two components of their variance were quantified: “Good” variance (variance within the UCM) that did not affect the performance variable, and “bad’ variance (variance orthogonal to the UCM) that did.

Note that in this context the word “stability” has a meaning of “low variability in sequential trials”, which is different from stability in a more direct sense as resistance to external perturbations. A recent study of multi-joint coordination has shown that high synergy indices with respect to a performance variable may be associated with poor stability when an external perturbation is applied (Gorniak et al. 2009).

In this study, we used a simple multi-finger constant force production task, smooth perturbations applied to one of the fingers, and an instruction “do not intervene voluntarily” (cf. Feldman 1966, 1986). Multi-finger synergies stabilizing total force have been documented in several studies with pressing tasks (Latash et al. 2001; Scholz et al. 2002; Shim et al. 2005), as well as with prehension tasks (Budgeon et al., 2008). Our first question was: Do synergies attenuate the effects of a perturbation applied to one of the fingers on the total force? We used an “inverse piano” apparatus to lift one of the fingers during the steady-state force production. Lifting a finger stretched the flexor muscles and was expected to lead to an increase in the pressing force due to the peripheral spring-like properties of the muscles and the action of the stretch reflex (Liddell and Sherrington 1924; Matthews 1959; Rack and Westbury 1969). We hypothesized that the three other fingers of the hand would show a force decrease such that the total force change will be smaller as compared to the force change of the lifted finger. Note that this prediction links multi-finger synergies to stability of the performance variable (total force) in a direct meaning of the word “stability”.

In an earlier study, we asked the subjects to produce a constant force level and then to tap with one of the fingers (Latash et al. 1998). When the tapping finger lost contact with the surface, its force dropped to zero. Other fingers of the hand showed an out-of-phase increase in their force such that the total force was nearly unaffected. In this experiment, we asked a question whether such error compensation could be observed in the absence of a voluntary action by the subject (under the “do-not-intervene” instruction). We hypothesized —this is our second hypothesis–that synergic mechanisms would act even if a change in force produced by one of the fingers is not produced by the subject voluntarily.

There is a well known mechanism of finger interaction that leads to positive co-variation of finger forces. It has been addressed as enslaving or lack of individuation (Schieber 1991; Kilbreath and Gandevia 1994; Zatsiorsky et al. 1998, 2000). When one finger increases its force, this mechanism is expected to lead to an increase in the forces produced by all other fingers. The increase depends on the proximity of the enslaved finger from the master finger: the closer the fingers the larger the enslaving (Zatsiorsky et al. 2000). Previous studies involving multi-finger force stabilizing synergies have not addressed whether or not a proximity effect existed. This study does investigate it. In our experiment, enslaving could be expected to lead to an increase in the forces of all four fingers, when one finger was lifted. We hypothesized, however, that synergic mechanisms that favor negative force co-variation would dominate such that total force is indeed stabilized (the 3^rd hypothesis).

To test the three main hypotheses, we used finger displacements of two magnitudes, performed at two rates, applied to each of the four fingers, and varied the initial pressing force between two levels. These manipulations were used to explore the generality of the findings and the dependence of the hypothesized synergic force adjustments on the magnitude of perturbation, possible transient force changes related to the speed of muscle stretch, and target finger.

Methods and Materials

Subjects

Ten male subjects participated in the experiment. The average age, weight, and height of the subjects were 26.6 ± 3.5 years, 74.7 ± 7.0 kg, and 177.9 ± 7.8 cm, respectively. All subjects were right-handed, in good health, and had no previous history of neuropathies or traumas to the upper limbs. None of the subjects had a history of long-term involvement in hand or finger activities such as professional typing or playing musical instruments. The subjects gave informed consent according to the procedures approved by the Institutional Review Board of the Pennsylvania State University.

Apparatus (the ‘inverse piano’ technique)

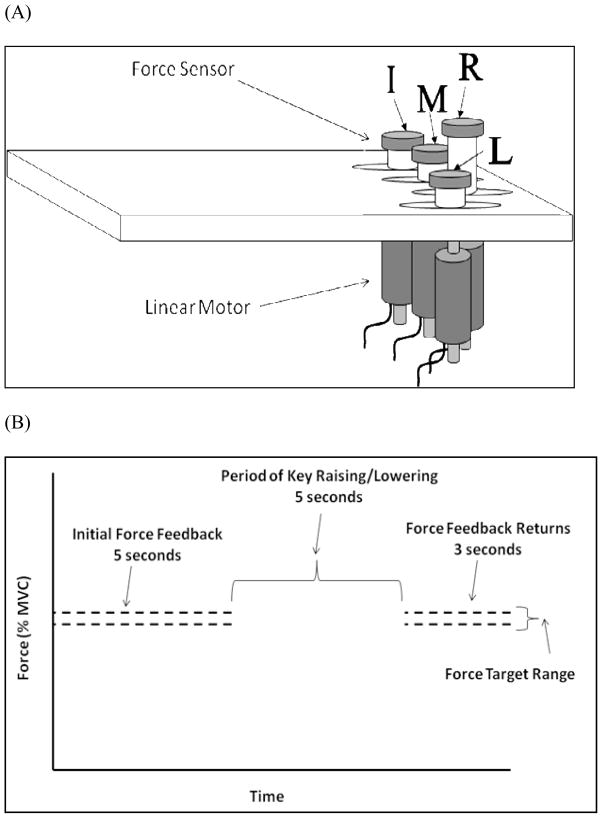
Four uni-directional piezoelectric sensors (208C02, PCB Piezotronics) were used for force measurement. The sensors were calibrated prior to data collection to ensure accuracy of data. The sensors were mounted on a steel frame, which was securely attached to the testing station. Sandpaper pads were attached to the face of the sensors to increase friction and to reduce the temperature effect from the skin. Sensors were spaced 30 mm apart in the direction of finger adduction-abduction. The position of the sensors could be adjusted in the finger longitudinal direction in a range of 75 mm to fit individual subject’s anatomy. A wooden support was made to support the wrist and forearm, as well as to ensure stable contact between the fingers and force sensors. A wooden block was placed under subject’s hand to promote stable hand configuration and avoid pronation/supination during pressing. Analog output signals from the sensors were connected to separate AC/DC conditioners (484B, PCB Piezotronics, Depew, NY, USA), then digitized using a 16-bit analog-digital converter (CA-1000, National Instruments, Austin, TX, USA), mounted on a microcomputer (Dimension 2400, Dell, Round Rock, TX, USA) that was utilized for control, acquisition, and processing of the data. Force sensors were connected to linear motors (PS01-23×80, Linmot, Spreitenbach, Switzerland) that raised and lowered the sensors (Fig. 1A). The motors were programmed using LabVIEW (LabVIEW Version 8.0, National Instruments) that sent commands to a controller (E400-AT, Linmot, Spreitenbach, Switzerland). Motors produced smooth vertical movements of the posts with the sensors (the ‘inverse piano’ technique).

Figure 1.

A. Schematic of force sensors mounted on linear motors. Linear motors produced motion of the force sensor in the vertical direction. The letters I, M, R, and L refer to the keys corresponding to the index, middle, ring and little fingers, respectively. In the schematic the key under the ring finger is raised. B. Illustration of feedback given to subjects. A target range (±5.0 % MVC) was given. The target was shown for the first 5 seconds, disappeared for the next 5 seconds during the key raising/lowering, and then returned for the last 3 seconds of the trial. C. Example force data from a single trial. Change in force was computed as the forces after the key was raised minus the background force before the key was raised. The background forces were the average finger forces 250 ms before the key was raised. D. Example full wave rectified EMG data from a single trial. EMG amplitude was averaged for 500 ms before key was raised and averaged from start of motor movement to cessation of key movement. The averages in these two windows were compared to see if there was a difference in muscle activity during key raising.

Surface electromyogram (EMG) was recorded from the flexor digitorum superficialis (FDS) during trials. EMG was collected to determine whether there was a change in muscle activity during key raising. The EMG data were collected with an amplifier (Burtec Octopus, AMT-8, Calgary, AB, Canada) connected to the same analog-digital converter as the force sensors. Electrodes were placed on the proximal, anterior region of the forearm. Subjects were asked to place their forearm on a table then perform repeated finger flexion while the experimenter palpated the forearm. The region in which the greatest amount of forearm muscle activity could be felt and observed was where the electrodes were positioned. Generally, it was slightly medial of the forearm midline and 5–7 cm distal of elbow. Skin was prepared with alcohol wipes to decrease electrical impedance. Electrodes were disposable and coated with an adhesive gel (A10041-60, Vermed, Bellows Falls, VT, USA). During experimental trials the EMG electrodes were only in contact with the skin and not in contact with any of the experimental equipment.

Experimental Procedure

During testing, subjects were seated facing the testing table with the right upper arm at approximately 45° shoulder abduction in the frontal plane, 45° shoulder flexion in the sagittal plane, and approximately 45° flexion of the elbow. The subjects participated in two measurement sessions. The goal of the first session was to measure maximal voluntary force of the individual fingers (MVC). Subjects were given a 5-s window to press with an instructed finger to achieve maximal force and maintain it for approximately 1 s. The peak force was taken as the MVC value. MVC trials were performed two times for each finger and the higher of the two was used for scaling forces in the experimental trials.

The task given to the subjects was to naturally press with all four fingers on the force sensors and match a target force given on the computer screen. The target force was scaled to the MVC of the finger to be raised and presented as a double line on the screen representing ± 5.0 % of the target force. The subjects were told that the target force represented the sum of the force of all four fingers. This deception was used so that subjects always press with the same natural sharing pattern (Martin et al., 2009). Subjects were told at the end of the experiment of this trick with the feedback and none were aware that the feedback was on one finger’s force, not all combined force of the four fingers. Trials were also visually inspected to ensure that the sharing pattern was consistent across trials, within subjects. After the first 5 seconds the force feedback was removed and one of the force sensors was raised. The beginning of key upward movement occurred 1 second after feedback was removed. Subjects were aware that a key would be raised but did not know which key it would be. The motor maintained its raised position for 2 seconds and then returned to its original height (Fig. 1B). Force feedback then returned for the remaining 3 seconds of the trial. Subjects were instructed to return to the force target when it re-appeared. Generally, small deviations of the total force of four fingers occurred during the interval of no feedback. These deviations decreased in magnitude with practice.

The instruction given to subjects was once the sensor began to rise “don’t pay attention to changes in finger forces rather maintain same commands sent to fingers prior to the perturbation” and more simply “do not intervene voluntarily”. This instruction may be verbally confusing to some subjects, however, after performance of several trials in which this command is given it tends to become very clear to the subjects. Many subjects, actually said phrases such as “now I understand” after they performed several practice trials. The “do not intervene voluntarily” command has been successfully used with previous experiments in which subjects were not supposed to voluntarily respond to a perturbation. Once the motor stopped its movement the subjects were told to maintain the current finger forces for the remainder of the trial. Subjects were given a short practice session to familiarize themselves with this instruction.

The final vertical displacement of key raised, speed of key raising, initial pressing force, and finger raised were the experimental variables. Two levels of final vertical displacement (1 cm and 2 cm), speed (1 cm/s and 3 cm/s), and initial target pressing force (5 % MVC and 20 % MVC) were used. There were four levels of finger raised (I, M, R, L). Each subject performed a total of 64 trials: 2 height levels × 2 speed levels × 2 target force levels × 4 fingers (I, M, R, L) × 2 trials of each condition = 64 trials. The trials were randomly ordered. If it appeared that the subject did not follow the instructions the trial was repeated. The forces of all the fingers during the trials were visible to the experimenter and thus any unusual pressing pattern, removal of fingers from force transducers, or lack of force increase by the raised finger were immediately detected. Subjects were given a one-minute rest after each of the MVC trials, a five minute rest following the MVC measuring session, and another five minute rest after completion of the first 32 key raising trials. These were given to ensure that fatigue did not affect performance.

Data Processing

A custom LabVIEW program (LabVIEW Version 8.0, National Instruments) was used to collect the force signals and display feedback to subjects. The same program was used to control the motors producing key movements to ensure that the force data was synchronized with the position of the keys. Force data were collected at a frequency of 300 Hz. The force data were digitally filtered using a 4^th order low-pass two-way Butterworth filter at 10 Hz using Matlab (Version R2006a, The Mathworks, Inc). The EMG data were collected at a frequency of 1000 Hz and filtered using a 4^th order low-pass two-way Butterworth filter at 300 Hz. All trials were visually inspected to verify that subjects followed the instructions. A criterion for an acceptable trial was the following: (1) the raised finger increased its force in a smooth manner and (2) it maintained the new force level, with no sudden drop in force and minimal downward drift, until the motor was lowered.

Data Analysis

The data of interest were the change in finger forces during the key raising. The change in finger force was defined as the difference between finger forces at the end of motor movement (to the raised position) minus the background force at the beginning. The forces after the finger was raised were taken as the average finger forces immediately when the key stopped the raising movement to 250 ms afterwards. The background force was computed as the average force 250 ms prior to the initiation of motor movement. For each trial the force changes were calculated for all four fingers. The finger force changes were computed in terms of magnitude of force change and percent MVC of a given finger. The force changes were then analyzed in several ways. First, for each combination of displacement, MVC, and speed the data were averaged across subjects. Averaging was not performed across fingers. Standard errors of the averages were computed.

Generally, all of the non-raised fingers showed a decrease in force. Therefore, another measure, which will be denoted ‘% compensation’, was computed. This quantity represents how much of the total force increase due to the force change of the raised finger was “compensated” for by the other fingers. The % compensation was calculated as: 100*(Δ f_raised − Σ Δ f_non-raised)/Δ f_raised. The EMG data was full wave rectified then averaged over two time periods and the average amplitude during these time periods was computed. The first time period was from 500 ms prior to initiation of key movement to initiation of key movement. The second time period was from initiation of key movement to the cessation of key movement. Exemplary data is shown in Figure 1D.

The average force change of fingers as a function of proximity to the raised finger was computed. The finger(s) adjacent to the raised finger were assigned a proximity of 1. Note: when M- and R-fingers were raised, there were two adjacent fingers. Fingers two and three digits away from the raised finger were assigned proximity values of 2 and 3, respectively.

Statistical Analysis

A four-way mixed effects MANOVA was performed to test for the effects of INITIAL FORCE (2 levels: 5% and 20%), DISPLACEMENT (2 levels: 1 cm and 2 cm), SPEED (2 levels: 1 cm/s and 3 cm/s), and FINGER (4 levels: I, M, R, and L). The responses tested were change in raised finger force, in terms of both N and % MVC, change in total non-raised finger force, change in total force (sum of individual finger force changes), and the % compensated values for each trial. A paired t-test was used to evaluate the difference in average EMG amplitude before and during key movement. To check whether proximity effects were significant, the proximity levels were quantified as corresponding to whether the finger was 1, 2, or 3 fingers away from the raised finger. Then, a one-way ANOVA with three levels of proximity was applied. The response was the change in force of the non-raised finger. Statistical analysis was performed using the statistical software Minitab 13.0 (Minitab, Inc., State College, PA, USA) and SPSS (SPSS Inc., Chicago, IL, USA). The data was tested for sphericity. No statistically significant deviation from sphericity was found. All statistical analysis was performed at a significance level of α = 0.05.

Passive Mechanical Effects of Lifting a Finger

To examine the effects of passively raising a finger one subject was asked to complete an additional set of experimental trials. The subject was instructed to rest their hand on the force sensors, close the eyes and keep their hand/forearm muscles as relaxed as possible. Each finger was then raised, using the IP, for all combinations of displacements and speeds used in the experiment. One trial of each condition was recorded. The force data were processed exactly the same as the data from the experimental trials.

Results

The results will be divided into two sections. The first section will focus on the force change in raised finger. The second section will address the finger interaction.

Force Changes in Raised Fingers

In all trials the force exerted by the raised finger increased. The changes were from 1.39 ± 0.13 N (R-finger, INITIAL FORCE 5% of MVC, DISPLACEMENT 1.0 cm, SPEED 1.0 cm/s) to 8.00 ± 1.00 N (L-finger, INITIAL FORCE 20% of MVC, DISPLACEMENT 2.0 cm, SPEED 3.0 cm/s). In percent of the MVC, the changes ranged from 4.66 ± 0.38 % (I-finger, INITIAL FORCE 5% of MVC, DISPLACEMENT 1.0 cm, SPEED 1.0 cm/s) to 31.88 ± 2.19 % (L-finger, INITIAL FORCE 20% of MVC, DISPLACEMENT 2.0 cm, SPEED 3.0 cm/s). All the main effects, with the exception of the SPEED effect on the FORCE and % of the MVC changes were statistically significant. The differences in the increases between the slow and fast speeds were the smallest of the three factors investigated. Of all the factors the INITIAL FORCE factor produced the largest difference between the two levels. Individual fingers were affected differently by the perturbations. I- finger showed the smallest % MVC change (on average around 7.5 % of its MVC) followed by R-, M-, and L-fingers (21%). ANOVA results are presented in Table 1. The interaction effects of the factors were non-significant in all cases.

Table 1.

Mixed Effects MANOVA results. P-values are given. Statistically significant values are boldfaced. Note all interactions were insignificant.

Factor	Responses
	Force	% MVC
INITIAL FORCE	0.001	0.019
DISPLACEMENT	0.004	0.042
SPEED	0.118	0.313
FINGER	0.008	0.022
INITIAL FORCE×DISPLACEMENT	0.193	0.363
INITIAL FORCE×SPEED	0.931	0.682
INITIAL FORCE×FINGER	0.065	0.321
DISPLACEMENT×SPEED	0.937	0.480
DISPLACEMENT×FINGER	0.470	0.533
SPEED×FINGER	0.792	0.893
INITIAL FORCE×DISPLACEMENT×SPEED	0.821	0.432
INITIAL FORCE×DISPLACEMENT×FINGER	0.551	0.738
INITIAL FORCE×SPEED×FINGER	0.890	0.898
DISPLACEMENT×SPEED×FINGER	0.885	0.622

EMG change

There was no significant difference in muscle activity during and before the key movement. Over 90 % of the trials resulted in the EMG difference in the range between −0.01 and 0.01 mV. The data appear to be normally distributed about zero. Furthermore, the p-value from the paired t-test on the difference between EMG amplitude before and during key upward movement was non-significant (p > 0.17).

Finger Interaction and Compensation

The results presented below address three questions: (a) the type of interaction – enslaving or compensation, (b) effect of a single-finger perturbation on the total force of all fingers, and (c) were the proximity effects observed?

Enslaving or compensation?

In all trials the forces of the non-raised fingers decreased. Hence, synergic mechanisms favoring negative force co-variation dominated over possible finger enslaving. The force changes ranged from −9.12 ± 1.49 N (L-finger, INITIAL FORCE 20% of MVC, DISPLACEMENT 2.0 cm, SPEED 1.0 cm/s) to −0.29 ± 0.10 N (I-finger, INITIAL FORCE 5% of MVC, DISPLACEMENT 1.0 cm, SPEED 1.0 cm/s). On a finger by finger comparison, the higher INITIAL FORCE level always produced a larger decrease in the total force of the non-raised fingers. For all other factors (FINGER, INITIAL FORCE, SPEED) being equal, the larger DISPLACEMENT level also always resulted in a larger decrease in the force of non-raised fingers. SPEED did not have a significant effect on the non-raised finger forces (p > 0.52). The raised finger, non-raised finger and total force changes are given in Table 2A.

Table 2.

A.The force changes in raised and non-raised fingers. Mean values were computed across subjects (± standard error). Units of force are newtons (N). B. Mixed effects MANOVA results on the effect of finger perturbation on the force changes of all fingers. P-values are given. Statistically significant values are boldfaced.

(A)
FINGER RAISED	INITIAL MVC (% MVC)	DISPLACEMENT (cm)	SPEED (cm/s)	RAISED ΔF (N)	NON- RAISED ΔF (N)	TOTAL ΔF (N)
I	5	1	1	1.83 ± 0.18	−0.29 ± 0.10	1.55 ± 0.20
			3	2.25 ± 0.14	−0.58 ± 0.08	1.67 ± 0.13
		2	1	2.79 ± 0.32	−0.87 ± 0.19	1.91 ± 0.35
			3	2.91 ± 0.29	−0.50 ± 0.17	2.41 ± 0.23
M	5	1	1	2.25 ± 0.31	−0.70 ± 0.19	1.55 ± 0.31
			3	2.87 ± 0.20	−0.56 ± 0.08	2.30 ± 0.21
		2	1	3.27 ± 0.31	−1.07 ± 0.29	2.19 ± 0.39
			3	4.09 ± 0.35	−0.67 ± 0.21	3.42 ± 0.27
R	5	1	1	1.33 ± 0.14	−0.30 ± 0.07	1.03 ± 0.18
			3	1.60 ± 0.16	−0.46 ± 0.10	1.14 ± 0.20
		2	1	2.47 ± 0.24	−0.66 ± 0.23	1.81 ± 0.27
			3	2.62 ± 0.20	−0.80 ± 0.17	1.83 ± 0.28
L	5	1	1	2.56 ± 0.30	−0.75 ± 0.18	1.80 ± 0.28
			3	2.57 ± 0.25	−0.94 ± 0.27	1.62 ± 0.36
		2	1	3.58 ± 0.41	−1.16 ± 0.28	2.42 ± 0.31
			3	3.95 ± 0.50	−1.35 ± 0.27	2.59 ± 0.43
I	20	1	1	2.88 ± 0.28	−1.63 ± 0.31	1.25 ±0.52
			3	2.31 ± 0.34	−1.48 ± 0.27	0.83 ± 0.45
		2	1	3.99 ± 0.51	−3.80 ± 0.47	0.19 ± 0.67
			3	4.96 ± 0.65	−3.34 ± 0.36	1.62 ± 0.65
M	20	1	1	4.18 ± 0.50	−2.16 ± 0.36	2.03 ±0.46
			3	5.02 ± 0.40	−2.06 ± 0.25	2.96 ± 0.49
		2	1	4.90 ± 0.67	−4.86 ± 0.90	0.04 ± 0.89
			3	5.72 ± 0.52	−3.35 ± 0.42	2.37 ± 0.42
R	20	1	1	2.31 ± 0.50	−2.36 ± 0.26	−0.05 ± 0.48
			3	3.30 ± 0.29	−1.92 ± 0.21	1.39 ± 0.33
		2	1	3.80 ± 0.56	−3.43 ± 0.95	0.36 ± 0.78
			3	4.71 ± 0.54	−3.70 ± 0.58	1.00 ± 0.55
L	20	1	1	4.98 ± 0.66	−2.81 ± 0.82	−1.20 ± 0.77
			3	5.67 ± 0.68	−2.18 ± 0.54	3.49 ± 0.52
		2	1	7.75 ± 1.11	−9.12 ± 1.49	−1.37 ± 0.60
			3	7.09 ± 1.11	−7.77 ± 1.66	−0.68 ± 0.68

(B)
Factor	Non-Raised Fingers	Total Force Change (N)	% Compensation
INITIAL FORCE	0.000	0.041	0.007
DISPLACEMENT	0.002	0.845	0.124
SPEED	0.139	0.065	0.114
FINGER	0.012	0.255	0.594

Effects on the total force

The total force change, in terms of force (N), during key raising was positive in all but four cases. This means that the compensation was not complete: while all of the non-raised fingers showed a negative change in force this force drop was not sufficient to fully compensate for the force increase in the perturbed finger. Three of the four cases in which the total force change was negative occurred when the L-finger was raised and the INITIAL MVC was 20%. The other case occurred when the R-finger was raised and the initial MVC was 20%. The total force change was the greatest when the M-finger was raised (the worst compensation). There was no clear difference between the levels of displacement (Table 2B).

Proximity effects

The proximity effect was found to be significant (p<0.005, F = 5.40), see Fig. 2. The general trend was that, as distance from the raised finger increased, the absolute magnitude of negative force change (in newtons) decreased.

Figure 2.

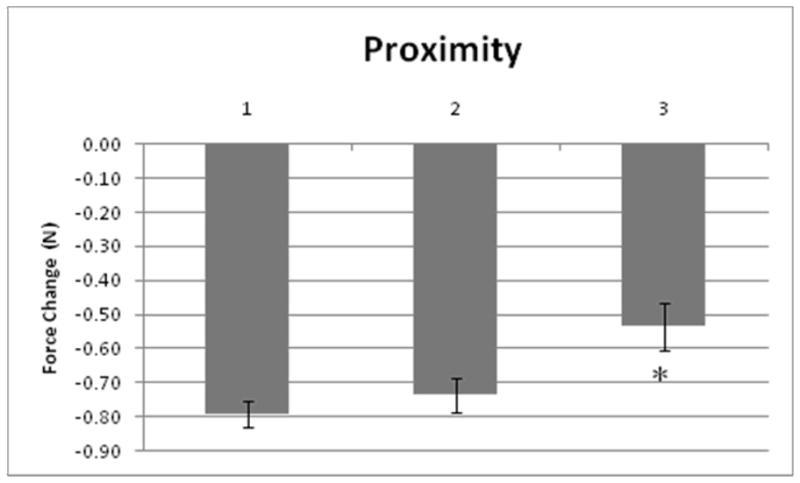
The effect of a non-raised finger location with respect to the raised finger (‘proximity’) on the force change (‘compensation’). The proximity values of 1, 2, and 3 refer to the distance of non-raised finger in relation to the raised finger. Values were averaged across all trials. Error bars are standard error.

Passive Mechanical Effects of Lifting a Finger

The passive mechanical effects (i.e. force changes) of lifting a finger on the non-raised fingers were found to be minimal (Table 3). The largest negative force change was −0.21 N and many non-raised fingers showed a positive force change. This data provides evidence that force changes during experimental trials were not due to passive mechanical mechanisms.

Table 3.

Force changes in fingers during passive lifting

Finger	Displacement (cm)	Speed (cm/s)	Change in Finger Forces (N)
			I	M	R	L
1	1	1	2.29	0.08	−0.10	−0.01
1	1	3	3.47	−0.08	−0.21	−0.04
1	2	1	2.09	0.06	−0.02	−0.03
1	2	3	3.52	−0.11	0.04	−0.17
2	1	1	0.19	1.21	0.11	−0.04
2	1	3	0.07	1.91	0.12	0.04
2	2	1	0.20	0.95	0.05	−0.01
2	2	3	0.07	2.19	−0.12	0.07
3	1	1	0.16	0.24	0.70	−0.01
3	1	3	0.08	0.28	1.11	−0.06
3	2	1	0.07	0.41	0.62	0.05
3	2	3	−0.05	0.54	1.56	0.07
4	1	1	0.05	−0.02	0.06	1.13
4	1	3	0.22	−0.09	−0.12	2.45
4	2	1	0.14	0.04	0.03	1.13
4	2	3	−0.02	−0.10	−0.16	1.80

Discussion

The experiment produced two main results, reproducible across subjects, which supported the three main hypotheses formulated in the introduction. In summary, these results showed that finger force adjustments during lifting of one of the fingers were dominated by synergic effects, not enslaving effects. These adjustments reduced the effects of the force change of the raised finger on total force, which may be interpreted as stabilization of the total force. We observed no signs of voluntary intervention by the subjects and hence interpret the data as resulting from involuntary synergic adjustments of finger forces.

The first result was that the raised finger always showed an increase in force, as expected. The effect depended on the initial force level, magnitude of finger displacement, and varied across the four fingers. The effect of speed was non-significant for the force changes (in N and % MVC).

The second result was that the non-raised fingers showed a decrease in force. The force decrease partially compensated for the increase in force of the raised finger such that the total force change was diminished. A strong proximity effect was observed: Fingers closer to the raised finger showed larger force adjustments as compared to relatively distant fingers. The following discussion will address implications of the findings for phenomena of finger interaction and features of synergic control.

Force Changes in Raised Fingers

The increase of force of the raised finger appears to be primarily due to peripheral (muscle and tendon) properties. Because the perturbations were applied to active muscles the reactions can barely be called ‘passive’ but it seems that the force increase was not induced by increased efferent stimulation to activation of the muscles. The main evidence for the increase in the force being due to ‘passive’ mechanisms is that no significant change in EMG was observed during finger perturbation and the associated force increase. We have to admit, however, that the EMG of only one muscle was recorded and the activity of the intrinsic hand muscles was not registered. It is quite likely that surface EMG is not sensitive enough for our purposes. Although we did not observe any change in the EMG of FDS during finger raising there may have been slight changes, or very significant changes in other muscles serving the fingers. This should be considered a delimitation limitation of the present study. The ‘passive’ nature of the force rise (in the sense that the level of activation was not substantially changed) does not contradict experimental facts that the amount of force increase depended on the initial force level, magnitude of finger displacement and to a smaller degree on the speed of finger displacement. Both the initial force and displacement magnitude affect the resistance of the muscle-tendon complexes to stretching: with the larger initial force and increased magnitude of displacement the resistance to stretching should increase.

Finger Interaction, Compensation, and Proximity Effect

The hypothesis that a force stabilizing synergy would emerge was supported. The non-raised fingers compensation was typically between 50 and 70 % of the increase in force of the raised finger. The provisional explanation that we offer is that during multi-finger pressing tasks a synergy is established and—in spite of the instruction ‘do not intervene’—the central controller is acting to stabilize the total output by compensating the immediate effect of perturbation to one finger by adjusting forces of other fingers. Such error compensation is the most prominent feature of the synergies (Latash, 2008).

The error compensation has been documented in several studies in which a finger was perturbed during multi-finger pressing. Types of perturbations that were previously used were finger-tapping (Latash et al., 1998), finger addition/removal (Li S. et al., 2003) and finger fatigue (Kruger et al., 2007). All of these studies found that the non-perturbed fingers compensated for the induced change in the total force to a higher degree than the non-raised fingers in this study, in some cases the compensation was 100 %. This may be due to the fact that in these studies the perturbations were induced by the subjects while in this study the perturbation came from an extrinsic source. Perhaps, this signifies an anticipatory component of error compensation, in which the CNS is able to “pre-plan” how it will adjust for an expected perturbation and as a result the % compensation is greater. The inter-finger error compensation was also observed in the prehension studies where the local and synergic effects to the perturbation have been reported (Zatsiorsky et al., 2006; Budgeon et al., 2008).

The effect of proximity of non-perturbed fingers to perturbed finger in previous enslaving studies (Zatsiorsky et al., 1998, 2000) has been found to be highly significant. The findings from this study agree with the aforementioned in the sense that fingers closer to the perturbed finger showed a greater force change; however, in this study the fingers in closer proximity showed a larger negative change. This result was unexpected and may be explained by one of two possibilities. The first is that non-raised finger’s force changes were purely compensatory and there was minimal enslaving between fingers. Had enslaving been involved in the finger interaction then it would have been expected that neighboring non-raised fingers to the raised finger would have displayed smaller negative force changes, or even positive force changes.

The second cause may be that raising a finger induced a mechanical effect on the entire hand, which was more pronounced in the neighboring fingers due to stronger peripheral connections to the raised finger. The data collected from the single subject contradicts this notion. The largest negative force change (−0.21 N) was substantially smaller than the average negative force changes observed during the experimental trials. Also, many of the non-raised fingers showed a positive increase in force, which may suggest that the total force stabilizing synergy was even stronger than originally thought.

Synergies and stability of performance

What do synergies do? In the original experiments within the UCM hypothesis framework (Scholz and Schöner 1999; Scholz et al. 2000; Latash et al. 2001), it was assumed that the main purpose of synergies was to reduce variability of an important performance variable by co-varying the inherently noisy outputs of the elements. However, later studies have shown that, during multi-finger tasks, each finger shows a large increase in the variance of its force (as compared to single-finger tasks), and the co-variation among the finger forces brings the total force variance down to values comparable to those observed in one-finger experiments (Shapkova et al. 2008; Gorniak et al. 2008). An alternative hypothesis has been suggested that synergies allow performing several tasks (ensuring low variability of several performance variables) simultaneously with the same set of elements without a negative interference among the tasks (Zhang et al. 2009; Gera et al. 2010; cf. the principle of superposition, Arimoto et al. 2001; Zatsiorsky et al. 2004). In other words, synergies allow to hold a glass of water and simultaneously point with the index finger of the same hand at a target without spilling the contents of the glass.

Our study addresses a basic feature of the notion of synergies: their relationship to stability of motor performance. The data suggest that multi-finger interaction may be directly related to stabilizing a performance variable, that is, to attenuating effects of perturbations applied to one of the elements (and, as a result, to the performance variable). Furthermore, the result that error compensation was observed rather than enslaving also agrees with this concept.

In a study by Gorniak et al. (2009), the subjects were asked to transport a brick-shaped, very light object held between the two palms and to transport an imaginary object to the same target location. Multi-joint synergies stabilizing the distance between the two midpoints of the palms were computed. They were higher during imaginary object transport. However, when, in some trials, an unexpected transient perturbation was applied to one of the hands, the other hand showed a very quick adjustment in the trials with the real object; these adjustments stabilized the distance between the hands and prevented the object from falling. No such adjustments were seen in the trials with an imaginary object. These results show that low variability in a performance variable ensured by a synergy does not necessarily provide stability of that performance variable if a perturbation takes place. Our results carry a different message: Lifting a finger perturbed the force it produced, but the force adjustments in other fingers attenuated the effects of this change on the total force.

There may be several reasons for the different results of this study and the study by Gorniak and her colleagues. Unlike the study of Gorniak, in our experiments, the perturbations were smooth and the system had ample time to produce corrective force adjustments. Our study did not involve manipulation of imaginary objects. The object of study (the fingers of the hand), the task (force production), and the instruction (do not intervene) differed from those in the two-hand object transport study. At this time, we cannot answer the question, which of the mentioned factors brought about the difference in the results.

Synergic reactions in voluntary and involuntary actions

Earlier studies of motor synergies explored co-variation of elemental variables across trials to quantify the relative amount of “good” variance in the total amount of variance (reviewed in Latash et al., 2007; Latash 2008). In those studies, the subjects were instructed to perform certain actions, and analyses of variance were run at comparable phases across trials. The current study shows that synergic adjustments of elemental variables are typical not only of voluntary actions but also of reactions to perturbations under the instruction to the subject not to intervene.

The instruction “do-not-intervene” used in our study had also been used in several studies within the equilibrium-point hypothesis of motor control (Feldman, 1966; Latash, 1994). Based on those studies, we have assumed that the reactions to finger lifting were compatible with an unchanged motor command that may be associated with setting a referent value for a salient variable that translated into a required constant total force in the initial state (Feldman and Levin, 1995; Pilon et al., 2007). As suggested in a recent study, multi-digit synergies may be produced by this pattern of control (Latash et al., 2010). When one finger was lifted, its actual coordinate was taken further away from the presumably unchanged referent coordinate resulting in an increase in that finger’s force. The observed changes in other (motionless) finger forces suggest that their referent coordinates changed as well, despite the instruction “not to intervene”, moving closer to the actual coordinates of the fingertips.

The results suggest that, despite the instruction, there were adjustments in the referent coordinates for the fingers, possibly mediated by sensory receptors (cf. Johansson and Westling, 1984). This suggests that referent coordinates are not set by the controller but emerge given values of (unidentified) neural control variables and sensory information about the actual body configuration (Feldman and Levin, 1995). Lastly, we would like to acknowledge that we strongly believe our observed results were due to a force-stabilizing synergy; but we do not dismiss the fact that passive mechanisms where undoubtedly intimately coupled with this synergy. Now the challenge for us is to better design experimental protocols, which will shed light onto the relative contribution of each.