Effect of gradient pulse duration on MRI estimation of the diffusional kurtosis for a two-compartment exchange model

Abstract

Hardware constraints typically require the use of extended gradient pulse durations for clinical applications of diffusion-weighted magnetic resonance imaging (DW-MRI), which can potentially influence the estimation of diffusion metrics. Prior studies have examined this effect for the apparent diffusion coefficient. This study employs a two-compartment exchange model in order to assess the gradient pulse duration sensitivity of the apparent diffusional kurtosis (ADK), a quantitative index of diffusional non-Gaussianity. An analytic expression is derived and numerically evaluated for parameter ranges relevant to DW-MRI of brain. It is found that the ADK differs from the true diffusional kurtosis by at most a few percent. This suggests that ADK estimates for brain may be robust with respect to changes in pulse gradient duration.

1. Introduction

Because of the limited gradient strengths available on human scanners, clinical applications of diffusion-weighted magnetic resonance imaging (DW-MRI) typically require the use of extended pulse durations for the diffusion-sensitizing gradients in order to obtain a sufficient degree of diffusion weighting [1]. As a consequence, apparent diffusion coefficient (ADC) estimates derived from clinical DW-MRI data may differ, in principle, from their ideal values as would be obtained in the narrow pulse limit. For closed geometries with impenetrable barriers, it has indeed been demonstrated that the diffusion-weighted NMR signal can be highly sensitive to the pulse duration [2]. However, for the more open geometries relevant to biological tissues, the effect of gradient pulse duration on ADC estimates is believed to be generally modest [3], supporting a view that clinical diffusivity maps are reasonably robust with respect to pulse duration changes.

Recently, it has been shown that the diffusional kurtosis, a measure of diffusional non-Gaussianity, can also be estimated with clinical DW-MRI [4–7]. Preliminary studies suggest that the diffusional kurtosis holds promise as a metric for characterizing neural tissue microstructure [8–12] and for studying pathologies such as tumors [13,14], ischemic stroke [15] and attention-deficit disorder [16]. Just as for the ADC, the apparent diffusional kurtosis (ADK) obtained with DW-MRI can potentially depend on the gradient pulse duration. Although one experiment has found the ADK in rat thalamus to be robust with respect to pulse duration changes [17], the pulse duration sensitivity of the ADK has not been previously addressed theoretically. In this article, we investigate the effect of pulse duration for a specific diffusion model that permits analytic solution.

The model we consider is the two-compartment version of the exchange model first proposed by Kärger and coworkers [18,19]. Although highly idealized, the Kärger model (KM) captures essential qualitative features of water diffusion in biological tissues, where the compartments plausibly represent intra- and extra-cellular spaces with differing compartmental diffusivities [20–23]. The exchange between compartments occurs via diffusion across the cell membranes. When the membrane permeability is sufficiently low, this transport can be accurately characterized by an exchange rate. Modifications of the KM have also been proposed [24,25] in order to better describe diffusion in certain types of tissues.

One special property of the KM is that the ADC is independent of the pulse duration, but this is largely consistent with empirical observations for water diffusion in brain [17]. The ADK for the KM does, in contrast, depend on the pulse duration, as we shall show explicitly for the case of two compartments. The magnitude of this dependence provides an indicator of the robustness of the ADK with respect to changes in gradient pulse duration and of how much the ADK may deviate from the true diffusional kurtosis.

2. Theory

2.1. Apparent diffusion metrics

The diffusion coefficient in a particular direction may be defined by

$$D(T)\equiv \frac{1}{2T}\langle x^2(T)\rangle ,$$ (1)

where x(T) is the net displacement of a diffusing spin over a time interval T and the angle brackets signify an averaging over all the spins within a region of interest (e.g., a voxel).

For pulsed gradient DW-MRI, the ADC measured with a signal readout time TE corresponds to

$$D_{\text{app}}\equiv \frac{{\gamma }^2}{2b}\underset{0}{\overset{\text{TE}}{\int }}{dt}_2\underset{0}{\overset{\text{TE}}{\int }}{dt}_1\sigma (t_1)\sigma (t_2)g(t_1)g(t_2)\langle x(t_1)x(t_2)\rangle ,$$ (2)

where g(t) gives the time dependence for the diffusion-sensitizing gradient pulse, b is the so-called b-value, σ (t) is the spin flip function, and γ is the gyromagnetic ratio for the spins [4]. In Eq. (2), we assume that the initial radiofrequency excitation occurs at a time t₀ = 0 and that x(t) represents, as in Eq. (1), the net displacement over a time interval t.

The b-value is given explicitly by

$$b\equiv 2{\gamma }^2\underset{0}{\overset{\text{TE}}{\int }}{dt}_2\underset{0}{\overset{t_2}{\int }}{dt}_1\sigma (t_1)\sigma (t_2)g(t_1)g(t_2)t_1,$$ (3)

while the spin flip function has unit magnitude and changes sign at times corresponding to any 180° radio frequency inversion pulses [26]. For the sake of simplicity, we have taken the gradients to be unidirectional and aligned with the diffusion direction of interest. The condition that the NMR signal be refocused requires that

$$0=\underset{0}{\overset{\text{TE}}{\int }}dt\sigma (t)g(t).$$ (4)

Note that Eqs. (2)–(3) imply that the ADC, as we have defined it, depends of the gradient time dependence but not on its strength (i.e., the ADC is invariant with respect to a rescaling of g). This definition of the ADC corresponds to minus the initial slope for the natural logarithm of NMR signal amplitude as a function of the b-value.

For the classic Stejskal-Tanner pulse sequence [27,28], the gradient pulse takes the form

$$\sigma (t)g(t)=g_0[H(t-\mathrm{\Delta })-H(\delta -t)],$$ (5)

for 0 ≤ t ≤ Δ +δ and with H (t) being the Heaviside step function (outside this interval the gradient pulse vanishes). The gradient amplitude is parameterized by g₀, the pulse duration is δ, and the diffusion time is Δ. Consistency requires that Δ ≥ δ.

By applying Eq. (5) to Eq. (3) and setting TE = Δ +δ, one may readily verify the familiar expression

$$b={(\gamma g_0\delta )}^2(\mathrm{\Delta }-\delta /3).$$ (6)

Moreover, one can show

$$\underset{\delta \to 0}{lim}{D}_{\text{app}}(\mathrm{\Delta },\delta )=D(\mathrm{\Delta }),$$ (7)

so that the ADC approaches the true diffusion coefficient in the narrow pulse limit.

The diffusional kurtosis is defined by [4,6]

$$K(T)\equiv \frac{\langle x^4(T)\rangle }{{\langle x^2(T)\rangle }^2}-3.$$ (8)

For Gaussian diffusion, K(T) vanishes and, more generally, it provides a dimensionless index of diffusional non-Gaussianity.

The ADK determined from DW-MRI data is given by [4]

$$K_{\text{app}}\equiv \frac{{\gamma }^4}{{(2b{D}_{\text{app}})}^2}\underset{0}{\overset{\text{TE}}{\int }}{dt}_4\underset{0}{\overset{\text{TE}}{\int }}{dt}_3\underset{0}{\overset{\text{TE}}{\int }}{dt}_2\underset{0}{\overset{\text{TE}}{\int }}{dt}_1\sigma (t_1)\sigma (t_2)\sigma (t_3)\sigma (t_4)g(t_1)g(t_2)g(t_3)g(t_4)\times [\langle x(t_1)x(t_2)x(t_3)x(t_4)\rangle -3\langle x(t_1)x(t_2)\rangle \langle x(t_3)x(t_4)\rangle ].$$ (9)

In analogy with Eq. (7), we have, for the Stejskal-Tanner pulse sequence, the narrow pulse limit

$$\underset{\delta \to 0}{lim}{K}_{\text{app}}(\mathrm{\Delta },\delta )=K(\mathrm{\Delta }).$$ (10)

As for the ADC, the ADK as defined by Eq. (9) is independent of the gradient strength.

2.2. Kärger model

The general KM is characterized by N compartments with intrinsic diffusivities D_i and relative particle number fractions f_i for i =1,2, …, N. The exchange between compartments is governed by the transition rate constants R_ij for a jump from compartment j to compartment i. For diffusion in the direction of the x coordinate, the basic KM equations are then [19]

$$\frac{\partial }{\partial t}{C}_i(x,t)=D_i\frac{{\partial }^2}{\partial x^2}{C}_i(x,t)+\sum _{j=1}^N{R}_{ij}{C}_j(x,t),\text{for}i=1,2,\dots ,N,$$ (11)

where C_i (x,t) is the particle concentration at position x and time t. The concentrations are related to the number fractions by

$$f_i=\underset{-\infty }{\overset{\infty }{\int }}dx{C}_i(x,t)/\sum _{j=1}^N\underset{-\infty }{\overset{\infty }{\int }}dx{C}_j(x,t).$$ (12)

By definition, the number fractions satisfy

$$1=\sum _{i=1}^N{f}_i.$$ (13)

For the f_i to be independent of time requires also that

$$0=\sum _{j=1}^N{R}_{ij}{f}_j.$$ (14)

In addition, detailed balance demands that [29]

$$R_{ji}{f}_i=R_{ij}{f}_j,$$ (15)

which follows from an assumption of time reversal symmetry in the underlying microscopic dynamics [30]. The equilibrium condition of Eq. (14) is explicitly stated by Kärger and coworkers [19]. While they do not mention the detailed balance condition of Eq. (15), it is generally appropriate for water diffusion in biological tissues and implicitly utilized in their analysis for the two-compartment case of N = 2 [18,19]. When R_ij = 0, Eq. (11) simply reduces to N independent diffusion equations for the concentrations C_i.

For the rate constants, we adopt the convention that R_ij is for a transition from j to i, rather than the i to j convention employed by Kärger et al. [19]. The j to i convention is often used in the context of master equations [29], which are the closely related to the KM, and has the advantage of being more consistent with the standard index notation used in linear algebra.

By taking into account the constraints of Eqs. (13)–(15), the N compartment KM is seen to be described by a total of (N ² + 3N − 2) / 2 free parameters. We emphasize the equilibrium and detailed balance conditions are fully independent. In particular, Eq. (14) restricts the diagonal components of R_ij, but Eq. (15) does not.

For the special case of N = 2, which we now consider in detail, the four free parameters may be taken as the compartmental diffusivities D₁ and D₂, the number fraction f₁ =1− f₂, and the exchange rate constant R_e ≡ R₁₂ / f₁ = R₂₁ / f₂.

The second order position correlation function for the KM with N = 2 is

$$\langle x(t_1)x(t_2)\rangle =2\overline{D}{t}_1,$$ (16)

assuming that t₁ ≤ t₂, where D̄ is the averaged diffusion coefficient for the total system given by

$$\overline{D}\equiv f_1{D}_1+f_2{D}_2.$$ (17)

It should be noted that Eq. (16) covers the general case since for t₁ > t₂ one may simply use the trivial identity x(t₁)x(t₂) = x(t₂)x(t₁) to find 〈x(t₁)x(t₂)〉 = 2D̄t₂. Since t₁ and t₂ refer to time intervals (i.e., time periods over which the diffusion is observed), Eq. (16) is consistent with time translation invariance, as is required for a stationary system. For t₁ = t₂, Eq. (16) is equivalent to the familiar expression of Eq. (1). The spatial averaging implied in Eq. (16) is elementary since the KM lacks geometrical structure. That the right side of Eq. (16) contains only a single time parameter is related to the fact that velocities for the KM are uncorrelated for different time intervals.

The fourth order position correlation function for the two-compartment KM is

$$\langle x(t_1)x(t_2)x(t_3)x(t_4)\rangle =4{\overline{D}}^2{t}_1(2t_2+t_3)+\frac{4{\overline{D}}^2{K}_0}{3R_e^2}[6R_e{t}_1+3e^{-R_e{t}_1}+2e^{-R_e{t}_2}+e^{-R_e{t}_3}-2e^{-R_e(t_2-t_1)}-e^{-R_e(t_3-t_1)}-3],$$ (18)

assuming that t₁ ≤ t₂ ≤ t₃ ≤ t₄. The parameter K₀ corresponds to the initial diffusional kurtosis and is given explicitly by

$$K_0\equiv 3f_1{f}_2\frac{{(D_1-D_2)}^2}{{\overline{D}}^2}.$$ (19)

Just as with Eq. (16), commutativity of the positions implies that the fourth order correlation function for an arbitrary time ordering can be derived from Eq. (18). The derivations of Eqs. (16) and (18) are outlined in the Appendix.

By using Eqs. (1), (8), (16), and (18), we find the two-compartment KM diffusion metrics:

$$D(T)=\overline{D},$$ (20)

and

$$K(T)=\frac{2K_0}{R_{e}T}\left[1-\frac{1}{R_{e}T}(1-e^{-R_{e}T})\right].$$ (21)

The KM kurtosis of Eq. (21) was derived first for f₁ = f₂ by Cao [31] and for arbitrary volume fractions by Jensen and co-workers [4]. Note that the kurtosis depends on the observation time interval and the exchange rate constant, but the diffusion coefficient is a constant and independent of the exchange rate constant as has been observed in several prior studies [6,20,21,23].

By performing the integrals in Eqs. (2) and (9) with TE = Δ +δ, the KM ADC and ADK for a Stejskal-Tanner sequence can be determined analytically as

$$D_{\text{app}}(\mathrm{\Delta },\delta )=\overline{D},$$ (22)

and

$$K_{\text{app}}(\mathrm{\Delta },\delta )=\frac{2K_0}{15{(X-Y/3)}^2{Y}^4}[15X{Y}^4-9Y^5-40Y^3+60Y^2-120+120(Y+1)e^{-Y}+120(Y-1)e^{-X}+60{(Y-1)}^2{e}^{-X+Y}+60e^{-X-Y}],$$ (23)

with X ≡ R_eΔ and Y ≡ R_eδ. So for the KM, the ADC is exactly equal to the true diffusion coefficient for any value of the gradient pulse duration. The ADK differs, in general, from the true kurtosis, but Eq. (23) is consistent with the narrow pulse limit of Eq. (10).

3. Results

In order to investigate the deviation of the KM ADK from the true kurtosis, we define the percent error as:

$$\epsilon \equiv 100·\frac{K_{\text{app}}(\mathrm{\Delta },\delta )-K(\mathrm{\Delta })}{K(\mathrm{\Delta })}.$$ (24)

By using Eqs. (21) and (23), this error was calculated for 0 ≤ δ / Δ ≤1and 0 ≤ R_e Δ ≤10. This includes the range of physical interest for standard DW-MRI of brain, since 0 ≤ δ ≤ Δ is required for any Stejskal-Tanner sequence, Δ is typically in the range of 20 to 200 ms, and R_e in brain has been estimated to be roughly 10 s⁻¹ [21]. We note that ε is independent of the diffusivities and the number fractions, as these enter the ADK only through the prefactor K₀ in Eq. (23).

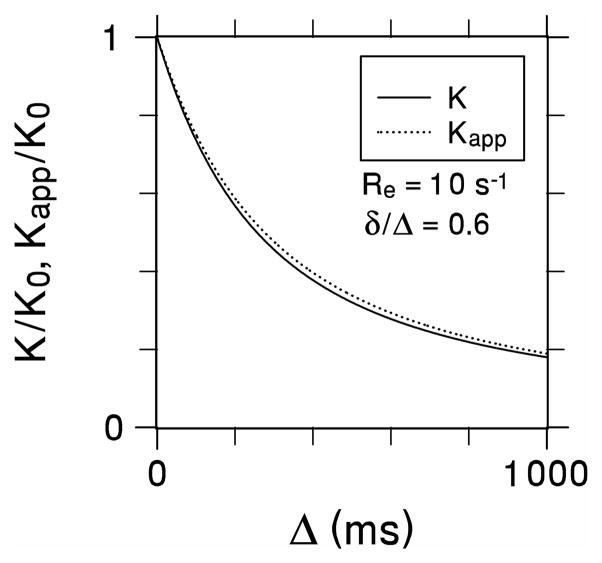
A contour plot for ε is shown in Fig. 1. The error vanishes for either δ / Δ = 0, in accord with Eq. (10), or for the no exchange limit of R_eΔ = 0. The error also vanishes for a line corresponding approximately toδ / Δ = 0.85; to the left of this line, the error is positive, while to the right it is negative. The maximum amplitude of the error is 6.2% for δ / Δ = 0.464 and R_eΔ = 6.82. As a specific example, Fig. 2 compares K(Δ) / K₀ with K_app (Δ,δ) / K₀ for δ / Δ = 0.6 and R_e = 10 s⁻¹. In this case, a maximum error of 5.63% occurs for Δ = 653ms.

Fig 1.

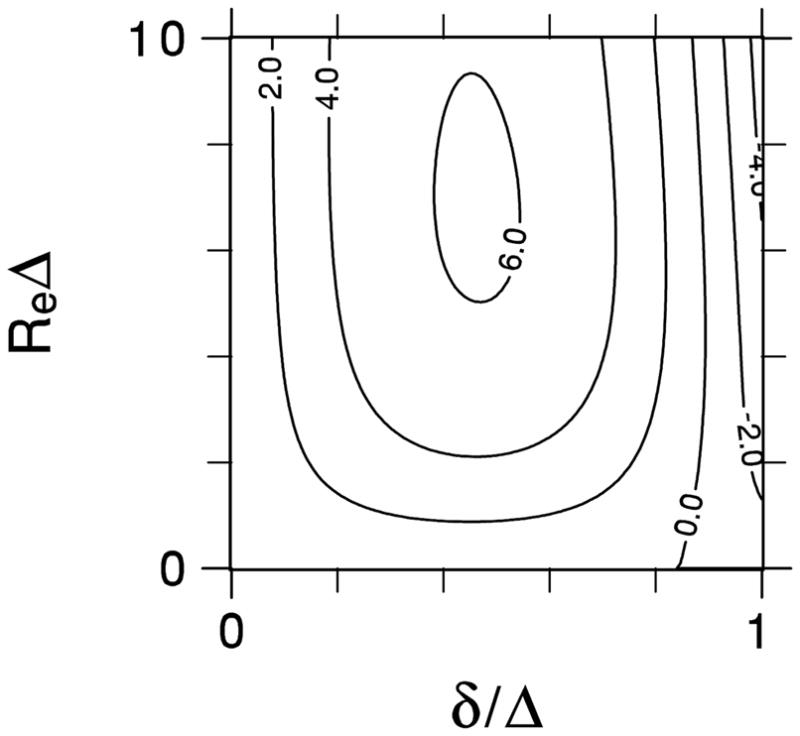
Contour plot of the percent error for the apparent diffusional kurtosis as calculated with the Kärger model and a Stejskal-Tanner pulse sequence.

Fig 2.

True (K) and apparent (K_app) diffusional kurtoses as functions of the diffusion time for R_e = 10 s⁻¹ and δ/Δ = 0.6. The two curves nearly coincide demonstrating the insensitivity of K_app to the gradient pulse duration.

4. Discussion

For clinical DW-MRI, hardware and time constraints substantially limit the diffusion information that is feasible to acquire. In most cases, only the ADC in selected directions and related quantities such as the diffusion tensor eigenvalues and the fractional anisotropy are estimated.

Recent work has demonstrated that the diffusional kurtosis may also be obtained using clinical scanners within scan times of a few minutes, thus adding a new diffusion metric to the clinical toolbox [4–7]. The practical estimation of the kurtosis is based of the formula

$$ln\left(\frac{S(b)}{S(0)}\right)=-{bD}_{\text{app}}+\frac{1}{6}{b}^2{D}_{\text{app}}^2{K}_{\text{app}}+O(b^3),$$ (25)

where S(b) is the signal amplitude as a function of the b-value. Fitting ln[S(b)] data for three or more b-values to Eq. (25), with the O(b³) terms excluded, then yields estimates for both the ADC and the ADK. This procedure is a simple extension of the conventional linear fit to ln[S(b)] used in diffusion tensor imaging. In brain, fits to Eq. (25) usually employ maximum b-values of about 2000 to 3000 s/mm². In practice, the accuracy of estimates for the ADC and ADK may depend on a variety of factors including the signal-to-noise ratio, choice of b-values, and intrinsic tissue properties such as inter-compartmental water exchange rates [6].

One potential confounding effect stems from the fact that the gradient pulse durations for clinical DW-MRI are typically long because of hardware limitations, often being comparable to the diffusion time Δ [1]. For this reason, the narrow pulse limit connections of Eqs. (7) and (10), for the ADC and ADK to the ideal diffusion coefficient and kurtosis, do not necessarily apply. Moreover, a strong dependence of the ADC and ADK on pulse duration would make them less attractive as clinical measures, since their values would depend significantly on the specific sequence parameters utilized.

However, a prior theoretical study of diffusion in open geometries [3] and an experimental study of water diffusion in rat thalamus [17] have both found the effect of pulse duration on the ADC to be relatively small. These results therefore help to justify use of the ADC for clinical applications.

Here we have performed a similar theoretical analysis for the KM ADK, finding that an extended pulse duration changes the ADK by at most a few percent for model parameters relevant to DW-MRI of brain. Although not definitive, our results do suggest that the water ADK in brain is insensitive to changes in the pulse duration, supporting the robustness of ADK estimates based on clinical DW-MRI. The previously mentioned rat thalamus experimental study also observed the water ADK to change very little with pulse duration [17], in consistency with our findings.

5. Appendix

In order to derive Eqs. (16) and (18), it is convenient to introduce the displacement probability density, P_ij (x,t), which corresponds to the solution of Eq. (11) with the initial condition

$$P_{ij}(x,0)={\delta }_{ij}\delta (x).$$ (26)

Physically, P_ij (x,t) is the probability density for moving a distance x over a time interval t, while beginning in compartment j and ending in compartment i. Given the probability density, the particle concentration is determined by

$$C_i(x,t)=\sum _{j=1}^N\underset{-\infty }{\overset{\infty }{\int }}dy{P}_{ij}(x-y,t)C_j(y,0),$$ (27)

so that P_ij (x,t) plays the role a Green’s function for Eq. (11).

If we define Fourier transformed probability P̃_ij (q,t) by

$$P_{ij}(x,t)=\underset{-\infty }{\overset{\infty }{\int }}\frac{dq}{2\pi }{\stackrel{\sim }{P}}_{ij}(q,t)e^{\mathit{iqx}},$$ (28)

then the KM equations can be rewritten as

$$\frac{\partial }{\partial t}{\stackrel{\sim }{P}}_{ij}(q,t)=-D_i{q}^2{\stackrel{\sim }{P}}_{ij}(q,t)+\sum _{k=1}^N{R}_{ik}{\stackrel{\sim }{P}}_{kj}(q,t),$$ (29)

with the initial condition

$${\stackrel{\sim }{P}}_{ij}(q,0)={\delta }_{ij}.$$ (30)

Here the parameter q is analogous to the wavenumber of q-space MRI [1].

By applying standard methods, one can obtain the solution

$${\stackrel{\sim }{P}}_{ij}(q,t)=\sqrt{\frac{f_i}{f_j}}\sum _{n=1}^N{\alpha }_{i,n}(q){\alpha }_{j,n}(q)e^{-{\lambda }_n(q)t}.$$ (31)

Here α_i,n (q) indicates a complete set of N orthonormal eigenvectors with the eigenvalues λ_n (q) so that

$${\lambda }_n(q){\alpha }_{i,n}(q)=D_i{q}^2{\alpha }_{i,n}(q)-\sum _{j=1}^N{R}_{ij}\sqrt{\frac{f_j}{f_i}}{\alpha }_{j,n}(q).$$ (32)

Note that α_i,n (q) and λ_n (q) are even functions of q and that λ_n (q) ≥ 0 for any physically sensible solution. The completeness and orthogonality of α_i,n (q) follow from the fact that they are the eigenvectors of a real symmetric matrix, which is a consequence of the detailed balance condition of Eq. (15).

In terms of the displacement probability, the second order position correlation function can be written

$$\langle x(t_1)x(t_2)\rangle =\sum _{i,j,k=1}^N\underset{-\infty }{\overset{\infty }{\int }}{x}_2{dx}_2\underset{-\infty }{\overset{\infty }{\int }}{x}_1{dx}_1{P}_{ij}(x_2-x_1,t_2-t_1)P_{jk}(x_1,t_1)f_k,$$ (33)

for t₁ ≤ t₂. By using Eq. (28), this can be reduced to

$$\langle x(t_1)x(t_2)\rangle =-\sum _{i,j=1}^N{\left[\frac{{\partial }^2}{{\partial }^{2}q}{\stackrel{\sim }{P}}_{ij}(q,t_1)f_j\right]|}_{q=0}.$$ (34)

An analogous argument for the fourth order position correlation function leads to

$$\langle x(t_1)x(t_2)x(t_3)x(t_4)\rangle =\sum _{i,j,k,l=1}^N{\left[\left(\frac{{\partial }^4}{{\partial }^4{q}_1}+3\frac{{\partial }^2}{{\partial }^2{q}_1}\frac{{\partial }^2}{{\partial }^2{q}_2}+\frac{{\partial }^2}{{\partial }^2{q}_1}\frac{{\partial }^2}{{\partial }^2{q}_3}\right){\stackrel{\sim }{P}}_{ij}(q_3,t_3-t_2)\times {\stackrel{\sim }{P}}_{jk}(q_2,t_2-t_1){\stackrel{\sim }{P}}_{kl}(q_1,t_1)f_l\right]|}_{q_1,q_2,q_3=0},$$ (35)

where t₁ ≤ t₂ ≤ t₃ ≤ t₄.

For the special case of N = 2, the transition rate constants may be written as the 2 × 2 matrix

$$\left(\begin{array}{cc}{R}_{11}& R_{12}\\ R_{21}& R_{22}\end{array}\right)=R_e\left(\begin{array}{cc}-f_2& f_1\\ f_2& -f_1\end{array}\right),$$ (36)

which automatically satisfies the constraints of Eqs. (14) and (15).

By solving the eigenvector problem of Eq. (32) for N = 2, one finds the KM eigenvalues to be

$${\lambda }_1=\frac{1}{2}[(D_1+D_2)q^2+R_e]-\frac{1}{2}\sqrt{{(D_1-D_2)}^2{q}^4-2R_e(f_1-f_2)(D_1-D_2)q^2+R_e^2}$$ (37)

and

$${\lambda }_2=\frac{1}{2}[(D_1+D_2)q^2+R_e]+\frac{1}{2}\sqrt{{(D_1-D_2)}^2{q}^4-2R_e(f_1-f_2)(D_1-D_2)q^2+R_e^2}.$$ (38)

The corresponding eigenvectors are

$${\alpha }_{i,1}=\frac{1}{\sqrt{1+c^2}}\left(\begin{array}{c}1\\ c\end{array}\right);{\alpha }_{i,2}=\frac{1}{\sqrt{1+c^2}}\left(\begin{array}{c}-c\\ 1\end{array}\right),$$ (39)

where

$$c=\frac{D_1{q}^2+R_e{f}_2-{\lambda }_1}{R_e\sqrt{f_1{f}_2}}.$$ (40)

A straightforward, albeit lengthy, calculation using Eqs. (31) and (34)–(40) leads then directly to the results of Eqs. (16) and (18).