Spike Correlations – What Can They Tell About Synchrony?

Abstract

Sensory and cognitive processing relies on the concerted activity of large populations of neurons. The advent of modern experimental techniques like two-photon population calcium imaging makes it possible to monitor the spiking activity of multiple neurons as they are participating in specific cognitive tasks. The development of appropriate theoretical tools to quantify and interpret the spiking activity of multiple neurons, however, is still in its infancy. One of the simplest and widely used measures of correlated activity is the pairwise correlation coefficient. While spike correlation coefficients are easy to compute using the available numerical toolboxes, it has remained largely an open question whether they are indeed a reliable measure of synchrony. Surprisingly, despite the intense use of correlation coefficients in the design of synthetic spike trains, the construction of population models and the assessment of the synchrony level in live neuronal networks very little was known about their computational properties. We showed that many features of pairwise spike correlations can be studied analytically in a tractable threshold model. Importantly, we demonstrated that under some circumstances the correlation coefficients can vanish, even though input and also pairwise spike cross correlations are present. This finding suggests that the most popular and frequently used measures can, by design, fail to capture the neuronal synchrony.

1. Functional Importance of Spike Correlations

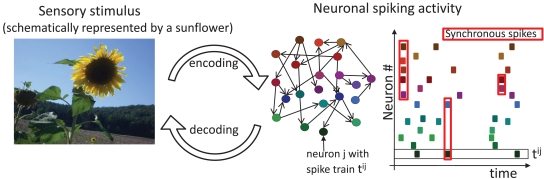
The first observations of spiking activity in groups of neurons in the 1960s and 1970s established that the spiking activity is correlated across neurons (Gerstein and Clark, 1964; Perkel et al., 1967; Moore et al., 1970; Eggermont, 1990). Subsequent studies have shown that these spike correlations of N neurons can depend on the similarity of preferred stimuli, distance between neurons, motion direction of a stimulus and may even change during the performance of cognitive tasks (Michalski et al., 1983; Krüger and Aiple, 1988; Kreiter and Singer, 1996). Recent studies exploiting a tour de force technique of dual intracellular recordings during visual stimulation demonstrated that correlations of membrane potential fluctuations, which reflect the cells’ input, can be stimulus-dependent too (Lampl et al., 1999; Yu and Ferster, 2010). These studies suggest that correlated activity may not just be an epiphenomenon but can carry crucial sensory information. Indeed, considerably more information about visual stimuli could be extracted from the activity of pairs of LGN cells if correlations between their spikes are taken into account (Dan et al., 1998). Similarly, decoding strategies that exploit the inter-neuron spike dependencies in the primate retina are capable of extracting 20% more information about the visual scene than decoding under the assumption of independence, and also preserve 40% more visual information than optimal linear decoding (Pillow et al., 2008). Pairwise correlations have been shown to predict multineuronal firing patterns in the vertebrate retina (Schneidman et al., 2006) and across larger distances in the cortex (Ohiorhenuan et al., 2010). Recently, Tkacik et al. (2010) have shown that a change in pairwise correlations can help to establish an optimal balance between efficient consumption of finite neural bandwidth and the necessary redundancy to mitigate noise. Figure 1 schematically illustrates how neuronal activity represents sensory information. The sensory stimulus, here schematically represented by the image of a sunflower, is encoded in the firing of a neuronal population. The total number of spikes, their timing, and particularly correlations between two or more neurons all carry important sensory information. Therefore decoding strategies can benefit from any of these sources.

Figure 1.

Sensory stimuli are represented in the spiking activity of cortical neurons. A sensory stimulus (left) is encoded, albeit with potential information loss, in the activity of an interconnected cortical population (middle). Colored circles and black arrows depict neurons and their connections. The spike times of each neuron (right, same color code as in the middle scheme) are depicted as dots. A black square highlights the spike train t^ij of neuron j and the red squares highlight examples of synchronous spikes. Sensory information is contained in the total number of spikes, their timing and the spike cross correlations between two or more neurons. Potential decoding strategies can benefit from any of these sources.

What is the origin of pairwise spike correlations? In physical systems the occurrence of synchronous events can emerge from a variety of mechanisms (Pikovsky et al., 2002). In neuronal networks, signal-evoked and intrinsic noise spike correlations both originate in the intricate connectivity of a neuronal network. Each cortical neuron receives inputs from approximately 10⁴ other neurons and sends out signals via its synapses to about 10⁴ others (Abeles, 1991; Braitenberg and Schüz, 1998). In such a neuronal network, spiking cross correlations in the activity of two neurons can emerge from direct synaptic connections or shared presynaptic partners. Because neurons are highly interconnected, it is almost unavoidable that two neurons in a network share some of their inputs (Figure 2 left, third from top). Apart from direct and shared connections, neurons can interact in any other complex multi-neuronal pattern, see for example Figure 2 (top left). The statistical structure of current and spike cross correlations in a pair of neurons can depend not only on the anatomical connections but also on the synaptic time constants. For example, synaptic connections mediated by glutamatergic AMPA channels contribute current fluctuations with a short time constant, while current fluctuations mediated by the NMDA channels lead to fluctuations with longer time constants (Stern et al., 1992; Hestrin, 1993). Experimental assessment of pairwise subthreshold and spike correlations in vivo generally reveals a wide variety of pairwise spike correlation functions (Ts'o et al., 1986; Lampl et al., 1999; Yu and Ferster, 2010), which depend on a multitude of parameters, e.g., the distance of cells in cortical space, receptive fields, or intrinsic properties of the cell membranes. Attempts to relate a particular spike correlation form to the underlying synaptic architecture, have so far proven difficult. Broad temporally symmetric pairwise spike and input correlations are thought to originate from non-specific common synaptic inputs (Krüger and Aiple, 1988; Abeles, 1991). On the other hand, systematic spiking delays of one neuron relative to the other and accompanying asymmetric spike cross correlations are traditionally interpreted as signatures of dominant direct monosynaptic connections from one cell to the other (Ts'o et al., 1986; Krüger and Aiple, 1988; Aertsen et al., 1989; Abeles, 1991; Ostojic et al., 2009). However, experimental reports of asymmetric spike cross correlations with little anatomic evidence of direct synaptic connections (Lampl et al., 1999) point to a more complex relation between spike correlation function and the underlying architecture. Just as multiple synaptic interaction structures can potentially give rise to the same pairwise correlations, a particular functional form of the spike correlation function may not be a unique signature of interneuronal interactions. While the transformation of the network interactions to the correlated input currents, changes of membrane potential and then correlated firing of neurons have a defined solution, the inverse problem of assigning a circuitry to spike cross correlations does not have a unique solution, and a given form of spike cross correlations could emerge in a multiple neuronal circuit.

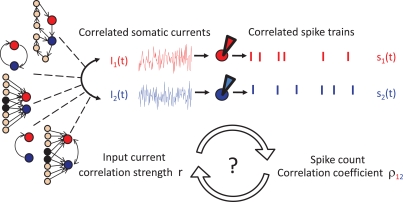
Figure 2.

The correlation transfer from input currents to spikes. Cross correlations in the net somatic currents of neurons 1 and 2 can originate from a multitude of synaptic interactions: direct or recurrent synaptic connections, common inputs or their combination. The presence of current cross correlations results in pairwise correlations in the spikes of neurons 1 and 2. Currently few neuronal models can offer tractable solutions describing how the pairwise input correlations translate to spike cross correlations.

2. Quantification of Correlated Neuronal Activity

The first step toward deciphering the information encoded in the spike trains of neurons is to simultaneously record the spike times of multiple neurons. Multiple electrodes implanted into the cortical tissue (Gerstein and Clark, 1964; Krüger and Aiple, 1988; Eggermont, 1992) or two-photon calcium imaging (Greenberg et al., 2008) can provide the necessary single neuron resolution. Since the spikes are all-or-none events, the spike train s(t) emitted by the neuron j is completely described by the sequence of spike times t^ij. The temporal structure of the spike train can be characterized using several measures. One is the spike auto correlation function, which describes the probability to emit a spike as a function of time elapsed from the previous spike (Moore et al., 1966; Tchumatchenko et al., 2010a). Alternative measures are the distribution of time intervals between adjacent spikes (Moore et al., 1966; Lindner, 2004; Verechtchaguina et al., 2007) and higher order spike interval dependencies (Moore et al., 1966). The spike cross correlations of two simultaneously recorded spike trains s₁(t) and s₂(t) can be quantified using the crosscorrelogram, which describes the probability of observing a spike in one spike train as a function of time before or after a spike in the other spike train (Moore et al., 1966). Its rate normalized analog is the conditional firing rate function ν_cond,12(τ) (Binder and Powers, 2001; Burak et al., 2009; Tchumatchenko et al., 2010a,b):

$${\nu }_{\text{cond},12}(\tau )=\langle s_1(t)s_2(t+\tau )\rangle /\sqrt{{\nu }_1{\nu }_2}.$$ (1)

Here ν₁ and ν₂ are the mean firing rates of neurons 1 and 2, respectively. 〈·〉 denotes the average over all spikes of the reference neuron 1 and subsequently averaged over multiple realizations of the same experimental condition. Because the temporal spike resolution can be limited, it is often beneficial to consider instead the number of spikes emitted in a given time period T. A frequently used measure based on spike count correlations is the pairwise correlation coefficient ρ₁₂ (Perkel et al., 1967; de la Rocha et al., 2007; Shea-Brown et al., 2008; Greenberg et al., 2008). It is defined as the covariance of spike counts normalized by the variances of individual neurons:

$${\rho }_{12}=\frac{\text{Cov}(n_1(T),n_2(T))}{\sqrt{\text{Var}(n_1(T),n_1(T))\cdot \text{Var}(n_2(T),n_2(T))}},$$ (2)

where n₁(T) and n₂(T) are spike counts of neuron 1 and 2 measured in synchronous time bins of width T. This correlation coefficient is often taken as a measure of spike correlation strength. The correlation coefficient is equal to one if the spike trains are identical, and it is 0 if the spike trains are independent. Inversely, values of correlation coefficients close to one are interpreted as perfect synchrony, while low values or those indistinguishable from 0 are commonly interpreted as weak or 0 spike cross correlations.

3. Spike Correlations in Integrate and Fire Models

The leaky integrate and fire (LIF) model has long served as the preferred neuron model for addressing the computational properties of spike cross correlations (Moreno-Bote and Parga, 2004; de la Rocha et al., 2007). The fluctuating current driving the neuron is modeled as a stationary Gaussian process (Destexhe et al., 2003). To study spike cross correlations in two LIF neurons which result from a common noise component, the input current is typically split into two statistically independent parts, one of which (n_C(t)) is common to both neurons:

$$\begin{array}{c}{I}_1(t)=\sqrt{1-r}{n}_1(t)+\sqrt{r}{n}_C(t),\\ I_2(t)=\sqrt{1-r}{n}_2(t)+\sqrt{r}{n}_C(t),\end{array}$$ (3)

The mixing ratio is determined by the correlation strength r. Typically, the dynamics of components n_C(t), n₁(t), and n₂(t) are assumed to be filtered white noise with a correlation time τ_I (Moreno-Bote and Parga, 2006; de la Rocha et al., 2007; Ostojic et al., 2009). The voltage dynamics of these two neurons can then be described by two differential equations:

$$\begin{array}{c}{\tau }_M\frac{d{V}_1}{dt}=-V_1(t)+\mu +\sigma \sqrt{{\tau }_M}{I}_1(t),\\ {\tau }_M\frac{d{V}_2}{dt}=-V_2(t)+\mu +\sigma \sqrt{{\tau }_M}{I}_2(t).\end{array}$$ (4)

Upon reaching the threshold value ψ₀ a spike is emitted and the voltage is reset to a subthreshold value. To obtain the firing rate, spike auto and cross correlations coupled Fokker–Planck differential equations for the probability densities of I₁(t), I₂(t), V₁(t), and V₂(t) need to be solved. In related classes of models such as exponential or quadratic integrate and fire models, the linear membrane filter in Eq. 4 is substituted by an exponential or a quadratic term and the corresponding Fokker–Planck equation for the voltage probability density is employed (Naundorf et al., 2005, 2006; Marella and Ermentrout, 2008; Vilela and Lindner, 2009; Barreiro et al., 2010).

Over the last two decades numerous authors have shed light on the spike statistics of integrate and fire neurons. Burkitt (2006) summarizes their contributions in an excellent review. Here, we would like to spotlight some of those findings. For a single LIF neuron driven by correlated noise, the firing rate was first obtained by Brunel and Sergi (1998). Spike autocorrelation and the Fano factor were provided by Moreno-Bote and Parga (2006). The case of two correlated neurons has proven to be particularly challenging, because the Fokker–Planck equations are analytically tractable only in the linear regime of correlation strengths (r ≈ 0) and only for a limited set of current correlation functions. Some analytical results for the spike cross correlation function have been obtained using advanced approximation techniques for the probability density and expressed as an infinite sum of implicit functions (Moreno-Bote and Parga, 2004, 2006). Similarly, the correlation coefficient of two weakly correlated LIF neurons has been obtained for identical neurons in the limit of large time bins (Moreno-Bote and Parga, 2004; de la Rocha et al., 2007) and studied in specific limits in rate-inhomogeneous pairs (Shea-Brown et al., 2008). These studies revealed a firing rate dependent increase of correlation coefficients in the LIF model and confirmed it in pyramidal neurons (de la Rocha et al., 2007; Shea-Brown et al., 2008). Building on these findings, Ostojic et al. (2009) examined how the amplitude and time course of the conditional firing rate depend on the synaptic parameters, surrounding network activity and local connectivity in the LIF and exponential integrate and fire model models. Using linear response theory Ostojic and colleagues identified the conditional firing rate in response to weak common input, direct and reciprocal synaptic connections in neuronal pairs with different firing statistics. They found that the amplitude and shape of functional interactions varied depending on the synaptic properties and background synaptic inputs to the post-synaptic neuron(s), i.e., the activity of the surrounding network.

4. Key Open Challenges

A key challenge for a viable theoretical framework is to quantify the impact of the input current correlations on pairwise spike correlations. A subtle change in the amount of synchrony can make a large difference for many cellular processes, such as synaptic plasticity or synaptogenesis. It can also strongly affect the information content conveyed by the spike trains. Therefore, it is crucial to understand the extent to which a change in input correlations affects spike synchrony. To achieve this goal, it is particularly important to obtain spike correlations while taking into account a broad range of correlation strengths and functional forms of input correlations that can occur under physiological conditions. While the integrate and fire framework provided first glimpses at how correlations in the currents are reflected in the spikes, several key points remained open:

• Do correlation coefficients depend linearly on the input correlation strength? For example, are experimentally recorded weak spike correlation coefficients truly indicative of weak spike and input correlations?

• Do vanishing correlation coefficients reliably indicate independent or uncorrelated spike trains and justify correlation-free decoding strategies?

• How does one best compare correlation coefficients obtained under different experimental conditions?

In the following, we address these questions in a novel threshold framework.

5. Novel Threshold Model Framework

As discussed above, even the most simple and popular integrate and fire models have severe restrictions on the type of accessible input correlations. However, neuronal dynamics might not always unfold within these artificial limits. Therefore, alternative methods with a broader analytically accessible range of correlation strengths and temporal forms of pairwise input correlations are needed. One of the main points contributing to the analytical complexity of the integrate and fire framework is the reset after each spike. Therefore, several reset-free threshold models have been proposed in the last few years. Using a specific temporal structure of Gaussian voltage fluctuations Jung calculated the spike autocorrelation function of a single neuron in a threshold model without reset (Jung, 1995). Dorn and Ringach, (2003) later suggested a similar Gaussian approach, but assumed that the spikes occur not specifically at the threshold crossings but at any voltage above threshold. Svirskis and Hounsgaard (2003) also introduced a reset-free model based on the positive threshold crossings of a Gaussian process and obtained a series expansion of the conditional firing rate of two neurons but did not provide closed-form expressions. Recently, two independent studies by Burak et al. (2009), and ourselves simultaneously proposed a model based on positive threshold crossings of correlated Gaussian potentials and provided analytical expressions for the firing rate, conditional firing rate of a single neuron and two correlated neurons (Tchumatchenko et al., 2008). Using this framework, we obtained a number of tractable expressions for the pairwise correlation coefficients (Tchumatchenko et al., 2010a), characterized the computational properties of spike correlations in number of important limits and confirmed all basic predictions of this model in in vitro cortical neurons (Tchumatchenko et al., 2010b).

In this model framework, the somatic voltage fluctuations of cortical neurons are approximated by a stationary, temporally correlated Gaussian process. Starting from a stationary Gaussian potential V(t) with a correlation function best suited for a particular experimental observation, spikes are included as positive crossings of a fixed threshold. We took the positive threshold crossings, to remain close to the integrate and fire models. An important difference to the integrate and fire models is the lack of a reset, because the continuity of the potential already imposes a spike-free period after the last spike. To keep the model's complexity at bay we assumed a fixed spiking threshold, however, the framework can be easily modified to incorporate specific threshold adaptation mechanisms, e.g., history-dependent threshold adaptation (Naundorf et al., 2006). The spike train s(t) of a neuron is then given by:

$$s(t)=\delta (V(t)-{\psi }_0)|\dot{V}(t)|\theta (\dot{V}(t)),$$ (5)

where δ(·) and θ(·) are the Dirac delta and Heaviside theta functions, respectively. To implement correlations between two neurons, we assumed a voltage cross correlation between the voltages of the two neurons: $\langle V_1(t)V_2(t+\tau )\rangle =r{\sigma }_{V_1}{\sigma }_{V_2}\tilde{c}(\tau )$. Here, r is the assumed correlation strength, $\tilde{c}(\tau )$ is the temporal voltage correlation function of each neuron and ${\sigma }_{V_i}$ is the standard deviation of the potential fluctuations at neuron i. This approach is equivalent to Eq. 3 and is consistent with the symmetrical voltage cross correlation function in cortical neurons in vivo (Lampl et al., 1999). Now, all that is needed to explicitly compute pairwise spike conditional firing rate ν_cond(τ) in Eq. 2 is the Gaussian probability density featuring covariances between the voltages and their derivatives. This approach is analytically much more tractable than the Fokker–Planck formalism associated with the coupled differential equations in Eq. 4.

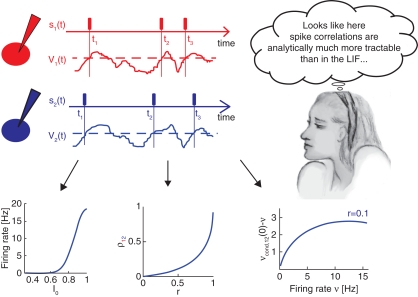
Figure 3 spotlights three analytical results obtained in the threshold framework and presented in more detail in Tchumatchenko et al. (2010a):

Figure 3.

Pairwise spike correlations in the novel threshold model framework. The spike times neurons t₁ − t₃ and the corresponding spike trains s₁(t) and s₂(t) represented by rectangles in red (top) or blue (center) are modeled in the threshold framework by positive threshold crossings (black dashed line) of a fluctuating potential V₁(t) or V₂(t), respectively. The correlations between neurons are incorporated as symmetric voltage cross correlations. Tractable analytical results can be obtained for the dependence of firing rate on the mean driving current I₀ (bottom left), correlation coefficient ρ₁₂ as a function of correlation strength r (bottom center) and the weak pairwise spike correlation ν_cond,12(0) − ν as a function of firing rate ν (bottom right).

• Firing rate as a function of mean current in Figure 3 (bottom left)

  $$\nu =\frac{\text{exp}\left(-{(I_0-{\psi }_0)}^2({\tau }_I+{\tau }_M)/(2{\sigma }_I^2{\tau }_I)\right)}{2\pi \sqrt{{\tau }_I{\tau }_M}}$$
• Pairwise spike cross correlations as a function of input strength in Figure 3 (bottom middle, ν = 6 Hz, τ_s = 10 ms).

  $$\begin{array}{l}{\rho }_{12}\propto \frac{1}{4{\pi }^2\nu {\tau }_s^2}\text{exp}\left(\frac{2\text{log}(\nu 2\pi {\tau }_s)}{(1+r)}\right).\\ \left[1+\frac{2r\text{\hspace{0.17em}arctan}\left(\sqrt{\frac{1+r}{1-r}}\right)}{\sqrt{1-r^2}}\right]\end{array}$$

  .
• Weak pairwise spike cross correlations as a function of rate dependence in 3 (bottom right, τ_s = 10 ms).

  $${\nu }_{\text{cond},12}(0)-\nu =\frac{r\nu }{2}\left(\pi +4|\text{log}(\nu 2\pi {\tau }_s|)\right)$$

As a reminder ν is the firing rate, ψ₀ the spiking threshold, τ_I current correlation time, τ_s voltage correlation time, τ_M membrane time constant, r input correlation strength, σ_I and σ_V the standard deviation of current and voltage fluctuations, respectively. The first result in Figure 3 describing the influence of the mean depolarization and current noise variance on the firing rates is consistent with previous observations in the integrate and fire framework (Brunel and Sergi, 1998; de la Rocha et al., 2007; Ostojic et al., 2009). The second result provides, to the best of our knowledge, the first analytical description of the sub-linear dependence of spike cross correlations on the input correlation strength which was reported in vitro by Binder and Powers (2001) and de la Rocha et al. (2007). The third result describes analytically the prominent firing rate dependence of weak spike cross correlations reported for LIF neurons (Moreno-Bote and Parga, 2006; de la Rocha et al., 2007; Shea-Brown et al., 2008), in vitro and in vivo (de la Rocha et al., 2007; Greenberg et al., 2008). The last two results are particularly remarkable because (1) they provide the first closed-form analytical description for spike cross correlations in a pair of neurons driven by a large class of temporal current structures and (2) they show that spike cross correlations progressively lose their firing rate dependence as the correlation strength increases.

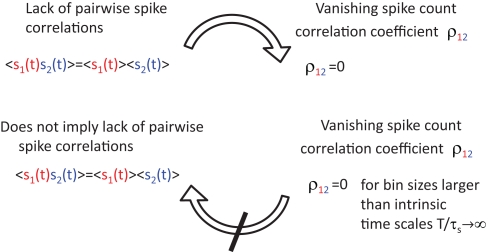
This framework also allows us to go one step further and explore a previously inaccessible territory: the influence of a broad range of correlation strengths and temporal form of spike correlations on various measures of spike synchrony. Studying the effect of the temporal form of input correlations on the correlation coefficient in (Tchumatchenko et al., 2010a) we found that the class of spike correlation functions fulfilling ${\displaystyle {\int }_{-\infty }^{\infty }{\nu }_{\text{cond}}(\tau )d\tau =0}$ leads to vanishing correlation coefficients in the limit of large time bins. In the threshold model, this class of cross spike correlation functions can be obtained from the class of voltage correlation functions with ${\displaystyle {\int }_{-\infty }^{\infty }C(\tau )d\tau =0}.$ As schematically demonstrated in Figure 4, a popular measure of synchrony, the spike correlation coefficient, can fail to indicate the presence of pairwise spike cross correlations. Particular care needs to be devoted to the time bin size to ensure that it is below the typical time scale of the spike cross correlation function. This finding is particularly important, because it directly demonstrates for the first time that vanishing correlation coefficients do not imply uncorrelated spike trains and therefore they do not readily justify correlation-free decoding strategies. In summary, we showed in Tchumatchenko et al. (2010a) that

Figure 4.

Vanishing spike count correlations do not imply uncorrelated spike trains. While a lack of spike cross correlations implies 0 correlation coefficients, the opposite does not always hold. We have shown that count correlation coefficient ρ₁₂ can vanish in pairs of cross correlated neurons. This effect can be expected if ρ₁₂ is computed for large time bins in neuronal pairs where the integral over the spike cross correlation function vanishes $\underset{-\infty }{\overset{\infty }{\int }}{\nu }_{\text{cond}}(\tau )d\tau =0$ (Tchumatchenko et al., 2010a).

• the firing rate, bin size, and temporal form of the voltage cross correlations play a crucial role for spike cross correlations. Importantly, weak spike correlation coefficients do not necessarily imply weak input correlations, because the conversion from inputs to spikes is in general substantially sub-linear.

• spike output correlations can vanish despite finite input cross correlations. In particular, spike count correlations on long time scales can vanish even if count correlations on shorter time scales do not.

• Relating a change in correlation coefficients to a change of input synchrony is best achieved in two pairs of equal firing rates and intrinsic time constants, where the coefficients are computed for small bin sizes.

With all the benefits and insights provided by the threshold model, what are its limits? One of its main limits is its restriction to the fluctuation-driven regime and Gaussian voltage statistics. Yet, these specific regimes are supported by growing experimental evidence showing that the fluctuation rather than mean depolarization driven regime is the primary operation scheme in cortical neurons. The first lines of evidence are the exceptionally low firing rates <1 Hz (Margrie et al., 2002; Greenberg et al., 2008). The second line of evidence is the remarkable cortical balance of excitation and inhibition such that neuronal firing is driven by fluctuations that transiently escape this cancellation (Shadlen and Newsome, 1994; Okun and Lampl, 2008). While mean and fluctuation driven regimes can differ significantly in their spike train regularity, yet they seem to exhibit very similar spike cross correlation (de la Rocha et al., 2007) and dynamical response properties (Koendgen et al., 2008). Therefore, numerous features of pairwise spike correlations can be understood by studying the fluctuation-driven regime. Even though skewed current distributions that violate the Gaussian assumption can be of interest in specific cases, experimental evidence suggests that the Gaussian distribution can be an excellent match for in vivo background fluctuations in the dominant cortical cell type of pyramidal neurons, e.g., see Box 1 (top) in Destexhe et al. (2003). Other neuron models with more involved spike generation mechanisms such as quadratic or exponential integrate and fire indicate the possibility that spike cross correlations in a pair of neurons can depend on the model specifics (Ostojic et al., 2009; Vilela and Lindner, 2009). Yet, realizing how remarkably accurate many cortical spike synchrony features can be modeled by a clearly barebone-threshold model, we are convinced that this model will find its place alongside the classical integrate and fire models.

6. Conclusions

Correlated activity has been shown to play an important role in sensory encoding and cognitive functions. Yet, understanding its properties has been difficult with the prevalent theoretical methods. In particular many questions regarding the implications of measured spike correlations remained open. Are weak correlation coefficients indicative of weak input correlations? Does a vanishing spike correlation coefficient in a pair of neurons imply that they are uncorrelated? Can spike synchrony across experimental conditions be compared simply by comparing correlation coefficients? Many of these basic questions were neglected in the quest for an easy-to-use measure of spike synchrony. To address such fundamental questions, there are two possible approaches to choose from. One approach is to resort to advanced simulations of specific neuronal morphology and ion channel composition, studying numerically the properties of spike correlation measures in various parameter regimes. Another approach is to take a minimal model, which can replicate the essential properties of spike correlations in real neurons, yet which is simple enough to deal with analytically. We took the second route and found that a minimal model based on the threshold crossings of correlated Gaussian potentials can do just that – replicate essential features of cortical spike correlations and offer an unprecedented analytical transparency to address the above questions. Using this model, we found that weak spike correlations, as characterized by a weak correlation coefficient, do not necessarily imply weak input correlations. In fact, substantial spike correlations and input correlations can be present in pairs with vanishing spike correlation coefficients. This implies that particular care needs to be given to the way correlation coefficients are computed. In particular they should be calculated with time scales shorter than the intrinsic time constants, and large integration times should be avoided. Let us stress again that many important features of neuronal activity can be emulated even if the biophysical basis of spiking mechanisms is not modeled in exquisite detail.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Key Concepts

Spike correlations in N neurons

Interdependencies in the spiking of multiple neurons. Pairwise spike correlations are correlations between the spike trains of two neurons, quantified by the spike (cross) correlation function. Higher order correlations include three-neuron, four-neuron, and the general N-neuron correlations, where the joint occurrence of N − 1 spiking events influence the Nth spiking event.

Correlation between two signals

Is a measure of interdependence between two signals. A pairwise (cross) correlation function quantifies their similarity at any two time points. It reaches its lowest negative values if the two points are each other's opposites, is positive if the two points are on average similar, and it is 0 if they are uncorrelated. It measures only linear interdependencies and therefore a lack of pairwise cross correlations does not imply statistical independence.

Pairwise spike correlations

The spike cross or auto correlation functions in a pair of neurons. Spike auto correlations quantify the temporal structure within a spike train, and cross correlations quantify the temporal coordination of spikes across the two spike trains.

Pairwise spike count correlation coefficient ρ₁₂

If the spike trains are identical then this commonly used figure of merit is equal to one, if they are independent of each other then the coefficient is 0. The inverse route is less straight forward; the interpretation of a correlation coefficient in terms of input correlation strength is not possible without prior knowledge of relevant time scales, firing rates and bin size.

Synchrony

Coincident events in the activity of multiple neurons. Synchronous spiking activity across neurons is characterized by a high degree of temporal fidelity in the emission of spikes. Figure 1 (right) schematically illustrates synchronous spikes in a population of neurons. The synchrony level can be quantified by the spike correlation function between two or more neurons.

Pairwise input correlations

Pairwise input correlations are the temporal auto and cross correlation functions of the net somatic input currents in two neurons. They determine the strength and temporal structure of pairwise voltage auto and cross correlations and ultimately give rise to pairwise cross correlations in two spike trains.

Biography

Tatjana Tchumatchenko defended her PhD thesis in 2010 at the Göttingen Graduate School for Neurosciences and Molecular Biosciences at the Georg August University and is now a postdoctoral fellow at the Bernstein Center and the Collaborative Research Center in Göttingen. She has combined theoretical and experimental methods to study the spike correlations and dynamical response properties in living neurons and hopes to someday understand how the cognitive functions emerge from the correlated activity of multiple neurons.