Interaural self-motion linear velocity thresholds are shifted by roll vection

Abstract

The otolith organs respond equivalently to changes in gravitational force due to head tilt and to changes in inertial force due to linear acceleration. It has been shown that the central nervous system (CNS) uses internal models of the laws of physics to distinguish tilt from translation. Models with these internal models predict that illusory tilt, if large enough, will be accompanied by an illusion of linear motion. To investigate this prediction, we measured interaural, self-motion, direction-detection thresholds in darkness and with roll optokinetic stimulation. Each lateral translation consisted of a single cycle of sinusoidal acceleration, after which subjects indicated whether they translated to the left or right. We found that the interaural direction-detection threshold measured during clockwise and counterclockwise optokinetic stimulation shifted in opposite directions relative to thresholds in darkness. Using a generalized linear model, we determined that this finding was statistically significant (P < 0.005) and is consistent with the prediction that illusory tilt should be accompanied by a non-zero neural estimate of linear velocity that, if large enough (supra-threshold), contributes to translation perception.

Introduction

The otolith organs—the physiologic linear accelerometers in our inner ear—measure gravito-inertial force (GIF), the sum of gravitational force and inertial force due to linear acceleration. Hence, otolithic signals are ambiguous. When considering how gravity and linear acceleration are centrally estimated, two internal models that work together have been hypothesized (e.g., Droulez and Darlot 1989; Merfeld et al. 1990; Glasauer 1992; Merfeld et al. 1993; Merfeld 1995; Merfeld and Young 1995; Angelaki et al. 1999; Merfeld et al. 1999; Zupan et al. 2002; Merfeld and Zupan 2003; Angelaki et al. 2004).

One internal model—mathematically represented by the relationship ¹ dĝ/dt = −ω̂ × ĝ—accounts for the influence of rotational cues on the estimation of gravity (ĝ) by mimicking the physical relationship (dg/dt = −ω × g) between gravity (g) and head angular velocity (ω). The second internal model is referred to as the GIF resolution hypothesis, which states that the CNS separates the ambiguous otolithic measurement of GIF (f = g − a) into estimates of gravity (ĝ) and linear acceleration (â) according to a neural internal model mathematically represented by the relationship, f ≈ ĝ − â.

Combining these two internal models with other dynamic influences, we predicted and then confirmed experimentally that illusory tilt induced by either canal (Merfeld et al. 1999; Zupan et al. 2000) or optokinetic (Wall et al. 1999; Zupan and Merfeld 2003) cues is accompanied by a horizontal VOR compensatory for an illusory central estimate of linear velocity. However, recent human studies have shown that vestibular action (i.e., VOR) and perception utilize qualitatively different mechanisms (Merfeld et al. 2005a, b; Zupan and Merfeld 2005). Specifically, vestibular perceptual responses are better accounted for by internal models across a broad range of frequencies, while human horizontal translational VOR responses are better accounted for by simple high-pass filters during high-frequency motion (Merfeld et al. 2005a, 2005b) and by internal models during low-frequency motion (Merfeld et al. 2001). Therefore, it is important to determine whether illusory tilt is accompanied by an illusory perception of linear motion.

Toward this goal, recent models have included specific predictions of linear velocity perception. Studies (Vingerhoets et al. 2006, 2007) have reported that human translation perception during off-vertical axis rotation (OVAR) can be modeled by adding a leaky integrator (time constant of 40 ms) to Merfeld’s model (Merfeld and Zupan 2002) to convert estimated linear acceleration to estimated linear velocity. Another model includes internal models and dynamics similar to those discussed above but additionally includes the influence of dynamic visual cues (Zupan et al. 2002). This model (Zupan et al. 2002) has been previously validated on a large set of human experimental data including visual–vestibular interactions during yaw rotation about an earth-vertical axis, eccentric rotations, off-vertical axis rotations, post-rotatory tilts in humans, optokinetic stimulation in various orientations (Zupan and Merfeld 2003), and caloric stimulation (Peterka et al. 2004).

When Zupan’s model² (Zupan et al. 2002) was provided a 60°/s roll optokinetic stimulation, the model predicted that it takes about 40 s for the illusory roll tilt to reach a near steady-state magnitude of 10°. For this predicted illusory 10° roll tilt, the perceived linear velocity estimate—named the sensory estimate of linear velocity in (Zupan et al. 2002)—was 8.7 cm/s (Fig. 1a). This falls below the human threshold to detect the direction of linear motion, since for low frequency horizontal linear velocity ramps, the average human velocity threshold was measured to be 22.6 cm/s (Jones and Young 1978; Young 1984). Consistent with these model predictions, subjects in earlier investigations did not perceive illusory translation when exposed to roll optokinetic stimulation alone (Zupan and Merfeld 2003).

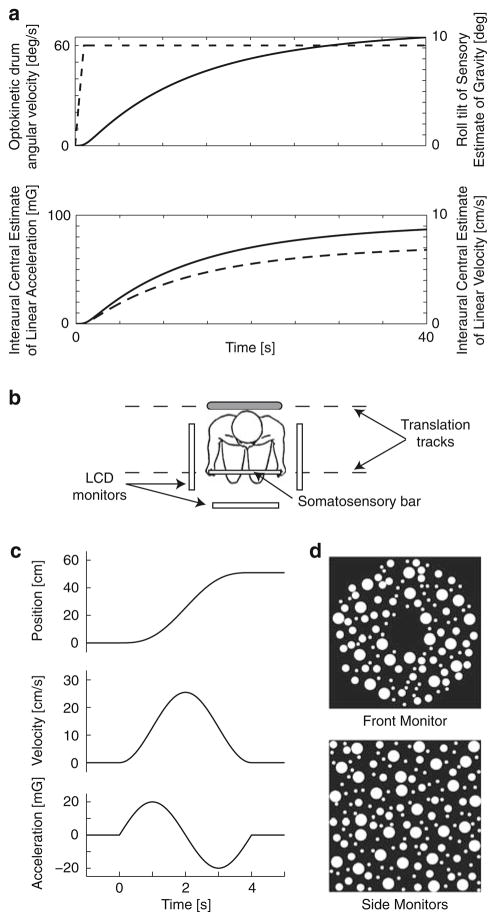
Fig. 1.

a Model predictions. A 60°/s roll optokinetic stimulus (dashed line, top) was provided as the input. This optokinetic stimulus evoked an illusory tilt of 10° (solid line, top) over a period of about 40 s. Interaural components of linear acceleration (dashed line, bottom) and linear velocity (solid line, bottom) were, in turn, evoked. These simulations were performed using an unmodified version of a published model (Zupan et al. 2002). b Bird’s eye view of experimental setup. c Change of lateral position (top), velocity (middle) and acceleration (bottom) during motion stimulus. Each lateral translation consisted of a single cycle of sinusoidal acceleration, a(t) = a_m sin 2πft, a velocity v(t) = a_m/(2πf)[1 − cos 2πft] and a lateral displacement Δp(t) = a_m/(2πf)[t − 1/(2πf) sin 2πft]. By definition, the total displacement, the peak velocity and the peak acceleration were linearly related (Δp = a_m/2πf ², v_m = a_m/πf). Examples of motion components for a_m = 20 mG, v_m = 25 cm/s, and f = 0.25 Hz are presented. d Front (top) and side (bottom) optokinetic patterns displayed on the three 18″ LCD monitors (14″ horizontal by 11.25″ vertical). When the front optokinetic pattern rotated in roll clockwise, the side optokinetic patterns translated upward on the left monitor and downward on the right monitor; optokinetic motion was reversed for counterclockwise optokinetic stimulation

On the other hand, studies using single cycles of sinusoidal linear acceleration have established substantially lower direction-detection thresholds for translational motion having higher frequency content. Specifically, at a frequency of about 0.25 Hz, Benson et al. (1986) measured a direction-detection threshold of 8 cm/s, which is just below the 8.7 cm/s linear velocity estimate predicted by Zupan’s model. Therefore, we hypothesized that small (circa 8.7 cm/s) shifts in the threshold to detect linear motion would be measured when single cycles of linear acceleration at 0.25 Hz were combined with constant velocity roll optokinetic stimulation.

Methods

There were two testing conditions: (1) total darkness (N = 7; 3 males, 4 females, age 23–36) and (2) continuous roll optokinetic stimulation (N = 10; 5 males, 5 females, age 23–39). Subjects were seated with their body restrained using a five-point harness and their head secured in an adjustable foam-lined head restraint. Subjects were passively translated along an earth-horizontal track aligned with their interaural axis (Fig. 1b). Each lateral translation consisted of a single zero-mean cycle of sinusoidal acceleration (Benson et al. 1986) that had a 4 s duration (Fig. 1c); the acceleration magnitude (a_m) varied between 0 and 20 mG to the left (+) or right (−), in increments of 2 mG (1 mG ≈ 1 cm/s²). Peak linear velocity was linearly proportional to peak acceleration and varied between −25 and 25 cm/s in increments of 2.5 cm/s. Trials with no net motion consisted of 4 s of zero mean vibration (0.23 cm/s RMS) designed to mimic that experienced during actual translations.

Dark

In total darkness, each subject reported a response for each of 210 total trials—10 repeats for each of the same 21 levels of linear velocity (10 trials to the left, 10 trials to the right, and one vibration trial with no net translation). Testing in the dark consisted of 5 sessions of 42 trials lasting about 5 min each with 5 min between sessions. Subjects held two ski pole handles—one in each hand—with a switch on top. Subjects indicated perceived motion to the left or right by pushing the switch in their left or right hand. Subjects were instructed to provide an answer, even if they had to guess (forced choice).

Optokinetic

We used a virtual optokinetic drum (Fig. 1d)—with a diameter equal to the distance between two side LCD monitors (76 cm) and the end of the virtual drum located 40 cm in front of subjects at the plane of a frontal monitor. Subjects were asked to look through the center of the 8 cm (11.4°) diameter circular central zone that included no dots (Fig. 1D) but to attend to the moving dots in their visual periphery. Subjects informed us in pilot studies that this virtual optokinetic drum yielded more stable illusory tilts than the real drum that we had used previously (Zupan and Merfeld 2003).

The direction of the constant-velocity (60°/s) roll optokinetic stimulation was maintained—clockwise (CW) or counterclockwise (CCW)—for each testing session, which repeated the same 21 velocity levels used for dark testing. Subjects were tested in six consecutive testing sessions lasting about 5 min each, alternating CW and CCW optokinetic stimulation.

Subjects were instructed to indicate their subjective roll tilt continuously using a somatosensory bar similar to one used previously (Zupan and Merfeld 2003). To make sure that illusory tilt was present during translation, the operator triggered each lateral displacement when the tilt measure exceeded threshold. For seven subjects, the threshold was 10°; for the remaining three subjects, who had weaker tilt illusions, the threshold was 5°. After each lateral translation, subjects indicated their perceived direction of motion by pressing a button located on the left or right of the somatosensory bar.

Data analysis

We used two analysis methods. For one method referred to as “individual normal cumulative distribution” (iNCD), a normal cumulative distribution function was fit to the individual data points—one point per subject at each velocity—using a generalized linear model (GLM) (McCullagh and Nelder 1983; Collett 1991). See Appendix for details. For the second method referred to as “averaged normal cumulative distribution” (aNCD), we first averaged the data across all subjects and then fit a normal cumulative distribution (similar to the right-side of Eq. A.2). For both methods, fit parameter μ represents both the inflection point and the velocity at which each subject reports motion equally in each direction, and the fit parameter σ represents the standard deviation.

Results

Dark

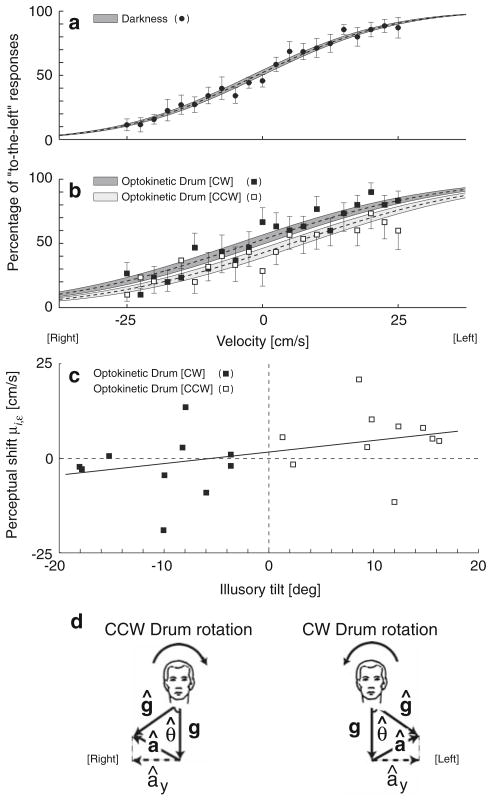
Subjects were able to detect large amplitude translations in the dark with nearly 100% accuracy (Fig. 2a), while they simply guessed at low velocities as demonstrated by the fact that the accuracy dropped nearer to 50%, as previously reported (Benson et al. 1986; Merfeld and Zupan 2003). As expected, in the dark the curve is symmetric with respect to translation direction; the inflection point occurs at −1 cm/s on average across subjects, which was not significantly different from 0 (P = 0.33). The threshold was 6.1 cm/s for both the iNCD and aNCD analyses.³

Fig. 2.

Thresholds for (a) total darkness (N = 7) and (b) constant roll optokinetic stimulation (N = 10) are shown. The percentage of responses where the subjects perceived being translated to-the-left is plotted versus peak velocity. Error bars indicate standard errors. Fitted normal cumulative distribution functions (dashed lines) are shown. Shading represents the standard error of the mean fit. c Offsets of the normal cumulative distributions μ_i,ε (see Eq. A.2) are plotted versus the mean illusory roll tilt for each subject. Solid line represents the fit linear regression (R = 0.4; P < 0.05, one-sided t test). d Optokinetic stimulation induces illusory roll tilt - represented by showing that the estimate of gravity (ĝ) tilts in roll away from gravity (g). The difference between estimated and measured gravity elicits a non-zero central estimate of linear acceleration (â = ĝ − g). The interaural acceleration component (â_y) is toward the subject’s right for CCW dome rotation and to the subject’s left for CW dome rotation and contributes to linear velocity perception via dynamic mechanisms like those included in earlier models (Zupan et al. 2002)

Optokinetic

A single illusory tilt value—for each subject and direction of optokinetic stimulation—was obtained by averaging the subjective tilt measurements across the 2-s period preceding each translation (Fig. 2c). We measured an average illusory tilt across subjects (±SE) of −10.1° ± 1.7° for CW trials and 10.2° ± 1.6° for CCW trials, which, not surprisingly, is near the threshold that the operator typically used to initiate the motion stimuli.

The response profiles during optokinetic stimulation (Fig. 2b) were qualitatively similar to the dark responses (Fig. 2a); however, we observed a shift that depended on the direction of optokinetic stimulation and a diminished accuracy at larger translations (~80% compared to near 100% accuracy in the dark). Using the iNCD, we determined that perception of translation was significantly different between CW and CCW optokinetic conditions (P < 0.005). Specifically, for the iNCD fit the average inflection point across subjects was −2.1 cm/s for CW drum rotation and +5.3 cm/s for CCW drum rotation (Fig. 2b). Relative to the dark responses (−1.0 cm/s), the shifts evoked by CW and CCW stimuli had magnitudes of 1.1 and 6.3 cm/s, respectively; the magnitude difference between 1.1 and 6.3 was not statistically significant (paired t test, P = 0.56). The average threshold during optokinetic stimulation was 8.4 cm/s for the iNCD analysis and 8.6 cm/s for the aNCD analysis.

Discussion

Because a normal cumulative distribution is a non-linear function of its parameters, the parameters found using the generalized linear model (iNCD), which can be interpreted as an average of the fit across subjects, are expected to be different from the parameters of a normal cumulative distribution (aNCD) fitted to the average. However, the fit parameters and thresholds were found to be similar (Table 1) because the variability of the fits is small (Fig. 2a, b).

Table 1.

Average fit parameters and thresholds (all in cm/s)

		Dark (N = 7)	Optokinetic (N = 10)
			CW	CCW
iNCD fit parameters	μ̄	−1.0 ± 1.0	−2.1 ± 2.6	5.3 ± 2.6
	σ	13.8	19.0	19.0
iNCD threshold	T	6.1	8.4	8.4
aNCD fit parameters	μ̄	−1.0	−2.1	5.4
	σ	13.9	20.0	20.0
aNCD threshold	T	6.1	8.6	8.6

Fit parameters include the curve inflection point (μ) and standard deviation (σ). The iNCD parameters represent the average fit across all data from all individual subjects, while the aNCD parameters represent the fit to the data averaged across subjects. To be consistent with (Benson et al. 1986), we defined threshold T as the velocity change for which the fit to the average data reaches 67% responses to the left

The threshold that we measured in the dark at 0.25 Hz was 6.1 cm/s, which is just a little lower than Benson’s reported threshold of 8 cm/s at 0.26 Hz. Given somewhat different procedures—different motion devices, different subjects, different motion frequency, etc.—these threshold values are indistinguishable given inter-subject variability.

Data showed that the motion direction detection threshold was 5.3 cm/s to the left for CCW optokinetic stimulation and 2.1 cm/s to the right for CW optokinetic stimulation. This total difference of 7.4 cm/s was statistically significant (P < 0.005) and was in the direction predicted by the models. During CW rotation (from subject’s perspective), the optokinetic stimulus induces an illusory tilt toward the subject’s left as represented by the estimate of gravity (ĝ) tilted toward the subject’s left (Fig. 2d, sketch on the right), as previously measured (Dichgans et al. 1972; Zupan and Merfeld 2003) and confirmed by our measure of roll tilt perception. When the estimate of gravity (ĝ) does not coincide with the measured GIF (f), an estimated linear acceleration (â) that equals the estimate of gravity ĝ minus measured GIF (f) is elicited (Fig. 2d). In this case, since the measured GIF equals gravity (f = g), we have f = ĝ − â = g, and therefore â = ĝ − g. This estimate of linear acceleration then contributes to an estimate of linear velocity. For example, as discussed earlier, Vingerhoets et al. (2006, 2007) use a leaky integrator with a time constant of 40 ms to convert estimated linear acceleration to estimated linear velocity. Zupan and Merfeld (2003) accomplishes the same conversion using internal models, a leaky integrator with a time constant of 130 ms, and sensory weighting. Since both approaches yield similar results, we cannot distinguish these models using these threshold data.

In summary, findings matched our hypothesis that illusory tilts to the right would be evoked by CCW optokinetic stimulation and should offset perceived linear velocity towards the right (or negative) and that CW optokinetic stimulation should offset perceived linear velocity towards the left (or positive).

The above explanation suggests that larger tilts should be accompanied by larger influences on translation perception. To evaluate this prediction, Fig. 2c shows the perceived translation shift for each individual subject during optokinetic stimulation trials versus the mean illusory roll tilt reported across the same set of trials. Consistent with the a priori hypothesis, a statistically significant (r = 0.4, P < 0.05) positive correlation was found.

The average magnitude of the threshold shift caused by the optokinetic stimulation was 3.7 cm/s ({5.3 − (−2.1)}/2), which is about half the linear velocity predicted by Zupan’s model (8.7 cm/s). This discrepancy may be because the model overestimates the perceived illusory linear velocity evoked by a 10° illusory tilt. Or it may be because the time constant of the leaky integration (130 ms) in Zupan’s model (Zupan et al. 2002) is too high; indeed, Vingerhoets et al. (2006, 2007) chose 40 ms for their model and if we choose 55 ms instead of 130 ms, the simulated threshold shift decreases to 3.7 cm/s without affecting the 10° illusory tilt. Alternatively, human threshold detection may involve additional high-pass filtering—like that reported for yaw rotation thresholds (Grabherr et al. 2008). Such a high-pass filter would be in addition to filtering included in existing models (Zupan et al. 2002; Vingerhoets et al. 2006, 2007). Such a high-pass filter would be consistent with the linear velocity thresholds reported by Benson (Benson et al. 1986) that decreased dramatically—from 19 cm/s (8.7 cm/s²) to 1 cm/s (4.5 cm/s²)—between 0.14 and 1.02 Hz.

Appendix: GLM implementation

For the individual normal cumulative distribution (iNCD) fit, we implemented a generalized linear model (McCullagh and Nelder 1983; Collett 1991) using the function glmfit in Matlab 7.3 (The Mathworks). Based on published data using similar translational motion stimuli (Benson et al. 1986), we hypothesized that our perceptual responses follow a probit distribution, which is the inverse cumulative distribution function of a normal distribution; it is a common model used to describe responses that are binomial. It is worth noting that glmfit is implemented using an iterative re-weighted least squares algorithm that converges to the maximum-likelihood estimate for each regression coefficient.

For our optokinetic data, the predictor variable X has 12 columns and 420 rows. The first 10 columns—one per subject—indicate the subject and are referred to as indicator columns. For example, the first ten elements of a row that represents subject #3 would be [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]. Column #11 indicates the interaural velocity (i.e., a number between −25 and 25 cm/s in 2.5 cm/s increments) for each trial. Column #12 indicates the optokinetic stimulation direction (1 for CW and −1 for CCW). Since we have 10 subjects, 21 levels of accelerations and 2 directions of optokinetic stimulation, the indicator matrix X must have 10 × 21 × 2 = 420 rows.

Since our data are binomial, Y is a 420-by-1 vector indicating the number of to-the-left responses. This will be 0, 1, 2, or 3 for 3 repeated trials for each direction of optokinetic stimulation. The percentage of to-the-left responses equals Y/n where n = 3 is the number of repeated optokinetic trials. The multiple regression model can be expressed in matrix notation by:

$$\text{norminv}(Y)=X\times B+E$$ (A.1)

where B is a 12-by-1 vector of regression coefficients (e.g., the 12th coefficient of regression corresponds to optokinetic stimulation direction), E is a 420-by-1 vector of residuals, and norminv is the inverse of a normal cumulative distribution function. Regression coefficients were obtained using the function glmval in Matlab 7.3.

Because we are using a probit model, the fitted models Ŷ_i,_ε/n are normal cumulative distribution functions defined for each subject (i) and direction of optokinetic stimulation (ε = 1 for CW and ε = −1 for CCW) by:

$${\widehat{\text{Y}}}_{i,\epsilon }(x)/n=1/\sqrt{2\pi {\sigma }^2}\underset{-\infty }{\overset{x}{\int }}exp\left(-{(\xi -{\mu }_{i,\epsilon })}^2/2{\sigma }^2\right)d\xi$$ (A.2)

where variables ξ and x are interaural linear velocity (in cm/s), and parameters σ and μ_i,ε are functions of the elements of the regression coefficient vector B = (b_j):

$$\sigma =\frac{1}{\sqrt{2\pi }{b}_{12}}\text{and}{\mu }_{i,\epsilon }=\frac{-b_i-\epsilon b_{11}}{b_{12}}.$$ (A.3)

We used a similar model for data in the dark except that there is no column for direction of the optokinetic stimulation. Therefore, the predictor variable X is a 147-by-8 matrix. The first 7 columns serve as subjects’ indicators and column #8 indicates the interaural velocity level. Similarly, Y is a 1-by-147 vector indicating the number of to-the-left responses (out of 10 repeated trials). The multiple regression model is similar to the one for data with optokinetic stimulation (Eq. A.2) with ε = 0.