Ultrahigh dimensional feature selection: beyond the linear model

Abstract

Variable selection in high-dimensional space characterizes many contemporary problems in scientific discovery and decision making. Many frequently-used techniques are based on independence screening; examples include correlation ranking (Fan and Lv, 2008) or feature selection using a two-sample t-test in high-dimensional classification (Tibshirani et al., 2003). Within the context of the linear model, Fan and Lv (2008) showed that this simple correlation ranking possesses a sure independence screening property under certain conditions and that its revision, called iteratively sure independent screening (ISIS), is needed when the features are marginally unrelated but jointly related to the response variable. In this paper, we extend ISIS, without explicit definition of residuals, to a general pseudo-likelihood framework, which includes generalized linear models as a special case. Even in the least-squares setting, the new method improves ISIS by allowing feature deletion in the iterative process. Our technique allows us to select important features in high-dimensional classification where the popularly used two-sample t-method fails. A new technique is introduced to reduce the false selection rate in the feature screening stage. Several simulated and two real data examples are presented to illustrate the methodology.

1. Introduction

The remarkable development of computing power and other technology has allowed scientists to collect data of unprecedented size and complexity. Examples include data from microarrays, proteomics, brain images, videos, functional data and high-frequency financial data. Such a demand from applications presents many new challenges as well as opportunities for those in statistics and machine learning, and while some significant progress has been made in recent years, there remains a great deal to do.

A very common statistical problem is to model the relationship between one or more output variables Y and their associated covariates (or features) X₁, …, X_p, based on a sample of size n. A characteristic feature of many of the modern problems mentioned in the previous paragraph is that the dimensionality p is large, potentially much larger than n. Mathematically, it makes sense to consider p as a function of n, which diverges to infinity. The dimensionality grows very rapidly when interactions of the features are considered, which is necessary for many scientific endeavors. For example, in disease classification using microarray gene expression data (Tibshirani et al., 2003; Fan and Ren, 2006), the number of arrays is usually in the order of tens or hundreds while the number of gene expression profiles is in the order of tens of thousands; in the study of protein-protein interactions, the sample size may be in the order of thousands, but the number of features can be in the order of millions.

The phenomenon of noise accumulation in high-dimensional classification and regression has long been observed by statisticians and computer scientists (see (Vapnik, 1995), Hastie et al. (2009) and references therein) and has been analytically demonstrated by Fan and Fan (2008). Various feature selection techniques have been proposed in both the statistics and machine learning literature, and introductions and overviews written for the machine learning community can be found in, e.g. Liu and Motoda (1998), Guyon and Elissee3 (2003) and Guyon et al. (2006). Specific algorithms proposed include but are not restricted to FCBF (Yu and Li, 2003), CFS (Hall, 2000), ReliefF (Kononenko, 1994), FOCUS (Almuallim and Dietterich, 1994) and INTERACT (Zhao and Liu, 2007). See also the special issue published by JMLR on “variable and feature selection”, including Bi et al. (2003), Bengio and Chapados (2003) and Guyon and Elissee3 (2003).

One particularly popular family of methods is based on penalized least-squares or, more generally, penalized pseudo-likelihood. Examples include the LASSO (Tibshirani, 1996), SCAD (Fan and Li, 2001), the Dantzig selector (Candes and Tao, 2007), and their related methods. These methods have attracted a great deal of theoretical study and algorithmic development recently. See Donoho and Elad (2003), Efron et al. (2004), Zou (2006), Meinshausen and Bühlmann (2006), Zhao and Yu (2006), Zou and Li (2008), Bickel et al. (2008), and references therein. However, computation inherent in those methods makes them hard to apply directly to ultrahigh-dimensional statistical learning problems, which involve the simultaneous challenges of computational expediency, statistical accuracy, and algorithmic stability.

A method that takes up the aforementioned three challenges is the idea of independent learning, proposed and demonstrated by Fan and Lv (2008) in the regression context. The method can be derived from an empirical likelihood point of view (Hall et al., 2008) and is related to supervised principal component analysis (Bair et al., 2006; Paul et al., 2008). In the important, but limited, context of the linear model, Fan and Lv (2008) proposed a two-stage procedure to deal with this problem. First, so-called independence screening is used as a fast but crude method of reducing the dimensionality to a more moderate size (usually below the sample size); then, a more sophisticated technique, such as a penalized likelihood method based on the smoothly clipped absolute deviation (SCAD) penalty, can be applied to perform the final feature selection and parameter estimation simultaneously.

Independence screening recruits those features having the best marginal utility, which corresponds to the largest marginal correlation with the response in the context of least-squares regression. Under certain regularity conditions, Fan and Lv (2008) show surprisingly that this fast feature selection method has a ‘sure screening property’; that is, with probability very close to 1, the independence screening technique retains all of the important features in the model. A remarkable feature of this theoretical result is that the dimensionality of the model is allowed to grow exponentially in the sample size; for this reason, we refer to the method as an ‘ultrahigh’ dimensional feature selection technique, to distinguish it from other ‘high’ dimensional methods where the dimensionality can grow only polynomially in the sample size. The sure screening property is described in greater detail in Section 3.2, and as a result of this theoretical justification, the method is referred to as Sure Independence Screening (SIS).

An important methodological extension, called Iterated Sure Independence Screening (ISIS), covers cases where the regularity conditions may fail, for instance if a feature is marginally uncorrelated, but jointly correlated with the response, or the reverse situation where a feature is jointly uncorrelated but has higher marginal correlation than some important features. Roughly, ISIS works by iteratively performing feature selection to recruit a small number of features, computing residuals based on the model fitted using these recruited features, and then using the working residuals as the response variable to continue recruiting new features. The crucial step is to compute the working residuals, which is easy for the least-squares regression problem but not obvious for other problems. The improved performance of ISIS has been documented in Fan and Lv (2008).

Independence screening is a commonly used techniques for feature selection. It has been widely used for gene selection or disease classification in bioinformatics. In those applications, the genes or proteins are called statistically significant if their associated expressions in the treatment group differ statistically from the control group, resulting in a large and active literature on the multiple testing problem. See, for example, Dudoit et al. (2003) and Efron (2008). The selected features are frequently used for tumor/disease classification. See, for example, Tibshirani et al. (2003), and Fan and Ren (2006). This screening method is indeed a form of independence screening and has been justified by Fan and Fan (2008) under some ideal situations. However, common sense can carry us only so far. As indicated above and illustrated further in Section 4.1, it is easy to construct features that are marginally unrelated, but jointly related with the response. Such features will be screened out by independent learning methods such as the two-sample t test. In other words, genes that are screened out by test statistics can indeed be important in disease classification and understanding molecular mechanisms of the disease. How can we construct better feature selection procedures in ultrahigh dimensional feature space than the independence screening popularly used in feature selection?

The first goal of this paper is to extend SIS and ISIS to much more general models. One challenge here is to make an appropriate definition of a residual in this context. We describe a procedure that effectively sidesteps this issue and therefore permits the desired extension of ISIS. In fact, our method even improves the original ISIS of Fan and Lv (2008) in that it allows variable deletion in the recruiting process. Our methodology applies to a very general pseudo-likelihood framework, in which the aim is to find the parameter vector β = (β₁, …, β_p)^T that is sparse and minimizes an objective function of the form

$$Q(\mathit{\beta })=\sum _{i=1}^{n}L(Y_i,{\beta }_0+{\mathbf{x}}_i^T\mathit{\beta }),$$

where ( ${\mathbf{x}}_i^T$, Y_i) are the covariate vector and response for the i^th individual. Important applications of this methodology, which is outlined in greater detail in Section 2, include the following:

1. Generalized linear models: All generalized linear models, including logistic regression and Poisson log-linear models, fit very naturally into our methodological framework. See McCullagh and Nelder (1989) for many applications of generalized linear models. Note in particular that logistic regression models yield a popular approach for studying classification problems. In Section 4, we present simulations in which our approach compares favorably with the competing LASSO technique (Tibshirani, 1996).

2. Classification: Other common approaches to classification assume the response takes values in {−1, 1} and also fit into our framework. For instance, support vector machine classifiers (Vapnik, 1995) use the hinge loss function $L(Y_i,{\beta }_0+{\mathbf{x}}_i^T\mathit{\beta })={\{1-Y_i({\beta }_0+{\mathbf{x}}_i^T\mathit{\beta })\}}_{+}$, while the boosting algorithm AdaBoost (Freund and Schapire, 1997) uses $L(Y_i,{\beta }_0+{\mathbf{x}}_i^T\mathit{\beta })=exp\{-Y_i({\beta }_0+{\mathbf{x}}_i^T\mathit{\beta })\}$.

3. Robust fitting: In a high-dimensional linear model setting, it is advisable to be cautious about the assumed relationship between the features and the response. Thus, instead of the conventional least squares loss function, we may prefer a robust loss function such as theL₁ loss $L(Y_i,{\beta }_0+{\mathbf{x}}_i^T\mathit{\beta })=\mid Y_i-{\beta }_0-{\mathbf{x}}_i^T\mathit{\beta }\mid$ or the Huber loss (Huber, 1964), which also fits into our framework.

Any screening method, by default, has a large false selection rate (FSR), namely, many unimportant features are selected after screening. A second aim of this paper, covered in Section 3, is to present two variants of the SIS methodology, which reduce significantly the FSR. Both are based on partitioning the data into (usually) two groups. The first has the desirable property that in high-dimensional problems the probability of incorrectly selecting unimportant features is small. Thus this method is particularly useful as a means of quickly identifying features that should be included in the final model. The second method is less aggressive, and for the linear model has the same sure screening property as the original SIS technique. The applications of our proposed methods are illustrated in Section 5.

2. ISIS methodology in a general framework

Let y = (Y₁, …, Y_n)^T be a vector of responses and let x₁, …, x_n be their associated covariate (column) vectors, each taking values in ℝ^p. The vectors ( ${\mathbf{x}}_1^T$, Y₁), …, ( ${\mathbf{x}}_n^T$, Y_n) are assumed to be independent and identically distributed realizations from the population (X₁, …, X_p, Y)^T. The n × p design matrix is X = (x₁, …, x_n)^T.

2.1 Feature ranking by marginal utilities

The relationship between Y and (X₁, …, X_p)^T is often modeled through a parameter vector β = (β₁, …, β_p)^T, and the fitting of the model amounts to minimizing a negative pseudo-likelihood function of the form

$$Q({\beta }_0,\mathit{\beta })=n^{-1}\sum _{i=1}^{n}L(Y_i,{\beta }_0+{\mathbf{x}}_i^T\mathit{\beta }).$$ (1)

Here, L can be regarded as the loss of using ${\beta }_0+{\mathbf{x}}_i^T\mathit{\beta }$ to predict Y_i. The marginal utility of the j^th feature is

$$L_j=\underset{{\beta }_0,{\beta }_j}{min}{n}^{-1}\sum _{i=1}^{n}L(Y_i,{\beta }_0+X_{ij}{\beta }_j),$$ (2)

which minimizes the loss function, where x_i = (X_i1, …, X_ip)^T. The idea of SIS in this framework is to compute the vector of marginal utilities L = (L₁, …, L_p)^T and rank them according to the marginal utilities: the smaller the more important. Note that in order to compute L_j, we need only fit a model with two parameters, β₀ and β_j, so computing the vector L can be done very quickly and stably, even for an ultrahigh dimensional problem. The feature X_j is selected by SIS if L_j is one of the d smallest components of L. Typically, we may take d = ⌊n/log n⌋, though the choice of d is discussed in greater detail in Section 4.

The procedure above is an independence screening method. It uses only a marginal relation between features and the response variable to screen variables. When d is large enough, it has high probability of selecting all of the important features. For this reason, we call the method Sure Independence Screening (SIS). For classification problems with quadratic loss L, Fan and Lv (2008) show that SIS reduces to feature screening using a two-sample t-statistic. See also Hall et al. (2008) for a derivation from an empirical likelihood point of view and §3.2 for some theoretical results on the sure screening property.

2.2 Penalized pseudo-likelihood

With features crudely selected by SIS, variable selection and parameter estimation can further be carried out simultaneously using a more refined penalized (pseudo)-likelihood method, as we now describe. The approach takes joint information into consideration. By reordering the features if necessary, we may assume without loss of generality that X₁, …, X_d are the features recruited by SIS. We let x_i,d = (X_i1, …, X_id)^T and redefine β = (β₁, …, β_d)^T. In the penalized likelihood approach, we seek to minimize

$$\ell ({\beta }_0,\mathit{\beta })=n^{-1}\sum _{i=1}^{n}L(Y_i,{\beta }_0+{\mathbf{x}}_{i,d}^T\mathit{\beta })+\sum _{j=1}^d{p}_{\lambda }(\mid {\beta }_j\mid ).$$ (3)

Here, p_λ(·) is a penalty function and λ > 0 is a regularization parameter, which may be chosen by five-fold cross-validation, for example. The penalty function should satisfy certain conditions in order for the resulting estimates to have desirable properties, and in particular to yield sparse solutions in which some of the coefficients may be set to zero; see Fan and Li (2001) for further details.

Commonly used examples of penalty functions include the L₁ penalty p_λ (|β|) = λ|β| (Tibshirani, 1996; Park and Hastie, 2007), the smoothly clipped absolute deviation (SCAD) penalty (Fan and Li, 2001), which is a quadratic spline with p_λ (0) = 0 and

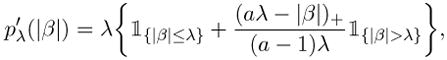for some a > 2 and |β| > 0, and the minimum concavity penalty (MCP), $p_{\lambda }^{\prime }(\mid \beta \mid )={(\lambda -\mid \beta \mid /a)}_{+}$ (Zhang, 2009). The choice a = 3.7 has been recommended in Fan and Li (2001). Unlike the L₁ penalty, SCAD and MC penalty functions have flat tails, which are fundamental in reducing biases due to penalization (Antoniadis and Fan, 2001; Fan and Li, 2001). Park and Hastie (2007) describe an iterative algorithm for minimizing the objective function for the L₁ penalty, and Zhang (2009) propose a PLUS algorithm for finding solution paths to the penalized least-squares problem with a general penalty p_λ (·). On the other hand, Fan and Li (2001) have shown that the SCAD-type of penalized loss function can be minimized iteratively using a local quadratic approximation, whereas Zou and Li (2008) propose a local linear approximation, taking the advantage of recently developed algorithms for penalized L₁ optimization (Efron et al., 2004). Starting from β⁽⁰⁾ = 0 as suggested by Fan and Lv (2008), using the local linear approximation

$$p_{\lambda }(\mid \beta \mid )\approx p_{\lambda }(\mid {\beta }^{(k)}\mid )+p_{\lambda }^{\prime }(\mid {\beta }^{(k)}\mid )(\mid \beta \mid -\mid {\beta }^{(k)}\mid ),$$

in (3), at the (k + 1)^th iteration we minimize the weighted L₁ penalty

$$n^{-1}\sum _{i=1}^{n}L(Y_i,{\beta }_0+{\mathbf{x}}_{i,d}^T\mathit{\beta })+\sum _{j=1}^d{w}_j^{(k)}\mid {\beta }_j\mid ,$$ (4)

where $w_j^{(k)}=p_{\lambda }^{\prime }(\mid {\beta }_j^{(k)}\mid )$. Note that with initial value β⁽⁰⁾ = 0, β⁽¹⁾ is indeed a LASSO estimate for the SCAD and MC penalties, since $p_{\lambda }^{\prime }(0+)=\lambda$. In other words, zero is not an absorbing state. Though motivated slightly differently, a weighted L₁ penalty is also the basis of the adaptive Lasso (Zou, 2006); in that case $w_j^{(k)}\equiv w_j=1/{\mid {\widehat{\beta }}_j\mid }^{\gamma }$, where β̂ = (β̂₁, …, β̂_d)^T may be taken to be the maximum likelihood estimator, and γ > 0 is chosen by the user. The drawback of such an approach is that zero is an absorbing state when (4) is iteratively used — components being estimated as zero at one iteration will never escape from zero.

For a class of penalty functions that includes the SCAD penalty and when d is fixed as n diverges, Fan and Li (2001) established an oracle property; that is, the penalized estimates perform asymptotically as well as if an oracle had told us in advance which components of β were non-zero. Fan and Peng (2004) extended this result to cover situations where d may diverge with d = d_n = o(n^1/5). Zou (2006) shows that the adaptive LASSO possesses the oracle property too, when d is finite. See also further theoretical studies by Zhang and Huang (2008) and Zhang (2009). We refer to the two-stage procedures described above as SIS-Lasso, SIS-SCAD and SIS-AdaLasso.

2.3 Iterative feature selection

The SIS methodology may break down if a feature is marginally unrelated, but jointly related with the response, or if a feature is jointly uncorrelated with the response but has higher marginal correlation with the response than some important features. In the former case, the important feature has already been screened at the first stage, whereas in the latter case, the unimportant feature is ranked too high by the independent screening technique. ISIS seeks to overcome these difficulties by using more fully the joint covariate information while retaining computational expedience and stability as in SIS.

In the first step, we apply SIS to pick a set 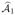of indices of size k₁, and then employ a penalized (pseudo)-likelihood method such as Lasso, SCAD, MCP or the adaptive Lasso to select a subset of these indices. This is our initial estimate of the set of indices of important features. The screening stage solves only bivariate optimizations (2) and the fitting part solves only a optimization problem (3) with moderate size k₁. This is an attractive feature in ultrahigh dimensional statistical learning.

Instead of computing residuals, as could be done in the linear model, we compute

$$L_j^{(2)}=\underset{{\beta }_0,{\mathit{\beta }}_{{\widehat{\mathcal{M}}}_1},{\beta }_j}{min}{n}^{-1}\sum _{i=1}^{n}L(Y_i,{\beta }_0+{\mathbf{x}}_{i,{\widehat{\mathcal{M}}}_1}^T{\mathit{\beta }}_{{\widehat{M}}_1}+X_{ij}{\beta }_j),$$ (5)

for $j\in {\widehat{\mathcal{M}}}_1^c=\{1,\dots ,p\}\backslash {\widehat{\mathcal{M}}}_1$, where 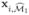is the sub-vector of x_i consisting of those elements in . This is again a low-dimensional optimization problem which can easily be solved. Note that $L_j^{(2)}$ [after subtracting the constant ${min}_{{\beta }_0,{\mathit{\beta }}_{{\widehat{\mathcal{M}}}_1}}{n}^{-1}{\sum }_{i=1}^{n}L(Y_i,{\beta }_0+{\mathbf{x}}_{i,{\widehat{\mathcal{M}}}_1}^T{\mathit{\beta }}_{{\widehat{\mathcal{M}}}_1})$ and changing the sign of the difference] can be interpreted as the additional contribution of variable X_j given the existence of variables in . After ordering { $L_j^{(2)}:j\in {\widehat{\mathcal{M}}}_1^c$}, we form the set 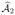consisting of the indices corresponding to the smallest k₂ elements, say. In this screening stage, an alternative approach is to substitute the fitted value 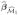from the first stage into (5) and the optimization problem (5) would only be bivariate. This approach is exactly an extension of Fan and Lv (2008) as we have

$$L(Y_i,{\beta }_0+{\mathbf{x}}_{i,{\widehat{\mathcal{M}}}_1}^T{\widehat{\mathit{\beta }}}_{{\widehat{\mathcal{M}}}_1}+X_{ij}{\beta }_j)={({\widehat{r}}_i-{\beta }_0-X_{ij}{\beta }_j)}^2,$$

for the quadratic loss, where ${\widehat{r}}_i=Y_i-{\mathbf{x}}_{i,{\widehat{\mathcal{M}}}_1}^T{\widehat{\mathit{\beta }}}_{{\widehat{\mathcal{M}}}_1}$ is the residual from the previous step of fitting. The conditional contributions of features are more relevant in recruiting variables at the second stage, but the computation is more expensive. Our numerical experiments in Section 4.4 shows the improvement of such a deviation from Fan and Lv (2008).

After the prescreening step, we use penalized likelihood to obtain

$${\widehat{\mathit{\beta }}}_2=\underset{{\beta }_{\text{0}},{\mathit{\beta }}_{{\widehat{\mathcal{M}}}_1},{\mathit{\beta }}_{{\mathcal{A}}_2}}{\text{argmin}}{n}^{-1}\sum _{i=1}^{n}L(Y_i,{\beta }_0+{\mathbf{x}}_{i,{\widehat{\mathcal{M}}}_1}^T{\mathit{\beta }}_{{\widehat{\mathcal{M}}}_1}+{\mathbf{x}}_{i,{\widehat{\mathcal{A}}}_2}^T{\mathit{\beta }}_{{\widehat{\mathcal{A}}}_2})+\sum _{j\in {\widehat{\mathcal{M}}}_1\cup {\widehat{\mathcal{A}}}_2}{p}_{\lambda }(\mid {\beta }_j\mid ).$$ (6)

Again, the penalty term encourages a sparse solution. The indices of β̂₂ that are non-zero yield a new estimated set 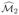of active indices. This step also deviates importantly from the approach in Fan and Lv (2008) even in the least-squares case. It allows the procedure to delete variables from the previously selected features with indices in .

The process, which iteratively recruits and deletes features, can then be repeated until we obtain a set of indices 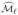which either has reached the prescribed size d, or satisfies 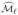= 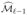. Of course, we also obtain a final estimated parameter vector β̂_ℓ. The above method can be considered as an analogue of the least squares ISIS procedure (Fan and Lv, 2008) without explicit definition of the residuals. In fact, it is an improvement even for the least-squares problem.

In general, choosing larger values of each k_r at each iteration decreases the computational cost and the probability that the ISIS procedure will terminate too early. However, it also makes the procedure more like its non-iterated counterpart, and so may offer less improvement in the awkward cases for SIS described in Section 1. In our implementation, we chose k₁ = ⌊2d/3⌋, and thereafter at the rth iteration, we took k_r = d − |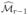|. This ensures that the iterated versions of SIS take at least two iterations to terminate; another possibility would be to take, for example, k_r = min(5, d − ||).

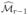Fan and Lv (2008) showed empirically that for the linear model ISIS improves significantly the performance of SIS in the difficult cases described above. The reason is that the fitting of the residuals from the (r − 1)^th iteration on the remaining features significantly weakens the priority of those unimportant features that are highly correlated with the response through their associations with {X_j: j ∈ 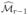}. This is due to the fact that the features {X_j: j ∈ 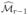} have lower correlation with the residuals than with the original responses. It also gives those important features that are missed in the previous step a chance to survive.

2.4 Generalized linear models

Recall that we say that Y is of exponential dispersion family form if its density can be written in terms of its mean μ and a dispersion parameter φ as

$$f_Y(y;\mu ,\phi )=exp\left\{\frac{y\theta (\mu )-b(\theta (\mu ))}{\phi }+c(y,\phi )\right\},$$

from some known functions θ(·), b(·) and c(·, ·). In a generalized linear model for independent responses Y₁, …, Y_n, we assert that the conditional density of Y_i given the covariate vector X_i = x_i is of exponential dispersion family form, with the conditional mean response μ_i related to x_i through $g({\mu }_i)={\mathbf{x}}_i^T\mathit{\beta }$ for some known link function g(·), and where the dispersion parameters are constrained by requiring that φ_i = φa_i, for some unknown dispersion parameter φ and known constants a₁, …, a_n. For simplicity, throughout the paper, we take a constant dispersion parameter.

It is immediate from the form of the likelihood function for a generalized linear model that such a model fits within the pseudo-likelihood framework of Section 4. In fact, we have in general that

$$L(Y_i,{\beta }_0+{\mathbf{x}}_i^T\mathit{\beta })=\sum _{i=1}^n\{b(\theta (g^{-1}({\beta }_0+{\mathbf{x}}_i^T\mathit{\beta }))-Y_i\theta (g^{-1}({\beta }_0+{\mathbf{x}}_i^T\mathit{\beta })))\}.$$ (7)

If we make the canonical choice of link function, g(·) = θ(·), then (7) simplifies to

$$L(Y_i,{\beta }_0+{\mathbf{x}}_i^T\mathit{\beta })=\sum _{i=1}^n\{b({\beta }_0+{\mathbf{x}}_i^T\mathit{\beta })-Y_i({\beta }_0+{\mathbf{x}}_i^T\mathit{\beta })\}.$$

An elegant way to handle classification problems is to assume the class label takes values 0 or 1, and fit a logistic regression model. For this particular generalized linear model, we have

$$L(Y_i,{\beta }_0+{\mathbf{x}}_i^T\mathit{\beta })=\sum _{i=1}^n\{log(1+e^{{\beta }_0+{\mathbf{x}}_i^T\mathit{\beta }})-Y_i({\beta }_0+{\mathbf{x}}_i^T\mathit{\beta })\},$$

while for Poisson log-linear models, we may take

$$L(Y_i,{\beta }_0+{\mathbf{x}}_i^T\mathit{\beta })=\sum _{i=1}^n\{e^{{\beta }_0+{\mathbf{x}}_i^T\mathit{\beta }}-Y_i({\beta }_0+{\mathbf{x}}_i^T\mathit{\beta })\}.$$

3. Reduction of false selection rates

Sure independence screening approaches are simple and quick methods to screen out irrelevant features. They are usually conservative and include many unimportant features. In this section, we outline two possible variants of SIS and ISIS that have attractive theoretical properties in terms of reducing the FSRs. The first is an aggressive feature selection method that is particularly useful when the dimensionality is very large relative to the sample size; the second is a more conservative procedure.

3.1 First variant of ISIS

It is convenient to introduce some new notation. We write 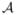for the set of active indices – that is, the set containing those indices j for which β_j ≠ 0 in the true model. Write 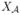= {X_j: j ∈ 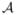} and 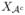= {X_j: j ∈ 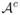} for the corresponding sets of active and inactive variables respectively.

Assume for simplicity that n is even, and split the sample into two halves at random. Apply SIS or ISIS separately to the data in each partition (with d = ⌊n/log n⌋ or larger, say), yielding two estimates 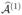and 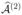of the set of active indices 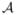. Both of them should have large FSRs, as they are constructed from a crude screening method. Assume that both sets have the satisfy

$$P(\mathcal{A}\subset {\widehat{\mathcal{A}}}^{(j)})\to 1,\text{for}j=1\text{and}2.$$

Then, the active features should appear in both sets with probability tending to one. We thus construct 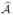= 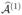∩ 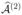as an estimate of 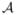. This estimate also satisfies

$$P(\mathcal{A}\subset \widehat{\mathcal{A}})\to 1.$$

However, this estimate contains many fewer indices corresponding to inactive features, as such indices have to appear twice at random in the sets 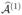and 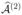. This is indeed shown in Theorem 1 below.

Just as in the original formulation of SIS in Section 2, we can now use a penalized (pseudo)-likelihood method such as SCAD to perform final feature selection from 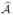and parameter estimation. We can even proceed without the penalization since the false selection rate is small.

In our theoretical support for this variant of SIS, we will make use of the following condition:

(A1) Let r ∈ ℕ, the set of natural numbers. We say the model satisfies the exchangeability condition at level r if the set of random vectors

$$\{(Y,X_{\mathcal{A}},X_{j_1},\dots ,X_{j_r}):j_1,\dots ,j_r\text{are}\text{distinct}\text{elements}\text{of}{\mathcal{A}}^c\}$$

is exchangeable.

This condition ensures that each inactive feature is equally likely to be recruited by SIS. Note that (A1) certainly allows inactive features to be correlated with the response, but does imply that each inactive feature has the same marginal distribution. In Theorem 1 below, the case r = 1 is particularly important, as it gives an upper bound on the probability of recruiting any inactive features into the model. Note that this upper bound requires only the weakest version (level 1) of the exchangeability condition.

Theorem 1

Let r ∈ ℕ, and assume the model satisfies the exchangeability condition (A1) at level r. If 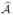denotes the estimator of 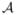from the above variant of SIS, then

$$P(\mid \widehat{\mathcal{A}}\cap {\mathcal{A}}^c\mid \ge r)\le \frac{{\left(\begin{array}{c}d\\ r\end{array}\right)}^2}{\left(\begin{array}{c}p-\mid \mathcal{A}\mid \\ r\end{array}\right)}\le \frac{1}{r!}{\left(\frac{d^2}{p-\mid \mathcal{A}\mid }\right)}^r,$$

where, for the second inequality, we require d² ≤ p − |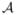| and d is the prescribed number of selected features in 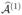or .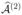

Proof

Fix r ∈ ℕ, and let 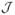= {(j₁, …, j_r): j₁, …, j_r are distinct elements of 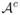}. Then

$$\begin{array}{l}P(\mid \widehat{\mathcal{A}}\cap {\mathcal{A}}^c\mid \ge r)\le \sum _{(j_1,\dots ,j_r)\in \mathcal{J}}P(j_1\in \widehat{\mathcal{A}},\cdots ,j_r\in \widehat{\mathcal{A}})\\ =\sum _{(j_1,\dots ,j_r)\in \mathcal{J}}P{(j_1\in {\widehat{\mathcal{A}}}^{(1)},\cdots ,j_r\in {\widehat{\mathcal{A}}}^{(1)})}^2,\end{array}$$

in which we use the random splitting in the last equality. Obviously, the last probability is bounded by

$$\underset{(j_1,\dots ,j_r)\in \mathcal{J}}{max}P(j_1\in {\widehat{\mathcal{A}}}^{(1)},\cdots ,j_r\in {\widehat{\mathcal{A}}}^{(1)})\sum _{(j_1,\dots ,j_r)\in \mathcal{J}}P(j_1\in {\widehat{\mathcal{A}}}^{(1)},\cdots ,j_r\in {\widehat{\mathcal{A}}}^{(1)}).$$ (8)

Since there are at most d inactive features from 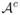in the set 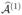, the number of r-tuples from 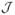falling in the set 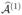can not be more than the total number of such r-tuples in 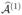, i.e.

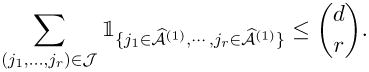Thus, we have

$$\sum _{(j_1,\dots ,j_r)\in \mathcal{J}}P(j_1\in {\widehat{\mathcal{A}}}^{(1)},\cdots ,j_r\in {\widehat{\mathcal{A}}}^{(1)})\le \left(\begin{array}{c}d\\ r\end{array}\right).$$ (9)

Substituting this into (8), we obtain

$$P(\mid \widehat{\mathcal{A}}\cap {\mathcal{A}}^c\mid \ge r)\le \left(\begin{array}{c}d\\ r\end{array}\right)\underset{(j_1,\dots ,j_r)\in \mathcal{J}}{max}P(j_1\in {\widehat{\mathcal{A}}}^{(1)},\cdots ,j_r\in {\widehat{\mathcal{A}}}^{(1)}).$$

Now, under the exchangeability condition (A1), each r-tuple of distinct indices in 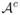is equally likely to be recruited into 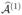. Hence, it follows from (9) that

$$\underset{(j_1,\dots ,j_r)\in \mathcal{J}}{max}P(j_1\in {\widehat{\mathcal{A}}}^{(1)},\cdots ,j_r\in {\widehat{\mathcal{A}}}^{(1)})\le \frac{\left(\begin{array}{c}d\\ r\end{array}\right)}{\left(\begin{array}{c}p-\mid \mathcal{A}\mid \\ r\end{array}\right)},$$

and the first result follows. The second result follows from the simple fact that

$$\frac{{(d-i)}^2}{p^{\ast }-i}\le \frac{d^2}{p^{\ast }},\text{for}\text{all}0\le i\le d,$$

where p^* = p − |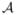|, and the simple calculation that

$$\frac{{\left(\begin{array}{c}d\\ r\end{array}\right)}^2}{\left(\begin{array}{c}{p}^{\ast }\\ r\end{array}\right)}=\frac{1}{r!}\frac{d^2(d-1^2)\cdots {(d-r+1)}^2}{p^{\ast }(p^{\ast }-1)\cdots (p^{\ast }-r+1)}\le \frac{1}{r!}{\left(\frac{d}{p^{\ast }}\right)}^r.$$

This completes the proof.

Theorem 1 gives a nonasymptotic bound, using only the symmetry arguments, and this bound is expected to be reasonably tight especially when p is large. From Theorem 1, we see that if the exchangeability condition at level 1 is satisfied and if p is large by comparison with n², then when the number of selected features d is smaller than n, we have with high probability this variant of SIS reports no ‘false positives’; that is, it is very likely that any index in the estimated active set also belongs to the active set in the true model. Intuitively, if p is large, then each inactive feature has small probability of being included in the estimated active set, so it is very unlikely indeed that it will appear in the estimated active sets from both partitions. The nature of this result is a little unusual in that it suggests a ‘blessing of dimensionality’ – the bound on the probability of false positives decreases with p. However, this is only part of the full story, because the probability of missing elements of the true active set is expected to increase with p.

Of course, it is possible to partition the data into K > 2 groups, say, each of size n/K, and estimate 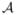by 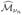∩ ∩ 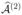… ∩ 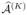, where 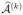represents the estimated set of active indices from the kth partition. Such a variable selection procedure would be even more aggressive than the K = 2 version; improved bounds in Theorem 1 could be obtained, but the probability of missing true active indices would be increased. As the K = 2 procedure is already quite aggressive, we consider this to be the most natural choice in practice.

In the iterated version of this first variant of SIS, we apply SIS to each partition separately to obtain two sets of indices ${\widehat{\mathcal{A}}}_1^{(1)}$ and ${\widehat{\mathcal{A}}}_1^{(2)}$, each having k₁ elements. After forming the intersection ${\widehat{\mathcal{A}}}_1={\widehat{\mathcal{A}}}_1^{(1)}\cap {\widehat{\mathcal{A}}}_1^{(2)}$, we carry out penalized likelihood estimation as before to give a first approximation to the true active set of features. We then perform a second stage of the ISIS procedure, as outlined in Section 2, to each partition separately to obtain sets of indices ${\widehat{\mathcal{M}}}_1\cup {\widehat{\mathcal{A}}}_2^{(1)}$ and ${\widehat{\mathcal{M}}}_1\cup {\widehat{A}}_2^{(2)}$. Taking the intersection of these sets and re-estimating parameters using penalized likelihood as in Section 2 gives a second approximation 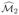to the true active set. This process can be continued until we reach an iteration ℓ with 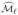= 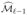, or we have recruited d indices.

3.2 Second variant of ISIS

Our second variant of SIS is a more conservative feature selection procedure and also relies on random partitioning the data into K = 2 groups as before. Again, we apply SIS to each partition separately, but now we recruit as many features into equal-sized sets of active indices 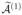and 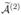as are required to ensure that the intersection 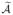= 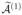∩ 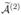has d elements. We then apply a penalized pseudo-likelihood method to the features 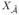= {X_j: j ∈ 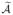} for final feature selection and parameter estimation.

Theoretical support for this method can be provided in the case of the linear model; namely, under certain regularity conditions, this variant of SIS possesses the sure screening property. More precisely, if Conditions (1)–(4) of Fan and Lv (2008) hold with 2κ + τ < 1, and we choose d = ⌊n/log n⌋, then there exists C > 0 such that

$$P(\mathcal{A}\subseteq \stackrel{\sim }{\mathcal{A}})=1-O\{exp(-{Cn}^{1-2\kappa }/logn+logp)\}.$$

The parameter κ ≥ 0 controls the rate at which the minimum signal |β_j| is allowed to converge to zero, while τ ≥ 0 controls the rate at which the maximal eigenvalue of the covariance matrix Σ = Cov(X₁, …, X_p) is allowed to diverge to infinity. In fact, we insist that |β_j| ≥ n^−κ and λ_max(Σ) ≤ n^τ for large n, where λ_max(Σ) denotes the maximal eigenvalue of Σ. Thus, these technical conditions ensure that any non-zero signal is not too small, and that the features are not too close to being collinear, and the dimensionality is also controlled via log p = o(n^1−2κ/log n), which is still of an exponential order. See Fan and Lv (2008) for further discussion of the sure screening property.

Recently, Fan and Song (2009) extended the result of Fan and Lv (2008) to generalized linear models. Let ${\widehat{L}}_0={min}_{{\beta }_0}{n}^{-1}{\sum }_{i=1}^{n}L(Y_i,{\beta }_0)$ be the baseline value to (2). The feature ranking procedure is equivalent to the thresholding method: 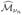= {j: L_j − L₀ ≥ νn}, in which ν_n is a given thresholding value. Under certainly regularity conditions, if

$$\underset{j\in \mathcal{A}}{min}\mid cov(X_j,Y)\mid \ge c_1{n}^{-\kappa },\text{for}\text{some}{c}_1>0\text{and}\kappa <1/2$$

and ν_n = c₀n^−2κ for a sufficiently small c₀, then we have

$$P(\mathcal{A}\subset {\widehat{\mathcal{M}}}_{{\nu }_n})\to 1,$$

exponentially fast, provided that log p_n = o(n^1−2κ). The sure screening property does not depend on the correlation of the features, as expected. However, the selected model size does depend on the correlation structure: The more correlated the features, the larger the selected model size. In fact, Fan and Song (2009) demonstrated further that with probability tending to one exponentially fast, $\mid {\widehat{\mathcal{M}}}_{{\nu }_n}\mid =O({\nu }_n^{-2}{\lambda }_{max}(\mathrm{\sum }))$. When λ_max(Σ) = O(n^τ) and λ_max(Σ) = O(n^−2κ), the selected model size is |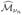| = O(n^2κ+τ). In particularly, if the condition 2κ + τ < 1 is imposed as in Fan and Lv (2008), we can reduce safely the model size to o(n) by independence learning.

An iterated version of this second variant of SIS is also available. At the first stage we apply SIS, taking enough features in equal-sized sets of active indices ${\stackrel{\sim }{\mathcal{A}}}_1^{(1)}$ and ${\stackrel{\sim }{\mathcal{A}}}_1^{(2)}$ to ensure that the intersection ${\stackrel{\sim }{\mathcal{A}}}_1={\stackrel{\sim }{\mathcal{A}}}_1^{(1)}\cap {\stackrel{\sim }{\mathcal{A}}}_1^{(2)}$ has k₁ elements. Applying penalized likelihood to the features with indices in 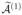gives a first approximation 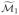to the true set of active indices. We then carry out a second stage of the ISIS procedure of Section 2 to each partition separately to obtain equal-sized new sets of indices ${\stackrel{\sim }{\mathcal{A}}}_2^{(1)}$ and ${\stackrel{\sim }{\mathcal{A}}}_2^{(2)}$, taking enough features to ensure that ${\stackrel{\sim }{\mathcal{A}}}_2={\stackrel{\sim }{\mathcal{A}}}_2^{(1)}\cap {\stackrel{\sim }{\mathcal{A}}}_2^{(2)}$ has k₂ elements. Penalized likelihood applied to 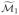∩ 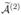gives a second approximation 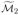to the true set of active indices. As with the first variant, we continue until we reach an iteration ℓ with 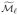= 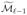, or we have recruited d indices.

4. Numerical results

We illustrate the breadth of applicability of (I)SIS and its variants by studying its performance on simulated data in four different contexts: logistic regression, Poisson regression, robust regression (with a least absolute deviation criterion) and multi-class classification with support vector machines. We will consider three different configurations of the p = 1000 features X₁, …, X_p:

• Case 1: X₁, …, X_p are independent and identically distributed N (0, 1) random variables

• Case 2: X₁, …, X_p are jointly Gaussian, marginally N(0, 1), and with $\text{corr}(X_i,X_4)=1/\sqrt{2}$ for all i ≠ 4 and corr(X_i, X_j) = 1/2 if i and j are distinct elements of {1, …, p}\{4}

• Case 3: X₁, …, X_p are jointly Gaussian, marginally N (0, 1), and with corr(X_i, X₅) = 0 for all i ≠ 5, $\text{corr}(X_i,X_4)=1/\sqrt{2}$ for all i ∉ {4, 5}, and corr(X_i, X_j) = 1/2 if i and j are distinct elements of {1, …, p} \ {4, 5}.

Case 1, with independent features, is the most straightforward for variable selection. In Cases 2 and 3, however, we have serial correlation such that corr(X_i, X_j) does not decay as |i − j| increases. We will see later that for both Case 2 and Case 3 the true coefficients are chosen such that the response is marginally uncorrelated with X₄. We therefore expect feature selection in these situations to be more challenging, especially for the non-iterated versions of SIS. Notice that in the asymptotic theory of SIS in Fan and Lv (2008), this type of dependence is ruled out by their Condition (4).

Regarding the choice of d, the asymptotic theory of Fan and Lv (2008) shows that in the linear model there exists θ^* > 0 such that we may obtain the sure screening property with ⌊n^1−θ*⌋ < d < n. However, θ^* is unknown in practice, and therefore Fan and Lv recommend d = ⌊n/log n⌋ as a sensible choice. Of course, choosing a larger value of d increases the probability that SIS will include all of the correct variables, but including more inactive variables will tend to have a slight detrimental effect on the performance of the final variable selection and parameter estimation method. We have found that this latter effect is most noticeable in models where the response provides less information. In particular, the binary response of a logistic regression model and, to a lesser extent, the integer-valued response in a Poisson regression model are less informative than the real-valued response in a linear model. We therefore used $d=\lfloor \frac{n}{4logn}\rfloor$ in the logistic regression and multicategory classification settings of Sections 4.1 and 4.5, $d=\lfloor \frac{n}{2logn}\rfloor$ in the Poisson regression settings of Section 4.2 and $d=\lfloor \frac{n}{2}\rfloor$ in Section 4.4. These model-based, rather than data-adaptive, choices of d seem to be satisfactory, as the performance of the procedures is quite robust to different choices of d (in fact using $d=\lfloor \frac{n}{logn}\rfloor$ for all models would still give good performance).

4.1 Logistic regression

In this example, the data ( ${\mathbf{x}}_1^T$, Y₁), …, ( ${\mathbf{x}}_n^T$, Y_n) are independent copies of a pair (x^T, Y) where Y is distributed, conditional on X = x, as Bin(1, p(x)), with $log(\frac{p(\mathbf{X})}{1-p(\mathbf{X})})={\beta }_0+{\mathbf{x}}^T\mathit{\beta }$. We choose n = 400.

As explained above, we chose $d=\lfloor \frac{n}{4logn}\rfloor =16$ in both the vanilla version of SIS outlined in Section 2 (Van-SIS), and the second variant (Var2-SIS) in Section 3.2. For the first variant (Var1-SIS), however, we used $d=\lfloor \frac{n}{logn}\rfloor =66$; note that since this means the selected features are in the intersection of two sets of size d, we typically end up with far fewer than d features selected by this method.

For the logistic regression example, the choice of final regularization parameter λ for the SCAD penalty (after all (I)SIS steps) was made by means of an independent validation data set of size n (generated from the same model as the original data, used only for tuning the parameters), rather than by cross-validation. This also applies for the LASSO and Nearest Shrunken Centroid (NSC, Tibshirani et al., 2003) methods which we include for comparison; instead of using SIS, this method regularizes the log-likelihood with an L₁-penalty. The reason for using the independent tuning data set is that the lack of information in the binary response means that cross-validation is particularly prone to overfitting in logistic regression, and therefore perfoms poorly for all methods.

The coefficients used in each of the three cases were as follows:

• Case 1: β₀ = 0, β₁ = 1.2439, β₂ = −1.3416, β₃ = −1.3500, β₄ = −1.7971, β₅ = −1.5810, β₆ = −1.5967, and β_j = 0 for j > 6. The corresponding Bayes test error is 0.1368.

• Case 2: β₀ = 0, β₁ = 4, β₂ = 4, β₃ = 4, ${\beta }_4=-6\sqrt{2}$, and β_j = 0 for j > 4. The Bayes test error is 0.1074.

• Case 3: β₀ = 0, β₁ = 4, β₂ = 4, β₃ = 4, ${\beta }_4=-6\sqrt{2}$, β₅ = 4/3, and β_j = 0 for j > 5. The Bayes test error is 0.1040.

In Case 1, the coefficients were chosen randomly, and were generated as $(4logn/\sqrt{n}+\mid Z\mid /4)U$ with Z ~ N(0, 1) and U = 1 with probability 0.5 and −1 with probability −0.5, independent of Z. For Cases 2 and 3, the choices ensure that even though β₄ ≠ 0, we have that X₄ and Y are independent. The fact that X₄ is marginally independent of the response is designed to make it difficult for a popular method such as the two-sample t test or other independent learning methods to recognize this important feature. Furthermore, for Case 3, we add another important variable X₅ with a small coefficient to make it even more difficult to identify the true model. For Case 2, the ideal variables picked up by the two sample test or independence screening technique are X₁, X₂ and X₃. Using these variables to build the ideal classifier, the Bayes risk is 0.3443, which is much larger than the Bayes error 0.1074 of the true model with X₁, X₂, X₃, X₄. In fact one may exaggerate Case 2 to make the Bayes error using the independence screening technique close to 0.5, which corresponds to random guessing, by setting β₀ = 0, β₁ = β₂ = β₃ = a, β_m = a for m = 5, 6, ···, j, ${\beta }_4=-a(j-1)\sqrt{2}/2$, and β_m = 0 for m > j. For example, the Bayes error using the independence screening technique, which deletes X₄, is 0.4290 when j = 20 and a = 4 while the corresponding Bayes error using X_m, m = 1, 2, ···, 20 is 0.0445.

In the tables below, we report several performance measures, all of which are based on 100 Monte Carlo repetitions. The first two rows give the median L₁ and squared L₂ estimation errors ${\left|\right|\mathit{\beta }-\widehat{\mathit{\beta }}\left|\right|}_1={\sum }_{j=0}^p\mid {\beta }_j-{\widehat{\beta }}_j\mid$ and ${\left|\right|\mathit{\beta }-\widehat{\mathit{\beta }}\left|\right|}_2^2={\sum }_{j=0}^p{({\beta }_j-{\widehat{\beta }}_j)}^2$. The third row gives the proportion of times that the (I)SIS procedure under consideration includes all of the important features in the model, while the fourth reports the corresponding proportion of times that the final features selected, after application of the SCAD or LASSO penalty as appropriate, include all of the important ones. The fifth row gives the median final number of features selected. Measures of fit to the training data are provided in the sixth, seventh and eighth rows, namely the median values of 2Q(β̂₀, β̂), defined in (1), Akaike’s information criterion (Akaike, 1974), which adds twice the number of features in the final model, and the Bayesian information criterion (Schwarz, 1978), which adds the product of log n and the number of features in the final model. Finally, an independent test data set of size 100n was used to evaluate the median value of 2Q(β̂₀, β̂) on the test data (Row 9), as well as to report the median 0–1 test error (Row 10), where we observe an error if the test response differs from the fitted response by more than 1/2.

Table 1 compares five methods, Van-SIS, Var1-SIS, Var2-SIS, LASSO, and NSC. The most noticeable observation is that while the LASSO always includes all of the important features, it does so by selecting very large models – a median of 94 variables, as opposed to the correct number, 6, which is the median model size reported by all three SIS-based methods. This is due to the bias of the LASSO, as pointed out by Fan and Li (2001) and Zou (2006), which encourages the choice of a small regularization parameter to make the overall mean squared error small. Consequently, many unwanted features are also recruited. This is also evidenced by comparing the differences between L₁ and L₂ losses in the first two rows. Thus the LASSO method has large estimation error, and while 2Q(β̂₀, β̂) is small on the training data set, this is a result of overfit, as seen by the large values of AIC/BIC, 2Q(β̂₀, β̂) on the test data and the 0–1 test error.

Table 1.

Logistic regression, Case 1

	Van-SIS	Var1-SIS	Var2-SIS	LASSO	NSC
||β – β̂||1	1.1093	1.2495	1.2134	8.4821	N/A
${\left|\right|\mathit{\beta }-\widehat{\mathit{\beta }}\left|\right|}_2^2$	0.4861	0.5237	0.5204	1.7029	N/A
Prop. incl. (I)SIS models	0.99	0.84	0.91	N/A	N/A
Prop. incl. final models	0.99	0.84	0.91	1.00	0.34
Median final model size	6	6	6	94	3
2Q(β̂0, β̂) (training)	237.21	247.00	242.85	163.64	N/A
AIC	250.43	259.87	256.26	352.54	N/A
BIC	277.77	284.90	282.04	724.70	N/A
2Q(β̂0, β̂) (test)	271.81	273.08	272.91	318.52	N/A
0–1 test error	0.1421	0.1425	0.1426	0.1720	0.3595

As the features are independent in Case 1, it is unsurprising to see that Van-SIS has the best performance of the three SIS-based methods. Even with the larger value of d used for Var1-SIS, it tends to miss important features more often than the other methods. Although the method appears to have value as a means of obtaining a minimal set of features that should be included in a final model, we will not consider Var1-SIS further in our simulation study.

Table 2 displays the results of repeating the Case 1 simulations for Van-SIS, Var1-SIS and Var2-SIS under the same conditions, but using the LASSO penalty function rather than the SCAD penalty function after the SIS step. These versions are called Van-SIS-LASSO, Var1-SIS-LASSO and Var2-SIS-LASSO respectively. We see that, as well as decreasing the computational cost, using any of the three versions of SIS before the LASSO improves performance substantially compared with applying the LASSO to the full set of features. On the other hand, the results are less successful than applying SIS and its variants in conjuction with the SCAD penalty for final feature selection and parameter estimation. We therefore do not consider Van-SIS-LASSO, Var1-SIS-LASSO and Var2-SIS-LASSO further.

Table 2.

Logistic regression, Case 1

	Van-SIS-LASSO	Var1-SIS-LASSO	Var2-SIS-LASSO
||β̂ – β̂||1	3.8500	2.1050	3.0055
${\left|\right|\mathit{\beta }-\widehat{\mathit{\beta }}\left|\right|}_2^2$	1.0762	0.7536	0.9227
Prop. incl. (I)SIS models	0.99	0.84	0.91
Prop. incl. final models	0.99	0.84	0.91
Median final model size	16.0	9.0	14.5
2Q(β̂0, β̂) (training)	207.86	240.44	226.95
AIC	239.69	260.49	255.99
BIC	302.98	295.40	316.36
2Q(β̂0, β̂) (test)	304.79	280.95	291.79
0–1 test error	0.1621	0.1476	0.1552

In Cases 2 and 3, we also consider the iterated versions of Van-SIS and Var2-SIS, which we denote Van-ISIS and Var2-ISIS respectively. At each intermediate stage of the ISIS procedures, the Bayesian information criterion was used as a fast way of choosing the SCAD regularization parameter.

From Tables 3 and 4, we see that the non-iterated SIS methods fail badly in these awkward cases. Their performance is similar to that of the LASSO method. On the other hand, both of the iterated methods Van-ISIS and Var2-ISIS perform extremely well (and similarly to each other).

Table 3.

Logistic regression, Case 2

	Van-SIS	Van-ISIS	Var2-SIS	Var2-ISIS	LASSO	NSC
||β̂ – β̂||1	20.0504	1.9445	20.1100	1.8450	21.6437	N/A
${\left|\right|\mathit{\beta }-\widehat{\mathit{\beta }}\left|\right|}_2^2$	9.4101	1.0523	9.3347	0.9801	9.1123	N/A
Prop. incl. (I)SIS models	0.00	1.00	0.00	1.00	N/A	N/A
Prop. incl. final models	0.00	1.00	0.00	1.00	0.00	0.21
Median final model size	16	4	16	4	91	16.5
2Q(β̂0, β̂) (training)	307.15	187.58	309.63	187.42	127.05	N/A
AIC	333.79	195.58	340.77	195.58	311.10	N/A
BIC	386.07	211.92	402.79	211.55	672.34	N/A
2Q(β̂0, β̂) (test)	344.25	204.23	335.21	204.28	258.65	N/A
0–1 test error	0.1925	0.1092	0.1899	0.1092	0.1409	0.3765

Table 4.

Logistic regression, Case 3

	Van-SIS	Van-ISIS	Var2-SIS	Var2-ISIS	LASSO	NSC
||β̂ – β̂||1	20.5774	2.6938	20.6967	3.2461	23.1661	N/A
${\left|\right|\mathit{\beta }-\widehat{\mathit{\beta }}\left|\right|}_2^2$	9.4568	1.3615	9.3821	1.5852	9.1057	N/A
Prop. incl. (I)SIS models	0.00	1.00	0.00	1.00	N/A	N/A
Prop. incl. final models	0.00	0.90	0.00	0.98	0.00	0.17
Median final model size	16	5	16	5	101.5	10
2Q(β̂0, β̂) (training)	269.20	187.89	296.18	187.89	109.32	N/A
AIC	289.20	197.59	327.66	198.65	310.68	N/A
BIC	337.05	218.10	389.17	219.18	713.78	N/A
2Q(β̂0, β̂) (test)	360.89	225.15	358.13	226.25	275.55	N/A
0–1 test error	0.1933	0.1120	0.1946	0.1119	0.1461	0.3866

4.2 Poisson regression

In our second example, the generic response Y is distributed, conditional on X = x, as Poisson(μ(x)), where log μ(x) = β₀ + x^T β.

Due to the extra information in the count response, we choose n = 200, and apply all versions of (I)SIS with $d=\lfloor \frac{n}{2logn}\rfloor =37$. We also use 10-fold cross-validation to choose the final regularization parameter for the SCAD and LASSO penalties. The coeffcients used were as follows:

• Case 1: β₀ = 5, β₁ = −0.5423, β₂ = 0.5314, β₃ = −0.5012, β₄ = −0.4850, β₅ = −0.4133, β₆ = 0.5234, and β_j = 0 for j > 6.

• Case 2: β₀ = 5, β₁ = 0.6, β₂ = 0.6, β₃ = 0.6, ${\beta }_4=-0.9\sqrt{2}$, and β_j = 0 for j > 4.

• Case 3: β₀ = 5, β₁ = 0.6, β₂ = 0.6, β₃ = 0.6, ${\beta }_4=-0.9\sqrt{2}$, β₅ = 0.15, and β_j = 0 for j > 5.

In Case 1, the magnitudes of the coefficients β₁,…,β₆ were generated as $(\frac{logn}{\sqrt{n}}+\mid Z\mid /8)U$ with Z ~ N(0,1) and U = 1 with probability 0.5 and −1 with probability 0.5, independently of Z. Again, the choices in Cases 2 and 3 ensure that, even though β₄ ≠ 0, we have corr(X₄, Y) = 0. The coefficients are a re-scaled version of those in the logistic regression model, except that β₀ = 5 is used to control an appropriate signal-to-noise ratio.

The results are shown in Tables 5, 6 and 7. Even in Case 1, with independent features, the ISIS methods outperform SIS, so we chose not to present the results for SIS in the other two cases. Again, both Van-ISIS and Var2-ISIS perform extremely well, almost always including all the important features in relatively small final models. The LASSO method continues to suffer from overfitting, particularly in the difficult Cases 2 and 3.

Table 5.

Poisson regression, Case 1

	Van-SIS	Van-ISIS	Var2-SIS	Var2-ISIS	LASSO
||β̂ – β̂||1	0.0695	0.1239	1.1773	0.1222	0.1969
${\left|\right|\mathit{\beta }-\widehat{\mathit{\beta }}\left|\right|}_2^2$	0.0225	0.0320	0.4775	0.0330	0.0537
Prop. incl. (I)SIS models	0.76	1.00	0.45	1.00	N/A
Prop. incl. final models	0.76	1.00	0.45	1.00	1.00
Median final model size	12	18	13	17	27
2Q(β̂0, β̂) (training)	1560.85	1501.80	7735.51	1510.38	1534.19
AIC	1586.32	1537.80	7764.51	1542.14	1587.23
BIC	1627.06	1597.17	7812.34	1595.30	1674.49
2Q(β̂0, β̂) (test)	1557.74	1594.10	14340.26	1589.51	1644.63

Table 6.

Poisson regression, Case 2

	Van-ISIS	Var2-ISIS	LASSO
||β̂ – β̂||1	0.2705	0.2252	3.0710
${\left|\right|\mathit{\beta }-\widehat{\mathit{\beta }}\left|\right|}_2^2$	0.0719	0.0667	1.2856
Prop. incl. (I)SIS models	1.00	0.97	N/A
Prop. incl. final models	1.00	0.97	0.00
Median final model size	18	16	174
2Q(β̂0, β̂) (training)	1494.53	1509.40	1369.96
AIC	1530.53	1541.17	1717.91
BIC	1589.90	1595.74	2293.29
2Q(β̂0, β̂) (test)	1629.49	1614.57	2213.10

Table 7.

Poisson regression, Case 3

	Van-ISIS	Var2-ISIS	LASSO
||β̂ – β̂||1	0.2541	0.2319	3.0942
${\left|\right|\beta -\widehat{\mathit{\beta }}\left|\right|}_2^2$	0.0682	0.0697	1.2856
Prop. incl. (I)SIS models	0.97	0.91	0.00
Prop. incl. final models	0.97	0.91	0.00
Median final model size	18	16	174
2Q(β̂0, β̂) (training)	1500.03	1516.14	1366.63
AIC	1536.03	1546.79	1715.35
BIC	1595.40	1600.17	2293.60
2Q(β̂0, β̂) (test)	1640.27	1630.58	2389.09

4.3 Robust regression

We have also conducted similar numerical experiments using L₁-regression for the three cases in an analogous manner to the previous two examples. We obtain similar results. Both versions of ISIS are effective in selecting important features with relatively low false positive rates. Hence, the prediction errors are also small. On the other hand, LASSO missed the difficult variables in cases 2 and 3 and also selected models with a large number of features to attenuate the bias of the variable selection procedure. As a result, its prediction errors are much larger. To save space, we omit the details of the results.

4.4 Linear regression

Note that our new ISIS procedure allows feature deletion in each step. It is an important improvement over the original proposal of Fan and Lv (2008) even in the ordinary least-squares setting. To demonstrate this, we choose Case 3, the most difficult one, with coefficients given as follows.

• Case 3: β₀ = 0, β₁ = 5, β₂ = 5, β₃ = 5, ${\beta }_4=-15\sqrt{2}/2$, β₅ = 1, and β_j = 0 for j > 5.

The response Y is set as Y = x^T β + ε with independent ε ~ N(0,1). This model is the same as Example 4.2.3 of Fan and Lv (2008). Using n = 70 and d = n/2, our new ISIS method includes all five important variables for 91 out of the 100 repetitions, while the original ISIS without feature deletion includes all the important features for only 36 out of the 100 repetitions. The median model size of our new variable selection procedure with variable deletion is 21, whereas the median model size corresponding to the original ISIS of Fan and Lv (2008) is 19.

We have also conducted the numerical experiment with a different sample size n = 100 and d = n/2 = 50. For 97 out of 100 repetitions, our new ISIS includes all the important features while ISIS without variable deletion includes all the important features for only 72 repetitions. Their median model sizes are both 26. This clearly demonstrates the improvement of allowing feature deletion in this example.

4.5 Multicategory classification

Our final example in this section is a four-class classification problem. Here we study two different feature configurations, both of which depend on first generating independent X̃₁,…,X̃_p such that X̃₁,…,X̃₄ are uniformly distributed on [ $-\sqrt{3},\sqrt{3}$], and X̃₅,…,X̃_p are distributed as N(0, 1). We use these random variables to generate the following cases:

• Case 1: X_j = X̃_j for j = 1,…,p

• Case 2: $X_1={\stackrel{\sim }{X}}_1-\sqrt{2}{\stackrel{\sim }{X}}_5,X_2={\stackrel{\sim }{X}}_2+\sqrt{2}{\stackrel{\sim }{X}}_5,X_3={\stackrel{\sim }{X}}_3-\sqrt{2}{\stackrel{\sim }{X}}_5,X_4={\stackrel{\sim }{X}}_4+\sqrt{2}{\stackrel{\sim }{X}}_5$, and $X_j=\sqrt{3}{\stackrel{\sim }{X}}_j$ for j = 5,…,p.

Conditional on X = x, the response Y was generated according to P(Y = k|X̃ = x̃) ∝ exp{f_k(x̃)}, for k = 1,…,4, where f₁(x̃) = −ax̃₁ + ax̃_4, f₂(x̃) = ax̃₁ − ax̃₂, f₃(x̃) = ax̃₂ − ax̃₃, and f₄ (x̃) = ax̃₃ − ax̃₄, with $a=5/\sqrt{3}$.

In both Case 1 and Case 2, all features have the same standard deviation since sd(X_j) = 1 for j = 1,2,…, p in Case 1 and $\text{sd}(X_j)=\sqrt{3}$ for j = 1,2,…, p in Case 2. Moreover, for this case, the variable X₅ is marginally unimportant, but jointly significant, so it represents a challenge to identify this as an important variable. For both Case 1 and Case 2, the Bayes error is 0.1373.

For the multicategory classification we use the loss function proposed by Lee et al. (2004). Denote the coefficients for the kth class by β_0k and β_k for k = 1,2,3,4, and let $\mathbf{B}=({({\beta }_{01},{\mathit{\beta }}_1^T)}^T,{({\beta }_{02},{\mathit{\beta }}_2^T)}^T,{({\beta }_{03},{\mathit{\beta }}_3^T)}^T,{({\beta }_{04},{\mathit{\beta }}_2^T)}^T)$. Let f_k(x) ≡ f_k(x, β_0k, β_k) = β_0k + x^Tβ_k, k = 1,2,3,4, and

$$\mathbf{f}(\mathbf{x})\equiv \mathbf{f}(\mathbf{x},\mathbf{B})={(f_1(\mathbf{x}),f_2(\mathbf{x}),f_3(\mathbf{x}),f_4(\mathbf{x}))}^T.$$

The loss function is given by L(Y, f(x)) = Σ_j≠Y [1 + f_j(x)]₊, where [ψ]₊ = ψ ≥ 0 and 0 otherwise. Deviating slightly from our standard procedure, the marginal utility of the j^th feature is defined by

$$L_j=\underset{\mathbf{B}}{min}\sum _{i=1}^{n}L(Y_i,\mathbf{f}(X_{ij},\mathbf{B}))+\frac{1}{2}\sum _{k=1}^4{\beta }_{jk}^2$$

to avoid possible unidentifiablity issues due to the hinge loss function. Analogous modification is applied to (5) in the iterative feature selection step. With estimated coefficients β̂_0k and β̂_k, and f̂_k(x) = β̂_0k + x^Tβ̂_k for k = 1, 2, 3, 4, the estimated classification rule is given by argmax_kf̂_k(x). There are some other appropriate multi-category loss functions such as the one proposed by Liu et al. (2005).

As with the logistic regression example in Section 4.1, we use n = 400, $d=\lfloor \frac{n}{4logn}\rfloor =16$ and an independent validation data set of size n to pick the final regularization parameter for the SCAD penalty.

The results are given in Table 8. The mean estimated testing error was based on a further testing data set of size 200n, and we also report the standard error of this mean estimate. In the case of independent features, all (I)SIS methods have similar performance. The benefits of using iterated versions of the ISIS methodology are again clear for Case 2, with dependent features.

Table 8.

Multicategory classification

	Van-SIS	Van-ISIS	Var2-SIS	Var2-ISIS	LASSO	NSC
	Case 1
Prop. incl. (I)SIS models	1.00	1.00	0.99	1.00	N/A	N/A
Prop. incl. final model	1.00	1.00	0.99	1.00	0.00	0.68
Median modal size	2.5	4	10	5	19	4
0–1 test error	0.3060	0.3010	0.2968	0.2924	0.3296	0.4524
Test error standard error	0.0067	0.0063	0.0067	0.0061	0.0078	0.0214
	Case 2
Prop. incl. (I)SIS models	0.10	1.00	0.03	1.00	N/A	N/A
Prop. incl. final models	0.10	1.00	0.03	1.00	0.33	0.30
Median modal size	4	11	5	9	54	9
0–1 test error	0.4362	0.3037	0.4801	0.2983	0.4296	0.6242
Test error standard error	0.0073	0.0065	0.0083	0.0063	0.0043	0.0084

5. Real data examples

In this section, we apply our proposed methods to two real data sets. The first one has a binary response while the second is multi-category. We treat both as classification problems and use the hinge loss discussed in Section 4.5. We compare our methods with two alternatives: the LASSO and NSC.

5.1 Neuroblastoma data

We first consider the neuroblastoma data used in Oberthuer et al. (2006). The study consists of 251 patients of the German Neuroblastoma Trials NB90-NB2004, diagnosed between 1989 and 2004. At diagnosis, patients’ ages range from 0 to 296 months with a median age of 15 months. They analyzed 251 neuroblastoma specimens using a customized oligonucleotide microarray with the goal of developing a gene expression-based classification rule for neuroblastoma patients to reliably predict courses of the disease. This also provides a comprehensive view on which set of genes is responsible for neuroblastoma.

The complete data set, obtained via the MicroArray Quality Control phase-II (MAQC-II) project, includes gene expression over 10,707 probe sites. Of particular interest is to predict the response labeled “3-year event-free survival” (3-year EFS) which is a binary variable indicating whether each patient survived 3 years after the diagnosis of neuroblastoma. Excluding five outlier arrays, there are 246 subjects out of which 239 subjects have 3-year EFS information available with 49 positives and 190 negatives. We apply SIS and ISIS to reduce dimensionality from p = 10,707 to d = 50. On the other hand, our competitive methods LASSO and NSC are applied directly to p = 10,707 genes. Whenever appropriate, five-fold cross validation is used to select tuning parameters. We randomly select 125 subjects (25 positives and 100 negatives) to be the training set and the remainder are used as the testing set. Results are reported in the top half of Table 9. Selected probes for LASSO and all different (I)SIS methods are reported in Table 10.

Table 9.

Results from analyzing two endpoints of the neuroblastoma data

End point		SIS	ISIS	var2-SIS	var2-ISIS	LASSO	NSC
3-year EFS	No. of features	5	23	10	12	57	9413
	Testing error	19/114	22/114	22/114	21/114	22/114	24/114
Gender	No. of features	6	2	4	2	42	3
	Testing error	4/126	4/126	4/126	4/126	5/126	4/126

Table 10.

Selected probes for the 3-year EFS end point

Probe	SIS	ISIS	var2-SIS	var2-ISIS	LASSO
‘A_23_P160638’					x
‘A_23_P168916’		x			x
‘A_23_P42882’		x
‘A_23_P145669’					x
‘A_32_P50522’					x
‘A_23_P34800’					x
‘A_23_P86774’		x
‘A_23_P417918’			x		x
‘A_23_P100711’					x
‘A_23_P145569’					x
‘A_23_P337201’					x
‘A_23_P56630’		x		x	x
‘A_23_P208030’		x			x
‘A_23_P211738’		x
‘A_23_P153692’					x
‘A_24_P148811’			x
‘A_23_P126844’			x		x
‘A_23_P25194’					x
‘A_24_P399174’					x
‘A_24_P183664’					x
‘A_23_P59051’				x
‘A_24_P14464’					x
‘A_23_P501831’	x		x
‘A_23_P103631’				x
‘A_23_P32558’			x
‘A_23_P25873’		x
‘A_23_P95553’					x
‘A_24_P227230’		x			x
‘A_23_P5131’					x
‘A_23_P218841’					x
‘A_23_P58036’					x
‘A_23_P89910’		x
‘A_24_P98783’					x
‘A_23_P121987’		x			x
‘A_32_P365452’					x
‘A_23_P109682’		x
‘Hs58251.2’				x
‘A_23_P121102’		x
‘A_23_P3242’					x
‘A_32_P177667’					x
‘Hs6806.2’					x
‘Hs376840.2’					x
‘A_24_P136691’					x
‘Pro25G_B35_D_7’		x		x
‘A_23_P87401’			x
‘A_32_P302472’					x
‘Hs343026.1’				x
‘A_23_P216225’		x		x	x
‘A_23_P203419’		x			x
‘A_24_P22163’		x			x
‘A_24_P187706’					x
‘C1_QC’					x
‘Hs190380.1’		x			x
‘Hs117120.1’				x
‘A_32_P133518’					x
‘EQCP1_Pro25G_T5’					x
‘A_24_P111061’				x
‘A_23_P20823’	x	x		x	x
‘A_24_P211151’			x
‘Hs265827.1’		x			x
‘Pro25G_B12_D_7’					x
‘Hs156406.1’					x
‘A_24_P902509’				x
‘A_32_P32653’					x
‘Hs42896.1’		x
‘A_32_P143793’	x		x		x
‘A_23_P391382’					x
‘A_23_P327134’					x
‘Pro25G_EQCP1_T5’					x
‘A_24_P351451’			x
‘Hs170298.1’					x
‘A_23_P159390’					x
‘Hs272191.1’		x
‘r60_a135’					x
‘Hs439489.1’					x
‘A_23_P107295’					x
‘A_23_P100764’	x	x	x	x	x
‘A_23_P157027’		x
‘A_24_P342055’					x
‘A_23_P1387’	x
‘Hs6911.1’					x
‘r60_1’					x

In MAQC-II, a specially designed end point is the gender of each subject, which should be an easy classification. The goal of this specially designed end point is to compare the performance of different classifiers for simple classification jobs. The gender information is available for all the non-outlier 246 arrays with 145 males and 101 females. We randomly select 70 males and 50 females to be in the training set and use the others as the testing set. We set d = 50 for our SIS and ISIS as in the case of the 3-year EFS end point. The results are given in the bottom half of Table 9. Selected probes for all different methods are reported in Table 11.

Table 11.

Selected probe for Gender end point

Probe	SIS	ISIS	var2-SIS	var2-ISIS	LASSO	NSC
‘A_23_P201035’					x
‘A_24_P167642’					x
‘A_24_P55295’					x
‘A_24_P82200’	x
‘A_23_P109614’					x
‘A_24_P102053’					x
‘A_23_P170551’					x
‘A_23_P329835’						x
‘A_23_P70571’					x
‘A_23_P259901’					x
‘A_24_P222000’					x
‘A_23_P160729’					x
‘A_23_P95553’	x		x
‘A_23_P100315’					x
‘A_23_P10172’					x
‘A_23_P137361’					x
‘A_23_P202484’					x
‘A_24_P56240’					x
‘A_32_P104448’					x
(−)3xSLv1’					x
‘A_24_P648880’	x				x
‘Hs446389.2’					x
‘A_23_P259314’	x	x	x	x	x	x
‘Hs386420.1’					x
‘Pro25G_B32_D_7’					x
‘Hs116364.2’					x
‘A_32_P375286’	x				x
‘A_32_P152400’					x
‘A_32_P105073’					x
‘Hs147756.1’	x
‘Hs110039.1’					x
‘r60_a107’					x
‘Hs439208.1’					x
‘A_32_P506090’					x
‘A_24_P706312’			x
‘Hs58042.1’					x
‘A_23_P128706’					x
‘Hs3569.1’					x
‘A_24_P182900’					x
‘A_23_P92042’					x
‘Hs170499.1’					x
‘A_24_P500584’	x	x	x	x	x	x
‘A_32_P843590’					x
‘Hs353080.1’					x
‘A_23_P388200’					x
‘C1_QC’					x
‘Hs452821.1’					x

We can see from Table 9 that our (I)SIS methods compare favorably with the LASSO and NSC. Especially for the end point 3-year EFS, our methods use fewer features while giving smaller testing error. For the end point GENDER, Table 11 indicates that the most parsimonious model given by ISIS and Var2-ISIS is a sub model of others.

5.2 SRBCT data

In this section, we apply our method to the children cancer data set reported in Khan et al. (2001). Khan et al. (2001) used artificial neural networks to develop a method of classifying the small, round blue cell tumors (SRBCTs) of childhood to one of the four categories: neuroblastoma (NB), rhabdomyosarcoma (RMS), non-Hodgkin lymphoma (NHL), and the Ewing family of tumors (EWS) using cDNA gene expression profiles. Accurate diagnosis of SRBCTs to these four distinct diagnostic categories is important in that the treatment options and responses to therapy are different from one category to another.

After filtering, 2308 gene profiles out of 6567 genes are given in the SRBCT data set. It is available online at http://research.nhgri.nih.gov/microarray/Supplement/. It includes a training set of size 63 (12 NBs, 20 RMSs, 8 NHLs, and 23 EWS) and an independent test set of size 20 (6 NBs, 5 RMSs, 3 NHLs, and 6 EWS).

Before performing classification, we standardize the data sets by applying a simple linear transformation to both the training set and the test set. The linear transformation is based on the training data so that, after standardizing, the training data have mean zero and standard deviation one. Our (I)SIS reduces dimensionality from p = 2308 to d = ⌊63/log 63⌋ = 15 first while alternative methods LASSO and NSC are applied to p = 2308 gene directly. Whenever appropriate, a four-fold cross validation is used to select tuning parameters.

ISIS, var2-ISIS, LASSO and NSC all achieve zero test error on the 20 samples in the test set. NSC uses 343 genes and LASSO requires 71 genes. However ISIS and var2-ISIS use 15 and 14 genes, respectively.

This real data application delivers the same message that our new ISIS and var2-ISIS methods can achieve competitive classification performance using fewer features.