Abstract
The little owl (Athene noctua) has declined significantly in many parts of Europe, including the Netherlands. To understand the demographic mechanisms underlying their decline, we analysed all available Dutch little owl ringing data. The data set spanned 35 years, and included more than 24,000 ringed owls, allowing detailed estimation of survival rates through multi-state capture–recapture modelling taking dispersal into account. We investigated geographical and temporal variation in age-specific survival rates and linked annual survival estimates to population growth rate in corresponding years, as well as to environmental covariates. The best model for estimating survival assumed time effects on both juvenile and adult survival rates, with average annual survival estimated at 0.258 (SE = 0.047) and 0.753 (SE = 0.019), respectively. Juvenile survival rates decreased with time whereas adult survival rates fluctuated regularly among years, low survival occurring about every 4 years. Years when the population declined were associated with low juvenile survival. More than 60% of the variation in juvenile survival was explained by the increase in road traffic intensity or in average temperature in spring, but these correlations rather reflect a gradual decrease in juvenile survival coinciding with long-term global change than direct causal effects. Surprisingly, vole dynamics did not explain the cyclic dynamics of adult survival rate. Instead, dry and cold years led to low adult survival rates. Low juvenile survival rates, that limit recruitment of first-year breeders, and the regular occurrence of years with poor adult survival, were the most important determinants of the population decline of the little owl.
Electronic supplementary material
The online version of this article (doi:10.1007/s00442-010-1868-x) contains supplementary material, which is available to authorized users.
Keywords: Demography, Conservation, Ringing data, Multistate capture–recapture, Vital rates
Introduction
Effective management to let declining populations recover depends critically on identifying which demographic variables are limiting and for what causes (Bro et al. 2000; Caughley 1994; Peery et al. 2004). Identifying which demographic parameters most strongly affect the population growth rate involves studying temporal or spatial variation in dynamics. However, collecting sufficient data to monitor vital rates over a long period and across large areas is difficult. Fortunately, for many bird species, volunteer ringers have collected a formidable amount of data on marked individuals (Saurola and Francis 2004), but its use is often compromised by the heterogeneity of ringing activity in space and time and the fact that recoveries by the general public are collected in a non-standardised way. Multi-state capture–recapture models allow one to reduce the effects of heterogeneity in the data on the survival rates obtained. This is achieved by taking into account that individuals in different, non-permanent states may have different capture probabilities (i.e. different sites; Hestbeck et al. 1991) and by including unobservable states (Kendall and Nichols 2002). Using both capture–recapture and mark–recovery data in the same multi-state models allows a more efficient use of all available data (Duriez et al. 2009). These models raise promising perspectives for the use of ringing and recovery data gathered on a large scale in identifying the key factors in population dynamics.
We used these new techniques to analyse data on the little owl (Athene noctua), a species in decline across Europe (Van Nieuwenhuyse et al. 2008). Degradation and fragmentation of the traditional agricultural and pastoral habitats, which may lead to food limitation during the breeding season, are thought to be the main factors explaining the decline (Martínez and Zuberogoitia 2004; Zabala et al. 2006; Thorup et al. 2010). Unfortunately, despite the fact that the little owl is widely distributed throughout Europe (Mikkola 1983), modelling demographic processes in little owl populations has not received much scientific attention until recently. Letty et al. (2001) found that survival rates of little owls varied between three small populations in eastern France, and population dynamics were highly sensitive to both adult and first-year survival rates. Schaub et al. (2006) found that variation in adult survival contributed most to variation in population growth rates in three of four local populations of little owls in Switzerland and Germany and that differences between these populations mainly stem from differences in immigration and in local juvenile survival rate. Both studies focused on local dynamics and local survival differences, and results are highly influenced by the scale of the studied populations. Therefore, long-term and large-scale studies of demography have been listed as research priorities for the little owl (Van Nieuwenhuyse et al. 2008).
In the Netherlands, the number of breeding pairs has decreased by 50–70% since the 1970s (Van Nieuwenhuyse et al. 2008; Fig. 1), and therefore the species is on the Dutch Red List. In 2000, 5,500–6,500 breeding pairs were estimated to be present. A large part of these birds breed in artificial nest boxes in which ringing and monitoring of birds is facilitated. Since the late 1990s, the effort of retrapping adult breeding birds increased due to the “Recapturing Adults for Survival” project. Moreover, the interest of the general public for this species increased the return of recovery information. A large scale dataset of ringed Dutch little owls is now available, spanning a period of 35 years.
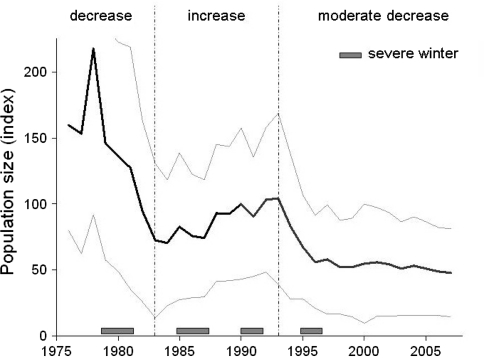
Fig. 1.
Trend of the little owl (Athene noctua) population in the Netherlands from the breeding bird monitoring scheme organised by SOVON and Statistics Netherlands (index: 1990 = 100). Thin lines represent lower and upper 95% confidence limits. Three trend periods have been defined for analyses. Severe winters (1978/79, 1981/82, 1984/85, 1985/86, 1986/87, 1995/96 and 1996/97) are also indicated
We estimated survival rates using this dataset of little owls ringed across all the Netherlands. We compared age-specific survival rates between geographical regions and time periods with different population trends. We investigated which age class contributed most to the dynamics of the species by correlating annual values of juvenile and adult survival to the rate of population change. In an attempt to explain the observed variation in survival rates, we correlated annual survival estimates with environmental factors such as weather conditions, habitat quality and the intensity of road traffic.
Materials and methods
Species
The little owl is sedentary, has a medium life span of c. 4 years, and lives in half-open and open landscapes. This small-sized owl feeds mainly on voles and large invertebrates. It breeds in cavities, traditionally mostly tree or rock cavities, and more recently also in man-made structures and nest boxes. The female lays 3–7 eggs in late April in western European populations, hatching occurs in late May and chicks fledge about 1 month later (Van Nieuwenhuyse et al. 2008). Juveniles leave their natal territory in September–October and settle on average about 2,700 m away from their natal site (Fuchs and van Laar 2008).
Data collection
In the areas where the little owl is monitored by ringers, at least one inspection round was conducted each year between March and July to check for occupancy of nest boxes. For occupied nest boxes, one more visit was performed during which the nestlings were ringed, with 98% of birds ringed as nestlings being ringed in May and June. Adults that were present in nest boxes during inspection were also ringed or controlled if they were already ringed. About 62% of the birds ringed as adults were ringed during the breeding season. Additional captures of adults took place using nets and playback of the species’ calls.
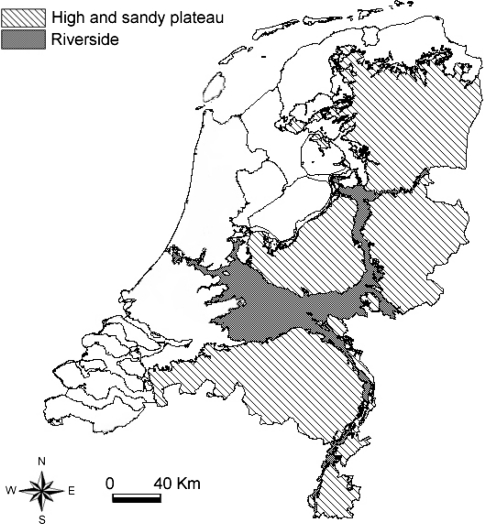
Between 1960 and 2007, 217 ringers were involved in little owl monitoring and 27,790 little owls were ringed in total in the Netherlands. These data are recorded and computerised in the standardised format by the national ringing schemes (van Noordwijk et al. 2003). Of all the little owls ringed, less than 9% were ringed in regions with a low proportion of suitable habitats (seaside, dunes, peat landscapes). We therefore used only data from the two geographical regions with the highest proportion of suitable habitat: the riverside area (R) and the high and sandy plateau area (H) (Fig. 2; Willems et al. 2004). We started the analyses from 1973 because of very low numbers of re-encounters in earlier data. Cases in which the accuracy of re-encounter data was poor (unknown date or fate of individual not recorded) were excluded as well as ringed nestlings that were recovered dead in their nest box within 30 days after ringing (the latter to avoid overlap with analyses of reproductive success; Willems et al. 2004). We were finally left with 25,729 ringed individuals (21,552 ringed as nestlings and 4,207 ringed as adults). Of these, 3,812 (2,273 nestlings and 1,539 adults, respectively) were later re-encountered at least once (1,672 dead recoveries and 2,140 live recaptures). Of the dead recoveries, 595 (35.6%) were reported by the general public.
Fig. 2.
The Netherlands with the two main geographical regions occupied by little owls (high and sandy plateau and riverside) used in the analyses
Model
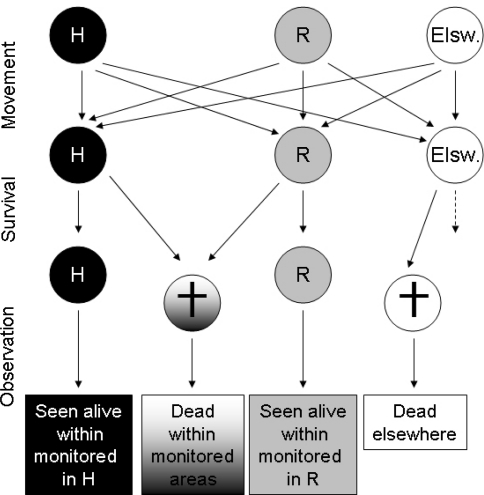
Annual survival estimates were computed using a capture–recapture approach (Lebreton et al. 1992). The large scale of the study is likely to induce strong capture heterogeneity between individuals because of different ringing and observation effort among regions. Preliminary tests on the single-state dataset of local observations confirmed that the data poorly supported the underlying assumptions of the Cormack–Jolly–Seber model, mainly because of a transient effect. We then used multi-state modelling to reduce heterogeneity in the capture–recapture dataset by defining the area where a bird is encountered as a state. This model permits us to separately estimate the encounter probability P At (the probability that an individual is encountered at site A and time t given that it is alive at site A and time t), the apparent survival ΦAt (the probability that an individual alive at site A and time t is still alive at time t + 1) and transition between sites, i.e. movements ΨABt (the probability that an individual moves from site A at time t to site B shortly after t in our case) for each area (Lebreton et al. 1992). When dealing with both recaptures and recoveries, survival is modelled as a transition from the state “alive” to the state “newly dead” (Lebreton et al. 1999). In the case of the little owl, live recaptures occurred mainly in monitored areas and were reported by ringers. Only 20 juveniles and 42 adults were re-encountered alive outside H and R and these encounters were excluded from analyses. In contrast, recoveries could be reported either by ringers within the monitored areas or by the general public outside monitored areas. When looking at spatio-temporal coverage, overlap between recoveries from the general public and from ringers reported in the same 1 × 1 km square was less than 1%, indicating a good spatio-temporal discrimination between monitored and unmonitored areas using the type of report. We thus accounted for six states: two alive states in monitored areas (in H or in R), one unseen alive elsewhere state, two newly dead states (dead in monitored area reported by ringer or dead elsewhere reported by the general public), and one unobserved dead state (dead but never reported). Since the two regions we used represent discontinuous parts of the country (Fig. 2), we did not use the model to specifically study dispersal between the monitored areas, and therefore we did not distinguish between the locations of death in those areas.
If a bird was found dead in an unmonitored area, it had necessarily moved from the monitored site where it had been ringed before dying. Therefore, movements were estimated prior to survival. Movement and survival are considered as two successive steps in transition matrices. Movement to “elsewhere” could be estimated with recoveries from the public since we assumed that only birds from elsewhere could be recovered by the public. Movements from monitored places to unmonitored places are considered as temporary emigration (i.e. transition to the state alive elsewhere from alive in monitored area was allowed for adults). Since the movement from alive elsewhere to alive in monitored area was not estimable for juveniles, we constrained it to 0. The schematic representation of dispersal and survival steps is presented in Fig. 3 and the corresponding matrices in Fig. S1.
Fig. 3.
Representation of the two step transitions (dispersal–survival) and the encounter events for the little owl context. H High sandy plateau, R riverside, Elsw elsewhere
Model selection
Details on multi-state GOF tests are given in Appendix S2. An overdispersion coefficient was examined by using the Median ĉ approach proposed in program MARK (White and Burnham 1999). The variance inflation factor, ĉ, estimated for the full model was 1.82, and this value was then used to scale the deviance of all subsequent models.
Model fitting and selection were performed using the program E-SURGE v1.4.6 (Choquet et al. 2009) using a generalised logit-link function. We used Akaike’s information criterion (QAICc), to compare models (Burnham and Anderson 1998). Models with smaller QAICc values were selected and two models were deemed to be equivalent when they differed by less than two.
We first analysed the model with many parameters including time, age and region effects on all the demographic parameters and we then sequentially reduced effects on each of these demographic parameters: first nuisance parameters like initial state and probabilities of capture and of recovery, then dispersal and finally the survival parameters. All the models tested are listed in Table S3. When comparing different models, we mainly tested the biologically relevant effects of age, time, region, and covariates (see below) on survival. Based on our monitoring data, we considered that little owls attained adult age 1 year after hatching. Thus, for birds ringed as nestlings, we considered two age classes, i.e. juvenile (0–1 year) and adult (>1 year). We assumed that survival and dispersal (both emigration and immigration) rates of birds ringed as nestlings that became adult were equal to the ones of birds ringed as adults.
We also tested whether survival and dispersal of juveniles and adults differed during different trend periods (1973–1983: declining; 1984–1993: increasing; 1994–2007: moderate decline; Fig. 1). To investigate whether discriminating between recoveries reported within monitored and unmonitored areas improved the fit of the model, we compared a model where reporting rates in both areas were constrained to be equal with a model in which they were different.
In order to check whether the model we used gave reliable estimates of survival rates, we performed the same analysis on two small-scale, well-monitored populations, and verified that survival estimates were in accordance with the observed dynamics (Appendix S5).
Population growth analysis
We investigated the relationship between juvenile and adult annual survival rates and annual changes in the size of the Dutch little owl population (indices from SOVON and Statistics Netherlands, available from 1976 to 2007; Fig. 1). We calculated the ratio of the population size at t + 1 and at t (i.e. population growth rate) and tested if this ratio co-varied with the logit of juvenile and adult survival rate during the same time interval, using a linear model. Finally, we checked for the presence of cyclic dynamics in survival over time using an autocorrelation function.
In order to compare true temporal variation (i.e. that does not account for sampling variability; Gould and Nichols 1998) of survival rates of juvenile and adult, we ran the best model selected in program MARK and used the variance component feature (White et al. 2002).
Temporal covariates and survival
We tested the effect of three different weather variables per season on survival: mean precipitation, mean minimum temperature, and the number of days with snow cover during winter (November–March). Data were taken from the meteorological station De Bilt (central Netherlands) and aggregated for the four seasons. The relationship between weather variables and survival rates is difficult to predict a priori. For example, precipitation could positively affect survival by increasing the availability of earthworms, or negatively by decreasing foraging efficiency. In the same way, minimum temperature could affect energy expenditure of the owls or the availability of worms and insects. To discriminate those factors, we performed two successive principal component analyses on monthly temperature and on annual precipitation, and then classified years on the resulting index integrating both temperature and precipitation. We thus discriminated dry and cold (DC), dry and warm (DW), wet and cold (WC), and wet and warm (WW) years, and tested if adult and juvenile survival rates differed among those years. Severe winters were determined according to IJnsen frost index (IJnsen 1991) which is calculated upon the number of frost days, ice days and very cold days for the winter season (November–March) at De Bilt. Winters for which the Ijsen frost index was superior at 44 were considered as severe.
As an index of the intensity of road traffic, we used the number of car kilometres per year (http://www.swov.nl/). Mortality due to road traffic is the cause of death that is reported most frequently (57%) for both juvenile and adults; we thus expected lower survival rates with the increase of road traffic.
As a measure of food abundance, we used indices of barn owl (Tyto alba) productivity and of the vole dynamics in the Netherlands. Barn owl productivity has been previously determined as a good proxy for vole density since the dynamics of the common vole population have a strong effect on the breeding performance of the species (De Bruijn 1994). We calculated barn owl productivity as the ratio of nestlings to adults ringed from ringing data for the same area as this little owl study. To correct for the general increase in the number of barn owl nestlings ringed annually, we used the residuals between the observed ratio and the regression of the ratio on year. We also discriminated years with high and low vole density based on a variety of monitoring sources as compiled by Dekker and Bekker (2008). The study of Dekker and Bekker (2008), making use of records on vole abundance gathered by farmers, showed that, as in western and continental Europe, the vole species have cyclic dynamics of 3 or 4 years, although the regular mice plagues observed during the last century became scarcer during the last decades. They also showed that the breeding success of barn owl is synchronised with the vole dynamics and used all available information to define good and bad years of vole density. Although little owls are more generalist predators than barn owls, and depend on other resources than voles (earthworms, insects; Van Nieuwenhuyse et al. 2008), we assume that the large amount of energy provided by voles compared to other prey items could influence the population dynamics of the little owl. All covariate models that were run are listed in Table S4.
In order to calculate the amount of variation in survival explained by the covariates, we used the analysis of deviance (Skalski et al. 1993). The proportion (V) of total variance in time explained by a particular covariate is calculated as V = [deviance (constant model)−deviance (covariate model)]/[deviance (constant model)−deviance (time dependent model)].
Results
In the best model, both the probability of live resighting and of dead recovery varied with year and age at ringing. The significant annual variation in resighting and recovery probability accommodated any changes in monitoring intensity or size of the monitored areas among years. Live resighting probabilities were also different between regions whereas the probability of dead recovery differed between monitored and unmonitored areas. The latter effect was very strong as constraining the reporting rate in monitored and unmonitored areas to be equal led to an increase of QAICc by more than 1,000. Dispersal rates in the best model were constant over time but varied between age classes and sites of departures and arrival (Table 1). Survival rate varied between age classes and years, with no difference between regions (Table 1). QAICc of models assuming survival rates differing between the three trend periods differed by more than 30 from the best model and hence were rejected.
Table 1.
The ten best models for little owl (Athene noctua) survival Φ selected with E-Surge
| Model | Other effects | Deviance | No./par | QAICc | Δ QAICc | ||
|---|---|---|---|---|---|---|---|
| No. | Φ juv | Φ ad | |||||
| 30 | Time | Time | 67,171.17 | 676 | 38,644.20 | ||
| 43 | tlin | Time | 67,194.31 | 644 | 38,646.09 | 1.89 | |
| 27 | Region | Region | 67,406.39 | 618 | 38,670.52 | 26.32 | |
| 37 | Region | Region | Additive time | 67,204.43 | 650 | 38,673.29 | 29.09 |
| 91 | Time | pp/t | 67,246.79 | 648 | 38,689.28 | 45.08 | |
| 88 | Time | Trend | 67,260.92 | 647 | 38,693.48 | 49.20 | |
| 36 | c | c | Additive time | 67,290.08 | 645 | 38,702.34 | 58.14 |
| 87 | Trend | Trend | 67,465.84 | 618 | 38,703.16 | 58.96 | |
| 80 | Road | Time | 67,293.42 | 645 | 38,704.17 | 59.96 | |
| 85 | Time | Swinter | 67,313.13 | 646 | 38,718.63 | 74.43 | |
Model number (No.) refers to the ones in Appendixes 3 and 4. For all these models, probability of dispersal varied among regions and between juveniles and adults; probability of re encountered dead or alive varied among states, years and between groups of age at ringing; initial state varied among year and groups of age at ringing
Φ juv First-year survival of birds ringed as nestlings, Φ ad survival of bird ringed as adults and after first year for bird ringed as nestlings.
Effects considered: time survival varied among years; tlin survival is linearly correlated to year; region survival differed between regions; pp/t different survival rates according to dry/cold–dry/warm–wet/cold–wet/warm years; trend survival rates varied according to the three trend periods defined in Fig. 1; c survival is constant over years and region; road survival rate is linearly correlated to road traffic index; swinter survival rates differed between years with severe winter and years with mild winter
Monitoring and dispersal parameter estimates
Parameter estimates and their standard errors are presented in Table 2. As expected, the overall reporting rate within unmonitored areas was lower than within monitored areas, but increased significantly from 1980 to 2007 (Spearman rank ρ = 0.49, df = 26, p = 0.008). The probability of resighting during the first year after ringing was lower for both regions and groups. Overall resighting rates in area R were higher than in area H. Dispersal rates were always higher for juveniles than for adults; they also differed between regions, but not in a systematic way (Table 2). Emigration rates of juveniles to elsewhere from both regions were especially high (65% in R and 73% in H; Table 2).
Table 2.
Estimates of survival, dispersal, resighting and recovery rates from the best capture–recapture model selected by E-Surge
| Parameters | Groups | Estimate | Variation |
|---|---|---|---|
| Survival rate | Juvenile (mean over all years) | 0.258 | 0.047 (SEt) |
| Adult (mean over all years) | 0.753 | 0.019 (SEt) | |
| Dispersal rate | H to R; juvenile | 0.030 | 0.006 (SE) |
| H to R; adult | 0.017 | 0.010 (SE) | |
| R to H; juvenile | 0.095 | 0.023 (SE) | |
| R to H; adult | 0.022 | 0.017 (SE) | |
| H to elsewhere; juvenile | 0.728 | 0.037 (SE) | |
| R to elsewhere; juvenile | 0.648 | 0.046 (SE) | |
| H to elsewhere; adult | 0.238 | 0.034 (SE) | |
| R to elsewhere; adult | 0.107 | 0.028 (SE) | |
| Elsewhere to H; adult | 0.029 | 0.004 (SE) | |
| Elsewhere to R; adult | 0.009 | 0.003 (SE) | |
| Probability of live resighting | In H: first-year probability for birds ringed as nestlings (mean on time) | 0.251 | 0.217 (SE) |
| In R: first-year probability for birds ringed as nestlings (mean on time) | 0.468 | 0.231 (SE) | |
| In H: long-term probability for birds ringed as nestlings (mean on time) | 0.340 | 0.305 (SE) | |
| In R: long-term probability for birds ringed as nestlings (mean on time) | 0.556 | 0.198 (SE) | |
| In H: first-year probability for birds ringed as adults (mean on time) | 0.292 | 0.235 (SE) | |
| In R: first-year probability for birds ringed as adults (mean on time) | 0.448 | 0.186 (SE) | |
| In H: long-term probability for birds ringed as adults (mean on time) | 0.380 | 0.278 (SE) | |
| In R: long-term probability for birds ringed as adults (mean on time) | 0.589 | 0.166 (SE) | |
| Probability of dead recovery | Reported within monitored areas, ringed as nestling (mean over all years) | 0.214 | 0.138 (SE) |
| Reported within monitored areas, ringed as adult (mean over all years) | 0.075 | 0.067 (SE) | |
| Reported within unmonitored areas, ringed as nestling (mean over all years) | 0.051 | 0.062 (SE) | |
| Reported within unmonitored areas, ringed as adult (mean over all years)a | 0.531 | 0.450 (SE) |
SEt Temporal process variation, SE standard error
aDue to scarce data, this parameter was poorly estimated
Survival rate estimates
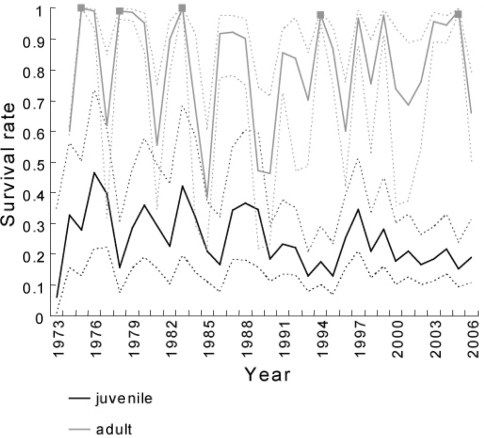
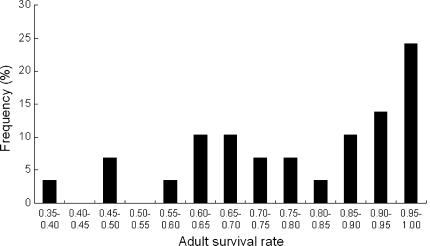
The average survival rate of juveniles was 0.258 (process temporal variation = 0.047, whereas for adults it was 0.753 (process temporal variation = 0.019). Temporal variability was significantly higher in juvenile survival rate than in adult survival rate (t test: t = −12, df = 32, p < 0.001). Juvenile survival rate significantly decreased over time (overall decrease was 42%, Fig. 4; the model assuming a linear trend in juvenile survival is the second best one, Table 1). For adult survival rate, we found a pattern with high survival rates (Φ > 0.85) in most years (Fig. 5), interspersed with bad years (Φ < 0.6) at more or less regular intervals of approximately 4 years (autocorrelation ACFt4 = 0.35, p < 0.05). Rather surprisingly, juvenile and adult survival rates were not correlated at t (Spearman ranked test ρ = 0.25, df = 26, p = 0.18). However, the correlations between juvenile survival rate at t and adult survival rate at t + 1 (ρ = 0.32, df = 26, p = 0.07), and between juvenile survival rate at t and adult survival rate at t−1 (ρ = 0.37, df = 26, p = 0.057) almost reached statistical significance.
Fig. 4.
Yearly estimates of juvenile and adult survival rates (continuous lines) and 95% confidence intervals (dotted lines) of the little owl from 1973 to 2007. Non estimable rates for adults are represented with gray squares
Fig. 5.
Frequency distribution of estimable annual survival rates for adults
Population growth analysis
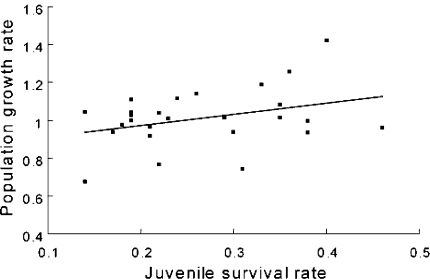
A linear model explaining annual variation in growth rates of the national population with logit-transformed estimates of juvenile and adult survival showed that population growth significantly increased when juvenile survival rate increased (F 1,14 = 17.7, p = 0.0008, β = 0.40, r 2 = 0.16; Fig. 6). No significant correlation was detected between population growth rate and adult survival rate (F 1,14 = 1.23, p = 0.28, r 2 < 0.01). However, we did find a significant but weak interaction between age and survival on the population growth rate (F 1,14 = 4.9, p = 0.04): for low values of juvenile survival rate, the relationship between adult survival rate and population growth rate was positive whereas it was negative for high values of juvenile survival rate.
Fig. 6.
Relationship between population growth rate and juvenile survival rate
Temporal covariates
None of the covariate models performed better than the best model without covariates as listed in Table 1. The best covariate model (fourth best among all models in Table 1) discriminated years based on an index of temperature and precipitation (i.e. dry-cold, dry-warm, wet-cold, wet-warm) for adult survival rate. Dry and cold years led to a lower adult survival rate [0.60 (0.59–0.62)95%CI] than all others years [dry-warm: 0.96 (0.93–0.98)95%CI; wet-cold: 0.709 (0.625–0.781)95%CI; wet-warm: 0.70 (0.60–0.78)95%CI]. In accordance with this result, adult survival rate during years with severe winter [0.53 (0.49–0.58)95%CI] was estimated lower than for years with mild winter [0.64 (0.62–0.66)95%CI, tenth best model; Table 1].
Models assuming different survival rates among trend periods were the second and third best models of covariate models (Table 1). Both models estimated lower adult survival rate during the decreasing period (first period of Fig. 1) than in other periods [0.61 (0.59–0.63)95%CI vs. 0.63 (0.57–0.69)95%CI and 0.73 (0.68–0.77)95%CI]. However, juvenile survival rate was higher during the first period of decrease [0.18 (0.15–0.22)95%CI] than during the increasing [0.097 (0.08–0.11)95%CI] and moderate decreasing [0.08 (0.07–0.09)95%CI] periods.
Among the covariate models assuming a linear relation between survival rate and an external covariate, the one assuming linear relationship between juvenile survival rate and road traffic index performed the best (Table 1), about 70% of the variance in juvenile survival was explained by this factor (Table S4). The model estimated negative trend of juvenile survival rate with road traffic (β = −0.01).
Discussion
Using ringing data from volunteers and state-of-the-art multi-state capture–recapture modelling, we estimated annual survival of Dutch little owls from 1973 to 2007 and its correlation with population growth. The length of our study permitted us to examine the effects of weather conditions and habitat quality indices. Moreover, integrating all information from the different areas monitored by volunteers and dead recoveries reported by the general public, through joint live recapture and dead recoveries multi-state modelling, allowed us to make efficient use of all available data (Barker and Kavalieris 2001). Our model thus provides a framework for general applicability to combine volunteer datasets and dead recoveries from members of the public.
Variation in survival rates and dynamics
Our aim was to understand the relationship between survival rates and little owl population dynamics. We found a positive correlation between juvenile survival rate and the annual population growth rate, i.e. years with a declining trend were associated with low juvenile survival, especially during the last two decades. This was true despite the fact that, on average, juvenile survival was high during the first phase of rapid population decline. Since most little owls breed when 1 year old, juvenile survival rate directly influences the recruitment rate of the population. When comparing survival estimates from two small-scale populations with contrasting dynamics (Appendix S5), we found no difference in juvenile survival rates between these populations, but lower and more variable adult survival in the declining population than in the stable one. Results at both scales point to juvenile survival being a key factor in little owl population dynamics, but also to variation in adult survival rate playing an important role. This corroborates to some extent the earlier results by Schaub et al. (2006), who showed that local juvenile survival rates and immigration largely explained the differences among four small populations, and that variation in adult local survival was the most important demographic factor explaining the variation in population growth rate across time, as was also found by Hone and Sibly (2002) for barn owls in Scotland. In eastern France, an increase in juvenile and adult little owl survival rate in the population was detected when the population trend shifted from declining to increasing (Letty et al. 2001). In a Swiss population of barn owls, two harsh winters that lead to simultaneously low juvenile and adult survival rates were associated with major population crashes (Altwegg et al. 2006). Among the 35 years of monitoring, no significant relationship between harsh winters, survival rate and population growth rate was detected, although one population size decrease seemed to coincide with harsh winter events (1978/79 and 1980/81; see Fig. 1). Because of a lack of little owl density data at the scale of the study, we did not investigate the possibility of population density interacting with winter severity on population dynamics, as suggested by Altwegg et al. (2006).
As expected by selection theory on life history traits for medium- to long-lived iteroparous species (Gaillard et al. 2000; Sæther and Bakke 2000; Stearns 1992) and previous work on other species of owls (Altwegg et al. 2003; Seamans and Gutiérrez 2007; Wisdom et al. 2000), population growth rate should be most sensitive to changes in adult survival rate, and adult survival rate should exhibit low temporal variation compared to juvenile survival rate. Our results supported the latter hypothesis since temporal variability was higher for juvenile than for adult survival. Due to the expected high sensitivity of population growth rate to adult survival rate, fluctuations in adult survival rates could be an important determinant of the decline in the population. However, the contribution of juvenile survival to the rate of population change in Dutch little owls seems to be more important than the contribution of adult survival because of its larger variation over time. These contrasting results are in accordance with the intermediate position of owls in the slow–fast continuum of species life history traits (Sæther et al. 2004). Nevertheless, the correlation between survival and population growth rate, although being significant, is quite weak (small r 2), leaving room for reproduction or immigration parameters to also explain a large part of the variation in population growth. An analysis of breeder recruitment is needed to complete the set of demographic parameters estimated for the Dutch little owl population. This would allow developing a model integrating both regular fluctuations as well as environmental stochasticity in parameters to further investigate the viability of the Dutch little owl population.
Variation in juvenile and adult survival rates
Our estimate of annual survival for juveniles (25.3%) is within the range of earlier studies (from 6 to 31%; Exo and Hennes 1980; Kämpfer-Lauenstein and Lederer 1995; Letty et al. 2001; Schaub et al. 2006; Thorup et al. 2010). By contrast, our estimate for adults (75.8%) is higher than found in previous studies (61–69%), except for an increasing population in eastern France where adult survival rate reached 80% (Letty et al. 2001). The integration of dispersal and dead recoveries could explain this discrepancy.
The best model we selected included variation in juvenile and adult survival rates between years. We also detected a decline in juvenile survival over time, and found a cyclic pattern in adult survival, with poor years occurring approximately at 4-year intervals. Previous studies only detected linear variation across years of juvenile or adult survival rates for this species (Letty et al. 2001, Schaub et al. 2006). Our dataset is an order of magnitude larger than previous ones with 3,812 individuals re-encountered at least once compared to 117–327 in previous studies.
We did not find any correlation between adult and juvenile survival rates in the same year, indicating that factors affecting each age class differed. Correlations between adult and juvenile survival with a time lag of plus or minus 1 year were almost significant, but given the uncertainty linked to survival estimation we will not speculate about it here. The decrease in juvenile survival was not due to a change in the age at ringing of nestlings as no such change was detected in our data (correlation test, p > 0.05). However, despite the fact that we discarded data from nestlings found dead within 30 days after ringing to limit overlap with reproductive success measurements, part of the nestlings that were not seen again could involve individuals that died during the early stage of their life but were not recovered. The juvenile survival rate we estimated therefore still included a small component of productivity that may have affected our estimate of survival during early life. Such early mortality is likely to be affected by the same factors that influence reproductive success, and reproductive success of the species in the Netherlands has indeed decreased, albeit by 16%, whereas the decrease in juvenile survival rate amounted to 42%. Therefore, about half the decrease is likely to be explained by other factors than the ones affecting productivity. An analysis of deviance of the various covariate models showed negative linear trends between juvenile survival and the amount of road traffic, explaining 70% of the variation, and between juvenile survival and the average minimum temperature in spring, explaining 63% of the variation. Both road traffic and spring temperature increased over time and could thus potentially explain the decline in juvenile survival. Road accidents are often pointed out as the main cause of mortality among the declining European populations of owls in rural areas, e.g. little owl (Hernandez 1988) and barn owl (Fajardo 2001; Meek et al. 2003). However, both correlations merely result from long-term temporal trends coinciding, and could equally well reflect the negative impacts of global change as habitat fragmentation and agriculture intensification instead of pointing towards direct causal effects. Studies of the causal effect of the impact of road traffic on survival of juvenile little owls should be conducted by comparing results from areas differing in traffic road intensity or monitoring activity of juveniles and adults around roads with different traffic intensity.
We found regular fluctuations of adult survival rate with low survival rates occurring about every 4 years. Short-term studies not running long enough to encompass low survival events may thus underestimate the temporal variance in fitness components, as was suggested for barn owl (Altwegg et al. 2003). We expected these fluctuations to be correlated with the dynamics of voles as observed for other owl species (Hakkarainen et al. 2002; Hone and Sibly 2002; Klok and de Roos 2007; Rohner 1995). However, models including measures of vole dynamics did not fit the data well. Karell et al. (2009) also showed that, for the tawny owl (Strix aluco) in southern Finland, variation in survival of breeding individuals were not related to vole abundance (but see Francis and Saurola 2004), and that vole dynamics mostly affected the offspring recruitment. The best covariate model explaining the fluctuation in adult survival rates included the index integrating annual mean temperature and precipitation. Dry and cold years led to reduced adult survival rates. Low temperatures could influence the energy expenditure of little owls especially during winter (Van Nieuwenhuyse et al. 2008). In a Swiss population of barn owls, winter harshness explained 17 and 49% of the variance in juvenile and adult survival, respectively (Altwegg et al. 2003, 2006). Although it seems that adult survival rate during years with severe winters was lower than during years with mild winters, the difference was not significant like the relationship between adult survival rate and snow cover.
Dry years could decrease the availability of insects and earthworms on which the species also feeds. Estimating the proportion of small invertebrates in the diet of little owl is difficult because their remains are poorly represented in pellets. However, some studies showed that the share of insects in the diet was large even in winter, and that earthworms were important during the feeding of nestlings (Van Nieuwenhuyse et al. 2008). Although insects and earthworms are less energetic than voles, they could be important alternative prey in intensively managed agricultural landscapes poor in voles.
Conclusion
This study has shown that both adult and juvenile survival rates are key determinants of changes in little owl population size. Adult survival rates were very high (>0.85) in most years but quite low (<0.65) in a quarter of the years. Thus, the average survival depends strongly on the frequency of these bad years and a study of several decades is essential to avoid absence or presence of a single bad year in the dataset having a large effect. The decline of the population is likely explained by declining juvenile survival rates whereas the regular occurrence of years with particularly low adult survival may be a cumulative deleterious factor when juvenile survival rate is already low. The failure to find strong relations with a number of potential explanatory variables strongly suggests that different factors affect the variation of age-specific survival rates and that variation in survival is due to complex interactions.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Acknowledgments
This research was funded under the project “Steenuil onder de pannen” lead by Birdlife Netherlands. The data analysed here were collected by 217 volunteer ringers and an even larger public reporting ringed little owls. We owe special thanks to Gert Speek and Woutéra van Andel for their management of the ringing data. Joep van de Laar made a major contribution to the digitisation of data from M.B. facilitating this study. We thank Olivier Duriez, Jean Baptiste Mihoub and Remi Choquet for their useful advice on E-Surge survival models. We thank the three anonymous referees for their helpful comments.
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
References
- Altwegg R, Roulin A, Kestenholz M, Jenni L. Variation and covariation in survival, dispersal, and population size in barn owls Tyto alba. J Anim Ecol. 2003;72:391–399. doi: 10.1046/j.1365-2656.2003.00706.x. [DOI] [Google Scholar]
- Altwegg R, Roulin A, Kestenholz M, Jenni L. Demographic effects of extreme winter weather in the barn owl. Oecologia. 2006;149:44–51. doi: 10.1007/s00442-006-0430-3. [DOI] [PubMed] [Google Scholar]
- Barker RJ, Kavalieris L. Efficiency gain from auxiliary data requiring additional nuisance parameters. Biometrics. 2001;57:563–566. doi: 10.1111/j.0006-341X.2001.00563.x. [DOI] [PubMed] [Google Scholar]
- Bro E, Sarrazin F, Clobert J, Reitz F. Demography and decline of the grey partridge Perdix perdix in France. J Appl Ecol. 2000;37:432–448. doi: 10.1046/j.1365-2664.2000.00511.x. [DOI] [Google Scholar]
- Burnham KP, Anderson DR (1998) Model selection and inference: a practical information-theoretic approach. Springer, New York
- Caughley G. Directions in conservation biology. J Anim Ecol. 1994;63:215–244. doi: 10.2307/5542. [DOI] [Google Scholar]
- Choquet R, Rouan L, Pradel R. Program E-SURGE: a software application for fitting multievent models. Environ Ecol Stat. 2009;16:847–868. [Google Scholar]
- De Bruijn O. Population ecology and conservation of the barn owl (Tyto alba) in farmland habitats in Liemers and Achterhoek (The Netherlands) Ardea. 1994;1:1–109. [Google Scholar]
- Dekker JJA, Bekker DL (2008) Veldmuispopulaties in Nederland: is er sprake van cycli en kunnen plagen voorspeld worden? In: VZZ rapport 2008.017. Zoogdiervereniging VZZ, Arnhem
- Duriez O, Sæther SA, Ens BJ, Choquet R, Pradel R, Lambeck RHD, Klaassen M. Estimating survival and movements using both live and dead recoveries: a case study of oystercatchers confronted with habitat change. J Appl Ecol. 2009;46:144–153. doi: 10.1111/j.1365-2664.2008.01592.x. [DOI] [Google Scholar]
- Exo KM, Hennes R. Beitrag zur Populationsökologie des Steinkauzes (Athene noctua)––eine Analyse deutscher und niederländischer Ringfunde. Die Vogelwarte. 1980;30:162–179. [Google Scholar]
- Fajardo I. Monitoring of non-natural mortality in the barn owl (Tyto alba), as an indicator of land use and social awareness in Spain. Biol Conserv. 2001;97:143–149. doi: 10.1016/S0006-3207(00)00091-4. [DOI] [Google Scholar]
- Francis CM, Saurola P. Estimating components of variance in demographic parameters of tawny owls, Strix aluco. Anim Biodivers Conserv. 2004;27:489–502. [Google Scholar]
- Fuchs P, Jvd Laar. Dispersie en vestiging van jonge Steenuilen. Limosa. 2008;81:129–138. [Google Scholar]
- Gaillard J-M, Festa-Bianchet M, Yoccoz N, Loison A, Toïgo C. Temporal variation in fitness components and population dynamics of large herbivores. Annu Rev Ecol Syst. 2000;31:367–393. doi: 10.1146/annurev.ecolsys.31.1.367. [DOI] [Google Scholar]
- Gould WR, Nichols JD. Estimation of temporal variability of survival in animal populations. Ecology. 1998;79:2531–2538. doi: 10.1890/0012-9658(1998)079[2531:EOTVOS]2.0.CO;2. [DOI] [Google Scholar]
- Hakkarainen H, Korpimäki E, Koivunen V, Ydenberg R. Survival of male Tengmalm’s owls under temporally varying food conditions. Oecologia. 2002;131:83–88. doi: 10.1007/s00442-001-0865-5. [DOI] [PubMed] [Google Scholar]
- Hernandez M. Road mortality of the little owl (Athene noctua) in Spain. J Raptor Res. 1988;22:81–84. [Google Scholar]
- Hestbeck JB, Nichols JD, Malecki RA. Estimates of movement and site fidelity using mark-resight data of wintering Canada geese. Ecology. 1991;72:523–533. doi: 10.2307/2937193. [DOI] [Google Scholar]
- Hone J, Sibly RM. Demographic, mechanistic and density-dependent determinants of population growth rate: a case study in an avian predator. Philos Trans R Soc Lond B. 2002;357:1171–1177. doi: 10.1098/rstb.2002.1118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- IJnsen F. Karaktergetallen van de winters vanaf 1707. Zenit. 1991;18:65–73. [Google Scholar]
- Kämpfer-Lauenstein A, Lederer W. Bestandsentwicklung einer Steinkauzpopulation (Athene noctua) in Mittelwestfalen (1974–1994) Charadrius. 1995;31:211–216. [Google Scholar]
- Karell P, Ahola K, Karstinene T, Zolei A, Brommer JE. Population dynamics in a cyclic environment: consequences of cyclic food abundance on tawny owl reproduction and survival. J Anim Ecol. 2009;78:1050–1062. doi: 10.1111/j.1365-2656.2009.01563.x. [DOI] [PubMed] [Google Scholar]
- Kendall WL, Nichols JD. Estimating state-transition probabilities for unobservable states using capture–recapture/resighting data. Ecology. 2002;83:3276–3284. [Google Scholar]
- Klok C, de Roos AM. Effects of vole fluctuations on the population dynamics of the barn owl Tyto alba. Acta Biotheorica. 2007;55:227–241. doi: 10.1007/s10441-007-9013-x. [DOI] [PubMed] [Google Scholar]
- Lebreton JD, Burnham KP, Clobert J, Anderson DR. Modeling survival and testing biological hypotheses using marked animals: a unified approach with case studies. Ecol Monogr. 1992;61:67–118. doi: 10.2307/2937171. [DOI] [Google Scholar]
- Lebreton JD, Almeras T, Pradel R. Competing events, mixture of information and multistratum recapture models. Bird Study. 1999;46S:S32–S38. [Google Scholar]
- Letty J, Génot J-C, Sarrazin F. Analysis of population viability of little owl (Athene noctua) in the Northern Vosges natural park (North-Eastern France) Alauda. 2001;69:359–372. [Google Scholar]
- Martínez JA, Zuberogoitia I. Effects of habitat loss on perceived and actual abundance of the little owl Athene noctua in Eastern Spain. Ardeola. 2004;51:215–219. [Google Scholar]
- Meek WR, Burman PJ, Nowakowski M, Sparks TH, Burman NJ. Barn owl release in lowland southern England–a twenty-one year study. Biol Conserv. 2003;109:271–282. doi: 10.1016/S0006-3207(02)00155-6. [DOI] [Google Scholar]
- Mikkola H, editor. Owls of Europe. London: Poyser; 1983. [Google Scholar]
- Peery MZ, Beissinger SR, Newman SH, Burkett EB, Williams TD. Applying the declining population paradigm: diagnosing causes of poor reproduction in the marbled murrelet. Conserv Biol. 2004;18:1088–1098. doi: 10.1111/j.1523-1739.2004.00134.x. [DOI] [Google Scholar]
- Rohner C. Great horned owls and snowshoe hares: what causes the time lag in the numerical response of predators to cyclic prey. Oikos. 1995;74:61–68. doi: 10.2307/3545675. [DOI] [Google Scholar]
- Sæther B-E, Bakke Ø. Avian life history variation and contribution of demographic traits to the population growth rate. Ecology. 2000;81:642–653. [Google Scholar]
- Sæther B-E, Engen S, Moeller A, Weimerskirch H, Visser M, Fiedler W, Matthysen E, Lambrechts M, Badyaev A, Becker P, Brommer J, Bukacinski D, Bukacinska M, Christensen H, Dickinson J, du Feu C, Gehlbach FR, Heg D, Hötker H, Merilä J, Tøttrup Nielsen J, Rendell W, Robertson RJ, Thomson DL, Török J, Van Hecke P. Life-history variation predicts the effects of demographic stochasticity on avian population dynamics. Am Nat. 2004;164:793–802. doi: 10.1086/425371. [DOI] [PubMed] [Google Scholar]
- Saurola P, Francis CM. Estimating population dynamics and dispersal distances of owls from nationally coordinated ringing data in Finland. Anim Biodivers Conserv. 2004;27:403–415. [Google Scholar]
- Schaub M, Ullrich B, Knötzsch G, Albrecht P, Meisser C. Local population dynamics and the impact of scale and isolation: a study on different little owl populations. Oikos. 2006;115:389–400. doi: 10.1111/j.2006.0030-1299.15374.x. [DOI] [Google Scholar]
- Seamans ME, Gutiérrez RJ. Sources of variability in spotted owl population growth rate: testing predictions using long-term mark-recapture data. Oecologia. 2007;152:57–70. doi: 10.1007/s00442-006-0622-x. [DOI] [PubMed] [Google Scholar]
- Skalski JR, Hoffmann A, Smith SG. Testing the significance of individual- and cohort-level covariates in animal survival studies. In: Lebreton JD, North PM, editors. Marked individuals in the study of bird populations. Basel: Birkäuser; 1993. pp. 9–28. [Google Scholar]
- Stearns SC. The evolution of life histories. Oxford: Oxford University Press; 1992. [Google Scholar]
- Thorup K, Sunde P, Jacobsen LB, Rahbek C (2010) Breeding season food limitation drives population decline of the little owl Athene noctua in Denmark. Ibis 152:803–814
- Van Nieuwenhuyse D, Génot J-C, Johnson DH, editors. The little owl: conservation, ecology and behavior of Athene noctua. UK: Cambridge University Press; 2008. [Google Scholar]
- van Noordwijk AJ, Speek G, Clark JA, Rohde Z, Wassenaar RD. The EURING exchange code 2000. J Ornithol. 2003;144:479–483. doi: 10.1007/BF02465510. [DOI] [Google Scholar]
- White GC, Burnham KP. Program MARK: survival estimation from populations of marked animals. Bird Study. 1999;46:120–139. doi: 10.1080/00063659909477239. [DOI] [Google Scholar]
- White GC, Burnham KP, Anderson DR. Advanced features of program MARK. In: Fields R, editor. Integrating people and wildlife for a sustainable future: Proceedings of the Second International Wildlife Management Congress. Bethesda: The Wildlife Society; 2002. [Google Scholar]
- Willems F, van Harxen R, Stroeken P, Majoor F (2004) Reproductie van de Steenuil in Nederland in de periode 1977–2003. In: SOVON-onderzoeksrapport, SOVON & STONE
- Wisdom M, Mills L, Doak D. Life stage simulation analysis: estimating vital-rate effects on population growth for conservation. Ecology. 2000;81:628–641. doi: 10.1890/0012-9658(2000)081[0628:LSSAEV]2.0.CO;2. [DOI] [Google Scholar]
- Zabala J, Zuberogoitia I, Martínez-Climent JA, Martínez JE, Azkona A, Hidalgo S, Iraeta A. Occupancy and abundance of little owl Athene noctua in an intensively managed forest area in Biscay. Ornis Fenn. 2006;83:97–107. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.