Skip to main content
NCBI home page
RNA logoLink to RNA
. 2011 Jun;17(6):1066–1075. doi: 10.1261/rna.2543711

Fully differentiable coarse-grained and all-atom knowledge-based potentials for RNA structure evaluation

Julie Bernauer 1,4, Xuhui Huang 2,4, Adelene YL Sim 3, Michael Levitt 4
PMCID: PMC3096039  PMID: 21521828

Abstract

RNA molecules play integral roles in gene regulation, and understanding their structures gives us important insights into their biological functions. Despite recent developments in template-based and parameterized energy functions, the structure of RNA—in particular the nonhelical regions—is still difficult to predict. Knowledge-based potentials have proven efficient in protein structure prediction. In this work, we describe two differentiable knowledge-based potentials derived from a curated data set of RNA structures, with all-atom or coarse-grained representation, respectively. We focus on one aspect of the prediction problem: the identification of native-like RNA conformations from a set of near-native models. Using a variety of near-native RNA models generated from three independent methods, we show that our potential is able to distinguish the native structure and identify native-like conformations, even at the coarse-grained level. The all-atom version of our knowledge-based potential performs better and appears to be more effective at discriminating near-native RNA conformations than one of the most highly regarded parameterized potential. The fully differentiable form of our potentials will additionally likely be useful for structure refinement and/or molecular dynamics simulations.

Keywords: RNA structure, knowledge-based potential, scoring

INTRODUCTION

RNA molecules are responsible for a wide range of biological processes occurring in the cell. To function, RNAs adopt detailed three-dimensional (3-D) folds (Gesteland et al. 2006). Understanding these structural intricacies gives insights to molecular evolution and structure-function relationships. Recently it was shown that, with high-resolution 3-D motifs, it is possible to design optimal sequences that improve RNA function (Das et al. 2010). This highlights the need for accurate RNA structure prediction and evaluation tools.

It had been hoped (Tinoco and Bustamante 1999) that the four nucleotides alphabet of RNA would make RNA structure prediction a more tractable problem than for proteins, since the latter have wider structural diversity arising from their 20 natural amino acids library. However, predicting the fold of RNA molecules, especially larger systems, is still a daunting task. Fortunately, RNA structure prediction is simplified by the hierarchical folding process of most RNAs (Brion and Westhof 1997; Batey et al. 1999; Tinoco and Bustamante 1999). An extended RNA first forms stable secondary structure defined by base-pairing, then packs into a globular 3-D form.

Given the efficient techniques developed for secondary structure prediction (Zuker 2003; Mathews 2006; Reeder et al. 2006; Shapiro et al. 2007; Hofacker 2009), the major remaining difficulty is determining the detailed local structure of bases and how they affect the RNA's global 3-D structure. Typical base interactions are base-pairing (canonical and noncanonical) and base-stacking. Even tertiary interactions—which usually contribute strongly to an RNA molecule's overall 3-D fold—like the tetraloop-tetraloop receptor (a well-defined base-pairing interaction between two distant small motifs) can be reduced to such local base interactions. Extensive work has been done to classify these base interactions (Murray et al. 2003; Sykes and Levitt 2005; Das and Baker 2007; Frellsen et al. 2009). Recent advances in RNA structure prediction techniques make use of base-pairing and stacking preferences either in the form of an energy function (Dima et al. 2005; Jonikas et al. 2009; Flores and Altman 2010) or through the use of fragment libraries taken from known RNA structures (Das and Baker 2007; Parisien and Major 2008).

Despite our understanding and classification of base interactions, for a given RNA, there are still many possible conformations consistent with reasonable secondary structures. Therefore the selection of good native-like models from an ensemble of conformations (also known as decoys) is a vital, yet very challenging task. Das and colleagues showed that a low resolution energy function was insufficient to discriminate good models (Das and Baker 2007)—defined by low root-mean-squared deviation (RMSD) to the native state—and that, with the addition of some higher resolution terms, its discriminatory power increased significantly (Das et al. 2010). This energy function—made available in the Rosetta package—tackles small RNA motifs more effectively than physics-based energy functions. However, the Rosetta RNA energy function is based on careful parameterization of weights for the various energetic components arising from preferred RNA base orientations and interactions, and therefore it is unclear how its efficacy scales with RNA size.

Similar problems in the protein folding world have led to the development of knowledge-based (KB) potentials. For instance, the potential of mean force (PMF) was generated from distance distributions between protein atoms, and was shown to be effective in screening and refining protein decoys (Samudrala and Moult 1998; Zhou and Zhou 2002; Zhang et al. 2004; Summa and Levitt 2007). To derive such a potential, a training set of high-resolution, nonredundant structures is required. The smaller number of high-resolution RNA structures available has thus far stalled the development of such distance-based KB potentials specifically designed for RNA.

In this study, we derive differentiable all-atom and coarse-grained KB potentials for RNA structures, using careful statistical treatment to handle low count regions. Unlike Rosetta, or other existing RNA potentials, our KB potentials implicitly incorporate all base interactions into distance-based potentials, eliminating the need for accurate weighting of energetic components. Our results show that our all-atom potential is effective in scoring RNA decoys for the selection of good native-like models in RNA systems of different sizes. When the native structure is derived by NMR, some of the near-native decoy structures scored with the all-atom potential have an energy that is below that of the NMR-determined native state: These structures may be closer to the true native state and thus constitute refined native states. The fully differential forms of our potentials facilitate their use in molecular dynamics (MD) and structure refinement.

RESULTS

Selection of representative RNA data set

The generation of an effective KB potential requires the careful selection of representative RNA structures. This data set of RNA structures should be high-resolution (to capture the intricate base–base interactions), nonredundant (to ensure that no particular RNA structure dominates), and sufficiently large (to provide good statistics). These conflicting criteria are difficult to meet and are not satisfied by the existing structure sets available in the literature such as RNAbase (Murthy and Rose 2003) or NDB (Murray et al. 2003).

We developed a protocol that combines automated and manual data curations designed to facilitate the extraction of high-quality, representative RNA structures (Supplemental Fig. 1; Materials and Methods). The process selects RNA-only structures that are solved by X-ray crystallography up to a resolution of at least 3.5 Å, in the absence of bound ligands or proteins. Structures that have identical sequences are filtered out to prevent redundancy in the data set.

The complete extraction procedure applied to the PDB (Berman et al. 2007) led to 77 selected RNA structures (total 7251 nucleotides [nt]). Fifty-four molecules in our data set also belong to the Stombaugh et al. (2009) data set, which contains 304 structures. Our data set is much smaller due to the stringent criteria used. The finalized data set used in the generation of the continuous RNA potential is summarized in Supplemental Table 1. Other than being useful for this work, the data set is generic enough to be used for other learning purposes and we have therefore made it publicly available (http://csb.stanford.edu/rna).

Generation of RNA potential

There are several ways to extract information from our structural data set. Some common methods to do this use known RNA base–base interactions like base-pairing and base-stacking, and generate independent potentials that are specific to these interactions (Sharma et al. 2008; Jonikas et al. 2009; Das et al. 2010). This approach, however, requires careful parameterization of the different energetic components. Alternatively, the BARNACLE model (Frellsen et al. 2009) uses dihedral angles from RNA rotamers (Murray et al. 2003) to train an angle-based RNA potential. While this appears to work well for sampling small RNA systems constrained by secondary structure information, it seems less likely that such a potential will capture tertiary interactions between distant motifs. Instead, we make use of distributions of inter-atomic distances, which allows us, in principle, to incorporate information from a wide array of interaction types.

We generated two RNA KB potentials: a coarse-grained five-point (P, C4′ backbone atoms, and C2, C4, and C6 base-planar atoms per base) version, and an all-atom version. The former is likely to be more effective for fast, efficient sampling due to the simplified representation of each base. This same five-atoms description was shown to be sufficient in describing base orientations (Sykes and Levitt 2005). The all-atom potential, on the other hand, may be useful for high-resolution RNA structure refinement, as a result of its inherent amount of structural detail, as it is for proteins (Chopra et al. 2010). Due to their nonoverlapping utility, both potentials were developed and tested here.

The distance computation led to ∼1 million distances <16 Å for the five-atoms per nucleotide model. Among them, 64% are due to the ribosomal RNA family (51% being due to the only complete ribosome structure included in our data set).

To obtain a potential from these distance measurements, we built a PMF as described previously for proteins (Samudrala and Moult 1998; Lu and Skolnick 2001). The potential between two atoms i and j at distance dij apart can be written as an energy function (Samudrala and Moult 1998) expressed as

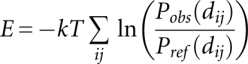graphic file with name 1066equ1.jpg

where T is the temperature (taken to be 300 K) and k the Boltzmann constant. Pobs(dij) and Pref(dij) represent the observed and reference probabilities, respectively, for the atoms i and j to be separated by distance dij.

Unlike previous work, in this study, Pobs(dij) and Pref(dij) are not computed by binning distances, which could significantly affect the results. Instead, these are probability distributions obtained from statistical analysis (see Materials and Methods): We used a Dirichlet Process Mixture Model to obtain the analytical form of the potential as a sum of Gaussian functions. Another feature of this potential is that it is fully differentiable, making it suitable for energy minimization or MD. To our knowledge, this is the first RNA KB potential that can be directly applied to continuum MD, though a KB potential for discrete MD has been designed (Sharma et al. 2008).

In developing KB potentials, the choice of the reference state is key. Some options include an ideal gas reference state (Zhou and Zhou 2002) or a quasi-chemical approximation (Lu and Skolnick 2001), which originates from “uniform density” reference state defined by Sippl (1990). This study used the latter with a composition-independent scale, i.e., the observed distances from all possible pairs are combined together to represent the reference state.

Assessment of potentials by decoy scoring

To assess the quality of our KB potentials we used them to score a variety of RNA decoys, and observed their abilities to distinguish good, near-native models. Scoring is a quick and simple way to evaluate the quality of a potential, compared to more computationally intensive methods like refinement and sampling. As a comparison, we scored the same decoys using the latest high-resolution scoring function from Rosetta (Das et al. 2010).

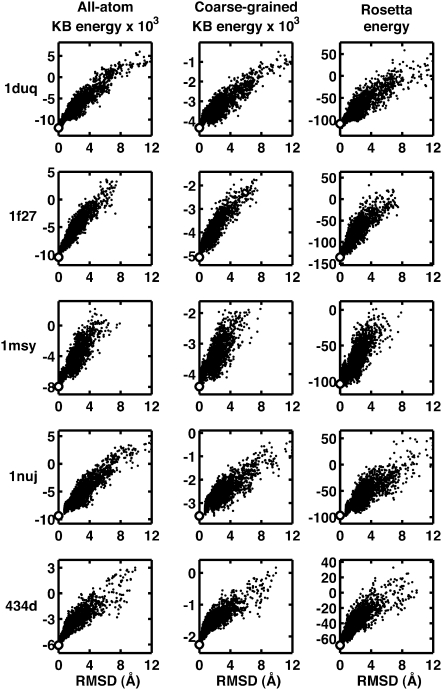
One set of decoys was generated by position-restrained molecular dynamics and replica-exchange molecular dynamics (REMD) simulations (see Materials and Methods), methods that cover a wide near-native RMSD range (from 0.1 to ∼12 Å). Five different RNA structures were used, and scores evaluated using the KB potentials generated from the full data set (Fig. 1). The cropped (using a data set where the five structures were all removed) and full versions of the KB potentials yield similar results (see Supplemental Fig. 2). In all five cases, the all-atom and coarse-grained KB potentials and Rosetta were very effective in identifying near-native decoys, as indicated by the strong scoring funnel toward the native structure.

FIGURE 1.

FIGURE 1.

Open in a new tab

Energy as a function of RMSD for decoys generated using position-restrained dynamics together with replica-exchange molecular dynamics for five different systems (rows). All-atom KB, coarse-grained KB, and Rosetta energies are shown in the left, middle, and right columns, respectively. In each case, a funnel shape toward the native structure (white circle) is seen, characteristic of a scoring function that is effective at distinguishing near-native structures from less native-like structures.

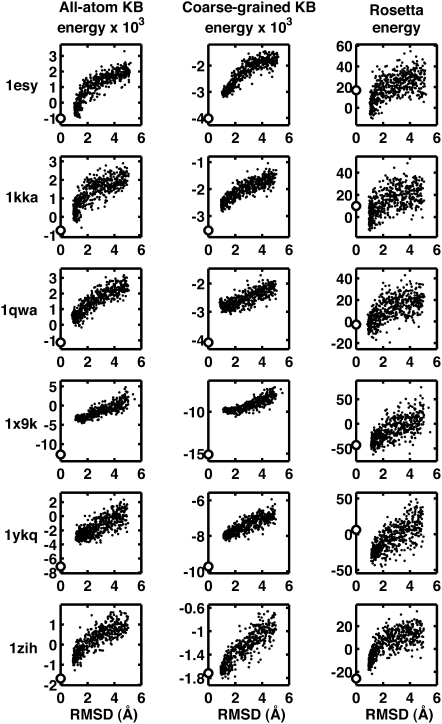
The assessment of potentials using a single method for decoy generation may be insufficient to determine their limitations (Handl et al. 2009). We therefore generated a second set of decoys using normal modes (NM). These decoys cover a narrower range of RMSD but present different geometrical distortions from the prior physics-based force-field methods. The all-atom, coarse-grained and Rosetta potentials show similar efficacy (Fig. 2; Supplemental Fig. 3): The funnel shape characteristic of good potentials is less pronounced, suggesting weaker ability of all three potentials to differentiate such decoys.

FIGURE 2.

FIGURE 2.

Open in a new tab

Energy as a function of RMSD for decoys generated by normal modes for six RNA structures (more in Supplemental Fig. 3). Scoring using our two KB potentials (all-atom on left, coarse-grained in middle) and Rosetta (right) are shown. Native scores are represented as white circles. A funnel toward low RMSD is seen in most cases. However, in several instances, some decoys score better than the native structure, a behavior that is more pronounced for the Rosetta scoring function.

Last, we tested the potentials' capabilities to score diverse RNA structures assembled by RNA-like fragments which had no native base-pairing enforced (see Supplemental Figs. 4–7). Not surprisingly, due to the reduced constraints, all three potentials were less effective in scoring these decoys. In general, our all-atom KB potential (full version) still appears to quantitatively do better than Rosetta (see Table 1). Das and colleagues showed that the combination of refinement and scoring improved the discriminatory power of the Rosetta potential (Das et al. 2010), suggesting that, with atomic refinement, our all-atom KB potential could possibly perform well too.

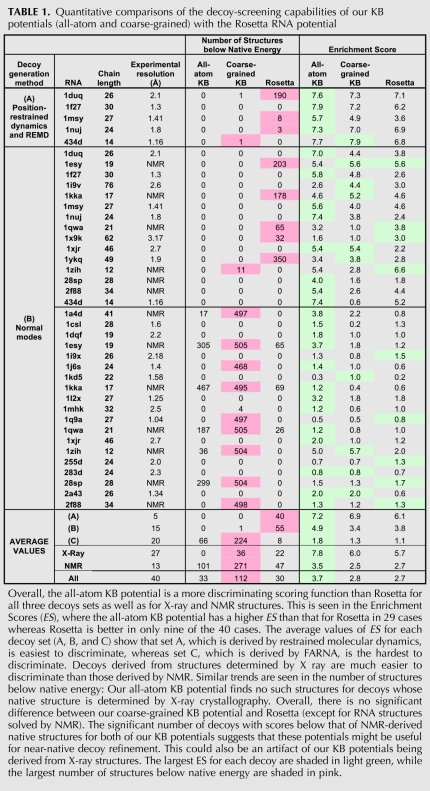
TABLE 1.

Quantitative comparisons of the decoy-screening capabilities of our KB potentials (all-atom and coarse-grained) with the Rosetta RNA potential

graphic file with name 1066tbl1.jpg

Open in a new tab

Evaluation metrics

For a quantitative comparison between all three potentials, we counted the number of decoys that scored lower than the native structure (Table 1). This gives us an indication of the number of structures that will be erroneously selected ahead of the native structure due to limitations in the potentials. Alternatively, we also define an Enrichment Score (ES), a useful metric based on identifying the top 10% scoring (Etop10%) and best 10% RMSD values (Rtop10%), then evaluating their degree of overlap (this choice percentage is somewhat arbitrary). The Enrichment Score (Tsai et al. 2003) is defined as

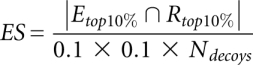graphic file with name 1066equ2.jpg

where |Etop10% ∩ Rtop10%| is the number of structures in the intersection of Etop10% and Rtop10%. Etop10% corresponds to the set of structures with energies in the best 10% of the energy range. Rtop10% corresponds to the set of structures having RMSD in the lowest 10% of the RMSD range.

For a perfectly linear scoring function for which Ei = c × Ri for each structure i and c is a constant, this would give

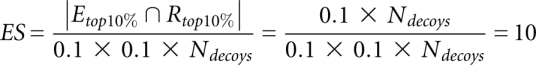graphic file with name 1066equ3.jpg

In a random scoring case, we would have

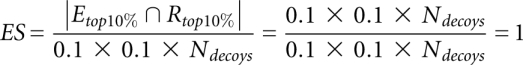graphic file with name 1066equ4.jpg

Hence, we have

graphic file with name 1066equ5.jpg

What constitutes a good scoring function is not obvious, though it clearly should have an ES between 1 and 10, the closer to 10 the better. For MD and NM, where RNA decoys have secondary structures similar to their respective native states, our all-atom KB potential appears to generally do best (Table 1).

DISCUSSION

Captured structural features

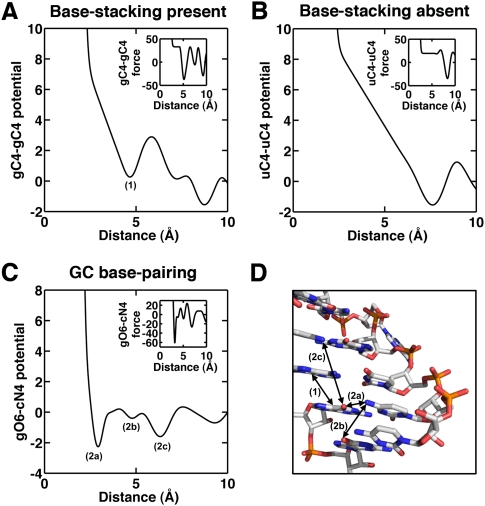
Common RNA base interactions typically explicitly represented in RNA potentials or force-fields are base-pairing and base-stacking. While we did not include these terms explicitly in our KB potentials, the distance-dependent potentials we developed should inherently include this information. Figure 3 shows that our potentials and their first derivatives are smooth and important base-interaction features are also captured as troughs in the potentials. For instance, base-stacking is more pronounced between purines, but least between pyrimidines (Saenger 1984). The potential between C4 atoms in guanines (purines; Fig. 3A) shows a well at ∼4.4 Å, which corresponds to the distance between base-stacked C4 atoms. On the contrary, this basin is absent for a similar potential between uracils (pyrimidines; Fig. 3B), consistent with the weak base-stacking interaction. The base-pairing interaction between guanine and cytosine (and adenine and uracil; not shown) is also captured (Fig. 3C).

FIGURE 3.

FIGURE 3.

Open in a new tab

Structural features captured by the KB potential. The plots (A–C) show the potentials for specific atom pairs. In each plot, the corresponding force is shown in the inset. (A) gC4-gC4 potential showing a base-stacking well ∼4.4 Å labeled (1). (B) uC4-uC4 potential showing no base-stacking well. (C) gO6-cN4 potential showing a deep base-pairing well (2a) and various structural wells (2b and 2c). (D) Distances represented in the different wells shown on the Rev binding element of HIV-1 structure (PDB id: 1duq).

The full energy landscape of an RNA is hyper-dimensional and cannot be adequately visualized from these potential plots, which are low-dimensional projections of the full energy surface. Nonetheless, the success of our potentials in scoring RNA decoys suggests that our KB representation of the RNA landscape is reasonable. Most native conformations can be accurately identified by our KB potentials even in its coarse-grained form (Figs. 1, 2; Supplemental Figs. 3–7). There are, however, structures that score close to, or lower than the native. To have a sense of which structural features are well captured by our potentials, we superimposed the best-scored decoys to the native state, and observed their structural differences.

Unsurprisingly, due to their dominance in KB statistics, helical topologies are well preserved and captured by our KB potential scoring (see Fig. 4). This also appears to be the case for Rosetta scoring. However, Rosetta is less effective in scoring the correct loop structure compared to our all-atom KB potential. The KB potential, unlike Rosetta, does not contain explicit base-pairing and base-stacking terms and hence does not necessarily favor a helix-like stacking for loops. This might be why our all-atom KB potential outperforms Rosetta in scoring the GUAA tetraloop (Fig. 4). Success in modeling such small motifs by Rosetta (Das et al. 2010) suggests that all-atom refinement of the models could improve scoring, but such analysis is beyond the scope of this current work.

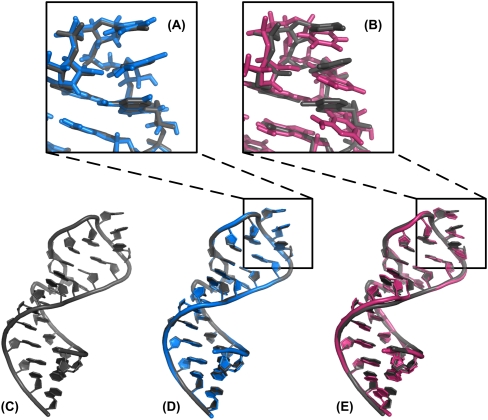
FIGURE 4.

FIGURE 4.

Open in a new tab

Comparison of the best scoring decoys for the GUAA tetraloop (PDB id: 1msy). The native structure is shown in C and the superimposed decoys selected by the all-atom KB potential and Rosetta are illustrated in D and E, respectively. In both D and E the native structure is also shown in gray. The close-up views of the tetraloop for both best scored decoys are shown in panels A and B, respectively. The Rosetta scoring function incorrectly selects a structure with stronger base planar stacking than found in the native structure.

From Table 1, the experimental method used to solve the native structure has an impact on the data: It seems to be more difficult to obtain good scoring for RNA structures solved by NMR. When the native structure is derived by NMR, some of the near-native decoy structures scored with the all-atom potential have energies below that of the NMR-determined native state. While this could likely be attributed to the use of X-ray structures in generating the KB and Rosetta potentials, the behavior could also be partly due to a single NMR reference structure not fully representing the true native state. NMR structures are usually more varied and their accuracies are hard to evaluate, in contrast to X-ray structures where resolution and Rfree factor provide good insights into the quality of structures.

The quality of scoring also depends on the nature of the decoy set. For example, for structures 1q9a and 28sp, FARNA failed to model bulge regions present in the native RNA, so all FARNA decoys used lacked such bulges. Hence scoring results were bad for both KB potentials and Rosetta (Table 1).

In general, the coarse-grained KB potential is less effective at screening decoys, likely because high-resolution information is omitted from its representation. This could explain the reduced ability of the coarse-grained KB potential to discriminate good decoys of small RNAs (e.g., 1zih, 12 bases; 434d, 14 bases).

Fully differentiable potentials for refinement and modeling

As mentioned previously, our KB potentials are fully differentiable and could be effective for refinement of near-native RNA decoys. The scoring results on the different types of RNA decoys (Figs. 1, 2; Supplemental Figs. 3–7) indicate that our potentials might be promising for refinement, since they show strong funnels toward the native state. However, being able to refine a structure well also depends on the energy landscape close to the native structure (Chopra et al. 2008)—we cannot visualize this by the simple scoring scheme we have adopted here.

We can also make use of our KB potentials to run MD simulations on different RNA systems. However, it is unclear whether these potentials can effectively model unfolded or intermediate RNA states. Modeling such extended conformations may require long-range interactions, but such distances are lacking in X-ray structures of globular native RNA. To better address this problem, and possibly improve the geometry of base-interactions, we envision having to explicitly include base-pairing interactions or other orientation-dependent interactions like those used in recent studies (Dima et al. 2005; Stombaugh et al. 2009; Zirbel et al. 2009). In future work, we will look at structural refinement of near-native decoys to investigate the quality of our potentials close to the native energy basins, and then evaluate the need for additional terms in our KB potentials.

Simplified treatment of solvent and electrostatics

A major advantage of using KB potentials is the implicit treatment of electrostatics and solvent, through the use of pairwise atomic distances in experimentally determined structures. This removes the need to include solvents and ions in any sampling or scoring procedure, reducing the size of the problem, thus allowing the handling of large RNA systems. Since distance statistics were taken from crystal structures grown under a diverse range of ionic conditions (albeit most crystals were grown in the presence of divalent ions), our KB potentials cannot be directly related to specific ionic conditions. Rather, our potentials are likely applicable to the broad range of ionic conditions under which most RNAs fold to their native form. Arguably our KB treatment of electrostatics and hydration is crude and unphysical, since we intentionally did not take into account differences in ionic conditions of the different crystallized RNAs, and also did not differentiate between diffuse ions from partially or fully dehydrated ones. However, the significant reduction in computational complexity definitely improves sampling efficiency. We can make use of the KB potential to seed different structures for more intricate explicit solvent and ions MD simulations.

CONCLUSION

We built fully differentiable KB potentials from a carefully curated data set of high-resolution RNA structures and used decoys to assess their qualities. While such an evaluation scheme has its limitations (Handl et al. 2009), it is a fast and easy method to determine the quality of potentials. We minimized any bias by scoring decoys generated from three different approaches. Even in the absence of a priori information, our RNA potentials—in particular that with all-atom representation—lead to effective discrimination of RNA decoys, comparable to, and in some cases bettering, existing parameterized or template-based techniques.

MATERIALS AND METHODS

RNA data set and distance collection

We built our RNA data set by selecting RNA structures that fulfill the following specific requirements:

  1. Each structure has been solved by X-ray crystallography to a resolution >3.5 Å.

  2. The solved RNA structure should not be bound to proteins or ligands.

  3. Less than 5% of the nucleotides in the RNA are modified or missing.

  4. The data set does not contain two structures with sequence identity >80%.

  5. The structure should be representative of the biologically active molecule (symmetric molecules are built if needed).

The RNA selection process consists of automated and manual portions. The PDB (2007 annual release) was scanned for suitability by using an in-house extension of the BioPython PDB module (Hamelryck and Manderick 2003) for nucleic acids. The lengths and sequences of RNA structures that meet criteria 1 and 2 (see above) were extracted and analyzed using the same module.

To account for identical RNAs, these sequences obtained were aligned using the program Blast (Altschul et al. 1990) and hierarchical clustering based on sequence identity was performed using the statistical program R (R Development Core Team 2008). These clusters of sequences were then manually evaluated. For each cluster, the structure corresponding to the longest sequence was retained. The structural details were manually curated and biological functions extracted from the relevant literature. When the biologically relevant molecule was not found in the asymmetric unit, symmetric chains were built using PyMOL (http://www.pymol.org/) (DeLano 2002) and added to the structure file.

Once selected, structures were labeled using a family tag (Ribosomal RNAs, Ribozymes, Transfer RNAs, Viral RNAs, SRP RNAs and miscellaneous; see Supplemental Table 1). This data set is available at http://csb.stanford.edu/rna.

Statistical analyses and functional forms

Computing Pobs(d) and Pref(d) as shown in Equation 1 from distance measurements is essentially a density estimation problem. The probabilities are inferred from the distances {d1,…,dn}, which are assumed to be exchangeable observations of Pobs and Pref. There are many alternative ways for performing density estimation in univariate sets. In previous studies, fixed binning and spline fitting were mainly used. This strategy can induce a lot of artifacts due to low count and noise and the resultant probability density often may not be a good representation of the data. Thus we decided to rely on classical statistical techniques. In this study, we used a Dirichlet process mixture model, which leads to analytically differentiable potential functions. Density estimation was performed using the implementation of Dirichlet process mixture models in the Flexible Bayesian Modeling package written by R.M. Neal. This software defines a hierarchical structure for the prior of the parameters φ = {μ,σ2}. The reader should refer to Neal (1998) for further details.

Normal mixture models are also widely used for density estimation. The density function is assumed to be a mixture of a number of Gaussian components weighted by factors ω = {ω1,…,ωn}. The density function has the form

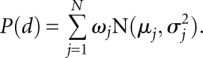graphic file with name 1066equ6.jpg

Given a fixed number of components N, it is easy to find the function P(d) that maximizes the likelihood of the data set. However, determining the optimal number of components in a statistically meaningful way is a difficult problem to which much research has been devoted (McLachlan and Peel 2000).

An alternative that has been investigated more recently is to extend the finite mixture model to an infinite mixture of components. One can then use a purely Bayesian approach to infer the parameters of the model, with a clever prior for the mixing proportions of the components. A good choice for this prior is a Dirichlet process, which results in what is known as a Dirichlet process mixture model. These models can have strong advantages over their finite counterparts (Rasmussen 2000):

  • In many applications it may be more appropriate not to limit the number of components.

  • The number of represented classes is automatically determined.

  • The use of reversible jump Markov Chain Monte Carlo (MCMC) effectively avoids local minima that plague mixtures trained by optimization methods.

  • It is simpler to work at the infinite limit than to work with finite mixtures of unknown size.

To overcome signal instabilities generated by the estimations at small distances where the number of counts is small for both Pobs (d) and Pref (d), the first part of the potential is assumed to be linear up to the first descending inflection point. The linear approximation proved to be sufficient to obtain reasonable looking potential shapes for the coarse-grained and all-atom potentials and shows better results than sigmoid estimates (data not shown). To ensure a smooth truncation at the distance cutoff (taken to be 14 Å), the whole signal was multiplied by a negative sigmoid function centered on the cutoff distance. Both of those assumptions lead to continuously differentiable energy and force functions, suitable for MD simulations.

Generation of decoy structures

In this study, we proposed a method to generate RNA decoy sets with RMSD ranging continuously from 0 Å to >10 Å. Our method is based on using MD simulations for sampling (Huang et al. 1996). Typical RNA MD simulations in explicit solvent will generate configurations that have RMSD values a few angstroms (typically 2 Å) away from the crystal structure. In order to generate near-native decoy structures (i.e., with RMSD <2 Å), we applied a position restraint potential on each heavy atom of the RNA molecule to constrain the motions of RNA. On the other hand, in order to generate decoy structures that are far from the native structure, we applied REMD, an enhanced sampling algorithm, to sample the configuration space far from the native structure.

MD simulations are often trapped in local free energy minima when sampling a rugged free energy landscape for biomolecular folding. REMD was developed to overcome this problem by inducing a random walk in temperature space, such that broad sampling is achieved at high temperature to avoid kinetic traps at low temperature (Hansmann and Okamoto 1999; Sugita and Okamoto 1999). In REMD, multiple simulations are run, each at a different temperature. A random walk in temperature space is achieved by periodically attempting to swap the conformations at two neighboring temperatures. The probability of accepting a swap is

graphic file with name 1066equ7.jpg

where P(i → j) is the probability of transitioning from temperature T(i) to temperature T(j), βi is 1/(kTi), with k the Boltzmann constant, and Ui is the potential energy of the conformation at T(i). Thus, the detailed balance condition is satisfied.

Our simulations used the AMBER 03 potential for nucleic acids (Chen and Pappu 2007). The GROMACS molecular dynamics simulation package (Hess et al. 2008) was used due to its speed. The RNA molecule was solvated in a water box with any solute atom at least 10 Å away from the wall of the box. Sodium cations (Na+) were added to neutralize the system. The simulation system was minimized using a steepest descent algorithm, followed by a 100 psec MD simulation applying a position restraint potential to the RNA heavy atoms. All simulations were run with constant NVT by coupling to a Nose-Hoover thermostat (Hoover 1985) with a coupling constant of 0.02 psec−1. A cutoff of 10 Å was used for nonbonded interactions. Long-range electrostatic interactions were treated with the Particle-Mesh Ewald (PME) method (Darden et al. 1995). Nonbonded pair lists were updated every 10 steps with an integration step size of 2 fsec in all simulations. All bonds were constrained using the LINCS algorithm (Hess et al. 1997).

Five representative RNA systems were chosen from our initial RNA data set to generate the decoy structures. For each RNA system, 20 1-nsec position restraint simulations were performed with each heavy atom constrained to its initial position by a harmonic potential,

graphic file with name 1066equ8.jpg

where k, the force constant, equals 0, 10, 20, … 90, 100, 200, 300, … 900 respectively in each of the 20 simulations. In addition, 1-nsec REMD simulations are also performed for each RNA system. The temperature list was roughly exponentially distributed, with 50 temperatures ranging from 285 to 592K.

Normal-mode decoys were generated using our normal-mode perturbation method (Summa and Levitt 2007). Quasi elastic modes of each native structure are computed using just the single-bond torsion angles as degrees of freedom. The potential energy and kinetic energy matrices, V and T, were generated by numerical differentiation (Levitt et al. 1985) using the Tirion-like (Tirion 1996) energy function:

graphic file with name 1066equ9.jpg

where r is the separation of atoms i and j, R is the constant separation of the same atoms in the native structure, and the constant a is set to 0.2. Using this function, the energy and its first derivative are zero at the native state (r = R) and the second derivative is always positive and decreases as R−6. Eigenvectors derived in torsion-angle space involve combinations of torsion angles that do not move atoms along straight lines in Cartesian coordinates. In the past (Summa and Levitt 2007), we used the shifts of atomic positions caused by a very small shift along a torsional mode denoted as υij for the ith Cartesian coordinate of the jth mode. These shift vectors are not necessarily orthogonal in Cartesian coordinates 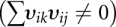Inline graphic so that adding components from such vectors can fail to span the subspace of K modes properly. We dealt with this problem by using the actual torsion angle changes associated with each normal mode. The angle changes for the 20 lowest modes were added together with random amplitudes and then used to perturb the native structure in torsion angle space. This gave a structure that still had stereochemically correct bond lengths and angles but could have bad contacts. The RMSD of this structure was recorded, as was the number of bad contacts. The procedure was then repeated 50,000 times using different random amplitudes whose magnitude slowly increased so as to ensure that we generated decoys with a uniform range of RMSD values up to some specified maximum value. The RMSD values of the structures were used to count how many structures fell in RMSD bins 0.1 Å wide. A required number of structures in each bin was specified (10 here) and the maximum RMSD value was set to 5 Å so that we aim to have 50 bins each containing 10 decoys. The 50,000 tries generated 100-fold more decoys and we chose the smallest RMSD with the smallest number of bad contacts in each bin. This gave ∼500 decoys that were then refined by Encad energy minimization to ensure that none of the decoys would be easy to discriminate due to bad contacts.

The FARNA decoys used in this study were obtained from http://www.stanford.edu/∼rhiju/data.html, and described in detail in the corresponding FARNA article (Das and Baker 2007).

Scoring with Rosetta RNA

Scoring of RNA decoys using the Rosetta scoring function was conducted with the Rosetta 3.0 package (http://www.rosettacommons.org). The addition of hydrogen atoms to native structures often introduces steric clashes. Therefore, for consistency, all hydrogen atoms were removed (decoys and native). In most cases, the terminal 5′-phosphate was missing, and was inserted based on ideal RNA base geometry. To relieve strain and steric clashes from the addition of the phosphate, only the corresponding bases were allowed to move in a simple implicit solvent minimization procedure (AMBER 99 force-field [Wang et al. 2000]; Generalized Born electrostatics [Tsui and Case 2000] with inverse Debye-Huckel length of 0.19 Å−1; maximum of 500 steps implemented in Nucleic Acid Builder [Macke and Case 1997]). Such a short and constrained minimization procedure adequately removes steric clashes introduced by the terminal phosphate, while appropriately maintaining the RNA fold. Atomic movements introduced were minimal in all cases, with small RMSD changes. These same structures were also used in our KB potential scoring.

SUPPLEMENTAL MATERIAL

Supplemental material is available for this article.

ACKNOWLEDGMENTS

This work is part of the “GNAPI Associate Team.” We thank the INRIA Équipe Associée program for financial support. This work was supported by a National Institutes of Health award (GM041455) to M.L., a Human Frontiers in Science Program grant to M.L., and a Hong Kong University Grants Council award (RPC10SC03) and RGCHKUST6/CRF/10 to X.H. A.Y.L.S. acknowledges support from the Agency for Science, Technology and Research (A*STAR), Singapore. The authors acknowledge support from NSF award CNS-0619926 for computer resources.

Footnotes

Article published online ahead of print. Article and publication date are at http://www.rnajournal.org/cgi/doi/10.1261/rna.2543711.

REFERENCES

  1. Altschul SF, Gish W, Miller W, Myers EW, Lipman DJ 1990. Basic local alignment search tool. J Mol Biol 215: 403–410 [DOI] [PubMed] [Google Scholar]
  2. Batey RT, Rambo RP, Doudna JA 1999. Tertiary motifs in RNA structure and folding. Angew Chem Int Ed Engl 38: 2326–2343 [DOI] [PubMed] [Google Scholar]
  3. Berman H, Henrick K, Nakamura H, Markley JL 2007. The worldwide Protein Data Bank (wwPDB): Ensuring a single, uniform archive of PDB data. Nucleic Acids Res 35: D301–D303 [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Brion P, Westhof E 1997. Hierarchy and dynamics of RNA folding. Annu Rev Biophys Biomol Struct 26: 113–137 [DOI] [PubMed] [Google Scholar]
  5. Chen AA, Pappu RV 2007. Parameters of monovalent ions in the AMBER-99 forcefield: Assessment of inaccuracies and proposed improvements. J Phys Chem B 111: 11884–11887 [DOI] [PubMed] [Google Scholar]
  6. Chopra G, Summa CM, Levitt M 2008. Solvent dramatically affects protein structure refinement. Proc Natl Acad Sci 105: 20239–20244 [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Chopra G, Kalisman N, Levitt M 2010. Consistent refinement of submitted models at CASP using a knowledge-based potential. Proteins 78: 2668–2678 [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Darden T, York D, Pedersen L 1995. A smooth particle mesh Ewald potential. J Chem Phys 103: 3014–3021 [Google Scholar]
  9. Das R, Baker D 2007. Automated de novo prediction of native-like RNA tertiary structures. Proc Natl Acad Sci 104: 14664–14669 [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Das R, Karanicolas J, Baker D 2010. Atomic accuracy in predicting and designing noncanonical RNA structure. Nat Methods 7: 291–294 [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. DeLano WL 2002. The PyMOL user's manual. DeLano Scientific, San Carlos, CA [Google Scholar]
  12. Dima RI, Hyeon C, Thirumalai D 2005. Extracting stacking interaction parameters for RNA from the data set of native structures. J Mol Biol 347: 53–69 [DOI] [PubMed] [Google Scholar]
  13. Flores SC, Altman RB 2010. Turning limited experimental information into 3D models of RNA. RNA 16: 1769–1778 [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Frellsen J, Moltke I, Thiim M, Mardia KV, Ferkinghoff-Borg J, Hamelryck T 2009. A probabilistic model of RNA conformational space. PLoS Comput Biol 5: e1000406 doi: 10.1371/journal.pcbi.1000406 [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Gesteland RF, Cech T, Atkins JF 2006. The RNA world: The nature of modern RNA suggests a prebiotic RNA. Cold Spring Harbor Laboratory Press, Cold Spring Harbor, NY [Google Scholar]
  16. Hamelryck T, Manderick B 2003. PDB file parser and structure class implemented in Python. Bioinformatics 19: 2308–2310 [DOI] [PubMed] [Google Scholar]
  17. Handl J, Knowles J, Lovell SC 2009. Artefacts and biases affecting the evaluation of scoring functions on decoy sets for protein structure prediction. Bioinformatics 25: 1271–1279 [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Hansmann UH, Okamoto Y 1999. New Monte Carlo algorithms for protein folding. Curr Opin Struct Biol 9: 177–183 [DOI] [PubMed] [Google Scholar]
  19. Hess B, Bekker H, Berendsen HJC, Fraaije JGEM 1997. LINCS: A linear constraint solver for molecular simulations. J Comput Chem 18: 1463–1472 [Google Scholar]
  20. Hess B, Kutzner C, Van der Spoel D, Lindahl E 2008. GROMACS 4: Algorithms for highly efficient, load-balanced, and scalable molecular simulation. J Chem Theory Comput 4: 435–447 [DOI] [PubMed] [Google Scholar]
  21. Hofacker IL 2009. RNA secondary structure analysis using the Vienna RNA package. Curr Protoc Bioinformatics Chapter 12: Unit12 12 doi: 10.1002/0471250953.bi1202s26 [DOI] [PubMed] [Google Scholar]
  22. Hoover W 1985. Canonical dynamics: Equilibrium phase-space distributions. Phys Rev A 31: 1695–1697 [DOI] [PubMed] [Google Scholar]
  23. Huang ES, Subbiah S, Tsai J, Levitt M 1996. Using a hydrophobic contact potential to evaluate native and near-native folds generated by molecular dynamics simulations. J Mol Biol 257: 716–725 [DOI] [PubMed] [Google Scholar]
  24. Jonikas MA, Radmer RJ, Laederach A, Das R, Pearlman S, Herschlag D, Altman RB 2009. Coarse-grained modeling of large RNA molecules with knowledge-based potentials and structural filters. RNA 15: 189–199 [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Levitt M, Sander C, Stern PS 1985. Protein normal-mode dynamics: Trypsin inhibitor, crambin, ribonuclease and lysozyme. J Mol Biol 181: 423–447 [DOI] [PubMed] [Google Scholar]
  26. Lu H, Skolnick J 2001. A distance-dependent atomic knowledge-based potential for improved protein structure selection. Proteins 44: 223–232 [DOI] [PubMed] [Google Scholar]
  27. Macke TJ, Case DA 1997. Modeling unusual nucleic acid structures. In Molecular modeling of nucleic acids (ed. Leontis NB, SantaLucia J Jr), Vol. 682, pp. 379–393 American Chemical Society [Google Scholar]
  28. Mathews DH 2006. Revolutions in RNA secondary structure prediction. J Mol Biol 359: 526–532 [DOI] [PubMed] [Google Scholar]
  29. McLachlan G, Peel D 2000. Finite mixture models. Wiley, New York [Google Scholar]
  30. Murray LJ, Arendall WB III, Richardson DC, Richardson JS 2003. RNA backbone is rotameric. Proc Natl Acad Sci 100: 13904–13909 [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Murthy VL, Rose GD 2003. RNABase: An annotated database of RNA structures. Nucleic Acids Res 31: 502–504 [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Neal RM 1998. Markov chain sampling methods for Dirichlet process mixture models. J Comput Graph Stat 9: 249–265 [Google Scholar]
  33. Parisien M, Major F 2008. The MC-Fold and MC-Sym pipeline infers RNA structure from sequence data. Nature 452: 51–55 [DOI] [PubMed] [Google Scholar]
  34. R Development Core Team 2008. R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria: [Google Scholar]
  35. Rasmussen CE 2000. The infinite Gaussian mixture model. In Advances in neural information processing systems (ed. Solla SA et al. ), Vol. 12, pp. 554–560 MIT Press, Boston [Google Scholar]
  36. Reeder J, Hochsmann M, Rehmsmeier M, Voss B, Giegerich R 2006. Beyond Mfold: Recent advances in RNA bioinformatics. J Biotechnol 124: 41–55 [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Saenger W 1984. Principles of nucleic acid structure. Springer-Verlag, New York [Google Scholar]
  38. Samudrala R, Moult J 1998. An all-atom distance-dependent conditional probability discriminatory function for protein structure prediction. J Mol Biol 275: 895–916 [DOI] [PubMed] [Google Scholar]
  39. Shapiro BA, Yingling YG, Kasprzak W, Bindewald E 2007. Bridging the gap in RNA structure prediction. Curr Opin Struct Biol 17: 157–165 [DOI] [PubMed] [Google Scholar]
  40. Sharma S, Ding F, Dokholyan NV 2008. iFoldRNA: Three-dimensional RNA structure prediction and folding. Bioinformatics 24: 1951–1952 [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Sippl MJ 1990. Calculation of conformational ensembles from potentials of mean force. An approach to the knowledge-based prediction of local structures in globular proteins. J Mol Biol 213: 859–883 [DOI] [PubMed] [Google Scholar]
  42. Stombaugh J, Zirbel CL, Westhof E, Leontis NB 2009. Frequency and isostericity of RNA base pairs. Nucleic Acids Res 37: 2294–2312 [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Sugita Y, Okamoto Y 1999. Replica-exchange molecular dynamics method for protein folding. Chem Phys Lett 314: 141–151 [Google Scholar]
  44. Summa CM, Levitt M 2007. Near-native structure refinement using in vacuo energy minimization. Proc Natl Acad Sci 104: 3177–3182 [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Sykes MT, Levitt M 2005. Describing RNA structure by libraries of clustered nucleotide doublets. J Mol Biol 351: 26–38 [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Tinoco I Jr, Bustamante C 1999. How RNA folds. J Mol Biol 293: 271–281 [DOI] [PubMed] [Google Scholar]
  47. Tirion MM 1996. Large amplitude elastic motions in proteins from a single-parameter, atomic analysis. Phys Rev Lett 77: 1905–1908 [DOI] [PubMed] [Google Scholar]
  48. Tsai J, Bonneau R, Morozov AV, Kuhlman B, Rohl CA, Baker D 2003. An improved protein decoy set for testing energy functions for protein structure prediction. Proteins 53: 76–87 [DOI] [PubMed] [Google Scholar]
  49. Tsui V, Case DA 2000. Theory and applications of the generalized Born solvation model in macromolecular simulations. Biopolymers 56: 275–291 [DOI] [PubMed] [Google Scholar]
  50. Wang J, Cieplak P, Kollman PA 2000. How well does a restrained electrostatic potential (RESP) model perform in calculating conformational energies of organic and biological molecules?. J Comput Chem 21: 1049–1074 [Google Scholar]
  51. Zhang C, Liu S, Zhou H, Zhou Y 2004. An accurate, residue-level, pair potential of mean force for folding and binding based on the distance-scaled, ideal-gas reference state. Protein Sci 13: 400–411 [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Zhou H, Zhou Y 2002. Distance-scaled, finite ideal-gas reference state improves structure-derived potentials of mean force for structure selection and stability prediction. Protein Sci 11: 2714–2726 [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Zirbel CL, Sponer JE, Sponer J, Stombaugh J, Leontis NB 2009. Classification and energetics of the base-phosphate interactions in RNA. Nucleic Acids Res 37: 4898–4918 [DOI] [PMC free article] [PubMed] [Google Scholar]
  54. Zuker M 2003. Mfold web server for nucleic acid folding and hybridization prediction. Nucleic Acids Res 31: 3406–3415 [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from RNA are provided here courtesy of The RNA Society

RESOURCES