Appraising relative and excess mortality in population-based studies of chronic diseases such as end-stage renal disease

Abstract

Purpose:

Modeling excess and relative mortality represents two ways of considering general population mortality rates (ie, background mortality) in cohort studies. Excess mortality is obtained by subtracting the expected mortality from the observed mortality (additive hazard model). Relative mortality is obtained by dividing the observed mortality by the expected mortality (multiplicative hazard model). Our first objective was to compare the results of these two models in a population-based cohort including 5115 dialyzed patients older than 70 years (mean age 79 years, range 70–97 years). Our second objective was to explore an alternative model combining both excess and relative mortality.

Patients and methods:

Effects of covariates on excess mortality and relative mortality were assessed using a generalized linear model and a Cox model, respectively. The model, combining both excess and relative mortality, is derived from the Aalen model.

Results:

The effect of age and sex was different according to the additive or multiplicative model used, whereas the effect of the first modality of dialysis or the primary nephropathy was similar. Because there was no evidence of lack of fit, the choice of one of these two models was not obvious. The combined model showed that the two components, additive and multiplicative, had to be kept. In this case, the combined model led to results similar to the pure additive and multiplicative univariate models, except for the method of dialysis, which did not exert an effect on both excess and relative mortality.

Conclusion:

We underlined the complementary interest of modeling excess and relative mortality in looking for factors associated with mortality related to end-stage renal disease. The combined model appeared attractive in offering the possibility of reducing the model to the most appropriate one. When both components have to be retained, it better describes the effect of covariates on excess and relative mortality.

Introduction

The increasing collection of registry-based data requires appropriate methodological approaches. One method of determining factors affecting chronic disease mortality is by analyzing cause of death. Deaths that can be directly attributed to the disease of interest are considered as events. Deaths from all other causes can either be censored to estimate the cause-specific mortality or be considered as competing events.^1,2 Unfortunately, in population-based cohorts, the cause of death is often unavailable or unreliable. Indeed, in patients with chronic diseases, such as end-stage renal disease (ESRD), the cause of death can be mistakenly imputed to their disease, whereas other factors, such as advanced age and associated comorbidities, play an important role leading to the death. This difficulty is illustrated by a poor concordance between the causes of death reported on death certificates and in registry reports.^3,4

When the cause of death cannot be used, another method consists of considering mortality rates from the general population as the natural mortality of the cohort, and thus the mortality due to all causes other than the cause of interest. Indeed, it is commonly assumed that most people from the general population do not present the disease of interest.⁵ The mortality rates from the general population, also called background mortality or expected mortality, are estimated from life tables reported in the national mortality statistics.^6–8 For each country, these life tables give the annual probability of death according to sex, calendar year, and age. To take into account the background mortality, two measures of mortality have been described: the excess mortality, related to the concept of relative survival,^5,9,10 and the relative mortality, related to the calculation of the standardized mortality ratio (SMR).^11,12

The excess mortality is obtained by subtracting the expected mortality from the observed mortality (additive hazard model).^9,10,13,14 The excess mortality can be interpreted as the mortality directly or indirectly related to the disease of interest, if one excludes all other causes of death. It is the extra number of deaths observed, beyond that expected, per person-years. For instance, an excess mortality rate of 40 deaths per 100 person-years means that there are 40 additional deaths per 100 person-years in excess of those expected. These deaths are supposed to be related to the disease of interest.

The relative mortality is obtained by dividing the observed mortality by the expected mortality (multiplicative hazard model).^11,13–15 The relative mortality compares the mortality of the cohort to the mortality of the general population. For instance, a relative mortality of 2 means that the observed mortality in the cohort is two-fold higher than expected in a similar subgroup of the general population.

It is worth noting that the terms “additive” and “multiplicative” refer to the manner in which the expected hazard is taken into account and not to how one considers the effect of covariates on excess or on relative mortality. In all this work, the effect of covariates on hazards is multiplicative, as is usually performed for common regression models (general linear model or Cox model).

Whereas excess and relative mortality represents different ways of considering background mortality, the results of the additive model are sometimes wrongly expressed as relative mortality, or conversely as excess mortality for the multiplicative model. In addition, to our knowledge, there are no strong arguments in the literature for choosing an additive hazard model rather than a multiplicative hazard model. Excess mortality has been widely used in cancer research to estimate mortality in population-based studies.^16–18 However, this method was not extensively applied to other chronic diseases,^19,20 contrary to relative mortality.^21,22

The aim of this study was to compare the information brought by the additive and multiplicative hazard models. We analyzed the independent impacts of sex, age at initiation of dialysis, first dialysis modality, and primary nephropathy on excess and relative mortality in a large population-based cohort of ESRD patients treated by dialysis. These models led to dissimilar conclusions, despite the absence of evidence of lack of fit. Thus, the choice of one model instead of the other was not obvious. We then explored an alternative model combining both excess and relative mortality.¹⁴ This model provides the possibility of testing the additive and multiplicative components and then to reduce the model to the most appropriate one, either additive or multiplicative. The potential interest of this model is to simultaneously measure the effect of a covariate on both excess and relative mortality. We then present the results obtained with the combined model in dialyzed patients.

Materials and methods

Adult patients older than 70 years for whom dialysis was initiated between 2002 and 2006 were selected from the French Renal Epidemiology and Information Network (REIN) registry, which includes all ESRD patients on dialysis living in eight French regions.^23,24

Duration of survival was calculated from the date of initiation of dialysis until the date of death, the date of transfer for renal transplantation, and the date of the most recent record, or as of December 31, 2008, whichever came first. All analyses were performed for the first 5 years of follow-up.

Individual expected hazards were calculated using sex s, age a, and calendar year c matched mortality rates based on the data of the French general population drawn from the Human Mortality Database (http://www.mortality.org).

All statistical analyses used R software (http://www.R-project.org) with the Epi package, the timereg package,²⁵ and the relsurv package.²⁶ The syntax is available in Appendix 1.

Excess mortality analysis (additive hazard model)

Calculation of excess mortality is based on an additive hazard model.^9,10,13,14 The observed hazard of a cohort of patients suffering from the disease of interest λ_obs(t) is the sum of the expected hazard of the general population ${\lambda }_{s,a,c}^{*}$ (t) and the excess hazard λ_excess (t) due to the disease:

$${\lambda }_{\mathit{\text{obs}}}\hspace{0.17em}(t,\hspace{0.17em}z)={\lambda }_{s,a,c}^{*}\hspace{0.17em}(t)+{\lambda }_{\mathit{\text{excess}}}\hspace{0.17em}(t,\hspace{0.17em}z)$$ (1)

with z the vector of covariates. Thus, the excess mortality is obtained by subtracting the expected mortality from the observed mortality:

$${\lambda }_{\mathit{\text{excess}}}\hspace{0.17em}(t,\hspace{0.17em}z)={\lambda }_{\mathit{\text{obs}}}\hspace{0.17em}(t,\hspace{0.17em}z)-{\lambda }_{s,a,c}^{*}\hspace{0.17em}(t)$$

The excess hazard is supposed to be a multiplicative function of the covariates z. The model (1) can be written as follows:

$${\lambda }_{\mathit{\text{obs}}}\hspace{0.17em}(t,\hspace{0.17em}z)={\lambda }_{s,a,c}^{*}\hspace{0.17em}(t)+\text{exp}({\beta }^{\prime }z){\lambda }_{0,\mathit{\text{excess}}}\hspace{0.17em}(t)$$

The model is a piecewise constant exponential model that assumes that the hazards are constant within prespecified follow-up intervals, with fu being the follow-up interval indicators:

$${\lambda }_{\mathit{\text{obs}}}\hspace{0.17em}(t,\hspace{0.17em}z,\hspace{0.17em}fu)={\lambda }_{s,a,c}^{*}\hspace{0.17em}(t)+\text{exp}({\beta }^{\prime }z+{{\beta }^{\prime }}_{fu}fu)$$

We chose to use a generalized linear model from individual data.^9,10 This model was estimated by splitting each subject i into several observations j according to the change in follow-up time interval (partitioned into 6-month intervals for the first year and into annual intervals thereafter), age of follow-up, and calendar year of follow-up.

We assumed that the number of deaths d_j for the observation j follows a Poisson distribution with parameter μ_j = λ_j · y_j where y_j is the person-time at risk for observation j. If $d_j^{*}$ is the expected number of deaths for observation j, this model can be written as:

$$\frac{{\mu }_j}{y_j}=\frac{d_j^{*}}{y_j}+\text{exp}({\beta }^{\prime }z+{{\beta }^{\prime }}_{fu}fu)$$

or

$$\text{ln}({\mu }_j-d_j^{*})={\beta }^{\prime }z+{{\beta }^{\prime }}_{fu}fu+\text{ln}(y_j)$$

It defines a Poisson model with the observed number of deaths d_j as response, $\text{ln}({\mu }_j-d_j^{*})$ as link function, and ln(y_j) as offset.

Because the effect of covariates is multiplicative, differences of excess mortality between patients with different covariate values (eg, Z = z₀ and Z = z₁) were expressed as excess mortality ratio (EMR) (EMR = exp(β′(z₁ – z₀))). For example, an EMR of 2 for males compared with females means that the excess mortality related to the disease of interest is two-fold higher in males than in females. An EMR of 1 means that the observed difference in mortality between males and females is similar to that observed in the general population.

A measure of the goodness of fit using the deviance statistic is not available with a generalized linear model from individual data.^10,27 Goodness of fit was thus evaluated from the model performed on collapsed data using the deviance statistics and graphical procedures as proposed by Stare et al.²⁸

The relative survival (RS), from the additive hazard model (1), can be written as follows:⁵

$$RS(t,\hspace{0.17em}z)=\frac{S_{\mathit{\text{obs}}}\hspace{0.17em}(t,\hspace{0.17em}z)}{S_{s,a,c}^{*}\hspace{0.17em}(t)}$$

Relative survival is a measure of the net survival, ie, the survival corrected for the effect of the other death causes. It is the probability of survival until the end of the follow-up period, provided that the only cause of death is the disease of interest.

Relative mortality analysis (multiplicative hazard model)

Calculation of relative mortality is based on a multiplicative hazard model.^11,14,15 The observed hazard λ_obs(t) is the product of the expected hazard of the general population ${\lambda }_{s,a,c}^{*}$(t) and the relative mortality λ_rel(t):

$${\lambda }_{\mathit{\text{obs}}}\hspace{0.17em}(t,\hspace{0.17em}z)={\lambda }_{s,a,c}^{*}\hspace{0.17em}(t)·{\lambda }_{\mathit{\text{rel}}}\hspace{0.17em}(t,\hspace{0.17em}z)$$ (2)

Thus, the relative mortality is obtained by dividing the observed mortality by the expected mortality:

$${\lambda }_{\mathit{\text{rel}}}\hspace{0.17em}(t,\hspace{0.17em}z)=\frac{{\lambda }_{\mathit{\text{obs}}}\hspace{0.17em}(t,\hspace{0.17em}z)}{{\lambda }_{s,a,c}^{*}\hspace{0.17em}(t)}$$

Relative mortality provides a direct comparison between the observed mortality in the cohort and the mortality of the general population. For example, if the relative mortality of a given group of patients is equal to 2, it means that the mortality of this group is two-fold higher than the expected.

Of note, λ_rel is a hazard ratio (HR) expressed without a unit (whereas λ_excess is a hazard, ie, a number of deaths per person-year).

Relative mortality can be estimated from individual data using a Cox model.¹⁵ The model (2) can be written as follows:

$${\lambda }_{\mathit{\text{obs}}}\hspace{0.17em}(t,\hspace{0.17em}z)={\lambda }_{s,a,c}^{*}\hspace{0.17em}(t)·{\lambda }_{0,\mathit{\text{rel}}}\hspace{0.17em}(t)·\text{exp}({\beta }^{\prime }z)$$

or

$${\lambda }_{\mathit{\text{obs}}}\hspace{0.17em}(t,\hspace{0.17em}z)={\lambda }_{0,\mathit{\text{rel}}}\hspace{0.17em}(t)·\text{exp}({\beta }^{\prime }z+\text{log}({\lambda }_{s,a,c}^{*}\hspace{0.17em}(t)))$$

where λ_0,rel (t) is an unknown underlying relative mortality, ie, the relative mortality at time t for an individual i with z = 0.

This model is a Cox model, including the log expected hazards as a time-dependent covariate with a known coefficient fixed to 1 (offset). Because the effect of covariates is multiplicative, differences of relative mortality between patients with different covariate values (eg, Z = z₀ and Z = z₁) were expressed as relative mortality ratio (RMR) (RMR = exp(β′(z₁ – z₀))). For example, an RMR of 2 for gender means that the ratio of the observed mortality of males and females is two-fold higher than the ratio of mortality of males and females in the general population.

Goodness of f it was evaluated using graphical procedures.²⁹

Combining excess and relative mortality

Because it is not obvious deciding which model to choose, we considered a model combining both the additive and the multiplicative hazard components.¹⁴ This combined model was written as:

$${\lambda }_{\mathit{\text{obs}}}\hspace{0.17em}(t)={\lambda }_{\mathit{\text{excess}}}\hspace{0.17em}(t)+{\lambda }_{\mathit{\text{rel}}}\hspace{0.17em}(t)·{\lambda }_{s,a,c}^{*}\hspace{0.17em}(t)$$

This model is a special case of the Aalen’s additive linear regression model,³⁰ where ${\lambda }_{s,a,c}^{*}$ (t) is introduced as a time-dependent covariate and where λ_excess (t) and λ_rel (t) are the parameters to be estimated. It is possible to test whether λ_excess (t) and λ_rel (t) depend on time using the Kolmogorov–Smirnov test.²⁵ As proposed by Andersen and Vaeth,¹⁴ because λ_excess (t) and λ_rel (t) do not depend on time in our cohort of ESRD patients (P = 0.46 and P = 0.78, respectively), the model can be simplified as follows:

$${\lambda }_{\mathit{\text{obs}}}\hspace{0.17em}(t)={\lambda }_{\mathit{\text{excess}}}+{\lambda }_{\mathit{\text{rel}}}·{\lambda }_{s,a,c}^{*}\hspace{0.17em}(t)$$ (3)

The reduction to the additive hazard model is possible by testing λ_rel to 1. In the same way, the reduction to the multiplicative hazard model is possible by testing λ_excess to 0.

Of note, in model (3), the component λ_excess is different from λ_excess (t) in model (1). Indeed, λ_excess estimated in the combined model does not depend on time and is estimated in combination with λ_rel. Similarly, the component λ_rel in model (3) is different from λ_rel (t) in model (2).

Estimation of λ_excess and λ_rel on the whole cohort

The additive λ_excess and multiplicative λ_rel components were estimated on the whole cohort by maximizing the log-likelihood function (see Appendix 2). The variances of the parameters were estimated from the second derivative of the log-likelihood function (see Appendix 2).

The Wald test was used to test λ_excess and λ_rel to 0 and 1, respectively.

Covariate effect on λ_excess and λ_rel

If the λ_excess is different from 0, and λ_rel is different from 1, model (3) is used to estimate the effect of the covariates on λ_excess and λ_rel. The effect of the covariates on λ_excess and λ_rel is considered as multiplicative, as for the additive (1) and multiplicative (2) hazard models presented previously. The first step is to test the global effect of each covariate. We compared the models with and without covariate using the likelihood ratio test. Because it is not possible to introduce a covariate both in the additive and in the multiplicative component of model (3), we calculated the log-likelihoods in subgroups as follows.¹⁴ For each covariate we performed K submodels, one for each modality k of the covariate, and we tested simultaneously whether λ_excess,k were identical and λ_rel,k were identical. The log-likelihood of the model with the covariate is the sum of the log-likelihoods of the K submodels. We thus compared a model with two parameters to a model with 2K parameters.

The second step was to test the effect of each covariate on the two components of the model separately. On one hand, we tested whether all λ_excess,k were identical. On the other hand, we tested whether all λ_rel,k were identical. For example, if a covariate has K = 2 modalities, we tested whether λ_excess,1 was equal to λ_excess,2 by comparing the model with four parameters (λ_excess,1, λ_excess,2, λ_rel,1, and λ_rel,2) with a simplified model with three parameters (common λ_excess, λ_rel,1, and λ_rel,2) by likelihood ratio test. We thus compared a model with K + 1 parameters to a model with 2K parameters.

Results

We identified 5206 patients who had begun dialysis between 2002 and 2006. We excluded 91 patients for the following reasons: pre-emptive graft (never dialyzed, n = 5) and absence of follow-up (n = 86). Finally, 5115 patients were included (Table 1). Mean age was 79 years (standard deviation = 5.3 years, range 70–97 years). The median follow-up was 3 years (1 day to 5 years), and 2871 deaths were observed for a total of 9396 person-years.

Table 1.

Patient characteristics at the beginning of dialysis

Characteristics (whole cohort), n = 5115	Number (%)
Sex
Male	3119 (61)
Female	1996 (39)
Age (years)
<80	3125 (61)
≥80	1990 (39)
First modality of dialysis
Hemodialysis	4467 (87)
Peritoneal dialysis	648 (13)
Primary nephropathy
Hypertensive and large vessel disease	1760 (34)
Diabetes	1204 (23)
Primary and secondary glomerulonephritis	360 (7)
Interstitial nephritis/pyelonephritis	368 (7)
Renal neoplasms/myeloma/light chain nephropathy/amyloidosis	241 (5)
Miscellaneous conditions/unknown/missinga	1182 (23)

Notes:

^aUnknown, missing (n = 824); miscellaneous primary nephropathies (n = 328), including genetic diseases, mainly represented by polycystic kidney diseases (n = 143); and few cases of developmental anomalies (renal dysplasia, hypoplasia), cystic diseases (infantile polycystic kidneys, nephronophthisis), tubular necrosis (no recovery), Alport syndrome, tuberous sclerosis, cystinosis, primary oxalosis, and Fabry’s disease.

Excess mortality analysis (additive hazard model)

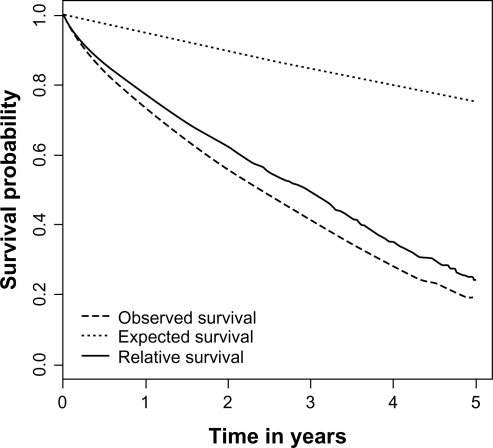
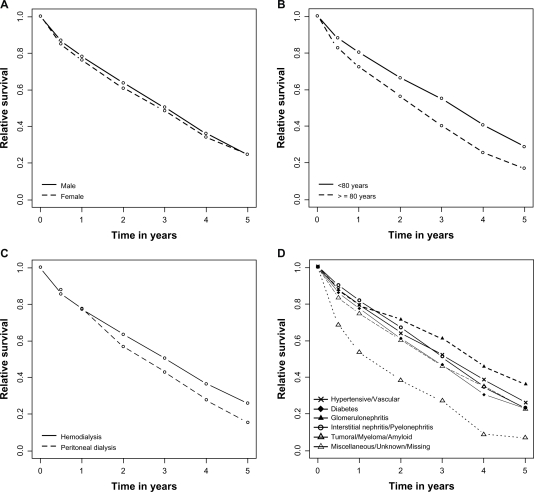
The expected number of deaths was 518 for 2871 observed deaths; the excess mortality was 25 per 100 person-years. The 1-, 2-, and 5-year relative survival rates were 77% (76%–79%), 62% (61%–64%), and 24% (21%–28%), respectively (Figure 1). Univariate analysis of factors determining excess mortality is presented in Table 2 and Figure 2. An older age, peritoneal dialysis, and diabetic and tumoral/myeloma/amyloid nephropathies (compared with hypertensive/vascular origin) were associated with a higher excess mortality (ie, a poorer relative survival). Multivariate analysis showed independent effects of age, first modality of dialysis, and diabetic and tumoral/myeloma/amyloid nephropathies on excess mortality (Table 3). The effect of sex was not significant in the multivariate analysis. There was no evidence of lack of fit by studying deviance on collapsed data (deviance =259 on 279 ddl, P = 0.23) or by graphical procedure. In particular, there was no interaction between age and follow-up time.

Figure 1.

Observed, expected, and relative survival of the whole cohort of patients with end-stage renal disease treated by dialysis.

Table 2.

Results of the univariate analysis of factors affecting excess mortality and relative mortality in dialyzed patients

	Excess mortality					Relative mortality
	5-year RS	EMR	95% CI	P value	LR testa	SMR	RMR	95% CI	P value	LR testa
Sex
Male	24%	1			3.2	4.74	1			73.6
Female	25%	1.09	0.99–1.19	0.069	(0.1)	7.61	1.61	1.49–1.74	<0.001	(<0.001)
Age (years)
<80	29%	1			65.1	7.29	1			96.1
≥80	17%	1.47	1.34–1.61	<0.001	(<0.001)	4.34	0.59	0.55–0.64	<0.001	(<0.001)
First modality of dialysis
Hemodialysis	26%	1			5.6	5.53	1			0.05
Peritoneal dialysis	15%	1.17	1.03–1.34	0.014	(0.017)	5.64	1.02	0.92–1.13	0.75	(0.75)
Primary nephropathy
Hypertensive/vascular	26%	1			98.5	4.62	1			106.4
Diabetes	22%	1.19	1.06–1.34	0.004	(<0.001)	7.32	1.59	1.43–1.75	<0.001	(<0.001)
Glomerulonephritis	36%	0.83	0.68–1.02	0.07		5.17	1.11	0.95–1.31	0.20
Interstitial nephritis/pyelonephritis	24%	0.91	0.75–1.11	0.36		5.32	1.15	0.98–1.34	0.09
Tumoral/myeloma/amyloid	7%	2.46	2.06–2.93	<0.001		14.28	3.04	2.60–3.56	<0.001
Miscellaneous/unknown/missing	25%	1.08	0.95–1.22	0.23		5.00	1.08	0.98–1.19	0.13

Note:

^aChi-squared test (P value) provided.

Abbreviations: CI, confidence interval; EMR, excess mortality ratio; LR, log-likelihood ratio; RMR, relative mortality ratio; RS relative survival, SMR, standardized mortality ratio.

Figure 2.

Relative survival curves according to A) sex, B) age group, C) first dialysis modality, and D) primary nephropathy in patients with end-stage renal disease on dialysis.

Table 3.

Results of the multivariate analysis of factors affecting excess mortality and relative mortality in dialyzed patients

	Excess mortality				Relative mortality
	EMR	95% CI	P value	LR testa	RMR	95% CI	Pvalue	LR testa
Sex
Male	1			1.1	1			158.2
Female	1.05	0.96–1.15	0.29	(0.29)	1.65	1.52–1.78	<0.001	(<0.001)
Age (years)
<80	1			78.5	1			162.9
≥80	1.54	1.41–1.69	<0.001	(<0.001)	0.61	0.56–0.66	<0.001	(<0.001)
First modality of dialysis
Hemodialysis	1			4.2	1			2.9
Peritoneal dialysis	1.15	1.01–1.30	0.036	(0.04)	1.10	0.99–1.22	0.08	(0.1)
Primary nephropathy
Hypertensive/vascular	1			114.9	1			138.6
Diabetes	1.29	1.14–1.45	<0.001	(<0.001)	1.36	1.23–1.50	<0.001	(<0.001)
Glomerulonephritis	0.92	0.75–1.13	0.42		0.99	0.84–1.16	0.88
Interstitial nephritis/pyelonephritis	0.97	0.80–1.19	0.78		1.05	0.90–1.23	0.54
Tumoral/myeloma/amyloid	2.75	2.30–3.28	<0.001		2.60	2.21–3.05	<0.001
Miscellaneous/unknown/missing	1.09	0.96–1.24	0.16		1.06	0.96–1.17	0.24

Note:

^aChi-squared test (P value) provided.

Abbreviations: CI, confidence interval; EMR, excess mortality ratio; LR, log-likelihood ratio; RMR, relative mortality ratio.

Relative mortality analysis (multiplicative hazard model)

The SMR on the whole cohort was 5.54 (5.34–5.75). In univariate analysis, relative mortality was higher for females and in diabetic and tumoral/myeloma/amyloid nephropathies (Table 2). Older patients have a lower relative mortality. Multivariate analysis showed that an advanced age was independently associated with a lower relative mortality (Table 3), whereas female gender and diabetic and tumoral/myeloma/amyloid nephropathies were independently associated with a higher relative mortality. There was no evidence of lack of fit by graphical procedure. In particular, there was no interaction between age and follow-up time.

Combining excess and relative mortality

Estimations of λ_excess and λ_rel on the whole cohort and in sub-groups are presented in Table 4. For the whole cohort, the maximum likelihood estimate of λ_excess was 0.19 (±0.01) and was different from 0 (P < 0.001). The maximum likelihood estimate of λ_rel was 2.17 (±0.17) and was different from 1 (P < 0.001). One might dread coping with a problem of identifiability in this instance. Indeed, the correlation between λ_excess and λ_rel is equal to −0.82. Unfortunately, this problem cannot be eliminated without simulations, ie, by simulating data based on the combined model and assessing the ability of the model to estimate parameters without bias. Nevertheless, the previous estimations appeared coherent.

Table 4.

Results of the combined model for modeling both excess and relative mortality in dialyzed patients

	λexcess(se)	Effect of the covariate onλexcessPvaluea	λrel(se)	Effect of the covariate onλrelPvaluea	Max log likelihood	Effect of the covariate on both componentsPvaluesb
Whole cohort	0.19 (0.01)		2.17 (0.17)		−6169
Sex
Male	0.17 (0.01)		2.11 (0.21)	0.0095	−3788	<0.001
Female	0.18 (0.01)	0.70	3.15 (0.35)		−2369
Age (years)
<80	0.18 (0.02)	0.001	2.04 (0.44)	0.22	−2500	<0.001
≥80	0.28 (0.03)		1.43 (0.25)		−2507
First modality of dialysis
Hemodialysis	0.19 (0.01)	0.90	2.07 (0.18)	0.26	−5347	0.096
Peritoneal dialysis	0.19 (0.03)		2.61 (0.45)		−820
Primary nephropathy
Hypertensive/vascular	0.17 (0.02)	0.002	1.86 (0.26)	0.077	−2097	<0.001
Diabetes	0.19 (0.02)		2.99 (0.48)		−1498
Glomerulonephritis	0.11 (0.03)		2.77 (0.67)		−409
Interstitial nephritis/pyelonephritis	0.10 (0.03)		3.32 (0.66)		−407
Tumoral/myeloma/amyloid	0.41 (0.08)		4.60 (1.71)		−275
Miscellaneous/unknown/missing	0.17 (0.02)		2.33 (0.31)		−1420

Notes:

^aLog-likelihood ratio test comparing the K λ_excess or the K λ_rel;

^bLog-likelihood ratio test comparing the model with and without each covariate (eg, sex: Chi-squared = −(3788 + 2369) + 6169).

Because the two components additive and multiplicative should be kept, this model did not enable selection of one of the pure additive or multiplicative models. We thus used this model to estimate the effect of the covariates on both excess and relative mortality (Table 4).

Sex, age, and primary nephropathy exerted an effect on mortality; conversely, the first modality of dialysis did not. Moreover, we showed that λ_excess was different between age groups and primary nephropathies, whereas λ_rel was higher in females. Both λ_excess and λ_rel were no different between hemodialysis and peritoneal dialysis.

Discussion

The use of expected mortality provides a useful perspective in mortality analysis of population-based cohorts of patients suffering from chronic disease such as cancer but also from other diseases. This is the reason why we were interested in comparing the two methods based on expected mortality rates in order to look for prognostic factors on ESRD-related mortality.

The additive hazard model is almost exclusively the first-choice model in population-based cancer studies. In other chronic diseases, it appears that a multiplicative hazard model is used more often. Noticeably, confusion between relative mortality and excess mortality is sometimes observed, ie, expressing the result of a multiplicative model in terms of excess mortality. As do Andersen and Vaeth,¹⁴ we advise using the term “excess mortality” when one assumes that the total hazard is the sum of expected and excess hazards (additive hazard model (1)). The term “relative mortality” should be used when one assumes that the total hazard is the product of expected and relative hazards (multiplicative hazard model (2)). We recall, in these two models, that the effect of covariates on excess or relative mortality is considered as multiplicative.

Estimations of the additive hazard model are based either on generalized linear models^10,31 or on likelihood estimation.³² All these models produce similar estimates.¹⁰ Another type of additive hazard model was described by Cortese and Scheike,³³ but this model assumes an additive effect of the covariates. The advantage of the additive hazard model is that it is interpretable in the context of competing risk settings. But under some circumstances, the additive hazard model may be inappropriate because it requires that the risk in the diseased group be higher than in the general population for all covariate levels. But in the case of chronic diseases, there are few instances for which the observed mortality is lower than the expected one.

Two formulations of the multiplicative hazard model have been described, based on generalized linear models¹² or the Cox proportional model,^13–15 leading to close estimates. In this instance, the choice of a multiplicative hazard model has been suggested,^13–15 though this was considered to be “biologically less appropriate” by some authors,^10,13 without additional explanation. However, to our knowledge, there are no strong arguments in the literature allowing the choice of an additive hazard model over a multiplicative hazard model. A usual way of deciding which of the two models is the most appropriate is to examine the likelihood ratio. This is a nontrivial problem, as these two classes of models (Poisson model and Cox model) are not nested here.

This study of a large cohort of patients with ESRD treated by dialysis prompted us to provide a comprehensive analysis of the mortality and compare the two types of models. We chose to limit the comparison of models containing the same four covariates without interactions. Indeed, the complexity of a model including both covariate by covariate interactions and time by covariate interactions, especially when covariates have several modalities, such as in our example (primary nephropathies), makes the model interpretation very difficult. In addition, selection of the more parsimonious model should lead to keeping only some covariates and their interactions in the final additive and multiplicative models. This approach might possibly lead to selecting different covariates and different interactions for the two final models considered.

Andersen and Vaeth¹⁴ suggest considering routinely both age and follow-up time as underlying time variables when the additive and multiplicative models are evaluated. Indeed, it may be interesting to consider age as the underlying time variable in two situations: i) if healthy subjects are followed up prospectively for the occurrence of a given disease (epidemiologic cohort studies), and ii) if the data are left truncated. The patients were included in our cohort on the day they initiated dialysis. Because we were interested in factors affecting mortality in dialysis, we only used the follow-up time as a time variable.

Interestingly, most of the covariates tested in the univariate models for excess or relative mortality led to different conclusions, particularly for age. Indeed, we observed that excess mortality increased with age, whereas the relative mortality decreased. That means that the absolute excess number of deaths is higher for older people (EMR = 1.54 [1.41–1.69]). However, relative to background mortality, which is higher in subjects older than 80 years, the excess of deaths was lower (RMR = 0.61 [0.56–0.66]). The difference between the two models for sex remained after adjusting for age, whereas the effects of first modality of dialysis and primary nephropathies were similar in multivariate models. Interpreting the differences between the results of additive and multiplicative models is not straightforward. Indeed, these results must be examined according to i) the size of the observed mortality in each subgroup and the observed HR, ii) the size of the expected mortality in each subgroup and the expected HR, and iii) the size of the expected mortality relative to the observed mortality. There are several cases where differences between the two models occur. An interesting example is the effect of gender in our cohort. Indeed, we found that the observed mortality in males was not different from the observed mortality in females (observed HR = 0.99 [0.92–1.07], P = 0.77). If gender does not exert an effect on mortality in ESRD, one should identify an observed HR for gender similar to the expected HR, ie, a worse prognostic in males (as in the general population). When performing the additive model, the EMR was not different from 1 (EMR = 1.09 [0.99–1.19]). We explained this absence of gender effect on excess mortality by the fact that the expected mortality is very low compared with the observed mortality in our cohort. The ratio (λ_obs females – λ^* females)/(λ_obs males – λ^* males) is thus close to the λ_obs females/λ_obs males ratio. On the contrary, when performing the multiplicative model, we underlined that the observed HR was different from the expected HR (RMR = 1.61 [1.49–1.74]) and thus that gender effectively exerted an effect on mortality in ESRD. The results of the two models are thus not contradictory but complementary. Both models are informative, and we recommend exploring the results of modeling excess and relative mortality separately in order to look for factors associated with mortality in chronic disease.

To our knowledge, few studies analyzed both excess and relative mortality using appropriate models.^34–36 Kvidal et al³⁴ performed such analyses in men who underwent aortic valve replacement, Favier et al³⁵ in Hodgkin’s lymphoma, and Reulen et al³⁶ in survivors of childhood cancer. In these studies, the opposite effect of age on relative and excess mortality in univariate analysis was described. In Reulen et al,³⁶ the opposite effect of age disappeared in multivariate analysis. This opposite effect of age was not assessable in Kvidal et al’s³⁴ and Favier et al’s³⁵ studies, as they only performed a multivariate model for excess mortality. For gender, in univariate analysis, both Reulen et al³⁶ and Favier et al³⁵ described a higher relative mortality in females than in males, whereas the excess mortality was higher in males. In Reulen et al,³⁶ the opposite effect of gender remained in multivariate analysis. Nevertheless, the authors did not interpret this discrepancy. In the particular context of ESRD, excess mortality has only been used to compare differences in mortality on dialysis across European countries by using specific expected mortality rates by countries.³⁷ In another study, only the relative mortality was estimated, and SMR was estimated and compared between various multiple subgroups.³⁸ However, our results were not comparable with this study, as the authors estimated SMR by subgroups and did not provide a multivariate analysis.

Because we observed apparent discrepancies in results obtained with the two models, we used the combined model already described by Andersen and Vaeth.¹⁴ We did not find in the literature a study that used such a model. This model has the advantage of giving the possibility of testing the additive and multiplicative components and then to reduce the model to the most appropriate one. In our data, the two components had to be kept in the combined model, underlying the potential interest of this model in simultaneously and separately measuring the effect of covariates on the excess mortality and relative mortality. It led to results similar to the pure additive and multiplicative univariate models. Particularly for age, the additive component became higher when age increased, whereas the inverse phenomenon was observed for the multiplicative component (even if it was nonsignificant). On the contrary, the modality of first dialysis did not exert a significant effect on both components. We can explain this result by the fact that the value of the additive component was very small relative to the multiplicative component. The omission of the multiplicative component (ie, if a pure additive model was used) led to an estimation of the additive component that might be biased, overestimating the effect of the covariate on excess mortality. The use of a pure additive or multiplicative model may thus lead to inappropriate conclusions. In our opinion, the combined model appeared useful to adequately estimate the effect of prognostic factors on mortality in chronic diseases. Nevertheless, a multivariate combined model is needed to confirm our results. To our knowledge, such a multivariate combined model has not been developed yet. Moreover, the interpretation of the parameters of the combined model is not straightforward. Presently, the parameters λ_excess and λ_rel can be estimated only in subgroups. We estimated these parameters only for testing an effect of one covariate on excess and relative mortality. Because these parameters are not directly interpretable, further developments are necessary to build a model that would estimate directly the HR for the two components. In this case, one might estimate both mortality related to a chronic disease and its relation to the expected mortality.

Conclusion

Excess hazard and relative hazard models allow the estimation of mortality related to a chronic disease, taking into account the background mortality. The choice between these two models depends on the purpose of the analysis and the fit to the data. More generally, it may be interesting to look for factors associated with mortality in a cohort of patients presenting a chronic disease. Even if the interpretation of the excess hazard model is different from the relative hazard model, and if these models may lead to apparent dissimilar conclusions, we underlined their complementary interest in looking for factors associated with mortality related to ESRD. Alternatively, a model combining both excess and relative mortality gives the possibility of testing the additive and multiplicative components and then of reducing the model to the most appropriate one. When both components must be retained, the interest of this model is to measure simultaneously and separately the effect of covariates on both excess and relative mortality.

Appendix 1: Syntaxes for fitting the models with R software

Fitting the additive hazard model (excess mortality analysis)

The additive hazard model is written as a generalized linear model as follows:

$$\text{ln}({\mu }_j-d_j^{*})={\beta }^{\prime }z+{\beta }_{fu}fu+\text{ln}(y_j)$$

The original dataset (data, one line per subject) can be easily split with the Lexis() function in the Epi package. For example, for one subject, data have the form:

num	sex	incl	age	futime	D	cov
70	2	04Jun2002	75.35	1.788	1	1

We need to split the follow-up of each subject into several observations j, according to change in age, calendar year, and follow-up time interval (using 1-year intervals). We can thus obtain for each observation of each subject (dataset named data1):

• Y: the length of the observation (y_j)

• rate: the expected hazard $({\lambda }_{s,a,c}^{*}\hspace{0.17em}(t))$. The website mortality.org provides a life table for each sex s (sex) containing the expected annual probability of death q_s,a,c for each age a (age) and each calendar year c (year). The expected annual hazard is calculated as ${\lambda }_{s,a,c}^{*}=-\text{log}(1-q_{s,a,c}^{*})$.

• E: the number of expected deaths $d_j^{*}$ calculated as the product of ${\lambda }_{s,a,c}^{*}$ (t) and y_j

• D: the indicator of death

• fu: the follow-up interval indicator and

• cov: the value of the covariate to be model.

For example, for the same subject, data1 have the form:

num	sex	age	year	rate	start	stop	Y	E	D	fu	cov
70	2	75	2002	0.0195	0.0000	0.5000	0.5000	0.0098	0	(0,0.5]	1
70	2	75	2002	0.0195	0.5000	0.5784	0.0784	0.0015	0	(0.5,1]	1
70	2	75	2003	0.0199	0.5784	0.6489	0.0705	0.0014	0	(0.5,1]	1
70	2	76	2003	0.0230	0.6489	1.0000	0.3511	0.0081	0	(0.5,1]	1
70	2	76	2003	0.0230	1.0000	1.5784	0.5784	0.0133	0	(1,2]	1
70	2	76	2004	0.0208	1.5784	1.6489	0.0705	0.0015	0	(1,2]	1
70	2	77	2004	0.0224	1.6489	1.7878	0.1389	0.0031	1	(1,2]	1

We need to specify the particular link function as presented here:

poi <- Mypoisson()

poi$link <- “Poisson excess risk model”

poi$linkfun <- function(mu) log(mu-E)

poi$linkinv <- function(eta) exp(eta)+E

assign(“E”, data1$E, env = .GlobalEnv)

if (any(data1$D – data1$E < 0)) {

poi$initialize <- expression({

n <- rep.int(1, nobs)

mustart <- pmax(y,E) + 0.1

})

}

The model can be performed as follows with the glm() function in R software:

Add<-glm(D∼-1+cov+fu,offset=log(Y),family=Mypoisson,data=data1)

The effect of the covariate is equal to the exponential of the coefficient:

EMR<-exp(coef(Add))

Fitting the multiplicative hazard model (relative mortality analysis)

The multiplicative hazard model is written as a Cox model as follows:

$${\lambda }_{\mathit{\text{obs}}}\hspace{0.17em}(t,\hspace{0.17em}z)={\lambda }_{0,\mathit{\text{rel}}}\hspace{0.17em}(t)·\text{exp}({\beta }^{\prime }z+\text{log}({\lambda }_{s,a,c}^{*}\hspace{0.17em}(t)))$$

The original dataset (data, one line per subject) can be easily split with the Lexis() function in the Epi package. We need to have ${\lambda }_{s,a,c}^{*}$ (t) for each event time and thus to split the follow-up of each subject into several observations j, according to change in age and calendar year.

We can thus obtain for each observation of each subject (dataset named data2):

• rate: calculated as above

• start and stop: the limits of the observation

• D: the indicator of death

• cov: the value of the covariate to be model.

For example, for the same subject, data2 have the form:

num	sex	age	year	rate	start	stop	D	cov
70	2	75	2002	0.0195	0.000	0.578	0	1
70	2	75	2003	0.0199	0.578	0.649	0	1
70	2	76	2003	0.0230	0.649	1.578	0	1
70	2	76	2004	0.0208	1.578	1.649	0	1
70	2	77	2004	0.0224	1.649	1.788	1	1

The model can be performed as follows with the coxph() function in R software:

Mult<-coxph(Surv(start,stop,D)∼cov+offset(log(rate)),data=data2)

The effect of the covariate is equal to the exponential of the coefficient:

RMR<-exp(coef(Mult))

Fitting the combined model

The combined model proposed by Andersen and Vaeth¹⁴ is written as follows:

$${\lambda }_{\mathit{\text{obs}}}\hspace{0.17em}(t)={\lambda }_{\mathit{\text{excess}}}\hspace{0.17em}(t)+{\lambda }_{\mathit{\text{rel}}}\hspace{0.17em}(t)·{\lambda }_{s,a,c}^{*}\hspace{0.17em}(t)$$

We need to split the dataset as for the multiplicative hazard model (data2).

The model can be performed as follows with the aalen() function in the timereg package:

Comb<-aalen(Surv(start,stop,D)∼rate,id=data2$num,data=data2)

This function allows to test whether the intercept (λ_excess(t)) and the coefficient of the covariate $(rate={\lambda }_{s,a,c}^{*}\hspace{0.17em}(t))$ depend on time using the Kolmogorov–Smirnov test.

Appendix 2: Log-likelihood function, score vector, and Fisher information for the combined model

The log-likelihood function of the combined model is written as:

$$LV=\sum _{i=1}^n{D}_i\text{ln}\left({\lambda }_{\mathit{\text{excess}}}+{\lambda }_{\mathit{\text{rel}}}·{\lambda }_{s,a,c}^{*}\hspace{0.17em}(t_i)\right)-{\lambda }_{\mathit{\text{excess}}}·\sum _{i=1}^n{t}_i-{\lambda }_{\mathit{\text{rel}}}·\sum _{i=1}^n{\Lambda }_{s,a,c}^{*}\hspace{0.17em}(t_i)$$

where t_i is the observation time, D_i is the indicator of failure, ${\lambda }_{s,a,c}^{*}\hspace{0.17em}(t_i)$ is the expected hazard, and ${\Lambda }_{s,a,c}^{*}\hspace{0.17em}(t_i)$ is the cumulative expected hazard for the subject i (i = 1, …, n). λ_excess and λ_rel are the excess and the relative hazard to be estimated.

The first-order derivative of the log-likelihood function (score vector) is written as:

$$\frac{\partial LV}{\partial {\lambda }_{\mathit{\text{excess}}}}=\sum _{i=1}^n\frac{D_i}{{\lambda }_{\mathit{\text{excess}}}+{\lambda }_{\mathit{\text{rel}}}·{\lambda }_{s,a,c}^{*}\hspace{0.17em}(t_i)}-\sum _{i=1}^n{t}_i$$

and

$$\frac{\partial LV}{\partial {\lambda }_{\mathit{\text{rel}}}}=\sum _{i=1}^n\frac{D_i·{\lambda }_{s,a,c}^{*}\hspace{0.17em}(t_i)}{{\lambda }_{\mathit{\text{excess}}}+{\lambda }_{\mathit{\text{rel}}}·{\lambda }_{s,a,c}^{*}\hspace{0.17em}(t_i)}-\sum _{i=1}^n{\Lambda }_{s,a,c}^{*}\hspace{0.17em}(t_i)$$

The Fisher matrix is thus equal to:

$$I=-E\left(\begin{array}{l}-\sum _{i=1}^n\frac{D_i}{{\left[{\lambda }_{\mathit{\text{excess}}}+{\lambda }_{\mathit{\text{rel}}}·{\lambda }_{s,a,c}^{*}\hspace{0.17em}(t_i)\right]}^2}-\sum _{i=1}^n\frac{D_i·{\lambda }_{s,a,c}^{*}\hspace{0.17em}(t_i)}{{\left[{\lambda }_{\mathit{\text{excess}}}+{\lambda }_{\mathit{\text{rel}}}·{\lambda }_{s,a,c}^{*}\hspace{0.17em}(t_i)\right]}^2}\hfill \\ -\sum _{i=1}^n\frac{D_i·{\lambda }_i^{*}\hspace{0.17em}(t_i)}{{\left[{\lambda }_{\mathit{\text{excess}}}+{\lambda }_{\mathit{\text{rel}}}·{\lambda }_{s,a,c}^{*}\hspace{0.17em}(t_i)\right]}^2}-\sum _{i=1}^n\frac{D_i·{\lambda }_i^{*2}\hspace{0.17em}(t_i)}{{\left[{\lambda }_{\mathit{\text{excess}}}+{\lambda }_{\mathit{\text{rel}}}·{\lambda }_{s,a,c}^{*}\hspace{0.17em}(t_i)\right]}^2}\hfill \end{array}\right)$$