Hybrid Median Filter Background Estimator for Correcting Distortions in Microtiter Plate Data

Abstract

Microtiter plate (MTP) assays often exhibit distortions, such as caused by edge-dependent drying and robotic fluid handling variation. Distortions vary by assay system but can have both systematic patterns (predictable from plate to plate) and random (sporadic and unpredictable) components. Random errors can be especially difficult to resolve by assay optimization alone, and postassay algorithms reported to date have smoothing effects that often blunt hits. We implemented a 5 × 5 bidirectional hybrid median filter (HMF) as a local background estimator to scale each data point to the MTP global background median and compared it with a recently described Discrete Fourier Transform (DFT) technique for correcting errors on computationally and experimentally generated MTP datasets. Experimental data were generated from a 384-well format fluorescent bioassay using cells engineered to express eGFP and DsRED. MTP arrays were produced with and without control treatments used to simulate hits in random wells. The HMF demonstrated the greatest improvements in MTP coefficients of variation and dynamic range (defined by the ratio of average hit amplitude to standard deviation, SD) for all synthetic and experimental MTPs examined. After HMF application to a MTP of eGFP signal from mouse insulinoma (MIN6) cells obtained by a plate-reader, the assay coefficient of variation (CV) decreased from 8.0% in the raw dataset to 5.1% and the hit amplitudes were reduced by only 1% while the DFT method increased the CV by 36.0% and reduced the hit amplitude by 21%. Thus, our results show that the bidirectional HMF provides superior corrections of MTP data distortions while at the same time preserving hit amplitudes and improving dynamic range.

The software to perform hybrid median filter MTP corrections is available at http://bccg.burnham.org/HTS/HMF_Download_Page.aspx, password is pbushway.

INTRODUCTION

Errors in microtiter plate (MTP) data can arise from many sources including robotic liquid handling, instrumentation, and atmospheric conditions, and are frequently exacerbated by lengthy or complex assays.^1–4 The detrimental localized data distortions in MTP data obtained from a chemical library screen can be random, such that sporadic errors are distributed unpredictably throughout a screen, or systematic, such that a similar pattern is repeated predictably. These distortions include edge artifacts that can be caused, for example, by variations in temperature and humidity over the area of a MTP. Even seemingly predictable patterns such as edge artifacts usually have random components that cannot be easily modeled or corrected.² Random components become more evident when comparing spatially patterned data distortions from MTP to MTP, as they often defy prediction by a concise error model. Strategies for rectifying systematic errors include defining and tracking the error sources and introducing methods to compensate for their effects. A common approach is to flag and remove errors from MTP data, but this has the undesirable effect of discarding potentially useful data.⁴ The primary challenge, therefore, is to design a method for correcting underlying data distortions while preserving the signal contributed by the hits, which can be modeled as sparse point noise, or outliers.

Local distortions, such as edge artifacts, can be thought of as local variations in background. This shifts the problem to one of finding a way to correct the background values to within a narrow and uniform range (eg, a flat surface in a 3D plot), thereby removing the distortions/artifacts and improving the confidence in resolving the sparse “point noise” of outliers that correspond to screening hits, while reducing the hit/background dynamic range as little as possible. We believe the simplest way to do this is to estimate the local background (L) within an appropriate sample neighborhood and scale each target data point (target value) centered in that neighborhood by the ratio of the global (G) and local backgrounds (L) as

where the corrected value replaces the target value in the corrected MTP dataset.

In chemical library or functional genomics (RNAi and cDNA) screens, hits are typically of high- or low-magnitude values compared to the background wells. Thus, error correction consists of correcting local background distortions by, for example, applying a median filter⁵ as illustrated in Figure 1A, while retaining sporadic, high/low magnitude events. That is, the hits are analogous to the “salt and pepper,” or “point” noise that typically comprises errors in many other applications. For chemical library or functional genomics screening applications, nonparametric data scaling should not remove or dwarf these rare, low- or high-magnitude events, since these correspond to assay hits and are the samples of interest. MTPs with local patterns designed into the assay, such as serial dilutions of compounds for dose responses, should be addressed with other methods such as LOcal regrESSion (LOESS) to fit and normalize data^1,6 via locally adaptive processes that use low-order polynomials to approximate a fit to neighborhood data.⁷

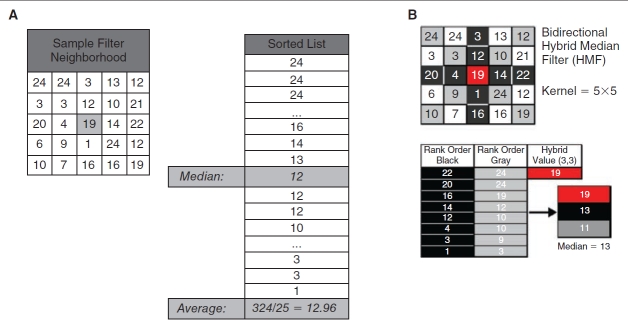
Fig. 1. .

Illustration of example 3 × 3 median and 5 × 5 hybrid median filters (HMFs). (A) Elements representing both common 3 × 3 median and average filters, where the median is obtained from the rank order of all 9 elements and the average is the arithmetic mean of the same elements, are shown. (B) For the bidirectional 5 × 5 HMF, the median values are extracted from neighborhood diagonals (gray), cross (black), and center value (red) and are used to generate a rank-ordered 3-number list from which a final hybrid median value is determined for each data element in a microtiter plate (MTP) array.

For primary screens, both the median filter and the hybrid median filter (HMF) can be used to estimate the local (empirically defined neighborhood) background to scale the center element by the global background (G/L, see Equation 1). G is the true or expected background, which can be estimated by the median or average of the whole dataset or a representative subset of values (eg, multiple plates in a batch, or one plate) in the screen; the global background estimate is a constant for a whole dataset, a batch of plates, or a single plate, respectively. Importantly, the median-based correction is outlier resistant in that a single hit/outlier will not alter the local estimate L of the background. By taking the statistical median stepwise over predetermined subregions of the neighborhood, the HMF provides additional freedom to ignore multiple hits/outliers within the neighborhood to create the background estimate. Because they completely ignore the hits/outliers in estimating the background, we hypothesized that median filters would be a better choice than typical smoothing operators/filters and methods based on the Discrete Fourier Transform (DFT), which invariably blunt the hits. The linear DFT views everything as spatial frequencies, which cannot always properly represent the spatially discrete properties inherent of the assay data. The nonlinear and inherently spatially digital/discrete properties of the HMF enable more complete insensitivity to hits/outliers and it can be applied to raw data arrays systematically and automatically without plate-by-plate operator input, which may improve consistency.

Other median-based methods have been previously introduced that make corrections to the systemic variations of MTP.⁸ Some prominent cases are the median polish⁹ and the B-score¹⁰ methods that estimate a residual value by employing a 2-way fit to the columns and rows of the target value. Through iterations, the row and then column medians are removed to minimize the residual value to the user-defined minimum or present number of iterations. Because of their iterative nature, these methods can be more computationally intensive than the single-pass HMF. Both iterative methods also require a user decision to stop iteration when the residual has reached a minimum value or a preset number of iterations have been completed. The HMF method, on the other hand, requires no input or decision making from the user.

In preliminary experiments, we tested various local background estimators on MTP data for their respective capacity to diminish spatial distortion while preserving hit amplitudes, and found the bidirectional HMF promising.^11,12 We then adapted the HMF for better operation at MTP edges and compared it to a recently described Small Laboratory Information Management System (SLIMS) DFT technique.^2,3 The strengths and weaknesses of the algorithms were evaluated by the reduction of background distortion and overall variations in MTP values (with hits removed), preservation of hit amplitudes, and/or hit:background dynamic range.

MATERIALS AND METHODS

Median-Based Array Correction

MTP data can be written in the matrix notation:

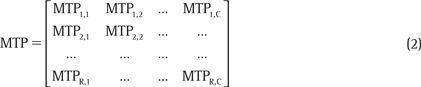where R and C represent the maximum number of rows and columns, respectively, in the MTP (eg, R =16, C = 24 for a 384-well MTP). Here, each element of the matrix represents the measurement originating from a well. In index notation, this can be simply expressed as MTP_i,j, where i = [1, 2, 3, …, R] and j = [1, 2, 3, …, C] are the row and column indices.

A square local neighborhood of the size d × d (eg, 3 × 3 and 5 × 5 in Figure 1A and 1B, respectively) is explicitly described with odd values of d for symmetry. The half-size of the filter, using integer math, is defined as h = d/2 (eg, h = 5/2 = 2 for d = 5). A local background L_i,j within each d × d neighborhood around MTP_i,j is estimated by the HMF such that the center element of the neighborhood falls on MTP_i,j. The medians of the diagonal and axial elements of each neighborhood are defined as

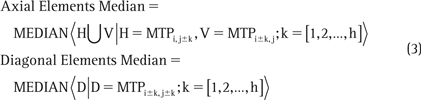Note that since k is a nonzero index, the central element is excluded from these median calculations. Moreover, when the neighborhood is close to the periphery of the MTP, the filter elements that fall outside of the defined range of MTP_i,j are simply ignored by dynamically shrinking the neighborhood size at the edges. Finally, the estimate of the local background is

Using the global background G of the entire MTP and this local background estimate, each data point MTP_i,j is then scaled to a corrected value C_i,j using a more specific version of Equation 1,

For the more common median and average filters, each element was also scaled in the manner described in Equations 1 and 4, with L defined as the median and average of the neighborhoods (Fig. 1A), respectively, and G defined as the MTP median (Fig. 1).

The kernel sizes of 3 × 3 and 5 × 5 for the HMF were chosen empirically. In preliminary experiments (data not shown), the 5 × 5 size appeared to be optimum for 384-well MTP arrays; however, application to higher density formats may require additional testing to confirm an optimal kernel size and it is possible that larger kernel sizes (eg, 7 × 7, 9 × 9, etc.) might perform better in higher density formats where, for example, edge artifacts might also extend inward over a larger number of wells. Since the local background estimation depends heavily on obtaining a representative sample population from the MTP, kernel size is important particularly at the MTP edges. An alternative to ignoring the kernel elements outside the array when operating at the edges (see Equation 3) is to keep the kernel size constant and move the target pixel within the kernel and appropriately alter the subregions for calculations of the intermediate medians. Alternatives from image processing are also available.^13–15

Applications of the common median and average filters (see Fig. 1A), and the bidirectional HMF (see Fig. 1B), are described as follows. For the example 5 × 5 neighborhood in Figure 1A (left), the median and average filters used all 25 of the elements to obtain local backgrounds of 12 and 12.96, respectively. Application of the bidirectional HMF in Figure 1B to the same neighborhood gave a median of the diagonal elements of 11 and a median of the axial elements of 13. With a central data element of 19, the final rank ordered list yields a hybrid median of 13.

The operation of the HMF is illustrated in more detail in the diagram of an example MTP (Fig. 2) created using Microsoft Excel by weighting array values appropriately to create a uniform contour with a pronounced edge artifact. The HMF with kernel (or neighborhood) size d = 5 was applied to the MTP and the medians of the diagonal (gray) and axial (black) elements are noted in the table (Fig. 2, bottom), along with the original and scaled value of the center MTP_i,j position (red). Note that elements of the HMF outside of the MTP array are ignored when they overhang the plate edge at the peripheral wells. The total number of contributing elements (N) is listed for each of the masks, which are located at center coordinates “ID_i,j.”

Fig. 2. .

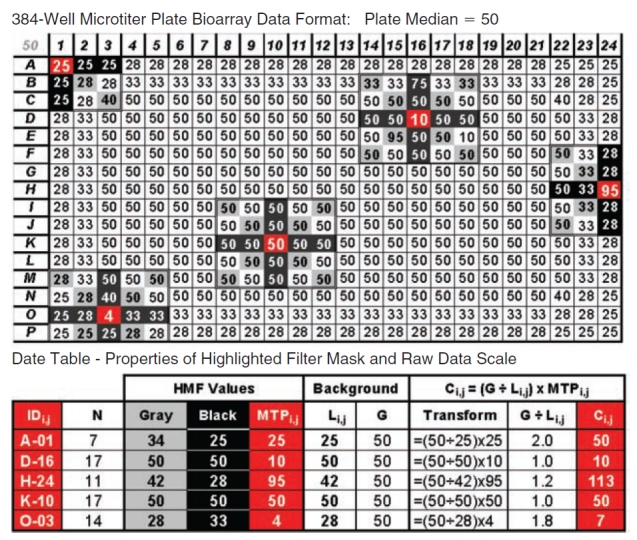
Application of the 5 × 5 bidirectional hybrid median filter (HMF) to a microtiter plate (MTP) array. Various placements of the HMF on an example array illustrate the function of the filter and the effect of peripheral wells on filter size and the total number (N) of sampled elements. As the 5 × 5 HMF passes over the array, it returns a unique value estimating the local neighborhood (L_i,j) corresponding to the raw data element at its center (MTP_i,j). A linear transform is then applied to the raw data center element. The linear transform divides the dataset global median (G) (50 as indicated in top left corner) by the filter hybrid median (L_i,j) to produce a simple scalar that is multiplied by MTP_i,j to yield the corrected value (C_i,j). The table (bottom) tracks MTP_i,j and C_i,j for the illustrated operations.

For the example targeting well A-01 for correction in Figure 2, there is no hit, but the modeled edge effect decreases the values toward the edge and Equation 5 scales MTP1,1 = 25 to the corrected value C1,1 = 50. At well D-16, MTP4,16 is a down hit, there are 2 up hits in the 5 × 5 neighborhood (95 in the diagonal and 75 on the vertical axis), and the well value is unchanged at C4,16 = 10. At H-24, there is an up hit distorted by the edge effect and MTP8,24 = 95 is scaled up to C8,24 = 113. At well K-10, MTP11,10 = 50 is the same as the global estimate, resulting in no change for C11,10 = 50. Well O-03 is a down hit of MTP15,3 = 4 that is distorted by the edge effect and is corrected up to C15,3 = 7. A program for implementing the bidirectional HMF can be downloaded at http://bccg.burnham.org/HTS/HMF_Download_Page.aspx (password pbushway).

Discrete Fourier Transform-Based Data Correction

DFT calculations of biological array experiments^2,3 can be used to create a periodogram of the array data.^16,17 The periodogram describes the degree of distortions that can be modeled by “patterning” in the original array data. In a MTP, plate-wide, well-by-well random variations including point noise (outliers; hits) represents low periodogram amplitudes and composes the bulk of the array data in a screen. Localized spatial distortion and patterning appears as high-magnitude signal on a periodogram due to spatial agreement in array values.

Our MTP data were processed with the Small Laboratory Information Management System (SLIMS) DFT software (downloaded from http://slims.sourceforge.net/) for comparison with the HMF. The VisTa standalone was used to confirm SLIMS-implemented DFT and DFT corrections (see http://www.columbia.edu/cu/biology/faculty/stockwell/StockwellLab/index/ to download).²

MIN6 eGFP/DsRED Cells

The MIN6 mouse insulinoma cell line¹⁸ was stably modified following lentiviral infection to express eGFP under the control of the human insulin promoter¹⁹ and DsRED under control of the phosphoglycerate kinase (PGK) minimal promoter.^20,21 The dual promoter system allows a direct comparison of insulin and PGK promoter activities.

Experimental Array Data

Our comparative analysis of correction methods used a combination of 3 computationally derived (“synthetic,” created in Microsoft Excel) and 4 experimentally derived cell-based (“experimental,” MIN6 eGFP/DsRED cells) MTP array data, which are summarized in Table 1. In the 3 synthetic arrays, a model 384-well MTP was created to mimic the edge artifact commonly observed in real-world assay data. Synthetic1 (Fig. 3) edge distortion was created in the outer wells (a distance of 3 or less from the edge), spanning the range 0.25–0.5 (out of 0.0–1.0). The Synthetic1 background values were generated randomly around a mean of 0.5 with a 5% deviation (using a uniform distribution) to mimic noise. Synthetic1 hits were inserted randomly with magnitudes 0.6 and 1.0 (Fig. 3A). Synthetic2 was created with edge effects within 3 wells of the edge but without background noise or hits (Fig. 4A). Sythethic3 is similar to Synthetic2 but with hits created by a random multiplier or divisor in the range 1–10 (Fig. 5A).

Table 1. .

Description of Datasets Used in the Experiments

MTP Dataset Name	Data Source
Synthetic1	Synthetic data created in Microsoft Excel with a background SD of 5%, containing hits less than or equal to 5 × SD (Fig. 3A)
Synthetic2	Synthetic data created in Microsoft Excel to represent edge effects in the 3 most peripheral wells (Fig. 4A)
Synthetic3	Synthetic data created in Microsoft Excel to represent edge effects in the most peripheral wells (within 3 from the edge), with hits created by a random multiplier or divisor in the range 1–10 (Fig. 5A)
Experimental1	eGFP Readout of MIN6 cells incubated for 2 days and imaged on an INCell1000 imager (Fig. 4D) with no hits implemented
Experimental2	eGFP Readout of MIN6 cells incubated for 2 days and imaged on an INCell1000 imager. Up hits were simulated using phalloidin-FITC for illustration in Figure 6 and analysis presented in Figure 7
Experimental3	Data are eGFP or DsRED (2 colors, same MTP) readout of MIN6 cells on an Envision plate-reader after incubation for 5 days
Experimental4	eGFP or DsRED readout of MIN6 cells on an Envision plate-reader (Fig. 5D and 5G, respectively) after incubation for 5 days. Down hits were simulated by addition of methanol as described in Methods.

 The datasets listed are created and used for gauging the performance of the correction methods as described in the Methods.

Fig. 3. .

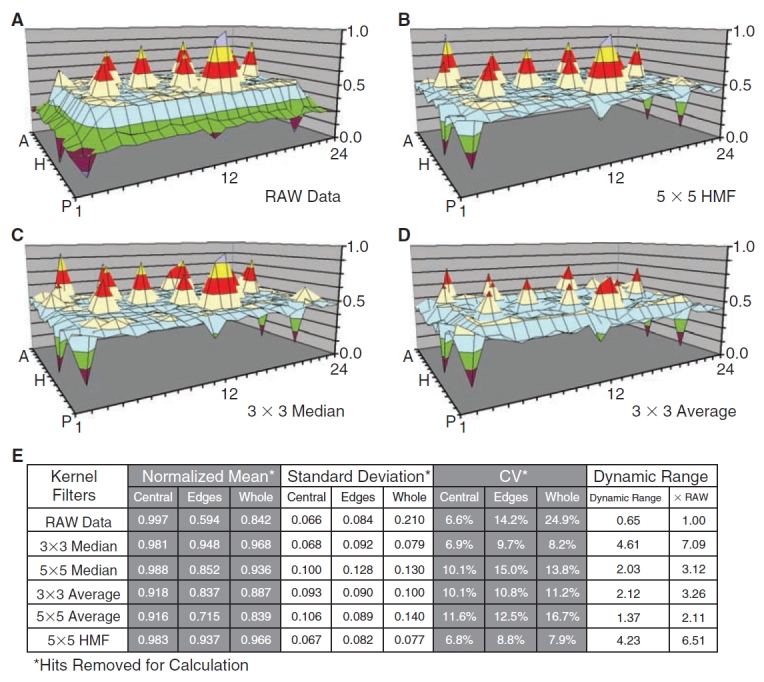
Comparison of local background estimators. The performances of the average, median, and bidirectional hybrid median filters (HMFs) are compared using the Synthetic1 dataset. The raw data are shown in (A) and the array corrections are shown in (B) for the 5 × 5 HMF, (C) for the 3 × 3 median filter, and (D) for the average filter. A data table (E) statistically summarizes the capacity of each filter to smooth localized background distortion while preserving hit amplitudes in the Excel array. Mean, standard deviation, and coefficient of variation (CV) were calculated with the simulated hits removed. Dynamic range was calculated according to Equation 7. The table breaks down corrective performance at the edges and central region of the array. Edge regions are defined by a 2-element wide border plus 1 element nested at each corner. The 5 × 5 median and average filters are not shown in surface plots because of reduced correction efficiency and method redundancy, but are summarized in (E). The scale and color codes are identical, with each color corresponding to 12.5% of the total range.

Fig. 4. .

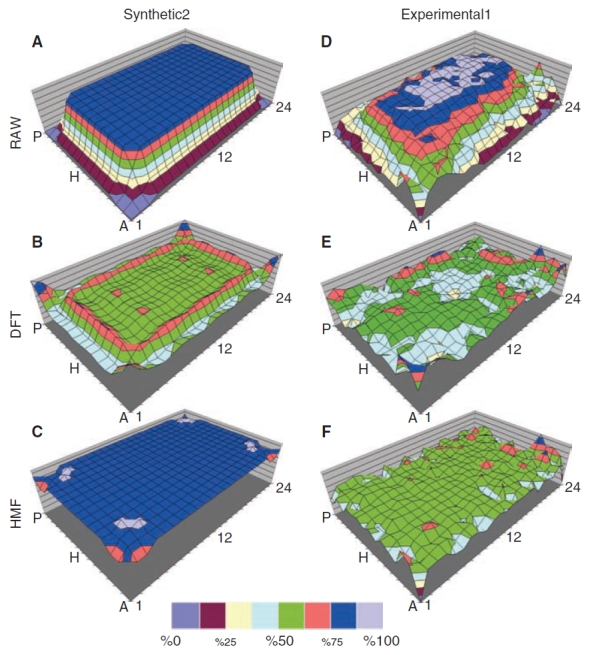
Panel of surface maps comparing Discrete Fourier Transform (DFT) and hybrid median filter (HMF) correction performances. 3D plots of Synthetic2 dataset (A) and Experimental1 data acquired on the INCell1000 high content microscope (D), both without simulated hits, are compared with 3D plots after correction by the DFT (B, E) and 5 × 5 bidirectional hybrid median (C, F) filters. Color intervals represent 12% of the RAW array range. All MTPs shown are normalized with respect to the maximum and minimum of their respective RAW dataset. The RAW datasets shown, therefore, span 0%–100%.

Fig. 5. .

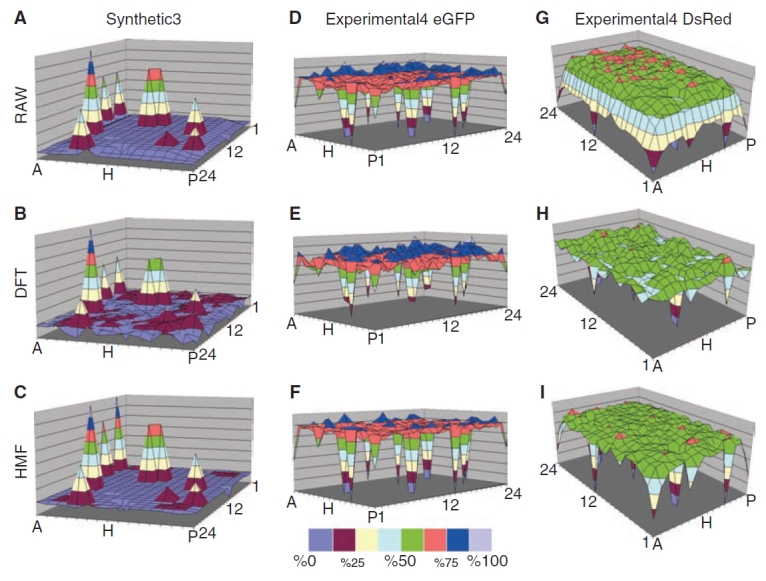
Panel of surface maps comparing corrections to arrays with nested outliers. Surface maps of the Synthetic3 dataset (A–C) and Experimental4 eGFP (D–F) and Experimental4 DsRed (G–I) are shown, as described in Methods and Table 1. The RAW data are shown in (A, D, and G) and the data as corrected by the 5 × 5 bidirectional hybrid median filter (HMF) (C, F, and I) and the Discrete Fourier Transform (DFT) (B, E, and H) methods. The Experimental4 eGFP and DsRED data are shown separately but each well contains both fluorescent proteins. The eGFP and DsRED differ in localized edge distortion prior to correction (see Discussion). Color intervals represent 12% of the RAW array range. All MTPs shown are normalized with respect to the maximum and minimum of their respective RAW dataset. The RAW datasets shown, therefore, span 0%–100%.

The 4 “experimental” datasets were created from 2 different MIN6 MTPs that were prepared to mimic minor edge distortion and hits (Experimental1 in Fig. 4D, Experimental2 in Figs. 6 and 7) MIN6 cells were seeded into a black-wall, clear-bottom 384-well MTP, using a Hamilton STAR fluid handler (Hamilton, NV) mounted with a 96 channel head, and incubated to achieve 60% confluence 24 h after seeding. Four image fields per well were acquired for both MTPs using a Nikon 10×, NA 0.45 objective at 12 bits/pixel binned 4 × 4 using the following filters: 360/40, 460/40 (DAPI), 475/20, 535/50 (eGFP), 535/50, 620/60 (DsRED) excitation/bandpass, emission/bandpass, respectively. TIFF images were analyzed using the IN Cell Analyzer 1000 Developer Toolbox. First, the eGFP image channel was flat-field corrected from previously acquired blank reference images and then an “isotropic diffusion filter” was passed over the image for 5 iterations to smooth image noise in image areas devoid of significant signal variation (terms and algorithms from INCell 1000 Developer Toolbox). Images were then segmented using threshold T = 1.04 × Mean_Image_Intensity for the eGFP channel. The well readouts were the density multiplied by the area under the segmented masks produced as a standard metric (D × A measurement) in the GE Developer Toolbox. The first plate was incubated for a total of 3 days at 37°C and 10% CO₂ until cells achieved 90%–100% confluence, then fixed in 5% paraformaldehyde (FLUKA) and imaged on the INCell 1,000 to generate the Experimental1 dataset. Then randomly positioned wells were incubated with 0.04% Phalloidin-Alexa488 (Invitrogen/Molecular Probes) in PBS to simulate up hits and the MTP was re-imaged to generate the Experimental2 dataset.

The second MIN6 MTP for datasets Experimental3 and Experimental4 was created to mimic more severe edge distortion and hits with decreased fluorescence intensity. Cells were seeded to achieve 40% confluence the day after seeding and maintained in culture for an extended incubation time of 5 days to maximize edge distortions, fixed, and read using the EnVision plate-reader (PerkinElmer, MA). Methanol was then added to randomly selected wells and groups of wells, to decrease fluorescence and thereby mimic down hits or toxic compounds for the Experimental4 dataset, which was also read on the Envision instrument. Both eGFP and DsRed spectra data were collected. This diverse collection of datasets helped delineate the differences in performance.

Calculations

The measurements used to gauge the performance of arrays are described as follows. The coefficient of variation of the background (CV = 100 × SD/mean) was used to describe the variation in the MTP data array background values. In arrays with hits, the hits were removed prior to calculating the CV, unless otherwise noted.

Over each MTP dataset, we define

and

where SD_Background is the SD of the plate with the hits excluded. Dynamic range and CV both distinguish array corrections that improve assay performance by decreasing background variation and/or increasing hit amplitudes, rather than by a simple multiplication that increases the amplitudes of both the hits and the background. The data are objectively improved—hit magnitudes increased and/or background variations decreased—with smaller background CV and larger dynamic range.

HMF Performance Vs. Hit Density

The HMF assumes that hits are relatively rare in the neighborhood. As hit density increases, the probability increases that enough hits reside within a given neighborhood to cause errors in the local background estimate. To investigate the sensitivity of the HMF to the number of hits in an MTP, we mathematically introduced increasing numbers of hits into the synthetic and experimental datasets and measured the corresponding changes in the CV and minimum dynamic range (which is defined by a variation of Equation 7 wherein the “average hit amplitude” is replaced by the minimum hit amplitude). For this experiment, variations of the Synthetic2 (Fig. 4A) and Experimental1 (Fig. 4D) MTPs were used. Originally, neither of these datasets contained any hits. To mimic a relatively weak hit, we chose a hit signal magnitude of mean plus 3 × SD, where SD is the standard deviation of the MTP without hits.

Hits were randomly positioned in the MTP and dynamic range and CV were measured with and without correction by the 5 × 5 HMF. This experiment was performed with number of hits varying from 1 to 381 in increments of 5.

RESULTS

Comparisons of Average, Median, and Bidirectional Hybrid Median Filter Corrections on a Synthetic MTP

In the first experiment, the background estimates provided by HMF were directly compared to those from the median and average filters (see Fig. 1) for their ability to correct localized distortions in the Synthetic1 dataset, which contains simulated hits (Fig. 3). All filters improved the dynamic range in Synthetic1 to some degree, but the HMF achieved the greatest reduction in CVs (Fig. 3E). The 5 × 5 HMF (Fig. 3B) and the 3 × 3 median filters (Fig. 3C) corrected the edge distortion and retained the amplitude of simulated hits. In contrast, the smoothing effects of the 3 × 3 average filter (Fig. 3D) reduced simulated hit magnitudes and demonstrated a diminished capacity to correct edge distortions (Fig. 3B and 3C).

Background smoothing was compared via the CVs as shown in Fig. 3E; a lower MTP background CV indicates a more uniform background. The 3 × 3 median filter (Fig. 3E) reduced the whole background CV to 8.2% from 24.9% for raw MTP and increased the dynamic range (see Equation 7) by 7.1-fold, while the 5 × 5 median filter decreased the whole background CV to 13.8% and increased dynamic range by 3.1-fold. The 3 × 3 average filter resulted in less improvement, with a whole background CV of 11.2% and dynamic range 3.3-fold better. The 5 × 5 average filter decreased the whole background CV to 16.7% and increased the dynamic range by 2.1-fold. The 3 × 3 median filter increased the dynamic range the most (7.1-fold), with the HMF next best (6.5-fold), whereas the HMF reduced the whole background CV the most (to 7.9%) and the 3 × 3 median next best (to 8.2%). At the edges, the HMF also reduced the CV the most (from 14.2% to 8.8%), with the 3 × 3 median filter next with a reduction to 9.7%. Inspection of the corrections along the 2-well-wide edges of the MTP in Figure 3C vs. 3A shows the differences. The 3 × 3 median filter results in Figure 3C demonstrate more corruption in at the edges (eg, regions A-15, A-09, D-02, and O-23 in Fig. 3C vs. 3A). Thus, the HMF enhanced dynamic range less than the 3 × 3 median filter, but created a lower background CV and left hit amplitudes closer to RAW data values. Also notable is how differently the HMF correction effected the CV of the peripheral wells compared to the central wells. HMF reduced the CV of the peripheral wells the most (14.2% in raw vs. 8.8% in corrected) while changing the CV of the center region the least (6.6% in raw vs. 6.8% in corrected). This shows the effectiveness of the HMF correction, especially for edge effects.

Performance Comparison of the 5 × 5 HMF and DFT Corrections on Spatially Distorted MTP Array Data

We compared the performances of the 5 × 5 HMF and DFT (as applied in the SLIMS software package) on synthetic and experimental datasets, both with and without simulated hits as described in the Methods. Example images from the Experimental2 dataset are shown in Figure 6 and include: (1) a negative control central well (Fig. 6A); (2) a dim negative control edge well (Fig. 6B) that resulted from long-term cell culture; and (3) a very bright simulated hit positioned at the MTP edge (Fig. 6C, note higher contrast vs. 6A and 6B) that were artificially brightened to visualize the cells.

Fig. 6. .

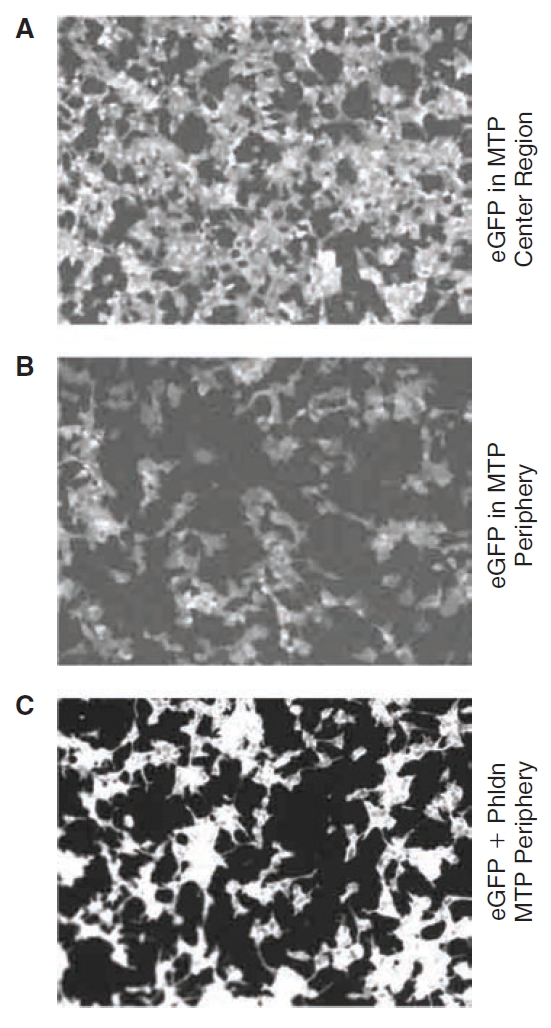
Example microtiter plate (MTP) edge distortion in the cell-based fluorescent assay. The example eGFP raw images from MTP used in the Experimental2 dataset are shown. Panel (A) from a central well is brighter than the image in (B) from a peripheral well, demonstrating an edge effect. (C) Shows an example simulated hit. Brightness was increased artificially in (A) and (B), relative to (C) for display, resulting in higher backgrounds—note the resulting higher backgrounds and lower contrast.

Figure 4A and 4D denotes surface plots of the Synthetic2 and Experimental1 datasets, respectively. These datasets did not contain simulated hits. Figure 4B illustrates the Synthetic2 MTP treated with the SLIMS DFT method. The waves in the surface plots that are especially prominent at the edges in Figure 4B (and present but less prominent in 4E) are the typical “ringing” artifacts of DFT methods, which are often a by-product of transforming the image data to the discrete frequency domain and back to the spatial domain.²² By inspection, the HMF produced a flatter 3D plot overall (Fig. 4F) vs. the DFT correction (Fig. 4E, compare, eg, areas M-J/13-16). Neither method completely corrected areas near corner wells A-1 and A-22 (Fig. 4E and 4F), where more prominent noise might be mistaken for hits.

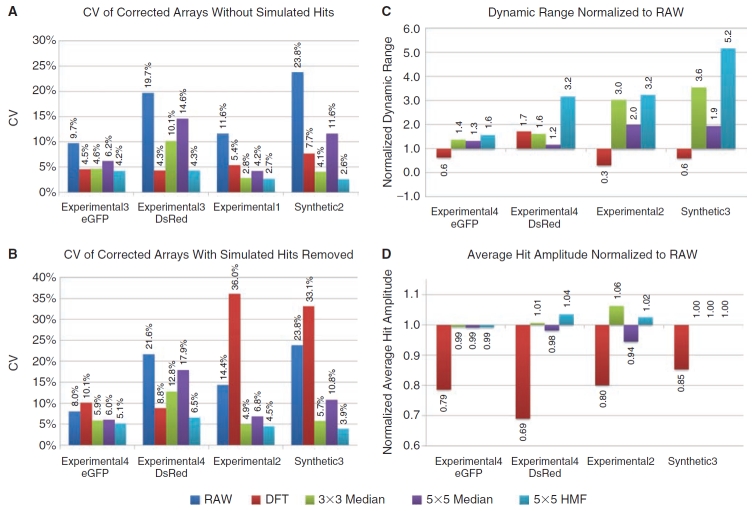
The Synthetic2, Synthetic3, Experimental1, Experimental2 and both eGFP and DsRed datasets of Experimental3 and Experimental4 were corrected using the DFT, 3 × 3 median, 5 × 5 median, and 5 × 5 HMF correction methods. The CVs were calculated and plotted in Figure 7A for datasets with no simulated hits and 6B for data arrays with simulated hits. In data arrays without hits (Fig. 7A), the 5 × 5 median background estimator performed the worst (decreased the CVs the least) on the eGFP and DsRed Experimental3 and Synthetic2 datasets, and the DFT performed the worst on the eGFP and DsRed Experimental3 dataset. The 5 × 5 HMF lowered the CVs the most on all datasets, with DFT second best on the Experimental3 eGFP dataset (4.2% vs. 4.5%), and tied with HMF in the Experimental3 DsRed dataset (both 4.3%). The 3 × 3 median was second to HMF on both the Experimental1 (2.7% vs. 2.8%) and the Synthetic2 (2.6% vs. 4.1%) datasets. For analogous corrections of the arrays with simulated hits included (Fig. 7B), the DFT performed the worst on all datasets, except for Experimental4 DsRed, and actually increased the CVs compared to the raw data on the Experimental2 and Synthetic3 datasets (to 36.0% from 14.4% and to 33.1% vs. 23.8%, respectively). The 5 × 5 HMF again performed the best on all datasets, with the 3 × 3 median second best on the Experimental4 eGFP dataset (5.1% vs. 5.9%), the DFT second best on the Experimental4 DsRed dataset (6.5% vs. 8.8%), and the 3 × 3 median second best on both the Experimental2 (4.5% vs. 4.9%) and Synthetic3 datasets (3.9% vs. 5.7%).

Fig. 7. .

Summary of background estimator performance. (A) The coefficient of variations (CVs) for the corrected Synthetic2, Experimental1, and the eGFP and DsRed datasets of Experimental3 that contained no simulated hits are shown. (B) The CVs of corrected Synthetic3, Experimental2, and the eGFP and DsRed datasets of Experimental4, which contained simulated hits that were removed prior to CV calculations, are shown. (C) Shows the effect of array corrections on dynamic range. The average absolute deviation of hits from the array mean is divided by the background standard deviation (values shown above dynamic range bars). The corrected arrays were then normalized to the RAW data dynamic range by division. (D) The average absolute deviations of hits from each array were normalized to the RAW data and shown as a percentage of the RAW data amplitude. Importantly, (C) shows the consolidated effect of the correction method (noise, localized distortion, and preservation of dynamic range), whereas (D) tests if dynamic range improvements were made by erosion or exaggeration of array hit amplitudes. See Methods for details on calculations.

In Table 2, the data of Figure 7A and 7B were further averaged across all datasets into 2 groups—with and without simulated hits—for comparison. Without simulated hits, the improvements in CV to an average of 0.2–0.3× of raw are similar except for the 5 × 5 median, which improved the CVs to an average of only 0.6× of raw. The differences are more dramatic with simulated hits, where the 5 × 5 HMF and 3 × 3 median average corrections were again similar at 0.3× and 0.4×, respectively, but the 5 × 5 median corrected by an average of 0.6× and the DFT actually made the average CV worse than the raw data by 1.3×. Thus, for the results in Figure 7A and 7B and averages shown in Table 2, the CV was decreased most consistently by the HMF method, and the DFT correction performed especially poorly on the Experimental2 and Synethetic3 datasets as a result of including simulated hits. That is, the presence of hits substantially compromised the ability of the DFT to correct background distortions.

Table 2. .

Performance of Correction Methods Without Hits Vs. With Hits Averaged for all Datasets

Correction Method	No Hits		With Hits
	CV (%)	CV/Raw	CV (%)	CV/Raw
Raw Data	16.2	1.0	17.0	1.0
5 × 5 HMF	3.5	0.2	5.0	0.3
3 × 3 median	5.4	0.3	7.3	0.4
SLIMS DFT	5.5	0.3	22.0	1.3
5 × 5 median	9.2	0.6	10.4	0.6

 The average CVs for the datasets are tabulated for experiments without and with simulated hits in the arrays, to further compare the performances of the DFT, 3 × 3 median, 5 × 5 median, and 5 × 5 HMF filters in the experiments of Figure 7A and 7B. CVs with hits were calculated only on non-hit wells.

 Abbreviations: CV, coefficient of variation; HMF, hybrid median filter; DFT, Discrete Fourier Transform; SLIMS, Small Laboratory Information Management System.

We next evaluated the dynamic ranges (see Equation 7) and average hit amplitudes after corrections by the median, HMF and DFT (both normalized to the raw data) methods. As shown in Figure 7C, the dynamic ranges increased most after correction by the HMF in all datasets, with the 3 × 3 median performing second best in the Experimental4 eGFP dataset (1.4 vs. 1.6), the DFT performing second best in the Experimental4 DsRed dataset (1.7 vs. 3.2), and the 3 × 3 median performing second best in both the Experimental2 (3.0 vs. 3.2) and Synthetic3 (3.6 vs. 5.2) datasets. The DFT method decreased the dynamic range in all datasets except in Experimental4 DsRed dataset.

Correction methods should preserve hit amplitudes, as with the HMF in Figure 7D, rather than blunt them as with the DFT. Interestingly, while the DFT blunted the hit amplitudes the most in the Experimental4 DsRed dataset (0.69×), it apparently also decreased the CV even more to still improve the dynamic range, second only to the HMF (Fig. 7C). Overall, the median-based background estimation methods (Equation 1) retained hit amplitudes most representative of the raw ones (0.99× to 1.06×). The preservation of raw data hit amplitudes was independent of median filter type and contrasted sharply with DFT corrections that consistently reduced hit amplitudes over all of the datasets. In addition, all of the background estimation methods (Equation 1) improved the dynamic ranges (Fig. 7C), whereas the DFT decreased them in 3 out of the 4 datasets.

The DFT and HMF corrective effects on simulated hit amplitudes are further illustrated in 3D surface plots of the Synthetic3 and Experimental4 eGFP and DsRed datasets in Figure 5A–5I. Note that artifacts in different channels in the same wells (eg, eGFP and DsRED) are independent from each other (see Fig. 5D–5F vs. 5G–5I), indicating that a background estimate derived from one reporter protein cannot be used to correct the distortion of another. The performance differences between these 2 methods can be viewed by comparing Figure 5B, Figure 5E, and Figure 5H with 5C, 5F, and 5I, respectively. In each case, the DFT largely blunts the hits more and decreases the background variations less than the HMF background estimator.

Effect of Hit Density on HMF Correction Performance

The HMF background estimation method was found to better retain hits than the other background estimators. This ability to ignore hits in the background estimate was expected to decrease as the hit densities increased. High hit density experiments, such as secondary screens, should be excluded from HMF correction, as should the regions with contiguous control wells. To determine at what hit densities HMF should no longer be used, simulated hits were randomly positioned in the Synthetic2 and Experimental1 datasets 100 times each for hit densities of 1 to 382 in 384 wells with the magnitude of 3 × SD as described in the methods. The resulting CV (Fig. 8A) and signal-to-noise ratio (SNR) (Fig. 8B) plots were created from the averages of each set of 100 trials at each density and the SD envelopes are also shown. The HMF reduced the CVs at all hit densities and as shown by the SNR, began blunting the hits as the hit densities increased. The SNRs improved by more than 50% at hit densities lower than 20% for the Synthetic2 dataset and lower than 25% for the Experimental1 dataset. Thus, the HMF decreased the CV and improved the SNR at hit densities an order of magnitude or more than are typical for primary screens.

Fig. 8. .

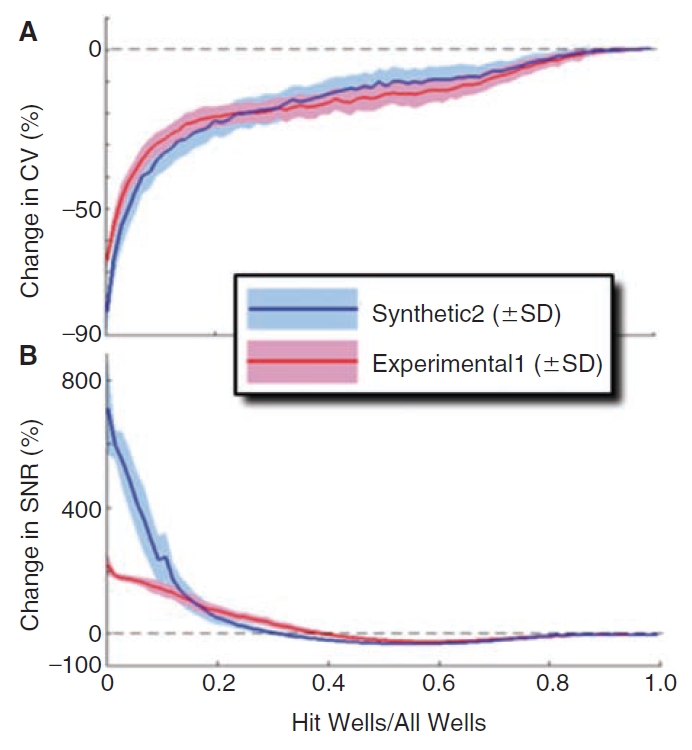
Effect of hit density on 5 × 5 hybrid median filter (HMF) function. Simulated hits were positioned randomly into the Synthetic2 and Experimental1 (Fig. 4A and 4D, respectively) and the effect on coefficient of variation (CV) and signal-to-noise ratio (SNR) were determined for increasing numbers of hits (from 1 to 382 in increments of 5) along with standard deviation obtained over 100 trials. (A) Effect on CV: a negative value in the vertical axis signifies an improvement (reduction) in CV. (B) Effect on SNR: a positive value in the vertical axis signifies an improvement in SNR. Note that the 5 × 5 HMF improves CV and SNR at all hit densities; however, the magnitude of the effect diminishes as the hit density increases.

DISCUSSION

One variable in the HMF that might be further optimized, especially for different (larger or smaller) MTP plate sizes, is the kernel size. The 5 × 5 size was empirically determined to be optimum for 384-well MTP arrays; however, for application to denser formats (eg, 1,536) it would be useful to test different kernel sizes such as 7 × 7 and 9 × 9. Since the local background estimation depends heavily on obtaining a representative sample population from the MTP, kernel size becomes a significant concern at the MTP edges. Although the total number of elements sampled by the kernel filter is reduced at the MTP periphery because a portion of the mask overhangs the MTP edge, the 5 × 5 HMF was robust enough to maintain a tight correlation between the obtained median value and the local sampling area in the 384-well MTP. Alternative ways to address array edges are well-documented for image processing.^13–15

HMFs, like all automated methods for correcting systematic errors, require spatially random MTP data without clustering of wells that have high or low magnitudes. As shown in Figure 8, the effectiveness of the filter diminishes as the hit density increases, with CVs significantly diminished at hit rates above 20%. High densities or clustering of positive wells, or organizing MTPs with dose series or controls positioned in rows or columns, would result in misrepresentation of the control values as background in the kernel and compromises filter function. One way to circumvent this problem is by nesting controls or dilution series within the MTP in such a way as to avoid having a low- or high-value clusters disturb the function of the filter (ie, by randomizing well positions). Also, in the case of controls positioned in rows or columns, the filter can be programmed to exclude the control wells from analysis. The SLIMS interface used in the DFT corrections offers such an option.^2,3 Alternatively, the HMF kernel could be customized by excluding axial elements (column or row) that might contain control wells and we are exploring this further.

In comparing MTPs before and after correction with DFT, the correction largely restored background values to the mean value range (compare Fig. 5G and 5H). With rare exceptions, however, the DFT corrections also reduced the amplitude of simulated hits (compare hits in Fig. 5E vs. 5D and 5H vs. 5G). For example, in the corners of the Experimental4 DsRed array, the DFT method failed to preserve simulated hits altogether and instead reduced the hit to background levels. This tendency to blunt hits is also common to the averaging correction methods (compare Fig. 3D with 3B and 3C). In contrast, the 5 × 5 HMF retained all simulated hits in our datasets, scaling them in agreement with local wells (eg, compare region A-1 in Fig. 5G–5I).

The case of Experimental4 DsRed illustrates an interesting point in the comparison of the DFT and median-based correction methods. The background CV measurements for Experimental4 DsRed (Fig. 7B) are higher in arrays corrected with 3 × 3 and 5 × 5 median as compared to the DFT. However, viewing Figure 7D reveals that while the DFT reduced the background CV more, it did so at the cost of blunting hits. The DFT correction is also accompanied with a reduction in dynamic range that is apparent in Figure 7C. The lower CVs, blunted hits, and reduced dynamic range after DFT treatment can be explained by a gross flattening of the array contour without regard to discrete hits. For example, the MTP edge correction appears extensive after treatment with the DFT-based method in the Experimental DsRed (compare data in the range 37.5%–50% in Fig. 5G vs. 5H), but the corrections also reduced the magnitude of many of the hits (eg, well A-13).

Further, correction of corner wells by the DFT was more aggressive than the correction of the other edge-proximal wells. The DFT also blunted the hits in MTP corners more aggressively than other edge-proximal wells (eg, compare corrections to A-1 and P-1 to M-1 and A-13 in Fig. 5G and 5H). This correction is unusual and suggests a DFT correction artifact based on highly conserved array symmetry (4 corners). The correction made by the HMF to MTP corner wells, however, appears to be consistent with that made to other edge-proximal wells (eg, compare corrections with A-1 and A-13 in Fig. 5H and 5I).

Although the DFT reduced the background CVs statistically over the entire MTP for both Synthetic2 and experimental arrays (Fig. 7B and Table 2), it introduced waves or “ringing artifacts” in Figure 4B and 4E (eg, area J-17) in the corrected Synthetic2 dataset. The DFT is based on continuous functions that require special treatment to deal with finite data arrays. That is, how does one model the region at the edge where the data ends? In order for continuous functions to work at the edges, assumptions have to be made to create “data” outside the original array. For example, if one produces an artificially larger plate where the “outside” values are zero, a step function is produced that generates distinctive ripple patterns.²² Various “windowing functions” have been designed to reduce this ripple. Primary screening data have hits that are fundamentally discrete on a background that can be modeled as continuous (a single mean with noise). Because of this, it may be possible to remove the ripple by iteratively refining the estimate of the data “outside” the MTP array to match the mean and noise of the background.

Median filters (Fig. 4C), which are nonlinear and natively spatially discrete, do not generate ringing artifacts. However, the HMF-corrected array Figure 4C exhibits symmetric artifacts in the corners of the plate due to the small sample size of the HMF kernel in the corners. This resulted in insufficient sampling of the background and in turn reduced the efficacy of the correction. The corner correction failures in the HMF correction had a much smaller effect than the DFT ringing on the CVs (Fig. 7A). One possible solution to this problem is to adaptively increase the kernel area at the corners. The kernel size could also be held constant by moving the target pixel. Alternatively, we have adjusted the kernel pattern to make it more or less sensitive to outliers as the sample size decreases.²³ In addition, we have found that the serial application of multiple discrete filters tuned to common MTP array patterns minimizes the introduction of artifacts at the MTP corner regions, while also having an additive beneficial effect on error correction.²³

The DFT method transforms MTP data into the Fourier space by fitting sinusoidal functions to the data.² Since sinusoidal functions are by definition continuous, this transformation assumes that the data are also continuous. For MTPs, this means that the DFT correction expects a hit, which by definition has an extreme magnitude, to resemble its surrounding background wells. However, MTP screening uses discrete wells, oftentimes each with diverse reagents (eg, library compounds) being tested, thus the datasets are discontinuous. Therefore, the magnitude of a signal from any one well is unrelated to that of surrounding wells and the piecewise continuity assumption of the DFT method is inappropriate. Fitting of a continuous function to discontinuous data reduces the hits toward background levels, that is, blunts them. The HMF method, on the other hand, is based on nonlinear rank order calculations for each neighborhood (ie, finding the median) and does not assume spatial continuity in the dataset. This inherently discrete method essentially ignores rare extreme values (hits) in its estimation of the background.

In summary, the 5 × 5 HMF performed best overall with regard to statistical improvement of the various datasets tested. The DFT method may benefit from case by case fine-tuning in the frequency domain. The bidirectional HMF might also be further tuned by optimizing the neighborhood size and subregions, but the easily implemented and computationally cheap 5 × 5 HMF performed well on all of the datasets tested here. We conclude that median-based array correction methods best-reduced localized data distortion and assay noise while preserving hit amplitudes, and that discrete background smoothing approaches are superior to ones based on continuous functions for this data type—rare hits in data arrays.

AUTHOR DISCLOSURE STATEMENT

No competing financial interests exist.