Abstract
Differential cell migration and growth drives the organization of specific tissue forms and plays a critical role in embryonic development, tissue morphogenesis, and tumor invasion. Localized gradients of soluble factors and extracellular matrix have been shown to modulate cell migration and proliferation. Here we show that in addition to these factors, initial tissue geometry can feedback to generate differential proliferation, cell polarity, and migration patterns. We apply layer by layer polyelectrolyte assembly to confine multicellular organization and subsequently release cells to demonstrate the spatial patterns of cell migration and growth. The cell shapes, spreading areas, and cell-cell contacts are influenced strongly by the confining geometry. Cells within geometric ensembles are morphologically polarized. Symmetry breaking was observed for cells on the circular pattern and cells migrate toward the corners and in the direction parallel to the longest dimension of the geometric shapes. This migration pattern is disrupted when actomyosin based tension was inhibited. Cells near the edge or corner of geometric shapes proliferate while cells within do not. Regions of higher rate of cell migration corresponded to regions of concentrated growth. These findings demonstrate the multicellular organization can result in spatial patterns of migration and proliferation.
Keywords: differential migration, differential proliferation, microscale, cell patterning
Introduction
Local differences in cell motility and proliferation influence the number and disposition of cells in different regions and direct tissue formation. The most observable examples of tissue patterning by differential migration occur during tissue morphogenesis. Notable examples of this include dorsal development of embryos [1–3] and wound healing [4, 5] wherein differential cellular motility effects closure. Tissue patterns can also arise from spatial inhomogenieties of cell growth wherein some cells proliferate while neighboring cells remain quiescence. Such differential growth rates generate stresses that influence tissue form [6, 7], for example, angiogenic proliferation at the tip leads to capillary blood vessels.
The underlying cause of differential migration has been the subject of extensive investigations. The migration of individual cells is influenced by their local microenvironment as set by cell-cell contacts [8, 9], cell-ECM contacts [10–14], and diffusible molecules [15, 16]. Individual cells undergo polarized extension and attachment of lamellipodia at their leading edges and detachment of their retracting ends [17]. On a larger scale, the coordinated migration of cell clusters requires initial spatial polarization of the cells [18–21] with the dominant leading edge formed by unbalanced lamellae on one side that pulls the entire cluster in that direction [9]. Differential migration of multicellular groups has been explained by spatial gradient of soluble molecules [22] and cell-adhesions [23] that determine cluster polarity [9, 21, 24]. The effect of cell adhesions on cell motility depends on the cell type. Contact inhibition of locomotion has been proposed as an explanation for the directional migration of neural crest cells that retract their protrusions and stop upon contact [25, 26]. Conversely, contact-stimulated migration is observed for fibroblasts that preferentially migrate in directions away from their contacting neighbors [25, 26].
Cell proliferation is influenced by soluble factors [27–29], cell shape and size [30, 31], cell-cell contacts [32, 33] and cell-ECM interactions [34–37]. For sheets of cells, geometry and mechanical stresses has been reported to initiate spatial variations in proliferation[7]. In general, most factors influencing cell migration also affect cell proliferation. This correlation is most evident in studies of wound healing [7, 38–41] wherein the loss of cell-cell contacts at the periphery of wounds is considered to be the principal cause of locally enhanced propagation and migration.
Spatial patterns of growth and migration lead naturally to a range of multicellular forms that have been extensively reported. However, feedback mechanisms through which complex structures and patterns of migration emerge from simpler ones has not been demonstrated. Symmetry breaking has been observed for pairs of mammalian cells confined within square and circular island geometries[42]. When two endothelial cells were confined within a circular or square adhesive islands, the two cells rotated synchronously about the geometric center of the island.[43] Fibroblast pairs however did not show coordinated motions under the same confinement conditions. Here, we focus on geometrically defined clusters of fibroblasts to demonstrate symmetry breaking on a larger scale and the concept of "Form from Form" wherein the initial spatial geometry of cell clusters sets the patterns of subsequent differential migration. We apply a novel non-invasive technique [44] to first confine and subsequently release ensembles of cells from different confining geometries to investigate how individual cells within specific geometric clusters alter their shape, polarization, motility, and proliferation.
Materials and Methods
Materials
Tissue culture dishes were purchased from Fisher Scientific (Catalog No. 430166) and used as received. Polydimethylsiloxane (PDMS; Sylgard 184) was obtained from Dow Corning (Midland, MI). The random copolymer of oligoethyleneglycol methacrylate and methacrylic acid poly(OEGMA-co-MA) with 80 wt% OEGMA was prepared following procedures described earlier [45]. Chitosan (182 kDaltons, 69% deacetylation) was a gift from Tri-Corporation (Alpharetta, GA). Alexa 488-phalloidin, 4',6-diamidino-2-phenylindole (DAPI), 5- bromo-2´-deoxyuridine (BrdU), anti-bromodeoxyuridine, mouse IgG1, monoclonal PRB-1 (anti-BrdU), Alexa Fluor® 488 goat anti-mouse IgG1 (γ1) (secondary antibody) were purchased form Molecular Probes (Eugene, OR). Phosphate buffer saline was purchased from Sigma (St. Louis, MO). Iscove’s modified Dulbecco’s medium (IMDM), Serum Supreme, were purchased from Cambrex biosciences (Walkersville, MD).
Preparation of poly(OEGMA-co-MA)
Random copolymers of OEGMA and MA (Scientific Polymer Products, NY) were prepared by free radical polymerization of 10 wt% methanolic solutions of the two monomers (80:20 OEGMA to MA mass ratio) at 60°C. Polymerizations were initiated with 1 wt% (with respect to monomer) of 2,2’-azobis(2-amidinopropane) dihydrochloride (Wako, VA) and allowed to react for 16 hours. Similar polymerizations, when carried out in water resulted in precipitation of the copolymer product. This water-insolubility is key to its use as a cell-resist in confining cells.
Preparation of patterned tissue culture dishes
Micropatterns consisting of different geometric shapes including squares, circles, ellipse and rectangles were fabricated on silicon wafers using standard photolithographic techniques. From this silicon master, complementary polydimethylsiloxane (PDMS) replicas were prepared following the soft lithography procedure of Whitesides and co-workers [46] and used as stamps in subsequent microcontact printing steps to form patterns of poly (OEGMA-co-MA) copolymer directly on cell culture dishes. Patterned dishes were sterilized under UV for 12 hours before cells were plated. Masking of poly(OEGMA-co-MA) printed regions by adsorption of chitosan to render these regions cell-adhesive again was accomplished by immersing the culture dish with media containing 2% water-soluble chitosan [44].
Cell culture
NIH 3T3 fibroblasts were cultured in Iscove’s modified Dulbecco’s medium (IMDM) supplemented with 10% serum supreme. Cultures were maintained at 37°C in a humidified atmosphere containing 5% CO2. Sub-confluent monolayers were dissociated with 0.01% trypsin solution, re-suspended in IMDM with 10% serum, and then plated on micropatterned culture dishes. The Rac1 and RhoA constitutively active mutants (Rac1L61 and RhoAL63) were gifted by Dr. Yi Zheng (Cincinnati Children's Hospital). Mutants were generated by site-directed mutagenesis based on oligonucleotide-mediated PCR.
Immunostaining
Cells were fixed with 3.7 % paraformaldehyde for 10 minutes, washed in phosphate buffered saline, and then permeabilized with 0.2 % Triton X100 for 5 minutes. Samples were then rinsed with PBS and incubated with Alexa 594-phalloidin, Alexa 488 conjugated anti-Golgin-97 (human) and DAPI to stain for F-actin, Golgi apparatus and nuclei respectively. Images of the patterned cells were acquired using a Nikon TE-2000 inverted microscope with Metamorph software (Ver 6.0r4, Universal Imaging, Westchester, PA).
Cell migration from different shapes
Cells were plated at a density of approximately 10,000 cells/cm2 and allowed to reach confluence within the cell-adhesive patterns on the tissue culture dishes. The cells were then released from confinement by incubating with complete media containing 2% chitosan (182 kDa, 69% deacetylation, TRI corporation, Alpharetta, GA) for 20 minutes, after which the cells were restored in complete media containing no chitosan. The patterns of migration following release were tracked by time-lapse recording of phase contrast images with a CCD camera (Spot CAM, Diagnostic Instruments Inc.). To disrupt actomyosin based tension, 10 µM or 20 µM Y27632 (Calbiochem) were added at the time of release.
BrdU labeling
NIH3T3 cells were synchronized by serum starvation for 24 hrs before plating over the micropatterned dishes. Cells were pulse labeled with BrdU (20mM) for 2 hours and washed with PBS, fixed with 3.7 % paraformaldehyde for 10 minutes, and then permeabilized with 0.2 % Triton X100 for 5 minutes. Fixed cells were then incubated with 1N HCl for 10 minutes at 2 °C to open the DNA structure of the labeled cells. Immediately after acid washing cells were exposed to PBS buffer for 30 minutes at room temperature. Cells were again washed with PBS with 0.1% Trition X-100 and incubated with anti-bromodeoxyuridine, mouse IgG1, monoclonal PRB-1 (anti-BrdU) overnight at room temperature. Following the overnight incubations labeled cells were washed with PBS with 0.1% Triton X-100 and treated with secondary antibody (flourescein labeled goat anti-mouse IgG1) to visualize anti-BrdU labeled cells. Cells were also counterstained with DAPI to visualize cell nuclei. Images of the labeled cell nuclei were acquired using a Nikon TE-2000 inverted microscope with Metamorph software (Ver 6.0r4, Universal Imaging, Westchester, PA).
Characterization of cell cluster
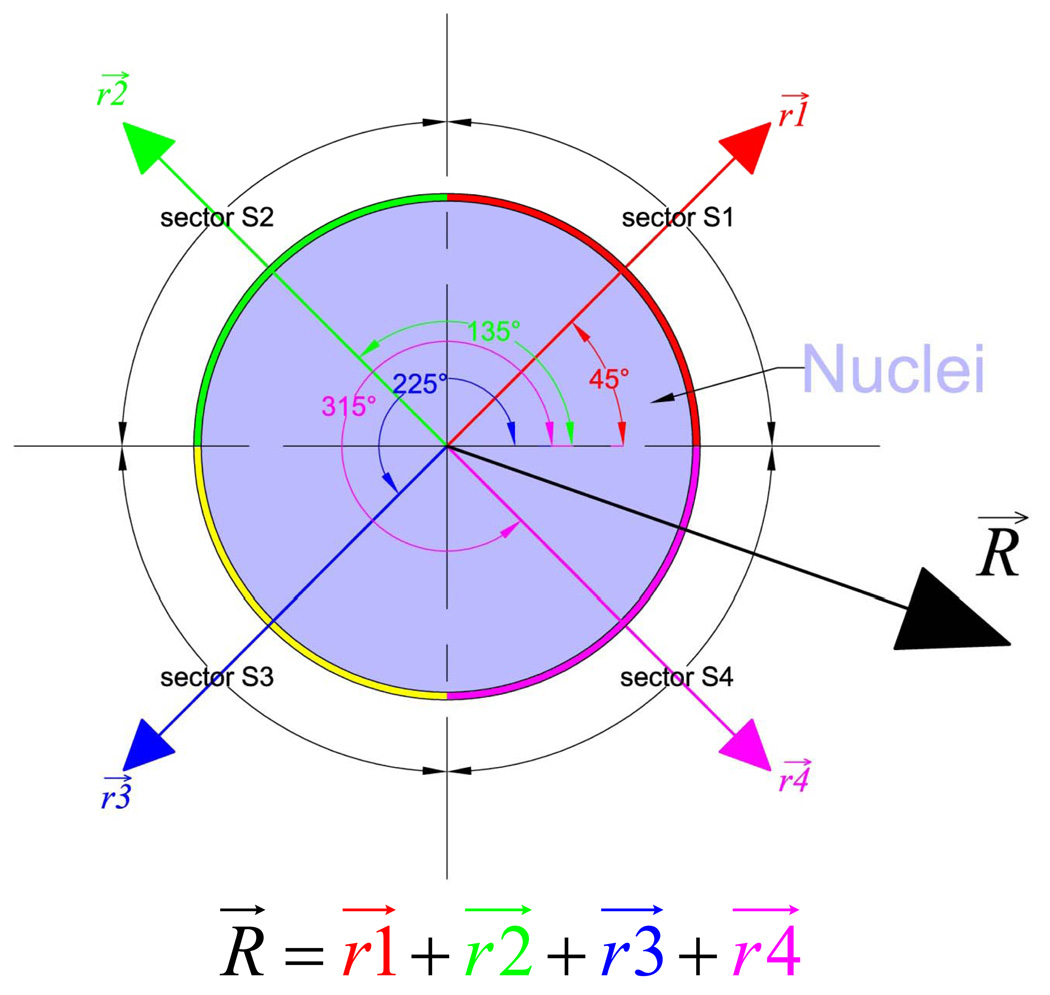
Cells patterned over different geometric shapes were characterized for their local average cell area, aspect ratio, cell-cell contacts and Golgi polarization. The average areas of individual cells within a cell clusters were calculated from their phase contrast images. Cell edges were traced manually and processed in MetaMorph imaging software to calculate projected cell area, largest projected X and Y dimensions, and aspect ratio. The fraction of the cell perimeter contacting neighboring cells was obtained by manually tracing the perimeter of individual cells. Golgi polarization of individual cells within cell clusters was calculated by interactive tracing of fluorescently labeled Golgi apparatus. Golgi polarization for a cell within a cell-cluster was reported in terms of a resultant vector R⃗ (Fig. 3), which is sum of four vectors set at angles of 45°,135°, 225°,315° whose individual magnitude is set to the fraction of Golgi apparatus in their corresponding sector (S1, S2, S3 and S4) when the origin is set at the center of the nuclei (Fig. 3).
Figure 3. Quantification of morphological polarization.
The overall polarization of each cell in a cluster is represented by the resultant vector R⃗ that is determined as follows. For each cell, the origin is centered to its nucleus and the surrounding region is divided into 4 sectors S1, S2, S3, and S4 respectively. The direction of the positive x-axis is fixed for all cells within a cluster and aligned to the major axis, edge, and longer edge of ellipsoidal, square, and rectangular clusters respectively. For each cell, the area of Golgi apparatus in each sector is assigned to the magnitude of their respective vectors .
Morphometric analysis
Immunofluorescence microscopy was carried out using a Nikon TE-2000 inverted microscope, and images of at least 50 islands for each shape. Subsequent image analysis and quantitation of cell invasion area were performed using Metamorph software. Statistical analysis of data was performed using SAS Software. The confidence interval around estimated area of cell migration are reported with a level of significance of p=0.05.
Results
Cell cluster shape induces cell polarization
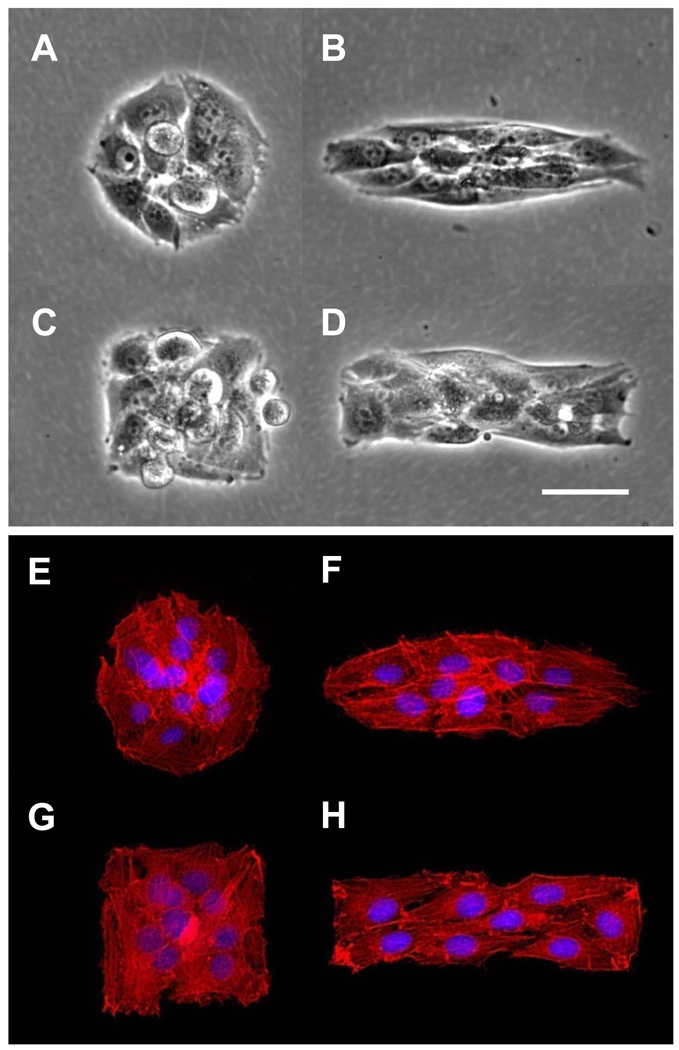
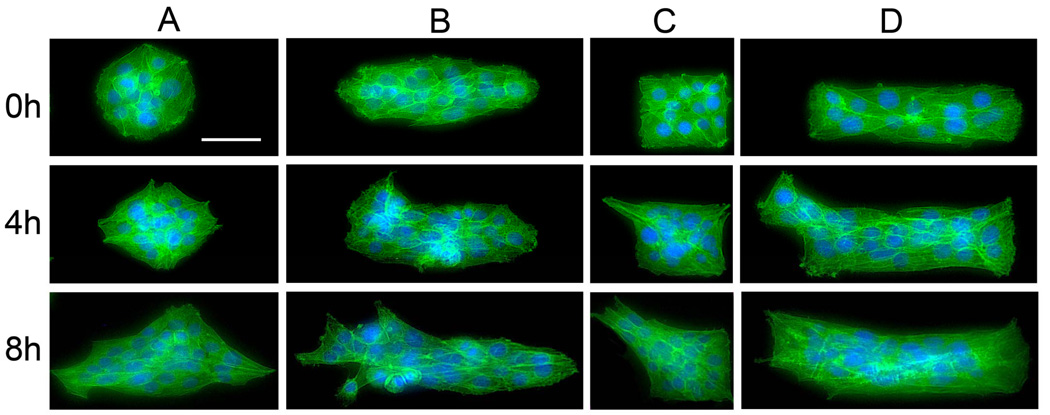
Four cluster shapes, shown in Figure 1, were designed to examine the role of initial cluster geometry on cell morphology and spreading. In each case, the geometry of the cell clusters are defined by the shape of adhesive islands of bare tissue culture dish surrounded by cell resistant poly(OEGMA-co-MA). The circular and elliptical cluster shapes probe the effects of asymmetry on the migration and proliferation of cells within clusters, whilst the square and rectangular shapes examine the effect of sharp corners and straight edges. The area of the islands is fixed (8100 µm2) to accommodate comparable number of cells (Table 1). One day after seeding, the number of cells within each shape varies from 10.9 ± 2.8 on circles to 12.0 ± 2.4 on ellipses (Table 1). These averages and standard deviations were determined from measurement of at least 150 islands for each shape. On circular islands, cells exhibit a random organization (Fig. 1E) while cells on elliptical or rectangular shape elongated along the major axis of the ellipse shape or the long edge of the rectangular shape (Fig. 1F and H). The anisotropic cell shape on the elliptical and rectangular shapes also correlate with the alignment of the actin filaments. Quantification of the cell elongation will be discussed in later sections. Next, we investigate how the influence of the cluster geometry on the cytoskeletal structure of constituent cells extends to the organization of organelles, Golgi apparatus and nucleus, which are indicators of cell polarization.
Figure 1. Cell cluster patterned over tissue culture dish.
NIH 3T3 cell cluster patterned over different geometric shapes (Area = 8,100µm2). A–D) Phase contrast micrographs of patterned NIH 3T3 fibroblasts. E–H) Cytoskeletal alignment of cell clusters. Actin microfilaments were visualized with Alexa -594® labelled phalliodin (red) and cell nuclei (blue) were visualized using DAPI. Scale bar = 50µm Magnification 20×.
Table 1.
Average spreading area of individual cell within a geometrically shaped cell cluster.
| Shape | Number of cells | Cell average area (µm2) |
|---|---|---|
| Circle | 11 ± 3 | 743 ± 177 |
| Ellipse | 12 ± 2 | 675 ± 146 |
| Square | 11 ± 2 | 724 ± 173 |
| Rectangle | 11 ± 2 | 711 ± 160 |
The location of Golgi apparatus relative to the nucleus is strongly correlated to the direction of cell migration [47]. Polarization of Golgi apparatus in front of the nucleus in the direction of travel is a general characteristic of motile cells. To probe if the ensemble geometry of cell clusters can influence the cell polarity and thus, their predisposition to migrate in specific directions, we analyzed the position of Golgi apparatus relative to the nucleus. Figure 2 shows representative images of confined cell clusters with their Golgi apparatus fluorescently labelled green. For each cell, we quantified the polarization of Golgi relative to the nucleus, by dividing the region around the nucleus into four quadrants labelled S1 to S4 (Fig 3) and assigning the relative fluorescent intensity in each quadrant to the corresponding vectors r1 to r4. The resultant vector sum, R, represents the direction and degree of Golgi polarization for each cell. The positive x-direction (zero angle) is fixed relative to the cluster geometry. Thus, while the origin is centered to the nucleus of each cell in calculating R, the component vectors r1 to r4 point in the same directions for all cells within a cluster. The x-axis is set to point along the major axis for the elliptical pattern, towards one side of the square pattern, and towards one of the shorter sides of the rectangular pattern.
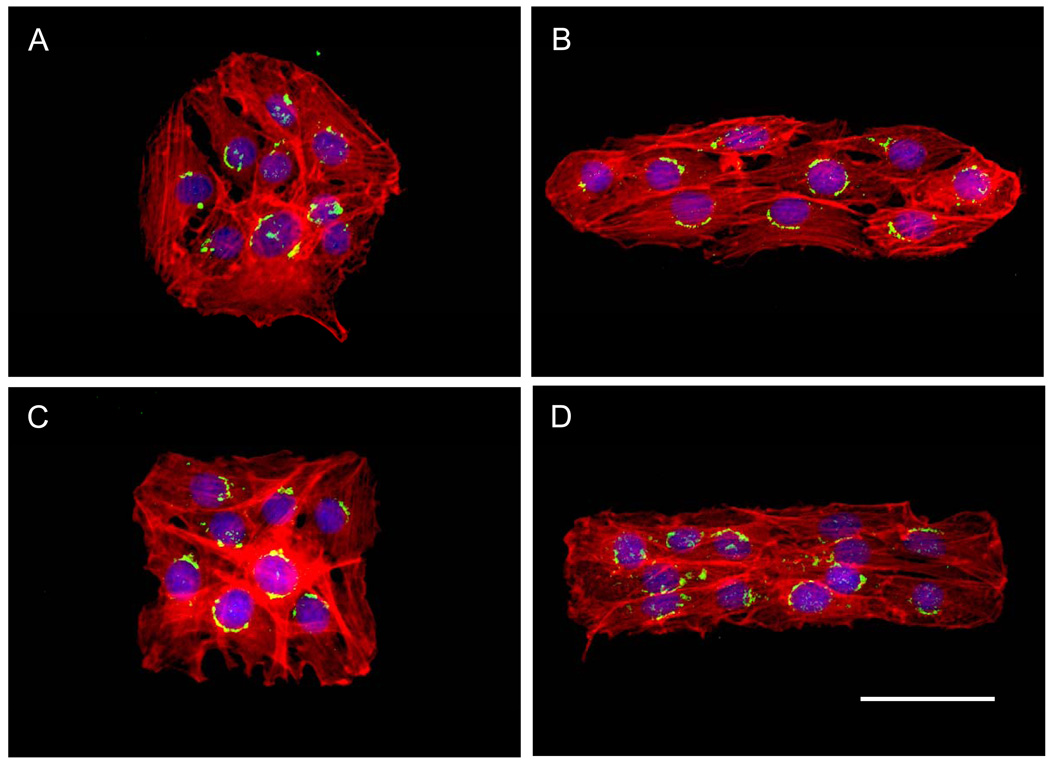
Figure 2. Polarization of Golgi apparatus within cell clusters.
NIH3T3 fibroblasts cells stained for cytoskeleton, Golgi apparatus and nuclei and viewed in color red, green and blue respectively. Cells patterned over A) circle, B) ellipse, C) square and D) rectangle. Scale bar = 50µm Magnification 20×.
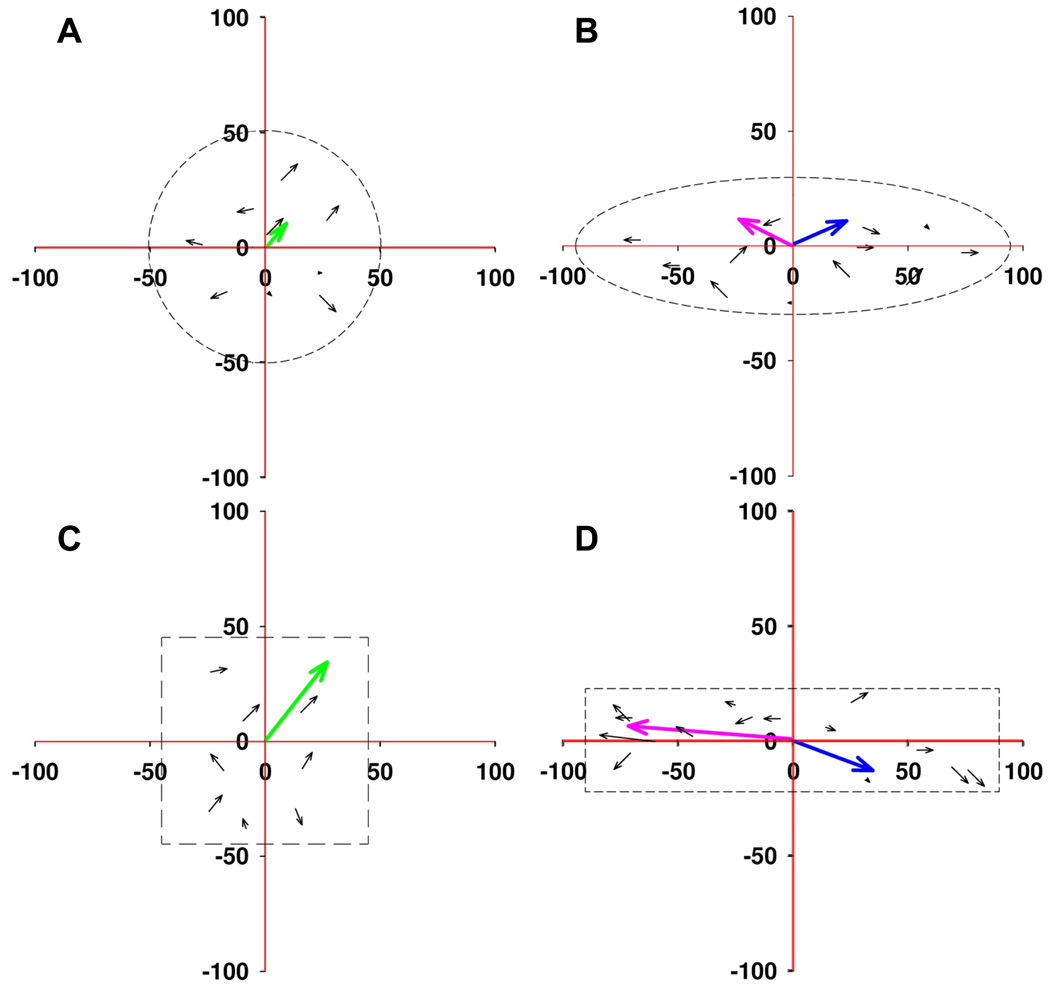
Figure 4 shows representative spatial distribution of Golgi polarization (R) for individual cells within the four cluster shapes. The green vector, representing the whole cluster polarization, is summed from the polarization of individual cells. Likewise, the blue and red vectors, show the overall polarization of cells in the left and right halves of the elliptical and rectangular geometries). Cells within circular clusters are generally polarized in the outward direction and the resultant cluster polarization is small. Cells within the elongated elliptical or rectangular clusters are preferentially polarized outwards along the major axis with minimal polarization along the minor axis. Cells on the right side of the pattern are preferentially polarized to the right, and cells on the left side preferentially polarized to the left, without preference for upwards or downwards polarization. For square clusters, cells coordinate to polarize their Golgi in one dominant diagonal direction (Fig. 4C). These results show that Golgi polarization of individual cells within a cluster depends on its location and the overall cluster geometry.
Figure 4. Quantification of Golgi polarization of individual cells within cell cluster patterned over geometric shapes.
Spatiotemporal quantification of Golgi apparatus polarization for NIH 3T3 fibroblasts cells patterned over geometric shapes. Cells show random Golgi polarization when patterned over (A) circle. Cells patterned over elliptical shape (B) shows that Golgi apparatus is polarized along semi-major axis. For square shape(C) cells Golgi apparatus is aligned along its diagonal and for rectangle (D) Golgi is polarized along its length.
Cells preferentially migrate from corners and along the major axis of elongated clusters
To determine if this polarity induced by the cell cluster results in differential migration, we cultured NIH 3T3 fibroblasts to confluence within the geometric patterns (24 hrs), then released the cell clusters by adsorbing cell-adhesive cationic chitosan to the cell-resistant anionic poly(OEGMA-co-MA) rendering these regions and in effect, the entire culture dish, cell-adhesive. Figure 5 and Figure 6 show the initial migration patterns of cell clusters. Cells in symmetric circular clusters do not migrate simultaneously outward, thus forming random asymmetric clusters with sharp corners. Cells released from square clusters migrate preferentially from one or two corners. Analysis of 52 square clusters show that cells migrate out from only one corner in 65% of the clusters examined and migrate out of out of two adjacent corners for the remaining 35%. Simultaneous migration from two diagonally opposite corners or collective migration from more than two corners was not observed. This indicates that the migration of cells from square clusters are coordinated and tied to the overall polarity of the cell cluster. Cells released from elliptical patterns migrate outwards along the major axis. Similarly cells released from rectangular island migrate outwards preferentially from the shorter sides, but like square clusters, cells also have a tendency to migrate out of corners. The migration pattern is consistent with the spatial patterns of cell polarity (Figure 4) and the actin filament organization.
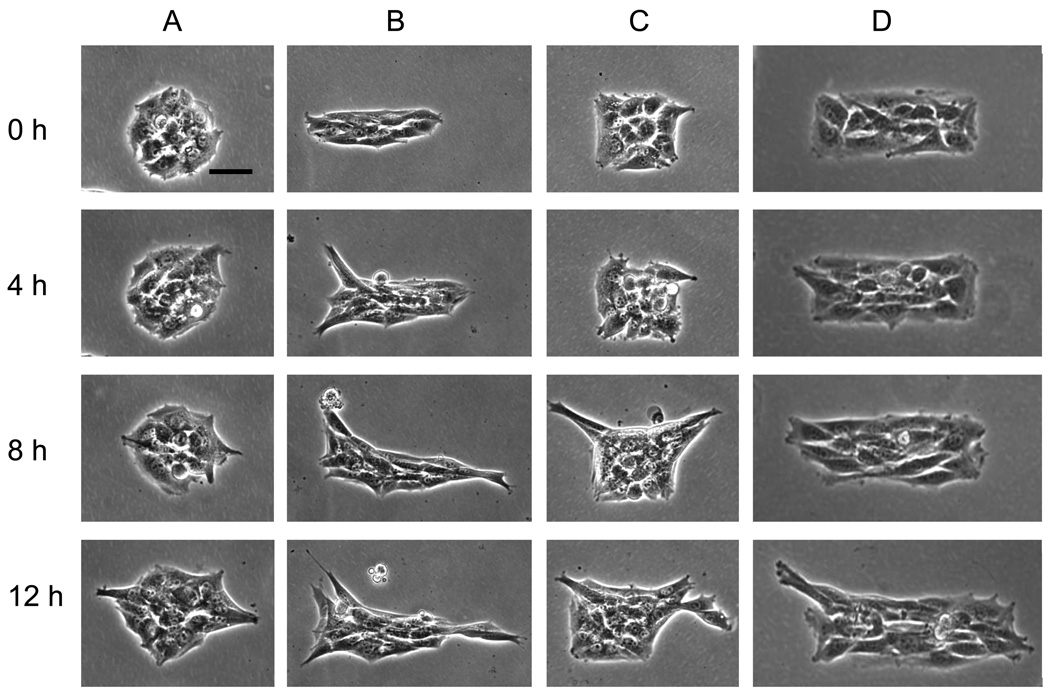
Figure 5. Directional migration of cell cluster.
Time lapse phase contrast images (in hours) show the directional migration of NIH 3T3 fibroblast cluster upon release from different shape adhesive islands. . (A) Cell cluster moves out randomly upon release from circular shape. (B) Cells migrate preferentially along semi-major axis from elliptical island. (C) Cells preferentially migrate out from the corners upon release. (D) Cells migrate out from corners and along the longer dimension. Magnification 20×. Scale bar = 50µm.
Figure 6. Cytoskeleton distribution within cell cluster upon release from various shaped adhesive islands.
Magnification 20×. Scale bar = 50µm
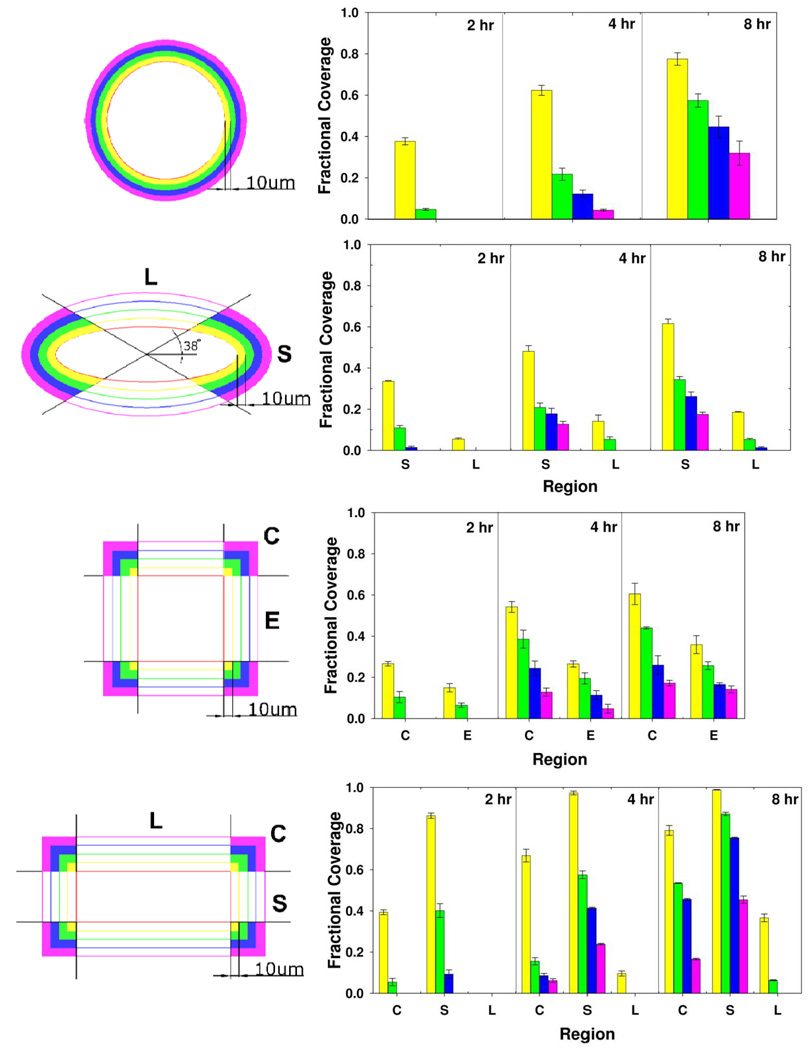
To quantify these observations of how cell clusters migrate and transform, we measured the fractional coverage in different regions around the initial cluster geometry (Fig. 7). Here, the surrounding region around each geometric shape is divided into four colored regions spaced incrementally 10 µm from the cluster perimeter. The surrounding area of elliptical clusters is further divided into S and L regions that are defined to be within and outside of 38° arcs from the major axis respectively. For square and rectangular clusters, corners (C), edges (E), short edge (S), and long edge (L) are defined accordingly.
Figure 7. Spatiotemporal characterization of migrating cell cluster.
Time lapse spatiotemporal characterization of migrating cell cluster. Cells preferentially migrate out from corners of squares, along length from rectangle, randomly from circle, and along semi-major axis of elliptical shape.
At the time of release (t = 0 hr), the fractional coverage in all regions by cells is zero. The fractional area of each region covered by cells as the cluster shapes transform over 2, 4, and 8 hours are shown in Figure 7. The outwards migration of cells from circular clusters over time increases the fractional coverage of regions further away from the initial cluster perimeter. The preferential migration of cells outwards along the major axis of elliptical clusters is clear from the significantly higher fractional coverage of S versus L regions (P<0.05). The migration into the S region is comparable to that for circular clusters, but migration along the minor axis into the L region is markedly less. Cells released from the square clusters preferentially migrate out from corners (region C) compared to edges (region E). Cells released from rectangular clusters are migrating from their short edge (S), corners (C), and long edge (L) in this order of preference. The migration from the short and long edges, are significantly enhanced and reduced respectively compared to the migration from edges of square clusters (P<0.05). These patterns of migration result in sharp corners becoming sharper, i.e., more acute in angle, elongated patterns becoming more elongated. This feedback mechanism in the shape transformation of cell clusters causes the symmetry breaking and transformation of circular symmetric cell clusters into elongated clusters with increasing number of sharp perimeter corners.
Spatial patterns of cell migration coincide with rates of proliferation
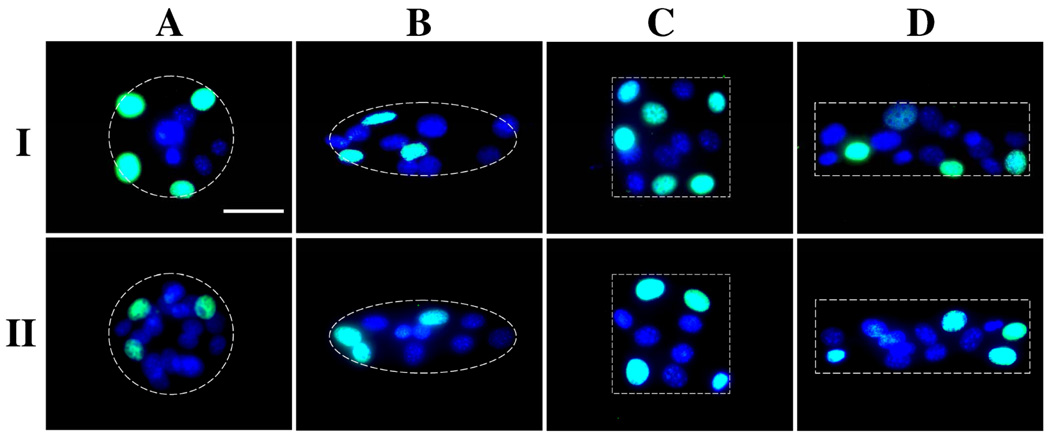
Over longer time periods, cell proliferation is expected to play an important role in the geometric transformation of cell clusters. We investigated with cell proliferation assays on the same circular, square, elliptical and rectangular geometries using NIH 3T3 fibroblasts. Cells, synchronized by serum starvation for 24 hours, were seeded and allowed to adhere onto the geometric patterns for 8 hours, then washed with PBS twice and replenished with growth media containing 10% serum. Cells in all geometric patterns reached confluence 32 hours after seeding after which they were pulse labeled with 5-bromo-2’-deoxyuridine (BrdU) for 2 hrs then immunostained with anti-BrdU to assess proliferation. As the representative images of this DNA assay (Fig. 8) shows, most cells in the interior of the clusters do not proliferate with DNA synthesis limited to cells with access to the perimeter of the cluster geometries.
Figure 8. Proliferation assay of cell cluster over geometric shapes.
DNA synthesis of patterned NIH 3T3 fibroblasts over different geometric islands (A–D) on culture dish. Cells with fewer cell-cell contacts showed increased DNA synthesis. DNA synthesis is visualized by immunofluorescent BrdU staining (green) with DAPI as counterstain (blue). Magnification 40×. Scale bar = 50µm.
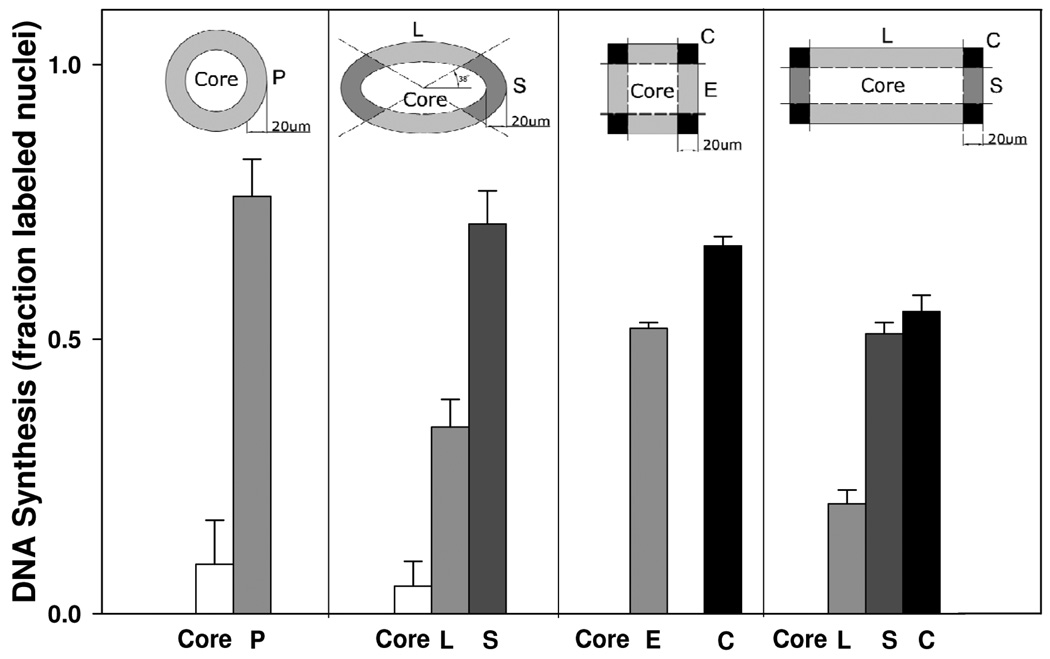
To facilitate statistical analysis of spatial distribution of DNA synthesis activity, we divided the clusters into a perimeter region 20 µm from the actual cluster perimeter, and defining the remaining internal area as the core (Fig. 9). Further defining P (circular periphery), E (edge), C (corner), S (short edge), and L (long edge), we analyzed 50 cell clusters of each shape and plot the fraction of nuclei in each region that is actively synthesizing DNA (Fig. 9). This analysis shows clearly that cells located on the periphery of the shapes exhibit significant higher rates of proliferation, compared to cells in the core. Less than 10% of cells in the core of circular or elliptical clusters are proliferating and no proliferating cells were detected within the core of square or rectangular clusters.
Figure 9. Quantification of DNA synthesis on various geometric shape.
Spatiotemporal quantification of DNA synthesis for patterned NIH 3T3 fibroblasts over different geometric islands. Cells located near the boundary form fewer cell-cell contacts and showed increased DNA synthesis. Cells within core of any geometric shape showed less activity of DNA synthesis. Error bar represents standard error.
For square clusters, more cells located in the corners (C) proliferate in comparison to edges (E) and the same trend was observed for rectangular clusters. For both elliptical and rectangular clusters, the analysis clearly shows that cells in the short edge (S) proliferate more than cells along the long edge (L). Altogether, these results demonstrate that cell proliferation is spatially heterogeneous and depends on the overall cluster geometry. Increased proliferation at corners and shorted edges (S) coincide with the outward migration patterns observed as the clusters transform in shape after release (Fig. 7). Thus, proliferation, which occurs over a longer time scale than migration, reinforces the patterns of cluster transformation that arise due to geometry induced polarization and migration of cells.
Individual cells assume different shapes and extent of cell-cell contact within clusters
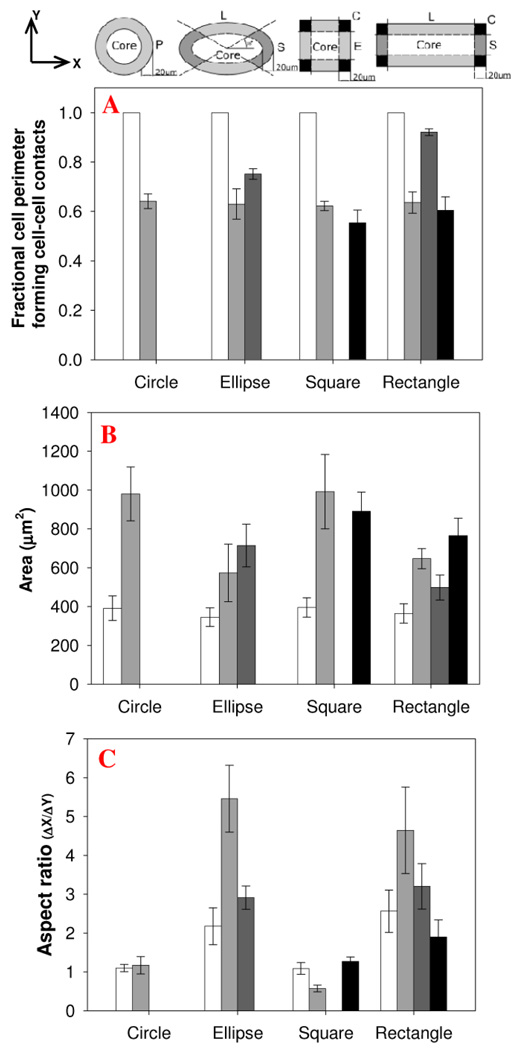
Cells located within cluster “cores” forms contacts with their surrounding cells, while cells at corners (region C) have the least opportunity to form cell-cell contacts. Here, we go further and measured statistically cell-cell perimeter adhesions, cell spreading areas, and aspect ratios for cells located in different regions of the clusters (Fig.10). As expected, cells near borders and corners have a smaller fraction of their perimeter in contact with neighboring cells (Fig. 10A). Cells located next to the borders have significantly higher cell spreading area compared to cells in the core of island suggestive of higher stress in the cells [7]. Independent of the cluster geometry, cells located in the core have areas of only 375±25µm2. In comparison, cells at the edge of circular clusters spread to 980±138 µm2, more than double the area of cells in the core (Fig. 10B). Cells in the perimeter region of ellipsoidal and rectangular clusters have similar spreading areas. However, perimeter cells along the longer edge (L region) of ellipsoidal clusters are highly elongated, with aspect ratios of 5.0±1.0 compared to cells along the shorter edge (S region) that have aspect ratios of 3.0±0.4 (Fig. 10C). A comparable difference in aspect ratios is observed for perimeter cells located along the long and short edges of rectangular clusters. The differential migration and proliferation observed on the various geometric shapes arises from a combination of mechanisms, including cell-cell contact, cell spreading, and cell aspect ratios.
Figure 10. Morphological characterization of cells over.
Morphological characterizations NIH 3T3 fibroblasts patterned over different geometric islands. Cells characterized for A) cell cell contact, B) Cell area and C) Aspect ratio. Error bar represents standard error.
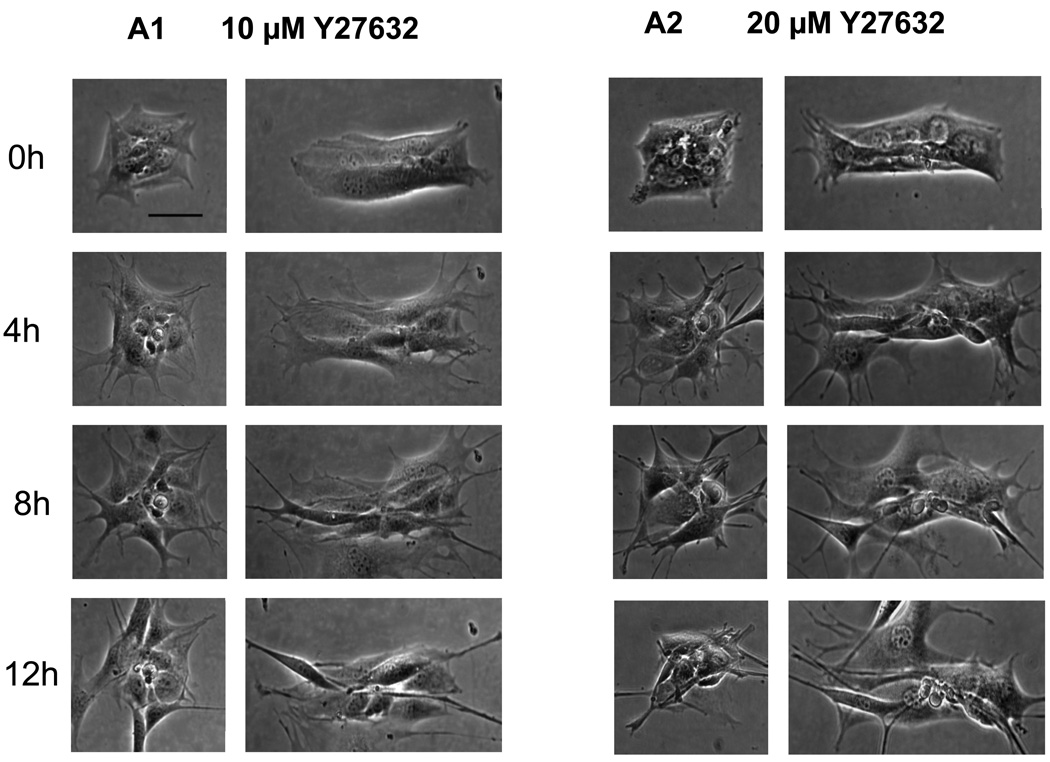
Tension within the monolayer is required for generating the patterns of migration
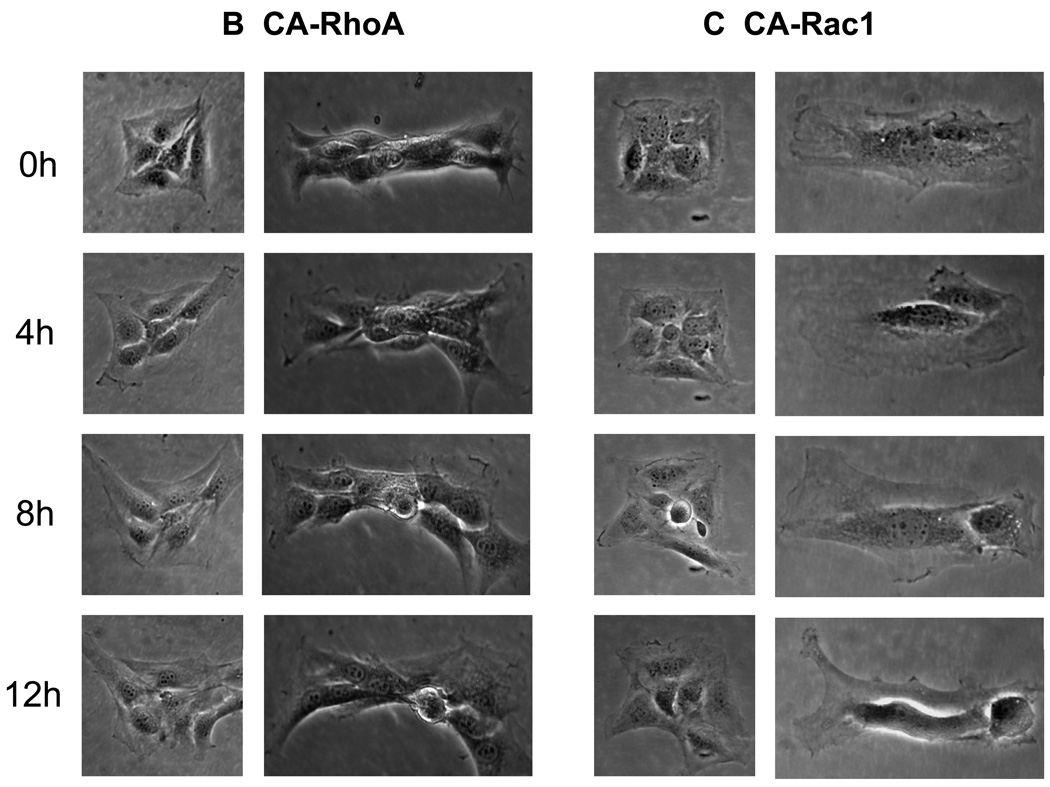
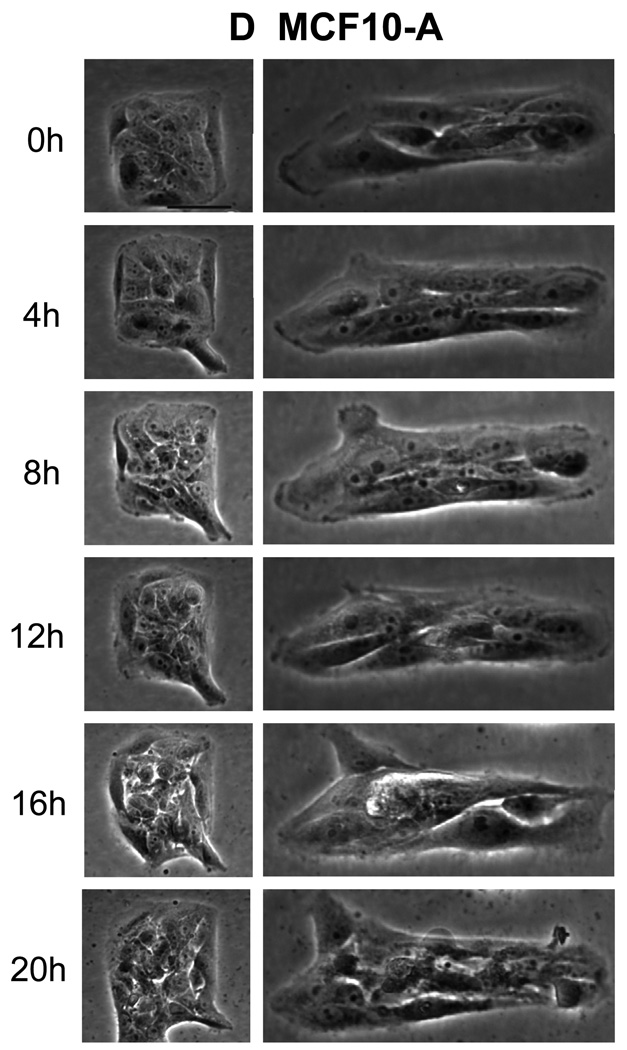
Previous studies have demonstrated that the mechanical forces originate from cytoskeletal tension generate patterns of proliferation [7]. To examine whether cell tension within the monolayer is also responsible for the observed patterns of migration, experiments were conducted using pharmacological or molecular interventions. Decreasing tension within the monolayer with Y27632 (Figure 11A) disrupted the migration pattern and cells released from the square and rectangular patterns migrate from both the edges and corners. Increasing the actomyosin cytoskeleton tension using cells expressing constitutively active RhoA caused substantially enhanced migration from corners and along the lengthwise direction (Figure 11B). Conversely, constitutively activated mutants of Rac1 that induces actin rich surface protrusions (lamellipodia) showed similar migration pattern as the unmodified fibroblasts (Figure11C). In addition to the fibroblasts examined initially, monolayers of epithelial cells such as MCF10A also shows similar patterns of migration (Figure 11D). These results suggest that contractile tension is important in formation of the patterns of migration in multicellular structures.
Figure 11. Cytoskeletal tension causes the patterns of migration.
Time lapse phase contrast images (in hours) show the directional migration of cells upon release from the square or rectangular adhesive islands. (A) NIH 3T3 fibroblasts treated with Y-27632 (B) NIH 3T3 fibroblasts expressing constitutively active RhoAL63 (C) NIH 3T3 fibroblasts expressing constitutively active Rac1L61 (D) MCF10A epithelial cells. Magnification 20×. Scale bar = 50µm.
Discussion
Unraveling the role of geometry and the spatial patterns of growth and migration within multicellular clusters is critical towards understanding embryonic development and tissue morphogenesis. By sequentially patterning then adsorbing oppositely charged cell-resistant and cell-adhesive polyelectrolytes on tissue culture dishes,[44] we have confined clusters of cells in precisely defined microscale geometries then track their migratory paths after release. These studies demonstrate clearly that the overall geometry of cell clusters has a strong influence on the cytoskeletal organization, polarization, and migration of individual cells. The spatial heterogeneity in these cell characteristics is furthermore coincident with patterns of cell spreading area, shape, and proliferation rates. This platform can be applied to investigate multicellular proliferation or migration such as wound healing and tumor growth.
Upon release from confinement, the symmetry breaking of circular cell clusters comes naturally from the non-synchronous outwards migration of cells. However, the continuous elongation of the circular clusters into shapes of increasing aspect ratio and number of perimeter corners was unexpected (Fig. 5). Controlled studies of differential migration rates from square clusters show a clear preference for cells to migrate outwards from corners. (Fig 5) Small protrusions from the cluster perimeter caused by the random motion of just one or two cells may thus trigger positive feedback driving the further development of these small protrusions into sharp perimeter corners. The tendency of 3T3 fibroblast clusters to develop acute perimeter angles is also observed for initially elliptical and rectangular clusters (Fig. 5). The pattern of migration is a result of contractile tension within the monolayer. Inducing the assembly of contractile actin and myosin filaments using constitutively activated RhoA enhances the observed migration pattern. Conversely, inhibiting actomyosin based tension with Y27632 disrupts this pattern.
From circular to square clusters, one would expect that cells will have different migratory preference between corners or edges. Here, it is useful to compare the polarization maps of the cells within the cluster and see which way they are inclined to move. For circular clusters, the constituent cells are polarized outwards in the direction of the perimeter leading to a small net polarization for the cluster as a whole. For square clusters, that have comparable symmetry to circular clusters, one would expect comparably small net polarization. Surprisingly however, the constituent cells of square clusters cooperatively polarize along a dominant diagonal resulting in a net cluster polarization that is much larger than that for circular clusters. The average net polarization vector for the square shape is more than double than that for the circular cluster. For cells released from square patterns, preferential migration from either one (65%) or two adjacent (35%) corners suggests that the overall cluster geometry itself can cause coordinated directional migration. These results provide the first example of net polarization and directional migration of groups of cells in a symmetric geometry.
The highest rate of cell migration is observed for cells released from rectangular patterns along the lengthwise direction. Previous studies on contact guidance[18, 23, 48] suggest that cell shape is influenced by the contacting boarder and adapt an elongated shape parallel to the edge. Our results indicate that the cell shape is not only influenced by the contacting border but also the overall geometry of the cell population defined by the adhesive island. For example as shown in Figure 10C, cells align parallel to the border in region L while in region S cells are aligned perpendicular to the border. This unique cell shape modulated by the shape of the cell cluster lead to cell polarization and preferential migration in the lengthwise direction. The preferential migration into the S regions are likely due to the alignment of actin filament, as shown in Fig. 1F. Cells on ellipse shaped adhesive island align their actin filaments parallel to the major axis and are likely to extend lamellipodia and migrate along this direction upon release.
The phenomenon of contact stimulated cell migration [25, 26] are observed for the preferential migration of cells in the S region as these regions has a higher cell- cell contact. Although it does not explain the preferential migration from the corners which actually has fewer cell - cell contact. It remains unknown why cells on the right half of the rectangular shape are polarized in the right direction and cells on the left half are polarized in the left. Possibly the polarization of the cell near the edge can be transmitted to the neighboring cells in the interior through gap type junctions[49–52]. The multicellular organization elicit a complex interplay between cell-cell, cell-boundary, cell shape and stress to emerge the unique patterns of cell migration.
The increased cell proliferation at borders relative to the core can be due to larger spreading areas and reduced cell-cell adhesions. This is consistent with earlier studies [53] relating proliferation rate to cell spreading area and how patterns of mechanical forces within multicellular groups can result in differential growth [7]. The increased DNA synthesis activity of cells located along the short edges (S) is likely related to their distinct morphology and higher mechanical forces they are subjected to.
We have demonstrated here that the spatial organization of cells also influence patterns of migration, which coincide with patterns of proliferation. Some of the results, particularly the observed preferential migration that transforms rectangular groups of cells into progressively longer and narrower assemblies, have physiological analogies. The convergent extent process wherein embryonic tissue restructures to elongate along the anteroposterior axis is one example, which plays an important role in embryonic development [54]. This principle of "Form from Form" is an important addition to extracellular morphogens and genetic cues, as mechanisms driving the shape and organization of multicellular assemblies.
References
- 1.Korff T, Augustin HG. Tensional forces in fibrillar extracellular matrices control directional capillary sprouting. Journal of Cell Science. 1999;112:3249–3258. doi: 10.1242/jcs.112.19.3249. [DOI] [PubMed] [Google Scholar]
- 2.Folkman J, Shing Y. Angiogenesis. Journal of Biological Chemistry. 1992;267:10931–10934. [PubMed] [Google Scholar]
- 3.Kiehart DP, Galbraith CG, Edwards KA, Rickoll WL, Montague RA. Multiple forces contribute to cell sheet morphogenesis for dorsal closure in Drosophila. Journal of Cell Biology. 2000;149:471–490. doi: 10.1083/jcb.149.2.471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Barfurth D. Zur regeneration der gewebe. Arch. Mikroskop. Anat. EntwMech. 1891;37:406–491. [Google Scholar]
- 5.Eycleshymer AC. The closing of wounds in the larval necturus. American journal of anatomy. 1907;1:317–325. [Google Scholar]
- 6.Michael L, Davies JA. Pattern and regulation of cell proliferation during murine ureteric bud development. Journal of Anatomy. 2004;204:241–255. doi: 10.1111/j.0021-8782.2004.00285.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Nelson CM, Jean RP, Tan JL, Liu WF, Sniadecki NJ, Spector AA, Chen CS. Emergent patterns of growth controlled by multicellular form and mechanics. Proceedings of the National Academy of Sciences of the United States of America. 2005;102:11594–11599. doi: 10.1073/pnas.0502575102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Tusch M, Hegerfeldt Y, Muradali S, Brocker EB, Friedl P. Invasion and migration of clustered cells from primary tumor explants: Differential expression and function of beta 1 integrins. Journal of Investigative Dermatology. 1998;110:504–504. [Google Scholar]
- 9.Kolega J. The movement of cell clusters invitro - morphology and directionality. Journal of Cell Science. 1981;49:15–32. doi: 10.1242/jcs.49.1.15. [DOI] [PubMed] [Google Scholar]
- 10.Boudreau N, Bissell MJ. Extracellular matrix signaling: integration of form and function in normal and malignant cells. Current Opinion in Cell Biology. 1998;10:640–646. doi: 10.1016/s0955-0674(98)80040-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Friedl P, Zanker KS, Brocker EB. Cell migration strategies in 3-D extracellular matrix: Differences in morphology, cell matrix interactions, and integrin function. Microscopy Research and Technique. 1998;43:369–378. doi: 10.1002/(SICI)1097-0029(19981201)43:5<369::AID-JEMT3>3.0.CO;2-6. [DOI] [PubMed] [Google Scholar]
- 12.Huttenlocher A, Ginsberg MH, Horwitz AF. Modulation of cell migration by integrin-mediated cytoskeletal linkages and ligand-binding affinity. Journal of Cell Biology. 1996;134:1551–1562. doi: 10.1083/jcb.134.6.1551. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Huttenlocher A, Sandborg RR, Horwitz AF. ADHESION IN CELL-MIGRATION. Current Opinion in Cell Biology. 1995;7:697–706. doi: 10.1016/0955-0674(95)80112-x. [DOI] [PubMed] [Google Scholar]
- 14.Sheetz MP, Felsenfeld DP, Galbraith CG. Cell migration: Regulation of force on extracellular-matrix-integrin complexes. Trends in Cell Biology. 1998;8:51–54. doi: 10.1016/s0962-8924(98)80005-6. [DOI] [PubMed] [Google Scholar]
- 15.Bailly M, Condeelis JS, Segall JE. Chemoattractant-induced lamellipod extension. Microscopy Research and Technique. 1998;43:433–443. doi: 10.1002/(SICI)1097-0029(19981201)43:5<433::AID-JEMT9>3.0.CO;2-2. [DOI] [PubMed] [Google Scholar]
- 16.Bailly M, Yan L, Whitesides GM, Condeelis JS, Segall JE. Regulation of protrusion shape and adhesion to the substratum during chemotactic responses of mammalian carcinoma cells. Experimental Cell Research. 1998;241:285–299. doi: 10.1006/excr.1998.4031. [DOI] [PubMed] [Google Scholar]
- 17.Lauffenburger DA, Horwitz AF. Cell migration: A physically integrated molecular process. Cell. 1996;84:359–369. doi: 10.1016/s0092-8674(00)81280-5. [DOI] [PubMed] [Google Scholar]
- 18.Friedl P, Brocker EB. The biology of cell locomotion within three-dimensional extracellular matrix. Cellular and Molecular Life Sciences. 2000;57:41–64. doi: 10.1007/s000180050498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Friedl P, Hegerfeldt Y, Tilisch M. Collective cell migration in morphogenesis and cancer. International Journal of Developmental Biology. 2004;48:441–449. doi: 10.1387/ijdb.041821pf. [DOI] [PubMed] [Google Scholar]
- 20.Friedl P, Wolf K. Tumour-cell invasion and migration: Diversity and escape mechanisms. Nature Reviews: Cancer. 2003;3:362–374. doi: 10.1038/nrc1075. [DOI] [PubMed] [Google Scholar]
- 21.Friedl P, Noble PB, Walton PA, Laird DW, Chauvin PJ, Tabah RJ, Black M, Zanker KS. Migration of coordinated cell clusters in mesenchymal and epithelial cancer explants in-vitro. Cancer Research. 1995;55:4557–4560. [PubMed] [Google Scholar]
- 22.Bianco A, Poukkula M, Cliffe A, Mathieu J, Luque CM, Fulga TA, Rorth P. Two distinct modes of guidance signalling during collective migration of border cells. Nature. 2007;448:362–U312. doi: 10.1038/nature05965. [DOI] [PubMed] [Google Scholar]
- 23.Haga H, Irahara C, Kobayashi R, Nakagaki T, Kawabata K. Collective movement of epithelial cells on a collagen gel substrate. Biophysical Journal. 2005;88:2250–2256. doi: 10.1529/biophysj.104.047654. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Nabeshima K, Inoue T, Shimao Y, Kataoka H, Koono M. Cohort migration of carcinoma cells: Differentiated colorectal carcinoma cells move as coherent cell clusters or sheets. Histology and Histopathology. 1999;14:1183–1197. doi: 10.14670/HH-14.1183. [DOI] [PubMed] [Google Scholar]
- 25.Abercrombie M. Contact Inhibition in Tissue Culture. In vitro. 1970;6:128–142. doi: 10.1007/BF02616114. [DOI] [PubMed] [Google Scholar]
- 26.Abercrombie M, Heaysman JEM. Observations on the social behaviour of cells in tissue culture I. Speed of movement of chick heart fibroblasts in relation to their mutual contacts. 1953:111–131. doi: 10.1016/0014-4827(53)90098-6. [DOI] [PubMed] [Google Scholar]
- 27.Bhora FY, Dunkin BJ, Batzri S, Aly HM, Bass BL, Sidawy AN, Harmon JW. Effect of growth-factors on cell-proliferation and epithelialization in human skin. Journal of Surgical Research. 1995;59:236–244. doi: 10.1006/jsre.1995.1160. [DOI] [PubMed] [Google Scholar]
- 28.Brown GL, Nanney LB, Griffen J, Cramer AB, Yancey JM, Curtsinger LJ, Holtzin L, Schultz GS, Jurkiewicz MJ, Lynch JB. Enhancement of wound-healing by topical treatment with epidermal growth-factor. New England Journal of Medicine. 1989;321:76–79. doi: 10.1056/NEJM198907133210203. [DOI] [PubMed] [Google Scholar]
- 29.Lynch SE, Nixon JC, Colvin RB, Antoniades HN. Role of platelet-derived growth-factor in wound-healing - synergistic effects with other growth-factors. Proceedings of the National Academy of Sciences of the United States of America. 1987;84:7696–7700. doi: 10.1073/pnas.84.21.7696. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Chen C, Mrksich M, Huang S, Whitesides G, Ingber D. Geometric control of cell life and death. Science. 1997;276:1425–1428. doi: 10.1126/science.276.5317.1425. [DOI] [PubMed] [Google Scholar]
- 31.Folkman J, Moscona A. Role of cell-shape in growth-control. Nature. 1978;273:345–349. doi: 10.1038/273345a0. [DOI] [PubMed] [Google Scholar]
- 32.Gray DS, Liu WF, Shen CJ, Bhadriraju K, Nelson CM, Chen CS. Engineering amount of cell-cell contact demonstrates biphasic proliferative regulation through RhoA and the actin cytoskeleton. Experimental Cell Research. 2008;314:2846–2854. doi: 10.1016/j.yexcr.2008.06.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Nelson CM, Chen CS. VE-cadherin simultaneously stimulates and inhibits cell proliferation by altering cytoskeletal structure and tension. Journal of Cell Science. 2003;116:3571–3581. doi: 10.1242/jcs.00680. [DOI] [PubMed] [Google Scholar]
- 34.Clark ERC, E.L. Microscopic observations on the growth of blood capillaries in the living mammal. American journal of anatomy. 1938;64:251–301. [Google Scholar]
- 35.Ingber D, Dike L, Hansen L, Karp S, Liley H, Maniotis A, Mcnamee H, Mooney D, Plopper G, Sims J, Wang N. Cellular Tensegrity - Exploring How Mechanical Changes in the Cytoskeleton Regulate Cell-Growth, Migration, and Tissue Pattern during Morphogenesis. International Review Of Cytology. 1994;150:150. doi: 10.1016/s0074-7696(08)61542-9. [DOI] [PubMed] [Google Scholar]
- 36.Ingber DE. FIbronectin controls capillary endothelial-cell growth by modulating cell-shape. Proceedings of the National Academy of Sciences of the United States of America. 1990;87:3579–3583. doi: 10.1073/pnas.87.9.3579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Ingber DE, Folkman J. Mechanochemical switching between growth and differentiation during fibroblast growth factor-stimulated angiogenesis invitro - role of extracellular-matrix. Journal of Cell Biology. 1989;109:317–330. doi: 10.1083/jcb.109.1.317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Reidy MA, Schwartz SM. Endothelial Regeneration .3. Time Course of Intimal Changes after Small Defined Injury to Rat Aortic Endothelium. Laboratory Investigation. 1981;44:301–308. [PubMed] [Google Scholar]
- 39.Ramsay MM, Walker LN, Bowyer DE. Narrow Superficial Injury to Rabbit Aortic Endothelium - the Healing-Process as Observed by Scanning Electron-Microscopy. Atherosclerosis. 1982;43:233–243. doi: 10.1016/0021-9150(82)90025-9. [DOI] [PubMed] [Google Scholar]
- 40.Selden SC, Rabinovitch PS, Schwartz SM. Effects of Cytoskeletal Disrupting Agents on Replication of Bovine Endothelium. Journal of Cellular Physiology. 1981;108:195–211. doi: 10.1002/jcp.1041080210. [DOI] [PubMed] [Google Scholar]
- 41.Coomber BL, Gotlieb AI. Invitro Endothelial Wound Repair - Interaction of Cell-Migration and Proliferation. Arteriosclerosis. 1990;10:215–222. doi: 10.1161/01.atv.10.2.215. [DOI] [PubMed] [Google Scholar]
- 42.Huang S, Brangwynne CP, Parker KK, Ingber DE. Symmetry-breaking in mammalian cell cohort migration during tissue pattern formation: Role of random-walk persistence. Cell Motility and the Cytoskeleton. 2005;61:201–213. doi: 10.1002/cm.20077. [DOI] [PubMed] [Google Scholar]
- 43.Brangwynne C, Huang S, Parker KK, Ingber DE. Symmetry breaking in cultured mammalian cells. In Vitro Cellular & Developmental Biology-Animal. 2000;36:563–565. doi: 10.1007/BF02577523. [DOI] [PubMed] [Google Scholar]
- 44.Kumar G, Meng JJ, Ip W, Co CC, Ho CC. Cell motility assays on tissue culture dishes via non-invasive confinement and release of cells. Langmuir. 2005;21:9267–9273. doi: 10.1021/la050332n. [DOI] [PubMed] [Google Scholar]
- 45.Kumar G, Wang YC, Co C, Ho CC. Spatially controlled cell engineering on biomaterials using polyelectrolytes. Langmuir. 2003;19:10550–10556. [Google Scholar]
- 46.Singhvi R, Kumar A, Lopez GP, Stephanopoulos GN, Wang DI, Whitesides GM, Ingber DE. Engineering cell shape and function. Science. 1994;264(5159):696–698. doi: 10.1126/science.8171320. [DOI] [PubMed] [Google Scholar]
- 47.Nobes CD, Hall A. Rho GTPases control polarity, protrusion, and adhesion during cell movement. Journal of Cell Biology. 1999;144:1235–1244. doi: 10.1083/jcb.144.6.1235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Wolf K, Muller R, Borgmann S, Brocker EB, Friedl P. Amoeboid shape change and contact guidance: T-lymphocyte crawling through fibrillar collagen is independent of matrix remodeling by MWs and other proteases. Blood. 2003;102:3262–3269. doi: 10.1182/blood-2002-12-3791. [DOI] [PubMed] [Google Scholar]
- 49.Larson DM, Haudenschild CC. Junctional Transfer in Wounded Cultures of Bovine Aortic Endothelial-Cells. Laboratory Investigation. 1988;59:373–379. [PubMed] [Google Scholar]
- 50.Larson DM, Sheridan JD. Inter-Cellular Junctions and Transfer of Small Molecules in Primary Vascular Endothelial Cultures. Journal of Cell Biology. 1982;92:183–191. doi: 10.1083/jcb.92.1.183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Zahm JM, Kaplan H, Herard AL, Doriot F, Pierrot D, Somelette P, Puchelle E. Cell migration and proliferation during the in vitro wound repair of the respiratory epithelium. Cell Motility and the Cytoskeleton. 1997;37:33–43. doi: 10.1002/(SICI)1097-0169(1997)37:1<33::AID-CM4>3.0.CO;2-I. [DOI] [PubMed] [Google Scholar]
- 52.Thomas LA, Yamada KM. Contact Stimulation of Cell-Migration. Journal of Cell Science. 1992;103:1211–1214. doi: 10.1242/jcs.103.4.1211. [DOI] [PubMed] [Google Scholar]
- 53.Chen CS, Mrksich M, Huang S, Whitesides GM, Ingber DE. Geometric control of cell life and death. Science. 1997;276(5317):1425–1428. doi: 10.1126/science.276.5317.1425. [DOI] [PubMed] [Google Scholar]
- 54.Elul T, Koehl MA, Keller R. Cellular mechanism underlying neural convergent extension in Xenopus laevis embryos. Dev. Biol. 1997;191:243–258. doi: 10.1006/dbio.1997.8711. [DOI] [PubMed] [Google Scholar]