Skip to main content
PMC home page
The Journal of the Acoustical Society of America logoLink to The Journal of the Acoustical Society of America
. 2011 Apr;129(4):2104–2111. doi: 10.1121/1.3543969

Auditory discrimination of force of impact

Robert A Lutfi 1,a), Ching-Ju Liu 1, Christophe N J Stoelinga 1
PMCID: PMC3097070  PMID: 21476666

Abstract

The auditory discrimination of force of impact was measured for three groups of listeners using sounds synthesized according to first-order equations of motion for the homogenous, isotropic bar [Morse and Ingard (1968). Theoretical Acoustics pp. 175–191]. The three groups were professional percussionists, nonmusicians, and individuals recruited from the general population without regard to musical background. In the two-interval, forced-choice procedure, listeners chose the sound corresponding to the greater force of impact as the length of the bar varied from one presentation to the next. From the equations of motion, a maximum-likelihood test for the task was determined to be of the form Δlog A + αΔ log f > 0, where A and f are the amplitude and frequency of any one partial and α = 0.5. Relative decision weights on Δ log f were obtained from the trial-by-trial responses of listeners and compared to α. Percussionists generally outperformed the other groups; however, the obtained decision weights of all listeners deviated significantly from α and showed variability within groups far in excess of the variability associated with replication. Providing correct feedback after each trial had little effect on the decision weights. The variability in these measures was comparable to that seen in studies involving the auditory discrimination of other source attributes.

INTRODUCTION

The sound of an object as it is struck conveys information about that object and the manner in which it is struck. But, how much of this information is a listener able to recover from the sound alone? For over a decade psychoacoustic research has pursued this question in order to gain understanding of how we perceive the world through sound. Much of the research has focused on the listener’s ability to identify the material properties of objects under restricted conditions of impact, rudimentary bars, plates, or membranes struck with a single mallet and constant force (Gaver, 1988, 1993a,b; Giordano and Petrini, 2003; Giordano and McAdams, 2006; Klatzky et al., 2000; Kunkler-Peck and Turvey, 2000; Lakatos et al., 1997; Liu and Lutfi, 2009; Lutfi, 2001, 2008; Lutfi and Liu, 2007; Lutfi and Oh, 1997; Tucker and Brown, 2003). Even under such constrained conditions, performance has varied widely within and across the studies. Listeners most often can identify the broad category of material to which the object belongs (i.e., wood, metal, or plastic), but the acoustic information on which listeners base their judgments can differ greatly across conditions (Giordano and McAdams, 2006; Lutfi and Oh, 1997) and, even within conditions, may not be the same for each listener (Lutfi, 2001; Lutfi and Liu, 2007). Similar variability in results has been observed for listener judgments regarding other properties of impact, including the size and shape of the object struck (Gaver, 1988; Kunkler-Peck and Turvey, 2000; Tucker and Brown, 2003), the size and hardness of the mallet used (Freed, 1990), and the point of contact of the mallet (Lutfi and Liu, 2007).

The variability of results in these studies is not well understood. One explanation implicates the use of synthetically generated sounds in many of these studies, the argument being that these sounds lack adequate information for identification (Carello et al., 2003). This explanation seems unlikely since similar results are obtained in studies that used exclusively live sounds or recordings as signals (Gaver, 1988, 1993a,b; Giordano and Petrini, 2003; Kunkler-Peck and Turvey, 2000; Tucker and Brown, 2003). Others have suggested that the acoustic information that would ensure accurate identification may not always be the most salient (Giordano et al., 2010) or even above the listener’s threshold for detection (Lutfi, 2000, 2001). This issue has been noted specifically with regard to judgments of the hardness (Giordano et al., 2010) and the material and geometric properties of objects (Giordano and McAdams, 2006; Lutfi, 2000, 2001; Lutfi and Stoelinga, 2010). Still a third potential factor is differences across studies in the amount of training, feedback, and prior information about the task given to listeners. Noteworthy in this regard is the fact that participants in studies are sometimes reported to have different degrees of musical training, which can be a factor influencing both decision strategy and performance (Lutfi and Liu, 2007; Liu and Lutfi, 2009; Micheyl et al., 2006; Oxenham et al., 2003).

Understanding the factors that contribute to the variability in results is important for the theories of sound source perception. The ecological approach to perception, credited to Gibson (1966) and more recently represented in the works of Carello et al. (2003), attributes to the listener the ability to extract from sound information that is lawfully related to properties of the source. This information is taken to be in the form of acoustic invariants that would allow a listener to uniquely identify one source property while others are allowed to vary (e.g., source material despite variation in size, shape, or the manner in which the source is driven to vibrate). The implication is that listeners would be rather uniform in their judgments regarding source properties if, indeed, their judgments were based on lawful acoustic invariants. The second major perceptual theory, inferential theory, emphasizes the ambiguous over the lawful nature of the stimulus and stresses the constraints limited sensitivity imposes on the processing of acoustic invariants (Ellis, 1996; Helmholtz, 1954; Martin, 1999). Because of the emphasis on stimulus ambiguity, inferential theory generally allows greater room for individual differences in the perception of sound sources based on past experience and prior knowledge of the stimulus.

The variability in results continues to be an issue in these studies, but there is at least one basic property of impact, largely ignored in this literature, for which the accuracy of judgments is expected to be quite good and variability quite small, that is, the force of impact. The first-order effect of the force of impact on sound has been worked out for the homogenous, isotropic bar (Morse and Ingard, 1968). For a given bar identically struck, the amplitudes of partials will vary in direct proportion to the force of impact. However, there is also an interaction with frequency as the properties of the bar are allowed to vary. For the same force of impact, the amplitudes will be less for bars emitting higher frequencies, the exact relation is given by an inverse proportionality of sound power and frequency, A2 ∝ l∕f. The relation is robust and it is more transparent and less subject to variation in the bar than the acoustic relations associated with the other source properties listeners have been asked to judge (Lutfi, 2000; Lutfi and Stoelinga, 2010). The relation also appears to be a general property of natural sounds in as much as the mean spectral densities of speech, music, animal vocalizations, and common environmental sounds are all found to vary in inverse proportion to frequency (Attias and Schreiner, 1997; Voss and Clark, 1975, 1978). Lewicki (2002) has gone so far as to suggest that frequency analysis by the cochlea, being roughly constant Q, is an adaptation of the auditory system to this general property that serves to maximize the transmission of information in natural sounds.

Given the ubiquitous nature of the inverse relation between amplitude and frequency and its salience as a cue, one might anticipate that listeners would be more uniform in their judgments regarding force of impact than they have been regarding other source attributes and, moreover, that their judgments would reflect an implicit knowledge of this relation. The goal of the present study was to test this idea. To evaluate the role experiential factors might play in contributing to individual differences the study included a group of professional percussionists as listeners as well as a group who had no musical training whatsoever. Conditions were also run with and without feedback. We hypothesized that the best performance would be achieved by the percussionists who have had many years of experience in striking objects to achieve desired nuances in sound and that, if feedback was at all effective, it would only be for the listeners who lacked such experience.

METHODS

Subjects

Three groups of listeners were included in the study—listeners with no musical training, professional percussionists, and listeners who were selected at from the population at large without regard to musical background. The last group was taken to be the representative of listeners as they have been typically recruited in past studies. The listeners without musical training were students at the University of Wisconsin, Madison, who reported never having any formal musical training or ever having seriously attempted to learn to play a musical instrument. Eight nonmusicians participated in the study, three males and five females, aged 23–34 yr. The percussionists were paid professionals who were either music majors in the School of Music at the University of Wisconsin or had were graduated with a music performance degree from the University. All of the percussionists reported having their first musical lessons before the age of 10 yr, and all reported playing their instrument for more than 10 yr. Moreover, at the time of their participation in the study, all had been practicing their instrument at least 5 days a week for several hours a day. Four percussionists participated in the study, three males and one female, aged 20–28 yr. The listeners selected without regard to musical background were recruited from the University at large and before we regularly collected reports regarding the musical training of our listeners. There were seven listeners in this group, two males and five females, aged 19–23 yr. None of the participants reported any prior history of auditory pathology, and the results of a standard hearing evaluation showed all listeners to have a hearing sensitivity of 15 dB hearing level (HL) or better from 250 Hz to 8 kHz (ANSI S3.6, 1996).

Stimuli

Approximations to the impact sounds of a cylindrical wood block and iron bar, clamped at one end and struck at the other, were synthesized using the theoretical equations for the motion of these sources from standard acoustic texts (Morse and Ingard, 1968).1 The synthesis was the same as that used in past studies by the authors and has received both subjective and objective psychophysical validation (Lutfi et al., 2005; McAdams et al., 2004). The resulting impact sounds are a sum of exponentially damped sinusoids with frequencies (fn, Hz), amplitudes (An, dyne∕cm2), and decay moduli (τn, s) that depend on the material and geometric parameters of the source, as well as the manner in which it is struck. Complete expressions describing these dependencies are given by Morse and Ingard (1968, pp. 175–191, 222).

The diameters of the wood block and iron bar used in the study were 4 and 1 cm, respectively; the length of both sources, however, varied for each presentation of a sound, as described shortly. For the iron bar, the nominal length was 10 cm, yielding values of fn = 517, 3237, and 9063 Hz and τn = 1.12, 0.005, and 0.0002 s for the audible partials. For the wood block, the length was 25 cm, yielding nominal values of fn = 2586 and 16 194 Hz and τn = 0.052 and 0.0002 s for the audible partials. The length and width of each bar were selected to cover a broad range of values of frequency and decay typical of everyday listening. Note that because of the very brief decay times of the higher partials, these partials affect only the onset transient of the signals. In the case of the iron bar, a 5-ms cosine-squared ramp was used to truncate the sounds after 1 s. This was done to keep the trial sequence at a reasonable length. The level of the partials for both the wood block and iron bar fell at 6 dB∕octave. A loudness balancing procedure was used (Lutfi et al., 2008) to calibrate the overall sound power so that it would vary with frequency around an approximate mean value of 70 dB sound pressure level (SPL) at the eardrum. Sounds were played at a 44 100-Hz sampling rate with 16-bit resolution using a MOTU 896 audio interface. From the interface, the sounds were buffered through a Rolls RA62c headphone amplifier and then delivered diotically to listeners over Beyerdynamic DT 990 headphones. Listeners were seated individually in a double-walled, Industrial Acoustics Company (IAC) sound-attenuated chamber.

Procedure

In the two-interval, forced-choice procedure listeners were asked to judge which impact sound corresponded to the source hit with the greater force, F. The length of the source varied at random about its nominal value (identified above) for each presentation of a sound. This was done to prevent the listener from performing the task simply by discriminating a fixed change in level. The distribution of length values was normal with standard deviation equal to 0.5 cm. Consistent with the equations of motion, the frequencies of the partials varied in inverse proportion to the square of the length, the decay moduli in inverse proportion to the cube of frequency, and the amplitudes in inverse proportion to the square-root of frequency (cf. Morse and Ingard, 1968, pp. 175–191, 222). For the iron bar, the difference in the force of impact ΔF within a block of trials was either 2 or 4 dB, corresponding to a 2 or 4 dB difference in overall sound level at any given fixed bar length. For the wood block, the corresponding values were 1, 2, or 3 dB. These values were selected to produce a range of performance levels between chance and perfect performance.

Listeners ran no more than one experimental session corresponding to one condition of the study per day. Each session lasted for 1 h and consisted of eight blocks of trials, 50 trials per block. The source was exclusively the wood block or iron bar within each session. No feedback or training was given during the initial experimental sessions. After completing one session and replication of each condition without feedback, sessions were repeated providing correct feedback after each trial. Listeners who were recruited without regard to musical background participated in a total of 16 sessions (two values of ΔF for the wood block and iron bar, with and without feedback and replication). Percussionists and nonmusicians participated in four sessions (one value of ΔF = 2 dB for the wood block, with and without feedback and replication).

Analysis

The goal of the study was to determine whether listeners make appropriate use of the amplitude dependence on frequency when judging force of impact. To this end, we derived a maximum-likelihood (ML) decision rule for the task, identifying how judgments should be based on An and fn so as to optimize performance. From the equations of motion, it is possible to show that for a homogenous bar varying only in length, the force of impact F can be recovered from the properties of any one partial according to the relation

F=kAf0.5, (1)

where k is a constant (see Appendix). Here, we drop the subscript n since the information in the partials regarding F is redundant. Rewriting this expression as A2 = F2∕(k2f), Eq. (1) can be seen to reflect the inverse proportionality between sound power and frequency when F is constant. 2 From Eq. (1), the ML decision rule for the two-interval, forced-choice procedure can be written as a linear combination of the log of A and f:

Respond Interval 1 iff ΔlogA+α(Δlogf)>0, (2)

where iff denotes “if and only if,” α = 0.5, and Δ log A (Δ log f) is the value of log A (log f) in the first interval minus its value in the second interval. Writing the decision rule in this way allows the optimal use of the dependence of A on f to be represented as an optimal relative decision weight on A andf given by α = 0.5. From the ML decision rule follows an empirical decision rule

Respond Interval 1 iff (ΔlogA+eA)+a(Δlogf+ef)+c+ec>0, (3)

where the e ∼ N(0,σ) are normal deviates representing different sources of additive internal noise, c is an interval bias, and a is the listener’s relative decision weight on log f comparable to α. Now, if the e are taken to be independent of A and f, they can be pooled to yield a single error term, ɛ. Equation (3) then provides a general linear model for estimating a empirically, which when compared to α can be used to determine whether listeners make optimal use of the inverse relation between A and f. The value of a is estimated by means of a logistic multiple regression of the listener’s trial-by-trial response on Δ log A and Δ log f, taking ɛ as the regression error. We use the glmfit routine of the software application MATLAB v.7.01. The resulting estimate is based on the unshared variance of predictors and is independent of all e. The empirical question is whether the obtained estimates of a for the different groups of listeners differ significantly from the optimal value of α = 0.5.

RESULTS

Discrimination of force of impact

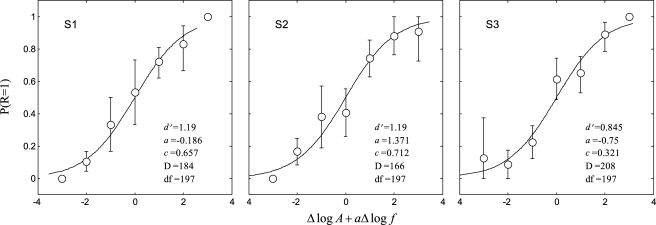
The first set of results reported is from the listeners recruited without regard to musical background. The conditions are the wood block (ΔF = 1 and 3 dB) and iron bar (ΔF = 2 and 4 dB) without feedback. Figure 1 shows the results of the regression analysis for three representative listeners (one listener for each panel) for the wood block condition, with ΔF = 1 dB. In each panel, the observed probabilities of a first-interval response (open symbols) are plotted against the predictions (continuous curve) of the decision model given by Eq. (3). Error bars show the 95% confidence intervals for the observed probabilities. Parameters of the fit are given in the lower right-hand corner of each panel. The fits are quite good and are representative of the fits for the other listeners in these conditions. For all listeners in all conditions, the deviance D of the fits was never more than twice the associated degrees of freedom df, ranging from D = 166–270 for df = 197. This indicates that a model with more free parameters would not provide a significantly better fit to the data (Snijders and Bosker, 1999). The values of c, moreover, were all quite close to 0, indicating no significant interval bias. In what follows then, we focus on the obtained values of a resulting from the regression and performance accuracy as given by d′ (Swets, 1996, pp.7–30).

Figure 1.

Figure 1

Open in a new tab

Representative results of the regression analysis for three listeners (panels) for the wood block condition without feedback, ΔF = 1 dB. The observed probabilities of a first-interval response (open symbols) are plotted against the predictions (continuous curve) of the decision model given by Eq. (3). Error bars give 95% confidence intervals. Parameters of the fit along with the associated deviance D and degrees of freedom, df, are given at the lower right-hand corner of each panel.

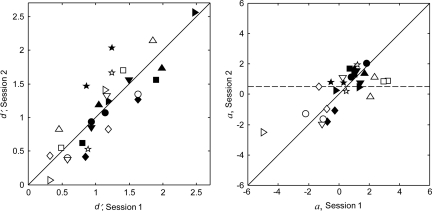
Figure 2 shows the results of the replication in estimates for the no-feedback condition, for both the iron bar (filled symbols) and the wood block (open symbols); repeated symbols represent the two values of ΔF for each condition. In the left panel, the two estimates of d′ obtained on different days are plotted against one another; perfect agreement is given by the diagonal. The panel shows wide variation across listeners (symbol type) and conditions, ranging from near chance performance (d′< 0.5) to near perfect performance (d′> 2.0). The agreement across replications, however, is reasonably good over the entire range, the data showing neither a consistent improvement nor deterioration in performance with replication. The right panel shows similarly good agreement in replication of the decision weights, a. In this case, an improvement in the decision weights with replication would be indicated by data for session 2 falling closer to the horizontal dashed line corresponding to the optimal decision weight of α = 0.5. The data clearly fall closer to the diagonal, although one listener (open squares) shows some apparent improvement in their decision weight. The results are consistent with those of past studies, involving different discrimination tasks, wherein individual differences in the decision weights of listeners have been reliably replicated on different days (Doherty and Lutfi, 1996).

Figure 2.

Figure 2

Open in a new tab

The left panel gives, for the no-feedback condition, the two estimates of d′ obtained on different days. The data are for the listeners recruited without regard to musical background (different symbol type for each listener). Data for the iron and wood bars are indicated, respectively, by filled and unfilled symbols. The right panel gives the corresponding estimates of the listeners’ decision weights, a. The decision weight for the ML decision rule, α = 0.5, is indicated by the horizontal dashed line. Note that values of |a| > 1.0 indicate a predominant weight on frequency.

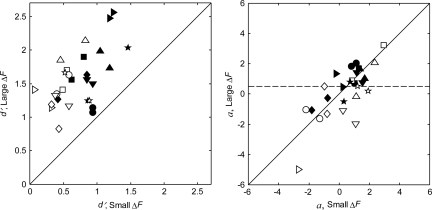
Figure 3 compares the results for the two values of ΔF in the no-feedback condition. The values of d′ obtained for the different values of ΔF (2 and 4 dB for the iron bar and 1 and 3 dB for the wood block) are plotted against one another in the left panel. The data show an expected improvement in d′ with the larger ΔF in each case, although the improvement varies widely across the listeners. The corresponding estimates of the decision weights are plotted against one another in the right panel. Here, by contrast to the estimates of d′, the data fall close to the diagonal, indicating little effect of ΔF on the decisions weights. Indeed, if the improvement in d′ were due to a change in the decision weights, one would again expect the data to fall closer to the horizontal dashed line corresponding to α = 0.5.

Figure 3.

Figure 3

Open in a new tab

As Fig. 2, except that the obtained values of d′ and a are given for the two values of ΔF for each sound source. For the iron bar, ΔF = 2 and 4 dB, while for the wood block ΔF = 1 and 3 dB.

Comparison of nonmusicians and professional percussionists

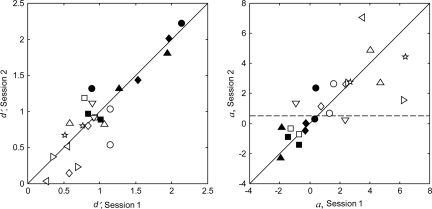
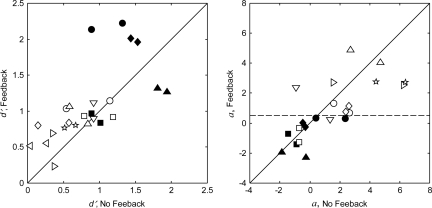
Figure 4 shows the results for the nonmusicians (open symbols) and professional percussionists (filled symbols) plotted in the same manner as Fig. 2. The data are for the wood block condition without feedback, ΔF = 2 dB. Once again the data show a wide range of performance across listeners and fairly good agreement with replication (left panel). A paired t-test showed a statistically significant difference in the performance of the two groups (t = 6.6, df = 46, p < 0.001). The best performers are clearly the percussionists, the worst performing percussionist (filled squares) roughly equaling the performance of the two best performing nonmusicians (open squares and downward triangles). The decision weights for these conditions (right panel) also show differences between the two groups. Within the group of nonmusicians the decision weights vary widely and show little agreement with replication. For the percussionists there is less variation and better agreement with replication. The percussionists also show fewer extreme values, |a |> 2, indicating near exclusive weight on differences in frequency (t = 1.9, df = 46, p < 0.05; one-tailed, paired t-test with unequal variances). These results are generally anticipated since past studies have shown musically trained listeners to often outperform musically naive listeners in auditory tasks prior to task-specific training (Liu and Lutfi, 2009; Micheyl et al., 2006; Oxenham, et al., 2003).

Figure 4.

Figure 4

Open in a new tab

As Fig. 2, except that the data are for the nonmusicians (open symbols) and professional percussionists (filled symbols) for the wood block condition without feedback. The value of ΔF was 2 dB.

Effect of feedback

The effect of providing feedback in the wood block condition (ΔF = 2 dB) is shown in Fig 5. Performance with feedback is plotted against performance without feedback for the percussionists (filled symbols) and nonmusicians (open symbols) in the left panel. The poorer performing nonmusicians tended to show a small improvement in performance with feedback, while the results for the percussionists were mixed. Two of the percussionists showed a substantial improvement in performance (filled circles and diamonds), a third showed no change (filled squares), while the fourth showed a decrease in performance with feedback (filled triangles). The effect of feedback for the nonmusicians was statistically significant (t = −3.3, df = 15, p < 0.01, paired t-test) while for the percussionists it was not (t = −1.0, df = 7, p > 0.05). The decision weights with and without feedback are shown for both groups of listener in the right panel of Fig. 5. There appears to be little improvement in the decision weights with feedback for either group of listeners as, once again, the data fall closer to the diagonal than to the horizontal dashed line representing α = 0.5. The one possible exception is the decision weights for the nonmusician given by the open diamonds. Overall the effect of feedback on the decision weights was nonsignificant (t = 1.5, df = 23, p > 0.05).

Figure 5.

Figure 5

Open in a new tab

As Fig. 4, except that the comparison is between the data obtained with and without feedback.

Relation of d′ and decision weights

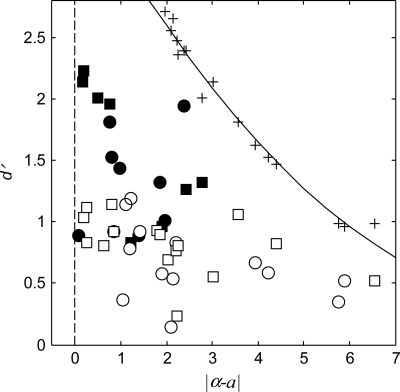
Figure 6 shows, for all conditions, each listener’s d′ performance plotted against the unsigned deviation of their decision weight from the optimal value of α = 0.5. Filled and unfilled symbols represent, as before, the data from the percussionists and nonmusicians; squares and circles represent, respectively, the conditions with and without feedback. Each small cross in the figure shows, for the data point projected vertically below it, the expected outcome if the deviation from the optimal decision weight was the only factor limiting performance. The expectations were computed from each listener’s trial-by-trial data using the decision weights obtained from each listener. Deviations from the theoretical prediction (continuous curve) reflect exclusively variability in the parameters of the impact sounds across blocks of trials. The figure reveals, across listeners and conditions, a rather weak relation of performance and decision weights. Although performance does tend to improve as the deviation from the optimal weight decreases, there is considerable scatter in the data. Moreover, the deviations of the data from the crosses indicate that factors other than the decision weights have a significant impact on performance. Such factors are identified collectively with interval bias, c, and the different sources of internal noise (regression error), e, in the decision model given in Eq. (3). Of these two factors, the most significant indicated by the analysis was, by far, that of e. This outcome is consistent with that of Lutfi and Liu (2007) who found internal noise to be the most significant factor underlying differences in performance across listeners in other source identification tasks.

Figure 6.

Figure 6

Open in a new tab

The figure shows d′ as a function of the deviation of the decision weight a from the optimal value of α = 0.5. The data are for the percussionists and nonmusicians (filled and unfilled symbols, respectively) with and without feedback (squares and circles, respectively). The continuous curve and small crosses give the expected outcome if the deviation from the optimal decision weight was the only factor limiting performance.

DISCUSSION AND CONCLUSIONS

Returning to the original question posed in the Introduction, the results of this study failed to support a special status for force of impact among the various source attributes listeners have been asked to judge from sound. As has been observed in past studies, the performance levels varied widely from one listener to the next. For the larger value of ΔF (left panel of Fig. 2), the performance of listeners recruited without regard to musical background ranged from d′= 0.8 – 2.2 and d′= 1.1 – 2.6, respectively, for the wood block and iron bar. For the smaller ΔF (left panel of Fig. 3), the range of variation was only slightly less. The professional percussionists tended to outperform listeners without any musical training (left panel of Fig. 4), suggesting that experience is a factor. This was, moreover, confirmed by the fact that feedback had a significant effect on performance only for the nonmusicians. However, within each group of listeners, the variability in performance was large and comparable to that for the listeners recruited without regard to musical background. Also, as in past studies, considerable variability was observed in the decision weights of listeners. In the right panels of Figs. 23, the decision weights appear near-uniformly distributed over the range a = −2.0 to 2.0. The endpoints of this range correspond to points for which differences in frequency have a much greater influence on the listener’s judgments than the differences in intensity. Indeed, for one listener, the decision weight (unfilled right-pointing triangle) fell well outside this range reflecting a near exclusive dependence of judgments on differences in frequency3. This is an unexpected result because, unlike the differences in intensity, the differences in frequency by themselves provide no information regarding force of impact; they only provide information when taken in combination with the differences in intensity.

A second unexpected result of this study was the failure of trial-by-trial feedback to yield any consistent improvement in the decision weights of listeners. Similar outcomes have been reported in the past involving judgments of other source attributes (Lutfi, 2001; Lutfi and Liu, 2007; Lutfi and Oh, 1997); however, in these studies, limits in auditory sensitivity or information capacity have been implicated as the likely cause. These explanations seem not to apply to the present study. The differences in frequency and intensity across trials were well in excess of the normal difference limens for these parameters for steady-state tones (Δf ⪢ 0.002, ΔI = ΔF > 1 dB; Wier et al., 1977; Jesteadt et al., 1977),4 and the informational demands of the task (processing a simple relation between frequency and intensity) were modest. The result, instead, seems to reflect a reluctance of listeners to modify their initial decision weights, even though they might improve their performance by doing so. Other unexplained failures of feedback to improve decision weights have been reported for the discrimination of multi-tone patterns by Berg (1990) and Lutfi and Jesteadt (2006).

If there is a single conclusion to be drawn from the last decade of research on human sound source identification, it is that individual listeners can differ greatly in their approach to identify even the most basic attributes of objects and events from the sound. The present study is no different in this regard, except that there were a priori reasons to expect that listeners would exhibit greater uniformity in their judgments. It remains unclear whether such results can be reconciled with current theories of sound source perception (Carello et al., 2003; Gibson, 1966).

ACKNOWLEDGMENT

The authors would like to thank Dr. Brian C.J. Moore and two anonymous reviewers for helpful comments on an earlier version of this manuscript. This research was supported by NIDCD Grant No. 5R01DC006875-05.

APPENDIX: DERIVATION OF EQ. (1)

The dependence of the amplitude of partials on an impulse striking force has been worked out for the homogenous, isotropic bar (Morse and Ingard, 1968, pp.181–185). For the cylindrical bar clamped at one end and a total impulse force F applied to the other, the unsigned amplitudes are

An=IFrSπ232ρQβn2, (A1)

where l, r, and S are, respectively, the length, radius, and cross-sectional area of the bar, ρ is the bar’s mass density, Q is Young’s modulus, and the βn are constants. In the present experiments only l and F were allowed to vary within a block of trials; all other properties of the bar had constant values. Hence, A1 can be rearranged to yield a simple expression for the force of impact in terms of the amplitude of any one partial,

F=c1Anlβn2, (A2)

where c1 takes on one of two values depending on whether the source is the wood block or the iron bar. Note from this expression that F could be determined exclusively from the amplitude of any one partial except for the fact that l varies. The variation in l introduces an additional level of complexity, causing the relation between amplitude and F to depend on frequency. This dependence can be determined from the expression for the frequencies derived for the bar (Morse and Ingard, 1968, p. 182),

fn=π4l2Qρβn2, (A3)

which for the present experiments can be rewritten

fn=c2l2βn2 (A4)

where c2 is another constant. Solving for l and substituting into Eq. (A2) gives

F=knAnfn0.5 (A5)

which is just the unabbreviated form of Eq. (1).

Footnotes

1

These equations assume that the predominant source of damping is external to the bar, as would be the case, for example, where much of the sound energy is dissipated through the supports. They also do not include the secondary effect of the time of contact associated with the impact force or the effect of radiation from the bar. The secondary effect of time of contact acts as a low-pass filter which would have a negligible effect on the synthesis of the impact sounds for the bars used in the present study (Zener, 1941; Stoelinga and Lutfi, 2010). The effect of radiation, however, is much more complex and not simply related to force of contact (cf. Kinsler et al., 2000).

2

A similar expression for F can be written in terms of A and τ, as the information in τ and f is entirely redundant.

3

The corresponding estimate for this listener is not shown as it fell well outside the range of the plot.

4

The comparison to these studies should be taken qualitatively since the tones in the present study were neither steady-state nor constant frequency as they were in the cited studies.

References

  1. ANSI (1996). S3.6,-1996 “American National Standard Specification for Audiometers” (American National Standards Institute, New York: ). [Google Scholar]
  2. Attias, H., and Schreiner, C. E. (1997). “Low-order temporal statistics of natural sounds,” Adv. Neural Inf. Process. Syst. 9, 27–33. [Google Scholar]
  3. Berg, B. G. (1990). “Observer efficiency and weights in a multiple observation task,” J. Acoust. Soc. Am. 88, 149–158. [DOI] [PubMed] [Google Scholar]
  4. Carello, C., Wagman, J. B., and Turvey, M. T. (2003). “Acoustical specification of object properties” in Moving Image Theory: Ecological Considerations, edited by Anderson J. and Anderson B.(Southern Illinois University Press, Carbondale, IL: ), pp. 79–104. [Google Scholar]
  5. Doherty, K. A., and Lutfi, R. A. (1996). “Spectral weights for overall level discrimination in listeners with sensorineural hearing loss,” J. Acoust. Soc. Am. 99, 1053–1058. [DOI] [PubMed] [Google Scholar]
  6. Ellis, D. P. W. (1996). “Prediction-driven computational auditory scene analysis,” Ph.D. thesis, Department of Electrical Engineering and Computer Science, Massachusetts Institute of Technology, Cambridge, MA. [Google Scholar]
  7. Freed, D. J. (1990). “Auditory correlates of perceived mallet hardness for a set of recorded percussive sound events,” J. Acoust. Soc. Am. 87, 311–322. [DOI] [PubMed] [Google Scholar]
  8. Gaver, W. W. (1988). “Everyday listening and auditory icons,” Ph.D. thesis, University of California, San Diego, CA. [Google Scholar]
  9. Gaver, W. W. (1993a). “What in the world do we hear?: An ecological approach to auditory event perception,” Ecological Psychol. 5, 1–29. [Google Scholar]
  10. Gaver, W. W. (1993b). “How do we hear in the world? explorations in ecological acoustics,” Ecological Psychol. 5, 285–313. [Google Scholar]
  11. Giordano, B. L., and McAdams, S. (2006). “Material identification of real impact sounds: Effects of size variation in steel, glass, wood, and plexiglass plates,” J. Acoust. Soc. Am. 119, 1171–1181. [DOI] [PubMed] [Google Scholar]
  12. Giordano, B. L., and Petrini, K. (2003). “Hardness recognition in synthetic sounds,” in Proceedings of the Stockholm Music Acoustics Conference, Stockholm, Sweden.
  13. Giordano, B. L., Rocchesso, D., and McAdams, S. (2010). “Integration of acoustical information in the perception of impacted sound sources: The role of information accuracy and exploitability,” J. Exp. Psychol. Hum. Percept. Perform. 36, 462–476. [DOI] [PubMed] [Google Scholar]
  14. Gibson, J. J. (1966). The Senses Considered as Perceptual Systems (Houghton-Mifflin, Boston: ), pp. 1–339. [Google Scholar]
  15. Helmholtz, H. (1954). On the Sensations of Tone as a Physiological Basis for the Theory of Music (Dover, New York: ), pp. 1–576. [Google Scholar]
  16. Jesteadt, W., Wier, C. C., and Green, D. M. (1977). “Intensity discrimination as a function of frequency and sensation level,” J. Acoust. Soc. Am. 61, 169–177. [DOI] [PubMed] [Google Scholar]
  17. Kinsler, L. E., Frey, A. R., Coppens, A. B., and Sanders, J. V. (2000). Fundamentals of Acoustics, 4th ed. (Wiley, New York: ), pp. 68–90. [Google Scholar]
  18. Klatzky, R. L., Pai, D. K., Krotkov, E. P. (2000). “Perception of material from contact sounds,” Presence: Teleop. Virtual Environ. 9, 399–410. [Google Scholar]
  19. Kunkler-Peck, A. J., and Turvey, M. T. (2000). “Hearing shape,” J. Exp. Psychol. 26, 279–294. [DOI] [PubMed] [Google Scholar]
  20. Lakatos, S., McAdams, S., and Causse, R. (1997). “The representation of auditory source characteristics: Simple geometric form,” Perspect. Psychol. Sci. 59, 1180–1190. [DOI] [PubMed] [Google Scholar]
  21. Lewicki, M. S. (2002). “Efficient coding of natural sounds,” Nature 5, 356–363 . [DOI] [PubMed] [Google Scholar]
  22. Liu, C. J., and Lutfi, R. A. (2009). “Identification of impact sounds by professional percussionists,” J. Acoust. Soc. Am. 125, 2684. [Google Scholar]
  23. Lutfi, R. A. (2000). “Source uncertainty, decision weights, and internal noise as factors in auditory identification of a simple resonant source,” Assoc. Res. Otolaryngol. Abstr. 23, 171. [Google Scholar]
  24. Lutfi, R. A. (2001). “Auditory detection of hollowness,” J. Acoust. Soc. Am. 110, 1010–1019. [DOI] [PubMed] [Google Scholar]
  25. Lutfi, R. A. (2008). “Human sound source identification,” in Springer Handbook of Auditory Research: Auditory Perception of Sound Sources, edited by Yost W. A. and Popper A. N. (Springer-Verlag, New York: ), pp. 13–42 . [Google Scholar]
  26. Lutfi, R. A., and Jesteadt, W. (2006). “Molecular analysis of the effect of relative tone level on multitone pattern discrimination,” J. Acoust. Soc. Am. 120, 3853–3860. [DOI] [PubMed] [Google Scholar]
  27. Lutfi, R. A., and Liu, C. J. (2007). “Individual differences in source identification from synthesized impact sounds,” J. Acoust. Soc. Am. 122, 1017–1028. [DOI] [PubMed] [Google Scholar]
  28. Lutfi, R. A., Liu, C. J., and Stoelinga, C. N. J. (2008). “Level dominance in sound source identification,” J. Acoust. Soc. Am. 124, 3784–3792. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Lutfi, R. A., and Oh, E. L. (1997). “Auditory discrimination of material changes in a struck-clamped bar,” J. Acoust. Soc. Am. 102, 3647–3656. [DOI] [PubMed] [Google Scholar]
  30. Lutfi, R. A., Oh, E., Storm, E., and Alexander, J. M. (2005). “Classification and identification of recorded and synthesized impact sounds by practiced listeners, musicians, and nonmusicians,” J. Acoust. Soc. Am. 118, 393–404. [DOI] [PubMed] [Google Scholar]
  31. Lutfi, R. A., and Stoelinga, C. N. J. (2009). “Sensory constraints on the identification of the geometric and material properties of struck bars,” J. Acoust. Soc. Am. 127, 350–360. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. McAdams, S., Chaigne, A., and Roussarie, V. (2004). “The psychomechanics of simulated sound sources: Material properties of impacted bars,” J. Acoust. Soc. Am. 115, 1306–1320. [DOI] [PubMed] [Google Scholar]
  33. Martin, K. D. (1999). Sound-source recognition: A theory and computational model, Ph. D. thesis, Department of Electrical Engineering and Computer Science, Massachusetts Institute of Technology, Cambridge, MA. [Google Scholar]
  34. Micheyl, C., Delhommeau, K., Perrot, X., and Oxenham, A. J. (2006). “Influence of musical and psychoacoustical training on pitch discrimination,” Hear. Res. 219, 36–47. [DOI] [PubMed] [Google Scholar]
  35. Morse, P. M., and Ingard, K. U. (1968). Theoretical Acoustics (Princeton University Press, Princeton, NJ: ), pp. 175–191. [Google Scholar]
  36. Oxenham, A. J., Fligor, B. J., Mason, C. R., and Kidd, G., Jr. (2003). “Informational masking and musical training,” J. Acoust. Soc. Am. 114, 1543–1549. [DOI] [PubMed] [Google Scholar]
  37. Snijders, T. A. B., and Bosker, R. J. (1999). Multilevel Analysis: An Introduction to Basic and Advanced Multilevel Modeling ( Sage Publishers, London: ) p. 49. [Google Scholar]
  38. Stoelinga, C. N. J., and Lutfi, R. A. (2010). “A method for including manner of contact in the synthesis of impact sounds for perceptual research,” J. Acoust. Soc. Am. 127, 1899. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Swets, J. A. (1996). Signal Detection Theory and ROC Analysis in Psychology and Diagnostics (Lawrence Erlbaum Association, Mahwah, NJ: ), pp. 7–30. [Google Scholar]
  40. Tucker, S., and Brown, G. J. (2003). “Modelling the auditory perception of size, shape and material: Applications to the classification of transient sonar sounds,” Presented at the 114th Audio Engineering Society Convention, Amsterdam, Netherlands. [Google Scholar]
  41. Voss R. F., and Clarke J. (1975). “1/f noise in music and speech,” Nature, 258, 317–318. [Google Scholar]
  42. Voss R. F., and Clarke J. (1978). “1/f noise in music: Music from 1/f noise,” J. Acoust. Soc. Am. 63, 258–263. [Google Scholar]
  43. Wier, C. C., Jesteadt, W., and Green, D. M. (1977). “Frequency discrimination as a function of frequency and sensation level,” J. Acoust. Soc. Am. 61, 178–184. [DOI] [PubMed] [Google Scholar]
  44. Zener, C. (1941). “The intrinsic inelasticity of large plates,” Phys. Rev. 59, 669–673. [Google Scholar]

Articles from The Journal of the Acoustical Society of America are provided here courtesy of Acoustical Society of America

RESOURCES