Abstract
Both helicases and polymerases perform their activities when bound to the nucleic acids, that is, the enzymes possess a nucleic acid-binding site. Functional complexity of the helicase or the polymerase action is reflected in the intricate structure of the total nucleic acid-binding site, which allows the enzymes to control and change their nucleic acid affinities during the catalysis. Understanding the fundamental aspects of the functional heterogeneity of the total nucleic acid-binding site of a polymerase or helicase can be achieved through quantitative thermodynamic analysis of the enzyme binding to the nucleic acids oligomers, which differ in their length. Such an analysis allows the experimenter to assess the presence of areas with strong and weak affinity for the nucleic acid, that is, the presence of the strong and the weak nucleic acid-binding subsites, determine the number of the nucleotide occlude by each subsite, and estimate their intrinsic free energies of interactions.
1. Introduction
Nonspecific interactions between enzymes involved in nucleic acid metabolism and the nucleic acids play a fundamental role in the transmission of genetic information from one cell generation to another. Both polymerases and helicases are essentially nonspecific nucleic acid-binding enzymes, that is, their interactions with the DNA or RNA have little dependence upon the specific nucleotide sequence (Baker et al., 1987; Enemark and Joshua-Tor, 2008; Heller and Marians, 2007; Hubscher et al., 2000; Joyce and Benkovic, 2004; Lohman and Bjornson, 1996; Morales and Kool, 2000; von Hippel and Delagoutte, 2002, 2003). Specific protein–nucleic acid interactions are predominantly engaged in carrying out a single physiological function, which is precisely defined by a short nucleotide sequence, for example, repressor–operator interactions. On the other hand, nonspecific interactions are primarily involved in metabolic pathways requiring multiple performances of the same reaction often on long stretches of the nucleic acid, regardless of the nucleotide sequence. In this context, recognition of specific nucleic acid conformational states, regardless of the nucleotide sequence of the DNA or RNA, is still a nonspecific protein–nucleic acid interaction. The intricate interactions between polymerases and the single-stranded conformation of the nucleic acids are well recognized, although not completely understood, particularly for different classes of polymerases, engaged in different metabolic pathways. On the other hand, there is still significant gap in our understanding of the corresponding interactions in the case of the helicases.
Helicases are a class of key enzymes that are involved in all major pathways of the DNA and RNA metabolism (Baker et al., 1987; Enemark and Joshua-Tor, 2008; Heller and Marians, 2007; Lohman and Bjornson, 1996; von Hippel and Delagoutte, 2002, 2003). The enzymes are motor proteins, which catalyze the vectorial unwinding of the duplex DNA to provide an active, single-stranded intermediate, which is required, for example, in replication, recombination, translation, and repair processes. The unwinding reaction, as well as the mechanical translocation of the helicase along the nucleic acid lattice, is fueled by NTP hydrolysis (Ali and Lohman, 1997; Baker et al., 1987; Enemark and Joshua-Tor, 2008; Galletto et al., 2004a,b; Heller and Marians, 2007; Jankowsky et al., 2002; Lohman and Bjornson, 1996; Lucius et al., 2002; Nanduri et al., 2002; von Hippel and Delagoutte, 2002, 2003). Helicases may also use the energy of NTP hydrolysis for activities in nucleic acid metabolism, different from duplex nucleic acid unwinding, for example, as molecular pumps (Bujalowski, 2003; Kaplan and O’Donnell, 2002; West, 1996). One of the fundamental elements of the helicase activity is the interaction with the ssDNA conformation of the nucleic acid. In fact, most of the helicases become active NTPases and are capable of free energy transduction only in the complex with the ssDNA or ssRNA (Ali and Lohman, 1997; Baker et al., 1987; Enemark and Joshua-Tor, 2008; Galletto et al., 2004a,b; Heller and Marians, 2007; Jankowsky et al., 2002; Lohman and Bjornson, 1996; Lucius et al., 2002; Nanduri et al., 2002; von Hippel and Delagoutte, 2002, 2003). The allosteric effect of the ssDNA on the NTPase activity of the helicase and the mechanical translocation of the enzyme along the nucleic acid lattice provided first clues, although only intuitive ones, that interactions of the helicase with the ssDNA is far more complex than the simple recognition of a specific conformational state of the DNA or RNA (Amaratunga and Lohman, 1993; Bjorson et al., 1996; Galletto et al., 2004c; Jezewska et al., 1996a, 1998a,b, 2000a,b, 2004; Lucius et al., 2006; Marcinowicz et al., 2007). Rather, they would more closely resemble the DNA or RNA polymerases with the intricate interplay among different areas of the total DNA-binding site of the enzyme with the nucleic acid.
In our discussion, we will first concentrate on the thermodynamic analyses of the Escherichia coli PriA helicase–ssDNA interactions, using spectroscopic approaches aimed at elucidation of the functional relationships in the PriA–ssDNA complex (Galletto et al., 2004c; Jezewska et al., 2000a,b; Lucius et al., 2006). The method is based on the quantitative spectroscopic titration technique to obtain model-independent binding isotherms, which allows the experimenter to address structure–function relationships within the total DNA-binding site of the enzyme (Galletto et al., 2004c; Jezewska et al., 2000a,b; Lucius et al., 2006). We will focus on the essential problem of obtaining thermodynamic parameters free of assumptions about the relationship between the observed signal and the degree of protein or nucleic acid saturation. The analogous approach will be next discussed in the case of the African swine fever virus (ASFV) polymerase X (pol X)–ssDNA complexes. ASFV pol X is engaged in the repair of the viral DNA. It is a small DNA polymerase whose complex interactions with the nucleic acid have been recently addressed. Although, in binding or kinetic studies, one generally monitors some spectroscopic signal (absorbance, fluorescence, fluorescence anisotropy, circular dichroism, NMR line width, or chemical shift), originating from either the protein or the nucleic acid, which changes upon the complex formation, we will discuss the quantitative analyses as applied to the use of fluorescence intensity. Fluorescence is the most widely used spectroscopic technique in energetics and dynamics studies of the protein–nucleic acid interactions in solution and its application will be illustrated in the case of the PriA–ssDNA complex (Bujalowski, 2006; Bujalowski and Jezewska, 2000; Bujalowski and Lohman, 1987; Galletto et al., 2004c; Jezewska and Bujalowski, 1996; Jezewska et al., 2000a,b; Lohman and Bujalowski, 1991; Lucius et al., 2006). Nevertheless, the derived relationships are general and applicable to any physicochemical signal used to monitor the ligand–macromolecule interactions (Bujalowski, 2006; Bujalowski and Jezewska, 2000; Bujalowski and Lohman, 1987; Galletto et al., 2004c; Jezewska and Bujalowski, 1996; Jezewska et al., 2000a,b; Lohman and Bujalowski, 1991; Lucius et al., 2006).
2. Thermodynamic Bases of Quantitative Equilibrium Spectroscopic Titrations
Determination of the binding isotherm is a fundamental first step in examining the energetics of the protein–nucleic acid association, or in general, any ligand–macromolecule interactions (Bujalowski, 2006; Bujalowski and Jezewska, 2000; Bujalowski and Lohman, 1987; Galletto et al., 2004c; Jezewska and Bujalowski, 1996; Jezewska et al., 2000a,b; Lohman and Bujalowski, 1991; Lucius et al., 2006). Equilibrium-binding isotherm represents a direct relationship between the average total degree of binding (moles of ligand molecules bound per mole of a macromolecule) and the free ligand concentration (Bujalowski, 2006; Bujalowski and Jezewska, 2000; Lohman and Bujalowski, 1991). In the case of protein binding to a long, one-dimensional nucleic acid lattice, a more convenient parameter than the total average degree of binding is the total average binding density (moles of ligand bound per mole of bases or base pairs) (Bujalowski, 2006; Bujalowski and Lohman, 1987; Bujalowski et al., 1989; Epstein, 1978; Lohman and Bujalowski, 1991; McGhee and von Hippel, 1974). The equilibrium-binding isotherm represents the direct relationship between the binding density and the free protein concentration (Bujalowski, 2006; Bujalowski and Jezewska, 2000; Bujalowski and Lohman, 1987; Bujalowski et al., 1989; Epstein, 1978; Jezewska and Bujalowski, 1996; Lohman and Bujalowski, 1991; McGhee and von Hippel, 1974). The extraction of physically meaningful interaction parameters that characterize the examined complex is only possible when such a relationship is available and is achieved by comparing the experimental isotherms to theoretical predictions that incorporate known molecular aspects of the examined system (Bujalowski, 2006; Bujalowski and Jezewska, 2000; Bujalowski and Lohman, 1987; Bujalowski et al., 1989; Epstein, 1978; Jezewska and Bujalowski, 1996; Lohman and Bujalowski, 1991; McGhee and von Hippel, 1974).
Fluorescence, or any spectroscopic titration method, is an indirect method of determining the binding isotherm, as the association of the ligand with a macromolecule is examined by monitoring changes in a spectroscopic parameter of the system accompanying the formation of the complex (Bujalowski, 2006; Lohman and Bujalowski, 1991). These changes are then correlated with the concentration of the free and bound ligand or with the fractional saturation of the macromolecule. Nevertheless, the functional relationship between the observed spectroscopic signal and the degree of binding or binding density is never a priori known, with exception of the systems where, at saturation, only a single ligand molecule binds to the macromolecule. But then, one has to establish that only one ligand molecule associates with the macromolecule, in the first place. On the other hand, in much more general cases where multiple ligand molecules can participate in the binding process, the observed fractional change of the spectroscopic signal and the extent of binding may not and, frequently will not, have such a simple linear relationship (Bujalowski, 2006; Bujalowski and Jezewska, 2000; Bujalowski and Lohman, 1987; Jezewska and Bujalowski, 1996; Lohman and Bujalowski, 1991).
Analysis of the binding of a protein to a nucleic acid can be performed using two different types of equilibrium spectroscopic titrations, “normal” or “reverse” titration approach (Bujalowski, 2006; Bujalowski and Jezewska, 2000; Bujalowski and Lohman, 1987; Jezewska and Bujalowski, 1996; Lohman and Bujalowski, 1991). Generally, the type of titration that is performed will depend on whether or not the monitored signal is from the macromolecule (normal) or the ligand (reverse). In the normal titration, a fluorescing macromolecule is titrated with a nonfluorescing ligand and the total average degree of binding, ΣΘi (average number of moles of ligand bound, LB, per mole of the macromolecule, NT), ΣΘi = LB/NT, increases as the titration progresses (Bujalowski, 2006; Bujalowski and Jezewska, 2000; Bujalowski and Lohman, 1987; Jezewska and Bujalowski, 1996; Lohman and Bujalowski, 1991). In the reverse titration approach, the fluorescing ligand is titrated with the nonfluorescing macromolecule and the total average degree of binding decreases throughout the titration (Bujalowski, 2006; Bujalowski and Jezewska, 2000; Bujalowski and Lohman, 1987; Jezewska and Bujalowski, 1996; Lohman and Bujalowski, 1991). In our studies of the PriA helicase binding to the ssDNA, we used the normal titration approach. The interactions have been examined using the fluorescent derivative of the homoadenosine oligomers and the binding was monitored through the changes of the nucleic acid fluorescence (Galletto et al., 2004c; Jezewska et al., 1998b, 2000a,b; Lucius et al., 2006). Thus, in the examined case the nucleic acid is treated as the macromolecule and the PriA helicase is treated as the ligand.
The major task in examining the protein–nucleic acid interactions using a spectroscopic titration method is to convert the titration curve, in our case, the fluorescence titration curve, that is, a change in the monitored fluorescence as a function of the total concentration of the protein, into a model-independent, thermodynamic binding isotherm, which can then be analyzed, using an appropriate binding model to extract binding parameters. The thermodynamic basis of the method is that for the total nucleic acid concentration, NT, the equilibrium distribution of the nucleic acid among its different states with a different number of bound protein molecules, Ni, is determined solely by the free protein concentration, LF (Bujalowski, 2006; Bujalowski and Jezewska, 2000; Bujalowski and Lohman, 1987; Jezewska and Bujalowski, 1996; Lohman and Bujalowski, 1991). Therefore, at each LF, the observed spectroscopic signal, Fobs, is the algebraic sum of the concentrations of the nucleic acid in each state, Ni, weighted by the value of the intensive spectroscopic property of that state, Fi. In general, a nucleic acid will have the ability to bind n protein molecules, hence the model-independent, “signal conservation” equation for the observed signal, Fobs, of a sample containing the ligand at a total concentration, LT, and the nucleic acid at a total concentration, NT, is given by (Bujalowski, 2006; Bujalowski and Jezewska, 2000; Bujalowski and Lohman, 1987; Jezewska and Bujalowski, 1996; Lohman and Bujalowski, 1991):
| (13.1) |
where FF is the molar fluorescence of the free nucleic acid and Fi is the molar fluorescence of the complex, Ni, which represents the nucleic acid with i, bound protein molecules (i = 1 to n). In Eq. (13.1), all bound species of the nucleic acid are grouped according to the number of bound protein molecules. Another mass conservation equation relates NF and Ni to NT by
| (13.2) |
Next, we define the partial degree of binding, Θi (“i” moles of protein bound per mole of nucleic acid), corresponding to all complexes with a given number “i” of bound protein molecules as
| (13.3) |
Therefore, the concentration of the nucleic acid with “i” protein molecules bound, Ni, is defined as
| (13.4) |
Introducing Eqs. (13.3) and (13.4) into Eq. (13.1) provides a general relationship for the observed fluorescence, Fobs, as
| (13.5) |
By rearranging Eq. (13.5), one can define the experimentally accessible quantity, ΔFobs, that is, the fluorescence change normalized with respect to the initial fluorescence intensity of the free nucleic acid, as
| (13.6) |
and
| (13.7) |
The quantity, ΔFobs, is the experimentally determined fractional fluorescence change observed at the selected total protein and nucleic acid concentrations, LT and NT. The quantity, ΔFi/i, is the average molar fluorescence change per bound protein in the complex containing “i” protein molecules. Because ΔFi/i is an intensive molecular property of the protein–nucleic acid complex with “i” protein molecules bound, Eq. (13.7) indicates that ΔFobs is only a function of the free protein concentration through the total average degree of binding, ΣΘi. Therefore, for a given and specific value of ΔFobs, the total average degree of binding, ΣΘi, must be the same for any value of LT and NT (Bujalowski, 2006; Bujalowski and Jezewska, 2000; Bujalowski and Lohman, 1987; Jezewska and Bujalowski, 1996; Lohman and Bujalowski, 1991). Thus, if one performs a fluorescence titration of the nucleic acid with the protein, at different total nucleic acid concentrations, NT, the same value of ΔFobs at different NTs indicates the same physical state of the nucleic acid, that is, the same degree of the nucleic acid saturation with the protein and the same ΣΘi. Since ΣΘi is a unique function of the free protein concentration, LF, then the value of LF, at the same total average degree of binding, must also be the same. Expression (13.7) is rigorous and independent of any binding model (Bujalowski, 2006; Bujalowski and Jezewska, 2000; Bujalowski and Lohman, 1987; Jezewska and Bujalowski, 1996; Lohman and Bujalowski, 1991). An analogous expression can be derived for the case where the spectroscopic signal originates from the ligand and the binding analysis is performed using reverse titration method (Bujalowski and Jezewska, 2000; Bujalowski and Lohman, 1987; Lohman and Bujalowski, 1991).
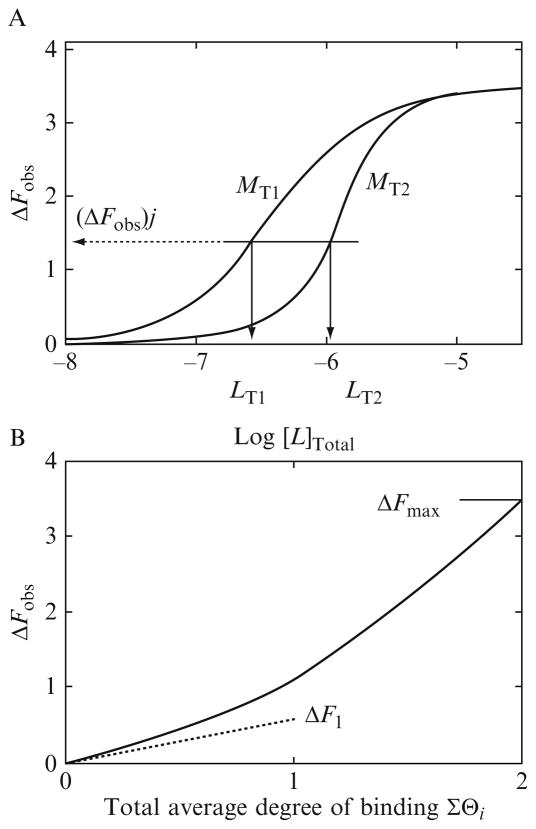
Expression (13.7) indicates a very effective method of transforming the fluorescence titration curve into a thermodynamic binding isotherm (Bujalowski, 2006; Bujalowski and Jezewska, 2000; Bujalowski and Lohman, 1987; Jezewska and Bujalowski, 1996; Lohman and Bujalowski, 1991). In optimal and minimal case, one can perform only two titrations at two different total concentrations of the macromolecule, that is, the nucleic acid, NT1 and NT2. At the same value of ΔFobs, the total average degree of binding, ΣΘi, and the free protein concentrations, LF, must be the same for both titration curves. Two hypothetical fluorescence titration curves are illustrated in Fig. 13.1A for the binding process where two ligand molecules bind to two different discrete binding sites on the macromolecule, characterized by intrinsic binding constants, K1 and K2, and the relative fluorescence changes, ΔF1 and ΔF2, respectively. The values of ΔFobs, as defined by Eq. (13.7), are plotted as a function of the logarithm of the total protein concentration, LT. At a higher nucleic acid concentration, a given relative fluorescence increase, ΔFobs, is reached at higher protein concentrations, as more protein is required to saturate the nucleic acid at its higher concentration. A set of values of (ΣΘi)j and (LF)j for the selected “j” value of (ΔSobs)j is obtained from these data in the following manner. One draws a horizontal line that intersects both titration curves at the same value of (ΔFobs)j (Fig. 13.1A). The point of intersection of the horizontal line with each titration curve defines two values of the total protein concentration, (LT1)j and (LT2)j, for which (LF)j and (ΣΘi)j are the same (Bujalowski, 2006; Bujalowski and Jezewska, 2000; Bujalowski and Lohman, 1987; Jezewska and Bujalowski, 1996; Lohman and Bujalowski, 1991). Then one has two mass conservation equations for the total concentrations of the protein, (LT1)j and (LT2)j, as
Table 13.1.
Macroscopic and intrinsic binding constants characterizing the association of the E. coli PriA helicase with ssDNA oligomers, which binds only one enzyme molecule
| 8-mer |
10-mer |
12-mer |
14-mer |
16-mer |
18-mer |
20-mer |
22-mer |
24-mer |
|
|---|---|---|---|---|---|---|---|---|---|
| dεA(pεA)7 | dεA(pεA)9 | dεA(pεA)11 | dεA(pεA)13 | dεA(pεA)15 | dεA(pεA)17 | dεA(pεA)19 | dεA(pεA)21 | dεA(pεA)23 | |
| KN (M−1) | (8.5 ± 03) × 104 | (1.7 ± 03) × 105 | (2.4 ± 03) × 105 | (3.6 ± 0.4) × 105 | (3.9 ± 0.5) × 105 | (4 ± 0.5) × 105 | (5.6 ± 0.6) × 105 | (6.4 ± 03) × 105 | (7.5 ± 03) × 105 |
| Kp (M−1) | (43 ± 0.3) × 104 | (4.3 ± 0.4) × 104 | (4.0 ± 0.4) × 104 | (4.5 ± 0.4) × 104 | (3.9 ± 0.3) × 104 | (33 ± 03) × 104 | (4.0 ± 0.5) × 104 | (4.0 ± 0.4) × 104 | (4.2 ± 0.5) × 104 |
Figure 13.1.
(A) Theoretical fluorescence titrations of a macromolecule with a ligand, obtained at two different macromolecule concentrations: (■) M1 = 1 × 10−7 M; (□) M2 = 8 × 10−7 M, respectively. The macromolecule has two discrete and different binding sites characterized by the intrinsic binding constants, K1 = 3 × 107 M−1 and K2 = 3 × 06 M−1. The partition of the system, ZD, is then ZD = 1 + K1LF + K2LF + K1K2LF2. The binding to the first ligand induces the relative change of the macromolecule fluorescence, ΔF1 = 0.5, while the relative fluorescence change accompanying binding of the second ligand is ΔF2 = 3. The arrows indicate the total ligand concentrations, LT1 and LT2, at the same selected value of the observed fluorescence change, marked by the dashed horizontal line, ΔFobs, at which the total average degree of binding of the ligand, ΣΘi, is the same at both titration curves. (B) Dependence of the relative fluorescence of the macromolecule, ΔFobs, upon the total average degree of binding, ΣΘi, of the ligand molecules. The short dashed line is an extrapolation of the initial slope of the plot, which indicates the value of ΔF1 = 0.5, characterizing the relative fluorescence change upon binding the first ligand molecules.
| (13.8a) |
and
| (13.8b) |
from which one obtains that at a given (ΔFobs)j the total average degree of binding and the free protein concentration are
| (13.9) |
and
| (13.10) |
where subscript x is 1 or 2 (Bujalowski, 2006; Bujalowski and Jezewska, 2000; Bujalowski and Lohman, 1987; Jezewska and Bujalowski, 1996; Lohman and Bujalowski, 1991). Performing a similar analysis along the titration curves at a selected interval of the observed signal change, one obtains model-independent values of (LF)j and (ΣΘi)j at any selected “j” value of (ΔSobs)j. Practically, the most accurate estimates of (LF)j and (ΣΘi)j are obtained in the region of the titration curves where the concentration of a bound protein is comparable to its total concentration, LT. In our practice, this limits the accurate determination of the total average degree of binding and LF to the region of the titration curves where the concentration of the bound ligand is at least ~10–15% of the LT. Selection of suitable concentrations of the nucleic acid is of paramount importance for obtaining (LF)j and (ΣΘi)j over the largest possible region of the titration curves. The selection of the nucleic acid (macromolecule) concentrations is based on preliminary titrations that provide initial estimates of the expected affinity. Nevertheless, the accuracy of the determination of (ΣΘi)j is mostly affected in the region of the high concentrations of the ligand, that is, where the binding process approaches the maximum saturation.
Usually, the maximum of the recorded fluorescence changes, that is, the saturation of the observed binding process, is attainable with adequate accuracy. What is mostly unknown is the maximum stoichiometry of the complex at saturation, as in the case of the PriA helicase (Jezewska et al., 2000a,b; Lucius et al., 2006). Another unknown is the relationship between the fluorescence change, ΔFobs, and the total average degree of binding (Bujalowski, 2006; Bujalowski and Jezewska, 2000; Bujalowski and Lohman, 1987; Jezewska and Bujalowski, 1996; Jezewska et al., 2000a; Lohman and Bujalowski, 1991; Lucius et al., 2006). Both unknowns can be determined by plotting ΔFobs as a function of ΣΘi, as depicted in Fig. 13.1B, for the hypothetical binding model where two ligand molecules associate with two different, discrete sites on the macromolecule. The relative fluorescence change, accompanying the binding of the first high-affinity ligand, ΔF1 = 0.5, is lower than ΔF2 = 3, characterizing the binding of the second low-affinity ligand. As a result, the plot is clearly nonlinear. As mentioned above, in practice, the maximum value of ΣΘi cannot be directly determined, due to the inaccuracy at the high ligand concentration region. However, knowing the maximum increase of the nucleic acid fluorescence ΔFmax, one can perform a short extrapolation of the plot (ΔFobs versus ΣΘi) to this maximum value of the observed fluorescence change, which establishes the maximum stoichiometry of the formed complex at saturation (Bujalowski, 2006; Bujalowski and Jezewska, 2000; Bujalowski and Lohman, 1987; Jezewska and Bujalowski, 1996; Lohman and Bujalowski, 1991). Moreover, often the initial of the plot ΔFobs versus ΣΘi can provide information on the value of the relative fluorescence change, ΔF1, accompanying the association of the first ligand molecule. Such an estimate of ΔF1 is illustrated in Fig. 13.1B.
3. Anatomy of the Total DNA-Binding Site in the PriA Helicase–ssDNA Complex
3.1. The site-size of the ssDNA-binding site proper of the PriA–ssDNA complex
The E. coli primosome is a multiprotein complex that catalyzes the DNA priming during the replication process (Jones and Nakai, 1999, 2001; Lee and Marians, 1987; Marians, 1999; Nurse et al., 1990; Sangler and Marians, 2000). The PriA helicase is a key DNA replication enzyme in the E. coli cell that plays a fundamental role in the ordered assembly of the primosome (Jones and Nakai, 1999, 2001; Lee and Marians, 1987; Marians, 1999; Nurse et al., 1990; Sangler and Marians, 2000). Originally, the PriA helicase was discovered as an essential factor during the synthesis of the complementary DNA strand of phage ΦX174 DNA (Lee and Marians, 1987). Current data indicate that the enzyme is involved not only in DNA replication but also in recombination and repair processes in the E. coli (Jones and Nakai, 1999, 2001). The native protein is a monomer with a molecular weight of 81.7 kDa and the monomer is the predominant form of the protein in solution (Galletto et al., 2004c; Jezewska et al., 1998b, 2000a, b; Jones and Nakai, 1999, 2001; Lee and Marians, 1987; Lucius et al., 2006; Marians, 1999; Nurse et al., 1990; Sangler and Marians, 2000).
The total site-size of a large protein ligand–DNA complex corresponds to the DNA fragment occluded by the protein, which includes nucleotides directly involved in interactions with the protein, its DNA-binding site proper and, in general, nucleotides that may not be engaged in direct interactions, or may interact differently with the protein matrix (Bujalowski, 2006; Bujalowski and Jezewska, 2000; Bujalowski and Lohman, 1987; Bujalowski et al., 1989; Epstein, 1978; Jezewska and Bujalowski, 1996; Lohman and Bujalowski, 1991; McGhee and von Hippel, 1974). The latter are prevented from interacting with another protein molecule by the protruding protein matrix of the previously bound protein molecule over nucleotides adjacent to the DNA-binding site proper. Binding of the monomeric E. coli PriA helicase to the ssDNA provides an example of such a complex structure of the total ssDNA-binding site of the protein interacting with the nucleic acid (Galletto et al., 2004c; Jezewska et al., 1998b, 2000a,b; Lucius et al., 2006). The most straightforward way of determining the total site-size of the ssDNA-binding site of a protein associating with the nucleic acid is to examine directly the protein binding to the homogeneous analog of the nucleic acid (Bujalowski, 2006; Bujalowski and Jezewska, 2000; Bujalowski and Lohman, 1987; Bujalowski et al., 1989; Epstein, 1978; Jezewska and Bujalowski, 1996; Lohman and Bujalowski, 1991; McGhee and von Hippel, 1974). However, such an approach, although it does provide an accurate estimate of the site-size of the total DNA-binding site, does not provide any information about the structural and functional complexity of the total DNA-binding site itself. Another experimental strategy is to use a large series of ssDNA oligomers of well-defined length. This approach dramatically increases the resolution of the binding experiments and allows the experimenter to determine not only the total site-size of the protein–ssDNA complex, n, but also the number of nucleotides directly engaged in interactions with the protein, m, that is, the site-size of the DNA-binding site proper. Only when these two parameters are known, the correct statistical thermodynamic model may be formulated and the intrinsic binding parameters extracted (Bujalowski, 2006; Bujalowski and Jezewska, 2000; Bujalowski and Lohman, 1987; Jezewska and Bujalowski, 1996; Lohman and Bujalowski, 1991).
The fluorescent etheno-derivatives of homo-adenosine DNA polymer or oligomers seem to be one of the most suitable fluorescent analogs in quantitative examinations of the protein–DNA interactions (Baker et al., 1978; Ledneva et al., 1978; Tolman et al., 1974). Binding of proteins to etheno-analogs is usually accompanied by a strong increase of the nucleic acid fluorescence (Chabbert et al., 1987; Jezewska et al., 1996b,c, 1998d, 2000a,b, 2001a,b, 2003; Lucius et al., 2006; Menetski and Kowalczykowski, 1985; Rajendran et al., 1998, 2001). The applied excitation and emission wavelengths, λex = 325 nm and λem = 410 nm, predominantly lead to the excitation of only the etheno-adenosine and observation of the nucleic acid fluorescence, without the excessive correction for the residual protein fluorescence. Thus the observed fluorescence change results exclusively from an increase of the quantum yield of the nucleic acid in the complex with the protein. The fluorescence change is usually very large (100–400%), greatly increasing the accuracy of the binding experiment. Moreover, fluorescence emission of etheno-analogs also allows the experimenter to access the nucleic structure in the complex. This is because the emission of etheno-adenosine, εA, has little dependence upon the nature of the environment but dramatically quenched (8–12-fold) in etheno-oligomers and poly(εA), as compared to free εAMP (Baker et al., 1978; Jones and Nakai, 1999, 2001; Ledneva et al., 1978; Lee and Marians, 1987; Nurse et al., 1990; Tolman et al., 1974). Stacking interactions between neighboring εA bases is similar to stacking interactions in unmodified adenosine polymers or oligomers (Baker et al., 1978). A dynamic model, in which the motion of εA leads to quenching via intramolecular collisions, has been proposed as a predominant mechanism of the observed strong quenching (Baker et al., 1978). Thus, increased viscosity of the solvent or immobilization and separation of the bases in the binding site partially eliminates the fluorescence quenching.
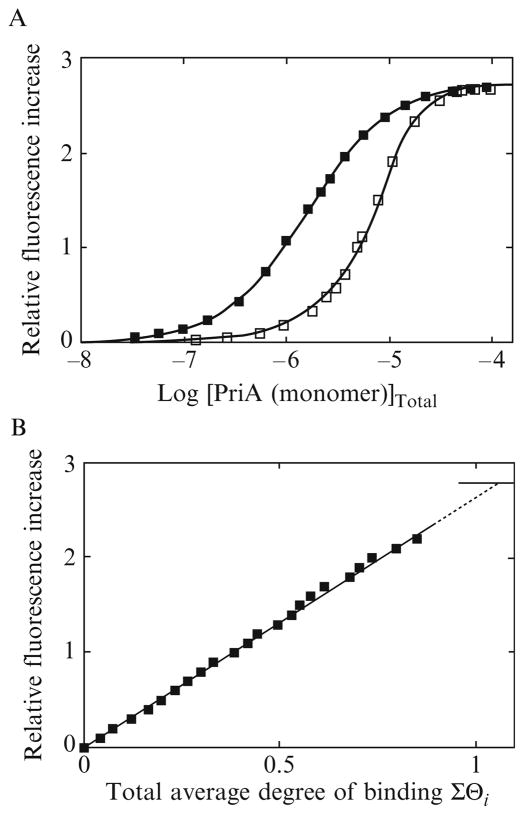
An example of fluorescence titrations of the ssDNA 24-mer, dεA(pεA)23, with the PriA helicase at two different nucleic acid concentrations, in 10 mM sodium cacodylate/HCl (pH 7.0, 10 °C), containing 100 mM NaCl, 0.1 mM EDTA, 1 mM DTT, and 25% glycerol (buffer C), is shown in Fig. 13.2A. Binding of the protein to the oligomer induces a large ~280% increase of the nucleic acid fluorescence. The selected DNA concentrations provide a significant separation of the titration curves, up to the relative fluorescence increase, ΔFobs ~2.3. The shift of the titration curve at a higher oligomer concentration results from the fact that more protein is required to obtain the same total average degree of binding, ΣΘi (Fig. 13.1A). The fluorescence titration curves in Fig. 13.2A have been analyzed, using the quantitative approach outlined above. A typical dependence of the observed relative fluorescence increase of the ssDNA 24-mer, ΔFobs, as a function of the total average degree of binding, ΣΘi, of the PriA helicase is shown in Fig. 13.2B. The values of ΣΘi could reliably be determined up to ΔFobs ~2.3. Short extrapolation to the maximum fluorescence change, ΔFmax = 2.8 ± 0.2 shows that only one molecule of the PriA helicase binds to the ssDNA 24-mer.
Figure 13.2.
(A) Fluorescence titrations of the 24-mer, dεA(pεA)23, with the PriA protein (λex = 325 nm, λem = 410 nm) in buffer C (10 mM sodium cacodylate adjusted to pH 7.0 with HCl, 0.1 mM EDTA, 1 mM DTT, 25% glycerol, 10 °C), containing 100 mM NaCl, at two different nucleic acid concentrations: (■) 4.7 × 10−7 M; (□) 1.2 × 10−5 M (oligomer). The solid lines are nonlinear least-squares fits of the titration curves, using a single-site binding isotherm (Eq. 13.11) with the macroscopic binding constant K24 = 7.5 × 105 M−1 and the relative fluorescence change ΔFmax = 2.8. (B) Dependence of the relative fluorescence of the 24-mer, ΔFobs, upon the total average degree of binding of the PriA protein, ΣΘi (■). The solid line follows the experimental points and has no theoretical basis. The dashed line is the extrapolation of ΔFobs to the maximum value of ΔFmax = 2.8.
The maximum stoichiometry of the enzyme–ssDNA oligomer is different in the case of the 30-mer, dεA(pεA)29, although this oligomer is only 6 nucleotides longer than the 24-mer. An example of fluorescence titrations of dεA(pεA)29 with the PriA helicase at two different nucleic acid concentrations is shown in Fig. 13.3A. Separation of the titration curves allowed us to determine the total average degree of binding, ΣΘi, up to ~1.8 at the value of ΔFobs ~1.8. The dependence of ΔFobs, as a function of the total average degree of binding of the PriA helicase on the 30-mer, is shown in Fig. 13.3B. The plot is also linear. Extrapolation to the maximum fluorescence increase ΔFmax = 2.5 ± 0.2 provides ΣΘi = 2.3 ± 0.2. Thus, the presence of an extra 6 nucleotides in the 30-mer, as compared to the 24-mer, provides enough interaction space for the binding of the second PriA protein molecule.
Figure 13.3.
(A) Fluorescence titrations of the 30-mer, dεA(pεA)29, with the PriA protein (λex = 325 nm, λem = 410 nm) in buffer C (pH 7.0, 10 °C), containing 100 mM NaCl, at two different nucleic acid concentrations: (■) 4.7 × 10−7 M; (□) 2.1 × 10−6 M. The solid lines are nonlinear least-squares fits of the titration curves, using the statistical thermodynamic model for the binding of two PriA molecules to the 30-mer, described by Eqs. (13.14)–(13.17). The intrinsic binding constant Kp = 1.3 × 105 M−1, cooperativity parameter ω = 11, and relative fluorescence change ΔF1 = 1.25, and ΔFmax = 2.5. (B) Dependence of the relative fluorescence of the 30-mer, ΔFobs, upon the total average degree of binding of the PriA protein, ΣΘi (■). The solid line follows the experimental points and has no theoretical basis. The dashed line is the extrapolation of ΔFobs to the maximum value of ΔFmax = 2.5.
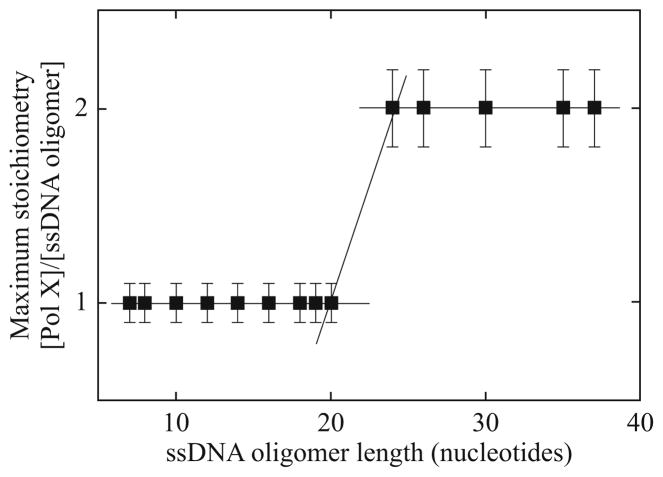
Analogous quantitative analysis of the maximum stoichiometry of the PriA–ssDNA complexes has been performed for a series of ssDNA oligomers. Recall, the discussed method of determining the maximum stoichiometry does not depend upon any binding model. The dependence of the maximum number of bound PriA molecules per selected ssDNA oligomer is shown in Fig. 13.4. Oligomers from 8 to 26 nucleotide residues bind a single PriA molecule. On the other hand, transition from a single enzyme bound per ssDNA oligomer to two bound protein molecules occurs between 26- and 30-mers (Fig. 13.4). Further, an increase in the length of the oligomer, up to 40 nucleotides, does not lead to an increased number of bound PriA molecules per ssDNA oligomer. These data provide the first indication that the total site-size of the PriA–ssDNA complex is definitely less than 24 nucleotides, but that it must contain at least 14–15 nucleotides per bound protein molecule to be compatible with the observed maximum stoichiometries of the examined complexes.
Figure 13.4.
The maximum number of bound PriA molecules, as a function of the length of the ssDNA oligomer in buffer C (pH, 10 °C), containing 100 mM NaCl. The solid lines follow the experimental points and have no theoretical bases.
3.2. Macroscopic affinities of PriA–ssDNA complexes containing a single PriA protein molecule bound
The next step in the analysis comprises examination of macroscopic affinities of the PriA helicase for different ssDNA oligomers. The striking feature of the data in Figs. 13.2–13.4 is that only a single PriA molecule binds to ssDNA oligomers of very different length. Thus, both 8- and 26-mer bind only a single enzyme molecule, yet the length of the 26-mer is more than three times longer than the length of the 8-mer. These data already indicate that only a part of the protein total DNA-binding site is engaged in direct interactions with the DNA, that is, the enzyme must possess an ssDNA-binding site proper within the total site, which predominantly interacts with the nucleic acid. However, the decisive evidence for the presence of the ssDNA-binding site proper comes from the determination of the macroscopic binding constant for enzyme binding to the ssDNA oligomers, which can accommodate only one protein molecule, as a function of the length of the nucleic acid (Galletto et al., 2004c; Jezewska et al., 2000a,b). Moreover, this analysis also allows us to determine the site-size of the ssDNA-binding site proper.
Binding of a single PriA molecule to 8-, 10-, 12-, 14-, 16-, 18-, 20-, 22-, 24-, and 26-mers can be analyzed using a single-site-binding isotherm described by
| (13.11) |
where KN is the macroscopic binding constant characterizing the affinity for a given ssDNA oligomer containing N nucleotides, and ΔFmax is the maximum relative fluorescence increase. The solid lines in Figs. 13.2A and 13.3A are nonlinear least-squares fits of the experimental titration curves, using Eq. (13.11). The values of KN and ΔFmax for the studied ssDNA oligomers are included in Table 13.1. The value of KN increases as the length of the ssDNA oligomers increase. The simplest explanation of this result is that the values of KN contain a statistical factor resulting from the fact that the number of nucleotides engaged in interactions with the ssDNA-binding site proper of the protein is lower than the length of the ssDNA oligomers. In other words, the enzyme engages a small number of the nucleotides in direct interactions, characterized by the intrinsic binding constant, Kp, while the macroscopic binding constant, KN, reflects the presence of extra potential binding sites on the ssDNA oligomers (Galletto et al., 2004c; Jezewska et al., 2000a,b). In terms of potential binding sites and the intrinsic binding constant, Kp, characterizing the interactions with the ssDNA-binding site proper, the macroscopic binding constant, KN, for the PriA helicase binding to the ssDNA oligomer containing N nucleotides, is analytically defined as (Bujalowski, 2006; Bujalowski and Jezewska, 2000; Bujalowski and Lohman, 1987; Galletto et al., 2004c; Jezewska and Bujalowski, 1996; Jezewska et al., 2000a; Lohman and Bujalowski, 1991):
| (13.12a) |
and
| (13.12b) |
Thus, the plot of KN as a function of N should be linear with respect to N. This is clearly evident in Fig. 13.5, which shows the overall equilibrium constant, KN, for PriA binding to ssDNA oligomers with a different number of nucleotides, as a function of the length of the ssDNA oligomer. Within experimental accuracy, the plot is linear. Moreover, the plot extrapolates to a zero value of the macroscopic binding constant, while intercepting the DNA length axis at a specific length. Such behavior of KN as a function of the length of ssDNA oligomers provides strong experimental evidence of the presence of the ssDNA-binding proper within the total site of the helicase, which explores several potential binding sites on the ssDNA oligomers (Galletto et al., 2004c; Jezewska et al., 2000a,b). The plot intercepts the nucleic acid length axis at N = m − 1 (Eq. (13.12b)). Extrapolation of the plot in Fig. 13.5 to KN = 0 provides the site-size of the ssDNA-binding site proper of the PriA helicase, m = 7.1 ± 1 (Jezewska et al., 2000a). This value is, within experimental accuracy, the same as the more conservative value of 8 ± 1, which we have estimated before (Jezewska et al., 2000a). The slight difference does not affect any structure–function conclusions of the previous studies and results discussed in this work. Additional crucial information, which often escapes in such analyses, is that the obtained data on the binding of different oligomers to the enzyme clearly show that the protein possesses only one ssDNA-binding site proper, in spite of the fact that the total site-size is at least 15 nucleotides in length. If there was more than one ssDNA-binding site proper on the enzyme, then the PriA helicase would bind two 8-mer molecules, which is not experimentally observed.
Figure 13.5.
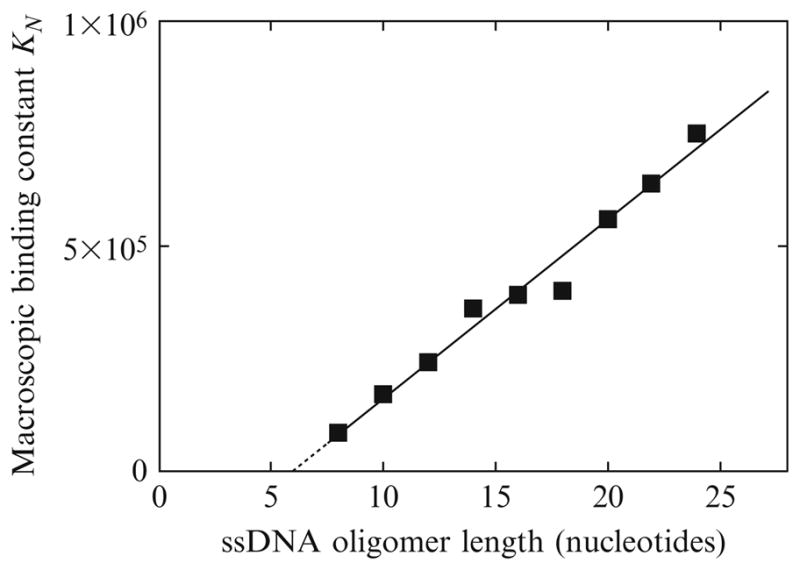
The dependence of the macroscopic binding constant, KN, for the PriA helicase binding to the etheno-derivatives of the ssDNA oligomers upon the length of the oligomer (nucleotides). The solid line is the linear least-squares fit of the plot to Eq. (13.12b). The dashed line is an extrapolation of the plot to the value of KN = 0. The plot intersects the DNA length axis at the value, m − 1 (details in text).
3.3. The site-size of the total DNA-binding site of the PriA helicase
3.3.1. Model of PriA protein–ssDNA interactions
As discussed above, the transition from a single PriA molecule bound per ssDNA oligomer to two molecules bound per the oligomer occurs between 26- and 30-mers, indicating that the minimum, total site-size of the PriA–ssDNA complex is at least 14–15 nucleotides per bound protein (Fig. 13.4). On the other hand, binding studies with oligomers, which can accommodate only one enzyme molecule, indicate that the protein engages only 7.1 ± 1 nucleotides in interactions with its ssDNA-binding site proper (see above). These results indicate that a significant part of the total site-size of the PriA helicase (at least ~7–8 nucleotides) results from the protruding of the large protein molecule over the nucleotides adjacent to the ssDNA-binding site proper.
Inspection of the data on the binding of the PriA helicase to the ssDNA oligomers of different lengths allows the experimenter to deduce the site-size of the total DNA-binding site of the enzyme, as well as the location of the ssDNA-binding site proper within the global structure of the protein matrix, using two, limiting binding models (Galletto et al., 2004c; Jezewska et al., 2000a,b). The first model of the structure of the total DNA-binding site of the PriA helicase is depicted in Fig. 13.6. The ssDNA-binding site proper, which encompasses ~7 nucleotides, is located on one side of the protein molecule (Fig. 13.6A). We are still assuming that the total DNA-binding site size is 14–15 nucleotides, that is, the protein matrix protrudes over 7–8 nucleotides outside of the ssDNA-binding site proper. However, if the ssDNA-binding site of the protein is located on one side of the molecule, with a part of the enzyme protruding over the extra 7–8 nucleotides, then the 24-, 26-, and 40-mers would be able to accommodate two and three PriA molecules, respectively (Fig. 13.6B). These are not experimentally observed maximum stoichiometries (Fig. 13.4). Only one PriA molecule binds to the 24- and 26-mers, and only two enzyme molecules bind to the 40-mer (Fig. 13.4). Therefore, the model shown in Fig. 13.6 cannot represent the PriA–ssDNA complex.
Figure 13.6.
Schematic model for the binding of the PriA helicase to the ssDNA, based on the minimum site-size of the protein–nucleic acid complex, n = 15, and the size of the binding site engaged in protein ssDNA interactions, m = 7. The helicase binds the ssDNA in a single orientation with respect to the polarity of the sugar-phosphate backbone of the ssDNA. The ssDNA-binding site proper, which encompasses 7–8 nucleotides, is located on one side of the enzyme molecule, with the rest of the protein matrix protruding over the extra 7–8 nucleotides, without engaging in thermodynamically significant interactions with the DNA (black ribbon) (A). When bound at the ends of the nucleic acid, or in its center, the protein can occlude 7 or 15 nucleotides (B). Therefore, this model would allow the binding of two molecules of the PriA helicase to the ssDNA 24-mer and three molecules of the enzyme to the 40-mer (C). However, this is not experimentally observed.
The second model where the ssDNA-binding site proper, which engages 7–8 nucleotides, is located in the central part of the protein and is depicted in Fig. 13.7. The protein molecule now has two parts that are protruding over 7–8 nucleotide residues on both sides of the ssDNA-binding site proper. In this model, only one PriA molecule can bind to the 24- and 26-mers (Fig. 13.7A). This is because the first bound molecule can now block at least 14–15 nucleotides. For efficient binding, the second protein molecule also needs a fragment of at least 14 nucleotides, which is larger than the remaining 11 and 12 residues of the 24- and 26-mers, respectively. On the other hand, such a location of the ssDNA-binding site proper allows two molecules of the enzyme to bind to the 30-, 33-, 35-, 37-, and 40-mers (Fig. 13.7B). In the case of the 40-mer, the remaining fragment of 4–5 nucleotides is too short, that is, it does not provide efficient interacting space to allow the third PriA protein to associate with the oligomer. This is exactly what is experimentally observed (Fig. 13.4). Therefore, the model of the protein–ssDNA, presented in Fig. 13.7, adequately describes all experimentally determined stoichiometries of the PriA with the series of ssDNA oligomers (Fig. 13.4). Moreover, these data and analyses indicate that the actual total site-size of the PriA–ssDNA complex is 20 ± 3 nucleotide residues and include the 7.1 ± 1 nucleotides encompassed by the ssDNA-binding site of the enzyme, as well as the 14–16 nucleotides occluded by the protruding protein matrix (Fig. 13.7B).
Figure 13.7.
Schematic model for the binding of the PriA helicase to the ssDNA, based on the total site-size of the protein–nucleic acid complex, n = 20, and the size of the ssDNA-binding site engaged in protein–ssDNA interactions, m = 7. The helicase binds the ssDNA in a single orientation with respect to the polarity of the sugar-phosphate backbone of the ssDNA. The ssDNA-binding site of the PriA helicase, which encompasses only 7–8 nucleotides, is located in the center of the enzyme molecule. The protein matrix protrudes over 7–8 nucleotides on both sides of the ssDNA-binding site without engaging in interactions with the nucleic acid (black ribbon). When bound at the 5′ or the 3′ end of the nucleic acid, the protein always occludes 14–15 nucleotides, while in the complex in the center of the ssDNA oligomer, 20–23 nucleotides are occluded (A). This model would allow the binding of only one molecule of the PriA helicase to the 24-mer and only two molecules of the enzyme to the 30-, 33-, 35-, 37-, and 40-mers (B). Such maximum stoichiometries are in complete agreement with the experimental data.
3.3.2. Intrinsic affinities of PriA–ssDNA interactions
Examination of the intrinsic affinities of the PriA helicase for different ssDNA oligomers, that is, the affinity of the ssDNA-binding site proper characterized by the binding constant, Kp, provides additional support for the proposed model of the PriA–ssDNA complex (Galletto et al., 2004c; Jezewska et al., 2000a,b; Lucius et al., 2006). The macroscopic binding constant, KN, for the binding of a single PriA molecule to 8- 10-, 12-, 14-, 16-, 18-, 20-, 22-, 24-, and 26-mers is defined in terms of m and Kp by Eq. (13.12a). Using the lattice model for the nucleic acid and taking integer value of m ≈ 7, one can recalculate the values of Kp, which are included in Table 13.1 (Galletto et al., 2004c; Jezewska et al., 2000a,b). As expected (Fig. 13.5), the values of Kp are very similar for all examined oligomers, indicating that very similar interactions are present in all examined complexes. However, if the model in Fig. 13.7B is correct, then the intrinsic affinity of the PriA helicase in the complexes with the ssDNA oligomers, which can accommodate two enzyme molecules, should also be similar to the value determined for the oligomers, which accommodate only a single protein molecule.
Quantitative determination of the value of Kp for the PriA helicase to the ssDNA 30-, 33-, 35-, 37-, and 40-mers, which can accommodate two enzyme molecules, requires a more complex statistical thermodynamic approach. In general, the binding process includes intrinsic affinity of the ssDNA-binding site proper, possible cooperative interactions between bound protein molecules, and the overlap between potential binding sites on the nucleic acid lattice (Bujalowski, 2006; Bujalowski and Jezewska, 2000; Bujalowski and Lohman, 1987; Galletto et al., 2004c; Jezewska and Bujalowski, 1996; Jezewska et al., 2000a,b; Lohman and Bujalowski, 1991). We know that the total site-size of the PriA–ssDNA complex is n = 20 ± 3. However, the number of nucleotides engaged in interactions with the ssDNA-binding site proper of the enzyme is only m = 7.1 ± 1, and that the protein protrudes over a distance of 7–8 nucleotides on both sides of the binding site proper (Fig. 13.7B). Therefore, the partial degree of binding that involves only the first PriA molecule bound to the ssDNA 30-, 35-, and 40-mers, is described by
| (13.13) |
where N = 30, 33, 35, 37, or 40, m = 7, and Kp is the intrinsic binding constant for the given N-mer. The factor, N + m + 1, indicates that the first single PriA molecule experiences the presence of a multitude of potential binding sites on each examined N-mer. However, as the protein concentration increases, this complex is replaced by the complex, in which two PriA molecules are bound to the oligomer and there are several different possible configurations of the two proteins on each N-mer (Fig. 13.7B). In order to derive the part of the partition function corresponding to the binding of two PriA molecules, we apply an exact combinatorial theory for the cooperative binding of a large ligand to a finite one-dimensional lattice (Epstein, 1978; Jezewska et al., 2000b). The complete partition function for the PriA–N-mer system, ZN, is then
| (13.14) |
where k = 2 and j is the number of cooperative contacts between the bound PriA molecules in a particular configuration on the lattice, and ω is the parameter characterizing the cooperative interactions. The factor SN(k, j) is the number of distinct ways that two protein ligands bind to a lattice with j cooperative contacts and is defined by (Jezewska et al., 2000a)
| (13.15) |
The factor, m + 7, arises from the fact that, with two protein molecules bound, each bound protein occludes the nucleic acid with its ssDNA-binding site proper (m nucleotides) and the protruding protein matrix on one side of the protein (in the considered case, 7 nucleotides). The total average degree of binding, ΣΘi, is defined as
| (13.16) |
The observed relative fluorescence increase of the nucleic acid, ΔFobs, is then
| (13.17) |
where ΔF1 and ΔFmax are relative molar fluorescence parameters that characterize the complexes with one and two PriA molecules bound to the N-mer, respectively.
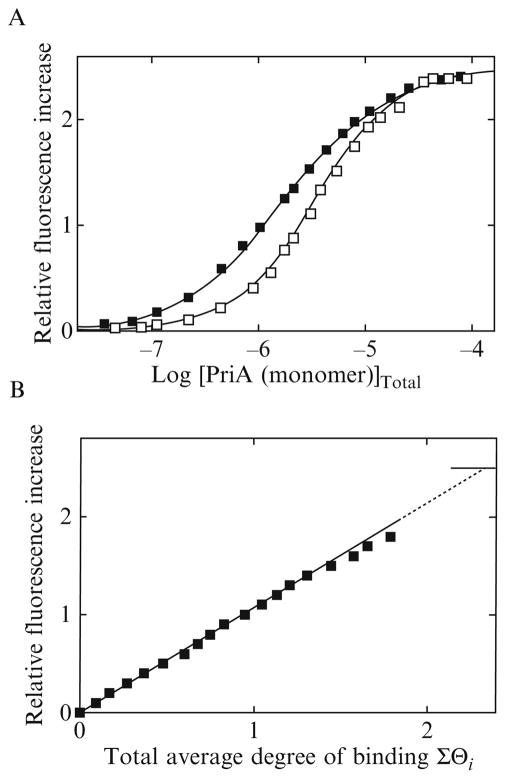
An example of fluorescence titrations of the 40-mer dA(pεA)39 with the PriA helicase at two different nucleic acid concentrations is shown in Fig. 13.8A. Separation of the titration curves allowed us to determine the total average degree of binding, ΣΘi, up to ~1.5 at the value of ΔFobs ~2.4. The dependence of ΔFobs, as a function of the total average degree of binding of the PriA helicase on the 40-mer, is shown in Fig. 13.8B. The plot is linear and extrapolation to the maximum fluorescence increase ΔFmax = 3.5 ± 0.2 provides ΣΘi = 2.0 ± 0.2. Also, using the plot in Fig. 13.8B, one can estimate the values of ΔF1 = 1.7 ± 0.05. Therefore, there are only two unknown parameters, Kp and ω, in Eqs. (13.14)–(13.17). The solid lines in Fig. 13.8A are nonlinear least-squares fits using Eqs. (13.14)–(13.17) with only two fitted parameters Kp and ω. The obtained values are Kp = (5.6 ± 0.3) × 104 M−1 and ω = 0.8 ± 0.3. Analogously, the solid lines in Fig. 13.3A are nonlinear least-squares fits using Eqs. (13.14)–(13.17) for the PriA binding to the 30-mer, dεA(pεA)29, with only two fitted parameters, Kp and ω, which provides Kp = (1.3 ± 0.3) × 105 M−1 and ω = 11 ± 3. The same analysis for the 35-mer, dεA(pεA)29, provides Kp = (1.3 ± 0.3) × 105 M−1 and ω = 2 ± 0.6 (Jezewska et al., 2000a).
Figure 13.8.
(A) Fluorescence titrations of the 40-mer, dεA(pεA)39, with the PriA protein (λex = 325 nm, λem = 410 nm) in buffer C (pH 7.0, 10 °C), containing 100 mM NaCl, at two different nucleic acid concentrations: (■) 4.6 × 10−7 M; (□) 4 × 10−6 M. The solid lines are nonlinear least-squares fits of the titration curves, using the statistical thermodynamic model for the binding of two PriA molecules to the 40-mer, described by Eqs. (13.14)–(13.17). The intrinsic binding constant Kp = 5.6 × 104 M−1, cooperativity parameter ω = 0.8, and relative fluorescence change ΔF1 = 1.7, and ΔFmax = 3.5, respectively. (B) Dependence of the relative fluorescence of the 40-mer, ΔFobs, upon the total average degree of binding of the PriA proteins, ΣΘi (■). The solid line follows the experimental points and has no theoretical basis. The dashed line is the extrapolation of ΔFobs to the maximum value of ΔFmax = 3.5.
The values of the intrinsic binding constant, Kp, for all examined oligomers fall between ~3.3 × 104 M−1 and 1.3 × 105 M−1. Such similar values of Kp, obtained with the ssDNA oligomers of different lengths, indicate similar types of intrinsic interactions between the PriA protein and the nucleic acid in the studied complexes, corroborating the proposed model of the PriA protein–ssDNA complex, which takes into account the total site-size of the protein–nucleic acid complex, n, the number of the nucleotide residues engaged in interactions with the ssDNA-binding site, m, and the central location of the ssDNA-binding site within the protein matrix. Moreover, the obtained value of ω ranging between 11 ± 3 and 0.8 ± 0.3 also indicates that the binding of the PriA helicase to the ssDNA is not accompanied by any significant cooperative interactions.
3.3.3. Binding modes in PriA–ssDNA interactions
It should be pointed out that the binding of the PriA protein to the ssDNA constitutes an example, albeit a very specific one, of a protein binding to the nucleic acid in two binding modes, differing by the number of the occluded nucleotides in the complex (Bujalowski and Lohman, 1986; Chabbert et al., 1987; Jezewska et al., 1998b, 2003b, 2006; Lohman and Ferrari, 1994; Menetski and Kowalczykowski, 1985; Rajendran et al., 1998, 2001). In one mode, the PriA protein forms a complex with the site size of 20± 3, that is, the total ssDNA-binding site is occluding the nucleic acid lattice and in the other binding mode, the protein can associate with the DNA using only its ssDNA-binding site proper, with the site size of ~7 nucleotides, with an additional ~7–8 nucleotides occluded by the protruding protein matrix (Fig. 13.7B). However, on the polymer ssDNA lattices only a single binding mode with the site size of 20 ± 3 nucleotides would be detectable, as in the predominant fraction of the bound protein molecules the PriA helicase occludes 20 ± 3 nucleotides. In other words, the detection of the PriA binding modes was only possible through the experimental strategy of examining the stoichiometry of the protein–ssDNA complex using an extensive series of ssDNA oligomers (Bujalowski and Lohman, 1986; Galletto et al., 2004c; Jezewska et al., 2000a,b, 2004; Lohman and Ferrari, 1994; Lucius et al., 2006).
4. Structure–Function Relationship in the Total ssDNA-Binding Site of the DNA Repair Pol X From ASFV
4.1. Model of the ASFV Pol X–ssDNA interactions
The DNA pol X from the ASFV provides an analogous, although more complex, system of the protein–ssDNA complex, as compared to the PriA–ssDNA complex. We will limit our discussion to studies of the structure–function relationship within the total ssDNA-binding site of the enzyme. The reader is advised to consult the original paper on the full analysis of the system (Jezewska et al., 2006). The DNA genome of the ASFV encodes a DNA polymerase, a member of the pol X family referred to as ASFV pol X, which is engaged in the repair processes of the viral DNA (Garcia-Escudero et al., 2003; Oliveros et al., 1997; Yanez et al., 1995). With a molecular weight of ~20,000, ASFV pol X is currently the smallest known DNA polymerase, whose structure has been solved by NMR (Maciejewski et al., 2001; Showwalter et al., 2003). The enzyme is built only of the palm domain, which includes the first 105 amino acids from the N-terminus of the protein and the C-terminal domain, which is built of the remaining 69 amino acid residues.
The strategy of addressing the function–structure relationship in the total DNA-binding site of the ASFV pol X has been analogous to the strategy discussed for the E. coli PriA helicase. Binding of the enzyme to the nucleic acid was examined using a series of etheno-homo-adenosine ssDNA oligomers (Jezewska et al., 2006). The first tactical step is to determine the maximum stoichiometry of the enzyme–ssDNA oligomer complex, as a function of the nucleic acid length. The stoichiometry of the complexes was determined using the quantitative fluorescence titrations method. The dependence of the maximum stoichiometry of the ASFV pol X–ssDNA oligomer for a series of ssDNA oligomers, dεA(pεA)N−1, as a function of the length of the ssDNA oligomer is shown in Fig. 13.9. Only a single ASFV pol X molecule binds to ssDNA oligomers, ranging from 7 to 20 nucleotides. A jump in the maximum stoichiometry of the complex, from one to two, occurs between the 20- and 24-mer. The maximum stoichiometry does not increase for the oligomer containing 37 nucleotides, which is 13 nucleotides longer than the 24-mer (Fig. 13.9). These data provide the first indication that a total site-size of the ASFV pol X–ssDNA complex is less than 19 nucleotides, but it must contain at least 12 nucleotides per bound protein molecule.
Figure 13.9.
The dependence of the total average degree of binding, ΣΘi, of the ASFV pol X–ssDNA complex upon the length of the ssDNA oligomer in buffer C (10 mM sodium cacodylate adjusted to pH 7.0 with HCl, 1 mM MgCl2, and 10% glycerol (10 °C), containing 100 mM NaCl and 1 mM MgCl2. The solid lines follow the experimental points and have no theoretical basis (Jezewska et al., 2006).
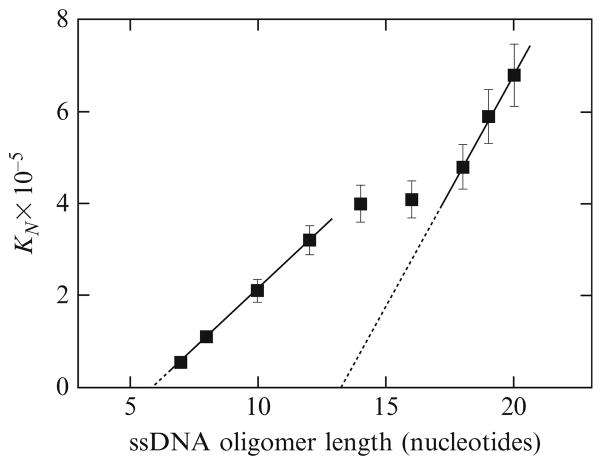
The dependence of the macroscopic binding constant, KN, for the ASFV pol X binding to the ssDNA oligomers, containing from 7 to 20 residues, that is, oligomers which can accommodate only a single enzyme molecule, upon the length of the ssDNA oligomer, is shown in Fig. 13.10. The plot has an unusual feature, when compared to the behavior of the PriA helicase. It is built of two linear regions separated by an intermediate plateau. For the ssDNA oligomers containing 7–12 nucleotides, the values of KN increase linearly with the length of the oligomers. As we discussed earlier, the simplest explanation of such empirical linear behavior of KN, as a function of the length of the ssDNA, is that there is a small, discrete binding region within the total DNA-binding site of the ASFV pol X that experiences the presence of several potential binding sites on the ssDNA oligomers, that is, there is the DNA-binding site proper within the total DNA-binding site. The DNA-binding site proper engages in interactions a number of p nucleotides, which must be smaller than the length of the examined ssDNA oligomers. Therefore, the values of KN contain a statistical factor that can be analytically defined in terms of the site-size, p, and the intrinsic binding constant, Kp, of the DNA-binding site proper, as defined by Eqs. (13.12a) and (13.12b). Extrapolation of the plot in Fig. 13.10 to the zero value of the macroscopic equilibrium constant, KN, intercepts the abscissa at the DNA length corresponding to the length of the ssDNA oligomer, which is too short to be able to form a complex with the enzyme. The plot in Fig. 13.10 gives that length as 6 ± 0.5. Therefore, the DNA-binding site proper of the ASFV pol X requires p = 7 ± 1 nucleotide residues of the ssDNA to engage in energetically efficient interactions with the nucleic acid. The intrinsic binding constant, Kp, can be determined from the slope of the first linear region in Fig. 13.10 (Eq. (13.12b)). For the ssDNA oligomers with the length between 7 and 12 nucleotides, the average value of Kp = (5.4 ± 0.8) × 104 M−1.
Figure 13.10.
(A) The dependence of the macroscopic binding constant KN, upon the length of the ssDNA for oligomers containing 7–20 nucleotides, that is, the oligomers that can accommodate only one ASFV pol X molecule. The solid line for the part of the plot corresponding to oligomers from 7 to 12 nucleotide residues is a linear least-squares fit to Eq. (13.12b). Extrapolation of the line to KN = 0 intercepts the DNA length axis at 6.0 ± 0.5. The solid line for the part of the plot corresponding to oligomers from 18 to 20 nucleotide residues is a linear least-squares fit to Eq. (13.18). Extrapolation of the line intercepts the DNA length axis at 13.2 ± 1.0 (Jezewska et al., 2006).
For the ssDNA oligomers, with the length exceeding 12 nucleotide residues, the plot in Fig. 13.7A becomes nonlinear and passes through an intermediate plateau into the second linear region for the oligomers, with the length longer than ~16–17 nucleotides. Such a transition between two linear regions of the plot of the macroscopic binding constant as a function of the length of the ssDNA oligomers indicates that different areas of the total DNA-binding site of the polymerase, beyond the DNA-binding site proper, become involved in interactions with the longer nucleic acid (Jezewska et al., 2006). The second linear region of the plot in Fig. 13.7A can be described by expressions analogous to Eqs. (13.12a) and (13.12b), as
| (13.18) |
However, the parameters in Eq. 13.18 now have different physical meanings. The quantity, q, is the minimum length of the ssDNA oligomer that can engage the total DNA-binding site of the polymerase, and Kq is the intrinsic binding constant for the total DNA-binding site. Extrapolation of this region to the KN = 0 provides q = 14.3 ± 1.0. Thus, the data indicate that in order to engage the total DNA-binding site of the ASFV pol X, the ssDNA must have at least ~14–15 nucleotides. Notice, this is a minimum estimate, not the actual site-size of the total DNA-binding site, which can be even larger (Jezewska et al., 2006). The slope of the linear region, for the ssDNA oligomers with the length between 18 and 20 nucleotides, provides Kq = (9.3 ± 2.1) × 104 M−1. This value is higher than the corresponding value of the intrinsic binding constant characterizing the interactions of the short ssDNA oligomers with the DNA-binding site proper of the polymerase. Such a difference reflects the fact that one observed different intrinsic interactions when the total DNA-binding site is engaged in interactions with the enzyme, as compared to the ssDNA-binding site proper (Jezewska et al., 2006).
4.2. Model of the ASFV Pol X–ssDNA complex
The next step is to address all obtained stoichiometry data to deduce the structural features of the total DNA-binding site. As discussed earlier, the transition of the maximum stoichiometry of the ASFV pol X–ssDNA oligomer complexes, from a single pol X molecule bound per an ssDNA oligomer to two molecules bound per oligomer, occurs between 20- and 24-mers (Fig. 13.9). However, binding studies with short ssDNA oligomers indicate that the polymerase engages only 7 ± 1 nucleotides in interactions with its DNA-binding site proper and the total DNA-binding site engages at least ~14–15 nucleotides. On the other hand, the 37-mer can still accommodate only two pol X molecules, that is, it does not allow the enzyme to associate with the nucleic acid using its ssDNA-binding site proper. These data indicate that the total site-size of the pol X–ssDNA complex is 16 ± 1 nucleotides per bound protein.
To address the structure of the total DNA-binding site of pol X, we consider the following two limiting models of the ASFV pol X–ssDNA complexes, depicted schematically in Fig. 13.11A and B (Jezewska et al., 2006). In Fig. 13.11A, the ssDNA-binding site proper, which engages 7 nucleotides, is located in the central part of the protein molecule. If this model of the total DNA-binding site applies, it would require that the protein molecule possesses two parts, each part protruding over ~8 nucleotides on both sides of the DNA-binding site proper giving a total DNA-site-size of ~23 nucleotides. This is because the minimum number of nucleotides engaged in interactions with the total DNA-binding site must be, at least, ~14–15, independent of the location of the DNA-binding site proper on the nucleic acid (Fig. 13.10). First, such a total site-size would be much larger than estimated from the fluorescence titration data. Second, the first bound pol X molecule would block ~15 nucleotides and the next bound molecule would also require an additional ~15 residues, giving the total requirement of 30 nucleotides. As a result, the ssDNA 24-mer would be able to accommodate only one pol X molecule. This is not experimentally observed (Fig. 13.9).
Figure 13.11.
(A) Schematic model for the binding of the ASFV pol X to the ssDNA 24-mer, based on the site-size of the DNA-binding site proper of the complex p = 7 nucleotides and the site-size of the total DNA-binding site of the polymerase, q = 16 (Jezewska et al., 2006). The DNA-binding site proper is located in the center of the enzyme molecule. In this model the protein matrix would have to protrude on both sides of the proper DNA-binding site over ~7–8 nucleotides in order to provide the minimum total DNA-binding site-size of ~15 nucleotides, independent of the location of the proper DNA-binding site. However, this model would allow the binding of only one molecule of pol X to the ssDNA 24-mer, which is not experimentally observed (Fig. 13.9). (A) Schematic model for the binding of the ASFV pol X to the ssDNA 24-mer, based on the site-size of the proper DNA-binding site of the complex p = 7 nucleotides and the site-size of the total DNA-binding site of the polymerase, q = 16. The enzyme binds the ssDNA in a single orientation with respect to the polarity of the sugar-phosphate backbone of the ssDNA. The DNA-binding site proper is located on one side of the enzyme molecule, with the rest of the protein matrix protruding over the extra 9 nucleotides. When bound at the ends of the nucleic acid, or in its center, the enzyme can occlude from 7 or 16 nucleotides. This model would allow the binding of two molecules of pol X to the ssDNA 24-mer (Jezewska et al., 2006).
Next, we consider a limiting model where the DNA-binding site proper of the enzyme engages 7 nucleotides and is asymmetrically located on one side of the polymerase molecule, as depicted in Fig. 13.11B. Part of the enzyme protrudes over the nucleic acid and engages an additional area in interactions at a distance from the proper binding site corresponding to ~8–9 nucleotides of the ssDNA. In this model, the total site-size of the complex is 16 nucleotides. The ssDNA oligomers with 20 or less nucleotides would bind only one ASFV pol X molecule, while oligomers from 24 to 37 residues would be able to accommodate two pol X molecules. This is exactly what is experimentally observed (Fig. 13.9). Therefore, the model of the ASFV pol X–ssDNA complex, depicted in Fig. 13.11B, adequately describes all experimentally determined stoichiometries of the ASFV pol X complexes with the examined series of ssDNA oligomers.
Notice, if the total DNA-binding site was only 15 nucleotides then the 37-mer would be able to accommodate three pol X molecules, which is not experimentally observed (Fig. 13.9). This is because two bound pol X molecules would block only ~30 nucleotides, leaving 7 nucleotides to accommodate an additional enzyme molecule, bound through its DNA-binding site proper. In other words, these data and analyses of the two alternative limiting models indicate that the actual total site-size of the pol X–ssDNA complex is 16 ± 1 nucleotides and includes 7 nucleotides encompassed by the DNA-binding site proper of the polymerase, as well as 9 nucleotides occluded by the protein only on one side of the DNA-binding site proper (Fig. 13.11B).
Acknowledgments
We thank Gloria Drennan Bellard for her help in preparing the manuscript. This work was supported by NIH Grants GM46679 and GM58565 (to W. B.).
Abbreviations
- DTT
dithiothreitol
- εA
1,N6-etheno adenosine
References
- Ali JA, Lohman TM. Science. 1997;275:377. doi: 10.1126/science.275.5298.377. [DOI] [PubMed] [Google Scholar]
- Amaratunga M, Lohman TM. Biochemistry. 1993;32:6815. doi: 10.1021/bi00078a003. [DOI] [PubMed] [Google Scholar]
- Baker BM, Vanderkooi J, Kallenbach NR. Biopolymers. 1978;17:1361. [Google Scholar]
- Baker TA, Funnell BE, Kornberg A. J Biol Chem. 1987;262:6877. [PubMed] [Google Scholar]
- Bjorson KP, Moore KJ, Lohman TM. Biochemistry. 1996;35:2268. doi: 10.1021/bi9522763. [DOI] [PubMed] [Google Scholar]
- Bujalowski W. Trends Biochem Sci. 2003;28:116. doi: 10.1016/S0968-0004(03)00034-3. [DOI] [PubMed] [Google Scholar]
- Bujalowski W. Chem Rev. 2006;106:556. doi: 10.1021/cr040462l. [DOI] [PubMed] [Google Scholar]
- Bujalowski W, Jezewska MJ. Spectrophotometry and Spectrofluorimetry. In: Gore MG, editor. A Practical Approach. Oxford University Press; Oxford: 2000. pp. 141–165. [Google Scholar]
- Bujalowski W, Lohman TM. Biochemistry. 1986;25:7779. doi: 10.1021/bi00372a003. [DOI] [PubMed] [Google Scholar]
- Bujalowski W, Lohman TM. Biochemistry. 1987;26:3099. doi: 10.1021/bi00385a023. [DOI] [PubMed] [Google Scholar]
- Bujalowski W, Lohman TM, Anderson CF. Biopolymers. 1989;28:1637. doi: 10.1002/bip.360280912. [DOI] [PubMed] [Google Scholar]
- Chabbert M, Cazenave C, Hélène C. Biochemistry. 1987;26:2218. doi: 10.1021/bi00382a022. [DOI] [PubMed] [Google Scholar]
- Enemark EJ, Joshua-Tor L. Curr Opin Struct Biol. 2008;18:243. doi: 10.1016/j.sbi.2008.01.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Epstein IR. Biophys Chem. 1978;8:327. doi: 10.1016/0301-4622(78)80015-5. [DOI] [PubMed] [Google Scholar]
- Galletto R, Jezewska MJ, Bujalowski W. J Mol Biol. 2004a;343:83. doi: 10.1016/j.jmb.2004.07.055. [DOI] [PubMed] [Google Scholar]
- Galletto R, Jezewska MJ, Bujalowski W. J Mol Biol. 2004b;343:101. doi: 10.1016/j.jmb.2004.07.056. [DOI] [PubMed] [Google Scholar]
- Galletto R, Jezewska MJ, Bujalowski W. Biochemistry. 2004c;43:11002. doi: 10.1021/bi049378q. [DOI] [PubMed] [Google Scholar]
- Garcia-Escudero R, Garcia-Diaz M, Salas ML, Blanco L, Salas J. J Mol Biol. 2003;326:1403. doi: 10.1016/s0022-2836(03)00019-6. [DOI] [PubMed] [Google Scholar]
- Heller RC, Marians KJ. DNA Repair. 2007;6:945. doi: 10.1016/j.dnarep.2007.02.014. [DOI] [PubMed] [Google Scholar]
- Hubscher U, Nasheuer HP, Syvaoja JE. Trends Biochem Sci. 2000;25:143. doi: 10.1016/s0968-0004(99)01523-6. [DOI] [PubMed] [Google Scholar]
- Jankowsky E, Gross CH, Shuman S, Pyle AM. Nature. 2002;403:447. doi: 10.1038/35000239. [DOI] [PubMed] [Google Scholar]
- Jezewska MJ, Bujalowski W. Biochemistry. 1996;35:2117. doi: 10.1021/bi952344l. [DOI] [PubMed] [Google Scholar]
- Jezewska MJ, Kim US, Bujalowski W. Biochemistry. 1996a;35:2129. doi: 10.1021/bi952345d. [DOI] [PubMed] [Google Scholar]
- Jezewska MJ, Kim US, Bujalowski W. Biochemistry. 1996b;35:2129. doi: 10.1021/bi952345d. [DOI] [PubMed] [Google Scholar]
- Jezewska MJ, Rajendran S, Bujalowski W. Biochemistry. 1998a;37:3116. doi: 10.1021/bi972564u. [DOI] [PubMed] [Google Scholar]
- Jezewska MJ, Rajendran S, Bujalowski W. J Biol Chem. 1998b;273:9058. doi: 10.1074/jbc.273.15.9058. [DOI] [PubMed] [Google Scholar]
- Jezewska MJ, Rajendran S, Bujalowski W. Biochemistry. 1998c;37:3116. doi: 10.1021/bi972564u. [DOI] [PubMed] [Google Scholar]
- Jezewska MJ, Rajendran S, Bujalowski W. J Mol Biol. 1998d;284:1113. doi: 10.1006/jmbi.1998.2252. [DOI] [PubMed] [Google Scholar]
- Jezewska M, Rajendran S, Bujalowski W. J Biol Chem. 2000a;275:27865. doi: 10.1074/jbc.M004104200. [DOI] [PubMed] [Google Scholar]
- Jezewska M, Rajendran S, Bujalowski W. Biochemistry. 2000b;39:10454. doi: 10.1021/bi001113y. [DOI] [PubMed] [Google Scholar]
- Jezewska MJ, Rajendran S, Bujalowski W. Biochemistry. 2001;40:3295. doi: 10.1021/bi002749s. [DOI] [PubMed] [Google Scholar]
- Jezewska MJ, Galletto R, Bujalowski W. Biochemistry. 2003;42:5955. doi: 10.1021/bi030046f. [DOI] [PubMed] [Google Scholar]
- Jezewska MJ, Galletto R, Bujalowski W. J Mol Biol. 2004;343:115. doi: 10.1016/j.jmb.2004.08.021. [DOI] [PubMed] [Google Scholar]
- Jezewska MJ, Marcinowicz A, Lucius AL, Bujalowski W. J Mol Biol. 2006;356:121. doi: 10.1016/j.jmb.2005.10.061. [DOI] [PubMed] [Google Scholar]
- Jones JM, Nakai H. J Mol Biol. 1999;289:503. doi: 10.1006/jmbi.1999.2783. [DOI] [PubMed] [Google Scholar]
- Jones JM, Nakai H. J Mol Biol. 2001;312:935. doi: 10.1006/jmbi.2001.4930. [DOI] [PubMed] [Google Scholar]
- Joyce KM, Benkovic SJ. Biochemistry. 2004;43:14317. doi: 10.1021/bi048422z. [DOI] [PubMed] [Google Scholar]
- Kaplan DL, O’Donnell M. Mol Cell. 2002;10:647. doi: 10.1016/s1097-2765(02)00642-1. [DOI] [PubMed] [Google Scholar]
- Ledneva RK, Razjivin AP, Kost AA, Bogdanov AA. Nucleic Acids Res. 1978;5:4225. doi: 10.1093/nar/5.11.4225. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee MS, Marians KJ. Proc Natl Acad Sci USA. 1987;84:8345. doi: 10.1073/pnas.84.23.8345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lohman TM, Bjornson KP. Annu Rev Biochem. 1996;65:169. doi: 10.1146/annurev.bi.65.070196.001125. [DOI] [PubMed] [Google Scholar]
- Lohman TM, Bujalowski W. Methods Enzymol. 1991;208:258. doi: 10.1016/0076-6879(91)08017-c. [DOI] [PubMed] [Google Scholar]
- Lohman TM, Ferrari ME. Annu Rev Biochem. 1994;63:527. doi: 10.1146/annurev.bi.63.070194.002523. [DOI] [PubMed] [Google Scholar]
- Lucius AL, Vindigni A, Gregorian R, Ali JA, Taylor AF, Smith GR, Lohman TM. J Mol Biol. 2002;324:409. doi: 10.1016/s0022-2836(02)01067-7. [DOI] [PubMed] [Google Scholar]
- Lucius AL, Jezewska MJ, Bujalowski W. Biochemistry. 2006;45:7217. doi: 10.1021/bi051827e. [DOI] [PubMed] [Google Scholar]
- Maciejewski M, Shin R, Pan B, Marintchev A, Denninger A, Mullen MA, Chen K, Gryk MR, Mullen GP. Nat Struct Biol. 2001;8:936. doi: 10.1038/nsb1101-936. [DOI] [PubMed] [Google Scholar]
- Marcinowicz A, Jezewska MJ, Bujalowski PJ, Bujalowski W. Biochemistry. 2007;46:13279. doi: 10.1021/bi700729k. [DOI] [PubMed] [Google Scholar]
- Marians KJ. Prog Nucleic Acid Res Mol Biol. 1999;63:39. doi: 10.1016/s0079-6603(08)60719-9. [DOI] [PubMed] [Google Scholar]
- McGhee JD, von Hippel PH. J Mol Biol. 1974;86:469. doi: 10.1016/0022-2836(74)90031-x. [DOI] [PubMed] [Google Scholar]
- Menetski JP, Kowalczykowski SC. J Mol Biol. 1985;181:281. doi: 10.1016/0022-2836(85)90092-0. [DOI] [PubMed] [Google Scholar]
- Morales JC, Kool ET. Biochemistry. 2000;39:12979. doi: 10.1021/bi001578o. [DOI] [PubMed] [Google Scholar]
- Nanduri B, Byrd AK, Eoff RL, Tackett AJ, Raney KD. Proc Natl Acad Sci USA. 2002;99:14722. doi: 10.1073/pnas.232401899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nurse P, DiGate RJ, Zavitz KH, Marians KJ. Proc Natl Acad Sci USA. 1990;87:4615. doi: 10.1073/pnas.87.12.4615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oliveros M, Yanez RR, Salas ML, Slas J, Vinuela E, Blanco L. J Biol Chem. 1997;272:30899. doi: 10.1074/jbc.272.49.30899. [DOI] [PubMed] [Google Scholar]
- Rajendran S, Jezewska MJ, Bujalowski W. J Biol Chem. 1998;273:31021. doi: 10.1074/jbc.273.47.31021. [DOI] [PubMed] [Google Scholar]
- Rajendran S, Jezewska MJ, Bujalowski W. J Mol Biol. 2001;308:477. doi: 10.1006/jmbi.2001.4571. [DOI] [PubMed] [Google Scholar]
- Sangler SJ, Marians KJ. J Bacteriol. 2000;182:9. doi: 10.1128/jb.182.1.9-13.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Showwalter AK, Byeon IJ, Su MI, Tsai MD. Nat Struct Biol. 2003;8:942. doi: 10.1038/nsb1101-942. [DOI] [PubMed] [Google Scholar]
- Tolman GL, Barrio JR, Leonard NJ. Biochemistry. 1974;13:4869. doi: 10.1021/bi00721a001. [DOI] [PubMed] [Google Scholar]
- von Hippel PH, Delagoutte E. Q Rev Biophys. 2002;35:431. doi: 10.1017/s0033583502003852. [DOI] [PubMed] [Google Scholar]
- von Hippel PH, Delagoutte E. Q Rev Biophys. 2003;36:1. doi: 10.1017/s0033583502003864. [DOI] [PubMed] [Google Scholar]
- West SC. Cell. 1996;86:177. doi: 10.1016/s0092-8674(00)80088-4. [DOI] [PubMed] [Google Scholar]
- Yanez RJ, Rodriguez JM, Nogal ML, Yuste L, Enriquez C, Rodriguez JF, Vinuela E. Virology. 1995;208:249. doi: 10.1006/viro.1995.1149. [DOI] [PubMed] [Google Scholar]