The executable pathway to biological networks

Abstract

As time goes by, it becomes more and more apparent that the puzzles of life involve more and more molecular pieces that fit together in increasingly complex ways. Genomics and Proteomics technologies nowadays, produce reliable and quantitative data that could potentially reveal all the molecular pieces of a particular puzzle. However, this is akin to the opening of Pandora’s box; and we are now facing the problem of integrating this vast amount of data with its incredible complexity into some coherent whole. With the aid of engineering methods designed to build and analyze computerized man-made systems, a new emerging field called ‘Executable Biology’ aims to create computer programmes that put together the pieces in ways that allows capturing their dynamicity and ultimately elucidating how molecular function generates cellular function. This review aspires to highlight the main features characterizing these kinds of executable models and what makes them uniquely qualified to reason about and analyze biological networks.

INTRODUCTION

The field of Executable Biology, which focuses on the design and analysis of executable computer programs that mimic biological phenomena [1], has emerged from several independent studies over the last decade. Regev and colleagues [2] were the first to propose treating biological signalling networks as distributed computer systems. They proposed to use π-calculus, which is a minimal language for describing concurrent systems, as a language for modelling biological systems [2–4]. This was the basis for a large body of work that uses continuous time Markov chains (CTMCs, see Glossary) as the underlying model of computation. Around the same time, Harel and colleagues [5] have noted the resemblance between biological systems and reactive systems which has led to various models of interacting state machines [5–8]. In addition, three independent studies have proposed to use hybrid systems as the underlying computational model for biological systems [9–11]. Modelling biological networks using Boolean networks started in the early 70 s [12] and modelling with Petri nets in the early 90 s [13, 14]. Over the last decade concepts and approaches from software engineering and computer science have started to penetrate the field of Systems Biology in an increasing pace.

The intended use of executable models is to complement informal graphical descriptions with executable formalisms that add formality and dynamicity to the knowledge base described. With the aid of formality, communication of models between researchers is enabled, making it possible to exchange information as well as to evaluate its accuracy. Modelling paradigms that are intended for constructing models of molecular interactions have the additional advantage that they can be built by first describing the structural connections between entities and then constant rates can be added for model refinement. Besides the basic ability to simulate such models, all these frameworks have additional analysis techniques that can be used to facilitate our understanding of complex biological systems. A major research challenge is to find ways to make these formalisms as convenient and user-friendly as possible for biologists, with the hope that these will become useful mainstream techniques without requiring biologists to become computer programmers.

In this review, we highlight the features of executable models that make them uniquely adequate for modelling biological systems, as well as the value of these features to the modelling of biological signalling networks.

COMPOSITIONALITY

One of the ways engineers handle complexity of systems is by using ‘compositionality’. Complex systems are built by breaking them down into parts of manageable size and complexity that are then composed to give rise to the whole. Compositionality is natural when coming to reason about biology as living systems are naturally built through compositionality. In many cases the complexity of an organism arises mainly from the interaction between the parts comprising it, while the parts have relatively simple behaviour and well defined boundaries. For example, a signal transduction pathway occurring inside a cell and carried out by individual proteins. Furthermore, the hierarchical structure often found in biological systems can be exploited more naturally (e.g. tissues are composed of cells that are composed of organelles, etc.). Executable models take advantage of compositionality in a natural way. If formalism also supports dual compilation (see Glossary), executable models effectively create a compositional way of describing traditional models. Compositionality is used almost in all executable models. Here, we choose to exhibit compositionality through two lines of work that highlight this feature.

The first line of work, by Fontana, Danos and colleagues [15, 16], use the Kappa-language (κ). A model in the κ-language describes the system that arises from a collection of agents and rules. Agents, which are entities in the model, have well defined interfaces through ‘interaction sites’. Rules describe how agents interact and may depend and change the state of interaction sites of each of the agents. A representation of a rule as a ‘contact’ map is shown in Figure 1. The κ-language is designed to closely match the style of reasoning applied to molecular interactions in cellular signalling. Simulations of κ models produce time course trajectories of quantities of entities in the system.

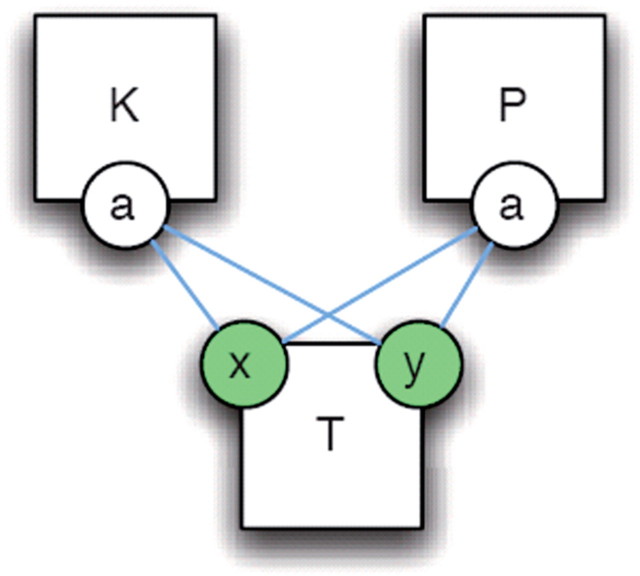
Figure 1:

A contact map. One view of the rule set is the contact map, which is akin to a protein–protein interaction map. This is a graph where nodes with interfaces represent agents and edges between interface sites represent possible bindings between sites. This system has three agents: a kinase (K), a target (T) with two phosphorylation sites (x and y), and a phosphatase (P). The Kinase K can bind to either the X or the Y site of T and changes their state to phosphorylated (change of state on binding indicated by green). Similarly, P can act on X and Y and changes their state from phosphrylated to dephosphorylated [20]. Figure reproduced with permission from Danos et al. [20].

One modelling work using the κ-language that highlights the usage of compositionality is the construction of a model for the repair mechanism of errors in DNA [17]. This work elucidates the simplicity of combining the model from its parts by considering agents, their sites, and possible interactions between systems. This is done with very local considerations that give rise to a global behaviour that explains the DNA repair mechanism. In a different modelling work, existing ODE models of the EGFR pathway [18, 19] are rewritten to take advantage of compositionality. Specifically, the different configurations of a substance that result in explosion of variables in the ODE representation are shown to be succinctly represented by using wisely the status of interaction sites and the rules that govern their changes [20]. Simple rules that relate to specific sites replace the reasoning about complete complexes. This highlights the power of compositionality by the behaviour of large complexes arising from the state of their interaction sites and the behaviour of the entire model arising from the entire set of rules. In a different line of work, it is shown how to take advantage of compositionality to improve scalability of simulations [21].

The main advantage of compositionality in the context of κ is that models can be constructed by introduction of rules in a modular fashion. Smaller models can be composed to larger models; and changes to existing rules can be performed without globally affecting the model. Models can be extended by addition of rules with a similar local effect.

A second line of work uses Statecharts [22] as a modelling language for biology [5]. State-based models define the behaviour of objects (elements of the system under description) over time, based on the various states that an object can be in over its lifetime. In other words, states are abstract situations in an object’s life cycle. Interacting state machines can specify causal relationships between state changes in different machines. These models describe both how objects communicate and collaborate, and how they behave under different circumstances. Interacting state machine models are particularly suitable for describing mechanistic models of biological systems that are well understood qualitatively. Such models do not require much quantitative data relating to the number of molecules and reaction rates. They allow the creation of abstract high-level models and the application of strong analysis tools such as model checking (see Glossary).

Usually, the state of an object is determined partly by the state of its sub-objects. For example, significant portions of the state of a cell would be determined by the state of the various genes and proteins comprising it. Each gene or protein would then have its own reaction to the presence or absence of some other molecules, and the change in the state of the cell would be influenced greatly by the interdependent state changes of all parts (Figure 2A). Initial work using this approach developed a model that described the various stages in the life span of a T cell, and the transitions between these stages [5]. Later work includes extensive animated model of T-cell differentiation in the thymus [6, 23]. The analysis of this model revealed several interesting emergent properties, which correspond well with biological phenomena. For example, the concurrent execution of T-cell development in the thymus led to the emergence of competition between T cells for sites of stimulation. This result suggest that such a behaviour could be important in generating the fine anatomy of the thymus, in selecting thymocytes with a range of migration velocities, and in explaining the paradox of CD4 to CD8 T-cell lineage ratios [6, 23]. A third model describes pancreatic organogenesis in embryonic mouse [8], which consists of a concurrent execution of pancreatic cells, leading to the formation of the unique 3D structure of the organ (Figure 2B).

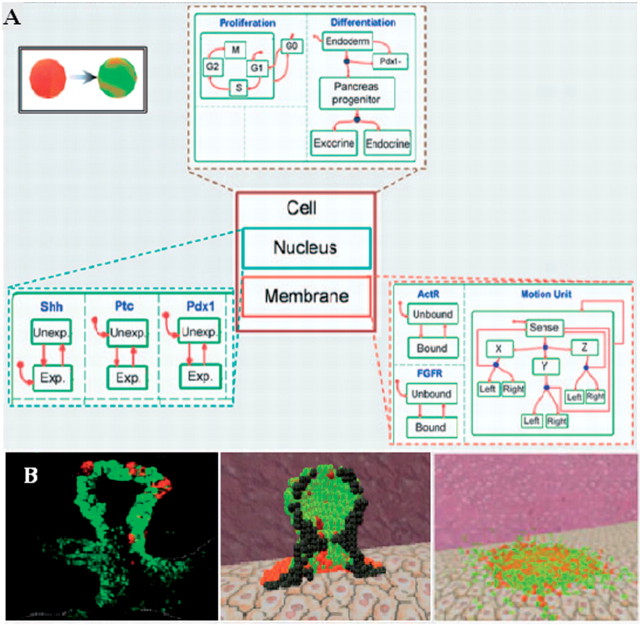
Figure 2:

StateCharts model of an autonomous pancreatic cell. (A) The cell is composed of a nucleus and a membrane and additional parts that control differentiation and proliferation. The Nucleus contains parts that follow the expression state of a few genes (Exp. or Unexp.), and the Membrane contains parts that follow the state of receptors and controls motion. (B) A histological cross-section of the pancreas (left), the emerging structure in the model at approximately the same developmental day (middle), and the result of an in silico experiment, in which the aorta was disabled, leading to a complete loss of structure (right) [8]. Figure reproduced with permission from Setty et al. [8].

Compositionality allows these models to scale to simulations of thousands of cells portraying the behaviour of organs. The behaviour of an organ arises from the behaviour of its parts and their interactions, which are described through their sub-parts.

DETERMINISTIC AND PROBABILISTIC SIMULATIONS

Another distinct advantage of the engineering approach arises from the ability to represent models in a high-level formalism that is detached from the actual implementation of the model. The high-level description can be then compiled (see Glossary) to various implementations, each highlighting a different aspect of the model. The most prominent example of this approach is in models that describe molecular interactions. Languages like Bio-Pepa [24] and BlenX [25] describe the molecular model through the interactions and rules that govern its behaviour. Both languages are process calculi (see Glossary), describing the entities that comprise the model, the different states that an entity can be in, the changes of state that an entity can undergo (either independently or by communicating with another entity), and the rates of such changes (see tutorials on the usage of these languages [26, 27]). These languages have two compilation paths—to ODEs and CTMCs—each having its own advantages (Figure 3). For example, well-established ODE models can serve as a reference. ODE simulations have fewer restrictions on the size of the models that can be analyzed, and ODE models can undergo analysis for steady state or other numerical solving techniques. CTMCs produce more accurate simulations; especially where stochastic behaviour arises from small numbers, and they support analysis techniques such as model checking and static analysis.

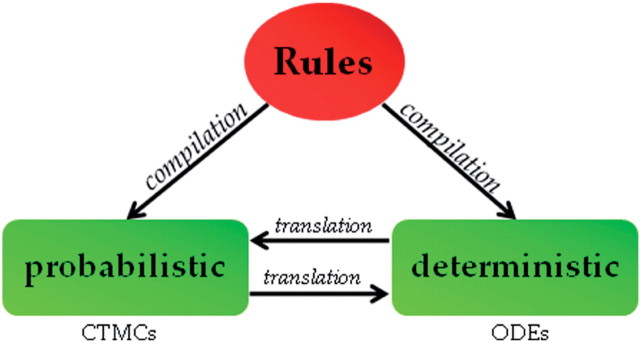
Figure 3:

Dual compilation. A high-level description through a set of rules can be compiled to a deterministic ODE model or to a stochastic CTMC model. Existing ODE models can be translated to rules and CTMCs, facilitating further refinement and affording additional analysis. Existing CTMC models can be translated to ODEs and compared to reference models.

As a first example, Calder and colleagues [28] constructed a model of the ERK signalling pathway, which was then contrasted with the ODE model of the same system. Analysis of the system, in the search of situations from which the system cannot perform any reactions, revealed a subtle problem with the original ODE model from which this model was derived. In a different work, a classical model of the EGFR signalling was translated to Bio-Pepa [29]. Simulations of the model, using the underlying CTMC model, were used to fine-tune the numerical analysis of the ODE model, and lead to the discovery of an error in previous simulations of the ODE model.

Another line of research builds automatic and semi-automatic translations from one type of model to the other. The existing large body of ODE models could benefit from translation to stochastic models. Models that are translated to rules notation can be more easily modified and refined. Additional types of analysis are available through probabilistic simulation and analysis. In particular, it is very simple to create mutated versions of models and test them ‘in silico’. For example, Palmisano and colleagues [30] have translated an ODE model to BlenX, compared the simulations of the two models, and created mutated versions of the model where only stochastic simulations were able to predict the experimental results. Similar motivation has lead to study direct translation from the Systems Biology Modelling Language (SBML) to BlenX [31] (and BlenX, as well as other formalisms, supports output to SBML). Dually, the translation from probabilistic models to ODE models serves to validate the probabilistic models [32]. In future, comparison of ODE models that arise from such translations, and ODE models that were constructed independently could serve to validate mechanistic understanding of signalling pathways by showing that similar models arise independently. Such comparisons could include both simulations of the two models as well as structurally comparing the resulting equations. Although such translations are currently ‘work in progress’, it is our view that translation between different formalisms with the advantages stated above will become more and more common.

Most efforts on dual compilation are currently in the area of molecular models, where the two underlying approaches are very closely related. In general, dual (or multiple) compilation could be very beneficial in applying different analysis to different parts of models. We believe that as the tools for Executable Biology will improve, this option will become more available for various types of models.

MODEL-CHECKING AND STATE-SPACE ANALYSIS

Executable models are also amenable to state-space analysis techniques. These techniques enable to explore all the possible states of the model or all its possible executions. The goal of exploration is to assert that all behaviours satisfy a given requirement. One such analysis technique is called ‘model checking’ (see Glossary), in which we try to assert that all possible behaviours of the system satisfy a given requirement [33]. If this assertion is false, we usually get a counter example: an execution of the system that does not satisfy the requirement. Model checking can be used either to assert that indeed a model behaves according to our expectations or to dig out interesting behaviours. Technically, model checking is enabled by efficient techniques to represent sets of states of a model. These techniques can also be used for other types of analysis as described below.

We have previously shown how model checking can be used to assert that all possible behaviours satisfy a given requirement through a state-based model describing the process of cell fate specification during Caenorhabditis elegans vulval development [34]. Our C. elegans model is discrete and non-deterministic (see Glossary). The fact that the model is non-deterministic implies that it has many possible executions for a given scenario (or mutation). In this particular case, there are millions of possible runs depending on the exact order in which cells in the model progress. We have used model checking for two purposes. First, to ascertain that our mechanistic model reproduces the biological behaviour observed in different mutant backgrounds. Second, we used model checking to query the behaviour of the model.

Model checking allowed us to test the consistency of the mechanistic model with an extensive set of observed behaviours and experimental perturbations affecting vulval formation. We have formalized the experimental results described in a set of papers (Table 1 in [34]) and verified that all possible executions satisfy these behaviours. That is, regardless of the order of interactions from a given set of initial conditions, different executions always reproduced the experimental observations. We found that 44 out of 48 perturbations affecting vulval development lead to a stable fate pattern, despite the vast number of possible executions of our model.

By phrasing queries such as ‘which mutations may lead to a stable or an unstable fate pattern’, we analyze the behaviour of the model. Once an unstable mutation was found, we determined what part of the execution allows this kind of mutation by disallowing different behavioural features of the model and checking when the instability disappears. To determine whether variations in the exact timing of the lateral signalling operating between the vulval precursor cells (VPCs) are the cause of this instability, we asked, using model checking, whether it is possible to get an unstable fate pattern without allowing variations in the timing of the lateral signal and found this not to be the case. We discovered that in order to adopt two different cell fates in two different executions, a VPC has to send the lateral signal before its neighbours in one execution, and after its neighbours in another execution. Specifically, we found that in the four cases containing the lin-15 knockout mutation, perturbation of the intricate timing dependency between the activation of the lateral signal and the inhibition of LIN-12 activity by the EGFR/RAS/MAPK pathway allows VPCs to adopt different fates in different executions of the model.

The analysis of this model predicted new genetic interactions between the two signalling pathways and provided new insights into the temporal aspects of EGFR and LIN-12/Notch signalling crosstalk during the process of cell fate determination. These temporal constraints may further elucidate the mechanisms underlying precise pattern formation during animal development (Figure 4). These predictions were also validated experimentally [34].

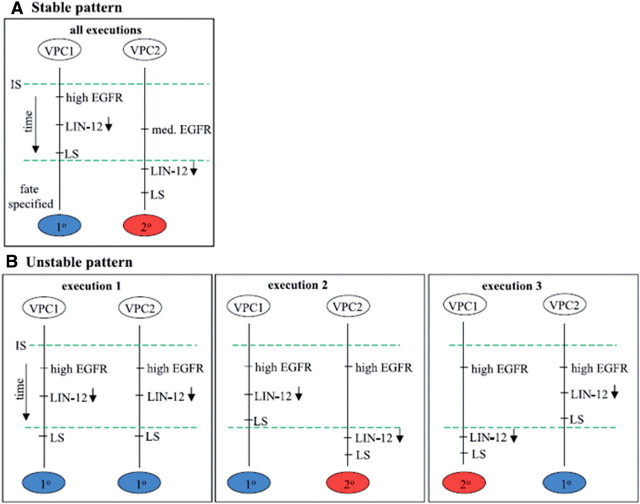
Figure 4:

Proposed sequence of events leading to a stable and unstable fate patterns as predicted by model checking. Time flows from top to bottom. Two events that appear on the same vertical line are ordered according to the time flow. The dashed lines synchronize the different vertical lines. All events that appear above a synchronization line occur before all events that appear below the synchronization line. The time-order between two events that appear on parallel vertical lines without a synchronization line is unknown. (A) Proposed sequence of events leading to a stable pattern. The left time line starts with a high inductive signal (IS) and the right time line with a medium IS. (B) Three diagrams that represent possible sequences of events leading to different fate patterns in the absence of IS (the AC is absent). Execution 1 represents the case where two cells are strongly coupled and they both reduce their lin-12 level simultaneously, send LS, which is ignored, and assume primary fates. Execution 2 represents the case where the left cell sends the lateral signal slightly before its neighbour reduces the level of lin-12, thus resulting in a 1⁰–2⁰ pattern. Execution 3 is the dual of execution 2 where the cell on the right inhibits the cell on the left. Figure reproduced with permission from Fisher et al. [34].

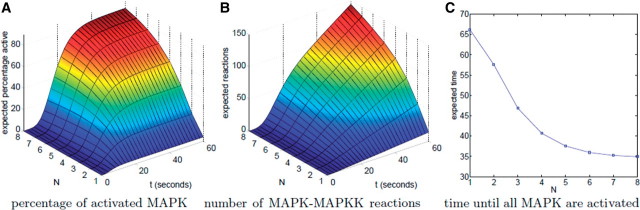
A different line of work uses probabilistic model checking to analyze molecular models. Here probabilistic model checking is applied to CTMCs and can compute exact quantitative measures. Using model checking, one can answer questions such as: ‘What is the expected time until the occurrence of an event? How many times is an event expected to occur in a given time? What is the probability of a certain event to occur in a given time?’ Heath, Kwiatkowska and colleagues have used probabilistic model checking to analyze a model of the FGF signalling pathway [35], looking at questions such as: ‘what is the probability that Grb2 is bound to FRS2 at a given time t? What is the expected number of times that Grb2 binds to FRS2 before degradation?’ And several more queries. The analysis of these questions sheds light for example on the roles of Shp2, Src, and Spry, in the FGF pathway. A similar study elucidates details of the MAPK cascade [36]. Results of model checking from this work are given in Figure 5 (see also review [37]).

Figure 5:

Results of model checking for the MAPK stochastic model. (A) The expected percentage of activated MAPK at time instant t, (B) the expected number of reactions between MAPK and MAPKK up until time t, and (C) the expected time until all MAPK are activated at the same time according to the number of MAPK, MAPKK, and MAPKKK that are initially available (N) [36]. These results demonstrate that, as the size of N grows, the percentage of MAPK that is activated increases and the time until all MAPK are activated decreases. They also show the expected dynamics that raising species quantities increases the number of reactions that occur between them. Figure reproduced with permission from Kwiatkowska et al. [36].

Another line of work uses Pathway Logic and the accompanying Assistant as a framework for the construction and analysis of signalling pathways [38–40] using Petri nets as the underlying formalism (see Glossary). Pathway Logic concentrates on the Boolean behaviour of signals. A model is constructed by collecting components and rules about their interaction. An execution starts by choosing which substances are available and proceeds by the rules activating or deactivating substances. Thus, a state of the system is a snapshot of which substances are active and states change by modifying the status of substances. The Pathway Logic Assistant enables to phrase general model checking queries but also has a default query: one may ask to reach a goal activation, while avoiding activation of other parts and hiding (i.e. not using) certain rules in the signalling network. The special feature of the Assistant is that after finding such a path it also enables to see only the part of the network that had actually participated in this path. This easily leads to the understanding of necessary and unnecessary reactions in order to achieve certain effects. In many cases, multiple possible activation paths that satisfy the required ‘goal,-avoid-or-hide’ requirement exist, and in this case the Assistant presents one of them [41, 42]. How to further combine the query with additional constraints that choose other paths (and consequently sub-networks) is in progress. One such attempt is to give weights to the reactions and try to produce the best such path according to these weights [43]. Overall, this additional analysis on top of model checking provides another layer of information along the winding path to decipher various signalling pathways.

Finally, the work of Schaub et al. [44] uses the techniques that underlie model checking for the analysis of large Boolean networks. Boolean networks abstract the behaviour of pathways by considering each substance as either active or inactive and change the status of substances according to inhibition and activation relations between substances. Analysis of Boolean networks tries to mimic the steady-state analysis applied to ODE models and checks which states of the Boolean network are stable. As Boolean networks grow in size, it is no longer possible to consider each of their states separately. One possible solution is to take a sample of the states. By taking advantage of state-space exploration techniques and techniques to reason about models composed from smaller parts, Schaub et al. were able to compute the set of steady states of a large Boolean network model. This work illustrates the usefulness of this approach through a model of the interaction between the Notch and the Wnt signalling pathways in mammalian skin. The analysis of the model predicted a new mode of interaction between the two pathways, which was also validated experimentally.

One of the major constraints of model checking is the size of the models that can be analyzed. This is especially true in the context of probabilistic model checking, where the capacity of the available tools is far from scaling to the size of the models constructed in practice. Still, this is a very useful technique that gives back important information. Extending the capacity of the tools is an open field of research within Computer Science.

VISUALIZATION AND USER-FRIENDLINESS

Executable models create an opportunity to transfer models from the hands of computational biologists to the hands of experimental biologists. In order to enable that, without requiring extensive training and at the same time allowing easy access to advanced analysis techniques, we need to establish formalisms and tools that will make the construction and analysis of models as transparent as possible. As models grow in size, it becomes harder to analyze them and to understand their simulations. Computer programmers have extended executable models with visualizations that enable to capture significant details of enormous models. Adding the option of such visualizations as another analysis technique adds a layer of complexity to the planning of such tools.

Several attempts at making executable models more accessible to non-experts are underway. The narrative language [45] translates a description written in high-level language to a molecular model. The description of the model is through simple rules (e.g. ‘if gp130 is not bound and gp130.typeI is not a dimer, then LIF binds gp130 on LIF’) in a restricted English structure. These rules then need to be augmented with rate information in order to create an executable model.

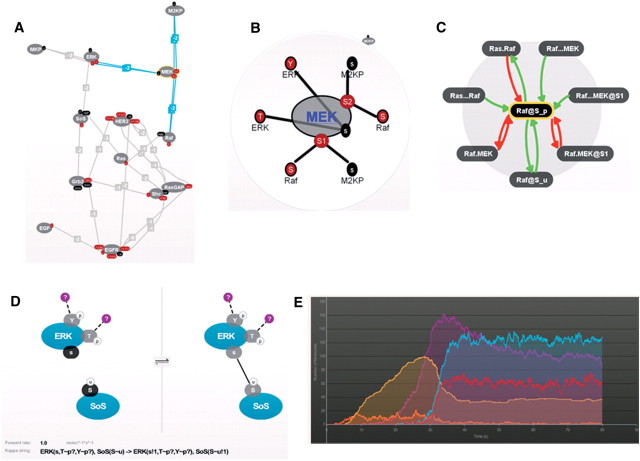
Another promising effort called Cellucidate [46] provides an extensive graphical user interface (GUI) for the construction, analysis, and simulation of models in the κ-language. In this tool the GUI takes advantage of the simple structure of the language, and enables to define entities, their sites, and rules. It also supports review of the structure of the model through many features such as zooming in on specific proteins and checking the rules that affect them (Figure 6). Cellucidate also aims to create an online archive and user community that will share and discuss models, leading to faster dissemination of knowledge and its expansion.

Figure 6:

Modelling with Cellucidate. (A) A model representing part of the EGFR cascade. Proteins and their interaction sites are the nodes with edges connecting interaction sites. (B) A zoom-in on MEK with its interaction sites and their connections. (C) A different view of Raf and its interactions, where activating relations are in green and inhibiting relations are in red. (D) A zoom-in into a rule: if sites Y and T of ERK are phosphorylated and may or may not be bound, and site S of SoS is ubiquitinated then site s of ERK and site S of SoS can bind, which changes their state from unbound (left) to bound (right). (E) A simulation of the model showing the change in number of molecules over time. Figure reproduced with permission from Plectix [46].

The Cell Illustrator [47] follows a similar path and builds a GUI on top of Hybrid Functional Petri Nets (HFPNe) with extensions. Petri Nets combine entities and the rules that govern their changes in an intuitive way. A unique feature of HPFNe is that they allow combining discrete and continuous parts in the same model [48]. The Cell Illustrator adds various visualization options (Figure 7), as well as the ability to animate simulations. Models written for Cell Illustrator, as well as automatic translation from SBML to the Cell Illustrator’s input language (CSML) are available for users [49].

Figure 7:

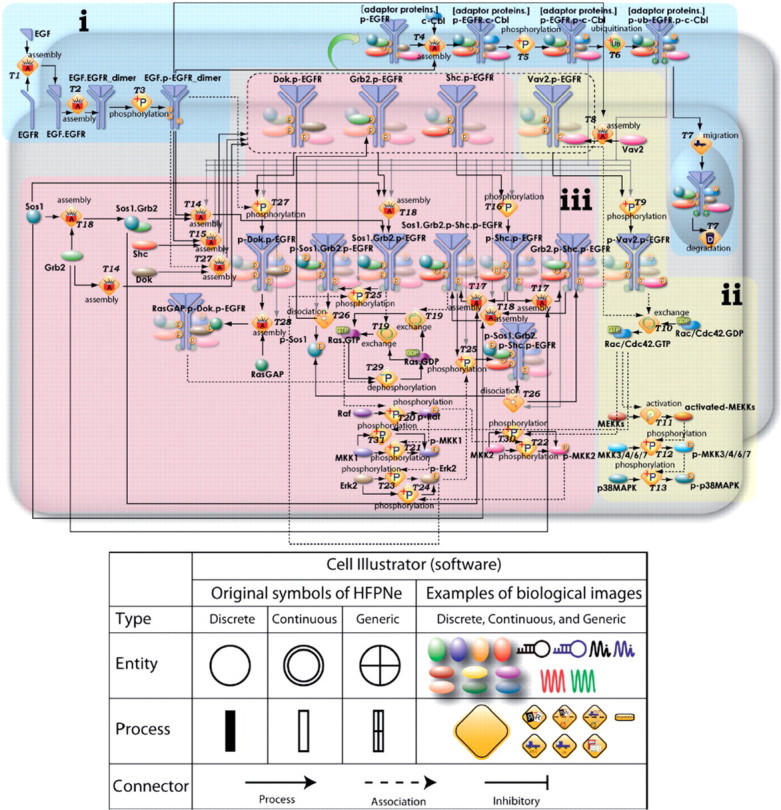
Hybrid Functional Petri Nets model of EGFR pathway in Cell Illustrator. (A) Sets of entities and processes are classified into discrete, continuous, and generic types, and entities and processes can be replaced with pictures reflecting the biological images. This replacement makes the hybrid functional Petri nets (HFPNe) model of a biological pathway more comprehensible for biologists. (B) For entities and processes, pictures reflecting the biological images may be used [52]. Figure reproduced with permission from Tasaki et al. [52].

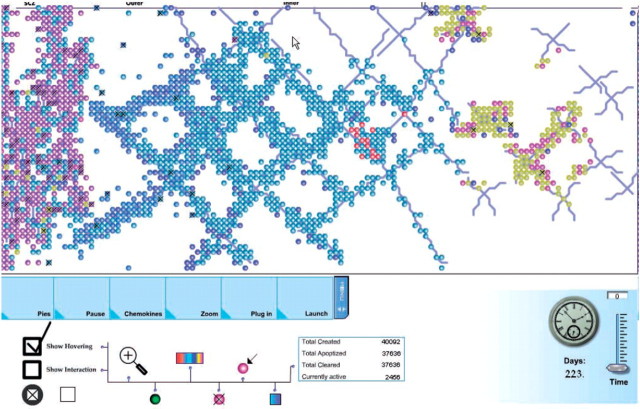
Animation is arising as a tool for overcoming the complexity of models and simulations also in ‘Reactive Animation’ [50]. We have previously mentioned the models of T-cell differentiation in the thymus [6, 23] and pancreatic development [8]. These models give rise to simulations of thousands of cells, including their movement as well as sub-cellular details. The amount of details in such simulations requires special mechanisms for understanding the simulations. Efroni et al. developed an animation engine that follows the execution of the underlying model and uses events in the simulation to drive a movie depicting this simulation (Figure 8). Through the animation the user has the ability to inject inputs, zoom-in and -out on specific sections or cells, and change parts of the simulation. Recently, the technique has been improved, resulting in a generic platform that enables interaction between various tools as well as 3D animation [51]. However, while the Statecharts language itself is relatively user-friendly and easy to master for non-programmers, visualizations as described here are intended to be created by expert programmers.

Figure 8:

A snapshot of the simulation during run time of the StateCharts Thymus model. This is a high-level front-end view of a lobule during execution. The buttons in the bottom left control the statistical representation of the data; pause the simulation; chemokine representation; different zooming in-and-out abilities; connection between the animation and simulation. The other buttons give different colour codes relevant to the display, enable the user to trace the motion of specific cells, control the connection between the simulation and specific statistical tool (such as Matlab), give the user the ability to avoid clutter made by overlapping cells, give the user the ability to receive visual indication to interactions, and more. The small circles are the visual representation of thymocytes [6]. Figure reproduced with permission from Efroni et al. [6].

User-friendly tools for creating executable models hold the promise of bringing the modelling work closer to the workbench; making it simpler to create, share and analyze models. Finding the right formalisms and building the appropriate tools that will enable biologists to remain experts in biology and not require them to become computing experts, and at the same time create effective models and analyze them, is a major task. All together, such tools should allow ‘the extra mile’ for expert programmers to add analysis layers such as complex visualization. We find this one of the major challenges facing the new emerging field of Executable Biology.

SUMMARY

This review aims to summarize the major unique features of executable models that make them especially adequate for reasoning about and analyzing biological signalling networks. We highlighted features that simplify the modelling work (compositionality and user-friendliness) as well as the analysis techniques that are available (multiple compilation, model checking and visualizations). All these different techniques can be aggregated and used in concert to shed more light on models. For example, a model can be written compositionally in a graphical and user-friendly language, dually compiled to ODEs and CTMCs, analyzed through model checking and simulated with the assistance of an animated graphical user interface. Obviously, the applicability of methods depends on the exact formalism chosen with respect to the biological question in mind, the size of the model, the expertise of the modeller and the amount of effort invested in the model construction. We have summarized numerous successes that highlight the potential power of the techniques we advocate here.

One of the major challenges facing the field of Executable Biology is to make such tools available to experimental biologists without requiring them to become expert programmers. The accessibility of these tools for biologists will further facilitate the incorporation of dynamic data into models, allowing faster dissemination and sharing of data. We look forward to the next 10 years, as these tools become more widely accepted and are developed to take an active mainstream role in Experimental Biology.

Key Points.

• We review the major unique features of executable models that make them especially adequate for reasoning and analyzing biological signalling networks.

• We highlight features that make the life of modellers simpler (compositionality and user-friendliness) and the analysis techniques that are available (multiple compilation, model checking and visualizations).

• One of the major challenges is to make such tools available to experimental biologists without requiring them to become programmers. The accessibility of these tools for biologists will further facilitate the incorporation of dynamic data into models allowing faster dissemination and sharing of data.

• Early successes have highlighted the potential power of the techniques, we advocate here. We look forward to the next 10 years, as these tools become more widely accepted and are developed to take an active mainstream role in Experimental Biology.

FUNDING

Nir Piterman is supported by the UK Engineering and Physical Sciences Research Council project Complete and Efficient Checks for Branching-Time Abstractions (EP/E028985/1).

Biographies

Dr Jasmin Fisher received her PhD in Neuroimmunology from the Weizmann Institute of Science and is currently an affiliated Lecturer at the Centre for Systems Biology in Cambridge University, the Computing Laboratory in Oxford University, and a Research Scientist in Microsoft Research Cambridge. Her research focuses on modelling of cell fate determination and signalling networks operating during normal development and cancer.

Dr Nir Piterman received his PhD in Computer Science from the Weizmann Institute of Science and is currently a Research Fellow at Imperial College London. His research interests include automata theory, formal methods and their application to validation and verification of systems.

GLOSSARY

Boolean Networks

These models provide an abstraction of ODE models through measuring the state of each species as one in a small range of values (on and off in Boolean Networks and, for example, off, low, medium, and high, in Qualitative Networks). Interactions between species are abstracted to simple functions like activation and inhibition. A state of the system is a value assignment to each of the components and an execution proceeds by changing the state of all species simultaneously according to the rules implied by the simplified interactions, thus approximating the deterministic behavior of ODEs. These models usually compute the steady states of the modeled system.

Compilation

The translation of a high-level programming language to a low-level machine language. In the context of software, high-level languages such as C++, or Java are translated to a low-level language composed of sequences of instructions that can be understood by the computer processor.

Continuous Time Markov Chains

A model used to describe systems with discrete states that change stochastically in real time. In a given state, a continuous time Markov chains (CTMC) defines a distribution over the possible next states and the time it takes to move to those states. In the context of biological networks a state of a CTMC relates to the numbers of all the different species in the model, and changes in states depict changes in these numbers. CTMCs can be simulated to produce possible trajectories, or model checked to analyze expectations and bounds on probabilities of certain events.

Non-deterministic Models

These are models that may have several possible reactions to the same stimulus. In biological systems, for example, we can observe various patterns of cell fate under the same genotype. Hence, non-deterministic models capture the diverse behavior often observed in biological systems by allowing different choices of execution, without assigning priorities or probabilities to each choice. Even small degrees of non-determinism can lead to a huge number of possible executions.

Model Checking

In non-deterministic models, simple simulations (i.e. testing) are not sufficient to verify the model’s consistency with the experimental data. The reason is that in non-deterministic models the number of possible behaviors resulting from the same initial condition could be enormous. Therefore, to test a non-deterministic model, one would have to run many simulations (one for each scenario). Another way to test non-deterministic models is to use model checking, which allows to formally check different executions of the system against a formal specification. By exploring all the possible states and transitions of a system, we can determine whether some property holds true for the system. In the case that the property does not hold, the model-checking algorithm supplies a ‘counterexample’, which is an execution of the system that does not satisfy the given requirement.

Petri Nets

A Petri net is a graph with two types of nodes: places, which represent the components of the system, and transitions, which correspond to events that can change the state of the components. The edges of the graph connect places to transitions and transitions to places. The state of the system is represented by places holding so-called tokens; one place may hold multiple tokens. Thus, different assignments of tokens to places induce different states of the system. Transitions change the state of the system by moving tokens along edges. In a given state of the system, there may be more than one transition that can move a token, leading to non-determinism. Petri nets are well-suited for modeling the concurrent behavior of biochemical networks and have been used to represent metabolic pathways and protein synthesis.

Process Calculi

Process calculi are an approach to describe concurrent systems—systems consisting of many components that interact with each other. The behaviour of the system is given through the description of its components. Each component has a state and it can change its state according to a given set of rules. Rules are conditioned upon the current state of the component and may include communication between two components. In case of such communication, both components change their states according to two rules that describe two sides of the communication. Modern process calculi include many features that make it very simple to describe many possible systems. A given state of the entire system includes the state of all the components comprising the system and their multiplicities. A change in the state of the system occurs by applying one of the rules that are applicable in a state to one or two of the components. The process calculi that are used in the context of biological modelling are usually stochastic, i.e. rules also have reaction rates and the next rule to change the state of the system is chosen according to some measure of probability that is defined by the reaction rates.

Steady States

Equilibrium points of the model. In the context of ODEs these are points where the model stays stable as time progress. In the context of Boolean Networks and Qualitative Networks these are cycles of states to which executions are drawn and keep cycling in as time evolves. Size of cycles indicates the network’s stability, with a cycle of size 1 relating to a classical stable point.