A new approach to auto-calibrated dynamic parallel imaging based on the Karhunen-Loeve transform: KL-TSENSE and KL-TGRAPPA

Abstract

TSENSE and TGRAPPA are auto-calibrated parallel imaging techniques that can improve the temporal resolution and/or spatial resolution needed in dynamic magnetic resonance imaging applications. In its original form, TSENSE uses temporal low-pass filtering of the under-sampled frames to create the sensitivity map. TGRAPPA uses a sliding-window moving average when finding the auto-calibrating signals. Both filtering methods are suboptimal in the least-squares sense, and may give rise to mismatches between the under-sampled k-space raw data and the corresponding coil sensitivities. Such mismatches may result in aliasing artifacts when imaging patients with heavy breathing, as in real time imaging of wall motion by MRI following a treadmill exercise stress test. In this study, we demonstrate the use of an optimal linear filter, i.e., the Karhunen-Loeve transform filter, to estimate the channel sensitivity for TSENSE, and acquire the auto-calibration signals for TGRAPPA. Phantom experiments show that the new reconstruction method has comparable SNR performance to traditional TSENSE / TGRAPPA reconstruction. In vivo real-time cardiac cine experiments performed in five healthy volunteers post-exercise during rapid respiration show that the new method significantly reduces the chest wall aliasing artifacts caused by respiratory motion (p<0.001).

1. Introduction

Real-time cine imaging of the heart eliminates the needs for breath-hold and regular cardiac rhythm, making it a robust and attractive method for many clinical applications. Real-time cine is limited in temporal and spatial resolution and may be inadequate for cardiovascular stress imaging and the evaluation of myocardial wall motion at high heart rates. Parallel imaging techniques such as SENSE (1) and GRAPPA (2) increase imaging efficiency by reducing the number of phase encoding steps, and have been used to significantly improve spatial resolution and temporal resolution in real-time cine (3-5). Both SENSE and GRAPPA require separate, full field-of-view (FOV) reference data to estimate the channel sensitivity of SENSE, or the autocalibration signals (ACS) of GRAPPA. TSENSE (6) and TGRAPPA (7) are autocalibrated parallel imaging techniques that interleave and temporally filter the k-lines of under-sampled adjacent frames to dynamically estimate coil sensitivity reference information. This autocalibration method has a few advantages. First, it increases scan efficiency by eliminating the need to acquire separate coil sensitivity data. Second, the method adapts the coil sensitivity estimate to temporal changes caused by motion. Third, TSENSE utilizes a temporal low-pass filter (LP), and TGRAPPA a sliding-window moving average (MA) of the under-sampled frames when deriving the coil reference data from the under-sampled data. Temporal filtering or averaging improves the signal-to-noise ratio (SNR) of the coil reference data, which in turn leads to improved SNR in the final reconstructed images.

The improved temporal resolution of cine MRI made possible by TSENSE or TGRAPPA is crucial in real time imaging of cardiac wall motion at the high heart rates encountered with dobutamine stress or immediately following peak exercise. While pharmacological stress (e.g. dobutamine or adenosine) is commonly combined with MRI, treadmill or bicycle exercise is actually the preferred method of cardiovascular stress testing as it reproduces symptoms and provides important physiological information. MRI immediately following exercise (8), however, poses a particularly difficult scenario for MRI in which the heart rate is extremely high and chest wall motion is exaggerated by rapid heavy breathing. Under these difficult conditions, the filter used to derive the coil reference data from the under-sampled data in TSENSE or TGRAPPA becomes critical. These filters used in the two parallel imaging techniques assume that coil sensitivity changes slowly with time (6), and hence the SNR of the coil reference data can be improved by removing high temporal frequency components without degrading the correspondence between the coil sensitivity map and the image data. While this is true when imaging patients during quiet breathing, it is no longer the case following exercise stress when the receiver coils move rapidly with the chest wall. As a result, these filters may excessively smooth out rapid temporal changes in the sensitivity map, giving rise to significant mismatches between the under-sampled k-space raw data and the corresponding coil sensitivity. Aliasing artifacts may arise, compromising the diagnostic image quality of the real time cine of the ventricular wall motion. We sought to improve the performance of TSENSE and TGRAPPA under conditions of rapid heart rate and deep rapid breathing encountered immediately following treadmill exercise by applying an improved method of filtering the dynamic coil sensitivity data.

In this study, we replace the previously described LP and MA temporal filtering approaches with the optimal linear filter, i.e., the Karhunen-Loeve (KL) transform filter (8), to estimate the channel sensitivity for TSENSE, and the ACS for TGRAPPA. The KL filter removes the eigenmodes of the temporal covariance matrix associated with low variance (i.e., small eigenvalues); the result is a low-rank approximation of the original data matrix that is optimal in the least square or Frobenius norm sense (9-12). Our hypothesis is that the temporal KL filter will minimize the mismatch between the coil sensitivity estimate and the k-space data, and thereby reduce aliasing artifacts. We present experimental results demonstrating the KL filter method of generating adaptive coil sensitivity data for TSENSE (KL-TSENSE) and adaptive ACS for TGRAPPA (KL-TGRAPPA) in real-time cardiac cine images acquired immediately following treadmill exercise. A new metric to automatically quantify chest wall aliasing artifact is described and used to compare the results from the different reconstruction methods.

2. Methods

Reconstruction Algorithm

Both TSENSE and TGRAPPA use the same basic approach to generate dynamically adaptive coil sensitivity reference data by temporally filtering time-interleaved under-sampled k-space data. As originally described, TSENSE (6) utilizes a Fourier low-pass filter, and TGRAPPA (2) a sliding window moving average, although the type of temporal filtering is not necessarily specific to either reconstruction method. Both filters smooth fast fluctuations and preserve slow-varying trends in the coil sensitivity profiles, but neither is optimal in the least-square sense; that is, for a given level of noise reduction, neither filter minimizes the effect on information content. We replaced the LP and MA filters in the TSENSE and TGRAPPA reconstruction methods by a KL filter. The KL filter is similar to other transform-based filters (such as Fourier or Wavelet filters) and follows the same three essential steps: first, apply the KL transform to the original image series in the temporal direction to generate the eigenmode series; second, truncate the eigenmode series (set the eigenmodes associated with small eigenvalues equal to zero); third, apply the inverse KL transform to the truncated eigenmodes to reconstruct the series of filtered images (13).

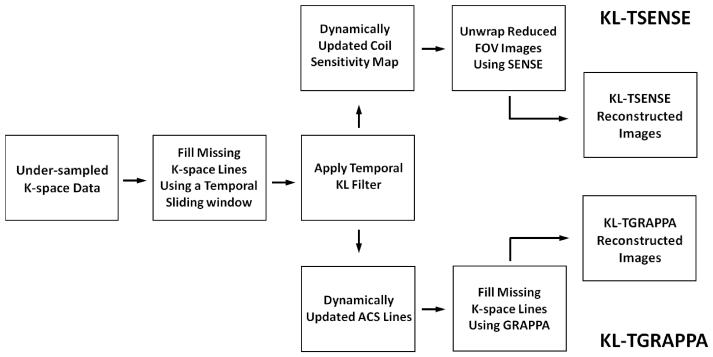
Replacing the LP filter in TSENSE and the MA filter in TGRAPPA by the KL filter results in the algorithm (hereby referred to as KL-TSENSE/KL-TGRAPPA) illustrated in Fig. 1. The algorithm can be described by the following steps. First, acquire p frames of under-sampled k-space data with parallel imaging reduction factor R (p >> R) using the time-interleaved acquisition scheme. Second, combine adjacent frames to generate p-R+1 full k-space raw data sets using a sliding window (width = R frames). Third, apply the KL filter to the p-R+1 full k-space raw data sets along the temporal direction (8), filtering out the eigenmodes with low eigenvalues. Fourth, use the KL filtered full k-space data sets to form dynamic estimates of the channel sensitivity for TSENSE reconstruction, or the ACS for TGRAPPA reconstruction. Finally, perform standard SENSE or GRAPPA reconstruction using a unique coil sensitivity estimate or ACS to reconstruct each frame. In the GRAPPA reconstruction used in this study, the block size was set to 4, and the number of ACS lines was set to be 90% of the phase encoding lines in the central k-space of the reference image.

Figure 1.

Block diagrams for KL-TSENSE and KL-TGRAPPA reconstruction algorithms. The temporal KL filter replaces the LP and the MA filters in the conventional TSENSE and TGRAPPA reconstruction algorithms.

Thus, the new algorithm differs from TSENSE and TGRAPPA in the use of a temporal KL filter to generate dynamic coil sensitivity maps or ACS lines. Also, the original description of TSENSE did not incorporate a sliding window in the second step; the combination of adjacent interleaved k-lines prior to filtering is necessary for KL filtering in the image domain, and does not substantially affect the results of LP or MA filtering. In order to demonstrate the effect of temporal filters on image quality in this study, no additional spatial smoothing of the coil sensitivity maps or any additional temporal filtering of the reconstructed image series was applied.

Filter Cutoff

To compare the various reconstruction algorithms, filter cutoff values for the LP and MA filters were chosen based on the original descriptions of the filters applied to TSENSE and TGRAPPA, and also to match their performance in temporal smoothing and noise reduction. In the original TSENSE description, a Fourier low pass filter with a cutoff of 0.75 Hz was used, although the paper also mentioned that filter cutoffs up to 2.5 Hz gave similar results (6). To compare the performance of the three filters, we chose to retain three Fourier modes in the LP filter, corresponding to a cutoff of 1.35 Hz. In the original TGRAPPA description, a sliding window moving average of three consecutive fully-sampled k-space frames was used, corresponding to a temporal frequency cutoff of approximately 1.51 Hz (the full width at half maximum of the corresponding sinc function). For the MA filter, we applied a sliding window of three fully-sampled k-space frames, matching the original description of TGRAPPA; this resulted in a temporal frequency cutoff of approximately 1.06 Hz at the sampling rates used in this study.

The KL filter has no well-defined pass-band frequency. Selection of eigenmodes was considered as follows. Since both the KL filter and the LP filter are unitary transform based filters, the SNR gain is identical when the same number of eigenmodes as Fourier modes are retained (8). Therefore, we chose to retain three eigenmodes in the KL filter, matching the noise reduction performance of the LP filter. The optimality of the KL filter ensures that it has minimal distortion on the original data for a given level of noise reduction. In the comparison, all the three filters, (LP, MA, and KL) were used to estimate channel sensitivity and ACS from time-interleaved under-sampled k-space data, which were then used by the SENSE and GRAPPA reconstruction methods.

Imaging Experiments

All imaging experiments were done on a 1.5T MRI system (MAGNETOM Avanto, Siemens Healthcare, Erlangen, Germany) equipped with 32 independent receiver channels. A standard 12-channel combined body and spine array coil was used for phantom imaging, and a 32-channel receiver array (Rapid MR International, Columbus, OH) was used for all volunteer imaging. The volunteer study was approved by our Institutional Review Board and all subjects gave written informed consent to participate. Image reconstruction was performed off-line in Matlab® 7.8 (MathWorks, Natick, Massachusetts) running on a personal computer with Intel® Core 2 Quad 3.00 GHz CPU and 8.0 GB RAM. When applying the KL filter to a 50-frame complex image series with 160 × 120 matrix, the processing time was less than 0.07 s.; i.e., the computational load of the KL filter is negligible.

2.1. Phantom Study

Images of a static phantom were acquired to compare the spatial mean SNR performance of the different filtering methods. Multiple-frame gradient echo images of a water bottle phantom from the scanner manufacturer (1.25g NiSO·₄⋅6H₂O + 5gNaCl per 1000g H₂O, T₁ = 578 ms, T₂ = 263 ms) were acquired with the following imaging parameters: 128 × 128 matrix, 10mm thick slice, flip angle=15°, TE/TR = 4.23/7.76 ms, pixel bandwidth=250 Hz/pixel, FOV = 100 × 100 mm², number of frames = 128. The fully sampled k-space raw data from multiple channels was collected, reconstructed, and combined using sum-of-squares. The raw data was then down-sampled by a factor of three and four (R = 3, 4). The resulting raw data was then reconstructed using TSENSE and TGRAPPA. The sensitivity data were obtained by each of the filtering schemes (LP, MA, and KL),

There is no well-accepted image SNR definition for MR images reconstructed using parallel imaging methods. In the phantom study, we used the spatial mean SNR as the SNR metric to evaluate the performance of different reconstruction algorithms. Spatial mean SNR was defined as the spatial average of the pixel-wise SNR measured by the multiple-acquisition method which was shown to be accurate in gradient echo images (14,15). The spatial mean SNR of the reconstructed images was assessed in a circular region of interest (ROI) with diameter =87 mm containing the entire phantom. Both signal and noise levels were evaluated in the same large ROI to minimize sensitivity of the SNR estimate to the spatial variation of noise (i.e., the g-factor effect).

2.2. Volunteer Study

Images acquired immediately after peak exercise stress and reconstructed using parallel imaging methods can be contaminated by severe chest wall aliasing artifacts due to the mismatch between coil sensitivity data and k-space data caused by heavy breathing. The volunteer study was performed to evaluate the performance of the proposed filter in reducing respiratory artifact in this scenario. We imaged 5 healthy volunteers immediately following maximal treadmill exercise performed inside the MRI room (16). Real-time cine images were acquired using a balanced steady-state free precession (SSFP) sequence at two acceleration rates (R = 3 and R = 4) in 6 views (vertical long-axis, horizontal long-axis, and four short-axis views) resulting in a total of 60 series of cine raw data (5 volunteers, 2 acceleration rates, 6 slices). Imaging parameters were: 160 × 84 matrix, 10mm thick slice, flip angle=68°, TE/TR = 0.99/2.26 ms, pixel bandwidth=1360 Hz/pixel, FOV = 380 × 300 mm². The views were scanned sequentially, and each slice was scanned for 2.2 seconds, resulting in 35 frames at a temporal resolution of 63.3 ms for R=3, and 46 frames at a temporal resolution of 47.5 ms for R=4. Each dataset was reconstructed with both TSENSE and TGRAPPA using each of the three different filter methods (LP, MA, and KL) to generate coil sensitivity data or ACS lines. The average heart rate was measured by counting the frames per cardiac cycle in the reconstructed images. The average maximum chest wall excursion was measured in a sagittal view cine. The severity of respiratory artifact of the resulting images was evaluated using the automated method described below.

Quantifying aliasing artifact

In the real time cines, the subcutaneous fat of the chest wall was extremely bright due to its proximity to the surface coil (see Fig. 2). The chest wall also moved significantly with breathing, causing the coil position to shift. The strong signal from subcutaneous fat together with motion led to aliasing of the chest wall fat when there was a mismatch between the sensitivity map and k-space data.

Figure 2.

Schematic showing the method used to calculate the artifact index. (a) The original image; (b) the template that contains the 1% of pixels with the highest intensity; (c) the cross-correlation function between the original image and the template. The peaks at FOV/3 and 2×FOV/3 are compared for acceleration rate R = 3. The highest peak in the cross correlation function is selected as the artifact index for this image.

Based on the above observation, a method was devised to quantitatively assess the aliasing artifact caused by chest wall motion in real time cine. For each phase in each cine series (of N images), an artifact index was calculated in the following way. For each image in a series, a template was defined by retaining the intensity of the 1% of pixels with the highest intensity and assigning a value of ‘0’ to all other pixels. This template outlined the subcutaneous fat that would contribute most to the aliasing artifact. We found that signal thresholds from 0.2% to 5% did not significantly impact the artifact index. The one-dimensional cross-correlation coefficient between each image and its template (consisting primarily of the chest wall) was calculated in the phase-encoded direction. Because of the chest wall ‘ghosts’ or other bright structures throughout the images, the cross-correlation coefficients will have local maxima at positions corresponding to fractions of the FOV in the phase encoding direction that match the reduction rate, R. For example, if R = 3, aliasing artifacts will be primarily located FOV/3 and 2×FOV/3 shifted away from the actual structure. The artifact index was defined as the maximum of the cross-correlation coefficients. Artifact indices associated with each image reconstructed using each of the different methods were calculated.

For each reconstruction method, and each acceleration rate, a paired t-test was used to compare the artifact indices of all images from all five volunteers between different filters. A paired t-test was also used to compare the artifact indices of all images from each of the individual volunteers.

3. Results

The mean SNR of the phantom images reconstructed from fully-sampled k-space raw data without parallel imaging was 76.3, and those of the phantom images reconstructed using each of the filter methods combined with both TSENSE and TGRAPPA, R=3 and R=4, are listed in Table 1. Images calculated using the MA filter had the highest SNR among the three adaptive reference map methods, and images calculated using the LP filter and KL filter had similar SNR (difference < 4%).

Table 1.

Comparison of SNR measurements in phantom images. R3 = rate 3, R4 = rate 4. Note that the effective cutoff of the MA filter was approximately 22% lower than the LP filter cutoff, resulting in higher SNR. KL filter cutoff was chosen to match the noise reduction of the LP filter.

	LP Filter		MA Filter		KL Filter		No Parallel Imaging
	TSENSE	TGRAPPA	TSENSE	TGRAPPA	TSENSE	TGRAPPA
R3	38.8	33.9	44.6	35.9	38.6	33.5	76.3
R4	28.6	22.4	33.9	25.0	28.1	21.6

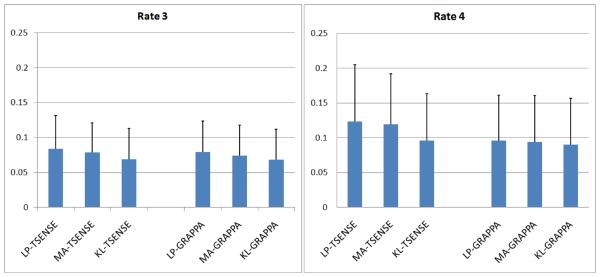
The volunteer cardiac cine images were acquired during high heart rate (153 ± 18 bpm) and heavy breathing (chest wall excursion: 13.2 ± 5.0 mm). The results of volunteer study are summarized in Fig. 3, Fig. 4, and Fig. 5. Figure 3 shows a bar chart of the average artifact index calculated for all combinations of filters, reconstruction methods, and acceleration rates based on all images from all five volunteers. Artifacts were more severe at R=4 than at R=3 independent of the filter used. The mean artifact indices across all images reconstructed using the KL filtered reference data were significantly lower (p-value<0.001) than both the MA and the LP filter methods for all combinations of reconstruction methods, cardiac views, and acceleration rates. The artifact reduction provided by the KL method was more pronounced at R=3, and the MA filter results showed significantly lower artifact indices (p-value<0.001) than the LP filter. When the artifact indices were averaged across all images for each individual volunteer and compared using a paired t-test, the KL filter had artifact indices significantly lower (p-value<0.05) than those obtained using the other filter methods for all images except in one case. In this single volunteer case where cine images were acquired with R=4, the TGRAPPA reconstruction yielded an artifact index not significantly different from that of KL-TGRAPPA.

Figure 3.

The mean artifact indices and the corresponding standard deviation for all five volunteers. The mean artifact score of KL-TSENSE/TGRAPPA reconstructed images is significantly lower (paired t-test, p<0.001) than those of LP-TSENSE/TGRAPPA and MA-TSENSE/TGRAPPA reconstructed images at both acceleration rates R = 3 and R = 4.

Figure 4.

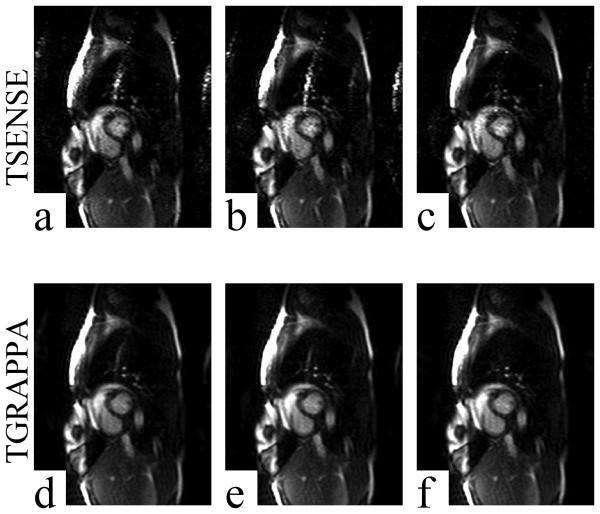
Example images acquired using acceleration rate R = 3 and reconstructed using TSENSE (a-c), TGRAPPA (d-f), and all three filter methods. All images shown are from the same raw data. LP, MA, and KL filters were used to generate channel sensitivity maps for the TSENSE reconstructions shown in panels a, b, and c, respectively. LP, MA, and KL filters were used to generate the autocalibration sensitivities for the TGRAPPA reconstructions shown in panels d, e, and f, respectively. Aliasing artifacts were reduced significantly in KL-TSENSE (c) and KL-TGRAPPA (f) reconstructed images compared to all other methods of sensitivity map filtering.

Figure 5.

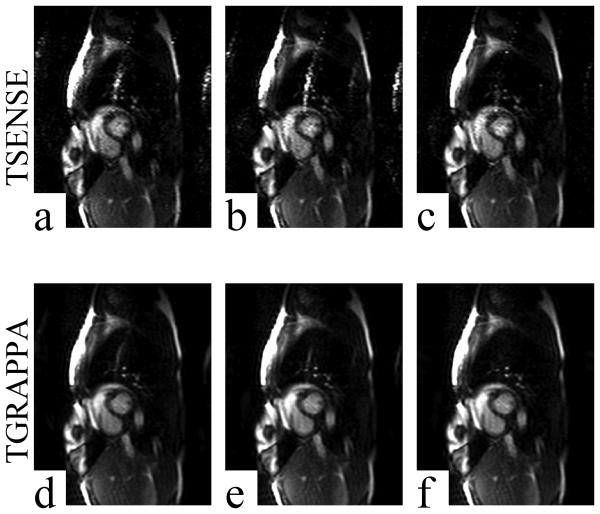
Example images acquired using acceleration rate R = 4 and reconstructed using TSENSE (a-c), TGRAPPA (d-f), and all three filter methods. All images shown are from the same raw data. LP, MA, and KL filters were used to generate channel sensitivity maps for the TSENSE reconstructions shown in panels a, b, and c, respectively. LP, MA, and KL filters were used to generate the autocalibration sensitivities for the TGRAPPA reconstructions shown in panels d, e, and f, respectively. Aliasing artifacts were reduced significantly in KL-TSENSE (c) and KL-TGRAPPA (f) reconstructed images compared to all other methods of sensitivity map filtering.

Figure 4a-c and Fig. 4d-f show results from a single raw data set acquired from one volunteer reconstructed using three filter methods combined with TSENSE and TGRAPPA at accelerate rate R = 3, respectively. Figure 5a-c and Fig. 5d-f show results from a raw data set acquired from the same volunteer reconstructed using three filter methods combined with TSENSE and TGRAPPA at accelerate rate R = 4, respectively. The images were all windowed to the same level. In both cases, the severity of the aliasing artifact was reduced significantly in KL-TSENSE and KL-TGRAPPA compared to other methods. Please note that in the example shown, the R = 3 images were acquired immediately post-exercise at a heart rate of 144 bpm, while the rate 4 images were acquired approximately 20 seconds later when the heart rate had dropped to 114 bpm. This may explain why quality of the R=4 images in Fig. 5 appears higher than the R=3 images in Fig. 4. Overall, however, the average artifact index was higher for R=4 images (Fig. 3) and the SNR was higher for R=3 (Table 1).

4. Discussion

A method of temporal filtering based on the Karhunen-Loeve transform was developed and used to adaptively estimate coil sensitivity for dynamic cardiac cine imaging. This KL filter replaced the low-pass and moving average filters previously described for the TSENSE and TGRAPPA reconstruction methods. We have shown that the optimality of the KL filter reduced the level of ghost artifacts in TSENSE and TGRAPPA real-time cardiac cine images acquired during rapid and heavy breathing immediately following treadmill exercise.

Fourier transform based temporal LP filtering (MA filter being a special case) removes noise and smoothes rapid fluctuations while preserving slow-varying trends. When sharp edges appear in the time course of pixel intensity caused, for example, by chest-wall motion, LP filtering will inevitably cause blurring and/or ringing in the filtered data. These artifacts will cause mismatches between the channel sensitivity map/ACS estimated from LP filtered images and the corresponding under-sampled k-space raw data, and such mismatches lead to aliasing artifacts in the reconstructed images. It has been shown that the KL filter, known to be the optimal linear filter in a least-squares sense, can minimize edge blurring and ringing artifacts compared to LP-filters (8). Minimization of these artifacts in the sensitivity map is thought to be the cause of the reduced aliasing artifacts demonstrated in this study.

It can be proven mathematically that if the respiratory motion and cardiac motion are strictly periodic, and the image series contains an integer number of cardiac and respiration cycles, or the acquisition time is long enough (>> respiration cycle), the temporal KL Transform and the Fourier Transform are equivalent, and the temporal low-pass filter and the KL filter can be identical (11). However, the above conditions can hardly be satisfied in practice. As such, the KL filter is the optimal linear filter in the least-squares sense. In the specific application of interest, post-exercise real-time cine imaging, the exaggerated motion due to deep, rapid, breathing strongly favors the KL filter in the TSENSE/TGRAPPA reconstruction.

Phantom images showed that the performance of the KL filter was comparable to the LP filter method for both TSENSE and TGRAPPA in terms of the SNR in the final reconstructed images (Table 1). This was expected since three eigenmodes and three Fourier modes were used in the filters, respectively. The MA filter resulted in the highest SNR of the adaptive filters, but this was also expected due to the approximately 22% lower effective frequency cutoff of the MA filter compared with the LP filter, based on the parameters chosen. The primary aim in replacing the previously used LP and MA filter with the KL filter was to reduce image artifacts, which we have shown to be successful. From our experience, the slightly reduced SNR did not cause any visible image quality degradation, while reducing respiratory artifact noticeably improved the quality of the real time cines.

Real-time cardiac cine results showed that the new KL-TSENSE and KL-TGRAPPA methods significantly reduced chest-wall aliasing artifacts compared to the other filtering approaches. This advantage is best appreciated in clinical applications where significant breathing motion can disrupt the correspondence between coil sensitivity map and the k-space data. The MA filter is a special type of temporal low-pass filter and it generated lower aliasing artifacts than the LP filter methods. We believe that the MA filter preserved sharp boundaries better than the LP filter used in our experiment, due possibly to the smoother transition bands in the frequency response of the MA filter.

The sensitivity maps used in TSENSE and TGRAPPA are essentially single-shot images acquired using an interleaved k-line ordering scheme. The combination of interleaved k-space acquisition and chest wall motion results in so-called “segmentation ghosts”, apart from the artifacts caused by temporal filtering. This is another potential source of error in the channel sensitivity map/ACS estimation, and its severity varies with the inter-leaved k-space sampling pattern. Unlike the artifacts caused by temporal filtering, the “segmentation artifacts” and the corresponding error in channel sensitivity/ACS estimation cannot be significantly reduced by the KL filter, or any linear filter for that matter. This helps explain why the degree of aliasing artifacts in the reconstructed images at R = 4 is higher than at R = 3. This effect may be reduced by optimizing the k-space sampling trajectory or applying motion correction strategies.

Another limitation of the KL filter is that it can only be applied after all data has been acquired; this precludes its use in applications where real-time reconstruction and display of the images is required. This limitation can be lifted to some degree by applying the KL filter to a narrower temporal sliding window, similar to the low-latency LP filter techniques proposed elsewhere (17,18).

In this study, we also introduced a new metric for quantifying aliasing artifacts using a template-based cross-correlation approach. The method may be useful in the investigation of other methods where the level of ghost artifact is of concern.

5. Conclusion

The Karhunen-Loeve Transform filter is an alternative to conventional low-pass and moving average filters. It provides a more accurate adaptive estimate of temporally changing coil sensitivity than the filters proposed in the original descriptions of TSENSE and TGRAPPA. This approach was shown to reduce ghosting artifacts in TSENSE and TGRAPPA reconstructed real-time cardiac cine images acquired during rapid and heavy breathing immediately following treadmill exercise. The method may be relevant to other applications where coil sensitivity is dynamically changing.