Abstract
The 4D extended cardiac-torso (XCAT) phantom was developed to provide a realistic and flexible model of the human anatomy and cardiac and respiratory motions for use in medical imaging research. A prior limitation to the phantom was that it did not accurately simulate altered functions of the heart that result from cardiac pathologies such as coronary artery disease (CAD). We overcame this limitation in a previous study by combining the phantom with a finite-element (FE) mechanical model of the left ventricle (LV) capable of more realistically simulating regional defects caused by ischemia. In the present work, we extend this model giving it the ability to accurately simulate motion abnormalities caused by myocardial infarction (MI), a far more complex situation in terms of altered mechanics compared with the modeling of acute ischemia. The FE model geometry is based on high resolution CT images of a normal male subject. An anterior region was defined as infarcted and the material properties and fiber distribution were altered, according to the bio-physiological properties of two types of infarction, i.e., fibrous and remodeled infarction (30% thinner wall than fibrous case). Compared with the original, surface-based 4D beating heart model of the XCAT, where regional abnormalities are modeled by simply scaling down the motion in those regions, the FE model was found to provide a more accurate representation of the abnormal motion of the LV due to the effects of fibrous infarction as well as depicting the motion of remodeled infarction. In particular, the FE models allow for the accurate depiction of dyskinetic motion. The average circumferential strain results were found to be consistent with measured dyskinetic experimental results. Combined with the 4D XCAT phantom, the FE model can be used to produce realistic multimodality sets of imaging data from a variety of patients in which the normal or abnormal cardiac function is accurately represented.
Index Terms: Cardiac imaging research, extended cardiac-torso (XCAT), finite element, ischemia, left ventricle, mechanical model, myocardial infarction, NURBS-based cardiac-torso (NCAT), single photon emission computed tomography (SPECT) phantom
I. INTRODUCTION
Computerized digital phantoms are gaining a wider and wider use in medical imaging research. A major advantage of using phantoms is that the exact anatomy and physiological functions are known, thus providing a gold standard from which to quantitatively evaluate and improve medical imaging devices and image reconstruction and processing techniques. A vital aspect of a simulation is to have realistic phantoms or models of the subject’s anatomy and physiology. The results need to be indicative of what would occur in actual patients in order to have practical value.
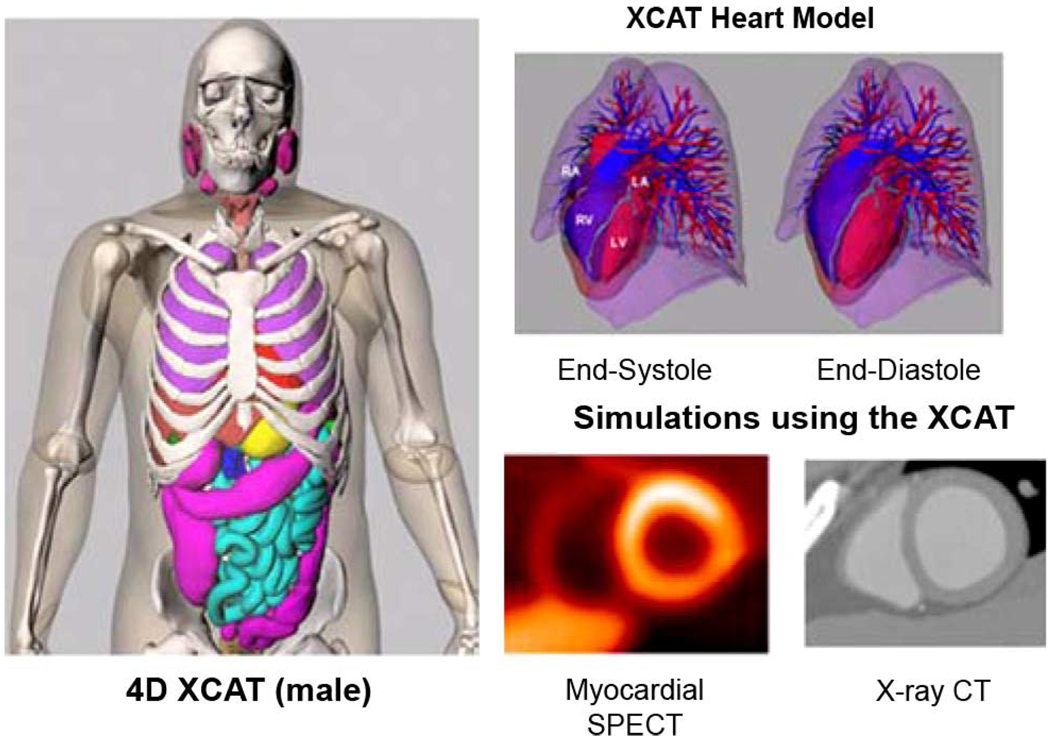
The 4D NURBS-based cardiac-torso (NCAT) phantom was developed to provide a realistic and flexible model of the human anatomy and cardiac and respiratory motions for use in medical imaging research [1]–[4]. Originally designed for low-resolution nuclear medicine research, the phantom has been recently updated to include a more detailed, whole body anatomy with improved resolution. The new extended 4D NCAT or XCAT phantom has now found application in higher resolution imaging modalities such as MRI and CT. The 4D XCAT phantom has also been used in conjunction with accurate simulation models of the imaging process, e.g., through the use of Monte Carlo techniques. When these accurate models of the imaging process are applied to the XCAT, it is capable of generating realistic multimodality imaging data, e.g., SPECT, PET, MRI, and CT (Fig. 1).
Fig. 1.
(Left) 4D phantom. (Top Right) Realistic cardiac model of the XCAT including model for coronary arteries of the LV. (Bottom right) Multimodality simulations from the phantom.
A prior limitation to the 4D NCAT/XCAT series of phantoms was that the cardiac motion was modeled based on a single set of gated tagged MRI data of a particular normal male volunteer. The effects of disease on the cardiac motion could be simulated to a limited extent by scaling down the motion in user-defined pie-shaped regions in the left ventricular wall. This definition of disease had no physiological basis. In a previous study [5], we sought to overcome this limitation by incorporating into the phantom a physiologically based finite-element (FE) mechanical model for the left ventricle (LV). This model was found to accurately simulate the normal motion of the LV as well as abnormal motions due to ischemia.
The focus of the following is to describe our extension of the FE model of a normal beating heart in the 4D XCAT phantom to include the simulation of dyskinetic myocardial infarction (MI). Myocardial infarction (MI) represents a far more complex situation in terms of altered mechanics compared with the modeling of acute ischemia in which the cessation of the contraction is the most notable alteration [6]. In acute ischemia (< 6 h after onset of ischemia), the behavior of the ischemic region is governed primarily by the passive properties of the normal myocardial tissue. The transition from contractile tissue to passive stretching becomes evident within the first 30 min following coronary ligation and then remains relatively stable for the next 6 hours [7]. After 6 h the tissue shows distinct stiffening [8]–[10] which is poorly quantified.
Once the lack of blood flow has caused cell death (necrotic phase), the tissue is considered infarcted. In the days that follow, the behavior of the infarcted regions is governed by processes associated with inflammation and necrosis [6] with tissue stiffening being evident. This phase lasts until the amount of new collagen, predominately types I and III, in the tissue begins to substantially increase (fibrotic phase) signaling the beginning of scar formation (seven days in humans [11]). The fibrous phase lasts approximately 21 days [11] in humans and is followed by the remodeling phase. This phase is marked by the thinning of the scar and an expansion of the surface area in the infarction LV wall. Histology indicates that the rise in collagen content slows but cross-linking continues to increase resulting in a stiffer scar [11].
Surrounding the scar tissue is a region known as the border zone (BZ). The presence of a border zone has been demonstrated though imaging [12]–[17] with these regions showing hypocontractile behavior while having normal perfusion. Mechanical factors such as tethering have been suggested to explain the underlying depressed function in the border zone myocardium [13, 18–22]. It is these two regions and their associated mechanical behavior that must be included in a realistic model of myocardial infarction. We have developed such a model for the beating heart model of the 4D XCAT phantom by expanding upon our previous FE techniques as outlined below.
We have demonstrated in our previous work that a finite element representation of the LV can be seamlessly combined with the 4D NCAT phantom to model normal and ischemic function. The FE model of the LV was necessary in order to define ischemia in the NCAT using a physiologically based model. We have continued this work and applied the newly developed infarction models to the successor to the 4D NCAT, the 4D XCAT phantoms. The XCAT is a full body implementation of the NCAT and can produce a much greater range of synthetic images than the NCAT. Modeling infarction represents a more complex modeling problem than the present modeling of ischemia. In acute ischemia, the passive behavior of the affected region is unchanged from the rest of the myocardium. The primary manifestation of ischemia is the alteration and cessation of active contraction. In the case of infarction, the geometry, fiber distribution and material behavior all change as described above.
One of the primary considerations of combining FE models with the NCAT or XCAT was that the geometry and the deformations of the LV model be consistent with the phantom LV. The FE LV geometry needed to fit into the phantom heart seamlessly. Furthermore, the gross deformations in the form of wall motion, wall thickening, and LV twist, had to be similar to that defined in the phantom so that the FE LV geometry would interact with the rest of the heart in a realistic manner over the entire cardiac cycle. The model must, therefore, provide subject-specific, mechanical behavior.
II. METHODS
A. Finite Element Model Generation
Complete details of the normal and ischemic models of the beating heart can be found in our previous publication [5]. The following is a short synopsis. A gated high resolution CT image set of a normal male subject acquired on a 32-slice Siemens X-ray multi-slice CT (MS CT) scanner (Siemens AG, Erlangen, Germany) was used to define the cardiac geometry of the finite element model. The patient study consisted of 9 time frames during the cardiac cycle. Each time frame consisted of a 512 × 512 × 231 image array with a pixel size and slice thickness of 0.42 mm.
The image dataset obtained near the beginning of diastole (approximately 1/3 of the way into diastole [23]) was used to define the undeformed reference configuration of the FE model. The boundaries of the epi- and endocardial surfaces of the left ventricle were manually segmented using the software program SURFdriver [24]. The segmented closed contours were used to define the FE mesh using TrueGrid [25] preprocessing program. Complete details of the normal and ischemic models can be found in Veress et al. [5].
1) Passive Material Behavior
The passive myocardium was represented as a transversely isotropic material with the strain energy function W defined as
| (1) |
where F1 represents the behavior of the ground substance surrounding the fibers while F2 represents the behavior of the fibers, and the final term represents the bulk behavior of the material where K is the bulk modulus of the material. F is the deformation gradient tensor and J is the determinant of the deformation gradient tensor F, i.e., J = det (F) [26], [27]. Ĩ is the first deviatoric invariant of the right Cauchy deformation tensor. The scalar λ̃ is the deviatoric stretch ratio along the fiber direction, a. A neo-Hookean form was used to represent the ground substance matrix, i.e.,
| (2) |
where µ is the shear modulus of the ground substance. The passive Cauchy stress tensor is
| (3) |
where W̃1, and W̃λare strain energy derivatives with respect to Ĩ1 and λ̃, B̃ is the deviatoric left deformation tensor, p is a pressure term which enforces incompressibility, 1 is the identity tensor, and “⊗” represents the vector outer product operation.
The stress-stretch behavior (λ̃Wλ̃) for the fiber direction is represented as an exponential function, with no resistance to a compressive load
| (4) |
The material coefficients C3 and C4 scale the fiber stress and control its rate of rise with increasing stretch, respectively. Further details of this material model can be found in the work of Weiss et al. [26]. The values of the constants µ, C3 and C4 were defined through least squares fit of biaxial testing of myocardial tissue [28]–[30].
2) Active Contraction
A “time varying elastance” active contraction model [29], [30] was added to the passive material model so that the total Cauchy stress T in the fiber direction is the sum of the active stress tensor T(a) (a ⊗ a) and the passive stress tensor T(p)
| (5) |
where a is the deformed fiber unit vector, defined as a = (F · a0)/λ. The active fiber stress T(a) is defined as
| (6) |
where Tmax = 135.7 KPa is the isometric tension under maximal activation and Ca0 = 4.35 µM is the peak intracellular calcium concentration. C governs the shape of the activation curve [30]. The length dependent calcium sensitivity ECa50 is governed by the following:
| (7) |
The active contraction was governed by the product TmaxCt (an active contraction stress) in (6), which was used to define a “load curve,” specifying the degree of contraction and subsequent relaxation during the cardiac cycle [5]. The intraventricular diastolic and systolic pressure-time curves were defined from literature values [30], [31]. The fiber distribution within the normal myocardium was based on diffusion tensor MRI measurements of cadaveric human hearts (−90° epi, to 90° endo) [32]. Each element within the FE mesh has a fiber direction associated with it in the form of a vector in 3D space. In this manner, the fiber distribution was defined for every element of the FE mesh. The activation of the myocardium is simultaneous as there is no electrical conduction in this model. In other words, the activation of every element occured exactly at the same time. The analyses were conducted using NIKE3D, a nonlinear, large deformation FE package [33], [34].
3) Scar Fiber Definition
The region defined as ischemic in our previous work [5] was redefined as the scar portion of the MI model and similar to the way the XCAT has defined the wedges of ischemic and infarcted tissue. In practice, any shape can be defined using the finite element preprocessor (TrueGrid, XYZ Scientific Applications, Livermore, CA) as well as other software developed for this work. The fiber distribution within the scar was defined using the strain and fiber distributions reported by Holmes et al. [6], [35], specifically, the epi and endocardial fiber angles were made more circumferential. Rather than rely on published values, the fiber distribution was defined by matching the diastolic longitudinal and circumferential strain stiffening evident in the Holmes studies. The scar was found to be stiffer in the circumferential direction than the noninfarcted controls manifesting in a 32% reduction in strain (Green–Lagrange). In contrast the longitudinal strains in the infarcted animals showed similar strain values as the noninfarcted controls. In order to reproduce this behavior, the fiber stiffness was increased by approximately 2.1 times that of the normal LV. However, stiffening alone did not reproduce the strain distribution described in the works by Holmes, thus requiring an alteration in fiber structure within the infarction region.
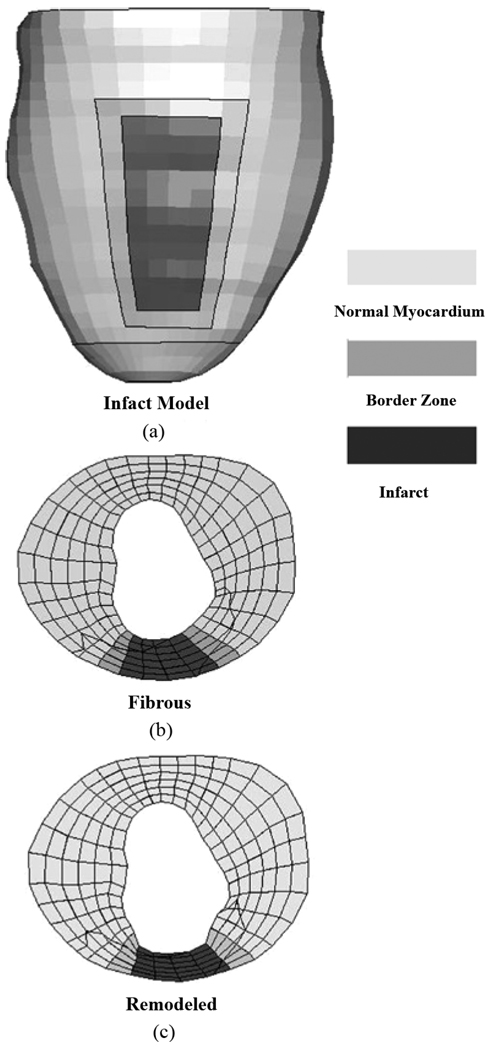
An iterative process was utilized to determine the appropriate fiber distribution. The fiber distribution was also made incrementally more circumferential in orientation until the fiber distribution showed a 32% reduction in strain in the circumferential direction yet the average longitudinal strain was nearly identical to the normal control model value within the infarct region. The fiber distribution of −40° at the epicardium to 42° at the endocardium in the infarcted region was found to produce circumferential strains that were approximately 32% reduction in strain than the normal model under diastolic pressures (1.6 KPa or 12 mmHg). The longitudinal strains were nearly identical to those found in the normal model for the same nodes. This then represents the stable post-infarct configuration at the end of the fibrous phase [Fig. 2(a) and (b)].
Fig. 2.
(a) Anterior infarction location in the left ventricle. Mid-ventricular short axis cross-sections for the (b) fibrous and (c) remodeled infarctions. Light gray is the normal myocardium, medium gray is the border zone (BZ) and the dark gray is the infarcted zone.
A second configuration of the heart was considered, that being the remodeled infarct. For this configuration, the wall of the infarcted myocardium was reduced by 30%. Within the infarcted region the endocardial surface was moved 30% closer to the epicardial surface [Fig. 2(c)]. The reference shape of the epicardial surface was not altered and the nodes within the wall were evenly distributed between the surfaces. It should be noted that the surface area of the infarcted region was not increased as has been reported in the literature for this type of infarction. The reasoning behind this was that the comparisons of the strains would be more relevant for identically sized infarcted regions within the two models. The material properties and fiber distribution within this region were initially not altered from those of the fibrous model. This model was then iteratively run to determine the amount of increased stiffness necessary for the remodeled LV to reproduce the strain values within the infarction region as reported in the literature.
Recent studies [36], [37] have found that the reorientation of the fiber architecture in the infarcted myocardium described by Holmes et al. [6], [35] have not been confirmed through imaging studies thus calling into question the validity of using an altered fiber structure when modeling the infarct. In order to explore the effects of the two types of fiber definitions, normal and altered, the fibrous and remodeled models were rerun using the fiber structure of the normal myocardium. The transmural strain distributions were then compared with the results of the models having the altered fibers distributions.
4) Scar Active Contraction
The active contraction within the infarcted region was simulated in the FE model for the LV by modifying the active contraction model as described by Mazhari et al. [38]. The active contraction stress was eliminated by employing a step change increase in calcium sensitivity Eca(50). This change in calcium concentration sensitivity causes a complete cessation of the contractile function within the ischemic region. This lack of any active contraction represents the baseline configuration of the fibrous and remodeled FE models.
5) Border Zone
The border zone (BZ) was defined as the elements surrounding the infarcted region (5–7 mm). In the remodeled case, the BZ was also the transition between the infarcted remodeled elements and the normal wall elements [Fig. 2(c)]. The fiber distribution in the BZ was not altered from that of the normal model. The active contraction stress in the BZ was reduced by 50% (0.5 Tmax) according to published literature values [39], [40].
B. Evaluation of the Finite Element Model
The transmural strain distributions resulting from the two definitions of infarction were compared with the strain distributions predicted by the normal FE model [5]. The transmural strain results of both infarction models were determined and the average circumferential and radial strains were determined and compared with those of the normal model as well as literature values. The strains predicted by the models could not be directly compared with the literature values due to inherent differences in the reference configurations of the experimental strain measurements and the FE model results. The reference (unloaded) configuration for the measurements found in the literature use end-diastole as the reference configuration while the FE models used in this study use the beginning of diastole. The tagged MRI strain measurements reported in the literature use end-diastole as the reference configuration while our FE models use the beginning of diastole. The end-diastolic node locations were substituted for the beginning-diastolic node locations. The displacements from end-diastole to end-systole from the FE analysis were then applied to the wall nodes. In other words, in these new models, the displacements going from beginning-diastole (reference configuration) to end-diastole (new reference configuration) in the original FE analysis were applied to the nodes of the original model to define the new ode locations. End diastole then became the new reference configuration. This new model was then run from end-diastole to end-systole (systolic contraction only) using the displacements defined for end-diastole to end-systole in the original model. The strains in the direction of the fibers reported using the shifted reference configuration are known as ejection strains [41]. The average strains within the infarction zones were then determined and compared with literature values.
Similar to what was done for ischemia [5], the FE deformation results for infarction were compared with results obtained using the 4D XCAT’s simplified model of disease. In the original 4D NCAT/XCAT phantom, regional motion abnormalities were modeled by just scaling down the motion of the LV myocardium in the infarcted region. The infarcted region in the FE mechanical model was adjusted to model this simple definition for two cases, 50% and 100% reductions in motion. The deformations defined by the existing definition of ischemia/infarction were used to define the infarction region in these additional models. The pressure loads were removed from the infarction regions, and the only loading was the displacements determined from the 0% or the 50% displacement settings in the 4D XCAT phantom. The end-systolic transmural strain distributions were determined and compared with the strain distributions predicted by the fibrous and remodeled infarction models.
It was assumed from the outset that the remodeled configuration would show an increased strain as there is simply less wall to take up the pressure load and this portion of the wall was assigned the same material properties as the fibrous case. In order to study the effects of cross-linking of the remodeled case, this model was iteratively run while selectively stiffening the scar tissue until the average strain values found in the literature were reached.
The computations were carried out on a four core Intel based Linux computer with 4 GB of core memory requiring approximately an hour of analysis time. This relatively short analysis time allowed for multiple iterations of the analyses for the fibrous model in order to find a scar fiber distribution that provided the appropriate circumferential and longitudinal strain distributions.
C. Incorporation of the FE Model Into the 4D XCAT Phantom
Complete details of the methods used to combine the FE results with the 4D XCAT phantom can be found in Veress et al. [5]. Briefly, the organ models in the 4D XCAT phantom are defined using 3D NURBS surfaces [4]. The size and shape of each NURBS surface model was determined by a set of control points. A surface can be altered by applying affine and other transformations to the control points in order to model anatomical variation or patient motion. The node points of the FE mesh at the beginning of diastole were used to define the control points for an inner, outer, and three mid-ventricular NURBS surfaces for the LV. The motion of the node points over the cardiac cycle as determined by the FE analysis were used to define the time-position curves for the control points of the surfaces which were used to replace the standard 3D XCAT LV beating heart model of the standard 4D XCAT. Atrial motions were modified to accommodate the new ventricular surfaces created from the mechanical model.
The FE based infarction models were incorporated into the 4D XCAT phantom and a gated myocardial perfusion SPECT simulation as performed. The distribution of radioactivity concentration was set to model the uptake of a typical Tc-99m sestamibi patient study [42]. The FE based beating heart model was divided into 16 time frames over a cardiac cycle (1 beat per second). Each generated 4D XCAT phantom with the heart models at the 16 time frames was stored in a 128 × 128 × 128 array with a pixel size and slice thickness of 0.31 cm. For each heart model, the 16 time frames were averaged to create phantom of the average beating heart motion for that case. Emission projection data were generated using a parallel projection model simulating an L-configured dual-camera SPECT system equipped with a transmission source. A complete projection dataset was generated over the typical 180° (45 right anterior oblique to 45° left posterior oblique) rotational arc around the patient. The simulations used a projection model that included the effects of nonuniform attenuation, detector response, and scatter. A low-energy high-resolution (LEHR) collimator with a thickness of 4.1 mm and hexagonal holes with a flat-to-flat size of 0.19 mm was simulated. The 128 × 128 simulated emission projection images were collapsed to 64 × 64 to simulate sampling used in a clinical data acquisition.
The noise-free emission projection data were reconstructed using the iterative ordered-subset expectation-maximization (OS-EM) reconstruction method with compensation for attenuation, scatter, and collimator-detector response [43]. The images were reconstructed into 64 × 64 arrays with 64 slices and a pixel width and slice thickness of 0.63 cm.
The intensity profiles through a representative mid-ventricular slice were compared for the normal, fibrous and remodeled reconstructed images for the case of full perfusion. The fibrous and infarct cases were reconstructed with the perfusion reduced to 50% of the normal. The intensity profiles through the walls were compared.
III. RESULTS
A. Analysis of the Finite Element Model for Infarction
The fibrous and remodeled models showed changes in both the systolic and diastolic volumes from the addition of the infarcted regions. The normal beating heart model had an end-diastolic volume of 107 ml and an end-systolic volume of 41 ml. The fibrous and remodeled simulations produced end-diastolic volumes of 106 ml and 108 ml, respectively, and end-systolic volumes of 47 ml and 55 ml. The remodeled case where the wall was defined as having been 10 times stiffer than the fibrous case had an end-diastolic volume of 106 ml and 51 ml for end-systole. The presence of the infarction decreased the ejection fraction from 62% in the normal to 56% for the fibrous case. This was further reduced to 49% for the remodel case (Table I) with the original material properties. The remodeled case with the wall stiffness increased tenfold showed an improved ejection fraction of 52%.
TABLE I.
Comparison of the LV Motion of the Normal Model to That of the 4D XCAT Phantom Indicate Excellent Agreement Between the Gross Deformations Predicted by the FE Models and Deformations of the XCAT Phantom. The XCAT Results are Based on Tagged MRI Displacements for a Normal Human Subject
| Heart | LV Twist (Base, Apex) |
Long. Cont. of LV Base (mm) |
LV Wall Thickening (lat., sep., inf., anterior)(%) |
Ejection Fraction (%) |
|---|---|---|---|---|
| 4D NCAT | (5°, −13°) | 14 | (27,31,41,29) | 60 |
| Normal FE Model | (6°, −11°) | 13 | (33,38,37,23) | 62 |
| Fibrous FE Model | (7°, −11°) | 11 | (31,34,37,−5) | 56 |
| Rem. FE Model | (7°, −11°) | 11 | (31,33,36,−9) | 49 |
| Rem. FE Model stiffened | (7°, −11°) | 11 | (31,33,36,−6) | 52 |
The gross deformations of the normal LV model was consistent with the 4D XCAT phantom (Table I) ensuring that the FE based LV would move and fit properly in the 4D XCAT heart. The wall thickening, and LV twist values were very similar to those of the XCAT LV. The infarcted regions of the LV in the fibrous model showed slight wall thinning. The remodel case showed nearly double the wall thinning as the fibrous case. The remodeled case with the tenfold increase in wall stiffness showed nearly half of the thinning (Table I) than the unaltered remodeled LV model.
The strain distribution of the normal LV was consistent with literature values from a number of studies (Table II). Our previous work further indicated that the strain distributions were consistent with highly detailed measurements conducted by Waldmen et al. [44]. The comparison of the Waldmen measured strains with those of the normal model can be found in our previous work [5].
TABLE II.
Comparison of the FE Strain predictions for the Normal Model to Values Found in the Literature. The Forward FE Results are in Reasonable Agreement With Published Experimental Results.
| Strain | FE Model | Sinusas[88] | Guccione[49] | Oments[60] | ||||
|---|---|---|---|---|---|---|---|---|
| Endo | Epi | Endo | Epi | Endo | Epi | Endo | Epi | |
| Circumferential | 0.29 | 0.07 | 0.15 | 0.07 | 0.15 | 0.09 | 0.22 | 0.05 |
| Radial | 0.33 | 0.15 | 0.25 | 0.15 | 0.34 | 0.19 | 0.18 | 0.12 |
| In-plane Shear | 0.01 | 0.01 | <0.02 | 0.06 | 0.01 | 0.03 | 0.02* | |
This table has been reproduced from our previous paper [5].
Reported a Mid-Wall Peak of 0.08
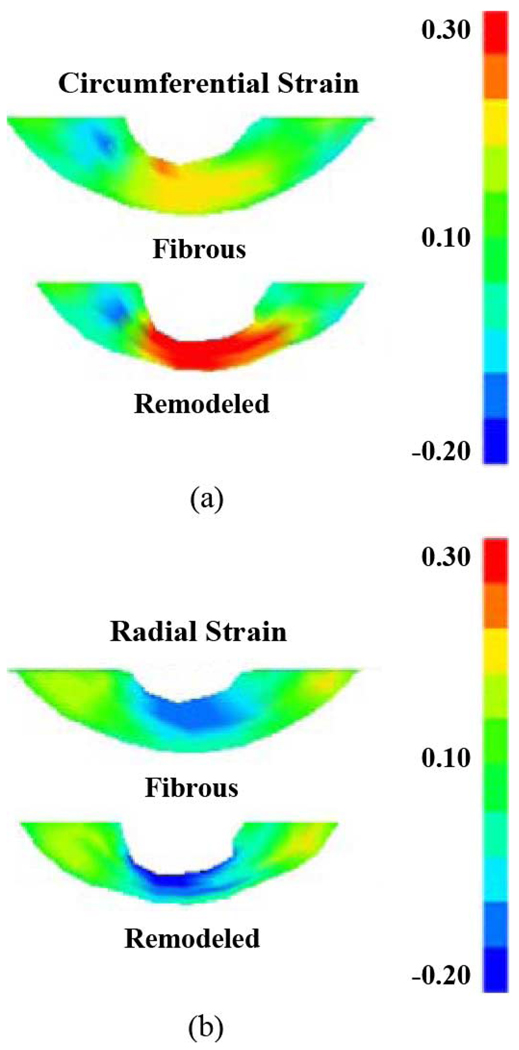
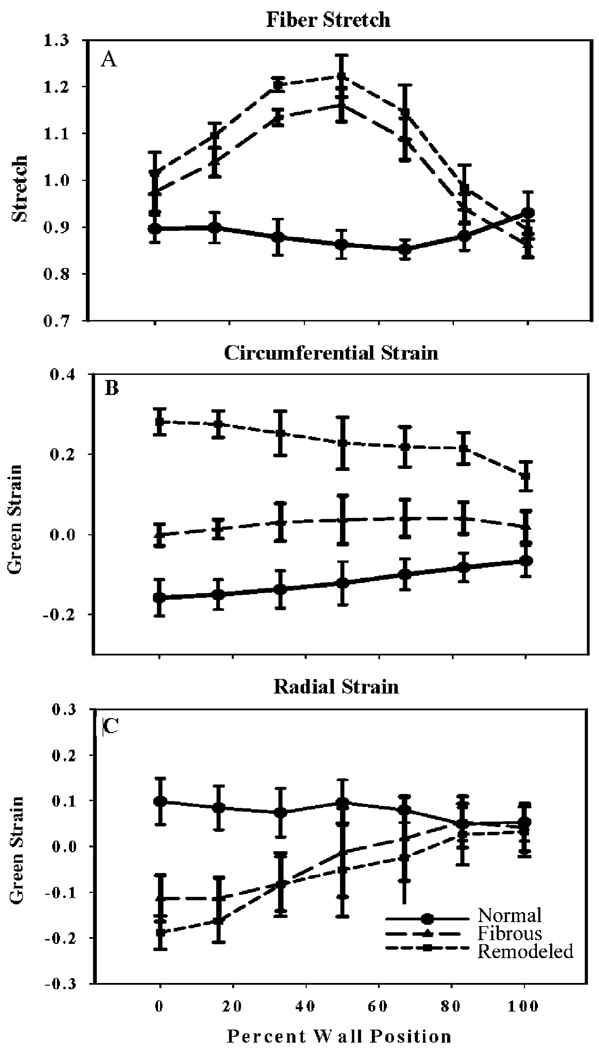
The end-systolic strain distributions within the infarction for the fibrous and remodeled cases showed the largest strain values at the endo-cardial surface with a semi-linear decrease toward the epicardial wall. The exception is the circumferential fibrous strain distribution which had the maximum near the epi-cardial wall (Figs. 3 and 4). The negative sign in the radial strain values indicates compression. For the fibrous infarction case, the average end-systolic circumferential strain was 0.125 indicating elongation, the average end-systolic radial strain was −0.03 indicating wall thinning and the fiber stretch of 1.03 indicating fiber elongation. The remodeled case had an average circumferential strain of 0.23, and an average end-systolic radial strain of −0.06 and a fiber stretch of 1.08. For comparison purposes, the normal model had an average end-systolic circumferential strain of −0.04, an average end-systolic radial strain of 0.01 indicating wall thickening and the fiber stretch was 0.93 indicating fiber contraction. It should be noted that these results are referenced to the beginning of diastole. The results for the fibrous and remodeled infarction models indicated nearly identical cross-sectional strain distributions for both circumferential and radial strains (Figs. 3 and 4).
Fig. 3.
Short axis cross-sections for end-systolic circumferential (a) and radial (b) Green-Lagrange Strains through infarcted regions with altered fiber distributions. Remodeled infarcted regions show elevated strains compared with fibrous models. Strains are with respect to beginning diastole.
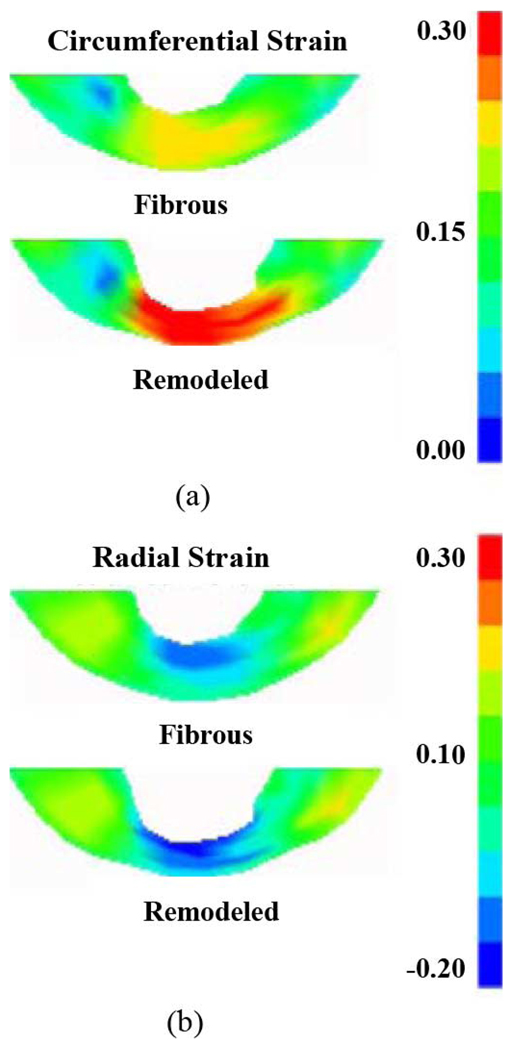
Fig. 4.
Short axis cross-sections for end-systolic circumferential (a) and radial (b) Green–Lagrange strains through infarcted regions with normal fiber distributions. The strain distributions are essentially equivalent to those produced by the altered fiber models depicted in Fig. 3.
The average circumferential systolic strain with the reference state shifted to end-diastole was 0.03 for the fibrous model and 0.08 for the remodeled model. Similar results were found for the radial strain with −0.07 for the average fibrous infarct strain and −0.03 for the remodeled case. In order for the remodeled infarct model to reproduce literature values the wall had to be stiffened to a value approximately 10 times that the fibrous stiffness [10 times C3 in (4)]. The infarcted region had an average circumferential strain of approximately 0.04 and an average radial strain of −0.05. The average ejection strains [41] (fiber strains from end-diastole to end-systole) were 0.05 for the fibrous model and 0.08 for the remodeled case. The remodeled case using the increased stiffness had an ejection strain of 0.02. The infarction models with the normal fiber distributions within the scar showed nearly identical transmural fiber distributions as the altered fiber models. The difference in transmural strains was less than 4% for the average transmural circumferential and radial strains depicted in Fig.5 (referenced to end-diastole). In most cases the difference was less than 3%. In contast, the longitudinal (long-axis strain) showed decreased values by 7%. This was due to the steeper fibers distribution within the scar so that the region was stiffer in this direction during diastolic filling and contracts more in this direction during systole.
Fig. 5.
Transmural strain distributions predicted by the normal FE model and the two infarct models with altered fiber distributions: (a) fiber stretch, (b) circumferential strain, and (c) radial strain, for the infarcted region shown in Fig. 2 for the normal (solid line) model, fibrous (long dashed line) model, and remodeled (short dashed line) model.
B. Comparison of the FE Infarction Models to the Original XCAT Model
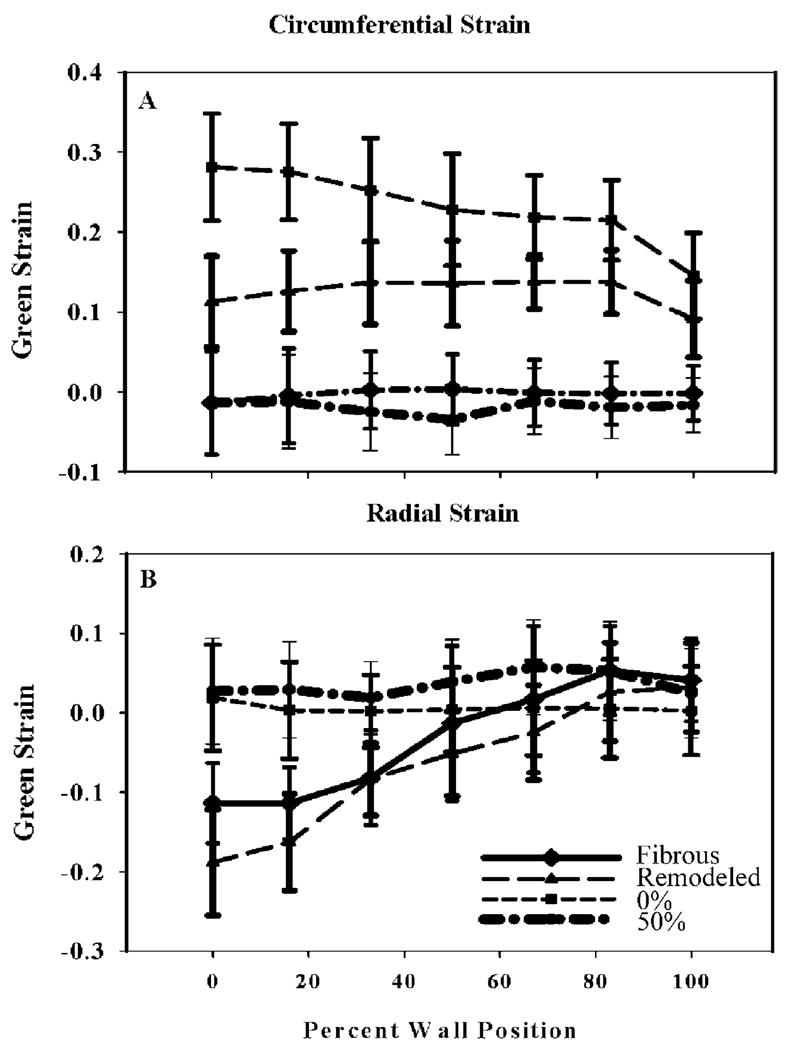
The comparison of the FE infarction results with the results using the 4D XCAT phantom’s original definition of ischemia/infarction show that the strain distributions predicted by the XCAT are of opposite sign as the dyskinetic model results (Fig. 6) and have relatively low end-systolic strain values.
Fig. 6.
The transmural strain distributions predicted by the XCAT definition of infarction shows relatively low strain values. These distributions are compared with the infarction model FE strain distributions with the altered fiber distributions: (a) Circumferential strain and (b) Radial strain. The XCAT results show reasonable strain distributions to indicate hypokinetic and akinetic behavior.
C. Myocardial SPECT Simulation Study
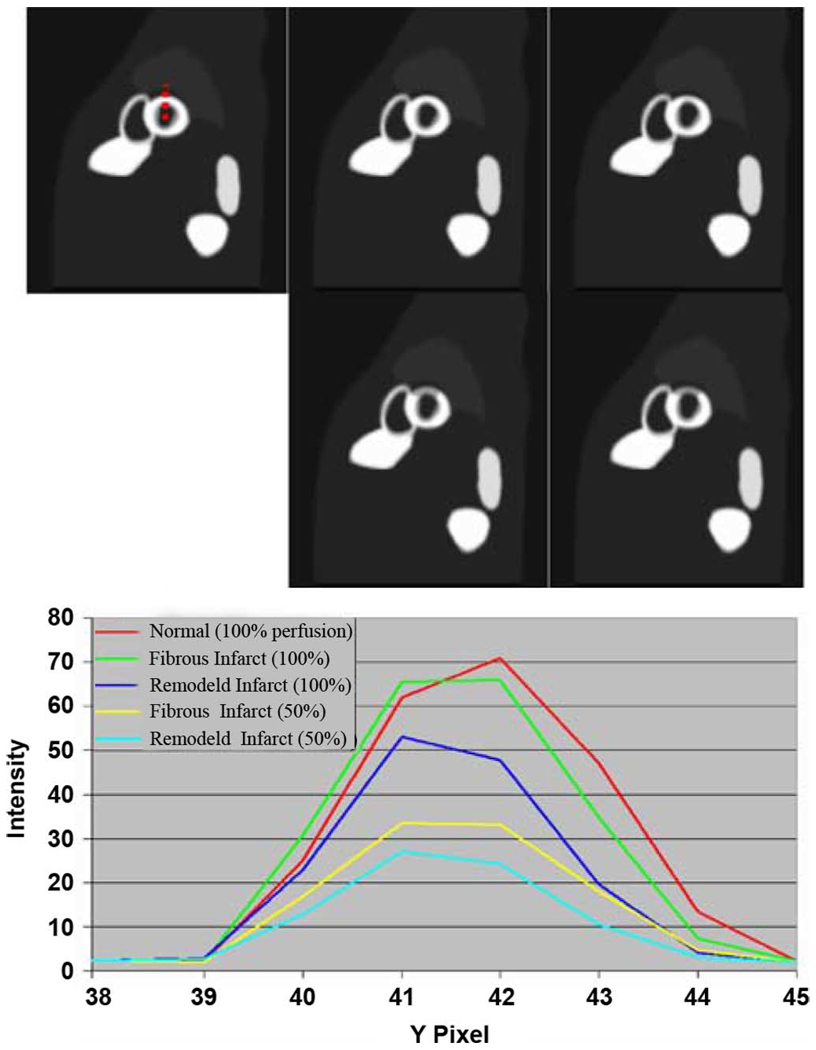
The intensity profile results based upon the reconstructed images (Fig. 7 top) indicate that for the normal perfusion cases the intensity profiles were nearly identical for the normal and the fibrous cases (Fig. 7 bottom). It should be noted that normal perfusion represents an unrealistic case that would never be found clinically. The intensity profiles for the reduced perfusion cases indicate that the difference in intensity values across the wall for the fibrous and remodeled infarcts were approximately 8–10 out of 256 gray levels. This difference in intensity is reflected in the deformation results. The maximum deformation difference between the normal FE model and the fibrous model, as measured from the models themselves, was 1.2. The maximum deformation difference between the normal and the remodeled models was 3.0.
Fig. 7.
Intensity profiles (bottom) across the anterior region (red dashed line) of the LV taken from short-axis images (top) indicate that the remodeled defect based on the FE model shows the greatest reduction in intensity with respect to the normal both with full perfusion and the 50% reduction in perfusion. The full perfusion fibrous infarct is indistinguishable from the normal but represents a case never found clinically. The 50% reduction in perfusion results in difficulty in distinguishing between the fibrous and remodeled cases due to the low resolution of the reconstructed gated SPECT images.
IV. DISCUSSION
The use of finite element models to drive a realistic computerized phantom designed originally for imaging research represents a unique and novel combination of technologies. It allows the phantom to model the full range of behavior found with infarction. These include hypokinetic behavior found in sub-endocardial ischemia [5] and infarction as well as akinetic behavior. Both the hypokinetic and akinetic behavior may be modeled in two ways. The wall motion in the 4D XCAT heart model can be reduced or fixed over the entire cardiac cycle. The second method involves reducing but not eliminating the contractile behavior within the infarcted region of the FE model. This was demonstrated by Dang et al. [39] to model akinetic behavior of an infarcted region. Their work suggested that infarcted tissue must have between 20% to 50% of the myocytes contracting in order for the tissue to behave in an akinetic manner. The exact amount of contracting myocytes depended upon the relative stiffness within the region [39]. This secondary method of defining hypo- and akinetic wall motion represents a physiologically based depiction of cardiac motion where one defines the relative myocyte function directly. This methodology can also be used to define subendocardial infarctions. The 4D XCAT heart model is ill equipped to mimic this type of infarction since only the overall wall motion is defined. Finite element models allow for the defining of a subendocardial region and the wall motion will then be a function of the contraction within the normally perfused myocardium and the passive mechanics of the scar tissue.
The primary focus of our work is reproducing dyskinetic behavior which the 4D XCAT heart model cannot accommodate. Two new infarction cases have been developed representing fibrous and remodeled infarctions. The presence of these relatively modest sized infarctions had a clear effect on the predicted volumes and ejection fractions of the LV. However, the models do not have any of the compensatory mechanisms resulting in increased contractility of the native heart so that the predicted changes in volume and EF are not likely to be seen the native heart with a similar sized anterior infarction. However, the models can easily be adjusted for an increased compensatory contraction provided the amount of increased contraction known.
The average circumferential strain results were consistent with the results of the dyskinetic infarction results reported in the literature (Table III). The average circumferential strain for the fibrous model was similar in magnitude and sign with the strain measurements reported by Walker et al. [45]. These studies were made in a sheep whose heart was 22.5 weeks post-infarct and was imaged using tagged MRI and subsequently analyzed to determine the strain distributions. The results were also consistent with those of Carlsson et al. [46] who measured strain within infarction scar tissue in pigs whose hearts were 50 days post-infarct and again using tagged MRI analysis. The radial strain results predicted for the fibrous model results were slightly higher than those measured by Pislaru et al. [47] using echocardiographic interrogation porcine subjects. The remodeled results using the same material properties as the fibrous were higher than the literature values. The tenfold increase in stiffness was found to reproduce the strain values reported in the literature. This indicates that there must be increased stiffening of the infarcted region even after it has reached a stable configuration this likely due to the cross-linking of collagen that goes on during remodeling [6], [48].
TABLE III.
Dyskinetic, Average Transmural Strain Data Compared to Published Data in the Literature
The results of our model produced results consistent with other FE based models of infarction. The radial strain results of −0.03 were consistent with the results of Dang et al. [39] whose model showed radial strains in the range of −0.01 to −0.07 for 10% dyskinetic infarction. The average ejection strain results were also consistent with the strain results predicted by Kerckhoffs et al. [41] for ejection strain within infarcted regions of hearts having left bundle branch block (~ +0.08) and these hearts undergoing bi-ventricular pacing (~ +0.07).
The simulated noise-free 4D gated myocardial perfusion SPECT images generated from the 4D XCAT phantom indicate that a 30% decrease in thickness is difficult to ascertain from the relatively low resolution available from this type of imaging (Fig. 7 top) particularly for the reduced perfusion case. The intensity profile results indicate that the difference in intensities between infarction types would be difficult to see for the reduced perfusion case. With the addition of noise both the difference in thickness between the two lesion types and the difference in the uptake would be even more difficult to distinguish. The differences, however, may be more distinguishable using higher resolution imaging such as PET, MRI, or CT.
The alteration of the fiber distributions to the normal distribution within the scar region had its greatest influence in the long-axis direction. The radial and circumferential transmural strain distributions (Figs. 3 and 4) remained largely unaltered. The average transmural values also showed little change. This may be due to the relatively small size of the infarcted area as well as the shape of the region. The scar is rectangular with the greater dimension being longitudinal rather than being circumferential. This shape may minimize the effects of the fiber distributions in the short-axis strains.
The fiber distribution determined by fitting the models to the strain distributions described by Holmes et al. [6], [35] showed less circumferential reorientation (−40° at the epicardium to 42° at the endocardium) than those reported in their work. They reported that the majority of large collagen fibers in the scar are oriented within 30° of the circumferential direction.
The sophistication of the FE model used for this study should be evaluated with respect to the application. The model was designed to provide realistic deformation distribution in order to produce reconstructed gated myocardial perfusion PET and SPECT synthetic images of dyskinetic infarctions which the XCAT cannot accommodate. As demonstrated in our previous work [5] as well as by the models described above, our FE LV models can provide strain distributions and gross changes in geometry consistent with literature values (Tables I–IV) [5]. The change in gross geometry suggests that both systolic and diastolic function was negatively affected by the presence of the infarct. The diastolic volume was reduced in both the fibrous and remodeled cases. Increasing the stiffness of the remodeled infarct improved overall cardiac function.
TABLE IV.
Comparison of the FE Strain Predictions for the Fibrous Infarct Model to Average Values Found in Ashikagi et al. (Estimated From Fig. 7 Dyskinetic Infarction Heart) Show Reasonable Agreement for all of the Regions. The Remainder of the Hearts in that Figure Displayed Akinetic and Hypokinetic Behavior
| Strain | FE Remodeled Stiffened | Ashikaga et al. [89] | ||||
|---|---|---|---|---|---|---|
| remote | BZ | infarct | remote | BZ | infarct | |
| Circumferential | −0.18 | 0.02 | 0.04 | −0.13 | 0.03 | 0.06 |
| Radial | 0.24 | 0.01 | −0.05 | 0.23 | 0.01 | −0.01 |
A. Limitations
The material model used in this study is similar to that proposed by Guccione et al. [49], [50] and utilized by Kerckoff [23], [41], [51], [52] and others [45], [53]–[55] where the fiber is an exponential function of the fiber strain. The primary difference is that the cross fiber stiffness terms are expressed in the Guccione model as an exponential while in the Weiss model they are represented as a linear function of the trace of the deviatoric deformation gradient [26], [27]. Our previous work as well as results shown in this paper demonstrates that this material model can produce realistic strain distributions for the normal LV wall. Finite element models based on transversely isotropy have been shown to be able accurately reproduce the observed strain distributions of the myocardium [50], [56]–[58]. One shortcoming of transverse isotropy is that this material model cannot accurately predict the transverse shear strains during systole [44], [59], [60]. Studies have indicated that the myocardium is structurally orthotropic [41], [61]–[64]. In order to address this problem, the Guccione model has been extended to be orthotropic [50] by adding additional cross fiber terms that represent the in-sheet and cross-sheet stiffness. Another orthotropic formulation was proposed by Peter Hunter’s group [65], [66]. It is based on the fitting of 18 material property parameters each of which have a structural basis. Assumptions based on the microstructure were used to reduce the number of material parameters since the fitting of a large number of material constants can be difficult [50]. Even with the increased accuracy of orthotropic material models, transversely isotropic material models continue to be used to model the myocardium [23], [39], [41], [45], [52], [54], [55], [67], [68], most likely due to their ease of use as well as the prevalence in the literature of published values for the material parameters definitions e.g., Guccione et al. [69], [70].
Another limitation of the current model is that there is no electrical conduction system. Conduction inhomogeneities [41] within the scar tissue are not taken into account by our model. These inhomogeneities affect the path and timing of the contraction sometimes leading to serious conduction abnormalities. The exploration of the effects of these infarction related conduction abnormalities [41], [51], [52] requires the use of a coupled electromechanical models. Work by Sermesant et al. [71] illustrates a 3D electromechanical model designed both for the simulation of the electrical and mechanical activity of the LV and RV as well as for the application of the models to image segmentation of a time series of medical images. The model incorporates a transversely isotropic material model that is coupled to a electrical propagation model based upon the FitzHugh–Nagumo reaction-diffusion equations. The nonlinearity of the myocardium is reproduced by piecewise linear sections of the stress/strain characteristics. In other words, multiple linear sections are combined to produce the hearts nonlinear behavior. The model was shown to be able to reproduce the twist and wall thickening characteristics of the LV. They further demonstrated that this type of model can be adjusted to model a patient-specific anatomy based upon MRI, and a framework to automatically estimate mechanical parameters, like local contractility, from tagged MRI based displacements [72]. Another coupled electromechanical model is the Continuity system.1 Recently, work of Kerchoff et al. [41] demonstrates that the system can reproduce most of the conduction abnormalities found in and around scar tissue with the exception of the transmural inhomogeneities. The results produced by our model simply cannot accommodate conduction abnormalities, however, these type of models without conduction systems can be used to accurately model myocardial infarction [45], [54], [55], [68], [73].
The work of McVeigh et al. [74] and Wyman et al. [75] suggests that uniform contraction may be a reasonable assumption for normal contraction or pathologies that do not directly affect the conduction pathways. Their work is based upon the direct measure of the temporal strain evolution through the use of tagged MRI. They found that the strain associated with activation is nearly uniform as a function of position within the LV based on right atrial paced subjects. From the mechanics prospective, this represents the best case. If the contraction is nearly uniform then there are no regions that are akinetic or dyskinesic. For example a large ischemic region with aneurymsal bulging would allow for less volume to be ejected thus reducing the efficiency of the pump. Another example of this type of behavior would be left bundle branch block (LBBB). In LBBB, the activation of the lateral wall is much delayed compared with the septal wall. The lateral wall must, therefore, work harder than the septal region because of the build up of pressure from the initial septal contraction. The effects of the increased lateral wall workload can be seen in imaging studies which found that LBBB causes increased wall thickening in the lateral wall [76]–[78] compared with the septal wall as well as increased remodeling following the same pattern [77], [78].
The model does not have a mechanism to mimic the compensatory increase in contraction due to the decreased cardiac output resulting from the infarct. A model capable of mimicking the response of the cardiovascular system would be necessary to provide an accurate increase in contraction. Work is currently underway to develop such a system [79]. Furthermore, such a system would allow for the modeling of other conditions such as hypertension and heart failure to be accurately reproduced and incorporated into the 4D XCAT. Another limitation is that the fiber distribution in the normal heart is based on literature values rather than measured values from the subject. Eventually, diffusion tensor MRI (DTMRI) should be able to provide subject-specific fiber distributions, however, current problems with motion artifacts and long acquisition times make in vivo measurement impractical. Our previous work showed that the model was able to reproduce the complex contraction and twisting motions of the heart observed using tagged MRI imaging of the native heart [5].
B. Fiber Composition and Distributions
Recent work has indicated that the scar is now considered living tissue, composed of fibroblast-like cells called myofibroblasts (myoFb) [80], [81]. These cells are active within the infarction site for years persisting long after the scar has formed [81], [82]. These cells are responsible for the turn over of type I and III collagens which are the primary structural components of stable scar tissue. Zimmerman et al. [48] has suggested that the original extracellular matrix acts as a scaffold along which fibroblasts migrate, laying down new collagen in approximately the same orientation as the original matrix with the non-ischemic myocardium acting as the source of the migrating fibroblasts. They also suggested that the dominant direction of deformation also influences infarct scar organization. The continuing addition and cross-linking of collagen in the infarction is likely responsible for increased stiffness necessary to reproduce the literature values in the established remodeled infraction. The driving force behind the remodeling may be similar to that described by Kroon et al. [55]. Their work suggests that the remodeling of microfibers were a local adaptation to local stress and strain distribution. The remodeling of the wall appears to be a function of the minimization of cross-fiber shear strain during the ejection phase of the cardiac cycle. Their work indicated that the result of this local remodeling was the increase in local tissue peak stress and strain during ejection. It is difficult to evaluate our results in terms of determining the driving force for the infarction remodeling as this is a function of passive stresses and strains during the cardiac cycle rather than the stresses and strains during active contraction of tissue as discussed in the Kroon work.
The comparison of the infarction model results with the strain distributions using the original definition of ischemia/infarction (defined simply by scaling down the motion) in the 4D XCAT phantom show that the strain distributions are of opposite sign suggesting the XCAT reproduces hypokinetic and akinetic infarction behavior compared with the dyskinetic behavior of the FE based models. In general, the strain distributions for the two XCAT infarction definitions (50% and 0%, Fig. 6) show reasonable strain distributions. The hypokinetic FE model would likely provide more reasonable strain distributions. However, more accurate strain distributions would not benefit the low-resolution reconstructed 4D gated myocardial perfusion PET and SPECT images generated from the 4D XCAT phantom. Also, one would expect very low strain values for the 0% displacement case [39] so the XCAT definition of infarction in this case seems quite reasonable.
The work of Walker and Chen [36], [37] found that the fiber orientations within the infarct regions remained unaltered after remodeling. In contrast, an imaging study by Wu et al. [83] found that the fibers did become more circumferentially oriented in infarcted regions after remodeling. As the imaging work becomes more sophisticated, the exact progression and change in fiber distribution will become better defined. Differences in imaging protocols and analysis likely affect the reported fiber architecture. For example, Dou et al. [84] demonstrated that fiber helix angle measurements were directly affected by the phase at which the images were studied. They demonstrated that the histogram of fiber helix angles becomes broader from early-systole to end-systole within the infarct region.
The noninfarcted regions adjacent to the infarct appear to undergo drastic changes in orientation. The Zimmerman et al. [85] porcine histological study found that adjacent tissue remodeled by expansion along the direction of the fibers and in the cross fiber direction three weeks post-infarct. Walker et al. [36] found that the fibers in the anterior region adjacent to the infarcts were circumferential at the epicardium and longitudinal at the endocardium. Wu et al. [86] found that the transmural fiber structure shifted toward a more left-handed orientation (positive fiber angles) in the adjacent tissue. The changes in orientation were found to be dependent upon the location of the tissue with respect to the infarcted region [36] as well as by the size of the infarcted region [87]. Wu et al. [87] suggested that larger scars lead to more LV remodeling in the adjacent regions. The changes in fiber architecture may also extend to the remote myocardium. Wu et al. found that the remote myocardium also showed a shift to a more left handed fiber orientation [86]. The alterations in the fiber distributions in the regions adjacent to the infarct have not been incorporated into the current model. These changes, as well as those in the remote myocardium will be added to the model once there is a general consensus on what the changes in the fiber structure are as well as having a firm delineation between the altered and normal myocardium. This has proven to be difficult [87] and determining the size of these regions remain undetermined. Furthermore, it appears likely that the post-infarct fiber distribution changes both within the infarct and in the adjacent regions will likely vary depending on the species being studied, the nature of the infarct as well as the time from infarction onset.
V. CONCLUSION
The 4D XCAT phantom, with its realistic model for the normal cardiac motion, is widely used in the evaluation and improvement of 4D cardiac imaging instrumentation, data acquisition techniques and image processing and reconstruction methods. It is necessary for the XCAT to be able to reproduce the full range of perfusion and deformation abnormalities seen in the clinical setting. The coupling of the continuum based FE models with the 4D XCAT phantom illustrates how the deformation characteristics due to infarction can be reproduced and incorporated into the XCAT phantom in order to produce synthetic images. In other words, the entire range of hyperkinetic, akinetic and dyskinetic motions are necessary to reflect ischemia and infarction. Being able to reproduce the full range of clinical presentations is extremely important in the development of new camera technologies and new data processing methodologies providing an invaluable tool with which to study the effects of anatomy and patient motions [1]–[4]. Simulations using the phantom provide a means to evaluate statistical requirements and temporal requirements needed to improve the diagnosis of cardiac abnormalities.
The 4D XCAT phantom, with its realistic model for normal cardiac motion, is widely used in the evaluation and improvement of 4D cardiac imaging instrumentation, data acquisition techniques and image processing and reconstruction methods. To develop a more versatile imaging simulation tool, it is necessary for the XCAT to be able to reproduce the full range of perfusion and deformations abnormalities seen in the clinical setting. Towards this goal, this paper creates an infarct model that couples continuum based FE models with the 4D XCAT phantom. This example illustrates how the deformation characteristics due to infarction can be reproduced and incorporated into the XCAT phantom in order to produce synthetic images that could reflect the entire range of hyperkinetic, akinetic and dyskinetic motions of the heart. Our previous paper demonstrated how this could be accomplished through the simulation of the deformations due to ischemia [5]. Simulations using the phantom provide a means to evaluate sensitivity and resolution (spatial and temporal) requirements needed to improve the diagnosis of cardiac abnormalities. The ability to reproduce the full range of clinical presentations will provide an invaluable tool with which to study the effects of anatomy and physiology, disease, and both anatomical and patient motion on image quality [1]–[5]. This is extremely important in the development of new camera technologies and data processing methodologies.
Acknowledgments
This work was supported in part by the National Institutes of Health under Grant R01 EB00121, Grant R01 EB07219, Grant R01 EB00168, Grant R01 HL091036 and in part by the Director, Office of Science, Office of Biological and Environmental Research, Medical Sciences Division of the U.S. Department of Energy under Contract DE-AC02-05CH11231.
Contributor Information
Alexander I. Veress, Department of Mechanical Engineering, University of Washington, Seattle, WA 98195 USA.
W. Paul Segars, Email: paul.segars@duke.edu, Department of Radiology, Duke University, Durham, NC 27705 USA.
Benjamin M. W. Tsui, Email: btsui@jhmi.edu, Department of Radiology, Johns Hopkins University, Baltimore, MD 21218 USA.
Grant T. Gullberg, Email: gtgullberg@lbl.gov, E. O. Lawrence Berkeley National Laboratory, Life Science Division, Berkeley, CA 94720 USA.
REFERENCES
- 1.Segars WP, Lalush DS, Tsui BMW. Development of an interactive software application to model patient populations in the 4D NURBS-based cardiac-torso phantom. IEEE Med. Imag. Nucl. Sci. Symp. Conf. Rec. 2000 [Google Scholar]
- 2.Segars WP, Lalush DS, Tsui BMW. A realistic spline-based dynamic heart phantom. IEEE Trans. Nucl. Sci. 1999 Jun.vol. 46(no. 3):503–506. [Google Scholar]
- 3.Segars WP, Tsui BM, Lalush DS, Frey EC, King MA, Manocha D. Development and application of the new dynamic NURBS-Based Cardiac-Torso (NCAT) phantom. J. Nucl. Med. 2001 May;vol. 42:7. [Google Scholar]
- 4.Segars WP. Ph.D. dissertation. Univ. North Carolina: Chapel Hill; 2001. Development of a new dynamic NURBS-based cardiac-torso (NCAT) phantom. [Google Scholar]
- 5.Veress AI, Segars WP, Weiss JA, Tsui BM, Gullberg GT. Normal and pathological NCAT image and phantom data based on physiologically realistic left ventricle finite-element models. IEEE Trans. Med. Imag. 2006 Dec.vol. 25(no. 12):1604–1616. doi: 10.1109/tmi.2006.884213. [DOI] [PubMed] [Google Scholar]
- 6.Holmes JW, Borg TK, Covell JW. Structure and mechanics of healing myocardial infarcts. Annu. Rev. Biomed. Eng. 2005;vol. 7:223–253. doi: 10.1146/annurev.bioeng.7.060804.100453. [DOI] [PubMed] [Google Scholar]
- 7.Gillam LD, Franklin TD, Foale RA, Wiske PS, Guyer DE, Hogan RD, Weyman AE. The natural history of regional wall motion in the acutely infarcted canine ventricle. J. Am. Coll. Cardiol. 1986 Jun.vol. 7:1325–1334. doi: 10.1016/s0735-1097(86)80154-1. [DOI] [PubMed] [Google Scholar]
- 8.Vokonas PS, Pirzada FA, Robbins SL, Hood WB., Jr Experimental myocardial infarction. XV. Segmental mechanical behavior and morphology of ischemic myocardium during hypothermia. Am. J. Physiol. 1978 Dec.vol. 235:H736–H744. doi: 10.1152/ajpheart.1978.235.6.H736. [DOI] [PubMed] [Google Scholar]
- 9.Pirzada FA, Ekong EA, Vokonas PS, Apstein CS, Hood WB., Jr Experimental myocardial infarction. XIII. Sequential changes in left ventricular pressure-length relationships in the acute phase. Circulation. 1976 Jun.vol. 53:970–975. doi: 10.1161/01.cir.53.6.970. [DOI] [PubMed] [Google Scholar]
- 10.Vokonas PS, Pirzada F, Hood WB., Jr Experimental myocardial infarction: XII. Dynamic changes in segmental mechanical behavior of infarcted and non-infarcted myocardium. Am. J. Cardiol. 1976 May;vol. 37:853–859. doi: 10.1016/0002-9149(76)90109-0. [DOI] [PubMed] [Google Scholar]
- 11.Fishbein MC, Maclean D, Maroko PR. The histopathologic evolution of myocardial infarction. Chest. 1978 Jun.vol. 73:843–849. doi: 10.1378/chest.73.6.843. [DOI] [PubMed] [Google Scholar]
- 12.Jackson BM, Gorman JH, Salgo IS, Moainie SL, Plappert T, St John-Sutton M, Edmunds LH, Jr, Gorman RC. Border zone geometry increases wall stress after myocardial infarction: Contrast echocardiographic assessment. Am. J. Physiol. Heart Circ. Physiol. 2003 Feb.vol. 284:H475–H479. doi: 10.1152/ajpheart.00360.2002. [DOI] [PubMed] [Google Scholar]
- 13.Lima JA, Becker LC, Melin JA, Lima S, Kallman CA, Weisfeldt ML, Weiss JL. Impaired thickening of nonischemic myocardium during acute regional ischemia in the dog. Circulation. 1985 May;vol. 71:1048–1059. doi: 10.1161/01.cir.71.5.1048. [DOI] [PubMed] [Google Scholar]
- 14.Epstein FH, Yang Z, Gilson WD, Berr SS, Kramer CM, French BA. MR tagging early after myocardial infarction in mice demonstrates contractile dysfunction in adjacent and remote regions. Magn. Reson. Med. 2002 Aug.vol. 48:399–403. doi: 10.1002/mrm.10210. [DOI] [PubMed] [Google Scholar]
- 15.Garot J, Lima JA, Gerber BL, Sampath S, Wu KC, Bluemke DA, Prince JL, Osman NF. Spatially resolved imaging of myocardial function with strain-encoded MR: Comparison with delayed contrast-enhanced MR imaging after myocardial infarction. Radiology. 2004 Nov.vol. 233:596–602. doi: 10.1148/radiol.2332031676. [DOI] [PubMed] [Google Scholar]
- 16.Gilson WD, Yang Z, French BA, Epstein FH. Measurement of myocardial mechanics in mice before and after infarction using multislice displacement-encoded MRI with 3D motion encoding. Am. J. Physiol. Heart Circ. Physiol. 2005 Mar.vol. 288:H1491–H1497. doi: 10.1152/ajpheart.00632.2004. [DOI] [PubMed] [Google Scholar]
- 17.Kramer W, Wizemann V, Thormann J, Bechthold A, Schutterle G, Lasch HG. Mechanisms of altered myocardial contractility during hemodialysis: Importance of changes in the ionized calcium to plasma potassium ratio. Klin Wochenschr. 1985 Mar.vol. 63:272–278. doi: 10.1007/BF01731474. [DOI] [PubMed] [Google Scholar]
- 18.Gallagher KP, Gerren RA, Choy M, Stirling MC, Dysko RC. Subendocardial segment length shortening at lateral margins of ischemic myocardium in dogs. Am. J. Physiol. 1987 Oct.vol. 253:H826–H837. doi: 10.1152/ajpheart.1987.253.4.H826. [DOI] [PubMed] [Google Scholar]
- 19.Gallagher KP, Gerren RA, Stirling MC, Choy M, Dysko RC, McManimon SP, Dunham WR. The distribution of functional impairment across the lateral border of acutely ischemic myocardium. Circ. Res. 1986 Apr.vol. 58:570–583. doi: 10.1161/01.res.58.4.570. [DOI] [PubMed] [Google Scholar]
- 20.Mazhari R, Omens JH, Covell JW, McCulloch AD. Structural basis of regional dysfunction in acutely ischemic myocardium. Cardiovasc. Res. 2000 Aug.vol. 47:284–293. doi: 10.1016/s0008-6363(00)00089-4. [DOI] [PubMed] [Google Scholar]
- 21.Sakai K, Watanabe K, Millard RW. Defining the mechanical border zone: A study in the pig heart. Am. J. Physiol. 1985 Jul.vol. 249:H88–H94. doi: 10.1152/ajpheart.1985.249.1.H88. [DOI] [PubMed] [Google Scholar]
- 22.Van Leuven SL, Waldman LK, McCulloch AD, Covell JW. Gradients of epicardial strain across the perfusion boundary during acute myocardial ischemia. Am. J. Physiol. 1994 Dec.vol. 267:H2348–H2362. doi: 10.1152/ajpheart.1994.267.6.H2348. [DOI] [PubMed] [Google Scholar]
- 23.Kerckhoffs RC, Neal ML, Gu Q, Bassingthwaighte JB, Omens JH, McCulloch AD. Coupling of a 3D finite element model of cardiac ventricular mechanics to lumped systems models of the systemic and pulmonic circulation. Ann. Biomed. Eng. 2007 Jan.vol. 35:1–18. doi: 10.1007/s10439-006-9212-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.SURFdriver. [Online]. Available: http://www.surfdriver.com. [Google Scholar]
- 25.TrueGrid XYZ Scientific Appl. [Online]. Available: http://www.truegrid. com. [Google Scholar]
- 26.Weiss JA, Maker BN, Govindjee S. Finite element implementation of incompressible, transversely isotropic hyperelasticity. Comput. Methods Appl. Mechan. Eng. 1996;vol. 135:107–128. [Google Scholar]
- 27.Spencer A. Continuum Mechanics. New York: Longman; 1980. [Google Scholar]
- 28.Humphrey JD. Cardiovascular Solid Mechanics Cells, Tissues and Organs. New York: Springer-Verlag; 2002. [Google Scholar]
- 29.Guccione JM, Waldman LK, McCulloch AD. Mechanics of active contraction in cardiac muscle: Part II—Cylindrical models of the systolic left ventricle. J. Biomech. Eng. 1993 Feb.vol. 115:82–90. doi: 10.1115/1.2895474. [DOI] [PubMed] [Google Scholar]
- 30.Guccione JM, McCulloch AD. Mechanics of active contraction in cardiac muscle: Part I—Constitutive relations for fiber stress that describe deactivation. J. Biomech. Eng. 1993 Feb.vol. 115:72–81. doi: 10.1115/1.2895473. [DOI] [PubMed] [Google Scholar]
- 31.Berne RM, Levy MN. Physiology. St. Louis, MO: Mosby; 1998. [Google Scholar]
- 32.Reese TG, Weisskoff RM, Smith RN, Rosen BR, Dinsmore RE, Wedeen VJ. Imaging myocardial fiber architecture in vivo with magnetic resonance. Magn. Reson. Med. 1995;vol. 34:786–791. doi: 10.1002/mrm.1910340603. [DOI] [PubMed] [Google Scholar]
- 33.Maker BN, Ferencz RM, Hallquist JO. NIKE3D: A nonlinear, implicit, three-dimensional finite element code for solid and structural mechanics. Lawrence Livermore Nat. Lab., Tech. Rep. 1990 UCRL-MA, #105268. [Google Scholar]
- 34.Engelmann BE. NIKE2D: A nonlinear, implicit, two-dimensional finite element code for solid mechanics—User manual. Lawrence Livermore Nat. Lab [Google Scholar]
- 35.Holmes JW, Nunez JA, Covell JW. Functional implications of myocardial scar structure. Am. J. Physiol. 1997 May;vol. 272:H2123–H2130. doi: 10.1152/ajpheart.1997.272.5.H2123. [DOI] [PubMed] [Google Scholar]
- 36.Walker JC, Guccione JM, Jiang Y, Zhang P, Wallace AW, Hsu EW, Ratcliffe MB. Helical myofiber orientation after myocardial infarction and left ventricular surgical restoration in sheep. J. Thorac. Cardiovasc. Surg. 2005 Feb.vol. 129:382–390. doi: 10.1016/j.jtcvs.2004.06.006. [DOI] [PubMed] [Google Scholar]
- 37.Chen J, Song SK, Liu W, McLean M, Allen JS, Tan J, Wickline SA, Yu X. Remodeling of cardiac fiber structure after infarction in rats quantified with diffusion tensor MRI. Am. J. Physiol. Heart Circ. Physiol. 2003 Sep.vol. 285:H946–H954. doi: 10.1152/ajpheart.00889.2002. [DOI] [PubMed] [Google Scholar]
- 38.Mazhari R, Omens JH, Waldman LK, McCulloch AD. Regional myocardial perfusion and mechanics: A model-based method of analysis. Ann. Biomed. Eng. 1998 Sep-Oct;vol. 26:743–755. doi: 10.1114/1.74. [DOI] [PubMed] [Google Scholar]
- 39.Dang AB, Guccione JM, Mishell JM, Zhang P, Wallace AW, Gorman RC, Gorman JH, Ratcliffe MB. Akinetic myocardial infarcts must contain contracting myocytes: Finite-element model study. Am. J. Physiol. Heart Circ. Physiol. 2005 Apr.vol. 288:H1844–H1850. doi: 10.1152/ajpheart.00961.2003. [DOI] [PubMed] [Google Scholar]
- 40.Guccione JM, Moonly SM, Wallace AW, Ratcliffe MB. Residual stress produced by ventricular volume reduction surgery has little effect on ventricular function and mechanics: A finite element model study. J. Thorac. Cardiovasc. Surg. 2001 Sep.vol. 122:592–599. doi: 10.1067/mtc.2001.114939. [DOI] [PubMed] [Google Scholar]
- 41.Kerckhoffs RC, McCulloch AD, Omens JH, Mulligan LJ. Effects of biventricular pacing and scar size in a computational model of the failing heart with left bundle branch block. Med. Image Anal. 2009 Apr.vol. 13:362–369. doi: 10.1016/j.media.2008.06.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Leslie WD, Tully SA, Yogendran MS, Ward LM, Nour KA, Metge CJ. Prognostic value of automated quantification of 99mTc-sestamibi myocardial perfusion imaging. J. Nucl. Med. 2005 Feb.vol. 46:204–211. [PubMed] [Google Scholar]
- 43.Hudson HM, Larkin RS. Accelerated image reconstruction using ordered subsets of projection data. IEEE Trans. Med. Imag. 1994 Dec.vol. 13(no. 4):601–609. doi: 10.1109/42.363108. [DOI] [PubMed] [Google Scholar]
- 44.Waldman LK, Fung Y-C, Covell JW. Transmural myocardial deformation in the canine left ventricle: Normal in vivo three-dimensional finite strains. Circ. Res. 1985;vol. 57:152–163. doi: 10.1161/01.res.57.1.152. [DOI] [PubMed] [Google Scholar]
- 45.Walker JC, Ratcliffe MB, Zhang P, Wallace AW, Fata B, Hsu EW, Saloner D, Guccione JM. MRI-based finite-element analysis of left ventricular aneurysm. Am. J. Physiol Heart Circ. Physiol. 2005 Aug.vol. 289:H692–H700. doi: 10.1152/ajpheart.01226.2004. [DOI] [PubMed] [Google Scholar]
- 46.Carlsson M, Osman NF, Ursell PC, Martin AJ, Saeed M. Quantitative MR measurements of regional and global left ventricular function and strain after intramyocardial transfer of VM202 into infarcted swine myocardium. Am. J. Physiol. Heart Circ. Physiol. 2008 Jun. doi: 10.1152/ajpheart.00280.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Pislaru C, Bruce CJ, Anagnostopoulos PC, Allen JL, Seward JB, Pellikka PA, Ritman EL, Greenleaf JF. Ultrasound strain imaging of altered myocardial stiffness: Stunned versus infarcted reperfused myocardium. Circulation. 2004 Jun.vol. 109:2905–2910. doi: 10.1161/01.CIR.0000129311.73402.EF. [DOI] [PubMed] [Google Scholar]
- 48.Zimmerman SD, Karlon WJ, Holmes JW, Omens JH, Covell JW. Structural and mechanical factors influencing infarct scar collagen organization. Am. J. Physiol. Heart Circ. Physiol. 2000 Jan.vol. 278:H194–H200. doi: 10.1152/ajpheart.2000.278.1.H194. [DOI] [PubMed] [Google Scholar]
- 49.Guccione JM, McCulloch AD, Waldman LK. Passive material properties of intact ventricular myocardium determined from a cylindrical model. J. Biomechan. Eng. 1991;vol. 113:42–55. doi: 10.1115/1.2894084. [DOI] [PubMed] [Google Scholar]
- 50.Costa KD, Holmes JW, McCulloch AD. Modeling cardiac mechanical properties in three dimensions. Phil. Trans. R. Soc. London Series A. 2001;vol. 359:1233–1250. [Google Scholar]
- 51.Kerckhoffs RC, Campbell SG, Flaim SN, Howard EJ, Sierra-Aguado J, Mulligan LJ, McCulloch AD. Multi-scale modeling of excitation-contraction coupling in the normal and failing heart. Conf. Proc. IEEE Eng. Med.Biol. Soc. 2009;vol. 2009:4281–4282. doi: 10.1109/IEMBS.2009.5332708. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Kerckhoffs RC, Lumens J, Vernooy K, Omens JH, Mulligan LJ, Delhaas T, Arts T, McCulloch AD, Prinzen FW. Cardiac resynchronization: Insight from experimental and computational models. Prog. Biophys. Mol. Biol. 2008 Jun-Jul;vol. 97:543–561. doi: 10.1016/j.pbiomolbio.2008.02.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Kroon W, Delhaas T, Arts T, Bovendeerd P. Computational modeling of volumetric soft tissue growth: Application to the cardiac left ventricle. Biomech. Model Mechanobiol. 2009 Aug.vol. 8:301–309. doi: 10.1007/s10237-008-0136-z. [DOI] [PubMed] [Google Scholar]
- 54.Kroon W, Delhaas T, Bovendeerd P, Arts T. Structure and torsion in the normal and situs inversus totalis cardiac left ventricle. II. Modeling cardiac adaptation to mechanical load. Am. J. Physiol. Heart Circ. Physiol. 2008 Jul.vol. 295:H202–H210. doi: 10.1152/ajpheart.00877.2007. [DOI] [PubMed] [Google Scholar]
- 55.Kroon W, Delhaas T, Bovendeerd P, Arts T. Computational analysis of the myocardial structure: Adaptation of cardiac myofiber orientations through deformation. Med Image Anal. 2009 Apr.vol. 13:346–353. doi: 10.1016/j.media.2008.06.015. [DOI] [PubMed] [Google Scholar]
- 56.Bovendeerd PH, Arts T, Delhaas T, Huyghe JM, van Campen DH, Reneman RS. Regional wall mechanics in the ischemic left ventricle: Numerical modeling and dog experiments. Am. J. Physiol. 1996 Jan.vol. 270:H398–H410. doi: 10.1152/ajpheart.1996.270.1.H398. [DOI] [PubMed] [Google Scholar]
- 57.Costa KD, Hunter PJ, Wayne JS, Waldman LK, Guccione JM, McCulloch AD. A three-dimensional finite element method for large elastic deformations of ventricular myocardium: II—Prolate spheroidal coordinates. J. Biomechan. Eng. 1996;vol. 118:464–472. doi: 10.1115/1.2796032. [DOI] [PubMed] [Google Scholar]
- 58.Vetter FJ, McCulloch AD. Three-dimensional stress and strain in passive rabbit left ventricle: A model study. Ann. Biomed. Eng. 2000 Jul.vol. 28:781–792. doi: 10.1114/1.1289469. [DOI] [PubMed] [Google Scholar]
- 59.Waldman LK, Nosan D, Villarreal F, Covell JW. Relation between transmural deformation and local myofiber direction in canine left ventricle. Circ. Res. 1988;vol. 63:550–562. doi: 10.1161/01.res.63.3.550. [DOI] [PubMed] [Google Scholar]
- 60.Omens JH, May KD, McCulloch AD. Transmural distribution of three-dimensional strain in the isolated arrested canine left ventricle. Am. J. Physiol.-Heart Circulation Physiol. 1991;vol. 261:H918–H928. doi: 10.1152/ajpheart.1991.261.3.H918. [DOI] [PubMed] [Google Scholar]
- 61.Arts T, Costa KD, Covell JW, McCulloch AD. Relating myocardial laminar architecture to shear strain and muscle fiber orientation. Am. J. Physiol.—Heart Circulatory Physiol. 2001 May;vol. 280:H2222–H2229. doi: 10.1152/ajpheart.2001.280.5.H2222. [DOI] [PubMed] [Google Scholar]
- 62.Costa KD, Takayama Y, McCulloch AD, Covell JW. Laminar fiber architecture and three-dimensional systolic mechanics in canine ventricular myocardium. Am. J. Physiol. Heart Circ. 1999;vol. 276:H595–H607. doi: 10.1152/ajpheart.1999.276.2.H595. [DOI] [PubMed] [Google Scholar]
- 63.Takayama Y, Costa KD, Covell JW. Contribution of laminar myofiber architecture to load-dependent changes in mechanics of LV myocardium. Am. J. Physiol.-Heart Circulation Physiol. 2002;vol. 282:H1510–H1520. doi: 10.1152/ajpheart.00261.2001. [DOI] [PubMed] [Google Scholar]
- 64.Le Grice IJ, Takayama Y, Covell JW. Transverse shear along myocardial cleavage planes provides a mechanism for normal systolic wall thickening. Circulat. Res. 1995;vol. 77:182–193. doi: 10.1161/01.res.77.1.182. [DOI] [PubMed] [Google Scholar]
- 65.Hunter PJ, Pullan AJ, Smaill BH. Modeling total heart function. Annu. Rev. Biomed. Eng. 2003;vol. 5:147–177. doi: 10.1146/annurev.bioeng.5.040202.121537. [DOI] [PubMed] [Google Scholar]
- 66.Nash MP, Hunter PJ. Computational mechanics of the heart. J. Elasticity. 2000;vol. 61 [Google Scholar]
- 67.Dang AB, Guccione JM, Zhang P, Wallace AW, Gorman RC, Gorman JH, Ratcliffe MB. Effect of ventricular size and patch stiffness in surgical anterior ventricular restoration: A finite element model study. Ann. Thorac. Surg. 2005 Jan.vol. 79:185–193. doi: 10.1016/j.athoracsur.2004.06.007. [DOI] [PubMed] [Google Scholar]
- 68.Guccione JM, Salahieh A, Moonly SM, Kortsmit J, Wallace AW, Ratcliffe MB. Myosplint decreases wall stress without depressing function in the failing heart: A finite element model study. Ann. Thorac. Surg. 2003 Oct.vol. 76:1171–1180. doi: 10.1016/s0003-4975(03)00731-8. [DOI] [PubMed] [Google Scholar]
- 69.Guccione JM, McCulloch AD. Mechanics of active contraction in cardiac muscle: Part I-Constitutive relations for fiber stress that describe deactivation. J. Biomechan. Eng. 1993;vol. 115:72–81. doi: 10.1115/1.2895473. [DOI] [PubMed] [Google Scholar]
- 70.Guccione JM, McCulloch AD. Mechanics of active contraction in cardiac muscle: Part II-Constitutive relations for fiber stress that describe deactivation. J. Biomechan. Eng. 1993;vol. 115:82–90. doi: 10.1115/1.2895473. [DOI] [PubMed] [Google Scholar]
- 71.Sermesant M, Delingette H, Ayache N. An electromechanical model of the heart for image analysis and simulation. IEEE Trans. Med. Imag. 2006 May;vol. 25(no. 5):612–625. doi: 10.1109/TMI.2006.872746. [DOI] [PubMed] [Google Scholar]
- 72.Sermesant M, Moireau P, Camara O, Sainte-Marie J, Andriantsimiavona R, Cimrman R, Hill DL, Chapelle D, Razavi R. Cardiac function estimation from MRI using a heart model and data assimilation: Advances and difficulties. Med. Image Anal. 2006 Aug.vol. 10:642–656. doi: 10.1016/j.media.2006.04.002. [DOI] [PubMed] [Google Scholar]
- 73.Walker JC, Ratcliffe MB, Zhang P, Wallace AW, Hsu EW, Saloner DA, Guccione JM. Magnetic resonance imaging-based finite element stress analysis after linear repair of left ventricular aneurysm. J. Thorac. Cardiovasc. Surg. 2008 May;vol. 135:1094–1102. doi: 10.1016/j.jtcvs.2007.11.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.McVeigh ER, Prinzen FW, Wyman BT, Tsitlik JE, Halperin HR, Hunter WC. Imaging asynchronous mechanical activation of the paced heart with tagged MRI. Magn. Reson. Med. 1998 Apr.vol. 39:507–513. doi: 10.1002/mrm.1910390402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Wyman BT, Hunter WC, Prinzen FW, McVeigh ER. Mapping propagation of mechanical activation in the paced heart with MRI tagging. Am. J. Physiol. 1999 Mar.vol. 276:H881–H891. doi: 10.1152/ajpheart.1999.276.3.H881. [DOI] [PubMed] [Google Scholar]
- 76.Sugihara H, Tamaki N, Nozawa M, Ohmura T, Inamoto Y, Taniguchi Y, Aoki E, Mitsunami K, Kinoshita M. Septal perfusion and wall thickening in patients with left bundle branch block assessed by technetium-99m-sestamibi gated tomography. J. Nucl. Med. 1997 Apr.vol. 38:545–547. [PubMed] [Google Scholar]
- 77.Mahrholdt H, Zhydkov A, Hager S, Meinhardt G, Vogelsberg H, Wagner A, Sechtem U. Left ventricular wall motion abnormalities as well as reduced wall thickness can cause false positive results of routine SPECT perfusion imaging for detection of myocardial infarction. Eur. Heart J. 2005 Oct.vol. 26:2127–2135. doi: 10.1093/eurheartj/ehi387. [DOI] [PubMed] [Google Scholar]
- 78.Kasai T, Depuey EG, Shah AA. Decreased septal wall thickening in patients with left bundle branch block. J. Nucl. Cardiol. 2004 Jan-Feb;vol. 11:32–37. doi: 10.1016/j.nuclcard.2003.11.004. [DOI] [PubMed] [Google Scholar]
- 79.Veress AI, Raymond GM, Gullberg GT, Bassingthwaighte JB. Coupled modeling of the left ventricle and the systemic circulatory system. SIAM News. 2009 Jun.vol. 42 [Google Scholar]
- 80.Cleutjens JP, Blankesteijn WM, Daemen MJ, Smits JF. The infarcted myocardium: Simply dead tissue, or a lively target for therapeutic interventions. Cardiovasc. Res. 1999 Nov.vol. 44:232–341. doi: 10.1016/s0008-6363(99)00212-6. [DOI] [PubMed] [Google Scholar]
- 81.Sun Y, Weber KT. Infarct scar: A dynamic tissue. Cardiovasc. Res. 2000 May;vol. 46:250–256. doi: 10.1016/s0008-6363(00)00032-8. [DOI] [PubMed] [Google Scholar]
- 82.Willems IE, Havenith MG, De Mey JG, Daemen MJ. The alpha-smooth muscle actin-positive cells in healing human myocardial scars. Am. J. Pathol. 1994 Oct.vol. 145:868–875. [PMC free article] [PubMed] [Google Scholar]
- 83.Wu Y, Tse HF, Wu EX. Diffusion tensor MRI study of myocardium structural remodeling after infarction in porcine model. Conf. Proc. IEEE Eng. Med. Biol. Soc. 2006;vol. 1:1069–1072. doi: 10.1109/IEMBS.2006.259840. [DOI] [PubMed] [Google Scholar]
- 84.Dou J, Reese TG, Tseng WY, Wedeen VJ. Cardiac diffusion MRI without motion effects. Magn. Reson. Med. 2002;vol. 48:105–114. doi: 10.1002/mrm.10188. [DOI] [PubMed] [Google Scholar]
- 85.Zimmerman SD, Criscione J, Covell JW. Remodeling in myocardium adjacent to an infarction in the pig left ventricle. Am. J. Physiol. Heart Circ. Physiol. 2004 Dec.vol. 287:H2697–H2704. doi: 10.1152/ajpheart.00160.2004. [DOI] [PubMed] [Google Scholar]
- 86.Wu EX, Wu Y, Nicholls JM, Wang J, Liao S, Zhu S, Lau CP, Tse HF. MR diffusion tensor imaging study of postinfarct myocardium structural remodeling in a porcine model. Magn. Reson. Med. 2007 Oct.vol. 58:687–695. doi: 10.1002/mrm.21350. [DOI] [PubMed] [Google Scholar]
- 87.Wu Y, Chan CW, Nicholls JM, Liao S, Tse HF, Wu EX. MR study of the effect of infarct size and location on left ventricular functional and microstructural alterations in porcine models. J. Magn. Reson. Imag. 2009 Feb.vol. 29:305–312. doi: 10.1002/jmri.21598. [DOI] [PubMed] [Google Scholar]
- 88.Sinusas AJ, Papdemetris X, Constable RT, Dione DP, Slade MD, Shi P, Duncan JS. Quantification of 3-D regional myocardial deformation: Shape-based analysis of magnetic resonance images. Am. J. Physiol.—Heart Circ. Physiol. 2001;vol. 281:H698–H714. doi: 10.1152/ajpheart.2001.281.2.H698. [DOI] [PubMed] [Google Scholar]
- 89.Ashikaga H, Mickelsen SR, Ennis DB, Rodriguez I, Kellman P, Wen H, McVeigh ER. Electromechanical analysis of infarct border zone in chronic myocardial infarction. Am. J. Physiol. Heart Circ. Physiol. 2005 Sep.vol. 289:H1099–H1105. doi: 10.1152/ajpheart.00423.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]