SOLVING PDES IN COMPLEX GEOMETRIES: A DIFFUSE DOMAIN APPROACH

Abstract

We extend previous work and present a general approach for solving partial differential equations in complex, stationary, or moving geometries with Dirichlet, Neumann, and Robin boundary conditions. Using an implicit representation of the geometry through an auxilliary phase field function, which replaces the sharp boundary of the domain with a diffuse layer (e.g. diffuse domain), the equation is reformulated on a larger regular domain. The resulting partial differential equation is of the same order as the original equation, with additional lower order terms to approximate the boundary conditions. The reformulated equation can be solved by standard numerical techniques. We use the method of matched asymptotic expansions to show that solutions of the re-formulated equations converge to those of the original equations. We provide numerical simulations which confirm this analysis. We also present applications of the method to growing domains and complex three-dimensional structures and we discuss applications to cell biology and heteroepitaxy.

1. Introduction

Complex geometric shapes are ubiquitous in our natural environment which arise in biological systems and man-made objects. A few illustrative examples include vein networks in plant leaves, tumors in human bodies, microstructures in materials, or simply a complicated engine in classical engineering applications. Here, we are interested in numerically solving partial differential equations (PDEs) in such geometries. Using standard discretization methods to solve these problems requires a triangulation of the complicated domain and thus rules out coarse-scale discretizations and with it efficient multi-level solutions. In addition the automatic generation of proper three-dimensional meshes for complex geometries remains a challenge. Furthermore, in many applications the complex geometry might even evolve in time, which would require a new discretization at each time step.

Various methods have been proposed to circumvent these problems. In one approach, known as the fictitious domain method, non-body fitted meshes are used and the complex geometry is embedded in a larger, simpler domain. This requires only a triangulation of the simpler domain. The PDE to be solved is extended to the larger domain, although now that the complex geometry is no longer resolved by the mesh one has to find a way to incorporate the original boundary conditions. Different strategies have been developed for doing this. One strategy, within a finite element context, is to build the necessary modifications in the vicinity of the boundary into the basis functions to account for the boundary conditions. Such an approach is known as the composite finite element method which was introduced in [18]. Recent work on image based computing [28] demonstrates the applicability of this approach in the case of zero flux boundary conditions. Extensions to Dirichlet boundary conditions are discussed in [41]. Other approaches in this direction enlarge the set of test functions to account for the boundary conditions. Such methods include the extended finite element method (e.g., [7, 34, 36]), the immersed interface method (e.g., [17, 27]) and generalized nonconforming finite element methods, e.g., [42]. In a similar approach it is also possible to only modify the quadrature in the assembly process for those elements in the vicinity of the boundary; see for example [2] for a treatment of Robin-type boundary conditions, and [45] for a general discussion. In the finite difference context similar treatments typically require a local modification of the scheme near the boundary; see the modified finite volume/embedded boundary/cut-cell methods (e.g., [20, 21, 22, 32, 33, 43]), the immersed interface method (e.g., [24, 26, 44, 49]) and the ghost fluid method (e.g., [9, 12, 13, 14, 30, 31]).

All methods discussed thus far require nonstandard tools and are therefore typically not available in standard finite element or finite difference software packages. Alternative methods for introducing the boundary conditions, e.g., using the penalty method [16] or using Lagrange multipliers [15], are typically restricted to Dirichlet or Neumann boundary conditions. Only recently have other boundary conditions been discussed; see for example [39] where a penalty method is used.

In the approaches described above the complex geometry is either given explicitly through a surface triangulation or implicitly as a level set function. Another approach, which we call the diffuse domain method and which we follow here, is to represent the complex geometry using a phase-field function. In this case, the phase-field function is an approximation of the characteristic function of the domain such that the sharp boundary of the domain is replaced by a narrow diffuse interface layer. In particular, the phase-field function is approximately equal to one in the domain interior and to zero in the exterior of the domain, with a rapid transition between the two. Thus, a diffuse domain is introduced. The phase-field function may be constructed from a signed-distance function that describes the distance of a spatial point to the domain boundary or the phase-field function may be constructed by solving an auxilliary equation.

The PDE is then reformulated on a larger, regular domain with additional source terms that approximate the boundary conditions. This diffuse domain approach does not require any modification of standard finite element or finite difference software. The diffuse domain method was introduced in [23] to study diffusion inside a cell with zero Neumann boundary conditions (no-flux) at the cell-boundary. The diffuse domain approach has also been used to simulate electrical waves in the heart [10]. In [25], this approach was extended to couple bulk diffusion with an ordinary-differential equation description of reaction-kinetics on the bounding surface of the domain to simulate membrane-bound Turing patterns. The coupling between the bulk and surface equations was through a flux condition for the bulk diffusion and a corresponding source term in the surface equations that relates the normal derivative of the bulk concentration to the bulk and surface concentrations at the boundary in a Robin-type boundary condition. In [3, 4], a similar diffuse domain approach was used for solving PDEs in complex domains with zero Neumann boundary conditions using spectral methods.

Here we extend this previous work and present a general diffuse domain approach for solving partial differential equations in complex, stationary, or moving geometries with Dirichlet, Neumann, and Robin boundary conditions. We use the method of matched asymptotic expansions to show that solutions of the reformulated equations converge to those of the original equations. We provide numerical simulations using adaptive, multi-level finite-difference, and finite-element methods, which confirm this analysis. We also present applications of the method to growing domains and complex three-dimensional structures and discuss applications to cell biology and heteroepitaxy.

The paper is organized as follows. In section 2 we review phase field methods, present the diffuse domain approximation, and discuss its applicability as a numerical tool to solve partial differential equations in complex geometries. In section 3 we give numerical examples to demonstrate convergence for simple two-dimensional problems and in section 4 we show simulations on growing domains and complex three-dimensional geometries. In section 5 we draw conclusions.

2. Diffuse domain approximation

Phase field models are typically used to describe complex evolution of patterns. An order parameter is introduced which smoothly varies between the values 0 and 1 in the two phases and has a rapid transition within a narrow diffuse interface layer between them. Phase field methods were originally developed to describe solid-liquid phase transitions and the method has since seen tremendous growth in use. It has been applied to a wide variety of physical and biological phenomena; see for example [8] for a recent review. Besides its success in modeling complex patterns, the phase field approach has also been recognized as a numerical tool to solve partial differential equations on surfaces [5, 29, 40]. The underlying idea is to describe the surface as the level set of the phase field function in a three-dimensional domain and solve an extended partial differential equation, while restricting the evolution to the diffuse interface. Using matched asymptotic expansions, it can be shown that if the diffuse interface width tends to zero the solution of the extended partial differential equation along the 1/2 level set of the phase field function approximates the solution of the original partial differential equation on the surface.

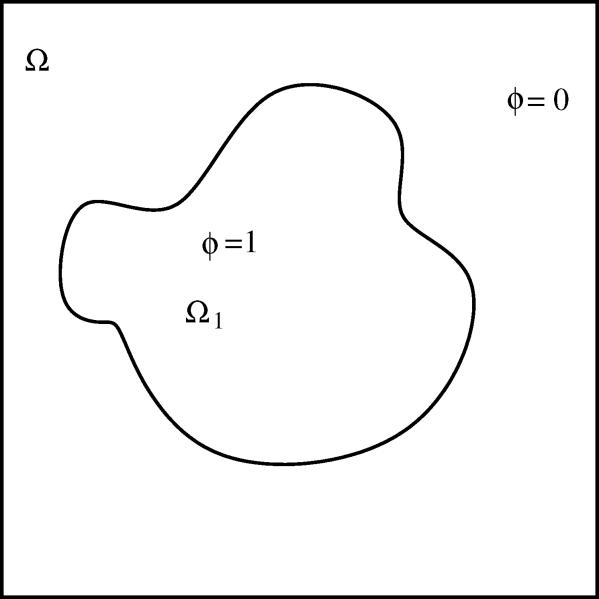
Here, we follow this and previous work described above, and use a similar approach, termed the diffuse domain method, to solve partial differential equations in complex geometries. Letting the phase field function be a smeared-out version of the characteristic function of the complex domain, the original PDE is reformulated and extended to a larger, regular domain. The original domain with a sharp boundary is thus replaced by a domain with a diffuse boundary. To be more precise we consider a time-dependent domain ${\Omega }_1\left(t\right)\subset \Omega \subset {\mathbb{R}}^n$ (see figure 2.1) implicitly described by a phase field function [40]

$$\varphi (\mathbf{x},t)≔\frac{1}{2}\left(1-\text{tanh}\left(\frac{3r(\mathbf{x},t)}{∊}\right)\right),\mathbf{x}\in \Omega ,$$ (2.1)

where r = r(x,t) denotes the signed distance function from the point x to the boundary ∂Ω₁(t) which is assumed to be negative in Ω₁(t) and positive in ΩΩ₁(t). The boundary ∂Ω₁(t) is given by the level set ∂Ω₁(t) = {x|ϕ(x,t) = 1/2}. In equation (2.1), ε is a small parameter that sets the width of the diffuse interface layer that bounds the diffuse domain (the actual width is 2ε). Note that different imaging tools for biological or medical structures today enable the construction of signed distance functions to represent the geometry. The same is true for modern construction tools such as computer aided design programs. In addition, there are efficient algorithms for calculating signed distance functions (e.g., [38, 46]). Alternatively, the phase-field function can be obtained by solving an auxilliary phase-field equation (e.g., [10, 29]).

Fig. 2.1.

Domain ${\Omega }_1\subset \Omega \subset {\mathbb{R}}^n$ described by a phase-field function ϕ.

We next reformulate partial differential equations in Ω₁ with boundary conditions on ∂Ω₁ into partial differential equations on Ω. The method of matched asymptotic expansions is used to show that when ε → 0 we recover the original partial differential equation in Ω₁ and its boundary conditions.

2.1. Model problem in Ω₁

Although the approach we take is general, we begin by describing the method for the Poisson equation on a fixed domain. Later, in section 2.6, we describe the approach for a general PDE. Consider the Poisson equation

$$\Delta u=f\text{in}{\Omega }_1,$$ (2.2)

for a right hand side function $f:{\Omega }_1\to \mathbb{R}$, with three different types of boundary conditions:

• Dirichlet boundary condition

  $$u=g\text{on}\partial {\Omega }_1,$$ (2.3)

  for a function $g:\partial {\Omega }_1\to \mathbb{R}$.
• Neumann boundary condition

  $$\nabla u\cdot \mathbf{n}=g\text{on}\partial {\Omega }_1,$$ (2.4)

  for a function $g:\partial {\Omega }_1\to \mathbb{R}$ and with n being the outward unit normal vector to ∂Ω₁. There is of course a compatibility condition for f ang g that must be satisfied.
• Robin boundary condition

  $$\nabla u\cdot \mathbf{n}=k(u-g)\text{on}\partial {\Omega }_1$$ (2.5)

  for a function $g:\partial {\Omega }_1\to \mathbb{R}$, and $k\in \mathbb{R}$ with k < 0.

Remark 2.1. For Neumann and Robin boundary conditions we can formally rewrite the problem on Ω using the characteristic function χ_Ω1 (x) = 1 for x∈Ω₁ and χ_Ω1 (x) = 0 for x∈ΩΩ₁ and the surface delta function δ_∂Ω1 ¹ as

$$\nabla \cdot ({\chi }_{{\Omega }_1}\nabla u)+{\delta }_{\partial {\Omega }_1}g={\chi }_{{\Omega }_1}f\text{in}\Omega ,$$ (2.6)

and

$$\nabla \cdot ({\chi }_{{\Omega }_1}\nabla u)+{\delta }_{\partial {\Omega }_1}k(u-g)={\chi }_{{\Omega }_1}f\text{in}\Omega ,$$ (2.7)

respectively. A derivation of these forms of the equations may be found in the appendix. The diffuse domain approximation of these equations will result from approximations of χ_Ω1 and δ_∂Ω1 obtained from ϕ and its derivatives, as described below.

Remark 2.2. For Dirichlet boundary conditions, the equations can also be formally rewritten as

$$\nabla \cdot ({\chi }_{{\Omega }_1}\nabla u)+(u-g)\nabla \cdot \nabla {\chi }_{\Omega }={\chi }_{{\Omega }_1}f\text{in}\Omega ,$$ (2.8)

where we have used that ∇χ_Ω = −δ_∂Ω1 n, where n is the outward unit normal of ∂Ω₁. A derivation may be found in the appendix. A direct diffuse domain approximation of this equation was found to be less robust than the other approximations described below.

2.2. Asymptotic analysis

In order to provide diffuse domain approximations for these boundary value problems, we consider extensions of f and g to the domain Ω which we again denote by f and g. The method of matched asymptotic expansions (e.g., see [37]) is used here to provide a formal justification of the diffuse domain approximations presented below. In this approach, the domain is separated into two regions — the regions far from ∂Ω₁ (the outer region) and the region near ∂Ω₁ (the inner region). In each region, the variables are expanded in powers of the diffuse interface thickness ε. In a region where both expansions are valid, the expansions are matched.

We first introduce a local coordinate system. Define r = r(x;ε) to be the signed distance of x from ∂Ω₁. Furthermore let $\mathbf{X}:S\to {\mathbb{R}}^d$ be a parametric representation of ∂Ω₁, where S is an oriented manifold of dimension d–1. Let n = n(s;ε) denote the outward unit normal, and let s be the arclength. Then we assume that for 0 < ρ << 1 there exists a neighborhood

$$U_{∊}=\{\mathbf{x}\in \Omega :\mid r(\mathbf{x};∊)\mid <\rho \}$$

of ∂Ω₁ such that one can write x = X(s;ε)+r(x;ε)n(s;ε) for x ∈ U_ε. Now one transforms u and ϕ to the new coordinate system:

$$u(r,s;∊)≔u(\mathbf{x};∊)=u(\mathbf{X}(s;∊)+r\mathbf{n}(s;∊);∊),\mathbf{x}\in U_{∊},$$ (2.9)

$$\varphi (r,s;∊)≔\varphi (\mathbf{x};∊)=\varphi (\mathbf{X}(s;∊)+r\mathbf{n}(s;∊);∊),\mathbf{x}\in U_{∊}.$$ (2.10)

Here, we simply expand u and ϕ in non-negative powers of ε:

$$u(r,s;∊)=u_0(r,s)+∊u_1(r,s)+\dots ,$$ (2.11)

$$\varphi (r,s;∊)={\varphi }_0(r,s)+∊{\varphi }_1(r,s)+\dots .$$ (2.12)

To find the inner expansion, we introduce a stretched variable $z:=\frac{r}{∊}$, and define

$$U(z,s;∊):=u(r,s;∊),$$ (2.13)

$$\Phi (z,s;∊)≔\varphi (r,s;∊).$$ (2.14)

As in the outer expansion, we expand U and Φ in non-negative powers of ε:

$$U(z,s;∊)=U_0(z,s)+∊U_1(z,s)+\dots ,$$ (2.15)

$$\Phi (z,s;∊)={\Phi }_0(z,s)+∊{\Phi }_1(z,s)+\dots .$$ (2.16)

By matching the inner and outer expansions in an overlapping region where both expansions are valid, the following matching conditions hold (e.g., [6, 37, 11]):

$$\underset{r\to \pm 0}{\text{lim}}{u}_0(r,s,t)=\underset{z\to \pm \infty }{\text{lim}}{U}_0(z,s,t),$$ (2.17)

$$\underset{r\to \pm 0}{\text{lim}}{\varphi }_0(r,s,t)=\underset{z\to \pm \infty }{\text{lim}}{\Phi }_0(z,s,t),$$ (2.18)

$$\underset{r\to \pm 0}{\text{lim}}\nabla u_0(r,s,t)\cdot \mathbf{n}=\underset{z\to \pm \infty }{\text{lim}}{\partial }_z{U}_1(z,s,t),$$ (2.19)

$$\underset{r\to \pm 0}{\text{lim}}\nabla {\varphi }_0(r,s,t)\cdot \mathbf{n}=\underset{z\to \pm \infty }{\text{lim}}{\partial }_z{\Phi }_1(z,s,t).$$ (2.20)

We further assume that there are analogous expansions for f and g.

2.3. Dirichlet boundary condition

2.3.1. Formulation

Below, we present four diffuse domain approximations for the Dirichlet problem:

$$\text{Approximation}1:\nabla \cdot (\varphi \nabla u)-{∊}^{-3}(1-\varphi )(u-g)=\varphi f\text{in}\Omega ,$$ (2.21)

$$\text{Approximation}2:\Delta u-{∊}^{-3}B\left(\varphi \right)(u-g)=\varphi f\text{in}\Omega ,$$ (2.22)

$$\text{Approximation}3:\nabla \cdot \left\{(1+{∊}^{-1}B\left(\varphi \right))\nabla u)\right\}-{∊}^{-2}B\left(\varphi \right)(u-g)=\varphi f\text{in}\Omega ,$$ (2.23)

$$\text{Approximation}4:\nabla \cdot (\varphi \nabla u)+(u-g)\nabla \varphi =\varphi f\text{in}\Omega ,$$ (2.24)

where B(ϕ) ~ ϕ²(1−ϕ)² (i.e. B(ϕ) = 36ϕ²(1−ϕ)²) in equations (2.22) and (2.23), assuming that ϕ is given by the hyperbolic tangent function in equation (2.1). In addition, Approximations 3 and 4 assume g to be extended such that the extension is constant in the normal direction off ∂Ω₁. Note that Approximation 4 is the direct diffuse domain approximation of equation (2.8). Numerical experimentation has shown that Approximation 4 is not as robust as Approximations 1–3. To justify these approximations, we use the method of matched asymptotic expansions. We note that this list is by no means exhaustive; there are many other possible diffuse domain approximations. If ϕ is not given by equation (2.1), then another choice of B may be required.

2.3.2. Matched asymptotic expansion for Approximation 1

Outer expansion:. At leading order $\mathcal{O}\left({∊}^0\right)$, we obtain

$$\Delta u_0=f_0\text{in}{\Omega }_1.$$

Thus we recover the Poisson equation (2.2) at leading order.

Inner expansion:. At $\mathcal{O}\left({∊}^{-3}\right)$, we obtain

$$(1-{\Phi }_0)(U_0-G_0)=0.$$

Since (1−Φ₀) > 0 for all $z\in \mathbb{R}$, we obtain

$$U_0=G_0\forall z\in \mathbb{R}.$$

Taking limits and using the matching conditions, we obtain

$$\underset{r\to -0}{\text{lim}}{u}_0=\underset{r\to -0}{\text{lim}}{g}_0.$$

Thus we also recover the boundary condition in equation (2.3) at leading order.

2.3.3. Matched asymptotic expansion for Approximation 2

Outer expansion:. The outer expansion is the same as in section 2.3.2.

Inner expansion:. At $\mathcal{O}\left({∊}^{-3}\right)$, we obtain

$$B\left({\Phi }_0\right)(U_0-G_0)=0.$$

Since B(Φ₀) > 0 for all $z\in \mathbb{R}$, we obtain

$$U_0=G_0\forall z\in \mathbb{R}$$

Arguing as above, we recover the boundary condition in equation (2.3) at leading order.

2.3.4. Matched asymptotic expansion for Approximation 3

Outer expansion:. The outer expansion is the same as in section 2.3.2.

Inner expansion:. At $\mathcal{O}\left({∊}^{-3}\right)$, we obtain

$${\partial }_z\left(B\left({\Phi }_0\right){\partial }_z{U}_0\right)=0.$$

It follows from the matching conditions that

$${\partial }_z{U}_0=0.$$

At the next order $\mathcal{O}\left({∊}^{-2}\right)$, we obtain:

$${\partial }_z\left(B\left({\Phi }_0\right){\partial }_z{U}_1\right)-B\left({\Phi }_0\right)(U_0-G_0)=0.$$

Assuming that G₀ is independent of z, integrating the above equation from −∞ to ∞, using the matching conditions, and the fact that

$$\partial z{\Phi }_0=-6{\Phi }_0(1-{\Phi }_0),$$

and

$${\int }_{-\infty }^{\infty }B\left({\Phi }_0\right)dz={\int }_1^0\frac{B\left({\Phi }_0\right)}{{\partial }_z{\Phi }_0}d{\Phi }_0=\frac{1}{6}{\int }_0^1\frac{B\left({\Phi }_0\right)}{{\Phi }_0(1-{\Phi }_0)}d{\Phi }_0\sim \frac{1}{6}{\int }_0^1{\Phi }_0(1-{\Phi }_0)d{\Phi }_0\ne 0,$$ (2.25)

we recover the boundary condition in equation (2.3) at leading order.

2.3.5. Matched asymptotic expansion for Approximation 4

Outer expansion:. The outer expansion is the same as in section 2.3.2.

Inner expansion:. At $\mathcal{O}\left({∊}^{-2}\right)$, we obtain

$${\partial }_z\left({\Phi }_0{\partial }_z{U}_0\right)+(U_0-G_0){\partial }_{zz}{\Phi }_0=0.$$ (2.26)

Defining W₀ = U₀ − G₀ and using that G₀ is independent of z, we may rewrite equation (2.26) as

$${\partial }_{zz}\left({\Phi }_0{W}_0\right)-{\partial }_z{W}_0{\partial }_z{\Phi }_0=0.$$

Integrating from −∞ to ∞ and using the matching conditions, we conclude that

$${\int }_{-\infty }^{+\infty }{\partial }_z{W}_0{\partial }_z{\Phi }_{0}dz=0.$$

Since ∂_zΦ₀ < 0, we conclude that ∂_zW₀ must have at least one zero. Denote the zero point by z = z*. An analysis of the equation shows that in fact W₀ and all its derivatives vanish in a neighborhood of z*. Thus, assuming sufficient smoothness of the solution, we conclude that W₀ = 0 identically, hence

$BD$ U _{ 0 _} = G _{ 0 _} $ED$

and so we recover the boundary condition in equation (2.3) at leading order.

2.4. Neumann boundary condition

2.4.1. Formulation

We next present four diffuse domain approximations for the Neumann problem:

$$\text{Approximation}1:\nabla \cdot (\varphi \nabla u)+\nabla \left(\varphi g\right)\cdot \frac{\nabla \varphi }{\mid \nabla \varphi \mid }=\varphi f\text{in}\Omega ,$$ (2.27)

$$\text{Approximation}2:\nabla \cdot (\varphi \nabla u)+g\mid \nabla \left(\varphi \right)\mid =\varphi f\text{in}\Omega ,$$ (2.28)

$$\text{Approximation}3:\nabla \cdot (\varphi \nabla u)+∊g{\mid \nabla \varphi \mid }^2=\varphi f\text{in}\Omega ,$$ (2.29)

$$\text{Approximation}4:\nabla \cdot (\varphi \nabla u)+{∊}^{-1}gB\left(\varphi \right)=\varphi f\text{in}\Omega ,$$ (2.30)

where B(ϕ) = 36ϕ²(1−ϕ)² in equation (2.30). Approximations 2–4 assume g to be extended such that the extension is constant in the normal direction off ∂Ω₁. Observe that in all these approximations, the characteristic function of Ω₁ is approximated by χ_Ω1 ≈ ϕ while the surface delta function δ_∂Ω1 is approximated by |∇ϕ|, φ |∇ϕ|² ε⁻¹B(ϕ), respectively. Note that in equation (2.28) lower order term ϕ∇g · ∇ϕ/|∇ϕ| is also present. Also, if ϕ is not given by equation (2.1), then the lower order terms in Approximations 3 and 4 need to be rescaled [25] and B may also need to be redefined.

2.4.2. Matched asymptotic expansion for Approximation 1

Outer expansion:. At $\mathcal{O}\left({∊}^0\right)$, we obtain

$$\nabla u_0=f_0\text{in}{\Omega }_1.$$

Thus we recover the Poisson equation (2.2) at leading order.

Inner expansion:. At $\mathcal{O}\left({∊}^{-2}\right)$, we obtain

$${\partial }_z\left({\Phi }_0{\partial }_z{U}_0\right)=0.$$

It follows that

$${\partial }_z{U}_0=0.$$

At $\mathcal{O}\left({∊}^{-1}\right)$, we obtain

$${\partial }_z\left({\Phi }_0{\partial }_z{U}_1\right)-{\partial }_z\left({\Phi }_0{G}_0\right)=0.$$

Integrating the above equation from −∞ to ∞ we obtain

$$\underset{z\to -\infty }{\text{lim}}{\partial }_z{U}_1=\underset{z\to -\infty }{\text{lim}}{G}_0,$$

and by matching the inner and outer expansions it follows that

$$\underset{r\to -0}{\text{lim}}\nabla u_0\cdot \mathbf{n}=\underset{r\to -0}{\text{lim}}{g}_0.$$

Thus we also recover the boundary condition in equation (2.4) at leading order.

2.4.3. Matched asymptotic expansion for Approximation 2

Outer expansion:. The outer expansion is the same as in section 2.4.2.

Inner expansion:. At $\mathcal{O}\left({∊}^{-2}\right)$, we obtain

$${\partial }_z\left({\Phi }_0{\partial }_z{U}_0\right)=0\Rightarrow {\partial }_z{U}_0=0.$$

At $\mathcal{O}\left({∊}^{-1}\right)$, we have

$${\partial }_z\left({\Phi }_0{\partial }_z{U}_1\right)-G_0\partial z{\Phi }_0=0.$$

Assuming that G₀ is independent of z, integrating the above equation from to −∞ to ∞, and using the matching conditions, we recover the boundary condition in equation (2.4) at leading order.

2.4.4. Matched asymptotic expansion for Approximation 3

Outer expansion:. The outer expansion is the same as in section 2.4.2.

Inner expansion:. At $\mathcal{O}\left({∊}^{-2}\right)$, we obtain

$${\partial }_z\left({\Phi }_0{\partial }_z{U}_0\right)=0\Rightarrow {\partial }_z{U}_0=0.$$

At $\mathcal{O}\left({∊}^{-1}\right)$, we obtain

$${\partial }_z\left({\Phi }_0{\partial }_z{U}_1\right)+G_0{(\partial z{\Phi }_0)}^2=0.$$

Assuming that G₀ is independent of z, integrating the above equation from −∞ to ∞, using the matching conditions, and the fact that

$${\int }_{-\infty }^{\infty }{(\partial z{\Phi }_0)}^{2}dz={\int }_1^0\partial z{\Phi }_{0}d{\Phi }_0=6{\int }_0^1{\Phi }_0(1-{\Phi }_0)d{\Phi }_0=1,$$

we recover the boundary condition in equation (2.4) at leading order.

2.4.5. Matched asymptotic expansion for Approximation 4

Outer expansion:. The outer expansion is the same as in section 2.4.2.

Inner expansion:. At $\mathcal{O}\left({∊}^{-2}\right)$, we have

$${\partial }_z\left({\Phi }_0{\partial }_z{U}_0\right)=0\Rightarrow {\partial }_z{U}_0=0.$$

At $\mathcal{O}\left({∊}^{-1}\right)$, we obtain

$${\partial }_z\left({\Phi }_0{\partial }_z{U}_1\right)+G_{0}B\left({\Phi }_0\right)=0.$$

Assuming G₀ is independent of z, integrating the above equation from to −∞ to ∞, and using that ${\int }_{-\infty }^{+\infty }B\left({\Phi }_0\right)dz=1$ (following the analysis in equation (2.25)) together with the matching conditions, we recover the boundary condition in equation (2.4) at leading order.

2.5. Robin boundary condition

2.5.1. Formulation

We next present two diffuse domain approximations for the Robin problem:

$$\text{Approximation}1:\nabla \cdot (\varphi \nabla u)+∊k(u-g){\mid \nabla \varphi \mid }^2=\varphi f\text{in}\Omega ,$$ (2.31)

$$\text{Approximation}2:\nabla \cdot (\varphi \nabla u)+{∊}^{-1}B\left(\varphi \right)k(u-g)=\varphi f\text{in}\Omega ,$$ (2.32)

where B(ϕ) = ϕ²(1−ϕ)². Actually, all four diffuse interface approximations of the Neumann problem described earlier could be used here. Approximation 1 was used previously in [25].

2.5.2. Matched asymptotic expansion for Approximation 1

Outer expansion:. At leading order $\mathcal{O}\left({∊}^0\right)$, we obtain

$$\Delta u_0=f_0\text{in}{\Omega }_1,$$

Thus we recover the partial differential equation in equation (2.2) at leading order.

Inner expansion:. At $\mathcal{O}\left({∊}^{-2}\right)$, we obtain

$${\partial }_z\left({\Phi }_0{\partial }_z{U}_0\right)=0\Rightarrow {\partial }_z{U}_0=0.$$

At $\mathcal{O}\left({∊}^{-1}\right)$, we have

$${\partial }_z\left({\Phi }_0{\partial }_z{U}_1\right)+k(U_0-G_0){(\partial z{\Phi }_0)}^2=0.$$

Assuming that G₀ is independent of z, integrating the above equation from −∞ to ∞ we obtain

$$\underset{z\to -\infty }{\text{lim}}{\partial }_z{U}_1=k\underset{z\to -\infty }{\text{lim}}(U_0-G_0).$$

By matching the inner and outer expansions we obtain

$$\underset{r\to -0}{\text{lim}}\nabla u_0\cdot \mathbf{n}=k\underset{r\to -0}{\text{lim}}(u_0-g_0).$$

Thus we also recover the boundary condition in equation (2.5) at leading order.

2.5.3. Matched asymptotic expansion for Approximation 2

Outer expansion:. The outer expansion is the same as in section 2.5.2.

Inner expansion:. At $\mathcal{O}\left({∊}^{-2}\right)$, we have

$${\partial }_z\left({\Phi }_0{\partial }_z{U}_0\right)=0\Rightarrow {\partial }_z{U}_0=0.$$

At $\mathcal{O}\left({∊}^{-1}\right)$, we have

$${\partial }_z\left({\Phi }_0{\partial }_z{U}_1\right)+B\left({\Phi }_0\right)k(U_0-G_0)=0.$$

Assuming that G₀ is independent of z, integrating the above equation from −∞ to ∞, and using the matching conditions, we recover the boundary condition in equation (2.5) at leading order.

2.6. Summary

The preceding analyses show that all that is needed to approximate a PDE in a complex geometry by a PDE on a larger regular domain is a restriction of the partial differential operators using the phase field variable ϕ and adding an additional lower order term to take care of the boundary conditions. Here, we consider a more general second order partial differential equation in an evolving domain Ω₁(t) of the form

$${\partial }_{t}u-\nabla \cdot (\mathbf{A}\nabla u)+\mathbf{b}\cdot \nabla u+cu=f\text{in}{\Omega }_1\left(t\right),$$ (2.33)

with A = A(u,∇u,x,t) :Ω₁(t) → Ω₁(t) a positive definite matrix, b = b(u,∇u,x,t): ${\Omega }_1\left(t\right)\to \mathbb{R}$ a vector, $c=c(u,\nabla u,x,t)\in \mathbb{R}$, and f = f(x,t), as well as approprioate boundary conditions:

• Dirichlet boundary condition

  $$u=g\text{on}\partial {\Omega }_1\left(t\right),$$ (2.34)
• Neumann boundary condition

  $$\mathbf{A}\nabla u\cdot \mathbf{n}+uV=g\text{on}\partial {\Omega }_1\left(t\right),$$ (2.35)

  where V is the normal velocity of ∂Ω₁(t), and
• Robin boundary condition

  $$\mathbf{A}\nabla u\cdot \mathbf{n}+uV=k(u-g)\text{on}\partial {\Omega }_1\left(t\right).$$ (2.36)

The Neumann and Robin boundary conditions (2.35) and (2.36) respectively are natural generalizations of the stationary domain conditions and are justified in the appendix (see also [23]). The diffuse domain approximation reads as

$${\partial }_t\left(\varphi u\right)-\nabla \cdot (\varphi \mathbf{A}\nabla u)+\varphi \mathbf{b}\cdot \nabla u+\varphi cu+\mathrm{B}.\mathrm{C}.=\varphi f\text{in}\Omega ,$$ (2.37)

where A, b, and c are now extended coefficients, with the only requirement for the extension of A is that it should remain positive definite. The notation B.C. refers to the appropriate diffuse domain forms for the boundary conditions discussed in the previous subsections. A justification of this diffuse domain formulation can be done by performing matched asymptotic expansions along the same lines as above using that in the inner expansion, ${\partial }_t=-\frac{V}{∊}{\partial }_z+O\left({∊}^0\right)$ where V is the normal velocity of ∂Ω₁(t). This is seen as follows. For simplicity, we perform the analysis using Approximation 1 of the Robin boundary condition (2.31) and we assume that ϕ is given by equation (2.1). That is, we consider

$${\partial }_t\left(\varphi u\right)-\nabla \cdot (\varphi \mathbf{A}\nabla u)+\varphi \mathbf{b}\cdot \nabla u+\varphi cu-∊k(u-g){\mid \nabla \varphi \mid }^2=\varphi f\text{in}\Omega .$$ (2.38)

In the outer expansion at O(ε⁰), we obtain equation (2.33). In the inner expansion, assuming A = Â₀ + Â₁ +..., and likewise for b and c, we obtain at $\mathcal{O}(1∕{∊}^2)$:

$${\partial }_z\left({\Phi }_0\left(\mathbf{n}{\widehat{\mathbf{A}}}_0\mathbf{n}\right){\partial }_z{U}_0\right)=0\Rightarrow {\partial }_z{U}_0=0.$$ (2.39)

At the next order $\mathcal{O}(1∕∊)$, we obtain

$$-V{\partial }_z\left({\Phi }_0{U}_0\right)-{\partial }_z\left({\Phi }_0\mathbf{n}{\widehat{\mathbf{A}}}_0(\mathbf{n}{\partial }_z{U}_1+\mathbf{s}{\partial }_s{U}_0)\right)-k(U_0-G_0){\left({\partial }_z{\Phi }_0\right)}^2=0.$$ (2.40)

Since V is independent of z, integrating from −∞ to ∞, and using the matching conditions (assuming also that G₀ is independent of z), the specific form of ϕ, and that A₀∇u₀ ·n = (nA₀n)∇u₀ ·n+(nA₀s)∇u₀ ·s, yields

$$\underset{r\to -0}{\text{lim}}(V{u}_0+{\mathbf{A}}_0\nabla u_0\cdot \mathbf{n})=k\underset{r\to -0}{\text{lim}}(u_0-g_0),$$

where A₀ is the leading order term in the outer expansion of A. Thus, equation (2.36) is recovered at leading order.

Alternatively, let us consider a conservative generalization of equation (2.33):

$${\partial }_{t}u-\nabla \cdot (\mathbf{A}\nabla u)+\nabla \cdot \left(u\mathbf{b}\right)+cu=f\text{in}{\Omega }_1\left(t\right).$$ (2.41)

For this equation, we may consider alternative forms of the Neumann and Robin boundary conditions considered above:

• Neumann boundary condition alternative

  $$\mathbf{A}\nabla u\cdot \mathbf{n}+u(V-\mathbf{b}\cdot \mathbf{n})=g\text{on}\partial {\Omega }_1\left(t\right),$$ (2.42)

  where b·n is the normal component of b on ∂Ω₁(t), and
• Robin boundary condition alternative

  $$\mathbf{A}\nabla u\cdot \mathbf{n}+u(V-\mathbf{b}\cdot \mathbf{n})=k(u-g)\text{on}\partial {\Omega }_1\left(t\right).$$ (2.43)

These boundary conditions are justified in the appendix. Note that if b·n = V, then these reduce to the stationary Neumann and Robin boundary conditions.

The diffuse domain approximation reads:

$${\partial }_t\left(\varphi u\right)-\nabla \cdot (\varphi \mathbf{A}\nabla u)+\nabla \cdot \left(\varphi u\mathbf{b}\right)+\varphi cu+\mathrm{B}.\mathrm{C}.=\varphi f\text{in}\Omega ,$$ (2.44)

where as before, the B.C. refers to the appropriate diffuse domain forms for the boundary conditions discussed in the previous subsections. As before, equation (2.44) can be justified using the method of matched asymptotic expansions. To see this, again use Approximation 1 of the Robin boundary conditions and ϕ given from equation (2.1). That is, we consider:

$${\partial }_t\left(\varphi u\right)-\nabla \cdot (\varphi \mathbf{A}\nabla u)+\nabla \cdot \left(\varphi u\mathbf{b}\right)+\varphi cu-∊k(u-g){\mid \nabla \varphi \mid }^2=\varphi f\text{in}\Omega .$$ (2.45)

In the outer expansion at $\mathcal{O}\left({∊}^0\right)$, equation (2.41) is recovered. In the inner expansion at $\mathcal{O}(1∕{∊}^2)$, equation (2.39) is obtained. At $\mathcal{O}(1∕∊)$, we obtain

$${\partial }_z\left({\Phi }_0{U}_0\left({\widehat{\mathbf{b}}}_0\cdot \mathbf{n}-V\right)\right)-{\partial }_z\left({\Phi }_0\mathbf{n}{\widehat{\mathbf{A}}}_0(\mathbf{n}{\partial }_z{U}_1+\mathbf{s}{\partial }_s{U}_0)\right)-k(U_0-G_0){(\partial z{\Phi }_0)}^2=0.$$ (2.46)

Integrating from −∞ to ∞ and using the matching conditions yields

$$\underset{r\to -0}{\text{lim}}((V-{\mathbf{b}}_0\cdot \mathbf{n})u_0+{\mathbf{A}}_0\nabla u_0\cdot \mathbf{n})=k\underset{r\to -0}{\text{lim}}(u_0-g_0),$$

so that equation (2.43) is recovered at leading order.

In summary, given a signed distance representation of the geometry Ω₁, a phase field function can be constructed either using equation (2.1) or by solving an auxilliary phase field equation. If ϕ differs from equation (2.1), then some of the diffuse domain approximations of the Neumann and Robin boundary conditions need to be rescaled, as indicated earlier. The PDE and its boundary conditions are then reformulated in the larger domain as described above. The reformulated PDE can be solved by standard approaches. In particular, since the larger domain Ω typically has a simple shape, most likely a box in ${\mathbb{R}}^3$, a coarse grid representation is easy to construct. Starting from this coarse grid a hierarchy of finer meshes can be created using adaptive or global refinements.

Remark 2.3. Since ϕ = 0 in ΩΩ₁, we ensure that the reformulated equations are well posed in Ω by replacing ϕ ϕ + δ with a small parameter δ. For the asymptotic analysis it is sufficient to set δ = ε. However, to obtain satisfactory numerical results a much smaller value of δ is required. In the simulations that follow, we set δ = 10⁻⁶.

3. Numerical examples

As a benchmark for the diffuse domain approach, we consider the Poisson equation with Dirichlet and Robin boundary conditions and the quasi-steady reaction-diffusion equation Δu−u = f on a circular domain ${\Omega }_1=B_1\left(0\right)\subset {\mathbb{R}}^2$ (with B₁(0) being the unit circle) with Neumann boundary conditions. The equations are reformulated as above using the phase field function in equation (2.1) and the computational domain Ω=(−2,2)² with periodic boundary conditions on ∂Ω. As indicated in [4], the boundary conditions imposed at ∂Ω do not influence the solution in Ω₁ provided ∂Ω₁ is sufficiently far from ∂Ω.

In the tests that follow, we set the right hand side f and the boundary function g such that we obtain the following analytic solution:

$$u(r,\theta )=\frac{1}{4}{r}^2=\frac{1}{4}(x^2+y^2).$$ (3.1)

This enables us to quantify the errors introduced by the diffuse domain approach. As discussed above, the reformulated problem can be solved using standard numerical techniques. In this section, we use a finite element discretization (FEM) implemented with the adaptive FEM toolbox AMDiS [47]. To discretize space, a conforming triangulation τ_h is introduced and the mesh is locally adapted using a bisection algorithm (see [47] and references therein) such that the mesh is refined near the domain boundary ∂Ω₁ and a coarse mesh is used elsewhere. Globally continuous piecewise linear finite elements are used with a standard weak form of the equations. To show the versatility of the diffuse domain approach, we also provide results using an adaptive finite difference method in section 4.1.

3.1. Dirichlet boundary conditions

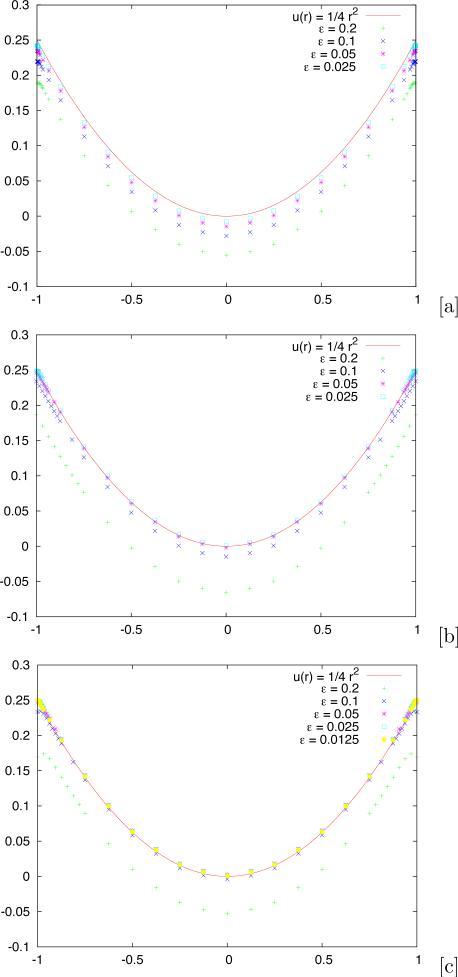
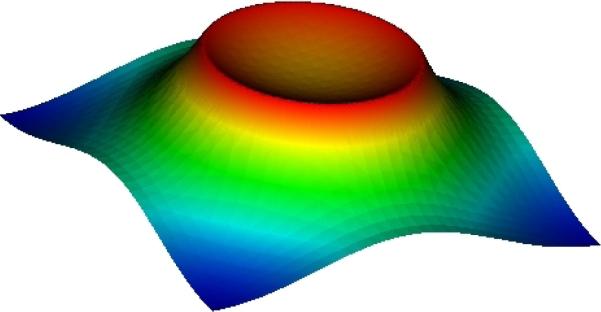
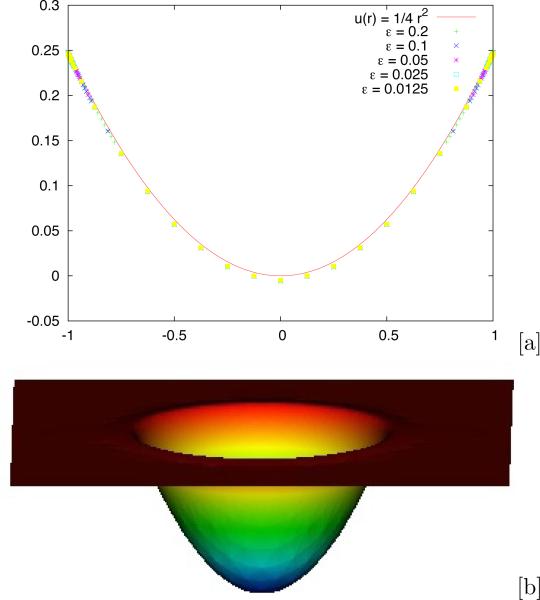
We set f(x,y) = 1, g(x,y) = 1/4 and solve Δu = f using each of the three diffuse domain Approximations (2.21)–(2.23). In figure 3.1, the y = 0 slices of the discrete solution for different values of ε are shown in comparison with the analytic solution. The results reproduce the convergence result from the asymptotic analysis in section 2.3. While extrapolation could be used in principle to obtain a more accurate solution (essentially second-order in ε), this requires interpolation since the meshes are different when ε is varied because of adaptivity. Hence we do not present extrapolated results here. We do not present results for Approximation 4 since this was found to be less robust than Approximations 1–3. Observe that Approximation 3 appears to provide more accurate results than the others. In figure 3.2, the numerical solution in the whole domain Ω is shown for Approximation 3.

Fig. 3.1.

diffuse interface approximation of Dirichlet problem for the Poisson equation. A slice of u(x,y) along y = 0 for different values of ε as labeled. [a]: result using Approximation 1 in equation (2.21), [b]: result using Approximation 2 in equation (2.22) and [c]: result using Approximation 3 in equation (2.23).

Fig. 3.2.

The numerical solution u(x,y) in the whole domain Ω using Approximation 3 in equation (2.23) with ε = 0.1.

3.2. Neumann boundary conditions

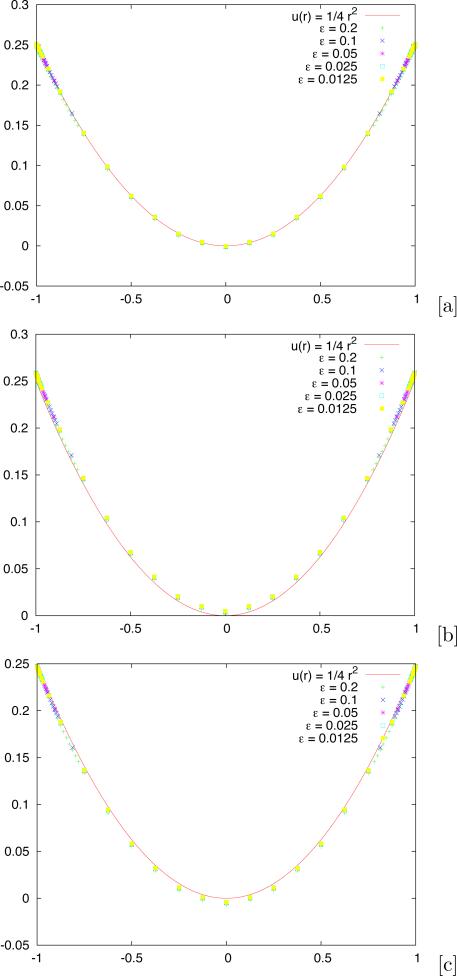
We set f(x,y) = 1−1/4(x² +y²), g(x,y) = 1/2 and solve Δu−u = f using the diffuse domain Approximations (2.27)–(2.29). The analytic solution is the same as in the previous example. The corresponding numerical results for the different diffuse domain approximations are shown in figure 3.3. The results reproduce the convergence result in the asymptotic analysis in section 2.4. In this case, Approximation 1 appears to be the most accurate of the three.

Fig. 3.3.

diffuse interface approximation of the Neumann problem. A slice of u(x,y) along y = 0 for different values of ε as labeled. [a]: result using Approximation 1 in equation (2.27), [b]: result using Approximation 2 in equation (2.28), and [c] result using Approximation 3 in equation (2.29).

3.3. Robin boundary conditions

We solve Δu = f with Robin boundary conditions using f(x,y) = 1, g(x,y) = 3/4, and k = −1. The analytic solution is the same as in the previous examples. We use Approximation 1 in equation (2.31). The corresponding numerical results are shown in figure 3.4, and again reproduce the convergence result in the asymptotic analysis in section 2.5.

Fig. 3.4.

The diffuse domain approximation of the Robin problem using Approximation 1 in equation (2.31). [a] The y = 0 slice of the numerical solution u(x,y) for different values of ε as labeled. [b]: The numerical solution u with ε = 0.1.

4. Applications

4.1. Time dependent and moving domains

We next consider the following PDE in an evolving domain Ω₁(t):

$${\partial }_{t}u+\nabla \cdot \left(u\mathbf{v}\right)-\nabla \cdot (\nabla u)+u=f\text{in}{\Omega }_1\left(t\right),$$ (4.1)

with Neumann boundary condition

$$\nabla u\cdot \mathbf{n}=g\text{on}\partial {\Omega }_1\left(\mathrm{t}\right).$$ (4.2)

We take Ω₁(t) to be a growing, perturbed circular domain and suppose that the velocity of the domain v(x,t) is given. The initial domain is enclosed by the polar curve

$$r(\theta ,0)=1+0.1\text{cos}\left(3\theta \right)+0.02\text{cos}\left(5\theta \right),$$ (4.3)

and the velocity v is given by

$$\mathbf{v}=\stackrel{.}{r}(\theta ,t)(\text{cos}\left(\theta \right),\text{sin}\left(\theta \right)),$$ (4.4)

where

$$\stackrel{.}{r}(\theta ,t)=0.2e^{2t}\text{cos}\left(3\theta \right)+0.12e^{6t}\text{cos}\left(5\theta \right).$$ (4.5)

Thus, the domain increasingly deviates from a circle as time proceeds and acquires a complex shape. We choose f and g such that the solution is $u(r,\theta ,t)=\frac{1}{4}{r}^2$. The initial condition is $u_0(r,\theta )=\frac{1}{4}{r}^2$.

To approximate equation (4.1), we solve the diffuse domain model using Approximation 2 in equation (2.28),

$${\partial }_t\left(\varphi u\right)+\nabla \cdot \left(\varphi u\mathbf{v}\right)-\nabla \cdot (\varphi \nabla u)-g\mid \nabla \varphi \mid +\varphi u+\varphi f\text{in}\Omega ,$$ (4.6)

in the square (−2,2)² with zero Neumann boundary conditions. To determine ϕ, we have several choices. Here, we reconstruct ϕ from the signed distance function r via equation (2.1). Because the velocity v is given analytically (see equation (4.4)), we construct r exactly. More generally, one could solve a Hamilton-Jacobi equation for the signed distance function

$${\partial }_{t}r+V\mid \nabla r\mid =0,$$ (4.7)

where V is an extension of v|∂Ω₁ · n off ∂Ω₁ such that ∇V · n = 0 in a neighborhood ∂Ω₁ (e.g., [1, 30]). Alternatively, one could solve for ϕ directly using an advective Cahn-Hilliard equation

$${\partial }_t\varphi +\mathbf{v}\cdot \nabla \varphi =\nabla \cdot (\nu \nabla (F^{\prime }\left(\varphi \right)-{∊}^2\Delta \varphi )),$$ (4.8)

where ν and F are appropriately defined mobility and double well free energy functions, respectively.

To solve equation (4.6) we use an adaptive finite-difference, multilevel-multigrid method with block-structured Cartesian mesh refinement (see [48]). Centered finite difference approximations are used for the space discretization and the time stepping is performed by the Crank-Nicholson method. The overall scheme is second order accurate in space and time. The complexity of this method is optimal, i.e., the number of operations to solve the equations is $\mathcal{O}\left(N\right)$, where N is the number of unknowns. The mesh is refined in the diffuse interface region around ∂Ω₁ where ϕ exhibits a sharp transition.

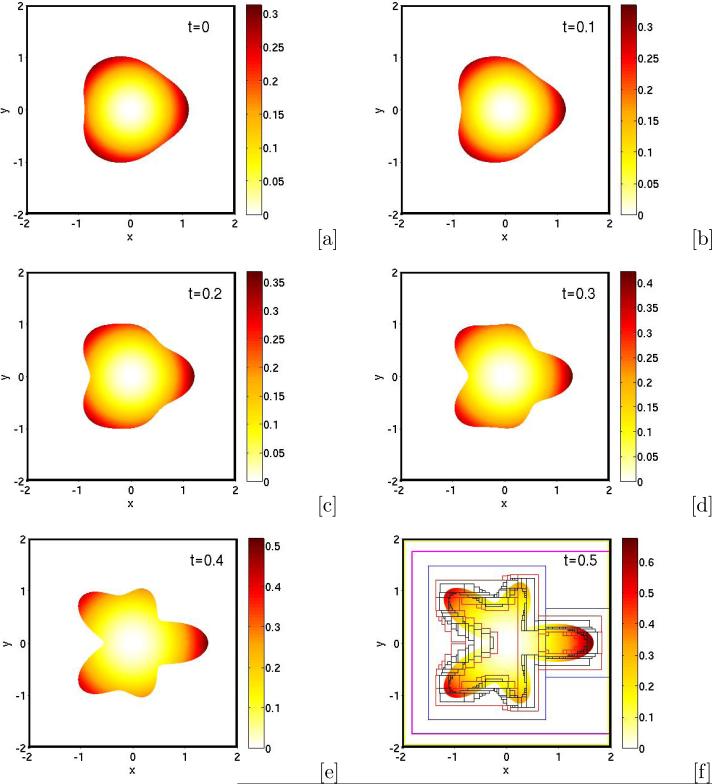
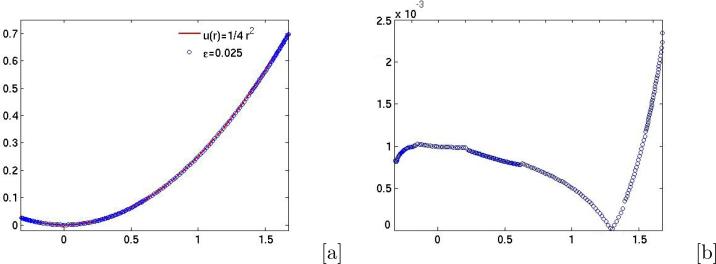
In figure 4.1 we present the results using an adaptive mesh with six levels of refinement. The mesh size ranges from h_coarse = 0.25 to h_fine = 4/1024≈0.0039. We use the interface thickness parameter ε = 0.025 in equation (2.1); there are approximately 10 grid points across the diffuse interface layer. The boxes correspond to the boundaries of the adaptive Cartesian patches. Each interior box contains a mesh that is one half of the size of the mesh in the box that contains it. The bounding box corresponding to coarsest mesh is the boundary of the computational domain itself. In figure 4.2[a], the numerical solution from figure 4.1[f] (‘o’) is shown together with the exact solution (solid line) along the y = 0 slice of the domain (restricted to Ω₁). The absolute value of the difference between the numerical and exact solutions (error) on the y = 0 slice is shown in figure 4.2[b]. The error is on the order of 10⁻³ with the largest error occurring near the rightmost finger. Clearly the solution of the diffuse domain model provides a good approximation of the true solution.

Fig. 4.1.

Solution of the diffuse domain approximation equation (4.6), at different times as labeled, with Ω₁ being a perturbed, growing growing circular domain. In [f], the boxes correspond to the boundaries of the adaptive Cartesian mesh patches. Each interior box contains a mesh that is one half of the size of the mesh in the box that contains it. See text for additional parameters.

Fig. 4.2.

The y = 0 slice of the result in figure 4.1[f]. [a]: The numerical solution (‘o’) and the exact solution (‘-’), [b]: The absolute value of the difference between the numerical and exact solutions along the y = 0 slice.

4.2. Three dimensional results

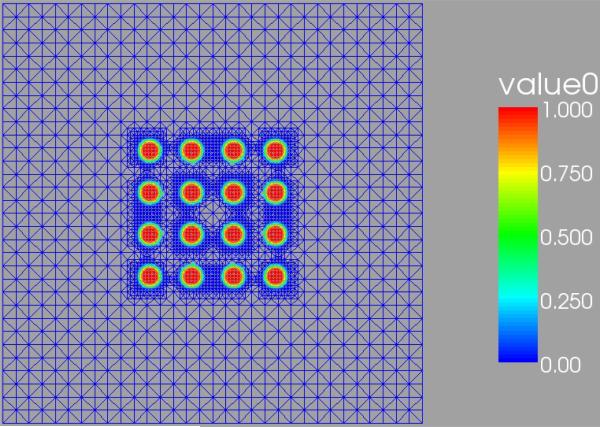
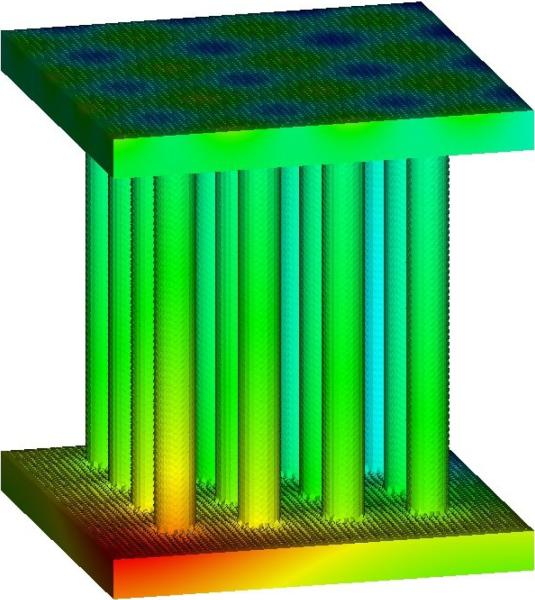
Next, we consider the solution of the Poisson equation Δu = f in a complex domain Ω₁ with boundary consisting of two rectangular cuboids and a 4×4 array of cylindrical connecting pillars. The height and radius of the pillars is 1.8 and 0.1, respectively. The rectangular cuboids have dimension 2×2×0.2; see figure 4.3. We apply Robin boundary conditions ∇u·n = k(u−g) on ∂Ω₁ with

$$g\left(\mathbf{x}\right)=g\left(x_3\right)=\frac{x_3-z_t}{z_b-z_t}{g}_b+\frac{x_3-z_b}{z_t-z_b}{g}_t,$$ (4.9)

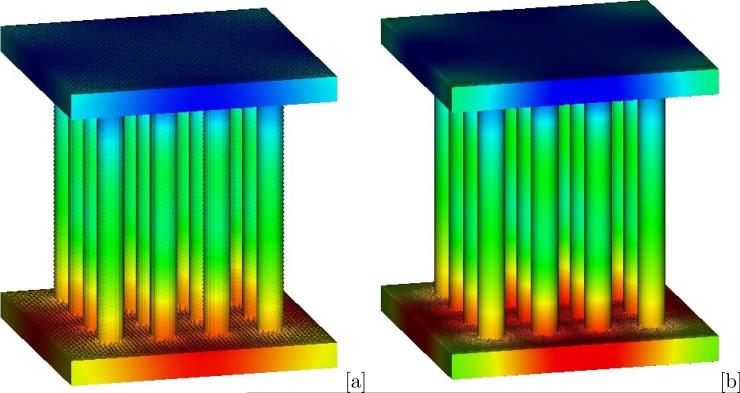
where x = (x₁,x₂,x₃). The numbers z_b and z_t denote x₃-values for which g attains the values g_b and g_t, respectively. In figure 4.3, we present the numerical solutions (shown on ∂Ω₁) obtained by solving the diffuse interface Approximation 1 from equation (2.31). The function ϕ is obtained from a level set description of the domain via equation (2.1) with ε = 0.05. The equations are solved in the computational domain Ω = (−4.0,4.0)³ with periodic boundary conditions using the AMDiS adaptive finite element framework described earlier. A BiCGStab algorithm is used to solve the system of discrete equations. In this simulation, we have taken k = 1, g_b = 2, g_t = 1, z_b = −2, z_t = 2. The right hand side is f = 1. In figure 4.3[a], the solution is shown with approximately 5 grid points across the diffuse interface layer (949,704 degrees of freedom (DOFs)) and in [b] the mesh is refined so that there are approximately 10 grid points across the layer (6,346,674 DOFs). The solution can be interpreted as a stationary temperature field (with blue and red denoting low and high temperatures respectively), where the structure is heated at the bottom and cooled at the top. In figure 4.4, a cross section of the mesh corresponding to figure 4.3[a] is shown together with the level contours of ϕ. Next, we modify the functions g and k in the Robin boundary conditions using the same complicated cuboid-pillar geometry as above. We take

$$g\left(x\right)=g_0-\mid \mathbf{x}-{\mathbf{x}}_0\mid ,$$ (4.10)

with g₀ = 10 and ${\mathbf{x}}_0=\left(\begin{array}{c}\hfill c_{bx}-l_x∕2\hfill \\ \hfill c_{by}-l_y∕2\hfill \\ \hfill c_{bz}-l_z∕2\hfill \end{array}\right)$, where $\left(\begin{array}{c}\hfill c_{bx}\hfill \\ \hfill c_{by}\hfill \\ \hfill c_{bz}\hfill \end{array}\right)$ denotes the center of the bottom cuboid and l_x, l_y and l_z denote the edge lengths in x₁-, x₂- and x₃-directions, respectively. For the function k, we take

$$k=k(\mathbf{x},\nabla \varphi )≔-h\left(x_3\right)\frac{\nabla \varphi }{\mid \nabla \varphi \mid }\cdot \left(\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 1\hfill \end{array}\right)=-h\left(x_3\right)\frac{{\partial }_{x_3}\varphi }{\mid \nabla \varphi \mid },$$ (4.11)

and

$$h\left(z\right)=h_0+(h_1-h_0)\frac{1}{2}\left(1-\text{tanh}\left(\frac{3z}{∊}\right)\right),$$

with h₀ = 10 and h₁ = 2. Thus, h is large in the lower part of the domain and moderate in the upper part. However, in the lateral directions k≈0 which approximates no flux boundary conditions. Again, the computational domain is Ω = (−4.0,4.0)³ with periodic boundary conditions. The result is shown in figure 4.5 using an adaptive mesh with at least 5 grid points across the diffuse interface (e.g. as in figure 4.3[a] and figure 4.4). Again the solution can be interpreted as a stationary temperature field.

Fig. 4.3.

Solution u of the diffuse domain Approximation 1 with Robin boundary conditions (4.9) on the boundary of the domain Ω₁. Blue and red denote small and large values of u. [a]: simulation using at least 5 grid points across the diffuse interface (949.704 DOFs), [b]. refined simulation using at least 10 grid points across the diffuse interface (6.346.674 DOFs).

Fig. 4.4.

Phase field function ϕ on cross section of the mesh from the simulation shown in figure 4.3[a].

Fig. 4.5.

Solution u of the diffuse domain Approximation 1 on the boundary of the domain Ω₁ with Robin boundary conditions (4.10) and (4.11) using at least 5 grid points across the diffuse interface (949,704 DOFs).

5. Conclusions and outlook

We have extended previous work and presented a general approach for solving PDEs in complex, stationary or moving geometries with Dirichlet, Neumann and Robin boundary conditions. Using a phase field approach, the partial differential equations are reformulated on a larger regular domain with additional lower order terms that approximate the boundary conditions. Matched asymptotic analyses were performed to demonstrate convergence to the original problem as the diffuse interface width tends to zero. Numerical simulations were performed which confirm the convergence analysis and show the effectiveness of the approach in simulating PDEs in complex domains.

Up to now, the geometry of the domain has been given analytically. This is not a restriction of the approach. For example, the phase field function can be the solution of another problem that determines the geometry. We now give an example of this in the context of heteroepitaxial growth where phase separation may occur in a growing thin crystal film. The model involves the solution of a Cahn-Hilliard equation in a film [19] which evolves due to surface diffusion (and also deposition/desorption). Neglecting deposition and desorption, the simplest set of governing equations for a binary film is

$$\begin{array}{cc}\hfill & V={\Delta }_{\Gamma }H\text{on}\partial {\Omega }_1\left(t\right),\hfill \\ \hfill & {\partial }_{t}u=\Delta \mu \text{in}{\Omega }_1\left(t\right),\hfill \\ \hfill & \mu =-∊\Delta u+\frac{1}{∊}{G}^{\prime }\left(u\right)\text{in}{\Omega }_1\left(t\right),\hfill \\ \hfill & \nabla \mu \cdot \mathbf{n}+uV=0\text{and}\nabla u\cdot \mathbf{n}=g\text{on}\partial {\Omega }_1\left(t\right),\hfill \end{array}$$

where Ω₁(t) is the evolving thin film domain, V is the normal velocity of the surface ∂Ω₁(t), n is the outward unit normal vector to ∂Ω₁(t), and H is the mean curvature. The operator Δ_Γ denotes the surface Laplacian on ∂Ω₁(t), u is the concentration of one of the film components, and μ is the chemical potential. A diffuse domain approximation for this system combines a phase field approach for both the evolving surface and a diffuse domain equation for the Cahn-Hilliard equation in the moving domain:

$$\begin{array}{cc}\hfill & {\partial }_t\varphi =\nabla \cdot ({∊}^{-1}B\left(\varphi \right)\nabla \omega )\text{in}\Omega ,\hfill \\ \hfill & g\left(\varphi \right)\omega =-∊\Delta \varphi +\frac{1}{∊}{G}^{\prime }\left(\varphi \right)\text{in}\Omega ,\hfill \\ \hfill & {\partial }_t\left(\varphi u\right)=\nabla \cdot (\varphi \nabla \mu )\text{in}\Omega ,\hfill \\ \hfill & \varphi \mu =-∊\nabla \cdot (\varphi \nabla u)+\frac{1}{∊}\varphi G^{\prime }\left(u\right)-∊g\mid \nabla \varphi \mid \text{in}\Omega ,\hfill \end{array}$$

where B(ϕ) = 36ϕ²(1−ϕ)², g(ϕ) = 30ϕ²(1−ϕ)² and we have used Approximation 2 for the Neumann boundary condition from equation (2.28) in the last equation. We could have used any of the diffuse domain approximations of the Neumann boundary conditions here, although Approximations 3 and 4 need to be rescaled where the rescaling is determined from the leading order term of the inner asymptotic expansion for ϕ.

An additional advantage of the diffuse domain approach is that it can easily be combined with a diffuse interface approximation of PDEs on surfaces introduced in [40], where the surfaces are implicitly described as a level set of a phase field function. Applications for these type of problems can for example be found in cell biology, where proteins diffusing inside the cell can bind to the membrane and diffuse along the membrane, whereas membrane-bound proteins can dissociate and become free to diffuse in the cytoplasm. Assuming a stationary membrane and cellular domain, a simple model for such a situation is (e.g., see [25, 35]):

$$\begin{array}{cc}\hfill & {\partial }_{t}v={\Delta }_{\Gamma }v+R_1+j\text{on}\partial {\Omega }_1\hfill \\ \hfill & {\partial }_{t}u=\Delta u+R_2\text{in}{\Omega }_1,\hfill \\ \hfill & j=-\nabla u\cdot \mathbf{n}=-r_{d}v+r_{a}u\text{on}\partial {\Omega }_1,\hfill \end{array}$$

where v and u are the surface and volume concentrations, respectively, the R_i, i = 1,2 are reaction terms depending on u and v, respectively, and r_d and r_a are desorption and absorption rate coefficients. The operator Δ_Γ again denotes the surface Laplacian on the boundary ∂Ω₁. A diffuse domain approximation for this system is

$$\begin{array}{cc}\hfill & B\left(\varphi \right){\partial }_{t}v=\nabla \cdot (B\left(\varphi \right)\nabla v)+B\left(\varphi \right)(R_1+j)\text{in}\Omega ,\hfill \\ \hfill & \varphi {\partial }_{t}u=\nabla \cdot (\varphi \nabla u)+\varphi R_2-∊j\mid \nabla \varphi \mid \text{in}\Omega ,\hfill \\ \hfill & j=-r_{d}v+r_{a}u\text{in}\Omega ,\hfill \end{array}$$

using Approximation 2 for the Neumann boundary condition from equation (2.28) in the volume concentration equation. Here, u, v and j are extended variables in Ω and B(ϕ) is as above. For a generalization in which a moving elastic membrane is considered and thus ϕ is evolving we refer the reader to [29].

Appendix A

In this appendix, we derive equations (2.6), (2.7) and (2.8). We also justify the Neumann and Robin boundary conditions given in equations (2.35), (2.36) and (2.42), (2.43) for moving domains.

Stationary domains. equations (2.6) and (2.7) are actually the distribution forms of equation (2.2) with Neumann and Robin boundary conditions. To see how these equations arise, we briefly derive the weak form of equation (2.2) with Neumann boundary conditions (the case with Robin boundary conditions is analogous). Multiply equation (2.2) by a test function ψ and integrate over Ω₁. Using integration by parts and that $\frac{\partial u}{\partial \mathbf{n}}=g$ on ∂Ω₁, it follows that:

$$-{\int }_{{\Omega }_1}\nabla \psi \cdot \nabla udx+{\int }_{\partial {\Omega }_1}\psi gds={\int }_{{\Omega }_1}\psi fdx,$$

which is the weak form of the equation (2.2) with Neumann boundary conditions. Introducing the characteristic function χ_Ω1 of the domain Ω₁ and the surface delta function δ_∂Ω1, and changing the integration domain to Ω, we obtain

$$-{\int }_{\Omega }{\chi }_{{\Omega }_1}\nabla \psi \cdot \nabla udx+{\int }_{\Omega }{\delta }_{\partial {\Omega }_1}\psi gdx={\int }_{\Omega }{\chi }_{{\Omega }_1}\psi fdx.$$

Next, integrate by parts and use that χ_Ω1 vanishes on ∂Ω. This gives

$${\int }_{\Omega }\psi \left(\nabla \cdot ({\chi }_{{\Omega }_1}\nabla u)+{\delta }_{\partial {\Omega }_1}g-{\chi }_{{\Omega }_1}f\right)dx=0,$$

and hence equation (2.6) follows.

The derivation of equation (2.8) follows from a similar line of reasoning, except that integration by parts is performed twice. Using that u = g on ∂Ω₁, we obtain

$${\int }_{{\Omega }_1}u\Delta \psi dx+{\int }_{\partial {\Omega }_1}(\psi \frac{\partial u}{\partial \mathbf{n}}-g\frac{\partial \psi }{\partial \mathbf{n}})ds={\int }_{{\Omega }_1}\psi fdx,$$

which is the weak form of the equation. Introducing χ_Ω1, δ_∂Ω1 and changing the domain of integration to Ω as before gives

$${\int }_{\Omega }{\chi }_{{\Omega }_1}u\Delta \psi dx+{\int }_{\Omega }{\delta }_{\partial {\Omega }_1}(\psi \frac{\partial u}{\partial \mathbf{n}}-g\frac{\partial \psi }{\partial \mathbf{n}})dx={\int }_{\Omega }{\chi }_{{\Omega }_1}\psi fdx.$$

Integrating by parts twice and using that χ_Ω1 vanishes on ∂Ω, it follows that

$${\int }_{\Omega }\psi \Delta \left({\chi }_{{\Omega }_1}u\right)dx+{\int }_{\Omega }{\delta }_{\partial {\Omega }_1}\psi \frac{\partial u}{\partial \mathbf{n}}dx-{\int }_{\Omega }{\delta }_{\partial {\Omega }_1}g\frac{\partial \psi }{\partial \mathbf{n}}dx={\int }_{\Omega }{\chi }_{{\Omega }_1}\psi fdx.$$

Using the fact that ∇χ_Ω1 = −δ_∂Ω1 n and that g is constant in the normal direction, we may write

$${\int }_{\Omega }{\delta }_{\partial {\Omega }_1}\psi \frac{\partial u}{\partial \mathbf{n}}dx=-{\int }_{\Omega }\psi \nabla {\chi }_{{\Omega }_1}\cdot \nabla udx,$$

and

$${\int }_{\Omega }{\delta }_{\partial {\Omega }_1}g\frac{\partial \psi }{\partial \mathbf{n}}dx={\int }_{\Omega }\psi g\nabla \cdot \nabla {\chi }_{{\Omega }_1}dx,$$

where we have also integrated by parts and used that δ_∂Ω1 vanishes on ∂Ω. Putting everything together gives

$${\int }_{\Omega }\psi \left(\nabla \cdot ({\chi }_{{\Omega }_1}\nabla u)+(u-g)\nabla \cdot \nabla {\chi }_{{\Omega }_1}-{\chi }_{{\Omega }_1}f\right)dx=0,$$

from which equation (2.8) follows.

Moving domains. To justify the Dirichlet and Robin boundary conditions in equations (2.35), (2.36) we derive the weak form of the equations as follows. The result in 1D can be found in [23]. Multiply equation (2.33) by a time and space dependent test function ψ and integrate from 0 to T in time and over Ω₁ in space. Integrating by parts in both space and time gives

$$\begin{array}{c}\hfill -{\int }_0^T{\int }_{{\Omega }_1}u{\partial }_t\psi dxdt+{\int }_0^T{\int }_{{\Omega }_1}\nabla \psi \cdot \mathbf{A}\nabla udxdt+{\int }_0^T{\int }_{{\Omega }_1}\psi (\mathbf{b}\cdot \nabla u+cu-f)dxdt\hfill \\ \hfill ={\int }_0^T{\int }_{\partial {\Omega }_1}\psi (\mathbf{n}\cdot \mathbf{A}\nabla u+uV)dsdt+{\int }_{{\Omega }_1\left(0\right)}\psi (\mathbf{x},0)u(\mathbf{x},0)dx-{\int }_{{\Omega }_1\left(T\right)}\psi (\mathbf{x},T)u(\mathbf{x},T)dx,\hfill \end{array}$$

which is the weak form of equation (2.33). Thus, the natural boundary condition is to specify n · A∇u+uV as in equations (2.35) and (2.36). In the above, we have used the fact that

$$\begin{array}{cc}\hfill {\int }_0^T{\int }_{{\Omega }_1}{\partial }_t\left(\psi u\right)dxdt=& -{\int }_0^T{\int }_{\partial {\Omega }_1}\psi uVdsdt\hfill \\ \hfill & +{\int }_{{\Omega }_1\left(T\right)}\psi (\mathbf{x},T)u(\mathbf{x},T)dx-{\int }_{{\Omega }_1\left(0\right)}\psi (\mathbf{x},0)u(\mathbf{x},0)dx.\hfill \end{array}$$

To derive the diffuse interface approximation (2.37) of equation (2.33) we follow the procedure outlined earlier and introduce φ ≈ χ_Ω1. Then, integrating over Ω and performing integration by parts in both space and time yields

$${\int }_0^T{\int }_{\Omega }\psi ({\partial }_t\left(\varphi u\right)-\nabla \cdot (\varphi \mathbf{A}\nabla u)+\varphi \mathbf{b}\cdot \nabla u+\varphi cu-\varphi f+B.C.)dxdt=0,$$

where B.C. stands for the approximation of the boundary conditions. For example, if approximation 1 of the Robin boundary conditions is used, then B.C. = −εk(u−g)|∇ϕ|². Finally, a similar analysis can be used to derive the boundary conditions (2.42) and (2.43) for the conservative equation (2.41) and to justify the corresponding diffuse interface approximation (2.44).