Biomechanical and Microstructural Properties of Common Carotid Arteries from Fibulin-5 Null Mice

Abstract

Alteration in the mechanical properties of arteries occurs with aging and disease, and arterial stiffening is a key risk factor for subsequent cardiovascular events. Arterial stiffening is associated with the loss of functional elastic fibers and increased collagen content in the wall of large arteries. Arterial mechanical properties are controlled largely by the turnover and reorganization of key structural proteins and cells, a process termed growth and remodeling. Fibulin-5 (fbln5) is a microfibrillar protein that binds tropoelastin, interacts with integrins, and localizes to elastin fibers; tropoelastin and microfibrillar proteins constitute functional elastic fibers. We performed biaxial mechanical testing and confocal imaging of common carotid arteries (CCAs) from fibulin-5 null mice (fbln5^−/−) and littermate controls (fbln5^+/+) to characterize the mechanical behavior and microstructural content of these arteries; mechanical testing data were fit to a four-fiber family constitutive model. We found that CCAs from fbln5^−/− mice exhibited lower in vivo axial stretch and lower in vivo stresses while maintaining a similar compliance over physiological pressures compared to littermate controls. Specifically, for fbln5^−/− the axial stretch λ = 1.41 ± 0.07, the circumferential stress σ_θ = 101 ± 32 kPa, and the axial stress σ_z = 74 ± 28 kPa; for fbln5^+/+ λ = 1.64 ± 0.03, σ_θ = 194 ± 38 kPa, and σ_z = 159 ± 29 kPa. Structurally, CCAs from fbln5^−/− mice lack distinct functional elastic fibers defined by the lamellar structure of alternating layers of smooth muscle cells and elastin sheets. These data suggest that structural differences in fbln5^−/− arteries correlate with significant differences in mechanical properties. Despite these significant differences fbln5^−/− CCAs exhibited nearly normal levels of cyclic strain over the cardiac cycle.

INTRODUCTION

Alteration in the mechanical properties of arteries occurs with aging and disease, and arterial stiffening is an independent predictor of cardiovascular risk.¹ Arterial stiffening is associated with the loss of functional elastic fibers and increased collagen content in the wall of large arteries. It is clear that vascular endothelial cells, smooth muscle cells, and fibroblasts demonstrate the remarkable ability to respond to mechanical stimuli via mechanotransduction mechanisms and to control the material properties and local mechanical environment in the arterial wall. This process occurs largely via delicate balances (or imbalances) in the synthesis, degradation, and reorganization of structural proteins and cells,^4,7 a process termed growth and remodeling.¹⁶ Genetically-modified animal models provide a unique opportunity to alter the content and organization of key microstructural proteins. ^8,30 Such models provide a platform to quantify the role of key structural proteins on the mechanical properties of arteries.

Fibulin-5, also known as DANCE (developmental arteries and neural crest EGF-like) or EVEC (embryonic vascular EGF-like repeat-containing protein), is an extracellular matrix protein that is essential for elastic fiber formation and is expressed in developing arteries as well as balloon-injured and atherosclerotic arteries.²¹ fbln5 localizes to elastic fibers and binds to tropoelastin and interacts with various integrins, including α_Vβ₃.²⁰ Mice lacking both alleles of the fbln5 gene experience loose skin, emphysema, tortuous blood vessels, and increased arterial stiffness.^24,32 Although adequate tropoelastin is present in large arteries of fbln5 knockout mice, this tropoelastin was not organized into functional elastic lamina in these vessels.³² Given these coincident microstructural and mechanical differences, fbln5^−/− mice provide a good model to study the effect of altered functional elastic fibers on the mechanical behavior of elastic arteries.

The purpose of this study is to quantify the biaxial biomechanical response and to qualitatively evaluate the microstructural content and organization of mouse common carotid arteries (CCAs) from fbln5^−/− mice and littermate controls. We performed biaxial mechanical tests and performed multiphoton (confocal) microscopy imaging on isolated carotid artery segments from fbln5^+/+ and fbln5^−/− mice. Biaxial tests revealed that arteries from fbln5^−/− mice were circumferentially and axially stiffer with a lower in vivo axial stretch than arteries from fbln5^+/+ mice. Confocal microscopy images showed that, in contrast to fbln5^+/+ CCAs, fbln5^−/− CCAs lacked organized elastic lamellae and that collagen fibers in fbln5^−/− CCAs engage at lower axial stretch ratios. Although vascular stiffness was elevated in fbln5^−/− vessels, since the in vivo pulse pressure is also higher in fbln5^−/− vessels, the cyclic strains in fbln5^−/− and fbln5^+/+ CCAs were not statistically different.

METHODS

Surgical Preparation and Vessel Isolation

Adult male mice, fbln5^−/− (13 ± 5 weeks old, n = 6) and fbln5^+/+ (13 ± 1 weeks old, n = 7) littermate controls on the C57BL/6 × 129/SvEv background were anesthetized with sodium pentobarbital (100 mg/kg IP). All mice were produced from a breeding pair originally obtained from Dr. Hiromi Yanagisawa (UT Southwestern). Under sterile conditions, both CCAs were excised, placed in fresh culture medium, dissected free of perivascular tissue, and mounted on the glass cannulae of our biomechanical testing device using sterile suture.¹¹ All animal procedures were approved by the Institute Animal Care and Use Committee (IACUC) at the Georgia Institute of Technology.

Biomechanical Testing

A device modified from one reported by Gleason et al.¹¹ was used to perform cylindrical biaxial biomechanical and vasoreactivity tests and to perform multi-photon, confocal microscopy. Pressure–diameter (P–d) data were collected from 0 to 180 mmHg at constant axial extensions, and axial force–length (f–ℓ) data were collected over cyclic axial extensions up to λ = 1.70 for fbln5^+/+ arteries and λ = 1.55 for fbln5^−/− arteries at constant pressures, P = 60, 100, and 160 mmHg. Here, λ = ℓ/L where ℓ is the current length and L is the original unloaded length; ℓ and L were measured as the distance between mounting sutures. The in vivo axial stretch ratio was defined as the stretch for which axial force remains nearly constant during the pressurization cycle.^5,27

P–d tests were performed at stretches above and below the in vivo axial stretch ratio and were performed at different sets of axial extensions for fbln5^−/− and fbln5^+/+ arteries. All P–d and f–ℓ tests were performed quasi-statically over 3 loading–unloading cycles, and to prevent damage from over stretching, the maximum axial load was limited to 9 and 4.4 mN for fbln5^+/+ and fbln5^−/− vessels, respectively. Tests were performed in the same order for all vessels; P–d at λ<in vivo axial stretch, P–d at λ ~ in vivo axial stretch, P–d at λ>in vivo axial stretch, f–ℓ at P = 60 mmHg, f–ℓ at P = 100 mmHg, and f–ℓ at P = 160 mmHg. Vessel wall thickness was measured using a custom videocaliper LabView subroutine by measuring the inner and outer diameter of the vessel following Gleason et al.¹¹

Immediately following these (‘basal’) biomechanical tests, vessels were loaded to P = 90 mmHg and λ = in vivo axial stretch ratio, and allowed to stabilize for 15 min. Contractile function was then assessed by measuring relative changes in diameter and axial force in response to the sequential administration vasoactive agents to the bathing media: phenylephrine (PE) or norepinephrine (NE) to elicit smooth muscle cell contraction, carbamylcholine chloride (CCh) to elicit endothelial-dependent dilation, and sodium nitroprusside (SNP) to elicit endothelial-independent dilation.¹¹ Values of diameter and axial force were normalized to values measured at the end of the 15-min recovery period.

Opening Angle

It is well known that the traction-free configuration of arteries is typically not stress-free; rather these unloaded vessels contain residual stresses.³ To quantify the degree of residual stress in these arteries, opening angle measurements were made. Multiple unloaded rings were cut from excised carotid arteries (17 fbln5^−/− and 12 fbln5^+/+ total), and a single radial cut was imposed, which caused the vessel rings to spring open, relieving much of the residual stress. The opening angle, Φ_o, was calculated as

$${\mathrm{\Phi }}_{\text{o}}=\pi -\frac{L_{\text{o}}-L_{\text{i}}}{2H}\text{and}A=\frac{H(L_{\text{o}}+L_{\text{i}})}{2}$$ (1)

where the second term on the right-hand side of Eq. (1)₁ is the half-angle of the open sector as defined by Chuong and Fung,³ L_o and L_i are the outer and inner arc lengths of the stress-free sector, H is the wall thickness of the stress-free sector and A is the cross-sectional area of the wall in the open sector. A mean value for H was calculated by measuring the area of the sector and using Eq. (1)₂.

Stress, Strain, and Compliance

The mean circumferential stress (σ_θ) and axial stress (σ_z) were then calculated as

$${\sigma }_{\theta }=\frac{Pa}{h}\text{and}{\sigma }_z=\frac{f}{\pi (b^2-a^2)}$$ (2)

where P is the transmural pressure, a is the current inner radius, b is the current outer radius, h is the current thickness, and f = f_m + πa²P is the force applied to the vessel wall; f_m is the force measured by the force transducer. The mean circumferential and axial components of the Green Strain were calculated as

$${\overline{E}}_{\theta \theta }=\frac{{\overline{\lambda }}_{\theta }^2-1}{2}\text{and}{\overline{E}}_{zz}=\frac{{\overline{\lambda }}^2-1}{2}$$ (3)

where the mean circumferential stretch was calculated as λ̄_θ = r_mid/ρ_mid, using mid-wall loaded and unloaded radii r_mid = (a + b)/2 and ρ_mid = (ρ_o − ρ_i)/2, respectively; here ρ_i and ρ_o are the unloaded inner and outer radii. Compliance is defined through the relation

$$C\mathrm{\Delta }P=\mathrm{\Delta }\epsilon =\frac{\mathrm{\Delta }{r}_{\text{m}}}{{\overline{r}}_{\text{m}}}$$ (4)

where C is compliance, Δr_m is the difference in the mid-wall radii measurements at two different pressures, r̄_m is the mid-wall radius at the mean pressure, ΔP is difference in the two pressures, and Δε is the local linearized cyclic strain experienced over ΔP. Physiological blood pressures were defined as 133/92 mmHg (systole/diastole) for fbln5^+/+ mice and 151/94 mmHg for fbln5^−/− mice.³²

Statistical Analysis

Mean values were compared using unpaired, two-tailed t-tests, with significance taken at p<0.05. Welch’s correction was used when variances between groups were unequal.

Multiphoton Microscopy

Freshly isolated vessels were imaged on an LSM 510 META inverted confocal microscope (Zeiss). The laser reached the sample through either a 40×/1.3NA or a 63×/1.4NAoil immersion objective (Zeiss). The META module of the microscope was configured as a 380–420-nm bandpass filter to detect backward scattering second-harmonic generation (SHG) signal from collagen.³³ Elastin was detected using a 500–550-nm bandpass filter with 488 nm laser excitation.³¹ Confocal microscopy of embedded sections showed nearly identical morphology of elastin and collagen as samples stained with Verhoeff’s and picro sirius red stains. Smooth muscle cells were visualized by staining the extracellular space with carboxyfluorescein.²² Imaris software (Bitplane) was used for 3D reconstruction of images.

Constitutive Modeling

Kinematics

We considered three configurations: a loaded configuration β_t, a traction-free (unloaded) configuration β_u, and a (nearly stress-free) reference configuration β_o; see Chuong and Fung.³ For inflation and extension of an axisymmetric tube, the deformation gradient, right Cauchy Green strain, and Green strain tensors have components

$$\begin{array}{l}[\mathbf{F}]=\text{diag}\{{\lambda }_r,{\lambda }_{\theta },{\lambda }_z\},[\mathbf{C}]=\text{diag}\{{\lambda }_r^2,{\lambda }_{\theta }^2,{\lambda }_z^2\},\\ [\mathbf{E}]=\text{diag}\{({\lambda }_r^2-1)/2,({\lambda }_{\theta }^2-1)/2,({\lambda }_z^2-1)/2\}\end{array}$$ (5)

where

$${\lambda }_r=\frac{\partial r}{\partial R},{\lambda }_{\theta }=\frac{\pi r}{{\mathrm{\Theta }}_{\text{o}}R}\text{and}{\lambda }_z=\lambda \mathrm{\Lambda },$$ (6)

and Λ and λ are the axial stretches for the motions from β_o to β_u and from β_u to β_t, respectively, and Θ_o = (π − Φ_o) is the sector angle in β_o. If the material is assumed to be incompressible, det(F) = 1, the current radius may be related to the reference radius (in β_o) as

$$r=\sqrt{\frac{{\mathrm{\Theta }}_{\text{o}}}{\pi \lambda \mathrm{\Lambda }}(R^2-R_{\text{i}}^2)+r_{\text{i}}^2}\text{or}r=\sqrt{r_{\text{o}}^2-\frac{{\mathrm{\Theta }}_{\text{o}}}{\pi \lambda \mathrm{\Lambda }}(R_{\text{o}}^2-R^2)},$$ (7)

where R_i and R_o are inner radii or outer radii in β_o and r_i and r_o are inner and outer radii in β_t. Thus, given measured values for the reference configuration (R_i, R_o, the unloaded axial length L_z, and Θ_o) and the current configuration (r_o, r_i, and the loaded length ℓ), the components of F, C, and E are easily calculated.

Equilibrium

Inflation and extension of a long, straight, axisymmetric, closed-ended tube in equilibrium requires that

$$\begin{array}{l}P=\underset{r_{\text{i}}}{\overset{r_{\text{o}}}{\int }}({\widehat{T}}_{\theta \theta }-{\widehat{T}}_{rr})\frac{dr}{r}\text{and}\\ f_{\text{m}}=\pi \underset{r_{\text{i}}}{\overset{r_{\text{o}}}{\int }}(2{\widehat{T}}_{zz}-{\widehat{T}}_{\theta \theta }-{\widehat{T}}_{rr})\mathit{rdr};\end{array}$$ (8)

where

$$\mathbf{T}=\widehat{\mathbf{T}}-p\mathbf{I}\text{where}\widehat{\mathbf{T}}=2\mathbf{F}(\partial W/\partial \mathbf{C}){\mathbf{F}}^{\text{T}}$$ (9)

T̂ is the so-called ‘extra’ stress due to the deformation, and W is the strain energy density function; see Humphrey.¹⁵

Constitutive Equation

We used a four fiber-family model proposed by Baek et al.² which is a simple extension of the model proposed by Holzapfel et al.¹³ and Spencer,²⁶ with strain energy function

$$W=\frac{b}{2}(I_1-3)+\sum _{k=1,2,3,4}\frac{b_1^k}{2b_2^k}\left\{exp\left[b_2^k{\left({({\lambda }^k)}^2-1\right)}^2\right]-1\right\}$$ (10)

where b, $b_1^k$, and $b_2^k$ are material parameters with k denoting a fiber family, I₁ = tr(C) = C_rr + C_θθ + C_zz is the first invariant of C, ${\lambda }^k=\sqrt{{\mathbf{M}}^k·\mathbf{C}{\mathbf{M}}^k}$ is the stretch of the kth fiber family, M^k = sin(α^k)e_θ + cos(α^k)e_z is the unit vector along the kth fiber direction in the reference configuration, and α^k is the associated angle between the axial and fiber directions. In general, (λ^k)² = C_θθ sin²(α^k) + 2C_θz sin(α^k) cos(α^k) + C_zz cos²(α^k), but C_θz = 0 for inflation and extension tests, given material symmetry. Under compression, the fiber families do not contribute to the mechanical response in an exponential fashion, as they do in tension. Thus, when λ^k<1, we set $b_1^k=0$; therefore, we model the vessel under compression as a neo-Hookean material. Here, we consider four-fiber families with α¹ = 90° (circumferential), α² = 0° (axial), and α³ = −α⁴ = α (diagonal) which is left as a variable to be determined along with the seven material parameters (with $b_1^3=b_1^4$ and $b_2^3=b_2^4$ for the diagonal fibers to ensure material symmetry) via non-linear regression.

Parameter Estimation

Equations (8)₁ and (8)₂ were used to calculate P and f based on measured values of outer diameter, axial length, unloaded radius, unloaded length and wall thickness. We employ Eq. (6), with Eq. (7), and specify the in vivo configuration and transmural strains in this configuration to determine F and C. Material parameters were identified via nonlinear regression by minimizing the error function

$$\text{Error}={\left\{\sum _{i=1}^N{\left(\frac{P_{\text{meas}}(i)-P_{\text{model}}(i)}{\overline{P}}\right)}^2+\sum _{i=1}^N\left(\frac{f_{\text{meas}}(i)-f_{\text{model}}(i)}{\overline{f}}\right)\right\}}^2$$ (11)

where P_meas(i) and f_meas(i) are measured values and P_model(i) and f_model(i) are predicted values of pressure and axial force for data point i and P̄ and f̄ are mean values of pressure and force over all data points. Thus, Eq. (11) quantifies the difference between experimental data and modeling predictions. Calculations were performed in MatLab 7.1 using the lsqnonlin subroutine.

RESULTS

Mechanical Response of fbln5^−/− Arteries and Controls

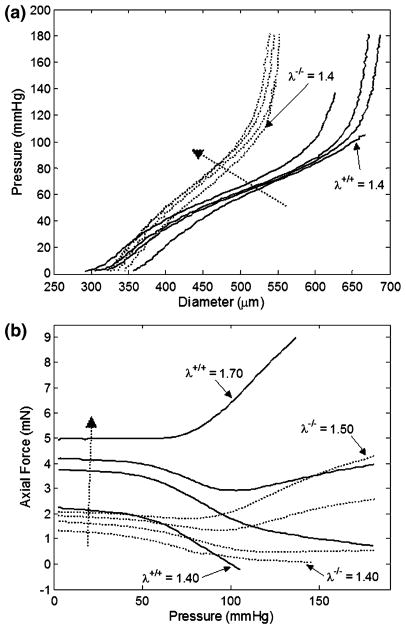
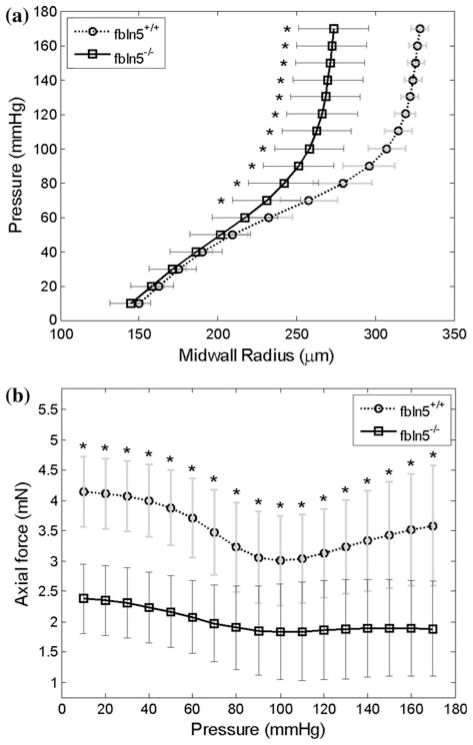
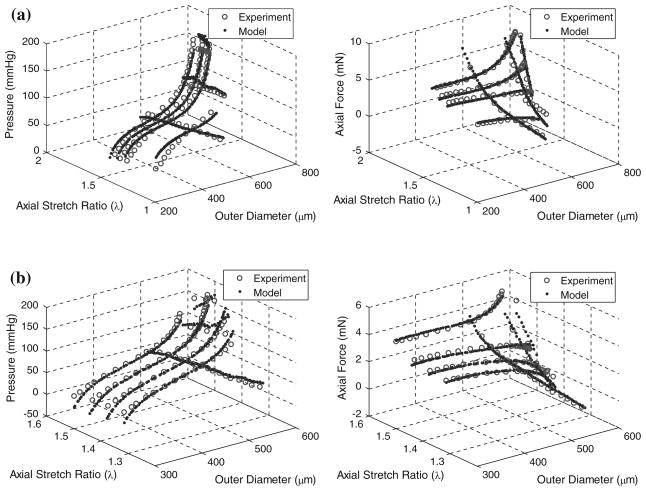
Pressure–diameter tests of fbln5^+/+ mice and fbln5^−/− mice revealed distinct regimes over lower pressure and higher pressure ranges characteristic of rodent large arteries (Fig. 1a). Not all curves reached 180 mmHg because tests were stopped when the axial force reached the maximum limit or when the axial force became negative. Force measurements taken during P–d tests indicated that at lower axial stretch ratios, axial force decreases with increased pressure while at higher axial stretch ratios, axial force increases with increased pressure (Fig. 1b). Although the range of axial stretch ratios used for testing was different for the fbln5^−/− and fbln5^+/+ groups, there were stretch ratios that overlapped both groups. Namely, at λ = 1.40, it is clear that the mechanical responses of the two types of vessels are different (Fig. 1b). For each vessel tested, there was an axial stretch ratio for which the force remains nearly constant with increased pressure, indicating the in vivo axial stretch ratio.^5,27 Mid-wall radii were calculated at the in vivo axial stretch ratio revealing significant differences in geometry at pressures greater than or equal to 70 mmHg (Fig. 2a and Table 1). In addition, the axial force was significantly different between groups when measured at the in vivo axial stretch ratio (Fig. 2b). Given the significantly lower in vivo axial stretch of the fbln5^−/− vessels, P–d tests for fbln5^−/− vessels were performed at lower axial stretch ratios than fbln5^+/+ vessels. Results from axial force–length tests (Fig. 3) revealed a cross-over point which represents the in vivo axial stretch ratio²⁸; the mean in vivo axial stretch ratio of fbln5^−/− arteries was λ = 1.41, compared to a mean in vivo axial stretch ratio of λ = 1.64 in fbln5^+/+ arteries (Table 1). The in vivo axial stretch ratios as determined from f–ℓ tests were similar to the axial stretch ratio determined from P–d tests.

FIGURE 1.

Representative plots of pressure–diameter (a) and pressure–force (b) results for fbln5 ^+/+ (solid lines) and fbln5 ^−/− (dotted lines) arteries. Curves for the fbln5 ^−/− plot indicate axial stretch ratios of λ = 1.40, λ = 1.45, λ = 1.48, and λ = 1.50, while curves for the fbln5 ^+/+ plot indicate axial stretch ratios of λ = 1.40, λ = 1.60, λ = 1.65, and λ = 1.70. Dotted arrow indicates direction of increasing axial stretch ratios. The exponentially stiffening portion of the mechanical response of P–d curves occurs at smaller diameters in fbln5 ^−/− arteries.

FIGURE 2.

Mean pressure-mid-wall radii (a) and pressure–force (b) plots for fbln5 ^+/+ (circles) and fbln5^−/− (squares) arteries. Data were collected at the in vivo axial stretch ratio and indicate that fbln5 ^−/− vessels had smaller circumferential dimensions. Asterisks indicate p<0.05; error bars indicate standard deviation.

TABLE 1.

Animal age and weight and vessel geometry, contractile response, and mechanical metrics for fbln5 ^+/+ and fbln5 ^−/− mice.

	fbln5+/+ (n = 6)	fbln5−/− (n = 7)
Age (weeks)	13 (1)	13 (5)
Body weight (g)	28.93 (1.88)	24.04 (2.65)*
Opening angle	86.6 (14.1)	150 (12)*
Unloaded dimensions (μm)
Inner diameter	248 (34)	202 (99)
Outer diameter	403 (21)	417 (23)
Wall thickness	77.1 (15.3)	108 (42)
In vivo dimensions (μm)
Inner diameter	603 (25)	492 (57)*
Outer diameter	652 (23)	577 (43)*
Wall thickness	24.3 (4.5)	42.6 (11.1)*
In vivo axial stretch ratio	1.64 (0.03)	1.41 (0.07)*
Maximal contraction (%)	12.6 (6.0)	4.60 (2.88)*
Physiological compliance (MPa−1)	14.0 (7.4)	8.51 (3.62)
Linearized cyclic strain (%)	7.76 (4.13)	6.46 (2.75)
Mean in vivo stresses (kPa)
Circumferential	194 (38)	101 (32)*
Axial	159 (29)	74.4 (27.9)*

Values are means (SD).

Asterisks indicate statistical significant differences (* p<0.05).

FIGURE 3.

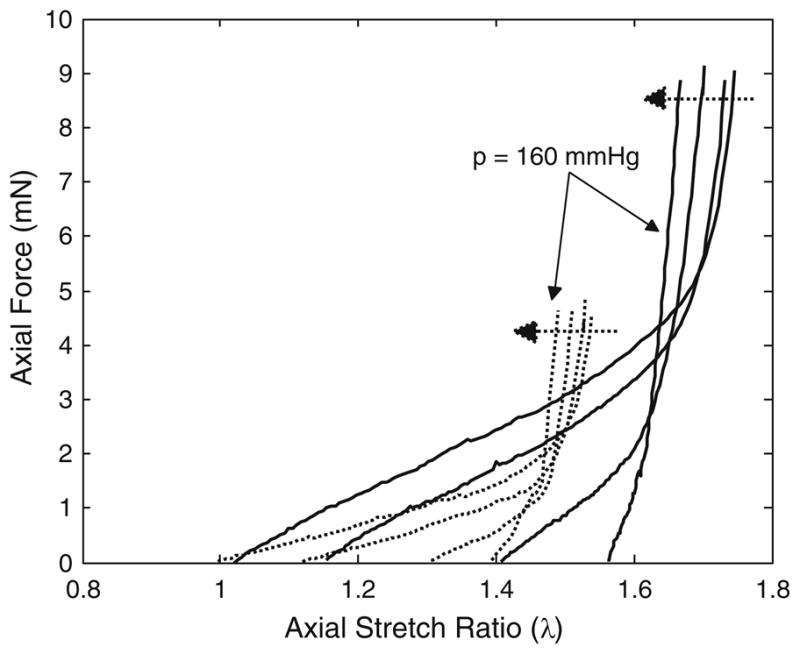
Representative plots of axial force-stretch results for fbln5 ^+/+ (solid lines) and fbln5 ^−/− (dotted lines) arteries. Axial force-stretch tests were conducted at pressures of P = 0, P = 60, P = 100, and P = 160 mmHg. Dotted arrows indicate direction of increasing pressure. The crossover points represent in vivo axial stretch ratios; and the data suggest that fbln5 ^−/− vessels have a lower in vivo axial stretch ratio.

Stress, Strain, and Compliance

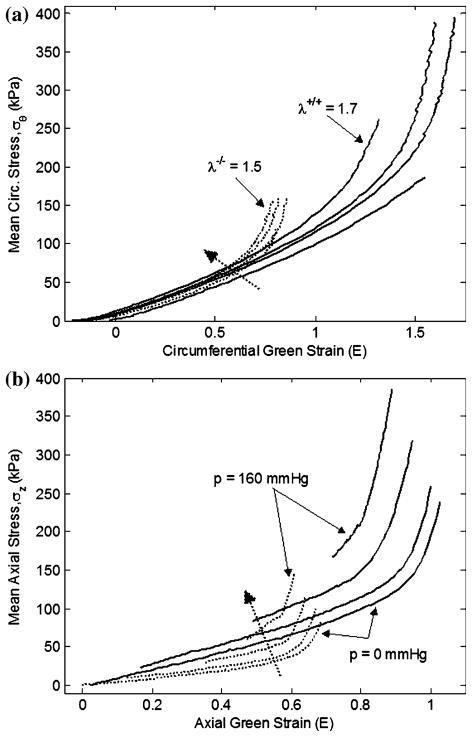
Since the pressure–diameter and axial force–length responses depend on both material properties and geometry, it is difficult to quantify differences in the material properties between different vessels from P–d and f–ℓ plots. Stress–strain plots, however, only depend on material properties; thus, differences in the stress–strain response indicate differences in the material properties. While large segments of the mean stress–strain plots in both circumferential and axial directions overlap (Fig. 4), calculations based on in vivo axial stretch and mean blood pressures reveal significant differences in both in vivo axial and circumferential stresses (Table 1). Mean circumferential and axial (Cauchy) stress vs. mid-wall Green strain reveal significant differences in the material response between fbln5^+/+ and fbln5^−/− vessels (Figs. 4a and 4b). In other words, the exponentially stiffening portion of the stress strain plots occurs at lower strains for fbln5^−/− vessels. The overall compliance, between systolic and diastolic pressures, of the fbln5^−/− CCAs was not statistically different than fbln5^+/+ CCAs. The in vivo local linearized cyclic strain Δε over the cardiac cycle was also not statistically different across groups (Table 1). The local compliance, calculated at 10 mmHg intervals, was also not significantly different at the overlapping physiological pressures; however, compliance was different at 50, 60, 70, 80, and 150 mmHg (Fig. 5).

FIGURE 4.

Representative plots of mean circumferential stress–strain (a) and mean axial stress–strain (b) results for fbln5 ^+/+ (solid lines) and fbln5 ^−/− (dotted lines) arteries. For the circumferential stress–strain plot, curves for the fbln5 ^−/− plot indicate axial stretch ratios of λ = 1.40, λ = 1.45, λ = 1.48, and λ = 1.50, while curves for the fbln5 ^+/+ plot indicate axial stretch ratios of λ = 1.40, λ = 1.60, λ = 1.65, and λ = 1.70. For the axial stress–strain plot, curves reflect tests conducted at pressures of P = 0, P = 60, P = 100, and P = 160 mmHg. Dotted arrows reflect the direction of increasing axial stretch ratio or direction of increasing pressure. The exponentially stiffening portion of the curves occurs at lower strains in the fbln5 ^−/− artery.

FIGURE 5.

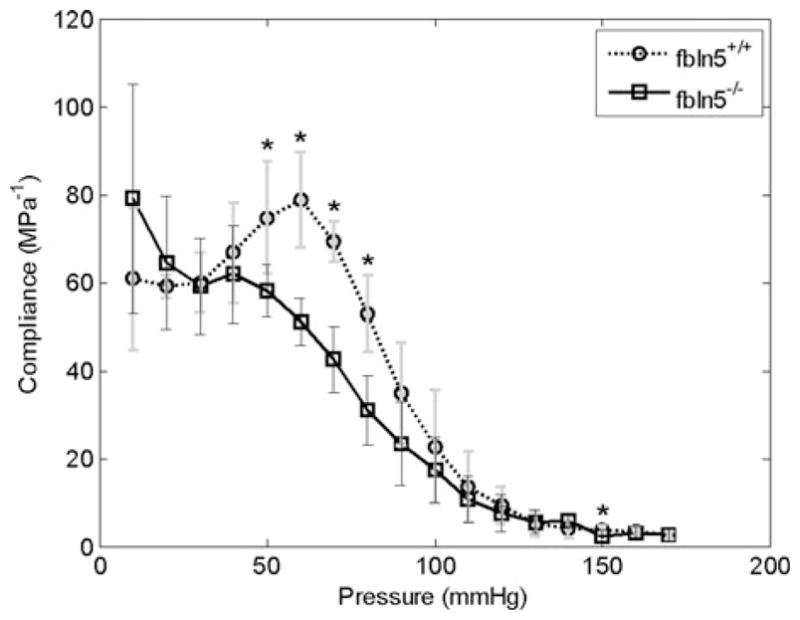
Compliance calculated at 10 mmHg intervals at the in vivo axial stretch ratio. At overlapping physiological pressures, there were no significant differences in compliance. Asterisks indicate p < 0.05; errors bars indicate one standard deviation.

Stress-Free, Unloaded, and Loaded Configuration

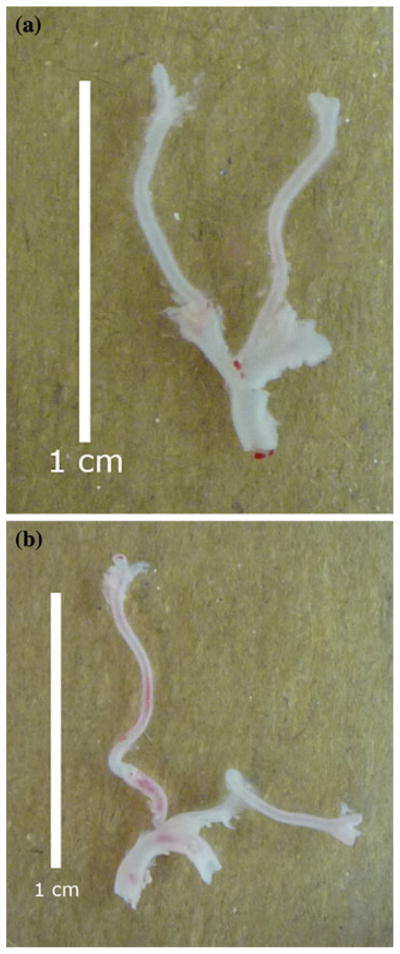
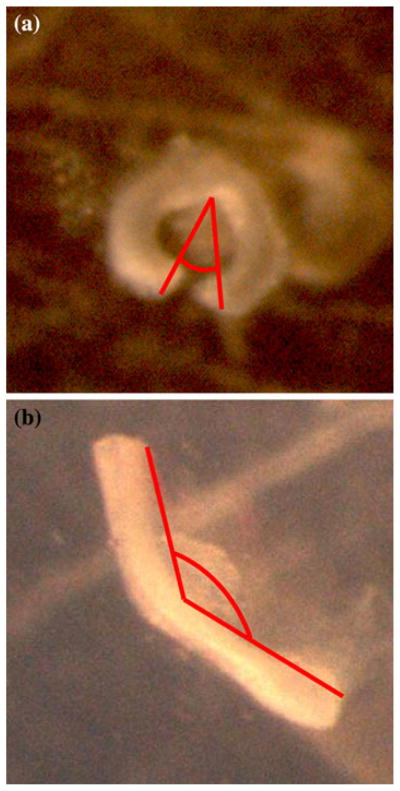
Excised fbln5^+/+ carotid arteries exhibited slight bending upon excision compared to the marked tortuosity of fbln5^−/− arteries (Fig. 6). Opening angles of sectors cut from fbln5^−/− arteries were statistically greater than angles of fbln5^+/+ arteries (Fig. 7 and Table 1), and there was also greater variability across samples in opening angle measurements from fbln5^−/− arteries. Inner diameter, outer diameter, and wall thickness were not statistically different in unloaded, traction-free configurations of fbln5^+/+ and fbln5^−/− arteries. Under physiological loading conditions, fbln5^−/− vessels had significantly smaller inner and outer diameters and larger wall thicknesses than the fbln5^+/+ vessels (Table 1).

FIGURE 6.

Representative images of excised arteries from fbln5 ^+/+ (a) and fbln5 ^−/− (b) vessels. Vessels in the unloaded state from knockout mice exhibit significant tortuosity compared with slight bending observed in wild-type vessels.

FIGURE 7.

Representative opening angle sectors from fbln5 ^+/+ (a) and fbln5 ^−/− (b) arteries.

Functional Response

Following ‘basal’ biomechanical testing, smooth muscle and endothelial cell function was confirmed by pharmacologically induced constriction and dilation. Both fbln5^−/− and fbln5^+/+ vessels decreased in diameter in response vasoconstrictors while relaxing to near basal levels of outer diameter in response to vasodilators (Table 1). Both wild-type and knockout vessels exhibited significant differences in normalized diameter at maximal contraction and normalized diameter at maximal relaxation.

Microstructural Organization

In the traction-free configuration, elastin from the fbln5^+/+ artery appeared undulated with a distinct internal elastic lamina while elastin in the fbln5^−/− artery appears disorganized with no distinct internal lamina (Fig. 8). Under in vivo conditions, distinct layers of elastin are visible in the fbln5^+/+ artery while the fbln5^−/− artery lacks noticeable lamellar units (Fig. 8). Collagen in the traction-free configuration appears to exist with varying degrees of undulation in the fbln5^−/− and the fbln5^+/+ arteries (Fig. 9). Under identical conditions of axial stretch and transmural pressure, collagen fibers in fbln5^−/− arteries appear to be straightened and engaged while collagen fibers in fbln5^+/+ arteries appear undulated (Fig. 9). Under in vivo conditions, individual smooth muscle cells show similar morphology in both fbln5^−/− and the fbln5^+/+ arteries; however, distinct lamellar units were visible in the fbln5^+/+ arteries (Fig. 10).

FIGURE 8.

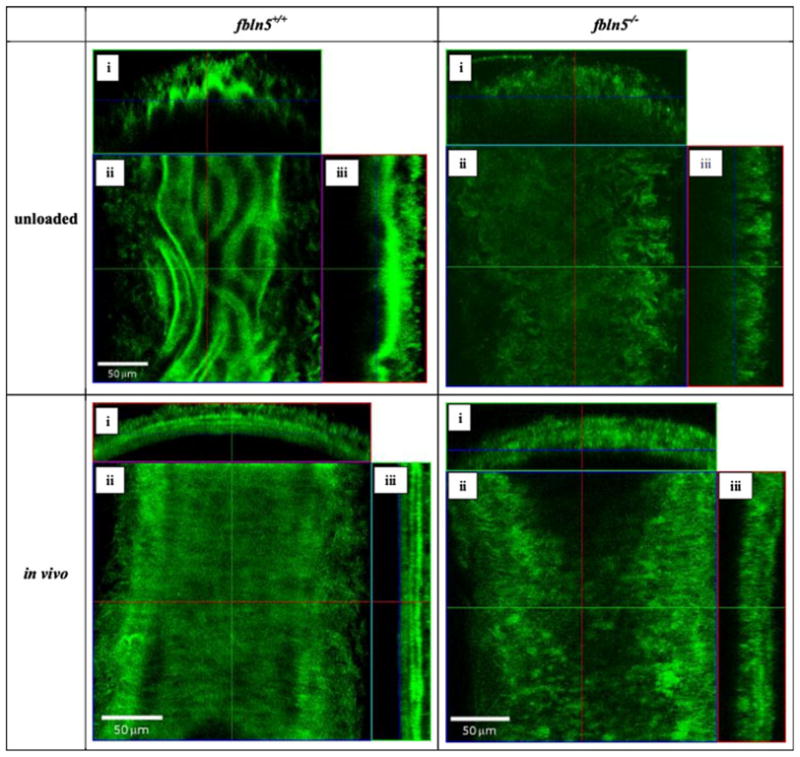
The undulated internal elastic lamina is clearly visible in the traction-free configuration of the fbln5 ^+/+ artery while elastin is more disorganized in the fbln5 ^−/− artery. When pressurized to in vivo conditions, elastin is organized into lamellar units and is visible in the fbln5 ^+/+ artery while in the fbln5 ^−/− artery, elastin remains disorganized. Panels i, ii, and iii show cross, en face, and longitudinal sections, respectively.

FIGURE 9.

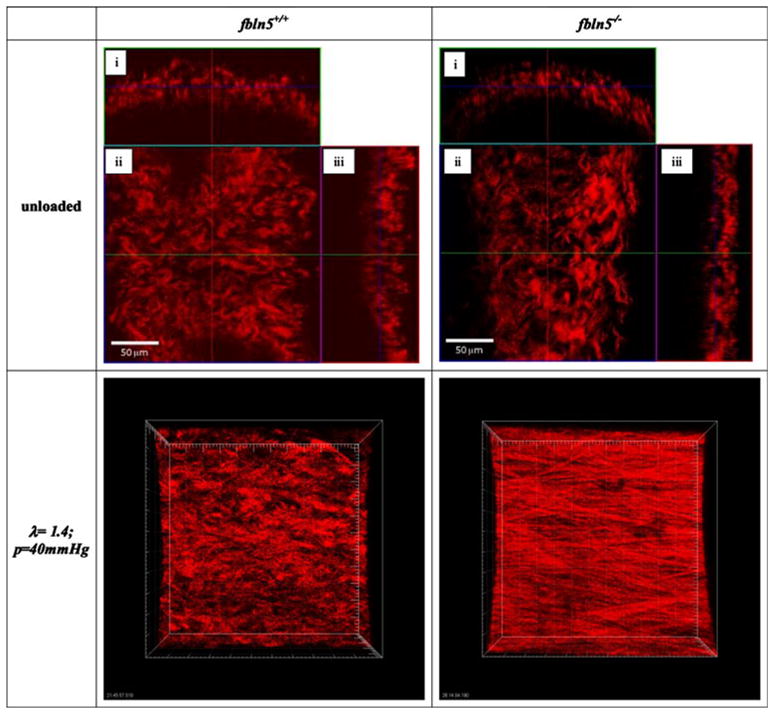
In the traction-free state, collagen fibers in the fbln5 ^+/+ artery and the fbln5 ^−/− artery have different degrees of undulation. Panels i, ii, and iii show cross, en face, and longitudinal sections, respectively. Collagen was imaged at an axial stretch of λ = 1.4 and transmural pressure of P = 40 mmHg for both knockout and wild-type arteries; images were stacked to generate a 3D reconstruction (axis of the vessel oriented horizontally). Collagen fibers from the fbln5 ^−/− vessel appear straightened while collagen fibers from the fbln5 ^+/+ vessel appear undulated, indicating that collagen fibers in fbln5 ^−/− vessels become engaged at a lower axial stretch ratio.

FIGURE 10.

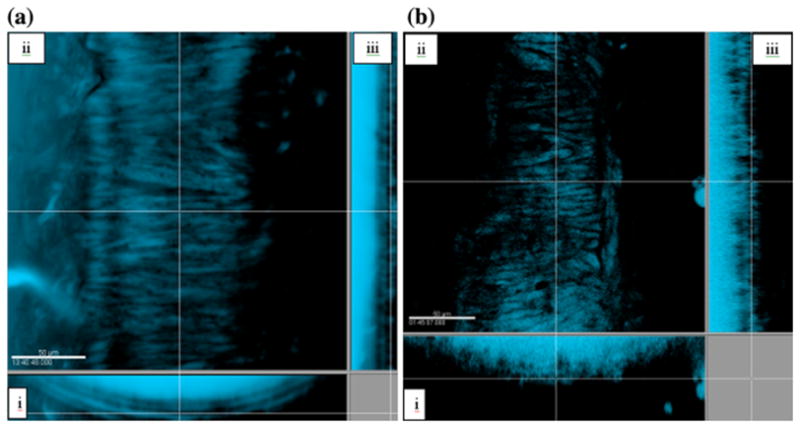
SMC from the fbln5 ^+/+ artery (a) are arranged into lamellar units while SMC from the fbln5 ^−/− artery (b) lack lamellar structure. Panels i, ii, and iii show cross, en face, and longitudinal sections, respectively.

Parameter Estimation

A four-fiber model was able to capture the full range of mechanical behaviors in both fbln5^−/− and the fbln5^+/+ arteries (Fig. 11). The lower and upper limits of the parameters were prescribed as b and $b_1^k\in [0,{10}^5],b_2^k\in [{10}^{-4},{10}^5]$, and α ∈ [0°, 90°]. The upper bounds were selected to encompass the full working range of individual parameters, and the non-zero lower bound for $b_2^k$ was selected to prevent the algorithm from searching for values close to zero. Final parameter values were insensitive to initial guesses. The mean values of Error = 0.058 and Error = 0.042 indicate reasonably good fits to experimental data; error values on (Table 2) reflect the error calculated from Eq. (11) normalized to the total number of data points for each vessel. A significant increase in $b_2^2$ and $b_2^3$ was seen for the fbln5^−/− groups (Table 2); these are the parameters in the exponential terms for the axially and diagonally oriented fiber families Eq. (10). Note that the elastic modulus term, b, was lower in fbln5^−/− vessels; however, this difference was not statistically significant.

FIGURE 11.

Illustrative plots of pressure and axial force vs. diameter and axial stretch ratio for model predictions (filled circle) and experimentally measured (open circle) for fbln5 ^+/+ (a) and fbln5 ^−/− (b) arteries. At lower diameters, these two cases show the model overestimating pressure for the fbln5 ^+/+ artery while underestimating pressure for the fbln5 ^−/− artery.

TABLE 2.

Material parameters for fbln5 ^+/+ and fbln5 ^−/− CCAs obtained for a four-fiber constitutive model.

	b (kPa)	$b_1^1(\text{kPa})$	$b_2^1$	$b_1^2(\text{kPa})$	$b_2^2$	$b_1^3(\text{kPa})$	$b_2^3$	α	Error
fbln5 +/+
1	26.295	0.036	0.709	0.141	1.201	0.576	0.835	43.1	0.104
2	26.905	3.569	0.129	0.611	0.768	0.803	0.885	32.9	0.060
3	17.004	0.431	0.216	0.418	0.783	0.246	0.850	32.0	0.033
4	40.516	0.974	0.278	0.105	0.932	0.012	1.562	41.2	0.055
5	31.285	0.385	0.290	0.333	1.004	0.370	0.861	33.6	0.071
6	13.805	3.153	0.044	17.744	0.000	0.274	0.726	30.7	0.024
Mean	25.968	1.425	0.278	3.225	0.781*	0.380	0.953*	35.6	0.058
SD	9.687	1.535	0.231	7.115	0.415	0.276	0.303	5.2	0.029
fbln5 −/−
1	26.735	5.077	0.859	0.000	5.537	0.050	3.426	36.1	0.033
2	24.002	2.940	0.633	0.610	2.659	1.080	2.026	40.7	0.025
3	26.699	0.963	0.625	0.032	5.305	0.368	2.688	34.9	0.051
4	0.189	0.727	0.068	4.876	1.078	2.682	0.399	36.5	0.070
5	0.133	2.313	0.023	9.448	0.000	1.688	0.717	25.9	0.054
6	11.716	0.992	0.353	0.990	5.638	0.447	3.450	29.9	0.017
7	19.889	6.527	0.306	0.000	9.086	0.081	3.139	34.4	0.041
Mean	15.623	2.791	0.410	2.279	4.186*	0.914	2.264*	34.1	0.042
SD	11.747	2.246	0.310	3.606	3.128	0.975	1.267	4.8	0.018

Values are means (SD).

Asterisks indicate that the parameter is statistically different between knockout and wild-type mice (* p<0.05).

DISCUSSION

Since the classic article by Roach and Burton, it is thought that functional elastic fibers in large arteries mediate the shape of the pressure–diameter curves at low pressures while collagen mediates this behavior at higher pressures.²⁵ Genetically altered mouse models that suppress expression of tropoelastin and microfibrillar proteins (e.g., fibrillins and fibulins) provide a unique platform to study the role of functional elastic fibers in the mechanical response of arteries.^8,30 In this study, we quantified the mechanical properties of fbln5^−/− CCAs, which lack functional elastic laminae, and the fbln5^+/+ arteries, which have normal elastic laminae. We performed biaxial mechanical tests and multiphoton (confocal) microscopy imaging on isolated carotid artery segments from fbln5^+/+ and fbln5^−/− mice. Biaxial tests revealed that arteries from fbln5^−/− mice were circumferentially and axially stiffer with a lower in vivo axial stretch ratio than arteries from fbln5^+/+ mice. Although vascular stiffness was elevated in fbln5^−/− vessels, since the in vivo pulse pressure is also higher in fbln5^−/− vessels, the cyclic strains in fbln5^−/− and fbln5^+/+ CCAs were not statistically different. This result suggests that, although significant microstructural differences exist between fbln5^−/− and fbln5^+/+ CCAs, growth and remodeling mechanisms that occur throughout development have altered the geometry and microstructural organization to achieve similar values of cyclic strain. Confocal microscopy images reveal significant differences in the structure of elastin and the organization of smooth muscle cells of fbln5^−/− CCAs. In contrast to fbln5^+/+ CCAs, fbln5^−/− CCAs lacked organized elastic lamellae and had collagen fibers that engaged in load bearing at lower axial stretch ratios. These differences in microstructure were coincident with elevated vascular stiffness and a lower in vivo axial stretch ratio in fbln5^−/− vessels. Constitutive modeling revealed that the mechanical behavior of fbln5^+/+ and fbln5^−/− vessels could be described well with the four-fiber family model of Baek et al.²

These microstructural differences manifest in significant differences in the biaxial biomechanical behavior across these groups. In particular, loss of functional elastic laminae results in vessels with an 15% reduction in in vivo mid-wall diameter, a 75% increase in vivo wall thickness, a 15% reduction in in vivo axial stretch, and a ~50% reduction in in vivo stresses. It appears that the presence of functional elastic laminae in control vessels serve to increase the in vivo axial stretch ratio and prevent vessel tortuosity. In fbln5^−/− arteries, the exponential stiffening region of the stress–strain plot occurs at lower axial and circumferential strains. This phenomenon can be further illustrated by images of collagen from knockout and wildtype arteries that are pressurized and stretched to identical loading conditions. Collagen fibers seen in fbln5^−/− CCAs at an axial stretch of λ = 1.4 and pressure of P = 40 mmHg appear straightened while collagen fibers from fbln5^+/+ arteries remain undulated (Fig. 9).

Decreases in in vivo axial stretch have been observed in mice deficient in elastin (eln), fibrillin-1 (fbn1), dystrophin (mdx), and sarcoglycan-δ (sgcd).^6,8,30 In addition to a lower in vivo axial stretch ratio and reduced elastin content, CCAs of elastin haploinsufficient mice also exhibit arterial tortuosity, and lower outer diameters. Despite these differences, and in contrast to our fbln5^−/− data, there were no significant differences in circumferential and axial stress-stretch relationships when held near the in vivo stretch and no differences in opening angles between the elastin haploinsufficient and control CCAs or abdominal aorta.³⁰ For a mouse model of Marfan’s Syndrome in which fibrillin-1 is reduced to 15–25% of normal levels (fbn1^R/R), CCAs exhibit similar in vivo outer diameters, but 5% reduction in in vivo axial stretches compared to control vessels; namely, the axial stretch in fbn1^R/R was 1.63 ± 0.02, compared to 1.71 ± 0.02 in wildtype controls. Again, in contrast to our data, there are no significant differences in the circumferential mechanical behavior at in vivo axial stretches between the fbn1^R/R and control CCAs. Force length tests, however, suggest differences in axial stress between fbn1^R/R arteries and wild-type controls at pressures from P = 60 mmHg to P = 100 mmHg and at axial stretches above λ = 1.64. In mouse models of muscular dystrophy pressure–diameter relationships near the in vivo axial stretch ratio are not statistically different.⁶ Thus, it appears that the presence of some functional elastic fibers, even in lowered quantities, is sufficient to allow large arteries to adapt to achieve normal circumferential in vivo mechanical behavior. Arterial tortuosity was also not noted in studies of mice deficient in fbln1, mdx and sgcd suggesting that the decrease in the production of functional elastic fibers is the cause of tortuosity.^6,8 Biomechanical properties of elastin knockout mice (Eln^−/−) show significant geometric and mechanical differences; however, these mice die within 72 h of birth.²⁹ Our study, as well as others, highlights the need to further investigate the axial mechanical behavior of arteries.

To quantify the local mechanobiological response of cells to their local mechanical environment, it is necessary to accurately predict their local mechanical environment; this requires a constitutive model with adequate predictive capability. Given that growth and remodeling are controlled through turnover and remodeling of key structural constituents, we submit that such a constitutive model should be structurally motivated; thus, we employed a fiber family model. Parameter estimation results suggest significant differences in the material properties of fbln5^−/− arteries. Each artery was modeled as anisotropic axial, circumferential and diagonal fibers embedded in an isotropic matrix. The isotropic portion of the vessel is associated with the parameter, b, while the anisotropic fibers are associated with $b_1^k$ and $b_2^k$. Parameter estimation studies indicated increases in exponential terms, $b_2^2$ and $b_2^3$, for fbln5^−/− arteries. These two parameters suggest differences in the mechanical behavior of axial and diagonal portions of the model. Because this constitutive relation does not account for mass fractions and altered crosslinking of constituents, differences in the structural configuration of constituents could have produced the changes observed in these parameters. A few parameters were zero highlighting the relative degree of exponential behavior of that fiber family. A fiber family with a $b_2^k$ term near zero or very much smaller than the $b_1^k$ term would exhibit high degree of exponentially stiffening behavior. There was also a large degree in variability in some of the parameters such as the case of b for fbln5^−/− mice and $b_1^2$ for both groups. Large variations in parameters describing experiments that exhibit similar mechanical behaviors highlights the sensitivity of parameters to small perturbations in biaxial test data and is characteristic of constitutive relations with exponential terms.^10,14 Results from parameter estimation studies illustrate the need for detailed investigation of the structure of arteries as well the need for constitutive relations that account for the structural components of the arterial wall.¹²

Mechanically induced vascular remodeling occurs as cells sense and adapt their local mechanical environment and plays a key role in many physiological and pathophysiological processes, as well as in the outcomes of many clinical interventions; examples include arterial stiffening with age, development of aneurysms, hypertension, atherosclerosis, and restenosis of vascular grafts. These adaptations (or maladaptations) are controlled largely by delicate balances (or imbalances) in the production, removal, and reorganization of structural proteins.

Whereas much attention has been paid to the role of wall shear stress and circumferential (hoop) stress in vascular remodeling and cardiovascular disease, the role of axial stress has been largely overlooked. Findings suggest, however, that altered axial stretch (or stress) induces remodeling at rates that are ‘unprecedented’ compared to that of pressure and flow.¹⁸ We submit that cells sense and respond to their local mechanical environment and grow and remodel to restore their local mechanical environment to a ‘desired’ state. Many clinical observations highlight the importance of axial remodeling in the vasculature; marked tortuosity in abdominal aortic aneurysms (AAAs), mammary artery by-pass grafts, and reduced axial strain in hypertension and aging are but a few examples. Circumferential expansion, wall thinning and axial lengthening of AAAs is coincident with a progressive loss of elastin and smooth muscle and a decrease in glycosaminoglycans. Indeed, the level of aortic tortuosity is among the greatest indicators of risk for AAA rupture.⁹ These observations suggest that elastic fibers endow arteries with their in vivo axial strain, and the loss of functional elastic fibers (which occurs in AAAs, hypertension, and aging) may be associated with impaired axial remodeling and development of tortuosity.

The lack of differences in compliance at pressures within the physiological range as well as differences in physiological geometry suggests that compliance (or cyclic strain) may be a primary target for adaptations in vascular growth and remodeling. In vivo mean stresses in the axial and circumferential directions were not restored suggesting that stress, while a target for growth and remodeling in cases of altered loading conditions,^17,19,23 may not be the primary target in development and maturation. Indeed, these results suggest that cyclic strain is restored during maturation, with in vivo stresses, perhaps being a secondary target for growth and remodeling. This speculation, however, warrants further investigation as other reports in the literature may suggest otherwise.²³

There are several limitations to the current approach. First, although we seek to identify the role of a single extracellular matrix protein (fibulin-5) on the overall biomechanical behavior of arteries, interpretation of these data is complicated by the fact that, throughout their development and maturation, mechanisms could compensate for the lack of fibulin-5. Nevertheless, given the striking differences in the mechanical and microstructural behavior of fbln5^−/− vs. fbln5^+/+, broad conclusion regarding the role of functional elastin fiber may be made. Second, we present plots of mean stress vs. mid-wall strain and perform stress analyses with the assumption that the tissue is homogeneous. Clearly, however, there are significant heterogeneities, particularly between the media and adventitia, in mouse CCAs. Future studies could include the incorporation of such heterogeneities, which may be based on heterogeneities in the content and organization of cells and extracellular matrix observed in our stacks of confocal microscopy images. Third, although the constitutive model employed here is microstructurally motivated, no direct correlations are made between material parameters and cell and extracellular matrix content and organization. Thus, future studies may include the use of constrained mixture models to ascribe such microstructural meaning to each parameter.¹²

In summary, biaxial mechanical tests have revealed distinct differences in the material properties of the fbln5^+/+ and fbln5^−/− arteries while confocal and multiphoton imaging have revealed structural differences in elastin, collagen and smooth muscle cell organization between fbln5^+/+ and fbln5^−/− arteries. Analysis of the fbln5^−/− mouse suggests that elastin plays a key role in the mechanical response of mouse carotid arteries and that functional elastic fibers appear to be necessary for the normal development of the in vivo axial stretch ratio. Further studies that quantify the microstructure and constitutive modeling with more advanced models will provide a more definitive link between the microstructure and mechanics of fbln5^−/− arteries.