Temperature Dependence of the Kinetic Isotope Effects in Thymidylate Synthase. A Theoretical Study

Abstract

In recent years, the temperature dependence of primary kinetic isotope effects (KIE) has been used as indicator for the physical nature of enzyme catalyzed H-transfer reactions. An interactive study where experimental data and calculations examine the same chemical transformation is a critical means to interpret more properly temperature dependence of KIEs. Here, the rate limiting step of the thymidylate synthase catalyzed reaction has been studied by means of hybrid Quantum Mechanics/ Molecular Mechanics (QM/MM) simulations in the theoretical framework of the ensemble-averaged variational transition state theory with multidimensional tunneling (EA-VTST/MT) combined with Grote-Hynes theory. The KIEs were calculated across the same temperature range examined experimentally, revealing a temperature independent behaviour, in agreement with experimental findings. The calculations show that the H-transfer proceeds with ca. 91 % by tunneling in the case of protium and ca. 80% when the transferred protium is replaced by tritium. Dynamic recrossing coefficients are almost invariant with temperature and in all cases far from unity, showing significant coupling between protein motions and the reaction coordinate. In particular, the relative movement of a conserved arginine (Arg166 in E. coli) promotes the departure of a conserved cysteine (Cys146 in E. coli) from the dUMP by polarizing the thioether bond thus facilitating this bond breaking that takes place concomitantly with the hydride transfer. These promoting vibrations of the enzyme, which represent some of the dimensions of the real reaction coordinate, would limit the search through configurational space to efficiently find those decreasing both barrier height and width, thereby enhancing the probability of H-transfer by either tunneling (through barrier) or classical (over-the-barrier) mechanisms. In other words, the thermal fluctuations that are coupled to the reaction coordinate, together with transition state geometries and tunneling, are the same in different bath temperatures (within the limited experimental range examined). All these terms contribute to the observed temperature independent KIEs in thymidylate synthase.

Introduction

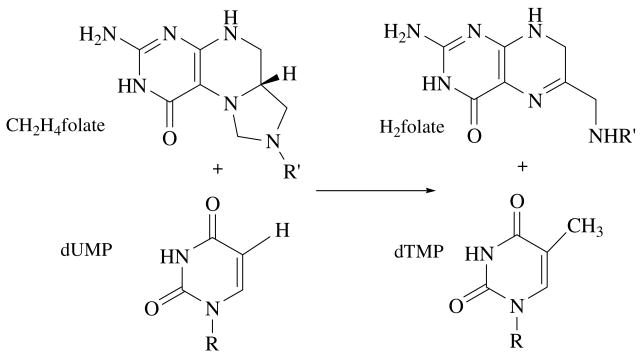
Thymidylate synthase (EC 2.1.1.45) catalyzes the reductive methylation of 2′-deoxyuridine 5′-monophosphate (dUMP) to 2′-deoxythymidine 5′-monophosphate (dTMP), using N5,N10-methylene-5,6,7,8-tetrahydrofolate (CH₂H₄folate) as both reductant agent and methylene donor, and producing 7,8-dihydrofolate (H₂folate).¹ This reaction is depicted in scheme 1.

Scheme 1.

Overall reaction catalyzed by thymidylate synthase.

In 2007, according to the World Health Organization, a quarter of all deaths occurred in developed countries were caused by cancer. Cancer appears when normal cells loose their capability to control its growth and multiplication. As dTMP is one of the building blocks of DNA, this enzyme is one of the main anticancer drug targets.¹

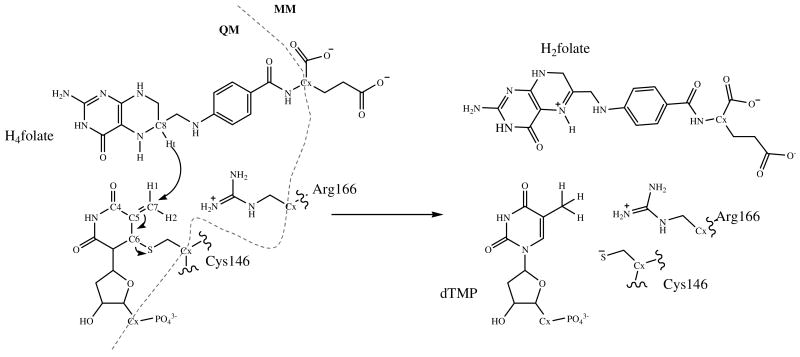
The complete molecular mechanism of the thymidylate synthase catalyzed reaction, as proposed by Carreras and Santi in the nineties,² has been studied by means of Quantum Mechanics/Molecular Mechanics (QM/MM) calculations in our laboratory.^3,4 From the mechanistic point of view, although our calculations were basically in agreement with the previously proposed mechanisms,² some critical differences were apparent. For instance, the role of protonation of carbonyl 4 and stabilization of enol intermediates throughout the path seems to play a minor role relative to the previous proposal. The C-S bond at C6 of dUMP, on the other hand appears to be much more labile than previously assumed. After evaluating the different energy barriers along the full complex cascade of reactions, the reduction of an exocyclic methylene intermediate by hydride transfer from the C6 position of 5,6,7,8-tetrahydrofolate, H₄folate (C8 in scheme 2), to form dTMP and H₂folate, appeared to be the rate determining step (r.d.s.), in agreement with the experimental observations.¹ This hydride transfer takes place with a concomitant breaking of the thioether bond between the C6 of the substrate and a conserved active site cysteine residue (Cys146 in E. coli), as shown in Scheme 2.^3,4

Scheme 2.

Proposed rate determining step of the thymidylate synthase catalyzed reaction. The partition between QM and MM regions is represented by the dashed line, and frontier QM-MM atoms are depicted as Cx.

A deep insight into the r.d.s. through analysis of free energy surfaces (in terms of two dimensional potential of mean force, 2D-PMF, performed at four different temperatures) revealed that the hydride transfer and the scission of Cys146 take place in a concerted but asynchronous fashion.⁴ This 1,3-S_N2 substitution appears to be assisted by arginine 166 and several other arginine residues in the active site that polarize the carbon-sulphur bond and stabilize the charge transferred from the cofactor to the substrate. It is also of critical importance that the features of our previous 2D-PMFs are temperature independent, which can dictate temperature independent KIEs, in agreement with measured intrinsic KIEs on the same H-transfer step.¹ The Marcus-like model^5-12 has been traditionally used to suggest that such a phenomenon could indicate H-tunneling from an ideal donor-acceptor distance and well-tuned reorganization of the reaction coordinate throughout the experimental temperature range. Thus, enzymes would be also working on the barrier width, that is, their ability to rearrange the heavy atoms toward a tunneling-ready donor–acceptor distance (DAD) of approximately 2.8 Å.¹² It is important to point out that barrier width does not only depend on DAD, but rather the whole shape of the multidimensional H-transfer coordinate. Considering the values of the distinguished reaction coordinate obtained at the transition states, an almost direct relationship can be drawn. In this article, quantum mechanical dynamical effects into the hydride transfer step of the thymidylate synthase catalyzed reaction have been accomplished by computing a potential of mean force (PMF) along a distinguished reaction coordinate, combined with multidimensional semiclassical transmission coefficients. These, introduced to overcome the limitations of the classical Transition State Theory (TST), incorporate the effects of barrier recrossing, quantized molecular vibrations and quantum mechanical tunneling. In the correction of the classical mechanical PMF (CM PMF), the transmission coefficient that incorporates the recrossings, i.e., trajectories that return to the reactant state once they have crossed the transition state dividing surface towards the products valley without equilibrating in that valley,^13-17 have been computed by means of the Grote-Hynes theory,^18,19 while quantized molecular vibrations and quantum mechanical tunneling have been estimated through the Ensemble-Averaged Variational Transition State Theory (EA-VTST).^20-22 Combination of such techniques allows obtaining both temporal and dynamic information of the catalytic activity of this important anticancer and antibiotic drug-target.

Other approaches to study enzyme barrier crossing, incorporating analysis of fast protein dynamics coupled with the chemical transformation, or “protein promoting vibrations” as termed by Schwartz and Schramm,^23-26 can be used by applying the Transition Path Sampling (TPS) method developed by Chandler and co-workers.^27,28 The main advantage of this method is to allow the study of reaction mechanisms in condensed media without prior knowledge of the reaction coordinate and transition state.²⁹ TPS has been previously applied to the enzymatic barrier crossing analysis of lactate dehydrogenase,³⁰ chorismate mutase³¹ and purine nucleoside phosphorylase³², showing that protein dynamic motions on the femtosecond timescale can contribute to transition state formation. These results, show the limitations of those descriptions based on equilibrium between a distinguished reaction coordinate, in agreement with our previous studies based on Grote-Hynes theory.^13-17

Furthermore, nuclear quantum effects can be estimated by means of other computational techniques, such as the coupled free-energy perturbation and umbrella-sampling technique in Feynman centroid path integral calculations (PI-FEP/UM) as employed by Gao and co-workers.³³ Nevertheless, and although this procedure avoids the great fluctuations associated with the explicit calculation of the difference between two free energy barriers (for light and heavy isotope species), thus rendering more accurate results (see for instance ref.34), the contributions of both nuclear effects (zero-point energies and nuclear tunneling) are not separable. Other methods based on the quantum classical paths (QCP) version of the centroid path integral approach and on an empirical valence bond (EVB) potential energy surface have been used by Warshel and co-workers to study the large KIEs in lipoxygenase,³⁵ and the origin of the temperature dependence of KIEs in Escherichia coli DHFR (ecDHFR).³⁶ This method, which considers explicitly the nuclear quantum mechanical effects, reproduced temperature dependence of the rate constant for the hydrogen transfer, but it was less successful with the deuterium transfer reaction. As pointed out by Warshel and co-workers, the difficulties of reproducing the temperature dependence of the rate constant reflect a well-known difficulty in reproducing temperature dependence of free energies by microscopic simulations.^37,38

Our computational protocol, described in detail in next section, has been applied at four different temperatures for protium and tritium transfer and allows a deep analysis into the different contributions to the finally estimated values of KIEs. The excellent agreement between our calculated KIEs and their temperature dependence with the experimental data we previously reported supports the high significance of these studies.

Computing Methods

The model

The starting geometry was obtained from the PDB entry 2TSC,^39-41 which consists of two subunits of 264 amino acids each, and an anti-folate inhibitor and a substrate in each one of the active sites. Once the inhibitor (10-propargyl-5,8-dideazafolate) was replaced by the cofactor in one of the active sites, the coordinates of the hydrogen atoms were placed using the HBUILD facility of CHARMM program.⁴² The pK_a value of ionisable amino acids was recalculated using the “cluster method”⁴³ at a pH of 7.5, as implemented by Field and co-workers,⁴⁴ in order to determine their proper protonation state in the protein environment.

A total of 24 sodium counterions were placed in optimal electrostatic positions around the enzyme (further than 10.5 Å from any atom of the system and 5 Å from any other counterion, using a regular grid of 0.5 Å) because the total charge of the system was not neutral. Finally, the system was solvated using a box of water molecules of 100 × 80 × 80 ų, and the water molecules with an oxygen atom lying within 2.8 Å of any heavy atom were removed.

The whole system was divided into a QM part and a MM part to perform combined QM/MM calculations.⁴⁵ The QM part considers 39 atoms of the folate, 25 atoms of the dUMP, Cys146 and Arg166, which gives a total of 80 QM atoms and four boundary atoms, represented by the GHO method⁴⁶ (see scheme 2). It must be pointed out that only one of the active sites of the dimer was modelled in the QM region, leaving the second active site, without any molecule inside, as part of the MM region. This approach is well justified for this enzyme that is known to have “half-of-the-sites-activity”,^47,48 i.e., only one active site is active at a time. The MM part comprises the rest of the folate and dUMP, the enzyme, the crystallization and solvation water molecules and the sodium counterions, which makes a total of 61137 atoms.

The QM atoms of the system are described by the semiempirical Austin Model 1 (AM1)⁴⁹ Hamiltonian, while the atoms of the MM region by the CHARMMc22⁵⁰ and TIP3P⁵¹ force fields. Cutoffs for the nonbonding interactions were applied using a switching function, within a radius range from 10.5 to 11.5 Å.

Potential Energy Surface, PES

After setting up the model, the full system was minimized using the Adopted Basis Newton Raphson (ABNR)⁴² method, keeping the backbone of the enzyme as frozen. Then, the system was gradually heated up until the desired temperature (278, 293, 303 and 313 K, respectively) by means of successive molecular dynamics (MD) simulations. Due to the huge dimensions of the system, all the residues further than 20 Å from the QM part were kept frozen (a total of 52614 out of 61221 atoms). All the MD simulations were performed using an integration step size of 1 fs and the velocity Verlet algorithm.⁵² In all cases, the resulting structure had an energy fluctuation lower than 0.1%, a kinetic energy fluctuation lower than 1% and a change in temperature lower than 2.5 K over the last 2 ps of the MD. The main interactions of the active site of these structures with the amino acids and crystallization water molecules were representative of the one proposed by Stroud and Finer-Moore,⁵³ which can be considered as a prove of the proper setting up of the molecular model. This structure was then used to generate a QM/MM potential energy surface (PES) for the r.d.s. of the thymidylate synthase catalyzed reaction (scheme 2).

It must be kept in mind that, in order to obtain the transition state (TS) of this chemical step, AM1/OPLS-AA/TIP3P 2D-PMFs were computed in our previous study,⁴ using the antisymmetric combination of distances describing the hydride transfer, dC8Ht-dHtC7, and the interatomic C6-S distance (see scheme 2) as the distinguished reaction coordinates. The results demonstrated that the reaction proceeds by a concerted but very asynchronous mechanism; at the four different tested temperatures,⁴ the two selected coordinates at the TS were about -0.06 and 2.02 Å, respectively. This indicated that in all TS structures, the transferring hydrogen was in between donor and acceptor atoms, while the carbon sulphur breaking bond process, defined by C6(UMP)-S(Cys146) distance, was in an early stage of the reaction. Moreover, the experimentally measured temperature independence of the KIEs,¹ suggests that the hydride is transferred from similar conformations at all temperatures, in accordance with our predictions.⁴ Thus, and considering the cost of two dimensional energy surfaces (especially in the case of PMFs required in next stage of our study), monodimensional PES were carried out as a function of the antisymmetric combination of the distances describing the breaking and forming bonds of the hydride transfer, dC8Ht-dHtC7. This potential energy surface had a total of 57 minimizations (dC8Ht-dHtC7 from -1.4 to 1.45 Å, with an interval of 0.05 Å), using the ABNR method and keeping frozen every residue outside the sphere of 20 Å previously explained.

Potential of Mean Force, PMF

Mono-dimensional PMFs were computed using the antisymmetric combination of distances describing the hydride transfer, dC8Ht-dHtC7, as the distinguished reaction coordinate, as in the PES calculations. The weighted histogram analysis method (WHAM), combined with the umbrella sampling approach,^54,55 was employed to scan the reaction coordinate in a range from -1.40 to 1.45 Å, with a window width of 0.025 Å (the total amount of windows was 116). This selection, together with an umbrella force constant of 590 kcal·mol^-1·Å^-2, allowed a perfect overlap among the windows. 5 ps of relaxation and 20 ps of production, with a time step of 0.5 fs, using the velocity Verlet algorithm⁵² to update the velocities were run in each window. The PMFs were performed at the same temperatures used for the experimental studies,¹ 278, 293, 303 and 313 K, using as starting points of each window structures from the previously obtained QM/MM PESs.

Quantum Mechanical Tunneling, Dynamic Effects and Rate Constants

In this section, the CHARMMRATE⁵⁶ module of CHARMM has been used to obtain rate constants of the hydride-transfer step of the thymidylate synthase catalyzed reaction at different temperatures, as well as primary tritium KIEs including the tunnel effect corrections.

The classical mechanical (CM) activation free energy profile is obtained from the CM PMF by means of equation 1:²⁰

$$\Delta G_{\mathit{\text{act}}}^{\mathit{\text{CM}}}(T,z)=W^{\mathit{\text{CM}}}(T,z)-[W^{\mathit{\text{CM}}}(T,z_R)+G_{R,T,F}^{\mathit{\text{CM}}}(T)]$$ (1)

where z_R is the value of z at the reactant (R) minimum of W^CM (T,z), and $G_{R,T,F}^{\mathit{\text{CM}}}(T)$ is the CM free energy of the normal mode (F) that corresponds to z at z_R. In general, we choose the zero of energies of W^CM (T,z) so that W^CM (T,z_R) = 0. The CM free energy barrier is $\Delta G_{\mathit{\text{act}}}^{\mathit{\text{CM}}}(T,z_{\ast }^{\mathit{\text{CM}}})$, where ${\mathit{\text{z}}}_{\ast }^{\mathit{\text{CM}}}$ is the value of the reaction coordinate corresponding to the maximum of W^CM (T,z). To correct the classical mechanical PMF, instantaneous normal mode analysis for a total of 2800 configurations (1200 at the reactant zone, 800 at the TS zone and 800 at the product zone) were calculated for the primary zone atoms, which involve the pteridine ring of the folate, the six-membered ring of the dUMP, the cysteine and the arginine (54 atoms). The Hessian was numerically determined by a central difference scheme with a step size of 0.01 bohr, and the generalized normal modes were calculated in rectilinear coordinates. When calculating generalized normal mode frequencies, the reaction coordinate was projected out of the Hessian as described in refs.20,57. The calculated frequencies for the various configurations were averaged over all the configurations that belong to a given bin of width 0.01 Å, and the quantum vibrational correction of the PMF, ΔW_vib(T,z), was calculated at the different bins.^20,57,58 The discrete values in individual bins were fitted to a polynomic function of fifth degree.

Then, the quasiclassical PMF, W^QC (T,z) which contains quantized vibrations for the primary zone atoms except for the degree of freedom corresponding to z, is obtained by:

$$W^{\mathit{\text{QC}}}(T,z)=W^{\mathit{\text{CM}}}(T,z)+\Delta W_{\mathit{\text{vib}}}(T,z)$$ (2)

The quasiclassical activation free energy profile $\Delta {\mathit{\text{G}}}_{\mathit{\text{act}}}^{\mathit{\text{QC}}}$, as described in ref.20, is obtained by:

$$\Delta G_{\mathit{\text{act}}}^{\mathit{\text{QC}}}(T,z)=W^{\mathit{\text{QC}}}(T,z)-[W^{\mathit{\text{CM}}}(T,z_R)+G_{R,T,F}^{\mathit{\text{CM}}}+\Delta W_{\mathit{\text{vib}},R}]$$ (3)

where ΔW_vib,R is the value of the quantum vibrational correction at the reactants state, including both the reaction coordinate and the vibrational modes orthogonal to it. The quasiclassical free energy barrier is $\Delta G_{\mathit{\text{act}}}^{\mathit{\text{QC}}}\left(z_{\ast }^{\mathit{\text{QC}}}\right)$, where ${\mathit{\text{z}}}_{\ast }^{\mathit{\text{QC}}}$ is the value of the reaction coordinate corresponding to the maximum of W^QC(z).

The next step was the calculation of the transmission coefficient in the static secondary zone (SSZ) approximation²⁰ and using the same primary zone definition as in the calculation of Δ W_vib(z). The transition-state ensemble was taken as 10 chosen configurations, which belonged to the ${\mathit{\text{z}}}_{\ast }^{\mathit{\text{QC}}}$ bin of the quasiclassical PMFs and optimized to the nearest saddle point, keeping frozen the atoms of its secondary zone. The same configurations were used for both protium and tritium calculations. The saddle point geometry was obtained using the Newton-Raphson method with Brent line minimization⁵⁹ with the gradient converged to 10^-7 atomic units. For each of them, the minimum energy path (MEP) as a function of the arc length reaction coordinate, s, was calculated as described elsewhere,^60-62 using the Euler steepest descent method⁶³ in mass-scaled coordinates with a reduced mass of 1 amu and a step size of 0.002 bohr. The range of the s for the MEP was -1.6 to 1.6 Å. Geometry optimizations of the primary zone of reactant and product species were performed using the BFGS (Broyden-Fletcher-Goldfarb-Shanno) method,⁵⁹ with the gradient converged to 10^-4 atomic units.

From these individual reaction paths, the net transmission coefficients γ_i are obtained as the product of two factors:^20,58 the quasiclassical transmission factor, Γ_i, which corrects the rate constant for dynamical recrossing, and the semiclassical transmission coefficient, κ_i, that accounts mainly for tunneling. In the present study Γ_i was obtained by means of the application of the Grote-Hynes theory, which has been demonstrated to be extremely useful even for reactions that imply the transfer of a light particle.¹⁶ From these coefficients, computed previously in our laboratory for this enzymatic reaction,⁶⁴ and using the quassiclassical activation free energies obtained with equation 3, the quasi-classical rate constants k^QC, which neglect contributions from tunneling effects, can be derived:

$$k^{\mathit{\text{QC}}}(T)=\Gamma (T)\frac{k_{B}T}{h}exp(-\frac{\Delta G_{\mathit{\text{act}}}^{\mathit{\text{QC}}}(T,z)}{\mathit{\text{RT}}})$$ (4)

The tunneling transmission coefficients, κ_i, were calculated by means of a least-imaginary-action tunneling approximation⁶⁵ that consists in finding the best tunneling paths within a predefined “basis set” of paths that interpolate between the best tunneling paths for small reaction-path curvature and large reaction-path curvature. The primitive approximation to the tunneling probability is e−^2θ/ħ where θ is the imaginary action integral^66,67 so least-imaginary action is equivalent to maximum tunneling. As performed by Truhlar and co-workers²², an approximation to the least-imaginary action method that involves comparing a small-curvature tunneling (SCT) approximation^68,69 to a large-curvature tunneling (LCT) approximation^65,70-72 was used, and choosing, at each tunneling energy, the one that maximizes the tunneling probability at that energy.⁷¹

In our case, the SCT approximation was the one finally employed to compute κ_i, since the reaction path curvature was found to be small over the region important for tunneling. Other hydrogen transfer enzymatic reactions, such as the tryptamine oxidation by aromatic amine dehydrogenase (AADH),⁷³ the deprotonation of methylamine by methylamine dehydrogenase (MADH)⁷⁴ or the 7,8-dihydrofolate reduction to 5,6,7,8-tetrahydrofolate catalyzed by ecDHFR⁷⁵, that presented temperature independent KIEs like in the case of thymidylate synthase studied here, have been properly studied with this SCT approximation. In fact, in the paper of Pu et al.,⁷⁵ the quantum effect transmission coefficient was computed by microcanonically optimizing the tunneling paths between small-curvature and large-curvature tunneling paths, and authors demonstrated that results would be only 2% smaller for hydride transfer (both for protium and deuterium) if calculations had been limited to small curvature tunneling paths. Then, the average net transmission coefficient can be written as:

$$\gamma =\langle {\Gamma }_i\cdot {\kappa }_i\rangle$$ (5)

From the value computed by equation 5, the final theoretical estimate of the phenomenological free energy of activation with the ensemble average variational transition-state theory with multidimensional tunneling (EA-VTST/MT) method would be:

$$\Delta G_{\mathit{\text{act}}}^{\mathit{\text{EA}}-\mathit{\text{VTST}}/\mathit{\text{MT}}}=\Delta G_{\mathit{\text{act}}}^{\mathit{\text{QC}}}\left(z_{\ast }^{\mathit{\text{QC}}}\right)-\mathit{\text{RT}}ln\gamma$$ (6)

From equation 6, the rate constant can be obtained;

$$k^{\mathit{\text{EA}}-\mathit{\text{VTST}}/\mathit{\text{MT}}}(T)=\gamma \frac{k_{B}T}{h}exp(-\frac{\Delta G_{\mathit{\text{act}}}^{\mathit{\text{QC}}}\left(z_{\ast }^{\mathit{\text{QC}}}\right)}{\mathit{\text{RT}}})$$ (7)

Finally, equation 7 can be straightforward used to obtain KIEs, as far as the transmission coefficient and the quasiclassical free energy of activation is computed for two different isotope labelled compounds. In our case, protium and tritium will be used as the transferred species in order to obtain the primary intrinsic KIEs. These values are compared below with the experimental data obtained for the same hydride transfer step.¹

Results and discussion

Potential of Mean Force

As explained in the Computing Methods section, the free energy profile for the r.d.s. of the thymidylate synthase catalyzed reaction (scheme 2) has been obtained in terms of CM PMFs at four different temperatures; 278, 293, 303 and 313 K. The resulting profiles are plotted in Figure 1, while averaged key distances of the three states involved in the reaction (reactants state, TS and products state) at the four temperatures are listed in Table 1 (other distances between substrate or cofactor and amino acids of the active site are reported in the Supporting Information).

Figure 1.

PMFs for the hydride transfer step (scheme 2) of the thymidylate synthase catalyzed reaction obtained at four temperatures. Distances are in Å and energies in kcal·mol^-1.

Table 1.

Averaged key distances of the reactants state, TS and products state obtained at 278, 293, 303 and 313 K (other distances corresponding to interactions between substrate and protein are reported in Supporting Information). Standard deviations were obtained during the PMFs generation. Distances are reported in Å and angles in degrees.

T = 278 K	Reactants	TS	Products
C8-Ht	1.15 ± 0.03	1.47 ± 0.05	3.22 ± 0.05
Ht-C7	2.46 ± 0.04	1.32 ± 0.05	1.13 ± 0.03
C8-C7	3.48 ± 0.11	2.77 ± 0.07	4.07 ± 0.18
C8-Ht-C7	151 ± 14	168 ± 6	135 ±14
C6-S	1.83 ± 0.04	1.87 ± 0.06	4.9 ± 0.7
S-Arg166	3.3 ± 0.4	3.9 ± 0.4	2.5 ± 0.3
T = 293 K	Reactants	TS	Products
C8-Ht	1.14 ± 0.04	1.43 ± 0.05	2.58 ± 0.04
Ht-C7	2.45 ± 0.05	1.34 ± 0.04	1.14 ± 0.03
C8-C7	3.34 ± 0.12	2.75 ± 0.06	3.59 ± 0.11
C8-Ht-C7	135 ± 12	167 ± 7	150 ± 12
C6-S	1.84 ± 0.05	1.89 ± 0.07	3.4 ± 0.4
S-Arg166	4.0 ± 0.4	3.9 ± 0.5	1.93 ± 0.15
T = 303 K	Reactants	TS	Products
C8-Ht	1.133 ± 0.024	1.47 ± 0.04	3.08 ± 0.04
Ht-C7	2.88 ± 0.04	1.31 ± 0.04	1.13 ± 0.03
C8-C7	3.46 ± 0.15	2.76 ± 0.07	4.01 ± 0.16
C8-Ht-C7	113 ± 11	166 ± 7	143 ± 16
C6-S	1.82 ± 0.04	1.89 ± 0.06	3.8 ± 0.9
S-Arg166	3.6 ± 0.4	3.8 ± 0.4	1.95 ± 0.16
T = 313 K	Reactants	TS	Products
C8-Ht	1.14 ± 0.03	1.47 ± 0.05	2.58 ± 0.05
Ht-C7	2.50 ± 0.05	1.32 ± 0.04	1.14 ± 0.03
C8-C7	3.31 ± 0.16	2.75 ± 0.07	3.58 ± 0.13
C8-Ht-C7	129 ± 14	166 ± 8	150 ± 14
C6-S	1.84 ± 0.05	1.92 ± 0.09	4.0 ± 0.7
S-Arg166	3.5 ± 0.4	3.6 ± 0.5	2.3 ± 0.5

First conclusion that can be derived from Figure 1 is that there is not a temperature dependence in the CM PMFs. The different activation free energies that can be deduced from the curves are in a range of just 2 kcal·mol^-1, from 15.8 to 17.9 kcal·mol^-1. The observed differences can be considered as the uncertainty associated with the method (± 1.0 kcal·mol^-1), but it also agrees with the dynamical disorder of the enzymes exhibiting fluctuations of catalytic rate constants, as shown by the experimental dispersion of reaction rate constants in single-molecule enzyme studies.^76-78 Thus, assuming not temperature dependence on CM PMF, a simple arithmetic average can be done, which gives a free energy barrier of 16.8 ± 1.0 kcal·mol^-1. This value, although not including quantum or dynamic effects, is in very good agreement with the experimental data,⁷⁹ 17.1 ± 0.2 kcal·mol^-1 which was measured at 293 K.

From the technical point of view, an infinity sampling carried out at all four temperatures would render closer curves and, thus, smaller deviations on the predicted free energy barriers. This prediction has been tested, at some extent, by computing the PMF at 303 K starting from structures initially used to obtain the PMF at 313 K (the two PMFs presenting the highest and lowest free energy barriers, as depicted in Figure 1). The results show that the new PMF at 303 was virtually equivalent to the previous PMF at 313 K (see Supplementary Information). Analysis of averaged structures on the TS reveals that the reaction coordinate of this state is almost invariant with temperature: 0.09 Å at 293 K, 0.15 Å at 278 and 313 K, and 0.16 Å at 303 K (see Table 1). This result, associated with an also invariant donor-acceptor distance (in the range of 2.75-2.77 Å), is in agreement with the non-monotonic isotopic difference in the vibrational energy as a function of temperature. The average C8-Ht-C7 angle obviously changes along the reaction reaching a maximum in the TS at all temperatures (see Table 1), in harmony with the maximum donor-acceptor orbital overlapping since it represents the closest value to the linearity.

Regarding the reactants state, the distance between the donor and acceptor carbon atoms at 278 and 303 K (3.48 ± 0.11 and 3.46 ± 0.15 Å) is slightly larger than the one obtained at 293 and 313 K (3.34 ± 0.12 and 3.31 ± 0.16 Å, respectively). This difference does not represent a significant change in the protein, cofactor or substrate conformations and is probably the result of limited conformational exploration, i.e., they would overlap at infinite sampling.

The energetic differences observed at products state in Figure 1 are only due to the fact that profiles are plotted using reactants state as the reference state. Nevertheless, the geometrical differences observed in the reaction coordinate in products state (2.09, 1.44, 1.95 and 1.44 Å at 278, 293, 303 and 313 K, respectively) do not have a significant effect in its stabilization respect to the TS and, again, this behaviour does not follow any particular trend with temperature. Representative snapshots of reactants, TS and products obtained at 293 K are depicted in Figure 2. It is important to note that as observed in the figure, and in data listed in Table 1, the products region is described by structures where not only the hydride has been transferred, but the C-S bond is also completely broken. This result confirms that the selected distinguished reaction coordinate, the antisymmetric combination of distances defining the hydride transfer, can be used to describe this chemical step, with the carbon-sulphur scissile bond implicitly controlled. Obviously, the real reaction coordinate is much more complex in this system, defined not only by the hydride transfer and the thioether bond cleavage, but also by some protein vibrations, as confirmed by the dynamic insights performed previously in our laboratory.^14,64 Nevertheless, the simple reaction coordinate used in this study allows a deep analysis of quantum effects on KIEs and their temperature dependency based on one dimension PMFs.

Figure 2.

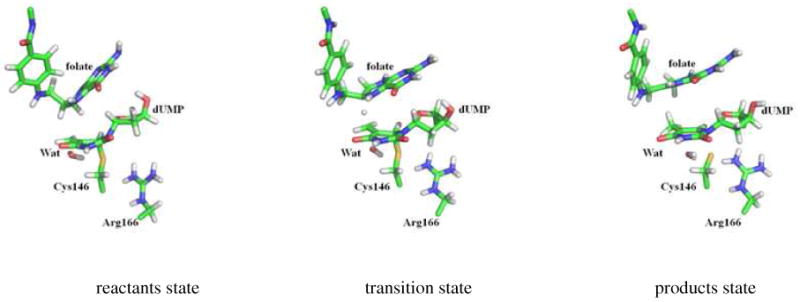
Representative snapshots of the averaged structures of reactants state, transition state and products state obtained from the potential of mean force at 293 K.

From the analysis of averaged structures obtained at the four temperatures, as well as the previous study of dynamic effects on this reaction,^14,64 it seems that the process, and in particular the carbon-sulphur breaking bond, is assisted by an arginine residue, Arg166, which polarizes this bond (see S-Arg166 in Table 1). This result justifies the quantum mechanical treatment of this residue in the QM/MM simulations since charge transfer, or at least important residue polarization, takes place.

These results emphasize that the problem in hand here is multi-dimensional and cannot be understood from a one dimensional reaction coordinate. A single dimensional reaction coordinate from PMF that is temperature independent is the textbook example for the KIEs that are temperature dependent, resulting from differences in zero point energies and different energies of activation for the different isotopes.

These results could be also used to compare the performance of two different force fields, since the PMFs presented in this article correspond to AM1/CHARMM/TIP3P calculations and the PMFs presented in our previous study⁴ were obtained within the AM1/OPLS-AA/TIP3P combination of methods, as implemented in the fDYNAMO library.⁸⁰ Nevertheless, comparison has to be done with caution, since different computational models and methods were used; the present QM/MM calculations are based on monodimensional PMFs with a larger QM region (Arg166 is treated quantum mechanically) and using GHO for the QM-MM frontier treatment; the previous results were based on 2D-PMFs, smaller QM region and link atoms to treat covalent bonds that are necessary in between the QM and the MM region.⁴ Anyway, it is quite encouraging that OPLS and CHARMM render results that led to conclusions that are equivalent, although quantitative results are slightly different.

Corrections to the CM PMFs

Once the CM PMFs were obtained, the next stage in our study was to compute the vibrational non-equilibrium and tunneling effect corrections. For clarity purposes, the results presented in this section correspond just to calculations carried out at 293 K but similar plots and tables, computed at the other three temperatures, can be found in Supporting Information.

Figure 3 shows the quantum mechanical vibrational energy correction for the protium and tritium transfers, as a function of the reaction coordinate, obtained at 293 K. The discrete values in individual bins were fitted to a polynomic function of fifth degree.

Figure 3.

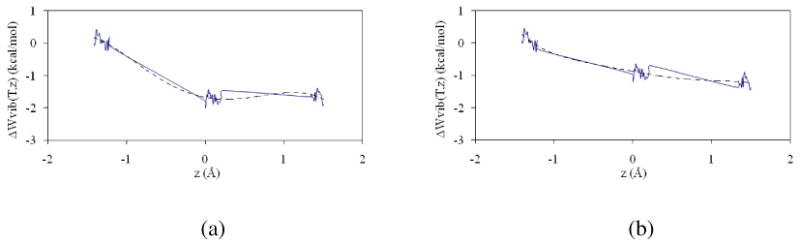
Quantum vibrational free energy correction for protium (a) and tritium (b) computed at 293 K.

From results plotted in Figure 3, a decrease in the activation free energy of 1.71 and 0.93 kcal·mol^-1 for protium and tritium, respectively, can be deduced. These quantum vibrational free energy corrections can be used to obtain the quasiclassical PMF. The results are shown in Figure 4 where a decrease in the free energy of activation is observed at 293 K from the 16.11 kcal·mol^-1 of the CM PMF to 14.40 and 15.18 kcal·mol^-1 for the quassiclassical PMF for protium and tritium transfers, respectively. We must also point out that reactants, TS and products zones appear almost at the same value of the reaction coordinate than in the CM PMF; a behaviour that is reproduced at the other three temperatures. In particular, the values of the reaction coordinate at the TS, after adding the quantum vibrational corrections, were 0.15, 0.11, 0.12, and 0.13 Å at 278, 293, 303 and 313 K, respectively. The fact that the reaction coordinate at the TS does not change with temperature can be interpreted, in the context of the Marcus-like model of tunneling,^8,10 as fluctuations or small variations of DAD which enable tunneling for both light and heavy isotopes of hydrogen (protium and tritium). It seems that promoting modes of the enzyme would limit the search through configurational space to efficiently find those decreasing both barrier height and width, thereby enhancing the probability of H-transfer by either tunneling (through barrier) or classical (over-the-barrier) mechanisms.^24,25,81 These findings can be considered similar to previous theoretical studies on DHFR by Warshel and co-workers, suggesting that the temperature dependence, or independence, of the KIE on DHFR appears to reflect mainly the temperature dependence of the distance between the donor and acceptor.³⁶ The findings are also reflecting the conclusions of Hammes-Schiffer and co-workers regarding soybean lipoxygenase (SLO),⁸² where the weak temperature dependence of the KIE for the proton-coupled electron transfer reaction catalyzed by SLO is predominantly determined by the proton donor-acceptor frequency and the distance dependence of the vibronic couplings for hydrogen and deuterium. This conclusion can be considered also in acordance with Klinman's phenomenological model used to study the temperature-dependent KIEs in Soybean Lipoxygenase-1,⁸³ where protein-gating modes and the modulation of potential energy barriers through environmental oscillations are proposed to play an inportant role in hydrogen tunneling reactions

Figure 4.

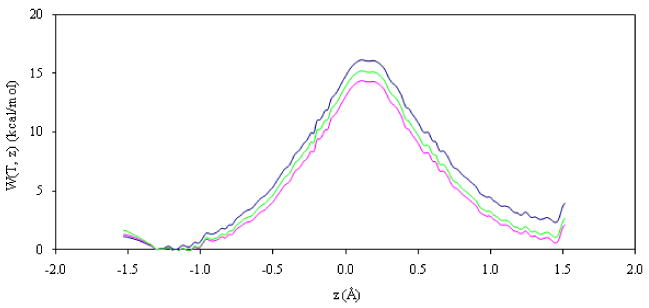
Classical mechanical PMF for hydride transfer (blue line), quasiclassical PMF including quantum vibrational free energy correction for protium (magenta line) and tritium (green line). Results obtained at 293 K.

Finally, the quantum mechanical vibrational contribution to the quasiclassical PMF in the reactants zone has been evaluated, producing a reduction in the barrier of 1.73 and 1.52 kcal·mol^-1 for protium and tritium, respectively. The magnitude of this last correction can be compared with previous corrections carried out for hydride transfer reactions in solution and in enzyme environments.^57,84,85

As explained in Computing Methods section, the MT transmission coefficient, κ(T), was calculated by using the centrifugal-dominant small curvature semiclassical adiabatic algorithm while the quasiclassical transmission factor, Γ(T), which corrects the rate constant for dynamical recrossing, was obtained by means of the application of the Grote-Hynes theory.⁶⁴ The results, together with a summary of the different correction terms and the phenomenological free energies of activation, are listed in Table 2.

Table 2.

Temperature dependence of classical free energy barriers and corrected after adding the classical and quantized nuclear vibrational corrections (in kcal·mol^-1). Overall average transmission coefficient (γ) together with the transmission coefficient components due to recrossing (Γ, obtained from ref.64) and tunneling (κ), phenomenological free energies of activation (kcal·mol¹) and rate constant (in s^-1) for protium and tritium transfer. Temperature in K.

Protium
Temperature	WCM	ΔWvib	GQC	ΔGQC	kQC
278	17.28	-1.92	-2.36	13.00	1.51·102
293	16.11	-1.71	-1.73	12.67	8.80·102
303	17.89	-2.11	-1.48	14.30	1.35·102
313	15.83	-1.95	-1.74	12.14	9.13·103
Temperature	Γ	κ	γ	$\Delta G_{\mathit{\text{act}}}^{\mathit{\text{EA}}-\mathit{\text{VTST}}/\mathit{\text{MT}}}$	kEA−VTST/MT
278	0.47 ± 0.06	11.92 ± 5.07	5.60 ± 3.10	12.05	1.8·103
293	0.44 ± 0.07	16.30 ± 7.93	7.17 ± 4.63	11.53	1.43·104
303	0.48 ± 0.07	10.64 ± 2.33	5.11 ± 2.33	13.32	1.43·103
313	0.45 ± 0.05	9.70 ± 3.95	4.37 ± 2.26	11.23	8.85·104
Tritium
Temperature	WCM	ΔWvib	GQC	ΔGQC	kQC
278	17.28	-1.32	-1.95	14.01	2.56·10
293	16.11	-0.93	-1.52	13.66	2.21·102
303	17.89	-1.24	-1.19	15.46	1.95·101
313	15.83	-1.18	-1.33	13.32	1.60·103
Temperature	Γ	κ	Γ	$\Delta G_{\mathit{\text{act}}}^{\mathit{\text{EA}}-\mathit{\text{VTST}}/\mathit{\text{MT}}}$	kEA−VTST/MT
278	0.50 ± 0.07	5.55 ± 1.43	2.78 ± 1.10	13.45	1.42·102
293	0.61 ± 0.05	5.99 ± 1.35	3.65 ± 1.12	12.91	1.33·103
303	0.48 ± 0.06	4.74 ± 0.72	2.28 ± 0.63	14.97	9.24·101
313	0.53 ± 0.06	4.30 ± 0.80	2.28 ± 0.68	12.81	6.88·103

Our calculations show how the classical free energy barriers, as well as the phenomenological ones, obtained after adding the different corrections, do not follow any indisputable tendency, indicating a temperature independence. An insight into the different corrections to the classical potential of mean force reveals that the most important contributions come basically from the classical and the quantum nuclear vibrational terms. In particular, the reduction on the PMFs for protium and tritium transfer reactions are in a range 4.3 – 3.4 kcal·mol^-1 for the former and 3.3 – 2.4 kcal·mol^-1 for the later.

The dynamic recrossing coefficients, Γ, marginally change from protium to tritium and, what is perhaps more significant in this context, do not follow any dependency with temperature. In both cases the values are far from unity, which means important dynamic coupling between some of the protein motions and the reaction coordinate. This result confirms once again that the simple distinguished reaction coordinate chosen in this study is far from the “real” reaction coordinate that involves also the coupling with the sulphur-carbon breaking bond, polarization by Arg166 and other promoting vibrations. Anyway, this coupling represents a small energy contribution to the barrier (+0.46 and +0.37 kcal·mol^-1 for the reaction with protium and tritium, respectively). Quantum mechanical tunneling makes also a significant contribution to the reaction rate at all temperatures and, apart from the value obtained at 293 K, a decrease is observed from 278 to 313 K (see κ columns). Such a decrease with the temperature was an expected trend but, as we will discuss later on, since the effect is observed in both isotopes, it will not affect the KIEs values. Comparison of κ^EA−^VTST/MT with κ^QC gives an indication of the degree of tunneling in the range between 94 to 90 % for the protium transfer and between 82 to 77 % for the tritium transfer. This result is of the same order of magnitude than previous theoretical predictions for hydride or proton transfers catalyzed by liver alcohol dehydrogenase (ca. 60%),⁸⁴ dihydrofolate reductase (ca. 80%),⁸⁶ methylamine dehydrogenase (ca. 90%),⁸⁷ morphinone reductase (ca. 99%),⁸⁸ or aromatic amine dehydrogenase (99.9%).⁷³ It is important to point out that in the work of Sutcliffe and co-workers,⁸⁸ tunneling mechanism of morphinone reductase appeared to be dependent on the nature of the isotopic label, changing from a LCT regime in the case of hydride transfer to a SCT regime for deuteride transfer. As mentioned before, this change was not observed in the work of Pu et al.,⁷⁵ where a small difference in quantum effect transmission coefficients was observed if computed by SCT or by microcanonically optimizing the tunneling paths between SCT and LCT paths, and it has not been observed neither in the present study. In energetic terms, tunneling effect represents a reduction in the free energy barrier of 1.37, 1.62, 1.42 and 1.41 kcal·mol^-1 for reaction with protium and 0.95, 1.04, 0.94 and 0.91 kcal·mol^-1 in the case of the tritium transfer at 278, 293, 303 and 313 K, respectively. These values of the barrier reduction are close to, for instance, the one obtained for lactate dehydrogenase in our laboratory;⁸⁹ a reaction where the hydride transfer is coupled to a proton transfer. In this later study, a decrease of the free energy barrier from tunnel effects of ca. 0.80 kcal·mol^-1 was obtained.

Kinetic Isotope Effects

From the rate constants listed in Table 2, tritium primary KIEs for the r.d.s of the thymidylate synthase catalyzed reaction can be computed and compared with experimental data. The results are presented in Table 3, together with the experimental data¹ and a decomposition of the quasi-classical and the quantum contributions to the final predicted value. Experimental and theoretical predicted KIEs are plotted in Figure 5.

Table 3.

Quasi-classical, quantum mechanical corrections and EA-VTST/MT temperature dependence of the primary tritium KIEs for the hydride transfer step of the thymidylate synthase catalyzed reaction. Experimental KIEs are obtained from ref.1

T (K)	KIEexp	KIEQC	KIEQM-corr	KIEEA-VTST/MT
278	7.62 ± 0.4	5.89	2.15	12.65
293	6.91 ± 0.05	3.97	2.72	10.81
303	7.4 ± 0.55	6.91	2.24	15.52
313	7.12 ± 0.17	5.70	2.26	12.86

Figure 5.

Temperature dependence KIEs. Comparison between experimental KIEs (black squares) and theoretical (red circles) KIEs. Experimental errors and theoretical standard deviations are reported as vertical segments on each point. Linear regressions on both set of data are presented for comparison purposes.

The first conclusion that can be derived from the results is that the final theoretical predicted KIEs appear clearly overestimated by comparison with the experimental data. Nevertheless, it is important to point out that, taking into account the high exponential dependence of the rate constants on the theoretical free energy barriers, any small error is amplified by the tunneling contribution introduced by the average net transmission coefficient factor. Thus, high quantum treatment of tunneling predicts usually values of KIEs that can quantitatively differ from the experimental data (see for instance the theoretical predictions of 1° KIEs in refs.86-88). Moreover, keeping in mind the deviations obtained for the different coefficients reported in Table 2, large deviations were expected for our calculated KIEs (see Figure 5). These are associated with the method employed to calculate the recrossing transmission coefficients and, specially, for the tunneling corrections. Nevertheless, it is also important to emphasize that, as previously pointed out by Pang et al.,⁸⁶ the standard deviations reported in Table 2 and in the theoretical predictions in Figure 5 are not error bars; they are standard deviations of the distribution corresponding to the TS and reactants ensembles, which can be equivalent to the real effect of the fluctuating protein environment (which causes fluctuations in the barrier widths, over barrier reaction paths, and tunneling paths). Single-molecule experiments have also demonstrated the broad distributions of rates in enzyme catalyzed reactions.^76-78 In accordance with this description, Allemann and co-workers have proposed that the temperature dependence of the KIEs of ecDHFR is a consequence of a variation in the populations of the different conformational sub-states with varying catalytic activity. Each reactive enzyme conformation is capable of catalysis by way of the same chemistry but the microscopic rate constants for each reaction will potentially differ as a consequence of different low amplitude promoting vibrations. The overall reaction rate achieved by this ensemble of enzymes would then be the statistic average over all sub-states.⁹⁰

From a computational point of view, and in accordance with Pu et al.,⁹¹ ensemble-averaged TST includes these fluctuations and the transmission coefficients can reflect the diversity of reaction paths that contribute to the ensemble-averaged experimental data. The wide distributions of transmission coefficients obtained for the thymidylate synthase are, in fact, of the same order of magnitude than previous studies based on similar methodology that estimate the tunnel effects in hydride transfer reactions catalyzed by other enzymes.^86,89,92

Even so, and more importantly, temperature independence is observed in the quasi-classical computed KIEs, KIE^QC, and also in the values computed after adding tunneling effects, KIE^EA-VTST/MT, in agreement with the trend of the experimental KIE values. This is clearly shown in the linear regressions performed from the two sets of data of Figure 5. The EA-VTST/MT correction is smaller than the absolute values of the KIEs computed by means of the quasi-classical approximation. This result means that, although tunneling effects are not negligible, the final values of the KIEs are dominated by contributions of bound vibrations. These vibrations do not show any particular trend with temperature, thus rendering temperature independent KIEs. The thermal fluctuations that are coupled to the reaction coordinate are the same in different bath temperatures (within the limited experimental range examined). And dynamics, geometries and tunneling seem to be perfectly coupled.

Finally, data reported in Table 3 reveals that if KIEs were computed just by means of the quasi-classical approximation, the predicted values would be underestimated, by comparison with the experimental data, thus demonstrating that quantum mechanical effects must be taken into account.

Conclusions

A theoretical study of the KIEs on the rate limiting step of the thymidylate synthase catalyzed reaction has been carried out by means of QM/MM simulations. The first step of our study has been obtaining the classical potential of mean force using the antisymmetric combination of distances defining the hydride transfer as the distinguished reaction coordinate. Several corrections to the TST rate constants were introduced, as the quantized nuclear vibrational, dynamic barrier recrossing and tunneling effects. The results show how the most important contributions in reducing the classical free energy barrier come basically from the classical and the quantum nuclear vibrational terms. The analysis of the different coefficients introduced to correct the limitations of the TST suggests that dynamic recrossings, computed by means of Grote-Hynes theory, do not depend on the temperature and in all cases they are far from unity, revealing a significant coupling of the environment motions and the selected reaction coordinate. The energetic contribution to the free energy barrier, however, was not significant (less than 0.5 kcal·mol^-1). The multidimensional tunneling transmission coefficient, κ(T), obtained through EA-VTST/MT simulations, render contributions of tunneling which decrease the classical free energy barrier by about 1.5 and 1.0 kcal·mol^-1 for protium and tritium, respectively. From the comparison of k^QC with k^EA-VTST/MT, it can be assessed that the catalyzed H-transfer proceeds with ca. 91 % by tunneling in the case of protium transfer, and ca. 80 % when protium is substituted by tritium. This result is in accordance with previous theoretical predictions for hydride transfer reactions catalyzed by different enzymes, but the effect on the free energy barrier is significantly larger, revealing important tunneling effects in the thymidylate synthase catalyzed hydride transfer.

Our predicted H/T KIEs, obtained at the same temperature range that was experimentally examined are overestimated with respect to the experimental data.¹ Nevertheless, the discrepancy between theoretical and experimental results is not very significant taking into account the high exponential dependence of the rate constants on the theoretical free energy barriers, whose deviations reflect the diversity of reaction paths that contribute to the ensemble-averaged experimental observations. A more substantial parameter from the standpoint of Marcus-like models is the fact that both experimental and calculated KIEs were temperature independent. This agreement between experimental and calculated data reveals that the enzyme has tuned the H-transfer so its KIEs are not sensitive to thermal population of the ensemble of DADs. The observed fluctuations in the active site do not produce large deviations in this hydride DADs, thus enabling tunneling by both light and heavy isotopes of hydrogen. This finding is in agreement with the estimated high contribution of tunneling for both tested isotopes, and with the temperature-independent KIEs measured in ref.1 and calculated here. In previous theoretical studies on temperature dependence of the KIEs for hydride transfer catalyzed by DHFR, two features were identified to reduce the temperature dependency by presenting opposite temperature dependency trends:⁷⁵ transition state position and effective potential barrier for tunneling. From the present study, it can be concluded that in the case of thymidylate synthase catalyzed hydride transfer, all terms contributing to the phenomenological free energies of activation appear to be temperature independent: classical and quantized nuclear vibrational corrections, transmission coefficient components due to recrossing and tunneling, and the classical potential of mean force. Our conclusions are based on arguments similar to the ones used in the studies of Warshel and co-workers on ecDHFR,³⁶ and with the studies of Hammes-Schiffer and co-workers on the enzyme soybean lipoxygenase SLO.⁸² The former concluded that the temperature dependence of the KIE on ecDHFR appears to reflect mainly the temperature dependence of the DAD, while the later showed that the weak temperature dependence of the KIEs for the proton-coupled electron transfer reaction catalyzed by SLO is due in part to the dominance of the local component of the proton donor-acceptor motion.

Another way to describe our findings is that the effective temperature in the active site (i.e., the thermal fluctuations that are coupled to the reaction coordinate) is the same at all four different bath temperatures. It looks like the protein serves as “temperature buffer” to maintain similar conditions (local environment) for H-transfer at different bath temperatures (global environment).

The most important outcome of these calculations is that they reveal the extent and complexity of the reaction coordinate, which includes H-transfer from H₂folate, the C-S cleavage by Cys 146 and the coupling of motions of active site residues. The analysis of averaged distances established along the reaction between the reactive system and the protein, measured and calculated at four temperatures, shows how the relative movements of some amino acids, especially an arginine (Arg166 in E. coli), are strongly coupled to the reaction coordinate. The C-S bond between C6 of dUMP and a cysteine (Cys146 in E. Coli), formed in previous steps of the catalytic cascade, is pre-polarized by Arg166 before the asynchronized H-transfer and scission of Cys146 take place. This finding demonstrates several features in enzymology that could be of general importance; the whole enzymatic complex works together to produce the right dynamic environment to the most difficult step in the reaction, the hydride transfer in this case; the apparent general role of H-tunneling in C-H bond activation in enzymes (based on comparison to previous calculations with other enzymes); and the reconciliation between phenomenological models (e.g.; TST, Marcus-like) and in depth analysis based on molecular simulations. The physical basis to the temperature independence KIEs would not be obvious from simple one-dimension reaction profile due to the multi-dimensionality of the problem. A reasonable agreement between TST results and observed rate constants does not imply a detailed understanding of the mechanism; a complete sampling of the reaction paths, including analysis of protein motions and breaking and forming bonds as well as tunneling effects, must be taken into account to obtain a realistic picture of such complex processes.