Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2012 Jul 1.
Published in final edited form as: Biotechnol Bioeng. 2011 Feb 19;108(7):1643–1650. doi: 10.1002/bit.23073

Targeted Cell Immobilization by Ultrasound Microbeam

Jungwoo Lee 1,†, Changyang Lee 1, Hyung Ham Kim 1, Anette Jakob 2, Robert Lemor 2, Shia-Yen Teh 3, Abraham Lee 3, K Kirk Shung 1
PMCID: PMC3098310  NIHMSID: NIHMS274393  PMID: 21328319

Abstract

Various techniques exerting mechanical stress on cells have been developed to investigate cellular responses to externally controlled stimuli. Fundamental mechanotransduction processes, how applied physical forces are converted into biochemical signals, have often been examined by transmitting such forces through cells and probing its pathway at cellular levels. In fact, many cellular biomechanics studies have been performed by trapping (or immobilizing) individual cells, either attached to solid substrates or suspended in liquid media. In that context, we demonstrated two-dimensional acoustic trapping, where a lipid droplet of 125 μm in diameter was directed transversely towards the focus (or the trap center) similar to that of optical tweezers. Under the influence of restoring forces created by a 30 MHz focused ultrasound beam, the trapped droplet behaved as if tethered to the focus by a linear spring. In order to apply this method to cellular manipulation in the Mie regime (cell diameter > wavelength), the availability of sound beams with its beamwidth approaching cell size is crucial. This can only be achieved at a frequency higher than 100 MHz. We define ultrasound beams in the frequency range from 100 MHz to a few GHz as ultrasound microbeams because the lateral beamwidth at the focus would be in the micron range (reviewer #1). Hence a zinc oxide (ZnO) transducer that was designed and fabricated to transmit a 200 MHz focused sound beam was employed to immobilize a 10 μm human leukemia cell (K-562) within the trap. The cell was laterally displaced with respect to the trap center by mechanically translating the transducer over the focal plane. Both lateral displacement and position trajectory of the trapped cell were probed in a two-dimensional space, indicating that the retracting motion of these cells was similar to that of the lipid droplets at 30 MHz. The potential of this tool for studying cellular adhesion between white blood cells and endothelial cells was discussed, suggesting its capability as a single cell manipulator.

INTRODUCTION

Laboratory-on-a-Chip (LOC) type devices have recently emerged as an important platform in which cells, proteins, or viruses can be manipulated and analyzed (Andersson and Berg, 2004; Sims and Allbritton, 2007). Biological experiments in such devices have been undertaken on a single-cell basis rather than in a homogeneous batch culture. The capability of precise cell positioning has thus become extremely crucial. In particular, non-inertial force-based approaches have been developed for cell entrapment (reviewer #2) by applying electrostatic, optical, magnetic, and acoustic waves on living cells. Dielectrophoresis (DEP) has been developed to manipulate polarizable particles (e.g., cells) in a fluid suspension with non-uniform electric fields generated from microfabricated electrode patterns (Choi and Park, 2005; Cummings and Singh, 2003). The DEP force is acted upon a cell along (positive DEP or pDEP) or against (negative DEP or nDEP) the field gradient that depends on cellular properties such as the size and the dielectric constant (Hu et al., 2005). Optical separation of a cell population has been achieved by a tightly focused laser beam and a momentum exchange with the scattered light at the cellular interface is the primary mechanism that makes such operation possible. A variety of beam configurations (Applegate et al., 2006; Cheong et al., 2006) have been combined with either static or dynamic microfluidic environment, where a specific cell is diverted and sorted from a main flow path. In a recent article (Paterson et al., 2005), it was reported that lymphocytes and erythrocytes were well separated in a circularly symmetric light pattern created by a Bessel beam without relying on fluid dynamics. Magnetically labeled particles have often been tagged with biological objects through antigen-antibody interactions, so that those particles were able to be controlled by magnetic forces (Pamme and Manz, 2004). The forces were produced from ferromagnetic elements in strongly localized field gradients. In some special cases like erythrocytes or magnetotactic bacteria, such labeling was unnecessary because their magnetic susceptibilities are higher than other naturally available cells (Han and Frazier, 2006; Schuler and Frankel, 1999). Acoustic standing waves have been able to aggregate and trap biological particles by utilizing multiple transducers or a transducer-reflector pair (Haake et al., 2004; Petersson et al., 2005). Two waves of the same wavelength and amplitude propagating in opposite directions form parallel stationary planes of node and anti-node, where particles like cell agglomerates are manipulated. Particle positions are spaced a half wavelength apart and mainly dependent on device geometries. By modulating phases of opposing waves, for example, those particles were able to be moved in a given direction (Courtney et al., 2010; Neumann et al., 2010).

More recently, a two-dimensional acoustic trapping was experimentally accomplished with a 30 MHz focused ultrasound beam. A 125 μm lipid droplet was thus shown to be laterally attracted towards the trap center (Lee et al., 2009, 2010). In this paper it will be demonstrated that the same approach could be used to trap a targeted cell. The use of highly focused ultrasound beam at frequencies higher than 100 MHz, referred to herein as ultrasound microbeam, is particularly critical in order to trap a single cell whose size is larger than the acoustic wavelength. In this work a 200 MHz ZnO transducer that was capable of producing a much more focused beam than previous experiments was used to demonstrate that a single K-562 leukemia cell (ATCC CCL-243) suspended in phosphate buffered saline (PBS) could be immobilized by the microbeam within the trap. The acoustic impedance for both leukemia cells (Taggart et al., 2007) and PBS media (Bedekar et al., 2003) has been reported to be approximately 1.5 MRayls. The validity of the previous finding (Lee and Shung, 2006) can be extended to even when those values are nearly equal, because the reflection (or the scattering force) becomes negligible and the trapping can readily be realized (reviewer #1). The lateral displacement and the position tracking of the trapped cell were measured with respect to the trap center, showing the capability of this technique as a single cell manipulator in cell biology applications.

Fundamental Physics of Acoustic Trap

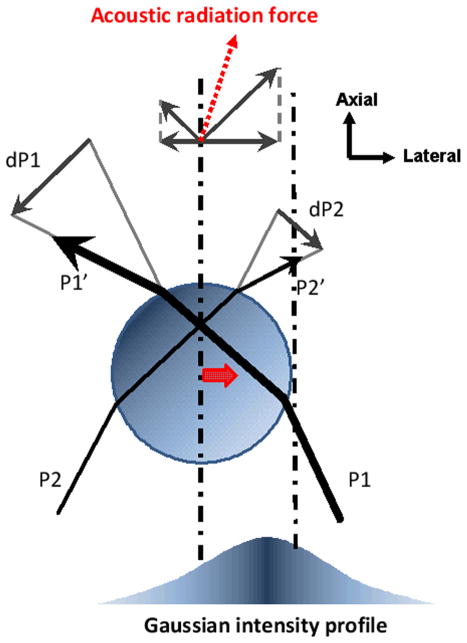
Ray acoustics is a valid trapping model for spheres in the Mie regime. This model describes trap formation being resulted from the redirection of incident beams at the interface, causing momentum transfer. Let two incident rays P1 and P2 incident upon a sphere in a sound field of Gaussian intensity profile as shown in Figure 1. In practice, a small fraction of the incident rays can penetrate into the sphere and leads to multiple internal scatterings, which are ignored here for the sake of simplicity. As both incident and outgoing rays P1′ and P2′ interact with the sphere, the momentum transfers from those rays to the sphere are defined by dP1 = P1′ -P1 and dP2 = P2′ - P2. Since a sound beam can be approximated as a group of rays, a net amount of momentum transfer is obtained by integrating such individual changes over the entire beam. The force applied on the rays is then determined by the rate of the momentum change. An equal and opposite force, called a trapping force, is thus acted on the sphere according to Newton’s third law. As a result, the sphere is directed towards the beam axis because P1 in higher intensity region is stronger than P2. As in optical tweezers (Ashkin et al., 1986), the magnitude and the direction of the force depend on the intensity difference between those rays involved. Therefore a sharp intensity gradient at the focus is an essential factor to form a strong acoustic trap. The radiation force may be separated into two components, scattering and gradient forces. The reflection at an interface between the sphere and the surrounding medium contributes to a scattering force that pushes the sphere away along the beam propagation. A gradient force produced by the refraction, on the other hand, attracts it towards the beam axis, serving as a restoring force (Ashkin, 1997). In order to make the magnitude of the refraction (or the gradient force) greater than that of the reflection (or the scattering force), the difference of acoustic impedances should be minimized at the interface (reviewer #1). Therefore steep intensity variation at the focus and minimal impedance difference are required to accomplish acoustic traps (Lee and Shung, 2006).

Figure 1.

Figure 1

Open in a new tab

Ray acoustics model of acoustic trapping. Two parallel rays (P1 and P2) are incident upon a sphere in a sound field of Gaussian intensity distribution, and their corresponding exiting rays are denoted as P1′ and P2′. The momentum transfers from the rays to the sphere are defined by dP1 and dP2, and redirect the sound propagation at the sphere. Resultant forces acted on the rays are determined by the rate of the momentum change. According to Newton’s third law, the sphere experiences an equal and opposite force that leads to an acoustic radiation force (a dotted arrow). Consequently the sphere is attracted to the beam axis. A thick arrow at the sphere’s center indicates the trapping direction.

MATERIALS AND METHODS

Transducer Fabrication and Characteristics

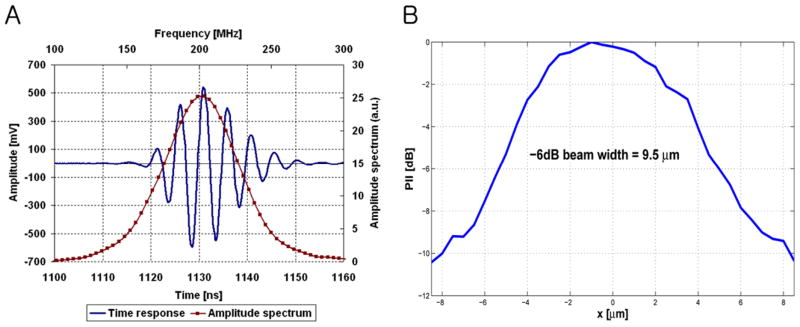
The single element 200 MHz ZnO transducer consisted of a sputtered 6 μm thick ZnO layer between two sputtered gold electrodes on the back surface of a sapphire (Al2O3) buffer rod, as depicted in Figure 2. Sound waves generated from the ZnO layer propagated through the buffer rod to a spherical cavity that was formed at the tip of the rod and served as an acoustic lens. The transducer was focused at 0.5 mm and its f-number was 1. For an efficient energy transfer from the lens to the acoustic coupling medium (or the PBS in this paper) (reviewer #1), a quarter-wavelength glass layer was added to the front surface of the cavity. Its acoustic impedance was determined by the geometric mean of the impedances of the lens and the coupling medium. More details on the design and fabrication of such a transducer can be found in Atalar et al. (1979). The transducer’s bandwidth was 30 % (Figure 3A). Neither calibrated hydrophones nor alternative standardized methods for measuring absolute pressure levels have been established at the frequency range of this work. Thus it was thus practically impossible at present to determine transmitted sound pressures from the transducer. Instead the lateral beam profile was measured by scanning a tungsten wire target whose diameter was 3 μm. These data at a bare minimum yielded information as to how tightly the beam was focused, and in turn, the intensity gradient. The pulse intensity integral (PII) was calculated from the received ultrasonic echoes (reviewer #1) reflected back from the wire target. PII is defined as the time integral of the intensity of a received echo (reviewer #1) taken over the time where the acoustic pressure is nonzero (Raum and O’Brien, 1997). As a result, a beam width equal to 9.5 μm was obtained by detecting a spatial point at which its PII value is reduced by 6 dB from the maximum (Figure 3B). This result was in approximate agreement with the predicted width of 7.5 μm (= f-number × wavelength). Note that the −6 dB contour has conventionally been used for depicting an ultrasonic beam in ultrasonic field characterization in the case of two-way transmission because within this area most of the beam’s energy is concentrated (reviewer #2).

Figure 2.

Figure 2

Open in a new tab

Fabricated ZnO transducer (by Fraunhofer IBMT). (A) Schematic structure and (B) Its photograph.

Figure 3.

Figure 3

Open in a new tab

Pulse echo response and lateral beam profile of ZnO transducer (by Fraunhofer IBMT). (A) A received RF waveform (solid line) and its frequency spectrum (solid-dotted line) show the resonant peak at 202 MHz. (B) The measured beam width was 9.5 μm.

Test Procedure

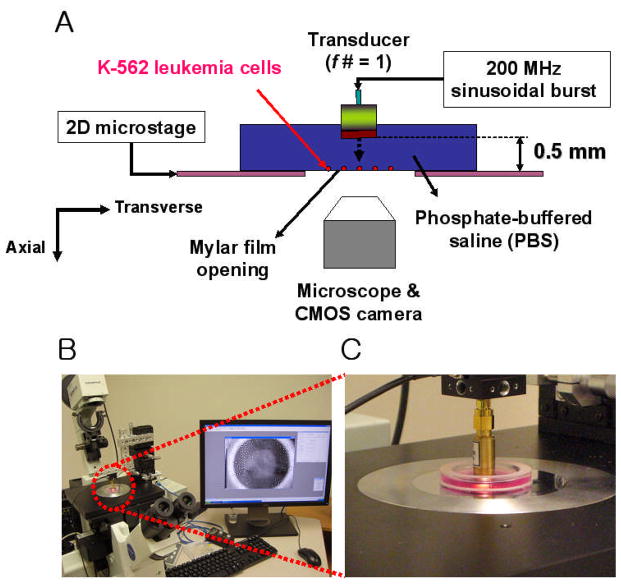
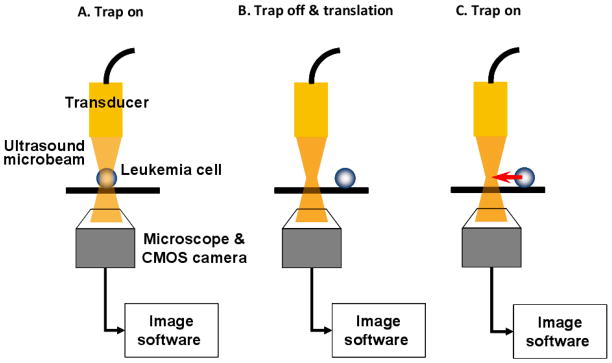
Figure 4 illustrates the experimental configuration for targeted cell immobilization. Human leukemia cells (K-562 cell line, ATCC CCL-243) were cultured in Dulbecco’s modified eagle medium (DMEM, GIBCO) supplemented with 10% fetal bovine serum (FBS) and 1% Penicillin-Streptomycin-Neomycin (PSN, GIBCO) in an incubator supplied with 5% CO2 and set at 37°C. The cultured cells were then suspended in a specially designed chamber filled with a phosphate buffered saline (PBS), sitting on top of a microstage. The chamber had an opening at its bottom, an acoustically transparent mylar film through which cell motions were detected by an inverted microscope (IX-71, Olympus, Japan). The transducer then interrogated the cells from above, as driven in a sinusoidal burst mode whose peak-to-peak voltage amplitude was as high as 2 V. The duty factor of the burst was 0.025 % and the pulse repetition frequency was set to 1 kHz. Prior to the cell trapping experiment, a pulse echo test was performed to ensure that the cells were located on the focal plane, 0.5 mm from the transducer’s aperture. A single cell was then randomly targeted within the microscope’s field of view and laterally scanned by the transducer in parallel with the focus. The procedure for cell displacement is illustrated in Figure 5. Immediately after the transducer was switched on, an acoustic trap was formed at the focus (step A) and the trapped cell motion was captured by a CMOS camera (ORCA-Flash2.8, Hamamatsu, Japan) connected to the microscope. Once the cell was immobilized, the transducer was subsequently turned off and moved by gradually increasing distance (step B). This protocol was repeated if the cell could still be retracted to its original location, i.e., the focus, when the transducer was turned back on (step C). Both lateral displacement and position tracking of the trapped cell were then analyzed by a commercial imaging software (Metamorph Advanced™, Olympus, Japan).

Figure 4.

Figure 4

Open in a new tab

Cell immobilization system. (A) Schematic diagram. (B) Experimental setup. (C) View of the measurement chamber along with the transducer.

Figure 5.

Figure 5

Open in a new tab

Test procedure for lateral cell displacement.

RESULTS

The immobilization process was initiated by placing the transducer in the acoustic far field, typically 1 mm, twice as far as the microbeam’s focal length (0.5 mm). Repulsive cell motions were readily induced and observed due to the beam divergence and a certain cell was isolated from the periphery of an aggregate nearby (reviewer #2). After an isolated cell was detected within the view of the microscope, the transducer was moved back to its focal length in the axial direction. Subsequently the cell was transversely scanned by the transducer to determine whether its motion was disturbed by the sound force. When the cell was instantaneously pushed back to a certain point during the scanning, that point was considered as the focus of the microbeam. In other words, the formation of an acoustic trap was accomplished after the focus was spatially identified. The voltage amplitude input to the transducer was first set to 0.1 V and increased by 0.2 V at a time. Below 1 V, no cells were observed to be moved by the microbeam.

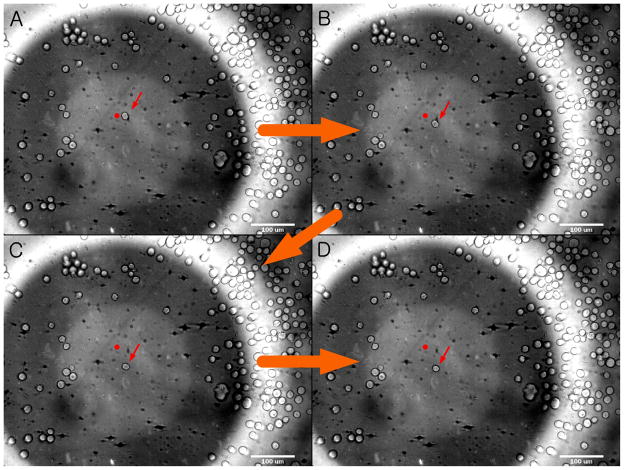
Figure 6 depicts an individual cell motion during the trap formation. The camera system captured a series of images with the numerical aperture of ×10 objective (reviewer #2) to illustrate a migrating and eventually immobilized cell at the focus. The average cell size was 10 μm in diameter and the input voltage for trapping was 2 V. Note that the transducer’s aperture was shown in the background. Before the transducer was switched on, a single cell was left unaffected and located at 50 μm from the focus (Figure 6A). As soon as it was turned on, the trap began to attract the cell towards its center (Figure 6B). As a result, the cell traveled through 50 μm (Figure 6C) and was immobilized at the focus (Figure 6D).

Figure 6.

Figure 6

Open in a new tab

Example of cell motion within acoustic trap (×10 objective). The cell location was recorded every 3 seconds. (A) The cell (see an arrow in the middle) is initially positioned at 50 μm from the trap center and (B) immediately directed to it when the transducer is excited. (C) After migrating over the focal plane, (D) the cell becomes finally settled at the focus. A dot is given as a reference point to show the change in the cell location.

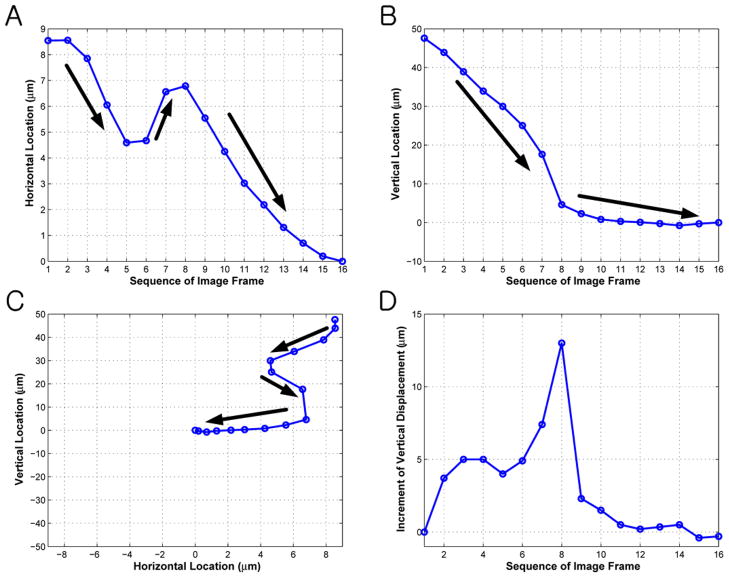
The trapped cell behaved like a particle as if tethered by an elastic spring. In contrast, the cell positioned beyond 50 μm from the focus was pushed away. The minimum intercellular distance for single cell trapping was 15 μm in this study (reviewer #2). Each spatial location of the cell was tracked in a two-dimensional domain and the results are given in Figure 7. The focus was assumed to be at the origin of the coordinate system. The cell motion was recorded until it reached the focus. Sixteen image frames were acquired in a total duration of 48 seconds. The spatial range within which the displacement fluctuates was much narrower in the horizontal direction (9 μm in Figure 7A) than in the vertical direction (50 μm in Figure 7B). The two-dimensional trajectory (Figure 7C) illustrated that the cell gradually migrated and settled at the focus. To validate the elastic behavior of the trap, the increment of the vertical displacement between successive frames was plotted in Figure 7D. Except for a sudden dip in frame #5, the vertical displacement was increased until frame #8 and then decreased afterwards. This approximated a similar pattern when a spring is released after being stretched beyond the equilibrium point (reviewer #2). The cell was then visually inspected through ×20 objective immediately after the transducer was turned off. The total beam exposure period was no longer than 5 minutes. No structural cell damage was observed and its original shape was retained throughout the experiment (reviewer #2).

Figure 7.

Figure 7

Open in a new tab

Trajectory of trapped cell as a function of image sequence. (A) Horizontal and (B) vertical coordinates are represented with respect to the trap center located at the origin. (C) Thick arrows indicate the moving direction of the cell whose position converged to the focus. (D) The increment of the vertical displacement is found until frame #8 and then decreased afterwards. This illustrates a spring-like pattern when it is released after being stretched beyond the equilibrium point (reviewer #2).

CONCLUSION

These results demonstrated that an acoustic trap generated by a 200 MHz ultrasound microbeam immobilized a single leukemia cell at the focus. The ZnO transducer driven in a burst mode directed a 10 μm cell to the trap center. The displaced cell traveled through 50 μm before being (reviewer #1) completely immobilized within the trap. By varying its axial distance from the transducer, the cell was able to be attracted towards or repelled away from the focus. Once trapped, the laterally displaced cell demonstrated a linear spring-like motion, retracted back to the trap as in optical tweezers. This cell behavior was similar to our previous observation with a droplet trapping at 30 MHz. The trajectory of the trapped cell was expressed in 2D, confirming the above results. The advantage of this method is the capability of handling an individual cell without affecting other cells in the vicinity. In order to emphasize such capability, the separation of a single cell was demonstrated against a population of leukemia cells (reviewer #2).

One of the potential applications using this microbeam technique is to investigate intercellular adhesion processes. In fact, it is well known that the adhesion of leukocytes (or white blood cells, WBCs) to vascular endothelial cells (ECs) gives rise to many inflammatory diseases (Chacko et al., 2005). In order to quantify interactions between them, a commonly used technique is to count the number of bound cells but this approach does not provide (reviewer #2) the underlying biophysical principle of the cell adhesion. Therefore adhesion force measurement was performed based on atomic force microscopy (AFM), and its magnitude was in the range of tens to a few hundred pico-newtons (Zhang et al., 2004) (reviewer #2). Fixation of WBCs to an AFM cantilever tip, however, often produced irregular deformation of receptor/ligand shape when microvilli were expanded, and further limited its accuracy of the measurement (Wang et al., 2006) (reviewer #2). Alternatively the AFM’s cantilever tip may be attached to a WBC – bead pair but additional surface interactions between the tip and the bead, which can possibly make the measurement more complicated, need to be considered (reviewer #1).

This microbeam trapping can be exploited as a remote sensing tool to examine the whole WBC-EC adhesion process because of its non-invasiveness and moderate energy use. The trapping forces produced by an ultrasound beam at 30 MHz were quantitatively estimated to be in the nano-newton range by adopting a fluid drag approach (Lee et al., 2010). By further increasing the beam’s frequency up to a few GHz, the force resolution is expected to be much finer than previously achieved (reviewer #2). A conceptual test scenario can be described as follows. Assume that trapping forces have been calibrated in advance by following the same approach. A single living WBC (typically, 10 – 15 μm in diameter) will be indirectly guided by controlling a microbead within an acoustic trap. The adhesion of the WBC to the bead can be mediated by adhesion receptors such as PSGL-1 (Ulbrich et al., 2003). The microbeam will be applied near the beam’s focus (or the center of the bead) where the intensity gradient is at its maximum. If the bead is much bigger than the WBC itself, then the WBC will be positioned outside of the focal zone of the microbeam. Although the WBC’s presence may affect the ultrasound intensity distribution of the focal zone slightly, its effect on the bead trapping is expected to be minimal (reviewer #1). A full cycle of contact-stretch-rupture of WBC-EC will be operated by displacing the trapped bead (in turn, WBC) from the EC. In every step, the cell displacement will be converted to the trapping force by the calibration data. As a result, the adhesion force between the two cells can be determined, providing important viscoelastic properties involved in those WBC-EC interactions. Due to its scalability of the trapping in the Mie regime, the bead size can proportionally be adjusted, depending on the cell size or the magnitude of the force. By binding a bead to various types of cells, therefore, the proposed approach can readily be applied to cells of irregular shape or different size, avoiding significant change in the trapping system including the transducer (reviewer #1).

Acknowledgments

This work has been supported by NIH grants R01-EB12058, and P41-EB2182.

References

  1. Andersson H, Berg A. Microtechnologies and nanotechnologies for single-cell analysis. Curr Opin Biotech. 2004;15(1):44–49. doi: 10.1016/j.copbio.2004.01.004. [DOI] [PubMed] [Google Scholar]
  2. Applegate RW, Squier J, Vestad T, Oakey J, Marr DWM. Optical trapping, manipulation, and sorting of cells and colloids in microfluidic systems with diode laser bars. Opt Express. 2004;12:4390–4398. doi: 10.1364/opex.12.004390. [DOI] [PubMed] [Google Scholar]
  3. Ashkin A, Dziedzic JM, Bjorkholm JM, Chu S. Observation of a single-beam gradient force optical trap for dielectric particles. Opt Lett. 1986;11:288–290. doi: 10.1364/ol.11.000288. [DOI] [PubMed] [Google Scholar]
  4. Ashkin A. Forces of a single beam gradient laser trap on a dielectric sphere in the ray optics regime. Biophys J. 1992;61:569–582. doi: 10.1016/S0006-3495(92)81860-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Ashkin A. Optical trapping and manipulation of neutral particles using lasers. Proc Natl Acad Sci USA. 1997;94:4853–4860. doi: 10.1073/pnas.94.10.4853. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Atalar A, Jipson V, Koch R, Quate CF. Acoustic microscopy with microwave frequencies. Ann Rev Mater Sci. 1979;9:255–281. [Google Scholar]
  7. Chacko BK, Chandler RT, Mundhekar A, Khoo N, Pruitt HM, Kucik DF, Parks DA, Kevil CG, Barnes S, Patel RP. Revealing anti-inflammatory mechanisms of soy isoflavones by flow: modulation of leukocyte-endothelial cell interaction. Am J Physiol Heart Circ Physiol. 2005;289:H908–H915. doi: 10.1152/ajpheart.00781.2004. [DOI] [PubMed] [Google Scholar]
  8. Bedekar D, Nair A, Vince DG. Atherosclerotic plaque characterization by acoustic impedance analysis of intravascular ultrasound data. IEEE Ultrasonic Symposium; 2003. pp. 1524–1527. [Google Scholar]
  9. Cheong FC, Sow CH, Wee ATS, Shao P, Bettiol AA, van Kan JA, Watt F. Optical travelator: transport and dynamic sorting of colloidal microspheres with an asymmetrical line optical tweezers. App Phys B – Lasers O. 2006;83:121–125. [Google Scholar]
  10. Choi S, Park JK. Microfluidic system for dielectrophoretic separation based on a trapezoidal electrode array. Lab Chip. 2005;5:1161–1167. doi: 10.1039/b505088j. [DOI] [PubMed] [Google Scholar]
  11. Coakley WT, Hawkes JJ, Sobanski MA, Cousins CM, Spengler J. Analytical scale ultrasonic standing wave manipulation of cells and microparticles. Ultrasonics. 2000;38:638–641. doi: 10.1016/s0041-624x(99)00151-1. [DOI] [PubMed] [Google Scholar]
  12. Courtney CRP, Ong CK, Drinkwater BW, Wilcox PD. Manipulation of microparticles using phase-controllable ultrasonic standing waves. J Acoust Soc Am. 2010;128(4):EL195–EL199. doi: 10.1121/1.3479976. [DOI] [PubMed] [Google Scholar]
  13. Cummings EB, Singh AK. Dielectrophoresis in microchips containing arrays of insulating posts: theoretical and experimental results. Anal Chem. 2003;75:4724–4731. doi: 10.1021/ac0340612. [DOI] [PubMed] [Google Scholar]
  14. Haake A, Neild A, Radziwill G, Dual J. Positioning, displacement, and localization of cells using ultrasonic forces. Biotechnol Bioeng. 2005;92(1):8–14. doi: 10.1002/bit.20540. [DOI] [PubMed] [Google Scholar]
  15. Han KH, Frazier AB. Paramagnetic capture mode magnetophoretic microseparator for blood cells. IEE Proc – Nanobiotechnol. 2006;153:67–73. doi: 10.1049/ip-nbt:20050019. [DOI] [PubMed] [Google Scholar]
  16. Hu XY, Bessette PH, Qian JR, Meinhart CD, Daugherty PS, Soh HT. Marker-specific sorting of rare cells using dielectrophoresis. Proc Natl Acad Sci USA. 2005;102:15757–15761. doi: 10.1073/pnas.0507719102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Lee J, Shung KK. Radiation forces exerted on arbitrarily located sphere by acoustic tweezer. J Acoust Soc Am. 2006;120:1084–1094. doi: 10.1121/1.2216899. [DOI] [PubMed] [Google Scholar]
  18. Lee J, Teh SY, Lee AP, Kim HH, Lee C, Shung KK. Single beam acoustic trapping. Appl Phys Lett. 2009;95:073701–073703. doi: 10.1063/1.3206910. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Lee J, Teh SY, Lee AP, Kim HH, Lee C, Shung KK. Transverse acoustic trapping using a Gaussian focused ultrasound. Ultrasound Med Biol. 2010;36:350–355. doi: 10.1016/j.ultrasmedbio.2009.10.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Lee J, Lee C, Shung KK. Calibration of sound forces in acoustic traps. IEEE Trans Ultrason Ferroelect Freq Contr. 2010;57(10):2305–2310. doi: 10.1109/TUFFC.2010.1691. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Neumann J, Hennig M, Wixforth A, Manus S, Radler JO, Schneider MF. Tranport, separation, and accumulation of proteins on supported lipid bilayers. Nano Lett. 2010;10:2903–2908. doi: 10.1021/nl100993r. [DOI] [PubMed] [Google Scholar]
  22. Pamme N, Manz A. On-chip free-flow magnetophoresis: continuous flow separation of magnetic particles and agglomerates. Anal Chem. 2004;76:7250–7256. doi: 10.1021/ac049183o. [DOI] [PubMed] [Google Scholar]
  23. Paterson L, Papagiakoumou E, Milne G, Garces-Chavez V, Tatarkova SA, Sibbett W, Gunn-Moore FJ, Bryant PE, Riches AC, Dholakia K. Light-induced cell separation in a tailored optical landscape. Appl Phys Lett. 2005;87:123901–123903. [Google Scholar]
  24. Petersson F, Nilsson A, Holm C, Jonsson H, Laurell T. Continuous separation of lipid particles from erythrocytes by means of laminar flow and acoustic standing wave forces. Lab Chip. 2005;5:20–22. doi: 10.1039/b405748c. [DOI] [PubMed] [Google Scholar]
  25. Raum K, O’Brien WD., Jr Pulse-echo field distribution measurement technique of high-frequency ultrasound sources. IEEE Trans Ultrason Ferroelect Freq Contr. 1997;44:810–815. [Google Scholar]
  26. Schuler D, Frankel RB. Bacterial magnetosomes: microbiology, biomineralization and biotechnological applications. Appl Microbiol Biotechnol. 1999;52:464–473. doi: 10.1007/s002530051547. [DOI] [PubMed] [Google Scholar]
  27. Sims CE, Allbritton NL. Analysis of single mammalian cells on-chip. Lab Chip. 2007;7(4):423–440. doi: 10.1039/b615235j. [DOI] [PubMed] [Google Scholar]
  28. Taggart LR, Baddour RE, Giles A, Czarnota GJ, Kolios MC. Ultrasonic characterization of whole cells and isolated nuclei. Ultrasound Med Biol. 2007;33:389–401. doi: 10.1016/j.ultrasmedbio.2006.07.037. [DOI] [PubMed] [Google Scholar]
  29. Ulbrich H, Eriksson EE, Lindbom L. Leukocyte and endothelial cell adhesion molecules as targets for therapeutic interventions in inflammatory disease. Trends Pharmacol Sci. 2003;24(12):640–647. doi: 10.1016/j.tips.2003.10.004. [DOI] [PubMed] [Google Scholar]
  30. Wang SK, Chiu JJ, Lee MR, Chou SC, Chen LJ, Hwang N. Leukocyte-endothelium interaction: measurement by laser tweezers force spectroscopy. Cardiovasc Eng. 2006;6:113–119. doi: 10.1007/s10558-006-9012-6. [DOI] [PubMed] [Google Scholar]
  31. Zhang X, Chen A, Leon DD, Li H, Noiri E, Moy VT, Goligorsky MS. Atomic force microscopy measurement of leukocyte-endothelial interaction. Am J Physiol Heart Circ Physiol. 2004;286(1):H359–H367. doi: 10.1152/ajpheart.00491.2003. [DOI] [PubMed] [Google Scholar]

RESOURCES