Power laws from individual differences in learning and forgetting: mathematical analyses

Abstract

It has frequently been claimed that learning performance improves with practice according to the so-called “Power Law of Learning.” Similarly, forgetting may follow a power law. It has been shown on the basis of extensive simulations that such power laws may emerge through averaging functions with other, nonpower function shapes. In the present article, we supplement these simulations with a mathematical proof that power functions will indeed emerge as a result of averaging over exponential functions, if the distribution of learning rates follows a gamma distribution, a uniform distribution, or a half-normal function. Through a number of simulations, we further investigate to what extent these findings may affect empirical results in practice.

Power laws of learning and forgetting

At what rate can we expect to learn and forget? We become faster and more accurate as we practice new activities, such as piano playing or speaking a foreign language. It has frequently been claimed that learning performance P improves with practice time t, according to the so-called “Power Law of Learning,” or that the forgetting of learned material follows a power function (J. R. Anderson & Schooler, 1991; Newell & Rosenbloom, 1981; Wixted & Ebbesen, 1991). In its simplest form, a power function is a function of the shape 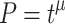, where μ is the learning (or forgetting) rate parameter, and t is number of learning episodes or time. P may refer to how accurate or how fast we carry out a learned activity.

Despite the compact form of P, it describes different types of behavior. For instance, the relative learning rate slows down with prolonged practice. There are situations, however, in which P needs some adjustment. The previous equation is not correct if P denotes a probability, μ is negative, and t is small. For example, for t = 0.5 and μ = −0.1, we have P = 0.5^-0.1 = 1.072. This would give a probability greater than 1, which is impossible. We can easily remedy this by adding 1 to t, thus obtaining 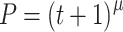. This form ensures that its value remains properly scaled as a probability (i.e., remains between 0 and 1) if μ is negative.

Several authors dispute that learning follows a power function (e.g., Heathcote, Brown, & Mewhort, 2000), reporting exponential curves for individuals. Exponential curves have basic shape P = μ ^t. If learning shows an exponential improvement, the learning process itself does not slow down but continues at the same relative pace. These opposing viewpoints can be reconciled, if averaging over individual exponential curves would yield an averaged power function. This has indeed been found in an extensive simulation study by R.B. Anderson (2001). This study showed for a variety of component-curve shapes, not just exponentials, that averaging tends to give power-like functions. There are also theoretical arguments based on a geometrical analysis that explain why there is a general tendency for averaged curves to give a superior fit for power functions as compared with exponential functions (Myung, Kim, & Pitt, 2000).

The motivation by R. B. Anderson (2001) for carrying out a simulation study rather than a mathematical analysis was that a mathematical proof had not been established and may, in fact, be impossible. As we will demonstrate in the present article, however, this is not the case. For certain relevant cases, a mathematical proof can in fact be derived, which we will outline below. We will limit our analysis to variations in learning rate, noting that there are several other possible sources of variation that we will ignore here, such as differences in asymptotes and intercept and individual levels of variability in learning performance. We will also ignore noise from sampling error, which tends to increase spurious power law fits (Brown & Heathcote, 2003b; Myung et al., 2000). Finally, note that although we use the Power Law of Learning as a starting point of our analysis, our proof is general and applies to any situation in which the assumptions are met. In particular, it also applies to the shape of forgetting functions.

Exponential learning curves

Our measure of learning performance is the probability p(t) that a student will make an error on a certain test item (e.g., knowing foreign language vocabulary) after study time t. In the analysis, we will first assume an exponential learning curve for each individual student i: 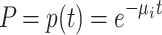with μ _i ≥ 0. Such a curve starts at 100% error at t = 0 and will reach an asymptote with 0 errors (100% correct), given enough study time. Our second assumption is that students’ learning rates are not all equal. Instead, we make the more reasonable assumption that some will be fast learners (high μ _i) and others slow learners (low μ _i). The aim of the present article is limited to showing that for certain common probability distributions, the shape of the averaged curve can be derived mathematically and that it conforms to a power function. We will also explore numerically the extent of the distortion introduced through averaging over exponential curves, which at times may give misleading averaged curves.

Analyses with different learning rate distributions

Gamma distribution

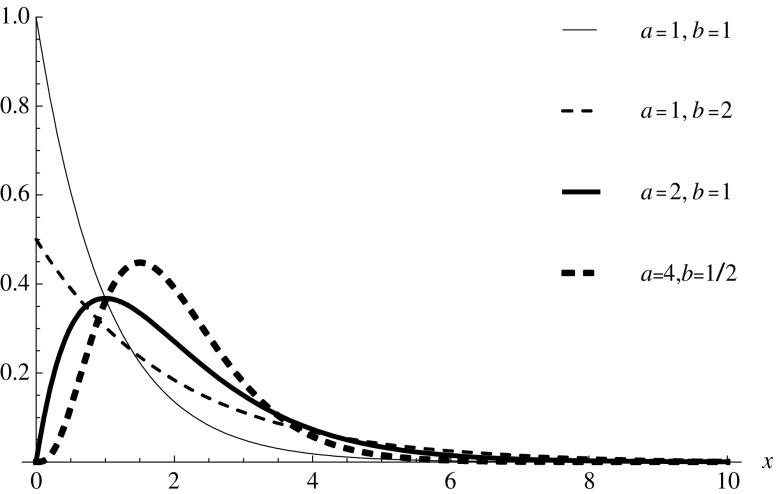
We will first consider the case in which learning rates follow a gamma distribution. This is a well-known probability distribution that can take different shapes, depending on its parameters a (the “shape” parameter) and b (the “scale” parameter). If the shape parameter a is 1, the gamma distribution becomes the exponential distribution as a special case. The mean of the gamma distribution is given by the product ab, and the variance by ab ². As can be seen from Fig. 1, its shape is flexible and may vary from a peaked distribution in which most learners tend to have low or average learning rates, to a broader distribution in which learning rates are more variable.

Fig. 1.

Illustration of the flexibility of the gamma distribution. Shown are plots for different values of a and b

In the Appendix, we show that, if we assume that the learning rates μ of individual participants follow a gamma distribution, the average p _A(t) of a (large) number of exponential learning curves will approach 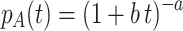(e.g., Feller, 1966, p. 48). This is a power function, which is properly scaled as a probability (i.e., remaining between 0 and 1) and starts at zero performance (100% error) at t = 0. Simulation studies with a range of parameter values of a and b, not reported here, confirm that averaged simulated learning curves approach the theoretical power function very closely.

Uniqueness of the result

We might wonder whether there are any other distributions for which we would find exactly this power function? This is not the case, because the method by which we calculate the expected value over exponential curves is identical to the Laplace transform (and is also very similar to the moment generating function in statistics). It is a well-known result from mathematics that the Laplace transform is a so-called “one-to-one transformation,” meaning that the transformed function is uniquely related to the resulting function. Hence, there is no other statistical distribution other than the gamma distribution that will give exactly the power function in this case. By a similar argument, we can immediately conclude that there is only one distribution that will retain exactly the shape of the exponential function when averaging, namely the Dirac delta function—a distribution that has all probability mass at a single point. In the present article, this means that only if the learning rates of all students are exactly identical will the averaged curve still be of the same exponential form; any deviations will compromise the exponential shape in some way or another.

There are, however, several distributions that will converge exactly to a power function in the limit, for higher t (the gamma distribution result is valid for all t ≥ 0) with only the initial portions of the averaged curve deviating (somewhat) from a power curve. We will discuss the result for two learning rate distributions: the uniform and the (truncated) normal distribution. Surprisingly, averaging exponential curves of which the learning rates follow either of these very different distributions still gives rise to a rapid convergence to a power function.

Uniform distribution

The form of the uniform distribution is not very flexible, but it is nonetheless informative for our analysis, since it is a closed distribution: Learning rates remain between set bounds, as compared with the gamma distribution, which allows a fraction of very high learning rates. We might encounter closed distributions if participants have passed a preselection test such that the slow and fast learners are eliminated (e.g., they are in a different group or class). This leaves us with participants who have learning rates higher than a and lower than b. Suppose that the number of participants is distributed evenly between a and b; we then have a uniform distribution of learning rates. If a = 0 and b = 1, we speak of a standard uniform distribution. In that case, only the fast learners have been eliminated.

In the Appendix, we show that with both exponential individual learning curves and uniformly distributed learning rates, the averaged curve for the uniform distribution with a = 0 and b > a, rapidly converges to (bt)^-1 with increasing t. This is also a power function, with exponent −1 (a so-called “hyperbolic function”). In Fig. 2b, one can see that this convergence is typically very rapid and that the averaged curve approaches a power function even for low t (e.g., t > 10). However, if a is higher than 0, and if b approaches a, the averaged curve approaches the exponential e ^{-a t} (see the Appendix), which is to be expected, because in that case, we then have nearly all learning rates similar to a (see previous remark about the Dirac function). For the in-between case, where b > a > 0, we have the mixture of a power function and exponentials, for which we were not able to find a useful closed-form expression for the limit. These results corroborate the simulations studies by Brown and Heathcote (2003a), who found that when averaging over exponential curves with high and low learning rates, a large variation in rates increased chances of finding spurious power function fits.

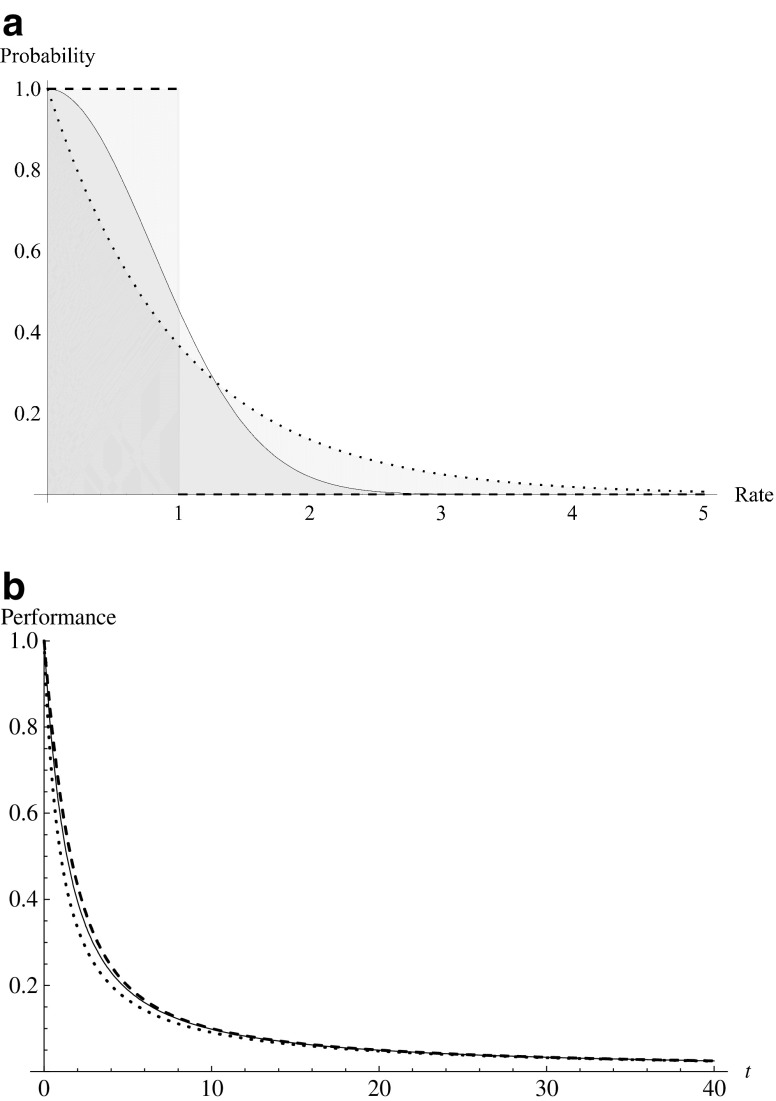
Fig. 2.

a Pdfs of three distributions: a gamma distribution (a = 1, b =1, dotted line; this is an exponential distribution, which is a special case of the gamma distribution), standard uniform distribution (dashed line), and half-normal distribution (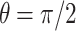, solid line). b Theoretical averaged exponential learning curves with learning rates distributed as in (a). The line styles in (b) refer to the same distributions as in (a). All curves converge to the curve t^-1

Half-normal distribution

The normal distribution is ubiquitous, and that alone merits its inclusion in the present article. Of course, negative learning rates are meaningless, so we must use the so-called “half-normal distribution,” which is a conditioned normal distribution with mean 0 but with the left half “chopped off.” In the Appendix, we prove that with increasing t, the averaged curve also converges to a power function of the form 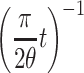, where θ is a parameter that determines the shape of the half-normal distribution.

Different distributions, yet similar averaged curves

Of particular interest is that there are many cases in which an observed averaged learning curve may be produced by different underlying learning rate distributions. This point is illustrated in Fig. 2, which shows the three predicted functions derived in this article. We have chosen parameter values such that the averaged curves converge to the same form t ^-1, with increasing learning time t. In Fig. 2a, it can be observed that the selected learning rate distributions are very different, whereas in Fig. 2b, we see a rapid convergence to the shape t ^-1. Only the initial portions of the learning curves differ visibly.

Application to small numbers of participants

One might wonder how the mathematical results apply to cases in which we average over small numbers of participants. In particular, what would happen if we fitted both a power function and an exponential function to averaged exponential learning curves? Would the power function always fit better, even with small numbers of participants, or would spurious power functions appear only with very large numbers of participants? To investigate, we simulated experiments with increasing numbers of participants. Each artificial participant contributed an exponential (noise-free) learning curve with a certain learning rate drawn from the gamma distribution. A learning curve averaged over all artificial participants was fitted to both an exponential function and a power function using a least-squares criterion. The goodness of fit of the two function types was compared using the r ² value (variance explained).

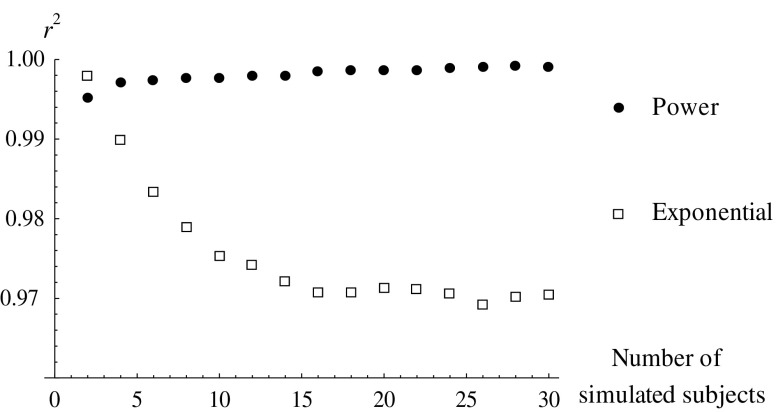
In Fig. 3, we show the r ² for one particular choice of learning rate distribution (a = 1, b = 1) and number of learning episodes (20), which was one of the distributions shown in Fig. 2. As can be observed, the power function fits better than the exponential function, as long as there are more than a few participants, even though the individual curves are exponential. When we repeated these simulations for the uniform and half-normal distribution, with parameters as in Fig. 2, the graphs were highly similar. We also explored this type of simulation for other parameter values of the gamma distribution with similar results. Only if the variance of the gamma distribution is very small (i.e., a strongly peaked distribution) does the exponential function fit better for nontrivial numbers (four or fewer) of participants.

Fig. 3.

For simulated experiments with increasing numbers of artificial participants, the r ² value (fraction of variance explained) is shown for the fits of exponential and power function. Each point is the average of 1,000 simulated experiments with gamma distribution parameters (a = 1, b = 1), and the number of learning episodes is 20

Discussion

In the present article, we discussed mathematical analyses of the effects of averaging exponential learning curves, where it is assumed that individuals have learning rates that follow a known probability distribution. We demonstrated mathematically that if the individual learning curves are exponential in shape, averaging over these curves gives rise to spurious power laws if the learning rates follow a gamma distribution, a uniform distribution, or a half-normal distribution.

The theoretical result can be generalized to forgetting functions in which we consider t to be time since the completion of learning. Using 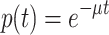for individual curves, and assuming a gamma distribution of the individual forgetting rates μ, we obtain for the averaged forgetting curve: 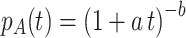. Our result is corroborated by a recent analysis (Lee, 2004) of over 200 forgetting studies taken from the literature, most of which average across participants. These forgetting curves are best modeled by the power function (1+t)^-1. If, as assumed here, this function is a result of averaging over exponential forgetting functions, we expect the distribution of the forgetting rates of individual participants to be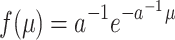, with a = 1 This is an exponential distribution, implying that in these experiments, we should observe rather many students who show little or no forgetting. This is not implausible, with the short retention intervals often encountered in the psychology laboratory, in which there may not be enough time to allow sufficient forgetting for many participants. The resulting ceiling effects would foster spurious power laws in the averaged forgetting curves.

Analyses such as these can also be applied to averaging over items rather than over students (R. B. Anderson, 2001; Newell & Rosenbloom, 1981). We then assume that single items to be learned (e.g., foreign language words) have different learning rates, according to a gamma distribution. The learning curve averaged over items will then appear as a power function. Thus, even a single student may show a power learning curve based on averaged performance of heterogeneous items to be learned. The analysis can be carried even further, to the level below that of a single item, namely to the features that make up its representation.

Our analysis complements earlier simulation studies (R. B. Anderson, 2001) and theoretical work (Myung, et al., 2000) by providing further mathematical analyses. Myung et al. show why, in general, averaging over exponentials will tend to produce good power function fits, with very general assumptions about the distribution of learning rates. R. B. Anderson’s results suggest that averaging over certain nonexponential types of curves may also give power-like functions. We will address this issue elsewhere. Clearly, our results do not rule out that processes other than averaging may give rise to power laws (Wixted, 2004). Nonetheless, we have presently adduced rigorous mathematical proof that power laws may arise as a result of mere data aggregation without reflecting directly the properties of fundamental cognitive processes, which may well be exponential in nature.

Appendix

The starting point of our analysis is the form of the function for the probability of correctly recalling a learned item for an individual participant. Let us denote the initial amount of learned information stored per unit of practice time t by μ. We take the following form for the recall function p(t) of an individual participant after learning time t:

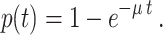1

Gamma distribution

We assume that individual learning rates μ follow a gamma distribution with density function

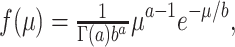2

with parameters a, b > 0, where Γ(a) is the gamma function.

Averaged exponential functions

The recall function, which we denote as p _A(t), averages over participants that learn exponentially but with different learning rates. It is equal to the mathematical expectation of function (1) with respect to μ:

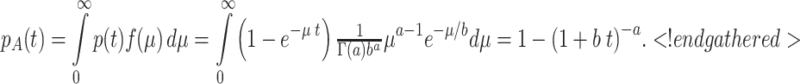3

This proof is based on elementary probability calculus (e.g., Feller, 1966, p. 48) and also applies when averaging over exponential forgetting curves with shape_s. A special case of this result (for a = 1 and b = 1, i.e., an exponential distribution) was derived by Killeen (2001, p. 34).

Uniform distribution

This distribution has pdf

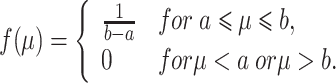If we integrate this function with the exponential individual learning curves, we obtain

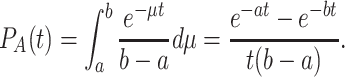For a = 0, this becomes

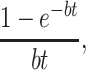which converges to 1/bt for large t. If b = 1, for increasing t, this rapidly converges to 1/t.

If b > a > 0, and if b approaches a very closely, we obtain an exponential function. This is to be expected because in that case (nearly) all participants will have the same learning rate a:

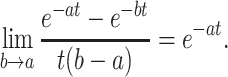Half-normal distribution

The half-normal distribution is a normal distribution with mean 0, of which the left half (i.e., below 0) is removed and the remaining part is multiplied by 2 to retain a total probability mass of 1. The pdf uses a different parameterization from the normal distribution where the familiar parameter σ is replaced by 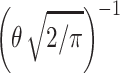, which gives the pdf:

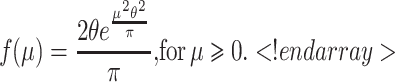The half-normal distribution has mean and variance .

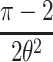As above, we derive the expected value for the exponential base function:

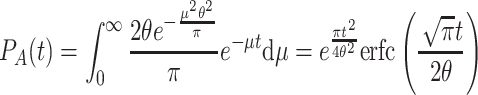Here, 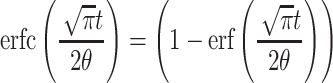, where erf(x) is the error function, which is an integral of form: .

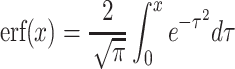For large t, we can derive the limit for P _A(t) as follows: We start with the following inequality (see Gautschi, 1965, p. 298):

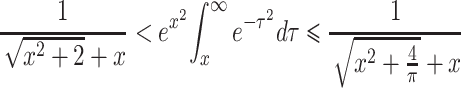Using

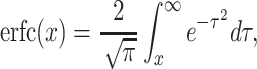we multiply all parts by :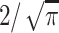

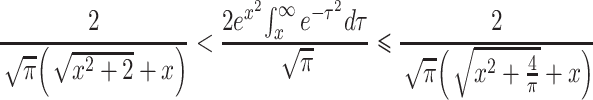and, thus, obtain

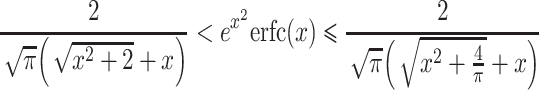The derived result for the averaged curve was

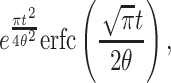so that, if we substitute 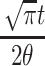for x, we obtain

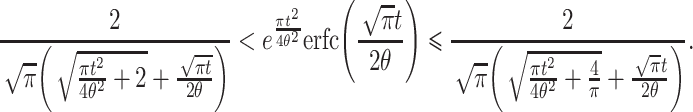This can be rewritten as

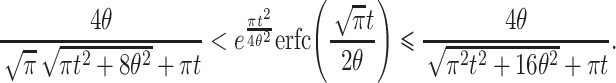We can now verify the limits for large t for the left- and right-hand sides of the inequality:

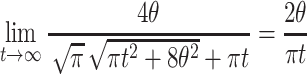and

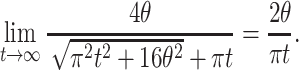We observe that both sides converge to 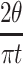and conclude that the expression itself converges to 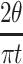for large t.