Grammatical Evolution for Features of Epileptic Oscillations in Clinical Intracranial Electroencephalograms

Abstract

This paper presents grammatical evolution (GE) as an approach to select and combine features for detecting epileptic oscillations within clinical intracranial electroencephalogram (iEEG) recordings of patients with epilepsy. Clinical iEEG is used in preoperative evaluations of a patient who may have surgery to treat epileptic seizures. Literature suggests that pathological oscillations may indicate the region(s) of brain that cause epileptic seizures, which could be surgically removed for therapy. If this presumption is true, then the effectiveness of surgical treatment could depend on the effectiveness in pinpointing critically diseased brain, which in turn depends on the most accurate detection of pathological oscillations. Moreover, the accuracy of detecting pathological oscillations depends greatly on the selected feature(s) that must objectively distinguish epileptic events from average activity, a task that visual review is inevitably too subjective and insufficient to resolve. Consequently, this work suggests an automated algorithm that incorporates grammatical evolution (GE) to construct the most sufficient feature(s) to detect epileptic oscillations within the iEEG of a patient. We estimate the performance of GE relative to three alternative methods of selecting or combining features that distinguish an epileptic gamma (~65-95 Hz) oscillation from normal activity: forward sequential feature-selection, backward sequential feature-selection, and genetic programming. We demonstrate that a detector with a grammatically evolved feature exhibits a sensitivity and selectivity that is comparable to a previous detector with a genetically programmed feature, making GE a useful alternative to designing detectors.

Introduction

The intracranial electroencephalogram (iEEG) is a very valuable diagnostic tool for surgical treatment of epilepsy. An electroencephalogram (EEG) measures the electrical activity of neuronal populations in the brain using a metallic electrode, and the iEEG is an invasive application of an EEG in which EEG electrodes are placed on top of or deep within the surface of the brain. For patients with epilepsy, the iEEG is reserved for preoperative evaluation of epileptic seizures prior to invasive treatment (e.g., surgery) and purposed to locate the area(s) of the brain from which epileptic seizures are generated and actually arise ((Diehl & Lüders, 2000; Engel, 1996)). Ultimately, with information about an estimated epileptic focus (i.e. the nucleus or nuclei for epileptic seizures), a neurosurgeon can excise the portion of brain that is putatively responsible for dysfunction without damaging important functional parts of brain ((Luders & Comair, 2000)). However, a means to reliably estimate the epileptic focus is obviously necessary for accurate and precise surgical treatment.

Recent studies suggest that an epileptic focus is possibly reliably identifiable according to particular pathological patterns in the epileptic brain, finding that certain electrographic signatures seemingly distinguish areas in which seizures do and do not occur in human epilepsy ((J. Jacobs, Chander, Dubeau, & Gotman, 2007; J. Jacobs, et al., 2008; Julia Jacobs, et al., 2009; Staba, Wilson, Bragin, Fried, & Engel, 2002; Worrell, et al., 2008; Worrell, et al., 2004)). For instance, oscillatory epileptic activity between 60-100 Hz, formerly called high-frequency epileptiform oscillations ((Worrell, et al., 2004)) but we call slow ripples ((Firpi, et al., 2007)), 100-200 Hz, called ripples ((Bragin, Engel, Wilson, Fried, & Buzsaki, 1999)), or 200–500 Hz, called fast ripples ((Bragin, et al., 1999)), in human iEEG are reported to spatially coincide with the location of epileptic seizures. Although, this information requires further study, especially a correlative analysis that contrasts the location of pathological biomarkers and surgically removed brain against the results of surgery, to determine any true usefulness, optimistically these findings make evident a potential biomarker that either alone or in combination with other relevant biomarkers may reveal the cause of epileptic seizures ((Engel Jr., Bragin, Staba, & Mody, 2009)) or improve the effectiveness of surgical treatment for patients with epilepsy. Consequently, there exists considerable value in designing an appropriate algorithm to automatically detect pathological oscillations within iEEG, which would provide an objective means to precisely pinpoint epileptic brain.

The detection of pathological oscillations is simply an application of classical binary classification. That is, a pathological oscillation must be quantitatively distinguished from noise (or normal background) with at least one feature in three basic stages: some improvement of the signal-to-noise ratio (e.g. band-pass filtering) for the iEEG, extraction of feature(s); and binary classification, which permits detection of the beginning and ending of an oscillation. Furthermore, we take the position that the success in classification highly depends upon the success in finding the best feature(s) that probabilistically separate(s) the two classes (refs), which would greatly simplify the task of a classifier. Previous approaches to automatically discriminate pathological oscillations and background from iEEG include techniques that rely on either an arbitrary manual selection of features ((Gardner, Worrell, Marsh, Dlugos, & Litt, 2007; O. L. Smart, Worrell, Litt, & Vachtsevanos, 2005; Staba, et al., 2002)), an automated selection of features using genetic programming ((Firpi, et al., 2007; O. Smart, Firpi, & Vachtsevanos, 2007)), or automatic creation of a feature directly from iEEG signals using particle swarm optimization ((Firpi, et al., 2007)). While manually selecting features—usually from intuition or some understanding of the problem—provides a means to detect pathological oscillations, it is usually not the best approach as demonstrated recently when compared against evolutionary algorithms ((Firpi, et al., 2007; O. Smart, et al., 2007)). On the other hand, evolutionary algorithms such as genetic programming (GP) or particle swarm optimization (PSO) may provide a better means to detect pathological oscillations, but there is still room to improve their usage. Therefore, we introduce an alternate evolutionary algorithm (EA), called grammatical evolution (GE), for selecting and combining features to distinguish pathological oscillations and normal activity within recorded iEEG signals. We propose GE rather than modifying the previously published applications of evolutionary algorithms (EAs) because GE can circumvent the technical limitations of the earlier EAs while constructing features that possibly improve detection over the state of the art.

Theory

Grammatical Evolution

Grammatical evolution ((O’Neill & Ryan, 2001)) parallels the creation of a protein from deoxyribonucleic acid (DNA) while simulating Darwinian processes of natural evolution to stochastically produce a solution for a given problem. Before we describe the operation of GE, we describe the process of creating a protein to help understand the inspiration for GE. A protein begins as DNA, which is a sequence of biological blocks called nucleotides. The DNA is transcribed to ribonucleic acid (RNA) by sequentially grouping three nucleotides of DNA, where each grouping is called a codon, and forming a sequence of codons as RNA. The RNA is translated to amino acids, which contribute to the structure and function of a protein. In GE, a solution, typically a mathematical expression, represents a protein and a randomly generated binary sequence with variable length represents DNA. Just as DNA is transcribed to RNA, the binary sequence is transcribed to a numerical sequence by grouping a predetermined number of bits, where each grouping is represents a codon. Lastly, the numerical sequence is translated to a sequence of grammatical symbols (e.g., variables, mathematical functions and operators, decimals), which represent amino acids and define the structure of a GE solution. For the GE, translation is dictated by two distinctive components in GE: a predefined context-free grammar in Backus-Naur form (BNF) that consists of terminal symbols, non-terminal symbols, rules to produce the symbols, and a starting symbol; and a mapping that first generates a sequence of non-terminal symbols from codons then substitutes terminal symbols for non-terminal symbols initiating with the starting symbol. The substitution is defined by the following mapping:

$$rule\#=\left(valueofcodon\right)MOD(numberofrulesforcurrentnon-terminal)$$

Meanwhile, Table 1 lists a typical grammar for GE, which we use in our experiments. Similar to GP ((Koza, 1992)), GE randomly initializes a population of individuals (i.e., DNA that ultimately converts to protein via above process), objectively computes a fitness for each individual and iteratively simulates Darwinian evolution (i.e., selection, crossover, mutation, duplication, and survival) to intermediately fabricate diversity in the population and ultimately find the best possible individual. The algorithm terminates when a specified number of generations (iterations) or value of fitness for the currently best individual is achieved. But contrary to GP, which explicitly encode each individual as a solution, GE uses a binary code that is transcribed and translated to compose a solution rather than randomly generating a solution and uses a grammar to produce a structured parsimonious solution rather than a seemingly spontaneous combinatorial solution.

Table 1.

We defined the below grammar for the grammatical evolution

		Rule	Rule Number
<start>	::=	<expr>	0
<expr>	::=	<expr> <op> <expr>	0
		|<func> ( <expr> )	1
		|<terminal>	2
<xlist>	::=	| x1 | x2 | … | xn	0 | 1 | 2 | … | n-1
<digitlist>	::=	<digit> | <digit><digitlist>	0 | 1
<terminal>	::=	<xlist> | <digitlist>.<digitlist>	0 | 1
<op>	::=	+ | − | * | /	0 | 1 | 2 | 3
<func>	::=	sin | cos | exp | log | sqrt | abs	0 | 1 | 2 | 3 | 4 | 5
<digit>	::=	0 | 1 | 2 | … | 9	0 | … | 9

In our application, we apply GE to select and combine features that distinguish pathological and normal iEEG activity. Thus, we define a BNF grammar that uses mathematical functions and operators as non-terminal symbols and original features and the numerical digits (0-9) as terminal symbols. As a result, the GE can produce an amalgamated feature in the form of a mathematical expression that involves a subset of operators, functions, digits, and features from the predefined grammar.

Data

We selected a sample of data to analyze (see ‘Methods’) from an existing large collection of clinical iEEG recordings from six patients with epilepsy. The patients underwent long-term continuous clinical video-iEEG monitoring and recording so that a neurosurgeon was able to preoperatively estimate an epileptic focus for surgical treatment. The preoperative video-iEEG recordings were used in an earlier medical study that involved the collection of the above data at Emory University (EUH), the University of Pennsylvania Hospital (UPH), and the Children’s Hospital of Philadelphia (CHP). The Internal Review Board (IRB) at each institution approved the medical study and each patient already provided their informed consent to enroll in the study. All collected data was de-identified before we sampled data for our study.

For the EUH and UPH patients, iEEG recordings were collected with a 64-channel digital EEG system (Nicolet Biomedical, Madison, WI) with an analog Butterworth bandpass filter (−3dB cutoff frequencies at 0.5 and 150 Hz) and digitization at 12 bits per sample and 400 samples per second. For the one patient from CHP, iEEG recordings were collected with a 128-channel digital EEG system (Grass-Telefactor, Philadelphia, PA) with an analog bandpass filter (−3dB cutoff frequencies at 0.5 and 100 Hz) and digitization at 12 bits per sample and 800 samples per second before digital lowpass filtering (−3dB cutoff at 70 Hz) and down-sampling to 200 samples per second. All digital data was archived to CD-ROM storage.

Methods

Manual Markings

For each patient, we prepared two sets of raw data across multiple iEEG electrodes using a MATLAB (Mathworks, Natick, MA) graphical user interface (GUI) ((Gardner, et al., 2007)) that automatically stored the time-stamp (i.e., the temporal beginning and ending) of a manually marked event: training data, with which to select and combine the best feature(s) using GE and cross-validate a chosen classifier, and testing data to verify the performance of a detector with a GE-feaure. For the training data, firstly we randomly marked isolated slow ripples (n = 21.3017±8.3116 seconds) and isolated segments of normal activity (n = 81.6667±21.8673 seconds) with the GUI, then secondly we ran an automated script to compile the actual iEEG data and corresponding labels for the type of marked activity (i.e., normal activity or slow ripple) according to the marked timestamps. For the testing data, firstly we randomly clipped continuous approximately three-minute segments of iEEG (n = 9.9963± 1.1651 clippings) with slow ripples and normal activity. Each clip came from one electrode, but not all clips came from the same electrode. Secondly, we concatenated the clips as one file of events, representing a single continuous iEEG signal (n = 29.9889±3.4952 minutes, 773.8333±162.5268 slow ripples) using another automated script. Thirdly, we marked each slow ripple (SR) within the concatenated file using the GUI.

Experiments

We conducted two main experiments: 1) comparison of four methods (in next sections) to find appropriate features for detecting slow ripples; and 2) evaluation of the best method in the comparison when used to actually detect slow ripples in quasi-continuous iEEG (i.e., concatenated clips of iEEG that appeared continuous to a detector). We made the comparison and evaluation after computing the projected performance of each method in distinguishing slow ripples and normal activity for the training data (first experiment) or testing data (second experiment). Both experiments involved three metrics of performance (see ‘Statistics’): one metric to serve as the objective function for the automated algorithms that selected and/or combined features and two metrics—other than the first metric—to define and compare the performance of the algorithms. The first metric also allowed a fair comparison between the algorithms, ensuring that any discovered difference in performance between the methods depended on the unique capability of the method rather than any uncontrollable confounding experimental factor (e.g., stochastic convergence, dissimilar parameters) due to the distinctive architectures. For the first experiment, we filtered the training data, extracted 25 features from a few domains (Table 2), and input the result into four methods for optimizing the selection and/or combination of at most three features. After filtering all data with a Chebychev highpass filter (61-100 Hz) and separating the filtered data into two classes of events (i.e., slow ripple or not slow ripple), the features operated in non-overlapping sliding windows over each class of data before appending the processed data as a single matrix. At this point, the data constituted a computed n_o x n_f matrix, where n_o was the number of observations and n_f = 25 was the number of features, and a corresponding n_o x 1 vector of labels. We referred to the n_o x n_f matrix as a feature-matrix. We controlled each method to return one, two, or three feature(s). For each number of returned features, we computed the mean projected performance of each method using 30 trials of 6-fold cross-validation with a selected classifier to determine whether one method performed better than others, whether a certain number of features delivered better performance than others, and whether any differences in mean performance between methods varied depending upon the number of features. In addition, because we measured performance as two metrics (see ‘Statistics’), we determined if each method performed with an expected difference between the metrics.

Table 2.

We selected twenty-five features with which a feature-matrix was computed as input for the four methods

Number	Feature	Description	Domain
1	Curve Length	Length of an irregular curve (i.e., similar to arc length)	Time
2	Energy	Average instantaneous energy	Time
3	Nonlinear Energy	Average change in amplitude and frequency	Time
4	Root Mean Square Time	Amplitude of time-varying wave (usually sinusoidal), quadratic mean
5	Mean Rectified Value	Mean magnitude (i.e., average of an absolute value)	Time
6	Sinusoidal Frequency	Estimate of frequency for sinusoidal (or periodic) signal	Time
7	Sinusoidal Phase	Estimate of phase for sinusoidal (or periodic) signal	Time
8	Periodicity	Estimate of regularity for sinusoidal (or periodic) signal	Time
9	Crossings	Mean number of intersections across an amplitude reference	Time
10	Peak PSD	Maximum value of power spectral density (PSD)	Frequency
11	Mean PSD Frequency	Mean value of power spectral density (PSD)
12	Peak Sign-PSD Frequency	Maximum value of power spectral density (PSD) for signed signal
13	Mean Statistics	Measure of central tendency, arithmetic mean (or average)
14	Median	Measure of central tendency, middle value	Statistics
15	Interquartile Range Statistics	Difference between the third and first quartiles, mid-spread
16	Mad Statistics	Mean (or median) absolute deviation from mean (or median) value
17	Range	Difference between the maximum and the minimum values	Statistics
18	Standard Deviation Statistics	Measure of the variability relative to a mean value
19	Variance Statistics	Mean square deviation from a mean value
20	Skewness	Asymmetry about a mean value	Statistics
21	Kurtosis	Affinity to statistical outliers	Statistics
22	Spectral Entropy Information	Measure of predictability (or regularity) in a sequence
23	Shannon Entropy Information	Average missing information when values are unknown
24	Renyi Entropy Information	Measure of the diversity (or randomness) in a sequence
25	Complexity	Level of intricacy in a sequence	Information

For the second experiment, we designed a detector that incorporated the feature(s) as determined from the first experiment and processed the testing data with the detector. The detector filtered the testing data with a Chebychev highpass filter (61-100 Hz), extracted a single feature with 75% overlap between consecutive sliding windows of filtered data as a time-series that we called a feature-series, classified the feature-series with a k-nearest-neighbor classifier (k = 10) to form a binary time-series, and registered the time-stamps (i.e., first moments of transition between two classes) of each detected event. We computed performance using the automatically registered time-stamps and the manually registered time-stamps (see ‘Manual Markings’). Additionally, we implemented a previously published detector for slow ripples ((O. Smart, et al., 2007)) and compared the implementations.

Grammatically Evolved Features

The feature-matrix entered a GE with predefined parameters (Table 3) and the GE returned one mathematical expression that included at least one of the 25 features but defined a single feature to quantitatively differentiate slow ripples from normal activity. We repeated the above procedure with the same parameters for the GE to simultaneously return two and three grammatically evolved features (GE-features). Also, we duplicated all above procedures for the GE with a radial basis function (RBF) classifier—five hidden nodes and one hidden layer—as well as a 10-nearest-neighbor classifier. We implemented the GE using a custom algorithm written in ANSI C++.

Table 3.

We set the below parameters for the GE and GP, which controlled each algorithm

GE Parameter	Value
POPULATION	200
GENERATIONS	200
SAMPLING	tournament
CROSSOVER	2 parents, 2 children
MUTATION	1 parent, 1 child
FITNESS	accuracy of k-NN classification
SURVIVAL	total elitism
MAXLENGTH	40·(number of desired features)

GP Parameter	Value
POPULATION	200
GENERATIONS	10
SAMPLING	tournament
CROSSOVER	2 parents, 2 children
MUTATION	1 parent, 1 child
FITNESS	accuracy of k-NN classification
SURVIVAL	total elitism
MAXLEVEL	9
INICMAXLEVEL	6
INICDYNLEVEL 6
FIXEDLEVEL	1
DYNAMICLEVEL	2
DEPTHNODES	1

Genetically Programmed Features

As with the GE, the feature-matrix entered a genetic program (GP) with predefined parameters (Table 3) and the GP returned one mathematical expression that included at least one of the 25 features but defined a single feature to quantitatively differentiate slow ripples from normal activity. We completed the above procedure for only one genetically programmed feature (GP-feature). We implemented the GP using an open-source MATLAB algorithm ((Silva & Almeida, 2003)).

Sequentially Selected Features

In addition, the n_o x n_f feature-matrix entered algorithms for forward sequential feature-selection (F-SFS) and backward sequential feature-selection (B-SFS), where each algorithm returned a single subset of features per patient as benchmarks for the GE. The sequentially selected features represent the most capable manual selection of features, since we suppose that a human at best essentially emulates F-SFS or B-SFS. We used the F-SFS and B-SFS algorithms in MATLAB.

Statistics

We performed the statistical analyses using SPSS software (SPSS Inc., Chicago, IL). For each analysis, we chose a probability value (p-value) less than the level 0.05 (alpha) to indicate a statistically significant observation. We computed the following three metrics for our experiments. The accuracy served as the fitness (objective function) for the automated algorithms that selected and/or combined feature, whereas both sensitivity and selectivity constituted the performance. For each statistical test, the mean value of each metric after 30 trials of 6-fold cross-validation became the dependent variable.

$$\begin{array}{cc}\hfill accuracy& =fitness\hfill \\ \hfill & =\frac{numberoftruepositives+numberoftruenegatives}{numberof(truepositives+truenegatives+falsepositives+falsenegatives)}\hfill \end{array}$$ (2)

$$sensitivity=\frac{numberoftruepositives}{numberoftruepositives+numberoffalsenegatives}$$ (3)

$$selectivity=\frac{numberoftruepositives}{numberoftruepositives+numberoffalsepositives}$$ (4)

For the first experiment, a two-factor repeated-measures analysis of variance (ANOVA) with multivariate assumptions for each above metric determined if a method differed from others, if a certain number of features differed from others, or if any differences in a metric between methods varied depending upon the number of features with the method and the number of features as the first and second factor, respectively. In addition, for the first experiment, a Wilcoxon sign-ranked paired t-test for each method determined if a method possessed balanced performance (i.e., no more sensitive than selective).

For the second experiment, a Wilcoxon sign-ranked paired t-test for each method determined whether our suggested detector performed equivalently—in terms of sensitivity or selectivity—to an earlier suggested detector (O. Smart, et al., 2007). In addition, as in the first experiment, a Wilcoxon sign-ranked paired t-test for each method determined if a method possessed balanced performance considering a more realistic task of detection.

Results

Experiment 1

We determined that some methods performed differently from others, that the number of features did not change the performance of each method, that the number of features did not affect the differences in performance between methods, and that each method demonstrated some unbalance in performance but the imbalanced performance of GE differed from the other methods. Figures 1-3 illustrated these findings.

Figure 1.

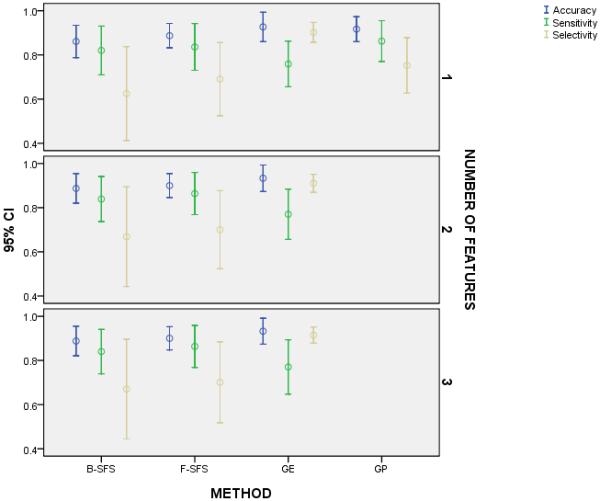
We compared the accuracy, sensitivity, and specificity of the selected methods with one, two, and three features; but we executed GP for only a single feature. For each number of features, all methods shared similar accuracy and sensitivity but GE appeared to project a higher selectivity despite no statistically significant difference. On the other hand, GE displayed higher selectivity than sensitivity, whereas the other methods practically demonstrated equal selectivity and sensitivity with a tendency for lower selectivity than sensitivity. We observed these findings regardless of the number of features for each algorithm.

Figure 3.

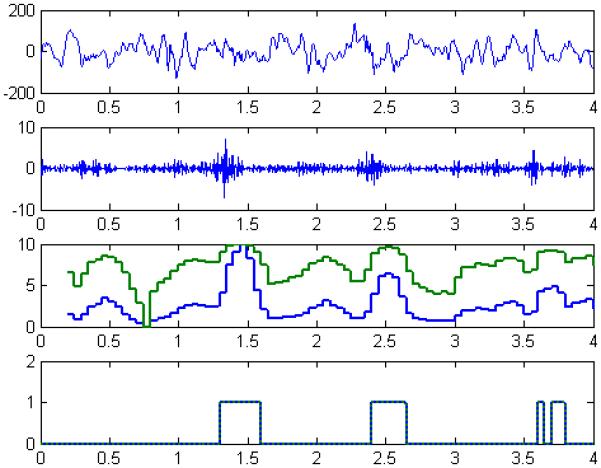
We illustrated the process and a representative outcome for detecting slow ripples with a four-second segment of processed iEEG from Patient A as an example. The raw iEEG (first panel) was filtered (61-100 Hz) to highlight slow ripples amongst background (second panel) before extracting each a GE-feature and a GP-feature and forming two feature-series (third panel). Each feature-series was classified using a nearest-neighbor classifier, resulting in a binary sequence (fourth panel) to discriminate epileptic events (1) and non-epileptic events (0). For this case, we noticed that although the feature-series did no overlap, the feature-series shared a similar end-behavior and ultimately the binary sequences were the same.

For a single feature, we found that none of the methods differed (p = 0.073) in mean accuracy, that at least one method differed (p = 0.010) from others in mean sensitivity, and one method ambiguously differed (p = 0.314, c.f. Table 4) from two other methods in mean selectivity according to conflicting statistics (Figure 1). That is, it appeared that GE produced a feature with higher projected selectivity than F-SFS and B-SFS and more exact (i.e., smaller confidence interval and standard error) projected selectivity than all other methods. When we repeated the analysis for only the methods that produced multiple features, we found that the methods did not differ (p = 0.054) in mean accuracy, that at least one method differed (p = 0.018) from others in mean sensitivity, and that again GE practically but not statistically differed (p = 0.130, c.f. Table 5 and Figure 1) from the other two methods in mean selectivity. Moreover, we determined that the number of features neither altered the accuracy (p = 0.476), sensitivity (p = 0.150), or selectivity (p = 0.459) for each method nor changed the accuracy (p = 0.891), sensitivity (p = 0.887), or selectivity (p = 0.817) across the methods (Figure 1). We also observed an interesting characteristic for each method regarding the relation between sensitivity and selectivity. Namely, we observed that GE produced features that led to higher selectivity than sensitivity (p = 0.028) and B-SFS barely produced features with less selectivity than sensitivity (p = 0.047), whereas F-SFS (p = 0.173) and GP (p = 0.075) produced features with equivalent selectivity and sensitivity. Lastly, when we compared the k-NN classifier and RBF classifier with each number of GE-features for each metric, we found no statistically or practically significant difference (p > 0.141, all nine pairs) in any of the comparisons.

Table 4.

We computed the marginal statistics for the mean selectivity of each method. The table showed that GE practically differed in selectivity from B-SFS and F-SFS and almost GP, yet the ANOVA found no statistically significant difference between any of the methods

SELECTIVITY
method	Mean	Std. Error	95% Confidence Interval
			Lower Bound	Upper Bound
B-SFS	.625	.083	.413	.837
F-SFS	.690	.065	.524	.856
GP	.753	.049	.627	.878
GE	.902	.018	.857	.948

Table 5.

We computed the marginal statistics for the mean selectivity for three of the four methods (i.e., B-SFS, F-SFS, and GE) for each number of features (i.e., one, two, or three). The table showed that GE practically differed in selectivity from B-SFS and F-SFS for each number of features, yet the ANOVA found no statistically significant difference between any of the methods

SELECTIVITY
method	nfeatures	Mean	Std. Error	95% Confidence Interval
				Lower Bound	Upper Bound
B-SFS	1	.625	.083	.413	.837
	2	.669	.088	.443	.894
	3	.670	.088	.444	.896
F-SFS	1	.690	.065	.524	.856
	2	.701	.069	.524	.877
	3	.701	.071	.518	.884
GE	1	.902	.018	.857	.948
	2	.910	.016	.870	.951
	3	.915	.014	.878	.951

Essentially, GE resulted in more selective features than the other methods but with similar sensitivity and demonstrated preferred selectivity over sensitivity while the other methods exhibited balanced performance. Furthermore, the type of classifier made no difference in performance, regardless of the number of produced features.

Experiment 2

Figure 3 illustrated the process of detecting slow ripples from raw iEEG using two distinct detectors (i.e., one with a GE-feature, one with a GP-feature) for two patients. Figure 4 illustrated the repeated process of detection for another patient. Both figures captured a visual finding for all patients regarding the GE-based and GP-based approaches: that the approaches appeared to similarly classify interictal epileptic and non-epileptic activity. For all patients, we quantitatively investigated whether the detectors performed equally for quasi-continuous iEEG with a null hypothesis of no difference in performance between methods and an unequal performance for at least one of the methods—considering the results of the first experiment.

Figure 4.

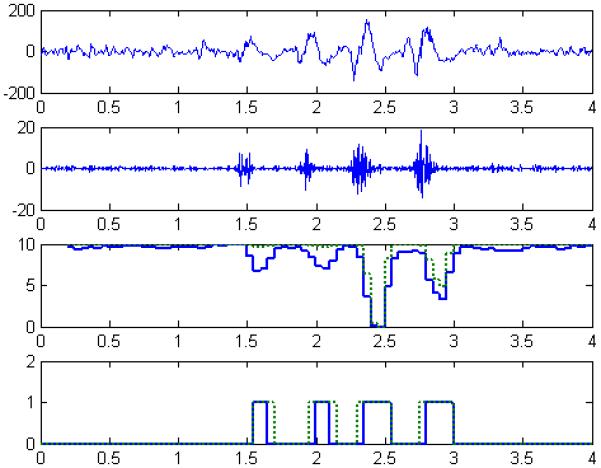
We illustrated the process and a representative outcome for detecting slow ripples with a four-second segment of processed iEEG from Patient C as an example. The raw iEEG (first panel) was filtered (61-100 Hz) to highlight slow ripples amongst background (second panel) before extracting each a GE-feature and a GP-feature and forming two feature-series (third panel). Each feature-series was classified using a nearest-neighbor classifier, resulting in a binary sequence (fourth panel) to discriminate epileptic events (1) and non-epileptic events (0). For this case, we noticed that the feature-series somewhat overlapped and paralleled in end-behavior but the binary sequences experienced some subtle differences (e.g., time-stamp(s) and duration of detected events).

According to the non-parametric (Wilcoxon) t-test, the methods did not differ in median sensitivity (p = 0.753) or median selectivity (p = 0.116), which agreed with earlier results from the first experiment (c.f., Figure 2, Figure 5). Unexpectedly, given the results of the first experiment, the detector with the GE-feature did not demonstrate a difference in selectivity and sensitivity (p = 0.600). Thus, we concluded that GE and GP performed similarly in sensitively and selectively detecting slow ripples, despite the drastic difference in the constructed features (Table 6).

Figure 2.

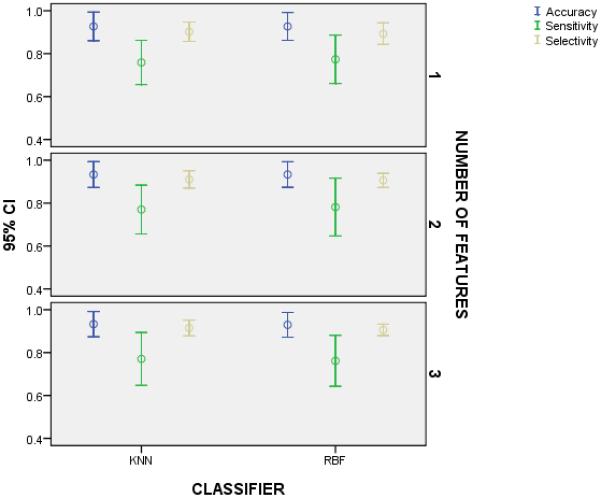
We compared the accuracy, sensitivity, and specificity of a k-NN classifier and a RBF classifier using the same GE-feature(s) to demonstrate that classification depends more on the computed feature than the classifier in this application. We observed no difference in the metrics for the classifiers with one, two, or three features.

Figure 5.

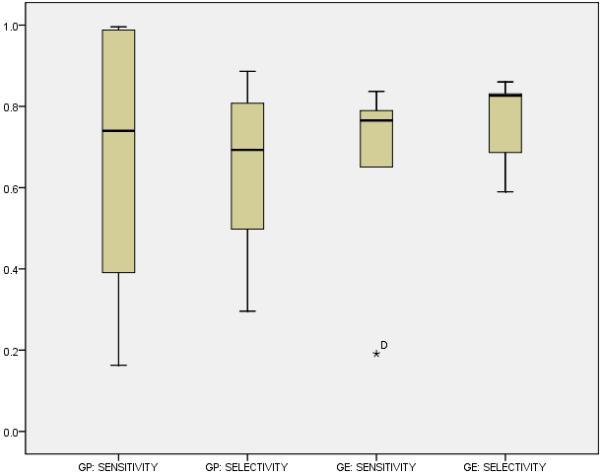
We compared the performance (i.e., sensitivity, and specificity) of our approach and a previously proposed approach for detecting slow ripples with one feature from an evolutionary algorithm. Overall, the approaches shared similar sensitivity and selectivity despite sweeping differences in the algorithmically constructed features.

Table 6.

We collected and contrasted the constructed features for the GE and GP algorithms

Patient	GE-Feature	GP-Feature
A	5.40·f1	√(atan(atan(atan(atan(atan(f1))))))
B	58.59·f1	atan(f17·f9·f17·f9·f9·f22·f22)·f9) = atan((f17)2·(f9)2·(f22)2)·f9)
C	(−517.61·f4+765.70·f1)·(−9.929)·f9	f16 - max((f16 - f1)2, f1)2
D	0.61·f1	max(f5,sin(f4)) + max(cos(f18), f10)3
E	−695.8·f1	|f19|3
F	65.4·f1	(f6)2 + (f6)2·max(f7, (f1)2)

Discussion

The findings in the presented experiments were important in several key aspects. First, we determined that forward and backward sequential selection and genetic programming returned features for detecting slow ripples with balanced sensitivity and selectivity whereas grammatical evolution returned features for detecting slow ripples with more selectivity than sensitivity. This finding was interesting since all four automatic approaches objectively maximized accuracy with no statistically significant difference in accuracy. The similarity between F-SFS and B-SFS was not surprising. Essentially, the algorithms iterated in the same manner, where only the order of processing the feature-maxtrix—subtract (or add) an individual feature-vector for B-SFS (or F-SFS)—defined the major difference in execution. On the other hand, although both GP and GE incorporate Darwinist evolutionary procedures, the GE clearly manipulated the feature-matrix in a different manner than the GP. We attributed this disparity to the more structured BNF grammar of GE, which GP lacked but perhaps introduced an increased level of selectivity in classification.

Second, we determined that GE presented higher mean selectivity, similar mean sensitivity, and more precise performance (i.e., smaller standard error in mean sensitivity and mean selectivity) when compared to the other three approaches. We attributed the contrast in precision and selectivity also to the unique BNF grammar, which introduced a specific structure in each returned solution.

Third, we observed that the number of features did not alter the previously mentioned findings. This analysis was especially important, since it dictated the number of needed features for properly processing the iEEG while minimizing computational burden for extraction and classification of features. For instance, with the presented data for each patient, we determined that one feature was just as effective as three features in classification. Thus, we opted for a single patient-specific feature for further analyses. Fourth, we observed that each patient-specific GE-feature simply scaled the ‘line-length,’ excluding Patient C for whom the GE-feature comprised ‘line-length’ and two other complementary features. This fourth finding was very interesting for two main reasons: 1) the unanimous selection of ‘line-length’ across patients not only presented a seemingly universal single feature that effectively discriminated epileptic gamma oscillations and non-epileptic background—at least according to the GE—but also agreed with prior literature in successfully building automated detectors for epileptic activity (Esteller, 2001; Gardner, et al., 2007; O. L. Smart, et al., 2005); 2) the execution of GP for the same experimental data indicated that multiple features were necessary for effective classification in 4 of the 6 patients with ‘line-length’ selected for 3 of the 6 patient-specific GP-features. The latter finding emphasized one of the disadvantages of the GP algorithm, namely the bloat rather than parsimony in the returned solutions.

Fifth, we found that the type of classifier did not significantly alter performance for the GE-features. We expected no difference between the RBF and the k-NN, despite the different architectures, since the GE produced a feature with very good discriminability per patient before classification. Lastly, using a new testing sample of continuous iEEG, our suggested detector (a GE-feature and a k-NN classifier) displayed similar sensitivity and selectivity to a previously implemented detector (a GP-feature and a k-NN classifier) with our detector exhibiting more expected precision in each metric than the previous detector. Unsurprisingly, these findings mirrored our results for the point-basis estimation of performance (i.e., using concatenated vectors of feature-values) because of the computed p-values. But contrary to the point-basis analysis, we observed no partiality of selectivity over sensitivity. Nonetheless, we ultimately concluded that the suggested detector presented an effective alternative to automatically registering epileptic oscillations in continuous clinical iEEG.

Conclusions

Overall, GE facilitated a sound approach to detect interictal epileptic oscillations in clinical iEEG. Because the GE required only a small sample of manually marked events and the general framework of the detector did limit detection to a certain event or electrographic recording, we presented a versatile approach that permitted the detection of interictal activity in different recordable bandwidths (e.g., fast ripples, ripples, spikes).