Efficacy of Weekly Docetaxel and Bevacizumab in Mesenchymal Chondrosarcoma: A New Theranostic Method Combining Xenografted Biopsies with a Mathematical Model

Abstract

The paucity of clinical treatment data on rare tumors, such as mesenchymal chondrosarcoma (MCS), emphasizes the need in theranostic tools for these diseases. We put forward and validated a new theranostic method, combining tumor xenografts and mathematical models, and used it to suggest an improved treatment schedule for a particular MCS patient. Growth curves and gene expression analysis of xenografts, derived from a patient’s lung metastasis, served for creating a mathematical model of MCS progression and adapting it to the xenograft setting. The pharmacokinetics and pharmaco-dynamics of six drugs were modeled, with model variables being adjusted by patient-specific chemosensitivity tests. The xenografted animals were treated by various monotherapy and combination schedules, and the MCS xenograft model was computer simulated under the same treatment scenario. The mathematical model for xenograft growth was then up-scaled to retrieve the MCS patient’s tumor progression under different treatment schedules. An average accuracy of 87.1% was obtained when comparing model predictions with the observed tumor growth inhibition in the xenografted animals. Simulation results suggested that a regimen containing bevacizumab applied i.v. in combination with once-weekly docetaxel would be more efficacious in the MCS patient than all other simulated schedules. Weekly docetaxel in the patient resulted in stable metastatic disease and relief of pancytopenia due to tumor infiltration. We suggest that the advantage of weekly docetaxel on the triweekly regimen is directly related to the angiogenesis rate of the tumor. Further validation of this conclusion, and the theranostic method we provide, may facilitate personalization of solid cancer pharmacotherapy.

Introduction

Mesenchymal chondrosarcoma (MCS) is a rare disease that accounts for about 1% of all chondrosarcomas. Overall, 5-year survival is 55%. This disease usually follows an aggressive course, with a high rate of distant metastases (1, 2). Lack of efficacious therapies for this and other rare tumors that progress rapidly accentuates the need to develop accurate, predictive personalization tools in a timely fashion.

Prediction of personalized therapy, or theranostics, is the process of selecting the best treatment for a given patient by accounting for patient-specific factors, such as gender, age, and genetic characteristics. A possible theranostic solution is to assess the relative efficacy of various treatments in laboratory animals, which bear the patient’s cancer (3). However, xenograft models suffer from three major impediments: slow, costly, and labor-intensive cellular acquisition from tumor biopsies and xenograft growth; animal physiology not reflecting the human pharmacokinetics (PK); and xenograft methods not accounting for patient safety.

Underlying these impediments is the complexity of the involved dynamics due to which one cannot estimate, by intuition alone, the relationships between measurable molecular biomarkers and the behavior of the organism as a whole. In contrast, mathematical models formally and systematically describe the major biological processes that relate the measured biomarkers to the phenotype in question. By integrating these mathematical models into comprehensive computer algorithms, one can compute what will be the effect on the phenotype of changes, even small changes, in biomarker levels. In theranostics, laboratory experiments in xenografted animals could be used in conjunction with mathematical models for the pathologic and physiologic growth dynamics and for drug PK and pharmacodynamics (PD).

Mathematical models for tumor progression (4–6), cancer therapy (7–10), and related genetic (11, 12), hematologic (13, 14), and immunologic processes (15, 16) have been developed. Using these models, the efficacy of various drug monotherapy and combination schedules was predicted (7, 8, 14, 15, 17, 18). These computer-implemented models allow clinicians to analyze the effects of drug regimens on disease progression, as well as provide the power to check various biomarkers for their suitability to represent different aspects of the disease in question. New methods for treatment optimization have also been developed, which grade the therapeutic potential of specific regimens according to clinical criteria, such as efficacy/toxicity ratio (17, 19). The biological process models, in conjunction with the optimization methods, introduce into clinical oncology a quantitative prediction-based decision-making facility.

Several preclinical and clinical trials have been carried out for testing the prediction accuracy of mathematical model for tumor progression (20–24). In the present work, we applied a validated model for vascular tumor progression (see below) to create a novel theranostic method for a large class of anticancer drugs. The method was validated in xenografts derived from a MCS patient’s lung metastasis and then used for predicting an improved therapy for the patient himself.

By controlling its variable values, the validated model was adapted to describe the metastatic tumor growth of a specific MCS patient as well as of its xenografted biopsy. We used these two new models to analyze the reasons underlying the relative advantage of one treatment option over another.

Materials and Methods

The Patient

A 45-y-old white male was in excellent health until a growing mediastinal mass was found in 2004. His primary tumor was resected and identified histologically as MCS. Despite the initial resection, multiple new bilateral pulmonary nodules were discovered 30 d after the operation. Despite aggressive chemotherapy with ifosphamide, cisplatin, and etoposide for six cycles, VACA (vincristine, doxorubicin, cyclophosphamide, and dactinomycin) for 2 cycles, and sunitinib p.o. for 8 wk, the patient progressed with additional liver and bone metastases. As a consequence of prolonged chemotherapy and documented bone marrow infiltration, the patient suffered severe myelosuppression with pancytopenia.

Study Design

The workflow of this study is described schematically in Supplementary Fig. S1.

Tumor fragments were taken from lung metastases of the MCS patient and implanted in mice. This xenograft model was established and amplified until sufficient tumor was available to implant a control and several treatment groups. In this model, cells are only propagated directly as smaller pieces from a previous xenograft and never propagated as a cell line. Mice were divided into groups, each treated by different drug regimen, in addition to a control group of untreated animals. In parallel to the laboratory work, a general mathematical model for vascular tumor growth dynamics was adapted to describe the growth of untreated xenografts of the MCS patient’s lung metastases. In silico experiments, similar to those performed in vivo, were conducted to predict growth of MCS xenografts and their response to various drug therapies. This was done by simulating the adapted tumor growth model in conjunction with the relevant PK/PD models and the particular dosing regimens. Where available, patient-specific chemosensitivity information was used to fine-tune the PD models. Otherwise, only publicly available data were used for the mathematical PK and PD models of the drugs in the xenograft experiments. Following the initial assessment of model prediction accuracy (25), the variables of several drug models were reevaluated and the accuracy was assessed again.

Subsequently, the mathematical model was adjusted to describe the patient’s metastatic growth dynamics. This was done using gene expression analysis of key proteins in mice and human and various treatment regimens were tested for efficacy in the MCS patient.

Experimental Setup

Immunohistochemistry

Tissue from the primary sarcoma was removed after surgery and fixed in 10% buffered formalin and embedded in paraffin. Tissue sections of 5 μm were deparaffinized in xylene and rehydrated in increasing concentrations of ethanol. Endogenous peroxidase activity was quenched with 0.01% H₂O₂, sections were boiled in 0.01 mol/L citric acid (pH 6.0), and nonspecific binding was blocked with 10% normal rabbit serum. After washing, rat anti-mouse CD34 monoclonal primary antibody (PharMingen) specific to vascular endothelium was applied at 25 μg/mL and incubated overnight at 4°C. After washing in PBS, biotinylated rabbit anti-mouse antibody, diluted 1:100, was applied followed by incubation at room temperature for 30 min. After washing again in PBS, avidin-biotin complex (Vector Laboratories), diluted 1:25, was applied and incubated at room temperature for 30 min and washed again in PBS. Tissue sections were developed with diaminobenzidine and peroxide and counter-stained with hematoxylin. Microvessel density (MVD) was assessed by counting the microvessels at ×200 in a field that had the highest vascularization by scanning at ×40 (12) and then converted to MVD/mm². Stained slides were examined blind and were also scored from one to four with increasing vascularity.

Animal model

For establishment and propagation, tumor fragments obtained from the MCS patient were s.c. implanted using an 11-gauge cancer trocar on the right flank of male CD-1 nude mice, as we assumed that mouse flank provides a good mirror of primary sarcoma growth in the soft tissue microenvironment of the patient from which it originated. Mice were weighed twice weekly and tumor measurements were taken with a Vernier caliper twice weekly, beginning 7 d after implantation. Tumors were considered established once growth reached log stage as determined by tumor measurements. Once established tumors reached a predetermined volume (1–3 cm³), they were excised and sectioned into 15 to 30 mm³ fragments, which were implanted s.c. as above; implantation was unilateral on the right flank. Once tumors grew to 50 to 150 mm³ in size, animals were pair matched by tumor size into treatment and control groups. The animals were ear tagged and followed individually throughout each experiment.

Data collection and analysis

Tumor volume was calculated by conversion of two-dimensional caliper measurements as follows (19):

$$V=\frac{1}{2}{W}^{2}L$$ (A)

where V, W, and L are the tumor volume, width, and length, respectively. Mean tumor growth inhibition (TGI) of each treated group was compared with vehicle control and a TGI value was calculated using the following formula:

$$\text{TGI}(\%)=100·\left(1-\frac{T-T_0}{C-C_0}\right)$$ (B)

where T ₀ and C ₀ are initial tumor sizes of the treated and the control tumor, respectively, and T and C are sizes of treated or control tumor, respectively.

In vitro proliferation assays

Patient-specific tumor cells were obtained from xenografts, generated by inoculation of lung metastases into immunocompromised mice, which were collected when they had grown beyond 150 mm³ in size. The tumors were minced into small pieces (<1 mm), digested for 2 h with collagenase-DNase, mechanically dissociated, and passed through sterile nylon mesh to produce single-cell suspensions. Viable tumor cells were enriched by elutriation and Ficoll-diatrizoate density centrifugations (26). Tumor cell suspensions were plated in microtiter wells (50,000 per well) and incubated in the presence or absence of the indicated drugs or combinations for 4 d in 3-(4,5-dimethylthiazol-2-yl)-2,5-diphenyltetrazolium bromide (MTT; ref. 27) or 7 d in the differential staining cytotoxicity (DiSC; ref. 28) assays.

Mathematically Modeling Vascular Tumor Growth

A mathematical model of angiogenesis-dependent tumor dynamics and its underlying assumptions is described in detail elsewhere (4, 5, 24). The reader is referred to Fig. 1 in ref. 24 for a schematic representation of the model. The model describes three main interactive growth dynamics: of tumor cells, of blood vessel formation (angiogenesis), and of new vessel maturation.

Generally, our model assumes that the tumor volume is formed by living cells, which undergo mitosis or death, and dying cells, which are progressively eliminated. The living cells consume nutrients and secrete proteins that affect angiogenesis. We distinguish between two types of vessels, mature and immature, which differ in their perfusion efficiency. Mature vessels are coated by pericytes, mesenchymal-like cells, which support these vessels and enable improved blood flow (29, 30). The immature vessels are only tubes of endothelial cells, which are more “leaky” than the mature ones, and conduct oxygen and nutrients less effectively to the tumor (31, 32). Another property of immature vessels in our model is their higher degradation tendency. The degree of tumor vascularization strongly affects its growth rate: higher and more effective vascularization triggers vigorous proliferation of tumor cells while inhibiting angiogenesis. In contrast, insufficient vasculature causes hypoxia and starvation of the tumor tissue, thus inhibiting cell proliferation and promoting angiogenesis (33–37). Four proteins that are related to angiogenesis are modeled: vascular endothelial growth factor (VEGF), platelet-derived growth factor (PDGF), angiopoietin-1 (Ang-1), and angiopoietin-2 (Ang-2). The growth factor VEGF drives angiogenesis by inducing endothelial cell proliferation and by serving as a survival factor for immature vessels. PDGF drives maturation by inducing the proliferation of pericytes, which coat the immature vessels and turn them mature. The proteins Ang-1 and Ang-2 also affect the processes of vessel maturation and destabilization. The protein Ang-1 promotes vessel maturation by facilitating the binding of free pericytes to the extracellular matrix. In contrast, Ang-2 causes pericyte dropout, thus promoting vessel destabilization (38, 39).

Personalizing the MCS Patient Model

The growth of six untreated xenografts was monitored for estimating the variables of the MCS patient tumor model when xenografted in mice. Only three of them actually grew in size. Results of histopathologic assays of the patient’s lung metastasis (e.g., tumor density, mitotic index, necrotic index, and vessel density) were used to define valid variable ranges in the evaluation process. Twelve model variables common to all the xenografts were evaluated. In addition, two variables, which represent the vascular bed at implantation site, were evaluated for each xenograft individually. Two additional xenograft growth curves were monitored for validating model predictability.

Mathematically Modeling PK/PD

We adopted linear compartmental PK models for all the drugs in this study (see refs. 40, 41 for general reviews on compartmental PK modeling). Each effect of the drug is mathematically defined as a function of drug concentration in a predefined model compartment. In general, the concentration-effect relationship is defined using a sigmoid function (42):

$$E(C)=E_{max}-\frac{E_{max}-E_{min}}{1+{(C/C_{\text{nor}})}^m}$$ (C)

where E is the measured effect at the given plasma concentration C; E _max and E _min are the maximal and the minimal possible effects, respectively; C _nor is the drug concentration that produces the effect that equals to the average of E _max and E _min; and m is the curve slope at the point [C _nor; E (C _nor)]. However, when the available information does not permit a reliable reconstruction of the variables for the sigmoid function, a more simplistic linear relationship is used:

$$E(C)=\{\begin{array}{ll}{E}_{min}\hfill & 0\le C<C_{min}\hfill \\ E_{min}+\frac{E_{max}-E_{min}}{C_{max}-C_{min}}·(C-C_{min})\hfill & C_{min}\le C\le C_{max},\hfill \\ E_{max}\hfill & C_{max}\hfill \end{array}$$ (D)

where E _max and E _min are the bounding maximum and minimum effects, respectively, and C _max and C _min are the respective drug concentrations that cause these effects.

The model of drug effect depends on its actual mechanism of action. For example, the effect of a cytotoxic drug, such as docetaxel, is modeled as a fraction of cells that are killed during the current time step (Eqs. C and D). Thus, in the context of docetaxel, E _max and E _min (Eqs. C and D) are taken as 1 and 0, respectively. The overall effect on treated tumor shrinkage compared with the untreated tumor is calculated by Eq. B.

The variable identification of the MCS model and the various PK and PD models was performed using a cross-entropy method, described in ref. 43, as well as experimental records of xenograft dynamic and publicly available PK data. The sources for PK and PD data can be found in Supplementary Tables S1 and S2, respectively.

Personalizing PK/PD Models Using Xenograft Experiments

Six drugs and their combinations were tested in mice bearing xenografts from the patient’s cancer tissue to determine the best possible treatment: bevacizumab, docetaxel, doxorubicin, gemcitabine, irinotecan (CPT-11), and sorafenib. Results of in vitro proliferation assays of the patient’s tumor cells were used to establish patient-specific concentration-effect curves for the chemotherapeutics (docetaxel, gemcitabine, CPT-11, doxorubicin, and docetaxel/gemcitabine combination). Two different concentrations of each drug were tested, enabling to construct linear dose-response functions (Eq. D). Response was measured using DiSC and MTT methods and concentration-effect equations were constructed separately for each method and then averaged. For docetaxel and gemcitabine/docetaxel, only DiSC results were used for parameterization. These data were modeled as the fraction of cells killed during the current time step.

Modeling PD of targeted drugs (bevacizumab and sorafenib) was based on relevant data of treated lung cancer xenografts and was implemented as a sigmoid dependence (Eq. C). In our mathematical model, we included bevacizumab single-action mechanism as a VEGF inhibitor and that of sorafenib triple-action mechanism (i.e., direct inhibition of tumor maturation, inhibition of pericyte activity, and decreasing the cell proliferation rate). The estimated individualized PD was combined with the corresponding PK to yield a complete PK/PD model. No PK individualization was performed in this work.

To model drug combinations, the independent effects of each drug in the combination were added. An additive effect was assumed due to lack of quantitative information on potential PK/PD interactions. An exception is the case of docetaxel/gemcitabine combination, where data from the patient-specific in vitro proliferation assays were available. Theoretically, the combined effects of docetaxel and gemcitabine may be synergistic or antagonistic depending on the type of tumor cells and on the order of drug administration (44, 45). PK interactions are partially responsible for the dependence of the combined effect on drug sequencing (45). As the chemosensitivity tests are PK independent, and due to the shortage of quantitative data, we assumed that no PD interactions exist between the modeled drugs.

Simulating MCS Xenograft Dynamics and Response to Drug Treatment

The full PK/PD models of numerous therapy schedules were simulated in conjunction with the MCS xenograft model. Mouse body weight was taken as 30 g. Efficacy was measured in terms of TGI (Eq. B). As stated above, necrotic tumor cells do not disappear from the system immediately, but are eliminated with a finite rate, and therefore contribute to tumor volume. Thus, the control and treated tumor sizes in Eq. B may refer to the total number of cells, or to living cells alone, resulting in TGI values that consider the tumor volume as a whole (TGI_T) or only the living fraction (TGI_L).

Xenograft simulations were carried out for a period of 22 d, similar to the period for TGI calculations in the experimental setup.

Validating the Model Predictions

Growth of MCS xenografts treated under various therapies was monitored for 22 d after treatment initiation. Model prediction accuracy was calculated as follows. For the control group, the growth of the tumor during the experiment, G, is given by

$$G=\frac{C}{C_0}$$ (E)

where C₀ and C are the initial and final sizes of untreated xenografts, respectively.

Prediction accuracy, A, for the control group was calculated using the observed, G _obs, and calculated, G _calc, G values as follows.

$$A_{\text{control}}(\%)=100·\left(\frac{\mid G_{\text{obs}}-G_{\text{calc}}\mid }{G_{\text{obs}}}\right)$$ (F)

Prediction accuracy for the treatment groups was calculated using the observed and predicted TGI values, TGI_obs and TGI_calc, respectively.

$$A_{\text{treated}}(\%)=100·\left(\frac{\mid {\text{TGI}}_{\text{obs}}-{\text{TGI}}_{\text{calc}}\mid }{{\text{TGI}}_{\text{obs}}}\right)$$ (G)

Refining the Models

Following the initial assessment of prediction accuracy, the PK and PD models of each drug were independently revisited by detailing the action mechanisms of the involved biological drug models and by additional refinement of PK/PD variables. Only publicly available data were used in this process. Unlike the original models, the reviewing process was performed only after receiving the experimental xenograft sensitivity. However, these were blinded in the refinement process. Thus, the results below may be regarded as prospective ones. Results of the initial assessment are also reported (25).

Simulating Tumor Dynamics and Response to Drug Treatment in the MSC Patient

The personalized disease model of the MCS xenografts served as the basis for the human model. Gene expression analyses of key proteins (e.g., VEGF; ref. 46) in the patient’s metastases and in the xenografted tumor (denoted as Met/F1 ratio) were used to scale relevant xenograft variables. For example, gene expression analysis shows that the Met/F1 ratio of Ang-2 is 0.7. Therefore, values of corresponding variables in the xenograft model were multiplied by this coefficient to yield a new value in the human model. Published data on the involved drugs were used to model their PK in human. We assumed that administering equivalent doses to a mouse and a human would result in effects of similar maximum magnitude but with different time profiles. Therefore, the same PD functions used in mice modeling were used in human models [i.e., patient-specific concentration-effect curves for cytotoxic drugs (CPT-11, docetaxel, doxorubicin, and gemcitabine) and literature-based functions for bevacizumab and sorafenib]. Note that for simplicity we describe here only our predictions about drug efficacy. Predictions about drug toxicity will be discussed elsewhere.

The full PK/PD models were simulated in conjunction with the MCS human model under various therapy regimens. A treatment period of 90 d was simulated, but simulations were carried out for a total period of 120 d to allow confirmation of response 4 wk after the end of treatment.

Results and Discussion

Experimental results

Personalized PD variables of the cytotoxic drugs docetaxel, doxorubicin, gemcitabine, and CPT-11 were estimated using the chemosensitivity tests of the patient’s tumor cells to the respective drugs. In addition to assessing the sensitivity to a single compound, docetaxel/gemcitabine combination was also tested (Table 1). This combination (docetaxel, 260 μg/mL; gemcitabine, 37.5 μg/mL) was found in vitro to be less efficacious than gemcitabine alone (70% versus 14% surviving cells, respectively). Moreover, after 1:2 dilution, the docetaxel/gemcitabine combination became completely inactive (100% surviving cells).

Table 1.

Chemosensitivity-tested response of the MCS patient’s tumor cells to cytotoxic drugs, as measured by DiSC and MTT methods

Drug	Concentration (Ag/mL)	Response
		DiSC	MTT
Docetaxel	37.5	96	N/A
	18.75	40	N/A
Gemcitabine	260	14	26
	130	10	15
Gemcitabine + docetaxel	260/37.5	30	N/A
	130/18.75	30	N/A
Doxorubicin	1.2	59	57
	0.6	20	27
Irinotecan	30	48	18
	15	24	20

NOTE: A higher response indicates a lower number of surviving cells (i.e., better efficacy).

Abbreviation: N/A, not available.

The xenografted animals were treated by five different drug schedules (regimens 1–5; Table 2). Tumor sizes of the treated and control animals were measured and registered at treatment onset (day 0) and on day 22. The calculation of TGI_T was performed according to Eq. B. In our experiments, the TGI_T values for the five regimens ranged from 38.9% (sorafenib monotherapy, regimen 4) to 109.3% (bevacizumab/docetaxel/gemcitabine, regimen 2).

Table 2.

Mathematical model validation

Regimen				Results*			Accuracy†
No.	Treatment	Dose (mg/kg)	Route	Schedule	Observed	Predicted
—	Control	—	—	—	2.11	2.01	94.8
1	Irinotecan	100	I.p.	q7dx3	59.40%	57.16%.	96.2
	Bevacizumab	10	I.p.	q3dx10
2	Gemcitabine	40	I.p.	q3dx4	109.27%	76.61%	70.1
	Docetaxel	6.3	I.v.	q2dx3
	Bevacizumab	10	I.p.	q3dx10
3	Doxorubicin	2	I.v.	qdx5	56.39%	65.31%	84.2
	Bevacizumab	10	I.p.	q3dx10
4	Sorafenib	60	P.o.	qdx10	38.85%	40.38%	96.1
5	Sorafenib	60	P.o.	qdx10	87.22%	71.02%	81.4
	Bevacizumab	10	I.p.	q3dx10
				Average accuracy			87.1%

NOTE: TGI of the different treatment schedules, as predicted by the mathematical model, compared with those measured in mice bearing xenografts originating from MCS patient’s tumor.

^*Results for control group: ratio of tumor size at day 22 to initial tumor size. Results for treatment groups: TGI_T.

^†As calculated using Eq. F for control and Eq. G for the treated cases.

Validating the predictions of the mathematical model

The mathematical model successfully retrieved the growth curves of the untreated MCS xenografts, including the calculated 3-month lag period between implantation and growth (Fig. 1). Validated for untreated tumor dynamics, the model was then simulated under different treatment regimens. The values of TGI_T were calculated from the predicted tumor sizes (Eq. B). Model predictions were compared with the experimentally observed values. In the initial assessment, the average prediction accuracy was 81.9% (25). Having refined the drug models, the accuracy of model predictions increased to 87.1% (Table 2). The analysis below refers to the results obtained using the refined models.

Figure 1.

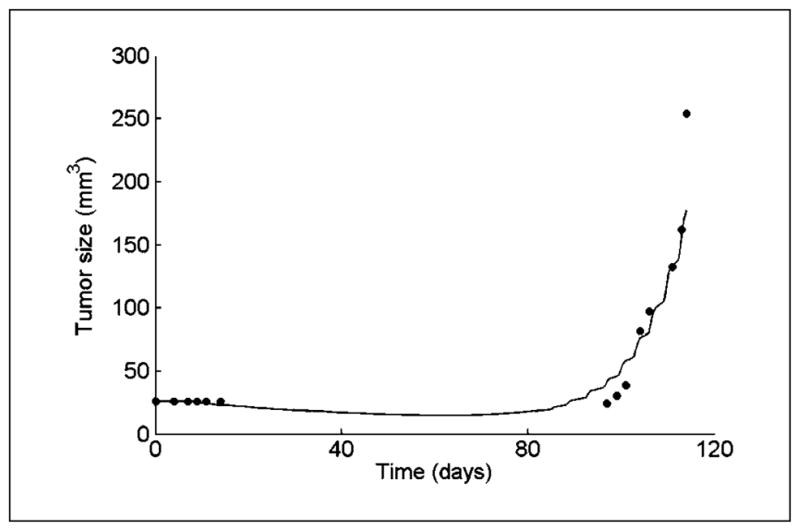
Growth in mouse of a tumor derived from a lung metastasis of a MCS patient. Simulation results of the MCS xenograft model (line) compared with experimental measurements of tumor size in a test mouse (circles). Tumor cells from the MCS patient biopsy were grown in vitro and implanted into the animal on day 0.

The predicted efficacy ranking of the different treatment regimens was correct, except for the swapping of rank 3 and 4 (regimens 3 and 1). Note the small difference in the experimental TGI values of these two regimens—59.4% for regimen 1 and 56.4% for regimen 3. This may suggest that the difference between these two schedules is not significant.

The most accurate prediction was achieved in the bevacizumab/CPT-11 combination (regimen 1). The model-predicted and measured TGI_T values were 57.2% and 59.4%, respectively (accuracy of 96.2%). The two most efficacious regimens, in terms of TGI, were regimen 2 (bevacizumab/gemcitabine/docetaxel) with measured TGI_T being 109.3% and regimen 5 (bevacizumab/sorafenib) with measured TGI_T being 87.22%. Our prediction for regimen 2 (TGI_T = 76.6% predicted versus 109.3% measured) was the less accurate of all the predictions (accuracy of 70.1%). Nevertheless, it was correctly identified as the most potent schedule. Note that excluding this lowest accuracy value results in mean accuracy of 90.5%.

Antagonism between gemcitabine and docetaxel was experimentally observed in vitro using the patient’s tumor cells (Table 1). This result is corroborated by our model simulations, which suggest that removing gemcitabine from regimen 2 (bevacizumab/gemcitabine/docetaxel) yields a slightly larger TGI_T: 78.6% versus 76.6%. However, whereas the in vitro result is probably related to the drug sequencing effects on cell kinetics, we believe that the in silico predicted antagonism better reflects the in vivo setting, where the added, relatively large, cytotoxic effect of the two drugs may generate intensive angiogenesis, eventually leading to excessive tumor recovery.

Proposing an improved treatment for the MCS patient

Drug efficacy experiments in the personalized xenograft model alone are of limited use as a theranostic tool (see above). Having validated our mathematical model, we could use it, jointly with the results of the empirical xenograft experiments, for analyzing putative treatment alternatives for the patient so as to maximize the TGI (Eq. B).

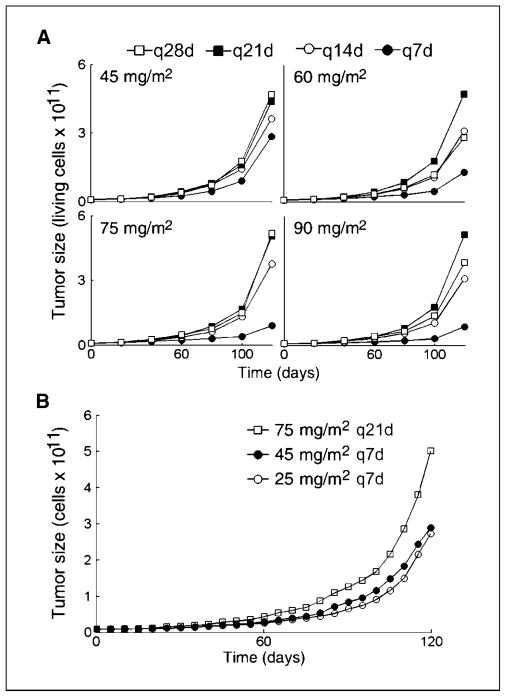
Many clinical trials have been reported comparing q7d with q21d docetaxel regimens for various indications. Nevertheless, no definitive conclusion about the superiority of either dosing interval can be made. In addition, several toxic effects have been associated with weekly regimens (47). Because our preliminary simulations pinpoint the bevacizumab/docetaxel combination as superior to most other therapies in suppressing the growth of the MCS patient’s xenografts (25), we wished to test whether the patient would benefit from weekly docetaxel administrations. To this end, a series of bevacizumab/docetaxel regimens was simulated (regimens 6–21; Table 3). In all the studied regimens, delivery of triweekly i.v. doses of 15 mg/kg bevacizumab combined with four alternative docetaxel doses (45, 60, 75, and 90 mg/m²) in four different dosing intervals (q7d, q14d, q21d, and q28d) was simulated. The associated treatment efficacy, in terms of time to progression and final tumor sizes, was predicted; time to progression is defined as the time needed for 20% increase in tumor size. Results are summarized in Table 3 and in Fig. 2A, where the predicted tumor growth curves of the 16 simulated treatments are shown. Our simulations suggested that once-weekly regimens (Fig. 2A, filled circles) would be superior to other simulated regimens for the MCS patient, both in terms of final tumor size and time to progression. The improvement in tumor dynamics that is predicted for once-weekly regimens is caused by the interdosing interval and not by increasing the total drug dose: dividing the total docetaxel dose from regimen 16 to once-weekly dosing interval [i.e., doses of 25 mg/m² (regimen 22)] results only in a minute decrease in the predicted efficiency compared with regimen 7 (75 mg/m² q7d). Both these weekly regimens are predicted to be more efficacious than the triweekly regimen 16 (Fig. 2). This result supports theory, suggesting that interdosing intervals per se significantly affect drug efficacy (7, 8).

Table 3.

Simulated docetaxel/bevacizumab combinations

Regimen				Total dose	TTP(d)†
No.	Drug	Dose	Schedule
6	Docetaxel	45 mg/m2	q7dx12	540 mg/m2	20.25
	Bevacizumab	15 mg/kg	q21dx4	60 mg/kg
7	Docetaxel	60 mg/m2	q7dx12	420 mg/m2	22.25
	Bevacizumab	15 mg/kg	q21dx4	60 mg/kg
8	Docetaxel	75 mg/m2	q7dx12	900 mg/m2	19
	Bevacizumab	15 mg/kg	q21dx4	60 mg/kg
9	Docetaxel	90 mg/m2	q7dx12	1080 mg/m2	29.75
	Bevacizumab	15 mg/kg	q21dx4	60 mg/kg
10	Docetaxel	45 mg/m2	q14dx6	270 mg/m2	18.5
	Bevacizumab	15 mg/m2	q21dx4	60 mg/kg
11	Docetaxel	60 mg/m2	q14dx6	360 mg/m2	18
	Bevacizumab	15 mg/kg	q21dx4	60 mg/kg
12	Docetaxel	75 mg/m2	q14dx6	450 mg/m2	17.75
	Bevacizumab	15 mg/kg	q21dx4	60 mg/kg
13	Docetaxel	90 mg/m2	q14dx6	540 mg/m2	18.5
	Bevacizumab	15 mg/kg	q21dx4	60 mg/kg
14	Docetaxel	45 mg/m2	q21dx4	180 mg/m2	18.5
	Bevacizumab	15 mg/kg	q21dx4	60 mg/kg
15	Docetaxel	60 mg/m2	q21dx4	240 mg/m2	17.75
	Bevacizumab	15 mg/kg	q21dx4	60 mg/kg
16	Docetaxel	75 mg/m2	q21dx4	300 mg/m2	17.5
	Bevacizumab	15 mg/kg	q21dx4	60 mg/kg
17	Docetaxel	90 mg/m2	q21dx4	360 mg/m2	18.25
	Bevacizumab	15 mg/kg	q21dx4	60 mg/kg
18	Docetaxel	45 mg/m2	q28dx3	135 mg/m2	18.5
	Bevacizumab	15 mg/kg	q21dx4	60 mg/kg
19	Docetaxel	60 mg/m2	q28dx3	180 mg/m2	17.75
	Bevacizumab	15 mg/kg	q21dx4	60 mg/kg
20	Docetaxel	75 mg/m2	q28dx3	225 mg/m2	17.5
	Bevacizumab	15 mg/kg	q21dx4	60 mg/kg
21	Docetaxel	90 mg/m2	q28dx3	270 mg/m2	18.25
	Bevacizumab	15 mg/kg	q21dx4	60 mg/kg
22	Docetaxel	25 mg/m2	q7dx12	360 mg/m2	18.75
	Bevacizumab	15 mg/kg	q21dx4	60 mg/kg

NOTE: The resulting predictions of tumor dynamics curves are presented on Fig. 2A.

Abbreviation: TTP, time to progression.

^†Simulated time to progression (±0.25 d).

Figure 2.

Effects of docetaxel scheduling on tumor dynamics as predicted by simulations of the in vivo MCS patient’s disease model under 16 bevacizumab and docetaxel treatment combinations. Schedules include bevacizumab (15 mg/kg i.v. q21d) combined with docetaxel (1-h i.v. infusion of 45, 60, 75, and 90 mg/m²; four docetaxel schedules are presented: q7d, q14d, q21d, and q28d; A) and docetaxel [i.v. infusion applied in three different schedules: 75 mg/m² q21d (regimen 16), 45 mg/m² q7d (regimen 7), and 25 mg/m² q7d (regimen 22)]. The simulated treatment period is 90 d.

Effect of angiogenesis on treatment outcome

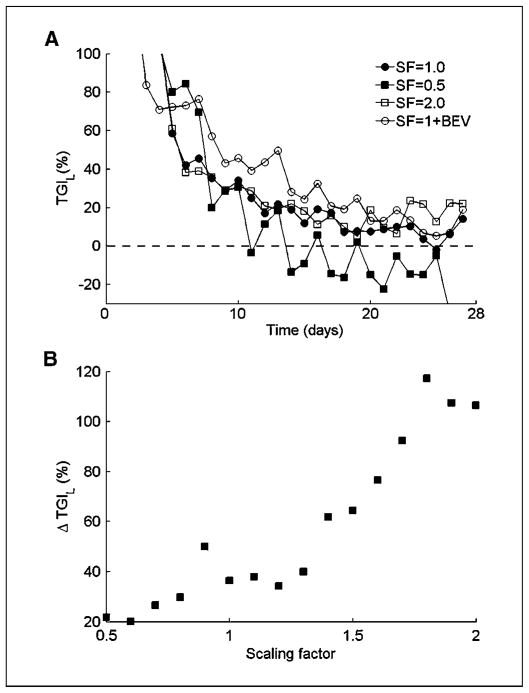
To understand the mechanism underlying the predicted q7d versus q21d superiority, we artificially changed various model variables and examined their effects on docetaxel efficacy. By altering the kinetic rate of new vessel formation, as influenced by VEGF secretion, density of VEGF receptors, etc., we could test the effect of angiogenesis on docetaxel effect over time. Our mathematical model simulations show that a single administration of the cytotoxic docetaxel perturbs the dynamic equilibrium between the living tumor cells and the blood vessels that support them, thus triggering a cascade of tumor recovery events. The more intensive the angiogenesis, the faster the tumor recovery is (Fig. 3A and B).

Figure 3.

Model simulations of MCS dynamics in the patient after a single docetaxel dosing (75 mg/m², 1-h i.v. infusion). A, estimated TGI_L after a single docetaxel dosing for tumors with different levels of angiogenesis intensity. Angiogenesis intensity is determined by scaling the model variable, which combines VEGF secretion and activity rates. Simulations using two arbitrary scaling factors (SF) are compared with those with estimated angiogenesis intensity of the MCS patient and, in combination with bevacizumab (BEV; 15 mg/kg i.v.), are presented. B, predicted decrease in TGI_L from day 7 to day 21 following docetaxel administration as a function of angiogenesis intensity.

Comparing the simulated tumor size in the MCS patient, after a single docetaxel dosing, with the predicted tumor size with no treatment, we calculated the expected TGI_L at each time point according to Eq. G. The calculated TGI_L on day 7 was 46%. On day 21, the effect almost disappears, as shown by a TGI_L value of only 10%—decrease of 36% (Fig. 3A). When the rate of new vessel formation is halved, the predicted reduction in TGI_L values from day 7 to day 21 is only 29% (39% and 10%, respectively), indicating slower recovery from drug-induced tumor inhibition. In contrast, if the rate of new vessel formation is doubled, compared with that calculated for the real MCS patient, the difference in the extent of tumor inhibition by docetaxel dose, between day 7 and day 21, increases to 92%: 69% at day 7 versus a negative value of −22% in day 21. The negative TGI_L value means that at this point, the number of living tumor cells is larger than it would have been if no treatment were administered. The dependence of tumor recovery rate on the rate of new vessel formation is almost monotonic over a wide range of kinetic rates (Fig. 3B). This suggests that angiogenesis-intensive tumors can be controlled by more frequent docetaxel dosing, whereas angiogenesis-poor tumors may be treated by less dense regimens. Adding to docetaxel, the anti-VEGF monoclonal antibody bevacizumab is shown in our simulations to slow down tumor recovery. The result is a predicted TGI_L value of 76% at day 7 compared with 45% without bevacizumab. As time goes on, bevacizumab is eliminated, which allows rapid tumor recovery resulting in 10% TGI_L on day 21 (a difference of 66%).

This work does not address drug-induced hematopoietic toxicity (48), which is the major dose-limiting factor in radiotherapy and chemotherapy of cancer (49). However, in another work, the superiority of calculated 10-day interdosing docetaxel intervals for alleviating neutropenia was theoretically shown, supporting the superiority of the weekly docetaxel regimens.⁶ A clinical decision was made to proceed with docetaxel therapy in addition to antiangiogenesis treatment with bevacizumab. For fear of aggravating the severe pancytopenia with larger q21d doses of docetaxel, a weekly schedule, as predicted here, was administered to the patient. The patient had a dramatic response to therapy with a marked decrease in serum alkaline phosphatase from bone and an immediate substantial recovery of all three blood elements (hemoglobin, WBCs, and platelet count). Soft tissue disease in the lungs and liver remained stable and the patient enjoyed a 6-month period of good quality of life, ending only after pulmonary progression of his disease to which he finally succumbed. Thus, a combined experimental and modeling approach for treatment personalization benefited this MCS patient.

Taken together, our results suggest that a methodology combining xenografted biopsies and mathematical modeling has promising prospects in personalized oncology. As our model had predicted, the patient showed a markedly improved clinical course after weekly docetaxel and bevacizumab combination. Our prediction, about the superiority of once-weekly docetaxel in patients with intensive angiogenesis, may explain observed variability in the relative efficacy of q7d versus q21d docetaxel regimens in cancer patients (47). This prediction should be validated in the preclinical and clinical setting. On further validation, it may aid physicians in identifying improved treatment schedules for individual patients.