Practical Signal-to-Noise Ratio Quantification for Sensitivity Encoding: Application to Coronary MRA

Abstract

Purpose

To develop and evaluate a practical method for the quantification of signal-to-noise ratio (SNR) on coronary magnetic resonance angiograms (MRA) acquired with parallel imaging.

Materials and Methods

To quantify the spatially varying noise due to parallel imaging reconstruction, a new method has been implemented incorporating image data acquisition followed by a fast noise scan during which radiofrequency pulses, cardiac triggering and navigator gating are disabled. The performance of this method was evaluated in a phantom study where SNR measurements were compared to those of a reference standard (multiple repetitions). Subsequently, SNR of myocardium and posterior skeletal muscle was determined on in vivo human coronary MRA.

Results

In a phantom, the SNR measured using the proposed method deviated less than 10.1% from the reference method for small geometry factors (<=2). In-vivo, the noise scan for a 10 minutes coronary MRA acquisition was acquired in 30s. Higher signal and lower SNR, due to spatially varying noise, were found in myocardium compared to posterior skeletal muscle.

Conclusion

SNR quantification based on a fast noise scan is a validated and easy-to-use method when applied to 3D coronary MRA obtained with parallel imaging as long as the geometry factor remains low.

INTRODUCTION

Accurate quantification of signal-to-noise ratio (SNR) is essential for objective evaluation of magnetic resonance (MR) images acquired with different hardware, imaging protocols, and reconstruction methods. Numerous scientific and clinical studies strongly depend on objective end-points including signal and noise quantification. The choice of a proper SNR measurement approach is therefore often a critical component of the experimental setup (1) and the analysis.

One of the most commonly used methods to measure SNR includes the division of the average signal from a region of interest (ROI) within the imaged object by the standard deviation (SD) of the signal in an ROI outside the object (2–4). This method is valid for conventional single or multi-channel coil imaging reconstructed by a sum-of-squares algorithm, where noise is distributed uniformly in the whole image. However, linear combination of multi-channel coil acquisitions based on coil sensitivity maps (5) and widely used parallel imaging acceleration techniques (6–8) cause a spatial variation in noise. Noise measured in one region of the image may therefore not necessarily represent the noise elsewhere in that same image (9).

One of the most accurate definitions of SNR is based on repetitive acquisitions of data under the same exact conditions at multiple time points. This method is referred to as SNR_mult, where SNR of each pixel is then defined as the ratio between the mean and the SD of the signal intensity time course of that pixel (9–10). When a very large number of time points are used, SNR_mult represents the true variation of the signal at a particular voxel and should be considered the gold standard for noise measurements. Another method described in the literature is based on just two identical acquisitions, which are either averaged or subtracted to determine signal or noise respectively (4,10). Both methods are generally not practical for in vivo measurements due to prolonged scanning time associated with repeated acquisitions. Also they are susceptible to system drift and to image misregistration related to physiological motion. Especially for 3D free breathing coronary magnetic resonance angiography (MRA) in combination with parallel imaging (11–12), such an SNR quantification may be adversely affected by respiratory and cardiac motion (13). Besides, repeated acquisitions of 3D coronary MRA data in vivo for SNR quantification is impractical due to prohibitively long scanning time.

As alternatives to multiple acquisitions, two methods have recently been proposed to measure SNR by reconstructing the image in SNR units directly (14) or by simulating repetitions of noise only images (15). However, both techniques suffer from a relatively high computational burden. In addition, the direct SNR determination necessitates detailed knowledge of all image reconstruction steps, which may not readily be available if image reconstruction is performed on a commercial MR system.

Hence, despite the availability of numerous and powerful methods, there is no practical, general SNR measurement method available for coronary MRA acquired with parallel imaging. An SNR quantification method that enables both the signal and the noise measurement at the exact same location is therefore needed.

For these reasons, an alternative, practical, and easy-to-use SNR quantification method has been implemented for coronary MRA and follows the recommendations of the National Electrical Manufacturers Association (NEMA) (4). This new approach, which currently comes at the expense of 30s of additional scanning time only, has been implemented on a commercial MR scanner. Subsequently, the method’s validity and suitability for quantitative coronary MRA SNR analysis have been investigated both in vitro and in vivo.

MATERIALS AND METHODS

Theory

An SNR measurement method recommended by NEMA (4) is based on the acquisition of a magnitude image and a second acquisition with identical settings but no radiofrequency (RF) pulses to obtain a pure noise image. Although this method has been known for years, to the best of our knowledge, there is limited literature investigating its performance and utility for MRI. Furthermore, a noise scan, which usually takes as long as the corresponding magnitude image acquisition, would not only double the scanning time but also significantly reduce overall practicality. For these reasons, this work will show that the duration of the noise scan can be abbreviated by an order of magnitude. The fast noise acquisitions could significantly increase the simplicity of SNR measurements in scans obtained with parallel imaging. In the following, we will refer to the SNR based on this noise scan as SNR_noRF.

The primary origin of random fluctuation in MRI signals is thermal noise. RF receiver thermal noise in MRI systems (16) can be determined according to:

$${\sigma }_{\mathit{thermal}}^2\propto 4kT·R_{\mathit{eff}}·BW,$$ [1]

where σ²_thermal is the variance of noise voltage, k is the Boltzmann constant, T is the resistor’s absolute temperature, R_eff is the effective resistance of the coil loaded by the body, and the BW is the bandwidth of the noise-voltage detecting system. Equation [1] indicates that data acquisitions with and without RF excitations have the same thermal noise variance - provided that coil loading and receiver bandwidth are identical.

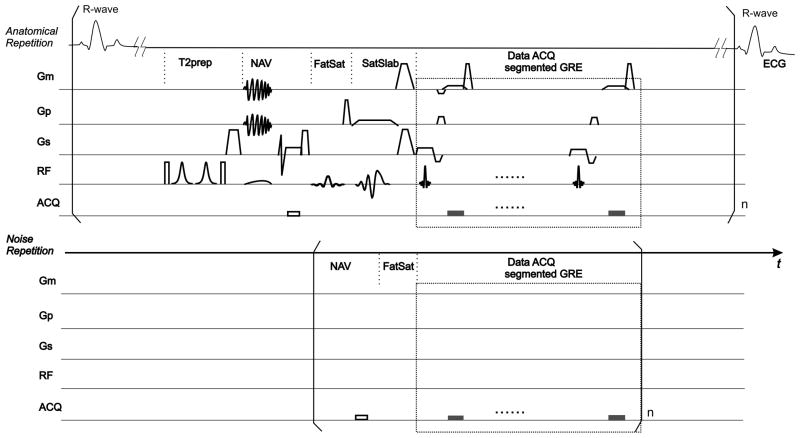
To measure noise, a fast noise acquisition scheme has been developed in the framework of a segmented k-space spoiled gradient echo imaging sequence (17) (Fig 1). The conventional or ‘anatomical’ scan is repeated with all the RF pulses and magnetic field gradient disabled (=noise scan). Furthermore, triggering to the R-wave of the electrocardiogram (ECG) is not used. The respiratory navigator, which is performed with both RF pulse and gradient disabled, is set to accept all data for reconstruction. Cardiac and respiratory motion during the noise scan acquisition are assumed to have little effect on the measured noise statistics since loading of the small phased array coil elements, and thus R_eff, is dominated by the chest, which is considered stationary relative to the coil. With this approach, the duration of noise scan is greatly abbreviated while the thermal noise statistics remain unaffected. It is important to note that both anatomical and noise scans have identical geometry, receiver gain, and reconstruction algorithm (The reconstruction algorithm should only include linear filters. Non-linear filters including image-based filters may affect the statistics of the anatomical and noise scan differently and thus-derived SNR values may no longer be valid.). After completion of the scan, both the anatomical dataset and the corresponding noise dataset are automatically reconstructed.

Fig 1.

Schematic of the pulse sequence: The anatomical scan consists of a conventional 3D coronary MRA sequence. The segmented k-space spoiled gradient echo (GRE) data acquisition (ACQ), starting at the predetermined trigger delay (Td) after the R-wave, is preceded by the magnetization preparation pulses including a T2prep pulse, a pencil-beam respiratory navigator pulse (NAV), a fat saturation pulse (FatSat) and a spatially selective saturation pulse (SatSlab). In the noise scan, however, data acquisition ACQ is executed without ECG triggering, RF excitations or gradient (Gm, Gp, Gs) pulses. Magnetization prepulses are omitted except NAV and FatSat, although their RF and GR are disabled as well. The modules as delineated by square brackets are repeated n times. By utilizing shorter modules without ECG triggering or respiratory gating, the duration of the noise scan can be greatly shortened compared to the anatomical scan.

On the anatomical images, ROIs are selected for signal measurements and these ROIs are automatically copied to the identical 3D location in the corresponding noise images. The signal (S_noRF) is defined as the average of the signal from the ROI in the anatomical image while the noise (N_noRF) is proportional to the standard deviation of the signal found in the equivalent ROI in the noise scan:

$$\begin{array}{l}{S}_{\mathit{noRF}}=\underset{\mathbf{r}\in \mathit{ROI}}{\mathit{mean}}(S(\mathbf{r})),\\ N_{\mathit{noRF}}=\sqrt{\frac{2}{4-\pi }}·\underset{\mathbf{r}\in \mathit{ROI}}{SD}(N(\mathbf{r})),\end{array}$$ [2]

where S(r) is the anatomical image intensity in pixel r=(r_x, r_y, r_z), N(r) is the noise image intensity in pixel r. The coefficient $\sqrt{2/(4-\pi )}$ accounts for the Rayleigh distribution of the noise in the magnitude image (2). This coefficient is different in the above mentioned sum-of-squares reconstruction (18). The SNR_noRF is thus obtained as

$${\mathit{SNR}}_{\mathit{noRF}}=S_{\mathit{noRF}}/N_{\mathit{noRF}}$$ [3]

Based on an error propagation calculation similar to that in the Appendix in (10), the error on estimates of the SNR (=σ_SNR) is proportional to $1/\sqrt{n_{\mathit{ROI}}}$ in presence of homogenous noise in that ROI, where n_ROI is the sample size (number of independent pixels) in that ROI.

Hardware

All phantom and in vivo studies were performed on a commercial whole body 3.0T MR scanner (Achieva R2.1, Philips Healthcare, Best, The Netherlands) equipped with a six-element cardiac phased-array coil for signal reception and vector-ECG (19) triggering. Parallel imaging was performed using sensitivity encoding (SENSE)(7).

Phantom Studies

Phantom experiments were performed to validate SNR_noRF in comparison to SNR_mult. First, noise maps for different acceleration factors were generated to show spatial variations as a qualitative comparison. Then, SNR maps were used in a quantitative comparison considering various acquisition and measurement parameters.

Image Acquisition

First, a multislice survey scan was obtained in axial, sagittal, and coronal views to identify the location of a cylindrical fluid phantom. This was followed by a SENSE reference scan with a spatial resolution of 3.0×3.0×4.0mm³. Then, a 2D segmented k-space spoiled gradient echo imaging sequence with centric k-space profile ordering was applied to acquire a 3mm thick coronal slice with a field-of-view (FOV) of 256×256mm² and an acquired matrix size of 128×128. The phase encoding direction was left-right (LR) and imaging was performed with artificial ECG triggering (RR interval = 800ms). The pulse sequence had 12 RF excitations per cardiac cycle, a repetition time (TR) of 5.2ms and an echo time (TE) of 2.6ms. No fractional echo signal-readout was used and the BW was 383.2 Hz/pixel, which remained unchanged for all phantom data acquisitions. The image acquisition was repeated 63 times (for SNR_mult) consecutively and paused for 5s, to ensure that all signal has decayed, before the fast noise image acquisition (for SNR_noRF) started. To investigate the influence of different levels of signal, scans with RF excitation angles of 20° and 8° were performed. For both experiments (20° and 8° RF excitation), SENSE acceleration factors ranging from 1 to 5 were applied in the LR direction. This resulted in a total of 10 individual scans each of which contained 63 anatomical and one noise image.

ROI Size

A small ROI (ROI_small) of 10×10 pixels was selected on the images. To assess the relationship between ROI size and SNR measurement, the SNR measurements were repeated with a larger ROI (ROI_large) of 20×20 pixels to ensure that more independent samples were included in the analysis.

SNR Measurement Methods

Based on the magnitude image data provided by the MRI system, SNR was measured using SNR_mult and SNR_noRF in MATLAB (MATLAB R14, The MathWorks Inc., Natick, MA). SNR_mult was calculated from repetitions 4 to 63 to avoid transient effects before steady-state of the magnetization was reached. Linear correction was applied to the signal intensity of repetitions 4– 63 to compensate for residual intensity drift during the acquisition. The signal of each pixel (Ψ_mult) was determined as the average of the pixel intensity from temporal repetitions, while the noise of each pixel (σ_mult) was determined as the SD of the pixel intensity series. SNR_mult of a user-specified ROI was the quotient of average signal (S_mult) over average noise (N_mult) among all the pixels in the ROI, as

$$\begin{array}{l}{\mathrm{\Psi }}_{\mathit{mult}}(\mathbf{r})=\underset{k=4,\cdots ,63}{\mathit{mean}}(S_k(\mathbf{r})),\\ S_{\mathit{mult}}=\underset{\mathbf{r}\in \mathit{ROI}}{\mathit{mean}}({\mathrm{\Psi }}_{\mathit{mult}}(\mathbf{r})),\\ {\sigma }_{\mathit{mult}}(\mathbf{r})=\underset{k=4,\cdots ,63}{SD}(S_k(\mathbf{r})),\\ N_{\mathit{mult}}=\underset{\mathbf{r}\in \mathit{ROI}}{\mathit{mean}}({\sigma }_{\mathit{mult}}(\mathbf{r})),\\ {\mathit{SNR}}_{\mathit{mult}}=S_{\mathit{mult}}/N_{\mathit{mult}},\end{array}$$ [4]

where S_k(r) is the anatomical image pixel intensity of the k^th repetition (9).

SNR_noRF was calculated from the 10^th repetition (steady state) of the anatomical scan and the noise from the noise scan (64^th repetition) as described in Equations [2] and [3].

Spatial Variation of Noise

The spatial variation of noise and its dependence on SENSE acceleration factors R was analyzed. To generate noise maps, the noise of each pixel was calculated from a ROI_small centered at the targeted pixel. Noise maps based on the noise statistics N_noRF (Equation [2]), N_mult and σ_mult (Equation [4]) were generated for data sets acquired with different R and an RF excitation angle of 20°. A comparison between N_noRF and σ_mult was made by computing |N_noRF − σ_mult|.

Quantitative Validation of SNR_noRF

SNR maps for SNR_noRF and SNR_mult were generated for a rectangular area in the center of the imaged phantom (rectangle in Fig 2a). The SNR in each pixel was calculated from a square shaped ROI centered at the targeted pixel. SNR measurements were performed for all possible 10×10 and 20×20 ROIs within the rectangle (20). For a quantitative validation, the relative differences between the proposed SNR_noRF and the reference standard SNR_mult, i.e., |SNR_noRF − SNR_mult|/SNR_mult, was calculated for all pixels in the rectangular area. The size of the rectangle was 60×54 on the images. The average and standard deviation of the relative differences over the area were reported as a scalar measure that describes the quality of the SNR measurement method.

Fig 2.

(a) The relative difference between SNR_noRF and SNR_mult was averaged over pixels within the depicted box. The box has a size of 60×54 pixels on the image. (b) SNR measurements from five locations (centered in the circles) were used for the linear regression between SNR_noRF and SNR_mult.

In addition, five locations, on the left, right, center, top, and bottom of the image (circles in Fig 2b), were selected. Their SNR values for all the RF excitation angles, ROI sizes and five locations in the image, were computed as a function of the different SENSE acceleration factors R and linear least-squares fitting was performed with SNR_mult on the x-axis vs. SNR_noRF on the y-axis.

G-Factor

G-factor maps based on the acquired SENSE reference scan can be generated by the standard MRI system using the coil sensitivity map. Alternatively, the g-factor can be determined according to the definition (7):

$$g(R)=\frac{{\mathit{SNR}}_1}{\sqrt{R}·{\mathit{SNR}}_R}.$$ [5]

Hereby, SNR₁ refers to the SNR on images acquired with a SENSE factor of R = 1, and SNR_R to that with R > 1.

G-factor maps calculated by the MRI system were exported and taken as the reference standard in the following g-factor comparison. The g-factor maps according to Equation [5] were also generated from the SNR_noRF data with an RF excitation angle of 20° and with ROI_small. For each SENSE acceleration factor, the average g-factor and one standard deviation over the rectangular area (Fig 2a) were computed for both g-factor maps reconstructed by MRI system and calculated based on SNR_noRF.

In Vivo Studies

For coronary MRA, SNR_mult can not be performed due to time constraints. Instead, to further demonstrate the ability of SNR_noRF to measure local SNR in vivo, we hypothesized that the signal ratio between myocardium and chest muscle is different from the SNR ratio between the two. At 3T, chest muscle has a T1 of 1420ms (21) and a T2 of 32ms (21), while myocardium has a T1 of 1220ms (22) and a T2 of 59ms (23). Therefore, and after T2-preparation, which generates T2 weighted image contrast (24–25), the signal of the chest muscle with the shorter T2 is expected to be smaller than that of the myocardium with the longer T2. When applying the uniform sensitivity reconstruction (5,7), the signal of each tissue and thus the relative signal depend only on the muscle tissue properties such as proton density, T1, T2, but not on coil sensitivity. However, the local noise does depend on (among other factors) coil sensitivity, i.e., on whether the ROI is located close to or more distant from the receive coils. Accordingly, in the case of spatially heterogeneous noise, the SNR ratio at two locations would differ from the signal ratio since SNR is determined by both signal and local noise.

Coronary MRA data obtained in ten healthy adult subjects (26) were analyzed. The study protocol was approved by our Institutional Review Board and all subjects gave written informed consent to participate. For each subject, two 3D segmented k-space spoiled gradient echo acquisitions of the right coronary artery (RCA) with identical scan times and acquisition windows of 40ms, but different SENSE acceleration factors (1 and 2), TR (3.3 and 6.6ms), TE (1.2 and 1.8ms), RF excitation number (12 and 6), and readout BW (724.1 and 149.3 Hz/pixel) were obtained. The three-dimensional fast noise scans always followed the anatomical scan immediately after a 5s pause.

The ‘Soap Bubble’ coronary analysis tool as described by Etienne et al. (27) was extended with the ability to quantify SNR_noRF. Rectangular ROIs were manually drawn on the anatomical images in the left ventricular wall and in the posterior chest wall, respectively, where signal and SNR of myocardium and skeletal muscle were calculated based on Equations [2] and [3]. In one representative coronary MRA dataset, the SNR map was calculated by a sliding ROI of 10×10 pixels size and for all the pixels in the slice.

All results are reported as mean ± 1 SD among all the subjects. For each SENSE acceleration factor, statistical tests were performed to compare the signal of myocardium and that of skeletal muscle, using a paired two tailed Student’s t-test, with a p-value<0.05 representing significant difference. The same statistical test was applied to SNR of myocardium and skeletal muscle. The above-described SNR ratio and signal ratio were calculated on all in vivo human datasets. Then, the SNR ratio was further compared to the signal ratio by using a paired two tailed Student’s t-test, with a p-value<0.05 representing significant difference.

RESULTS

Phantom Studies

Fig 3 shows representative magnitude images of anatomical scans and the corresponding noise scans (no RF) at various SENSE acceleration factors. With higher SENSE factors, the intensity of noise increases as SNR decreases in the anatomical images. Consistent with earlier findings of others (7), structured regions of high noise are seen centrally and more prominently as the SENSE acceleration factor increases. In addition, the spatial coherence visible on the noise images in the lower row is in good agreement with the artifacts seen on the anatomical images in the upper row.

Fig 3.

Phantom images (row a) and noise images (row b) when SENSE acceleration factors R = 1, 2, 3, 4, 5 were applied. All the images were acquired with an RF excitation angle of 20°. All phantom images are displayed with an identical window level, while the noise images with individually adapted window levels. The minimal and maximal intensities in each window level are labeled under the corresponding image.

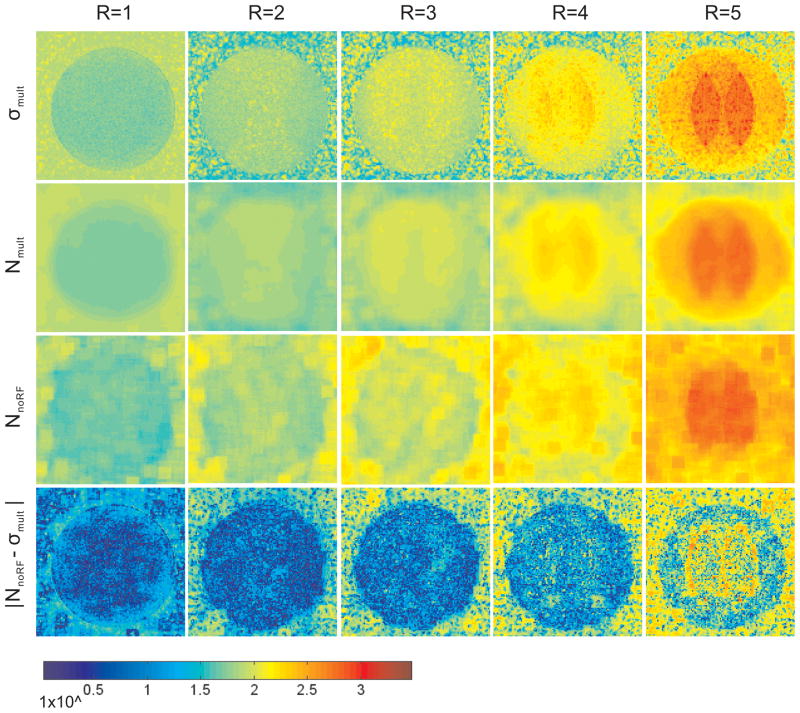
The noise statistics σ_mult, N_mult and N_noRF are displayed as pseudo color images in Fig 4. N_noRF demonstrates similar spatial distribution and magnitude of noise statistics as N_mult, which corresponds to a spatial average of σ_mult. By subtracting N_noRF from σ_mult, the coherent structures shown in σ_mult are largely removed and a minor residual difference signal remains at the edges of these structures due to the lower spatial resolution of the N_noRF image. The difference between N_noRF and σ_mult is one order of magnitude lower than the measured noise levels. It is noticed that, for an acceleration factor R larger than 2, N_noRF differs considerably from σ_mult in background areas outside of the object. The image reconstruction at these locations in background areas is unpredictable due to the absence of coil sensitivity in the SENSE reference scan, and thus the noise quantification in the background is not recommended.

Fig 4.

Spatial noise in phantom study calculated by σ_mult (row a), N_mult (row b) and N_noRF (row c) at five SENSE acceleration factors (R = 1, 2, 3, 4, 5) respectively. σ_mult, N_mult and N_noRF (rows a–c) showed structured regions of high noise centrally and more prominently as the acceleration factor increases. The absolute difference |N_noRF − σ_mult | is displayed in row d, on which edges are still seen, but the magnitude of absolute difference is reduced. For all images the phase encoding direction was oriented left-right, RF excitation angle was 20°, and the window level is identical. ROI size of 10×10 was used in N_mult and N_noRF computation.

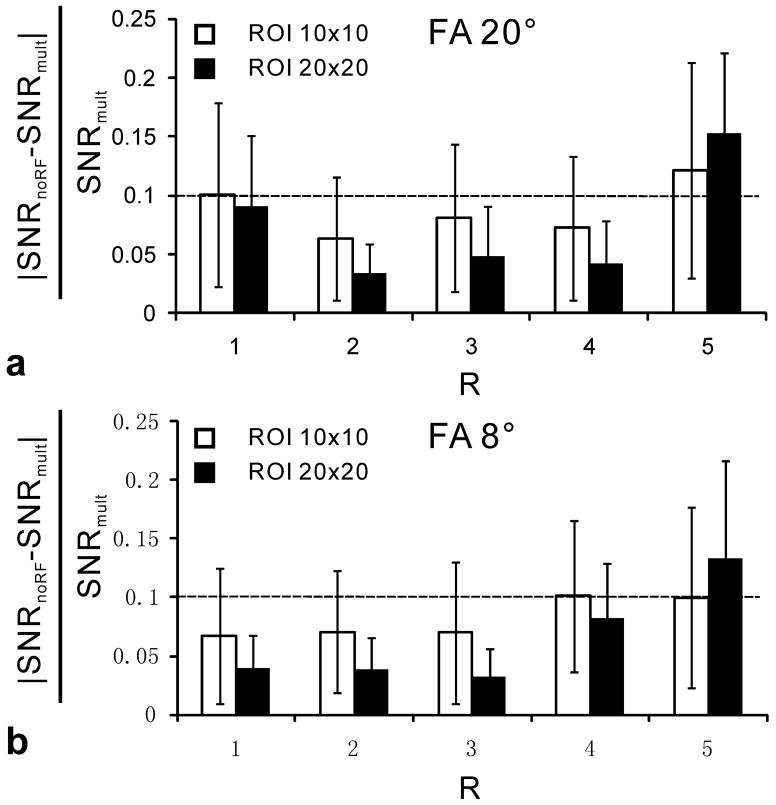
Quantitative results in Fig 5 represent the average relative differences between SNR_noRF and the reference standard SNR_mult as a function of ROI size and the RF excitation angle. These data are shown for acceleration factors R ranging from 1 to 5. The average relative differences for SENSE acceleration factors from 1 to 4 are below 10.1%. In contrast, SNR_noRF measurements obtained at a SENSE acceleration factor of 5 may differ up to 15% relative to the reference standard SNR_mult. Comparing RF excitation angles of 8° and 20°, the relative difference increased slightly for some SENSE acceleration factors but decreased for others. Therefore, the choice of the RF excitation angle, and thus the absolute signal level, does not seem to have a major effect on the SNR measurement using SNR_noRF. However, and as expected, the ROI size is a major determinant for differences between SNR_mult and SNR_noRF. ROIs of larger size help to reduce the error of SNR_noRF relative to the SNR_mult method for SENSE acceleration factors ranging from 1 to 4, although increasing ROI size decreases sensitivity to spatial variation.

Fig 5.

The average relative differences between SNR_mult and SNR_noRF (|SNR_noRF−SNR_mult|/SNR_mult) as a function of SENSE acceleration factor (R) in the phantom study. The average and SD (error bars) are determined among voxels within the center area on the image (rectangle shown in Fig 2a). The horizontal dashed line shows a relative difference level of 10%. a) shows data acquired with an RF excitation flip angle (FA) of 20°, while b) were acquired with a FA of 8°.

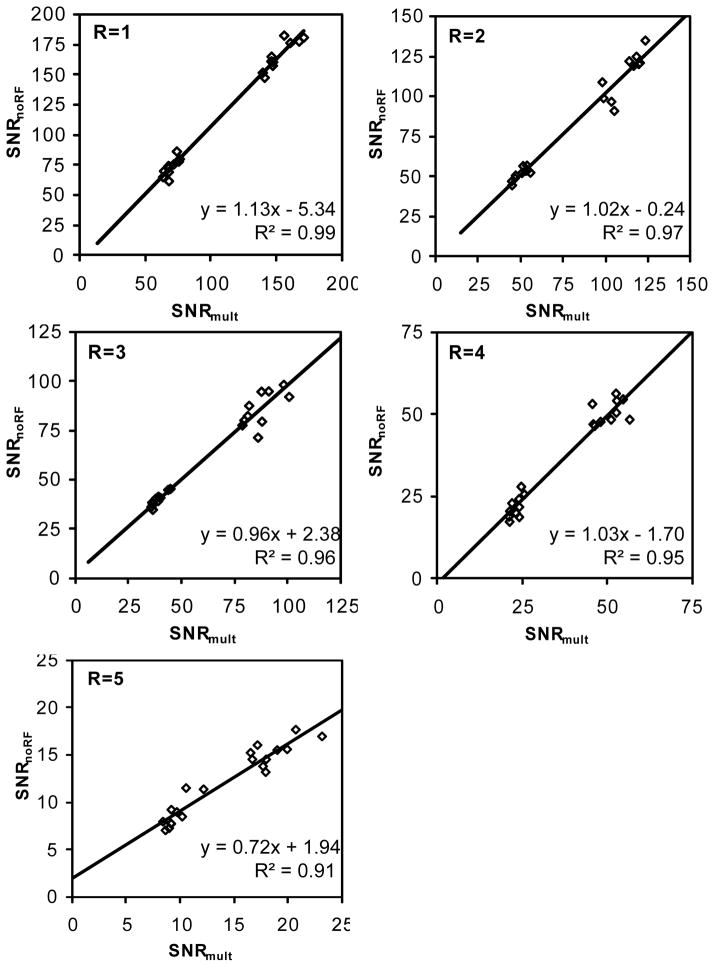
Linear regressions demonstrate a high correlation between SNR_noRF and SNR_mult (Fig 6). For each SENSE acceleration factor, SNR values of five selected locations from two different RF excitation angles and two ROI sizes are combined. These dots cluster into two separate SNR ranges on the plots because two different RF excitation angles (8° and 20°) were used for image acquisition. R² is above 0.93 for all SENSE acceleration factors. The slopes in the linear regression function with SENSE acceleration factors ranging from 1 to 4 are close to 1 (1.13, 1.02, 0.96, and 1.03 for R=1, 2, 3, and 4, respectively), and the intercepts are small. The linear regression reflects that SNR_noRF has negligible systematic bias compared to SNR_mult. However, with a SENSE acceleration factor of 5, the slope is 0.72, which indicate that SNR_noRF may underestimate the “true” SNR at higher acceleration factors. The average g-factors (Table 1) that are calculated based on SNR_noRF agree well with those generated by the MRI system. The average g-factors are indicators of noise inhomogeneity over the image, and the SD of g-factors reflect that the g-factors are spatially varying.

Fig 6.

Scatter plot of SNR_mult vs. SNR_noRF measured in the phantom study at different SENSE acceleration factors. SNR_mult and SNR_noRF were measured in five pixels within the phantom (Fig 2b). The least squares fit of linear functions and the corresponding R² are shown on the scatter plot. Each plot has its axis scales adjusted to SNR ranges at individual SENSE acceleration factors.

Table 1.

Comparison of g-factors obtained by coil sensitivity profile and SNR_noRF. All the g-maps were from data acquired with an RF excitation angle of 20°. For SNR_noRF, ROI size of 10×10 was used to calculate the g-factor. The average and standard deviation were measured within the center area of 60×54 pixels in the g-map.

SENSE acceleration factor	Coil Sensitivity	no RF
R = 2	1.06±0.08	1.04±0.12
R = 3	1.21±0.15	1.14±0.17
R = 4	1.90±0.43	1.64±0.25
R = 5	4.57±1.61	4.78±1.08

In Vivo Studies

The acquisition of the 3D volumetric noise image was completed in 30s only, while no ECG triggering, breath-holds, or navigators for respiratory motion suppression were needed. Representative anatomical and noise images, acquired with a SENSE factor of 2, and the corresponding SNR map are shown in Fig 7. Noise amplification (Fig 7b) is observed in the center of the body and in cranial direction consistent with regions with reduced coil sensitivity. In this representative example, the ROI localized in the left ventricular myocardium is in an area with an increased noise level (Fig 7, solid arrow). Conversely, the ROI localized in posterior skeletal muscle represents an area closer to the surface coil with a reduced noise level (Fig 7, dashed arrow). Quantitative measurements show that the signal of myocardium is significantly higher than that of skeletal muscle (for R=1: 161.3±30.6 vs.121.7±25.5, p < 0.05; for R =2: 165.9±35.2 vs. 117.1±16.4, p < 0.05), but simultaneously, the SNR of myocardium is significantly lower than that of skeletal muscle (for R=1: 12.3±2.5 vs. 15.4±3.8, p < 0.05; for R=2: 17.0±3.8 vs. 22.6±4.8, p < 0.05). Statistical tests also show that the SNR ratio is significantly smaller than the signal ratio (for R=1: 0.81±0.11 vs. 1.34±0.20, p<0.05; for R = 2: 0.75±0.10 vs. 1.42±0.18, p<0.05; both are SNR ratio vs. signal ratio).

Fig 7.

One slice of anatomical (a) and noise (b) image from the representative in vivo 3D volumetric coronary MRA, which was acquired with a SENSE acceleration factor of 2. The myocardium ROI (solid arrow) and skeletal muscle ROI (dashed arrow) are located at identical position on the anatomical and noise image. The SNR map (c) of the slice was generated using a moving ROI of 10×10 for illustration only. The minimal and maximal intensities in each window level are labeled under the corresponding image.

DISCUSSION

In this work, we have described a fast and easy-to-use method for quantifying SNR on coronary MRA images acquired with SENSE acceleration. This fast SNR_noRF method has been characterized and validated in phantom studies in comparison to a reference standard method SNR_mult. Good agreement of measured noise statistics and SNR behavior between the two methods was observed both qualitatively and quantitatively. The capability of SNR_noRF in measuring spatially dependent SNR was also demonstrated with in vivo studies.

The SNR_noRF method consists of a noise image that is acquired without RF pulses and magnetic field gradients. This is enabled by the linearity of parallel imaging reconstruction methods. As a result, the reconstruction process can be regarded as an operator that acts on both signal and noise separately (15). A noise image acquired with SNR_noRF offers several remarkable advantages when compared to a noise image that is obtained through the acquisition of serial identical anatomical images. First, the noise scan can be acquired orders of magnitude faster, which makes it perfectly well suited for lengthy volumetric coronary MRA scans. In practice, a noise scan can be completed within 30s for a 3D coronary MRA scan that takes 10 minutes to acquire. In the current implementation, one order of magnitude faster scan duration was achieved by removing most of the magnetization preparation pulses and the waiting period between the acquisition windows. However, during each TR, only the time for signal sampling is theoretically required to fill the noise k-space. This suggests that the 30s noise scan may be further abbreviated to 4s only. Secondly, without MR signal from the object, the noise images are free from artifacts induced by motion or physiological fluctuation. This important feature permits SNR_noRF to be computed for quantitative cardiac and time resolved contrast enhanced imaging, which cannot easily be performed using the multiple acquisitions method. The SNR for each repetition of the anatomical scan is determined by the signal measured in that repetition and the noise extracted from the noise scan. Should the anatomical scan require breath holding as a mechanism to suppress respiratory motion artifacts, the breath-hold duration does not have to be prolonged by the acquisition of the noise scan since it may be acquired during free breathing as long as the coil loading remains similar. Moreover, the SNR_mult method may be adversely affected by misregistration originating from object motion during the time course of data acquisition. This can be avoided with the SNR_noRF technique since a noise image is no longer contaminated by motion artifacts. In addition, the noise acquisition comes at no extra costs such as preparatory steps, extra setup time or offline processing. Finally, measurement of contrast-to-noise ratio (CNR) is based on local signal and noise measurements, and therefore can be obtained conveniently in the same manner as SNR_noRF. All these favorable properties may make the SNR_noRF method useful to be adopted in routine clinical scanning where quantitative analyses or systematic protocol optimization steps, and quantitative end-points related to image quality are essential.

An assumption underlying SNR_noRF is that all pixels in the user selected ROI have the same statistical noise distribution. SENSE reconstruction leads to inhomogeneous noise across the image. Since SNR_noRF is a ROI based measurement, its sensitivity to spatial variations is reduced when compared to SNR_mult. However, the noise statistics change slowly as a function of the location and can be considered regionally homogeneous as long as the g-factor remains low. In our phantom study, mean g-factors were lower than 2 and their standard deviation were less than 0.5 as long as the SENSE acceleration factor remained below 5 (see Table 1) with the current coil setup. For these moderate acceleration factors, the average relative deviations of SNR_noRF from SNR_mult are below 10.1% (see Fig 5). However, when the SENSE acceleration factor is 5, more coherent geometrical structures of noise amplification were observed. These might be responsible for the relatively sharp increase in relative SNR deviations for higher R values, especially if larger ROIs are used. In practice, adequate SENSE acceleration factors are usually chosen which are well supported by the coil arrangement. A g-factor beyond 2 is most commonly avoided since severe image degradation due to incomplete SENSE unfolding may occur. Therefore, over a reasonable range of g-factors and SENSE acceleration factors, the SNR_noRF method is reliable and fast for the quantification of SNR from homogeneous regions.

The ROI position and size should also be considered to ensure that the noise distribution in the ROI is sufficiently homogeneous. ROI positions in areas of fold over, or other kinds of artifacts on the anatomical image should be avoided. In practice, the ROI size is also limited by the homogeneity of the target area on the anatomical image and the noise statistics at that same location. In homogeneous regions, larger ROI sizes contribute to measurement precision, because the error in N_noRF is proportional to $1/\sqrt{n_{\mathit{ROI}}}$, where n_ROI is the number of independent pixels in the ROI. With SENSE acceleration factors 1 to 4, noise amplification and local variation are moderate. Thus enlarging ROI and including more samples contribute to reduce the relative error of SNR_noRF relative to the SNR_mult method. Our studies have demonstrated that the SNR_noRF method performed consistently well over a range of SNR levels.

In general, all previous knowledge about ROI based SNR measurement can be readily applied with the SNR_noRF method. For example, the magnitude bias correction can be applied to reduce the overall error of the signal estimation at low SNR (28).

Our measurements in vivo confirm that SNR_noRF is well-suited to measure spatially dependent SNR on MR images acquired with SENSE. The relative signals obtained in our study show that the myocardium has ~30–40% higher signal intensity than skeletal muscle. These results agree well with values in normal subjects in the literature (29–31) and may be attributable to shorter T2 that has been reported of chest muscle. However, the noise power in the myocardium which is located more distant from the signal receive surface coils is elevated compared to the noise in the skeletal muscle which is much closer to the coils (Fig 7). Therefore, despite the higher signal intensity of myocardium, the SNR of myocardium is reduced when compared to skeletal muscle. One may notice that SNR obtained with a SENSE acceleration factor of 2 is higher than that with factor of 1 for both cardiac and skeletal muscles. As previously reported, this is attributable to a longer TR, a lower receiver bandwidth and an improved RF transmit to receive duty cycle used in the sequence with a SENSE acceleration factor of 2 (26,32).

In the current study, experiments were performed with a specific coil, pulse sequence and parallel imaging technique. However, by compacting the reconstruction processes into a “black box” as available on most commercial MRI systems, the SNR_noRF method is expected to be applicable with other coils, signal acquisition techniques, k-space sampling schemes or trajectories, image reconstruction methods, and linear processing associated with coronary MRA. Therefore, the combination with balanced steady state free precession (bSSFP) (12) or spin echo pulse sequences (33) seems straightforward but remains to be explored. For parallel imaging approaches that rely on calibrating k-space lines that are acquired along with the normal image acquisition, such as generalized autocalibrating partially parallel acquisitions (GRAPPA) (8) and modified SENSE (34) reconstruction, the current method may not directly be applied and modifications of the reconstruction algorithm may be needed. However, if the “black-box” contains any nonlinear filtering, which may violate the condition of identical reconstruction for both the anatomical and the noise image, the proposed technique should not be used.

In conclusion, the SNR_noRF method demonstrated here is a practical and easy-to-use method to quantify SNR on coronary MRA when parallel imaging is employed. It allows SNR measurement in any user specified ROI on the image with very little extra cost in scanning time and no extra off-line image processing or analysis is required. The proposed method is also not jeopardized by misregistration in contrast to those approaches that depend on repeated image acquisitions. One limitation of SNR_noRF, like any other ROI based measurement, is its reduced sensitivity to spatial variation of noise when compared to the gold standard SNR_mult. SNR_noRF quantification may not be well-suited for high acceleration factors and non-linear filters during reconstruction or post processing. In general, the proposed methodology will provide a useful tool for objective and quantitative evaluation of coronary MRA acquired with different pulse sequences, MRI platforms, coil arrays, and reconstruction methods and may also find applications outside of coronary imaging.