Multi-scale lung modeling

Abstract

Multi-scale modeling of biological systems has recently become fashionable due to the growing power of digital computers as well as to the growing realization that integrative systems behavior is as important to life as is the genome. While it is true that the behavior of a living organism must ultimately be traceable to all its components and their myriad interactions, attempting to codify this in its entirety in a model misses the insights gained from understanding how collections of system components at one level of scale conspire to produce qualitatively different behavior at higher levels. The essence of multi-scale modeling thus lies not in the inclusion of every conceivable biological detail, but rather in the judicious selection of emergent phenomena appropriate to the level of scale being modeled. These principles are exemplified in recent computational models of the lung. Airways responsiveness, for example, is an organ-level manifestation of events that begin at the molecular level within airway smooth muscle cells, yet it is not necessary to invoke all these molecular events to accurately describe the contraction dynamics of a cell, nor is it necessary to invoke all phenomena observable at the level of the cell to account for the changes in overall lung function that occur following methacholine challenge. Similarly, the regulation of pulmonary vascular tone has complex origins within the individual smooth muscle cells that line the blood vessels but, again, many of the fine details of cell behavior average out at the level of the organ to produce an effect on pulmonary vascular pressure that can be described in much simpler terms. The art of multi-scale lung modeling thus reduces not to being limitlessly inclusive, but rather to knowing what biological details to leave out.

when a liter of gas is enclosed within a rigid container at a certain temperature, it exerts a certain pressure. In principle, one could calculate how pressure varies with volume by modeling the individual motions of each gas molecule inside the container, together with its collisions with the other gas molecules and with the walls of the container. Of course, the ludicrousness of such an undertaking, even if we had computers capable of doing it, should be immediately apparent to anyone who has gone through the relatively straightforward but highly enlightening exercise of deriving the perfect gas law using the concept of average momentum transfer. Modeling the pressure-volume behavior of a gas in terms of its individual components is thus not only impractical, it misses the crucial insights gained from an understanding of how the behavior of its microscopic constituents conspire to produce behavior at the macroscopic level. Importantly, the macroscopic behavior of a liter of gas bears no qualitative behavior whatsoever to the behavior of any of its molecular constituents. In fact, the macroscopic behavior is only apparent when the components are sufficiently numerous as to act as an ensemble. Accordingly, we say that the macroscopic behavior “emerges” in a way that can only be understood by considering the group dynamics of the constituents. The perfect gas law is thus an emergent property of a system consisting of a large number of independent molecules confined to a container.

The above simple example illustrates the principle challenge in multi-scale modeling. What are the important properties of a complex system that emerge from the ensemble behavior of its constituents at one level of scale and which need to be carried forward to higher levels, and what lower-level properties effectively average out and can be safely ignored? In the case of a perfect gas, we can answer these questions precisely. In the case of biological systems, which are vastly more complicated, answering such questions remains the principle challenge to our understanding of how these systems work. Actually, it may not be possible to formalize in a general way the process of moving between different levels of scale when modeling complex biological systems; each situation may have to be considered on its own merits. Nevertheless, we believe that seeing how multi-scale modeling applies in one area of biology may be useful for generalizing the process to other areas.

In the present review, we examine how multi-scale computational modeling has been applied to two important aspects of lung function. First we consider the phenomenon known as bronchoconstriction, or narrowing of the pulmonary airways, which in excess is a hallmark feature of asthma. Here, multi-scale modeling has proven crucial to our current understanding of how events that begin at the molecular level eventually result in global loss of lung mechanical function. Second, we examine multi-scale models of the pulmonary circulation that have led to a deep understanding of the way in which the distributed structure of the pulmonary vasculature determines much of overall lung physiology. In both cases, at each level of scale, an underlying consideration is always the question of which biological details have to be included in the model and which can be left out.

MODELING BRONCHOCONSTRICTION

Two of the most influential molecules in the lung, from the point of view of its day-to-day macroscopic function, are actin and myosin found in airway and vascular smooth muscle. These molecules interact to provide the mechanism by which smooth muscle contracts. Although still of unclear teleological benefit (20), there can be no doubt of the importance of airway smooth muscle (ASM) contraction; bronchoconstriction is the seminal event behind an acute attack of asthma (2). The pulmonary vascular smooth muscle is even more important to the lung, as it provides the primary dynamic control for matching perfusion to ventilation (50).

There has been a great deal of interest in recent years in understanding how the functional unit of ASM contraction, the cross-bridge cycle, translates into narrowing of the pulmonary airways. This is a multi-scale problem that has its genesis at a length scale of nanometers and a time scale of milliseconds, yet manifests in the lives of human beings at length scales of millimeters to centimeters and times scales of anything from a few seconds to years. A key question, then, is which details of cross-bridge cycling propagate up to higher levels of scale and are thus required for an accurate quantitative description of bronchoconstriction at the level of the whole lung.

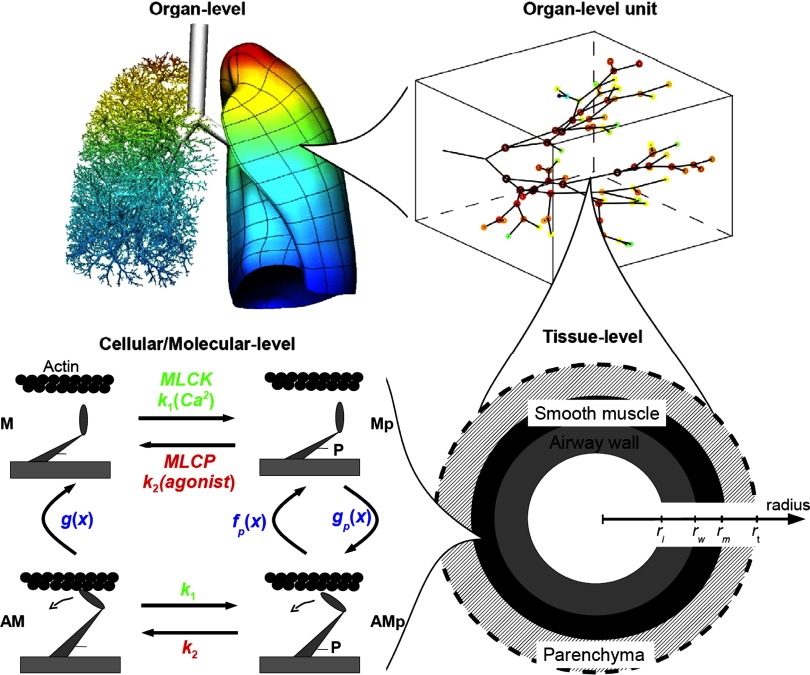
ASM cross-bridge cycling involves a four-state cycle of interactions between actin, myosin, and the phosphorylation enzymes that mediate the energy required for contraction (2, 21; Fig. ). Furthermore, the probabilities of attachment between myosin cross-bridge heads and their actin binding sites are affected by whether the actin and myosin fibers are able to move relative to each other, so ASM contraction affects the very processes that give rise to it in the first place. This illustrates another very important principle in multi-scale systems; although we usually think of emergence as occurring in the direction of increasing scale, in fact it can operate in the reverse direction. In this case, an ensemble of cycling cross bridges leads to emergence at a higher level of scale by causing bulk muscle shortening, but this then feeds back to the lower level of scale to influence cross-bridge binding itself. Such bidirectionality of influence between scales is actually characteristic of multi-scale systems and can lead to richly complex dynamic behavior.

The dynamic effects described above have been modeled for ASM using an adaptation of the Huxley equation that was originally developed for skeletal muscle. Such modeling predicts complex dynamic stress-strain behavior for activated ASM that includes amplitude-dependent loop widths and a peak steady-state stress that is virtually independent of strain amplitude (21, 41). While this can account for key features in the force-length data that have been observed in strips of activated trachealis muscle, it does so on the assumption that the actin and myosin fibers are perfectly aligned with the direction of strain and that the forces generated by the cross bridges are transmitted immediately and completely across the entire muscle tissue. Neither assumption is entirely valid because strips of ASM contain substantial amounts of passive connective tissue, and the contractile fibers themselves are arranged in a somewhat haphazard manner in contradistinction to the orderly sarcomeres of skeletal muscle. Indeed, the steady-state force-length loops of activated ASM can be equally well mimicked using a force generator having a single-valued hyperbolic force-velocity relationship connected in series with a nonlinear spring (7).

This raises the question as to whether the strain-rate dependence of cross-bridge attachment needs to be included at all in a more macroscopic description of the ASM strip. It turns out, however, that a complete description of the transient force-length behavior of activated ASM requires both connective tissue rheology as well as the influence of strain rate on cross-bridge kinetics (5). Even so, these two phenomena do not have to be modeled at the molecular level to accurately reproduce macroscopic behavior. Connective tissue rheology, for example, is well accounted for empirically in terms of spring-and-dashpot constructs (22). Importantly, the individual springs and dashpots do not correspond to anything in particular at the molecular level. Obviously, it is ultimately the interactions between molecules that produce the observed passive viscoelastic behavior, but the precise nature of these interactions remains a matter of debate (3, 4, 42, 49). Similarly, the effects of strain rate on cross-bridge attachment kinetics can be well accounted for using a simple empirical model based on first-order ordinary differential equations (5) instead of the structurally motivated but much more complicated partial differential equation of the type originally proposed by Huxley (33).

Thus, while the effects of cross-bridge detachment due to strain rate are clearly apparent at the level of the ASM strip, the complex dynamics of each of the many cross bridges that cycle throughout the strip average out in a way that causes a simpler overall behavior to emerge. Likewise, the genesis of passive viscoelastic behavior at the molecular level is presumably extremely complex, involving many different types of interactions between many different players, yet at the level of the ASM strip it can be modeled with great accuracy in terms of empirical elastic and resistive elements connected together appropriately. This is not to say, of course, that one can simply forget about everything at the level of molecules when modeling the ASM strip. On the contrary, the molecular level interactions are crucial for determining what behavior emerges at the tissue level, but it is this emergent behavior that should be included in the tissue level model rather than the individual behaviors of all the molecules. In other words, the tissue level model should be informed by what happens at the molecular level rather than including it specifically.

This process of emergence continues up to higher levels of scale in the lung. For example, one might be tempted to think that the empirical rheological and contractile properties identified as necessary for modeling the ASM strip should be carried on up to the level of the airway, the latter modeled in two dimensions as a circle of ASM tissue surrounding an annulus embedded in outwardly tethering alveolar parenchyma (Fig. 1). Experiments show this to be equivocal, however. For example, ascribing only a hyperbolic force-velocity relationship to the ASM in such a model leads to accurate predictions of the experimentally observed effects of tidal volume and transpulmonary pressure on the dynamics of bronchoconstriction in animal models (8), with almost no evidence of the need to invoke strain-rate dependence of cross-bridge kinetics. There is a suggestion that such dependence may become apparent following large deep inflations of the lung (6), but apart from that the complex dynamics of ASM contraction observed at the tissue level seem to manifest in somewhat simpler form at the level of the entire lung.

Fig. 1.

Schematic representation of the key levels of scale involved in modeling the mechanical consequences of bronchoconstriction from the level of the molecule up to the whole organ. [Reproduced with permission (44)].

Even at the level of the single airway, experimental data seem to reflect only relatively simple ASM behavior (34). This presumably reflects the fact that, again, some of the dynamic details observable at the level of the ASM strip average out in a way that yields apparently simpler behavior at higher levels of scale. Indeed, at the level of the whole organ, the dynamics of bronchoconstriction can be modeled quite well in terms of the narrowing of a small number of airways leading into their respective elastic compartments (9), although what is observed reflects the net effect of topographic heterogeneities throughout the lung (25, 35, 52), which may be due in part to the distribution of contractile agonist and its receptor binding (1). It is important to remember, however, that the level of detail required in a computational model is dictated, above all, by the nature of the experimental data it is designed to explain. Although data related to the dynamics of lung mechanical function during bronchoconstriction seem to require relatively simple models, various imaging modalities have shown that severe regional heterogeneities develop throughout the lung as bronchoconstriction proceeds. A particularly striking example is the model of Venegas et al. (54) showing that bidirectional influences between the level of a single airway and the entire lung can explain the patchy ventilation defects observed by positron emission tomography. Of course, the most complete possible model of bronchoconstriction would have to include events taking place at all levels of scale (44; Fig. 1), but the most important insights gained from such a model arise from the way in which behavior at one scale can be seen to emerge from that at other levels, both lower and higher.

MODELING THE PULMONARY CIRCULATION

Unlike the airways, in which contraction of the smooth muscle is generally considered an abnormality, active regulation of tone in the pulmonary vascular smooth muscle is an important mechanism for effective gas exchange function in the healthy lung. Active pulmonary vascular smooth muscle (PVSM) contraction/dilation acts to divert flow from/to regions of low/high partial pressure of oxygen, hence contributing to the matching of ventilation and perfusion to maintain adequate gas exchange. It could therefore be argued that understanding the balance of forces acting over multiple length and time scales to determine the extent of SM contraction or relaxation is even more important in the pulmonary vasculature than it is in the airways. While computational models to date have not considered the dynamics of this system, ultimately this will be essential for any integrative theoretical model that aims to explain experimental observations. Again, as in the example of modeling bronchoconstriction, judicious choices must be made about model scale and simplifying model assumptions.

A complete model for the pulmonary circulation must ultimately include active as well as passive processes. Here “complete” does not mean the simultaneous inclusion of each physical structure or biophysical process in detail; instead it means that these processes must each be accounted for and their importance understood with respect to model predictions and experimental interpretation. “Passive” here refers to the structural components of the lung (the lungs, lobes, and vascular branching geometry) that contribute baseline tissue elasticity and vascular resistance, as well as the fluid dynamic properties of blood, and the forces of breathing. As in the bronchial airways, the pulmonary blood vessels are suspended within a deforming tissue matrix that transmits tidally varying forces to the vessel wall during breathing. These tethering forces act differently on the large and small blood vessels (58). The radius of a blood vessel is partly determined by the balance of these passive tethering forces as well as the internal blood pressure, but importantly it is also determined by the SM tone of the vessel that is mediated by vasoconstrictive and vasodilatative control mechanisms, the most apparent of which are the “myogenic response” (45) and shear stress acting on the endothelium (29). The myogenic response is characterized by the local contraction of vascular SM in response to increased transmural pressure or local relaxation in response to decreased transmural pressure. Griffith (29) noted that the myogenic response could be considered as “an inherently unstable positive feedback mechanism;” however, the concomitant increase in wall shear stress during constriction counteracts the myogenic response, providing system stability. The mechanosensing of changes in shear stress by the endothelial cytoskeleton, elegantly reviewed by Griffith (29), leads to NO production and thus vasodilatation. Shear stress is dependent on vessel diameter, blood flow rate, and blood viscosity, which means that the determination of shear stress in a computational model involves solution of a nonlinear dynamic system. Hence, the mechanosensing mechanisms that initiate the myogenic response and NO production provide a second coupled non-linear system to consider in modeling.

“Active” components abound in the pulmonary circulation, such as shear stress, which has already been described, and hypoxic vasoconstriction in small pulmonary arteries acting to direct blood flow away from poorly ventilated lung regions (30). The commonality between these active mechanisms is that they both involve signaling to the PVSM, which constricts or dilates in response. These active mechanisms coexist in a fascinating dynamic system that to date has not been encapsulated in a descriptive and predictive theoretical model, but would be a well suited area for a multi-scale analysis. Several theoretical models already exist to describe NO transport and production at the cellular level, as well as at the level of a single arteriole or capillary (see Ref. 53 for a review of this type of model). The effect of hypoxic vasoconstriction on pulmonary function has also been modeled using simple representations of the whole lung (11, 39), without detail at the cellular or single vessel level. The second type of model quickly becomes limited in its predictive capability; the first type of model is important for detailed analysis at the smallest scales and lends itself to integration into a larger scale model to examine emergence of function. A challenge is to determine what the fundamental behaviors at the cellular level are that should be carried forward to the next spatial scale—and a rigorous methodology for achieving this—to create a tractable but insightful model. Incorporating existing and new models of each of the active and passive components of perfusion into a meaningful description of the pulmonary circulation is a challenge. However, a multi-scale model that appropriately describes each process by carefully integrating experimental measurements and observations is the only way to make sense of the dynamic interactions in this system. “Dynamic” here refers to phasic breathing, ventilation distribution (and hence alveolar partial pressures of oxygen) and pulsatile cardiac output at the organ scale, and the dynamic equilibrium of the active components at the cellular and vessel wall scales; these mechanisms interact to determine how the distribution of perfusion changes over short and long time scales in response to, for example, a deep breath or a sudden increase in cardiac output.

Modeling the passive transport of blood in the lung is a multi-scale problem in itself. Blood is a non-Newtonian fluid, yet it is often approximated as Newtonian in models of blood flow in “large” (pre-capillary) vessels. A Newtonian fluid has viscosity that is independent of its shear rate. Because blood comprises primarily a mixture of plasma and red blood cells, its viscosity does depend on shear rate. However, because the aggregation of red blood cells that give blood this property only form at relatively low velocities or within very small vessels, the approximation of blood in large vessels with high flow as Newtonian is appropriate. This approximation allows blood flow to be studied using classic fluid dynamics analysis, either solving the general 3-D Navier-Stokes and continuity equations in small domains (19, 38) or 1-D equations in more extensive domains (13, 15, 16, 46, 48), as well as by coupling 1-D and 3-D approaches (10). As the size of the blood vessel or the velocity decreases, it becomes less appropriate to treat the blood as Newtonian, and the two-phase behavior of the fluid must be considered. Any multi-scale model that seeks to study blood transit from the right to the left heart via the pulmonary circulation must account for this change in fluid properties. Fung and Sobin and colleagues (22–24, 47) in a series of papers, described blood flow at the microcirculatory level in their classic ‘sheet-flow’ model for the capillary bed. This model approximated flow in the pulmonary capillaries as occurring between parallel sheets connected by posts of connective tissue, providing an averaged description of blood flow. Alternative models that capture heterogeneity in capillary blood flow, but are computationally expensive, use 1-D “tubes” to represent capillary vessels (17, 32). The two-phase nature of blood flow in these models is accounted for via an empirically derived apparent viscosity that is dependent on blood hematocrit.

A model should only be as complex as is necessary, which essentially means it should be as simple as possible but not simpler, to paraphrase a famous quote from Einstein. Unfortunately, if the motivation is to study the factors that contribute to the distribution of blood in the lung, then even the simplest computational models have to be quite complex. Experimental studies have demonstrated both significant heterogeneity in blood flow within iso-gravitational planes (e.g., Refs. 27, 28) and multiple (potentially compound) effects of gravity (31, 43, 55, 56). There is still uncertainty and debate about the relative importance of gravity compared with mechanisms that are nongravitational in origin and presumably introduce heterogeneity. A recent Point:Counterpoint debate on this can be found in Ref. 26. The lack of a single multi-scale model that integrates an anatomically based structure, tissue tethering forces, and the effect of gravity on blood flow has hampered modeling attempts to contribute meaningfully to this debate. Theoretical models have long been important tools in pulmonary physiology for conceptualizing and explaining function in an organ that is notoriously difficult to “pull apart” and measure. However, these models have typically not been of the type to give rise to emergent behavior via interactions over multiple spatial scales.

The most prevalent model for explaining the distribution of perfusion in the lung (West's zonal model) considers only a single scale: the microcirculation. This model considers the balance of pressures acting on the pulmonary capillary, but by its nature does not include “larger scale” effects, such as extra-alveolar vessel resistance. While the zonal model is an important concept for the action of gravity at the microcirculatory level, it cannot explain heterogeneity within isogravitational planes that has been measured in microsphere and imaging studies, nor can it explain the incomplete reversal of flow gradient with reversal of posture. This does not suggest that a concept that is as important as the zonal model should be discarded, but instead we should ask whether physiologically consistent behavior emerges when the zonal model is integrated into a more extensive model that includes “larger scale” functions.

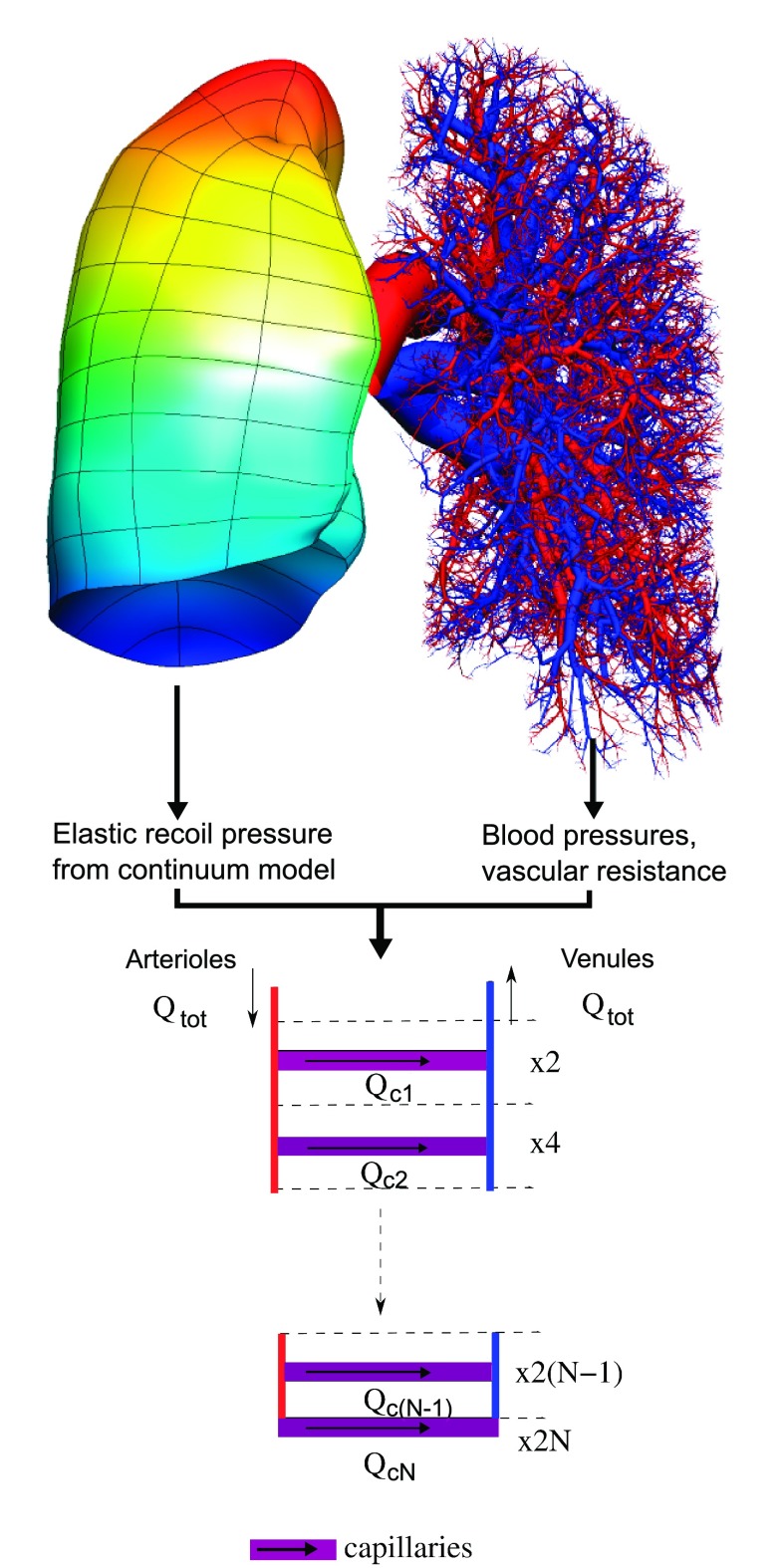
Burrowes and colleagues (12, 16) recently developed a model that is aimed at addressing this question. Large-scale effects are captured via heterogeneous (passive) vascular resistance within anatomically structured arterial and venous geometries (14), embedded within a continuum model for the parenchyma that deforms under its own weight (51). Mid-level “resistance” vessels in the pulmonary acinus are specifically included and are connected in series and parallel [in a ladderlike structure (18)] via capillaries described using the sheet-flow model. Scale-specific equations are used for the blood rheology. Components in this multi-scale model are illustrated schematically in Fig. 2. An advantage of this model is that the contribution of each component can be assessed independently of the others under completely artificial conditions that could not be replicated experimentally, e.g., tissue deformation under gravity, but with “weightless” blood, to isolate the “Slinky” effect (31). The model is also amenable to analysis at different scales, for comparison with relatively high-resolution (microsphere, SPECT, MRI) or low-resolution (scintillation counter) measurements. Coupling of each component into a single model gives rise to integrated function that is consistent with experiment (with respect to blood flow heterogeneity and gravitationally dependent perfusion gradients). The model predicts that each component makes an important and distinct contribution to the distribution of blood in the lung: tissue deformation is the primary cause of postural differences in perfusion gradients; vascular asymmetry is the primary cause of heterogeneity; and the microcirculation amplifies heterogeneity from the larger vessels due to the complex balance of forces at the microlevel. Some of these insights could be hinted at by using models that consider only a single component. For example, simulations of blood flow in a model of the arteries in isolation from the other model components had already suggested marked perfusion heterogeneity due to the vascular branching geometry (15). However, such a simple model cannot address whether this would continue to be significant in the presence of tissue deformation and when the balance of pressures within the microcirculation is altered.

Fig. 2.

Schematic illustration of the passive components of a multi-scale model of the pulmonary circulation, as presented by Burrowes and colleagues (12, 16). The arteries (red) and veins (blue) are distributed within a deforming model of the lung tissue (colored by pleural pressure for the right lung). These “large scale” components couple to the “microscale” at each precapillary artery and vein via elastic recoil and blood pressures. Q_tot is the total blood flow into an acinus, Q_cj is flow into the jth level capillary sheet, and the right hand side lists the number of sheets at each level of the ladder model. [Adapted with permission (18)].

Conclusions

The goal of a multi-scale model is to describe, in mechanistic terms, the important interactions that occur between subsystems operating at different spatial and/or temporal scales. This does not mean accounting for every known detail in the system being modeled; such an undertaking is usually impractical, but most importantly it provides little insight into how emergent behavior arises. Multi-scale modeling thus invariably requires that the mathematical equations governing the function of the model be simplified as much as possible through judicious assumptions that amount to elimination of unnecessary detail. Indeed, with the development of ever more complex models that span multiple spatial and temporal scales (44), the need for this type of model reduction becomes increasingly important. Advances in model complexity also lead to increased challenges in terms of model validation against experimental data. In fact, it is often the case that validation data are not available. There are many cases, however, in which multi-scale models serve as “virtual laboratories” themselves, allowing the consequences of specific hypotheses to be predicted with precision and then examined for physiological reasonableness.

Finally, we must stress that although we have focused on two application areas of multi-scale modeling in the lung in the present review, these are by no means the only cases worthy of mention. Multi-scale models have also been developed to describe, for example, the details of airflow throughout the airway tree (57), deposition of aerosols in the lung (1, 37), and the recruitment and derecruitment of airways in acute lung injury (36, 40). Multi-scale computational modeling has thus become central to the study of pulmonary physiology, and is clearly going to become increasingly important to the advancement of our understanding of the lung.

GRANTS

The authors acknowledge the financial support of the National Institutes of Health through NCRR-COBRE RR-15557, HL-76273, HL-75593, HL-87788, and HL-87789.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.