Emergent behavior of regional heterogeneity in the lung and its effects on respiratory impedance

Abstract

The ability to maintain adequate gas exchange depends on the relatively homogeneous distribution of inhaled gas throughout the lung. Structural alterations associated with many respiratory diseases may significantly depress this function during tidal breathing. These alterations frequently occur in a heterogeneous manner due to complex, emergent interactions among the many constitutive elements of the airways and parenchyma, resulting in unique signature changes in the mechanical impedance spectrum of the lungs and total respiratory system as measured by forced oscillations techniques (FOT). When such impedance spectra are characterized by appropriate inverse models, one may obtain functional insight into derangements in global respiratory mechanics. In this review, we provide an overview of the impact of structural heterogeneity with respect to dynamic lung function. Recent studies linking functional impedance measurements to the structural heterogeneity observed in acute lung injury, asthma, and chronic obstructive pulmonary disease are highlighted, as well as current approaches for the modeling and interpretation of impedance. Finally, we discuss the potential diagnostic role of FOT in the context of therapeutic interventions.

the lung consists of an asymmetrically branching airway tree embedded in a matrix of parenchymal tissue. For cyclic, tidal-like breathing, airflow to and from the gas-exchanging regions of the lung is governed by a distribution of mechanical time constants. These time constants arise from parallel and serial arrangements of effective airway and tissue resistances with tissue elastances (63, 69). Each airway behaves as a compliant tube with a longitudinal flow resistance and viscoelastic walls (78). The airway network eventually leads to alveoli embedded in viscoelastic tissues where gas exchange takes place. The structural arrangements of these numerous branching airways and viscoelastic tissues uniquely contribute to the overall mechanical function of the respiratory system.

The forced oscillation approach, in which time-varying flows of different frequencies are forced into the lungs at the airway opening, is a useful method for assessing the dynamic mechanical status of the respiratory system (24, 68). The complex ratio of the resulting driving pressure to delivered flow as a function of frequency is defined as the mechanical impedance. Using impedance terminology, one may theoretically characterize the oscillatory behavior for each individual element in the lung (i.e., the airway, the airway wall, or the alveolar tissues) by an effective real part that governs the energy loss, as well as an imaginary part representing energy storage (24, 64, 71). The mechanical impedance for the entire organ at a given frequency is thus determined by the parallel and serial arrangements of all these individual elements. The dynamic behavior of the lung is inherently nonlinear, especially for large volume perturbations (76, 77, 79); however, for the purposes of this paper, we will limit our analyses to small perturbations (i.e., tidal breathing or less) such that mechanical properties can be reasonably approximated by linear descriptions (71, 80).

The lung is exquisitely sensitive to small perturbations in its normally uniform function; that is, its capacity to maintain gas exchange. However, small structural alterations associated with many diseases may significantly depress this capability during tidal breathing. For example, the airway walls ordinarily have much lower effective compliance compared with overall lung compliance (63), such that insignificant portions of flow are lost to airway wall motion (30). However, under certain conditions, such as when downstream impedance becomes high due to peripheral lung disease, the unevenness of parallel time constants will create heterogeneous distribution of inhaled gas, and the airway walls will become an influential shunt pathway altering overall flow distribution (53, 56).

The motivation for measuring whole lung or whole respiratory system impedance is the notion that disease-based changes in specific structures (e.g., the airways or tissues) manifest themselves as unique signature changes when examined over a particular frequency range (56). These signatures may then provide insight into the primary causes for altered ventilation distribution. For example, the heterogeneous airway constriction observed in asthma not only increases total lung resistance, but also the dependence of resistance and elastance on frequency (48). Similarly, destruction of alveolar walls associated with emphysema or the accumulation of fluid in the air spaces with pneumonia or lung injury will alter regional tissue compliances, thus creating unique alterations in the imaginary part of impedance (22, 23, 47, 52, 53).

Under healthy conditions, tidal breathing results in relatively homogeneous distribution of the inhaled gas, even in the presence of asymmetries in anatomy and gravity. In striking contrast, most pathologies of the respiratory system manifest themselves as markedly heterogeneous alterations in structure. The mapping of such structural alterations to deviations in measured impedance spectra of the lungs is confounded by several factors. For example, the nonlinear elasticity of the airway wall can result in mechanical instabilities that allow an airway to transition rapidly from nearly opened to nearly closed (4). The implication of this is that airway constriction must occur heterogeneously, even if the lung is perfectly healthy (93, 95). In the acutely injured lung, alveoli that are derecuited at low lung volumes can spontaneously open when exposed to certain critical opening pressures (12, 60). How these critical opening pressures are distributed throughout the lung will influence its pressure-volume characteristic (91). Moreover, some lung diseases may impact both airways and tissues heterogeneously, making it difficult to determine the relative influences from impedance data alone (44, 46, 52).

This paper provides a detailed overview of many of these issues in the context of specific diseases. Our focus is to describe recent modeling and experimental techniques currently used to detect and quantify mechanical heterogeneity in the lung with respect to overall function. We first provide a general overview of mathematical modeling useful for interpreting impedance data during heterogeneous disease. We then provide a review of recent studies linking functional impedance measurements to heterogeneous lung structure for three common respiratory diseases: acute lung injury (ALI), asthma, and chronic obstructive pulmonary disease (COPD). Finally, we summarize likely future trends in this field as well as potential implications for therapy.

INVERSE MODELS AND INTERPRETATION OF IMPEDANCE

When measured over low frequencies (0.1–10 Hz), impedance can be a very sensitive, although not specific, indicator of pathology (64). A method often used to provide interpretations of the physiological alterations contributing to impedance is inverse model analysis, in which mechanical analogs of the respiratory system are proposed to characterize its dynamic oscillatory behavior (8, 13, 46, 51). These models generally consist of a limited number of lumped physical elements, ideally corresponding to precise physiological quantities such as airway resistance or tissue elastance (13, 43). These parameters are then estimated by fitting the model to impedance data using various least-squares approaches (19, 34, 43, 51), yielding functional insight into global respiratory mechanics.

Over the years, many inverse models have been developed to characterize the observed oscillatory behavior of the lungs and total respiratory system in several mammals, with emphasis on distinct physiological mechanisms: parenchymal viscoelasticity (65), serial and parallel time-constant heterogeneity (63, 69), and collateral ventilation (61). Until recently, the relative contribution of any of these mechanisms to the observed mechanical behavior of healthy or diseased lungs was largely speculative, as these lumped parameter representations were devoid of structural information or anatomic fidelity (8).

The development and use of alveolar capsules in the 1980s and 1990s allowed for the direct measurement of pressures across the airways and within the lung parenchyma (27). With this technique, it was observed that the frequency dependence of impedance in healthy mammalian lungs was due almost entirely to parenchymal viscoelasticity, as lung tissue resistance decreased near hyperbolically with increasing frequency, but airway resistance remained fairly constant (36, 40, 84). This behavior led to the development by Hantos et al. of what is now the most widely used model for characterizing oscillatory impedance: the so-called “constant-phase” model (37). This model consists of a single lumped airway compartment, with parameters representing Newtonian (i.e., frequency independent) airway resistance (R) and inertance (I), in series with a viscoelastic tissue compartment with parameters for tissue damping (G) and elastance (H). Its predicted mechanical impedance (Ẑ) as a function of frequency (ω) is given by:

$$\widehat{Z}(\omega )=R+j\omega I+\frac{G-jH}{{\omega }^{\alpha }}$$ (1)

where α = (2/π)tan⁻¹(H/G), and tissue hysteresivity, defined as the ratio of energy dissipation to energy storage (28), is η = G/H. This formulation has been validated by direct partitioning of the airway and tissue compartments with the alveolar capsule technique (27, 73) in normal dog lungs (73), and selectively affecting the airway impedance by using resident gases of different viscosity and density in rats (58, 72). A limitation of this model, however, is the assumption that impedance can be sufficiently described by serial compartments representing homogenous airways and tissues. Such an assumption may not always be valid, especially under pathological conditions for which heterogeneity results in additional frequency dependence in impedance that is not due to viscoelasticity alone (10, 46, 51, 58). For example during heterogeneous methacholine-induced bronchoconstriction, changing the physical properties of the resident gas (which ideally should only change airway resistance) also leads to artifactual increases in G and hence η (58, 72). This indicates that these viscoelastic tissue parameters can be influenced by parallel airway heterogeneity (10, 44). Nonetheless, the good overall fitting quality of the constant-phase model is preserved up to high degrees of bronchoconstriction (37, 55, 58, 72, 97), suggesting that even an extremely inhomogeneous lung structure can exhibit virtually homogeneous mechanical behavior. While the associated changes in some parameter values with higher levels of heterogeneous bronchoconstriction may obscure their corresponding physical interpretations, they nonetheless remain simple and useful indicators of developing inhomogeneity.

For certain patterns of heterogeneity, the above model can be modified for a more accurate description of mechanical behavior. For example, in asthma or COPD, a significant portion of oscillatory flow may be shunted into the central airway walls in the presence of high peripheral airway resistance (47, 57, 58). Thus the homogeneous airway compartment of Eq. 1 can be divided into two equal halves by an additional shunt airway compliance parameter to account for these nonrigid airway walls (48, 50, 75). To compensate for parallel heterogeneities in mechanical properties of those regions in communication with the airway opening, distributed inverse models based on Eq. 1 have been developed and applied to impedance data, allowing for a more accurate assessment of the regional mechanics associated with bronchoconstriction (44, 82, 96), emphysema (42, 74), acute lung injury (16, 46), and pneumonia (52). These topologies allow for stochastic variability in R or H, depending on whether one seeks to quantify airway or tissue heterogeneity, respectively. For example, if we seek to characterize heterogeneous bronchoconstriction, we may assume that a parallel distribution of airway resistances are sufficient to characterize impedance and can be approximated with a predefined probability density function, P(R), with lower and upper bounds R_min and R_max, respectively. The predicted impedance of such a model is given by:

$$\widehat{Z}(\omega )={\left[{\displaystyle \underset{R_{\min }}{\overset{R_{\max }}{\int }}\frac{P\left(R\right)}{R+j\omega I+\frac{G-jH}{{\omega }^{\alpha }}}\text{d}R}\right]}^{-1}$$ (2)

In contrast to the model described by Eq. 1 with four independent parameters, this model requires the estimation of five parameters (R_min, R_max, I, G, and H). Likewise, for pathologies associated with variations in tissue elastance between H_min and H_max, we may assume a similar topology whose predicted impedance becomes:

$$\widehat{Z}(\omega )={\left[{\displaystyle \underset{H_{\min }}{\overset{H_{\max }}{\int }}\frac{P\left(H\right)}{R+j\omega I+\frac{G-jH}{{\omega }^{\alpha }}}\text{d}H}\right]}^{-1}$$ (3)

Using the appropriate model, an estimate of effective airway resistance or tissue elastance can be obtained from the mean of the distribution function P, while the corresponding heterogeneity of the airways or tissues can be obtained from the standard deviation of P (51).

It should be noted that obtaining a model with the best fit statistically to any data set does not necessarily imply that all of the mechanisms contributing to frequency dependence in impedance have been accounted for, especially when the number of data points to be fit may be only slightly larger than the number of parameters in the model (51). It may be that many different physiological mechanisms contribute simultaneously to any observed global mechanical behavior (48). While increasing the complexity of a model to account for additional mechanisms may significantly improve the quality of fit, the resulting parameters may become unreliable with large confidence bounds (87, 96). Nonetheless, an appropriate comparison of various model fits can be useful in distinguishing which physiological mechanisms dominate a particular data set (44, 48, 50–52, 75).

The distributed models described by Eqs. 2 and 3 do not provide specific information on anatomy or structural alterations during chronic disease or acute physiological perturbations. However, they have the ability to quantify mechanical heterogeneity and characterize global dynamic lung function with a minimal number of physical parameters (51, 82). An ongoing challenge in the interpretation and validation of any candidate model of lung mechanics is the difficulty of obtaining reliable and simultaneous information on the structural alterations associated with heterogeneous pathology for comparison with model predication (9, 44, 45, 51). Nonetheless, recent studies combining functional lung imaging with impedance measurements demonstrate surprising concordance between heterogeneous structure and function (15, 44, 45, 85, 86).

ACUTE LUNG INJURY

Acute lung injury (ALI) and the more severe acute respiratory distress syndrome (ARDS) are complex pathological processes characterized by respiratory failure in the presence of airway closure and atelectasis, alveolar flooding, increased lung resistance, reduced lung compliance, and impairments in gas exchange (94). The mainstay of treatment, intubation and supportive positive pressure ventilation, may actually worsen existing lung injury through parenchymal overdistension from the maldistribution of tidal volume (volutrauma), as well as the shear stresses associated with cyclic, repetitive opening and closing of individual lung units (atelectrauma). The extremely heterogeneous interactions of these mechanical processes result in the release of inflammatory cytokines that further contribute to injury (biotrauma). Given that ALI/ARDS is associated with a 40% mortality rate (94), much emphasis has been on the improvement of existing ventilator protocols, specifically by adjusting positive end-expiratory pressure (PEEP) to maximize the recruited lung (3), and limiting tidal volume to minimize overdistension (5). However, the design of such protocols have been somewhat ad hoc, based on gas exchange indexes, which have a poor predictive value in terms of outcome (5), or on quasi-static pressure-volume curves representing aggregate static mechanical behavior of many different lung units (39). These approaches provide no insight into the heterogeneous mechanical derangements under dynamic conditions. Since ventilator-associated injury is due primarily to the maldistribution of ventilation arising from variations in regional mechanics throughout the lung (15, 29, 33), the ability to quantify mechanical heterogeneity under dynamic conditions may have potential for optimizing ventilatory parameters such as PEEP, tidal volume, or frequency (14).

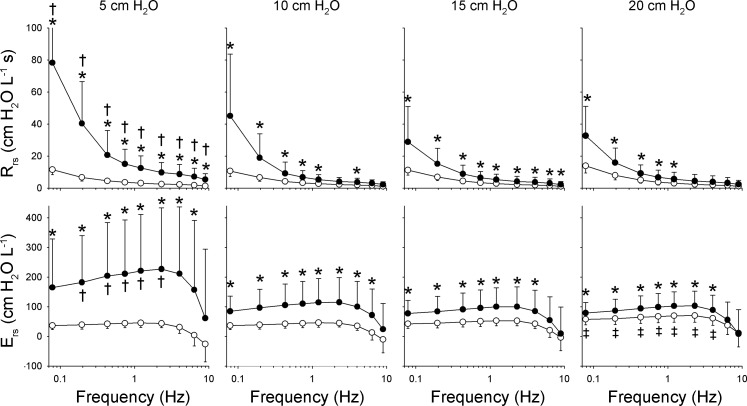
Recent studies, from the authors as well as other groups, have demonstrated a strong association between the heterogeneity of lung injury and the mechanical impedance spectrum of the total respiratory system, Z_rs (1, 2, 6, 7, 14–16, 22, 46, 51). An example of this is illustrated in Fig. 1, which shows a summary of such Z_rs spectra for 11 dogs at baseline and following lung injury with oleic acid during oscillations from 0.078 to 8.9 Hz and at mean airway pressures of 5, 10, 15, and 20 cmH₂O. The spectra are expressed as respiratory resistance R_rs = Re{Z_rs} and elastance E_rs = −ωIm{Z_rs}. While both the level and frequency dependence of R_rs increases following injury at all mean airway pressures, the greatest difference between baseline and postinjury R_rs occurs at 5 cmH₂O, and the minimal increase occurred at 15 cmH₂O. Such changes in the mechanical impedance spectra are consistent with progressive recruitment of lung units (56, 59). At 20 cmH₂O, further increases in postinjury R_rs and E_rs are consistent with strain stiffening of the parenchyma, an indicator of alveolar overdistension. These Z_rs data then qualitatively suggest that ventilation with mean airway pressures near 15 cmH₂O for this population of lung-injured animals would be optimal in terms of maximizing recruitment while minimizing overdistension.

Fig. 1.

Summary of respiratory resistance (R_rs) and elastance (E_rs) vs. frequency at baseline (○) and following lung injury (●) at 4 different mean airway pressures. Values are presented as means ± SD. *Significantly higher than baseline data at same frequency and airway pressure. †Significantly higher than corresponding data at 10, 15, and 20 cmH₂O at same condition and frequency. ‡Significantly higher than corresponding data at 5, 10, and 15 cmH₂O at same condition and frequency using analysis of variance and least significant difference criterion. [Modified from Kaczka et al. (46) with permission. Copyright Wolters Kluwer Health.]

Figure 2 summarizes derived parameters corresponding to effective tissue elastance as well as the tissue heterogeneity based on fits of Eq. 3 to the data of Fig. 1. At baseline, effective elastance was constant with mean airway pressures up to 15 cmH₂O, and then increased at 20 cmH₂O, reflecting increased lung stiffness. Baseline tissue heterogeneity demonstrated a tendency to decrease with increasing mean airway pressure, although there was a slight increase at 20 cmH₂O, suggesting that overdistension occurs in a somewhat heterogeneous manner. Following lung injury, the effective elastance and tissue heterogeneity increased compared with baseline, and both tended to decrease with increasing airway pressure in a parallel fashion, consistent with progressive recruitment of lung units with similar distributions of tissue elastances.

Fig. 2.

Summary of effective tissue elastance [i.e., mean of P(H) distribution function in Eq. 3] and tissue heterogeneity [SD of P(H) distribution function] for 11 dogs before (○) and after (●) lung injury *Significantly higher than baseline data at same airway pressure. †Significantly higher than corresponding data at same condition at 10, 15, and 20 cmH₂O. [Modified from Kaczka et al. (46) with permission. Copyright Wolters Kluwer Health.]

These data are consistent with the notion that the distribution of tissue elastances in the injured lung, as well as the degree of recruitment and overdistension, are dependent not only on the severity of injury, but also on degree of inflation (12, 60). As the measurement of Z_rs can be easily incorporated into existing ventilator platforms and clinical protocols (47, 49, 66, 67, 70), such techniques may have the potential to assist in the development of improved ventilator protocols in patients with ALI, with the goal of individualizing ventilator management to minimize the injurious processes of intratidal derecruitment and parenchymal overdistension for each patient.

ASTHMA

Asthma is a chronic disease characterized by hyperresponsiveness of airway smooth muscle and variable airflow obstruction. The amplified heterogeneous conditions during transient asthmatic exacerbations can have dire consequences on the ability to maintain gas exchange. This occurs because 1) some lung regions receive less than their typical portion of fresh gas with respect to their perfusion; and 2) airflow heterogeneities amplify lung impedance disproportionately at breathing frequencies (56, 59, 69). The latter means that one must expend greater energy to maintain adequate ventilation.

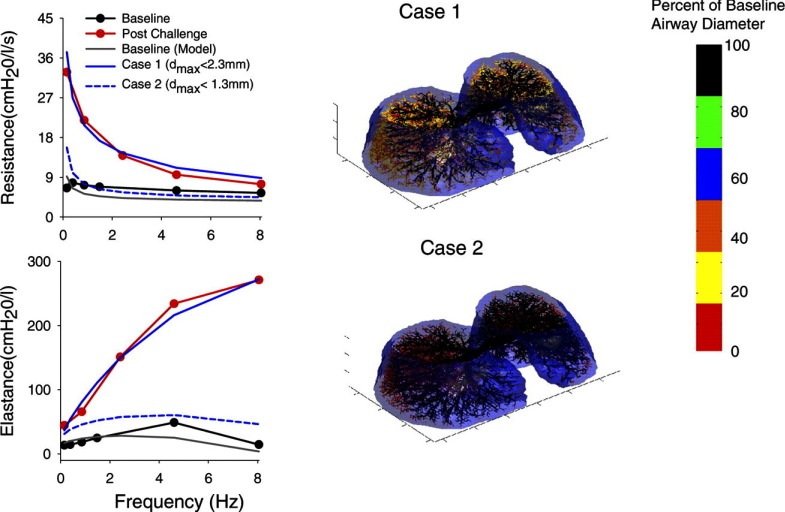
In the late 1990s, computational modeling of the mammalian lung evolved to permit the incorporation of viscoelastic tissues with airway trees of high anatomic fidelity (30, 31, 56, 57, 88). This allowed for the simulation of various patterns of heterogeneous airway constriction, as well as their effects on global lung impedance and ventilation distribution. These studies demonstrated that heterogeneous constriction, especially in small airways, produces dramatic increases in levels and the frequency dependence of total lung resistance (R_L) and elastance (E_L) near 0–2 Hz. In fact, while mean airway resistance might increase only a small amount for frequencies above 2 Hz, the increases in R_L and E_L at typical breathing frequencies greatly amplify the mechanical load against which tidal breathing occurs (59). Moreover, experimental measurements of R_L and E_L from 0.15 to 8.0 Hz in healthy and asthmatic subjects were highly consistent with these model predictions (48, 50). Subsequent airway tree models incorporating three-dimensional geometry (Fig. 3) demonstrated that heterogeneous small airway constriction was the major contributor to the observed changes in R_L and E_L during bronchoprovocation (85). During the early 2000s, various functional imaging techniques utilizing positron emission tomography (PET) and hyperpolarized MRI confirmed that induced constriction in healthy and asthmatic lungs occurs heterogeneously, resulting in clustered ventilation defects (89, 90, 92). While these imaging data suggested that near closure of larger bronchi was responsible for such clusters, computational modeling demonstrated that extensive small airway constriction was still essential to mimic the changes observed in measured lung impedance (17).

Fig. 3.

Left: lung resistance and elastance vs. frequency for an asthmatic subject at baseline (black circles) and following inhaled methacholine challenge (red circles). Baseline data are shown with prediction based on the 3-dimensional (3D), asymmetric 26-generation model of Tawhai et al. (83) (gray). Postchallenge data are shown with 2 different predictions from the model (blue lines), consistent with ventilation defects observed with PET imaging. Solid blue line (case 1) is model prediction when constrictions are confined to generations 14 and below (diameter < 2.3 mm), whereas dashed blue line (case 2) is model prediction with airway constrictions confined to generations 16 and below (diameter < 1.3 mm). Right: 3D surface rendering of the model airway tree superimposed inside the pleural surface for the 2 postchallenge conditions. Each airway segment of the model within the pleural surface is color coded (bar) to represent the degree of airway constriction as a percentage of maximum diameter (d_max). These data illustrate that constriction of small airways (i.e., with diameters between 1.3 and 2.3 mm) are required to mimic the observed changes in resistance and elastance during bronchoprovocation. [Modified from Tgavalekos et al. (85) with permission.]

These discrepancies were later reconciled by the modeling studies of Venegas, Winkler, and colleagues (93, 95), who demonstrated that small airways will constrict heterogeneously with clustered ventilation defects if a specific form of instability was built into the mechanics of the terminal airway system (4). These terminal airways are subjected to a nonlinear balance of forces between constricted smooth muscle and parenchymal tethering, such that during tidal breathing they will exist in one of two states: fully opened or nearly closed. Winkler and Venegas (95) imposed this mechanism on the airways of a symmetric tree, and stimulated constriction in a single airway during breathing. The result was a steady-state constriction pattern that was very spatially heterogeneous with clustered ventilation defects. Thus even a perfectly symmetric tree will converge on a heterogeneous pattern of ventilation if the constriction occurs during tidal breathing. This may at first seem counterintuitive. But when a single airway starts to constrict, the breathing dynamics in concert with a balance of forces will redistribute airflow asymmetrically and result in clustered defects. The symmetric airway pattern is broken and with each breath, areas not yet constricted receive a greater fraction of tidal volume and hence are exposed to more distending forces, while airways more constricted receive less tidal volume and are exposed to lower distending forces. This positive-feedback mechanism propagates ventilation defects to cluster in specific regions.

The above modeling approaches do not address the observation that many mild-to-moderate asthmatics exhibit ventilation defects in identical anatomic locations (20, 21, 38). An intriguing possibility is that airway remodeling due to longstanding inflammation is not homogeneously distributed throughout the tree, making certain airways more reactive than others, even if they are of similar size or of the same generation number. If such airways drive initial constrictions similar to the model of Winkler and Venegas (95), the resulting ventilation defects will always occur in the same locations. Thus asthma may be a localized disease and not a global organ defect, raising the possibility that targeted therapy to key airways may result in better patient outcomes (18). Unfortunately, some of these key airways may be <2 mm in diameter (85), which would make such an approach challenging at best. Nonetheless these phenomena, if confirmed, would offer a novel paradigm of what drives global functional deficiency in reactive airway disease and provide further motivation to aggressively treat early disease and potentially prevent these structural changes.

CHRONIC OBSTRUCTIVE PULMONARY DISEASE

COPD refers to intrinsic, irreversible airway obstruction (bronchitis), parenchymal tissue destruction (emphysema), or a combination of the two. Pulmonary function usually deteriorates in a slow and progressive manner. Chronic bronchitis is defined clinically as the presence of a chronic productive cough without a discernible cause for more than half the time over a period of two years. Emphysema, however, is characterized by a pathological enlargement of air spaces distal to terminal bronchioles with progressive destruction of the alveolar walls. There are many etiologies for emphysema (e.g., free radical damage via cigarette smoking, α₁-antitrypsin deficiency), but a common factor appears to be a reduction in activity of elastase inhibitors, resulting in heterogeneous destruction and disorganization of elastin fibers in the parenchyma (11). Macroscopically, such destruction emerges as an increase in overall lung compliance and reduced elastic recoil pressure for a given lung volume (81). This parenchymal destruction also may cause a loss of radial traction on the airways. This loss of airway tethering combined with the loss of elastic recoil pressure enhances the dynamic compression of the airways during expiration, often resulting in flow limitation that can severely compromise tidal breathing.

Studies on the peripheral lung in experimental emphysema have revealed heterogeneous changes in structure associated with functional inhomogeneity as assessed by its global dynamic behavior. Treatment of mice with porcine pancreatic elastase (PPE) increased both the mean size and the heterogeneity of alveolar size, and the fitting of impedance data by the distributed elastance model of Eq. 3 resulted in significantly larger values of mean elastance and a wider distribution in emphysema (40%) than that in control animals (32%) (42). Ito et al. (41) assessed the mechanical and structural properties of the lungs from tight skin (Tsk) mice and compared them to those of pallid mice (Pa) and their common background, the C57BL/6 mice. Tsk animals exhibited much larger alveolar sizes with a wider distribution and lower values of H_min and H_max compared with other groups. Whereas mean alveolar diameter was similar in the Pa and C57BL/6 mice, its variability was higher in the former; this, together with the reduced H_max, may indicate the early development of emphysema in the Pa mice attributable to lower serum α₁-antitrypsin concentrations (62).

However, a characteristic feature of these murine models of emphysema is the lack of impairment in airway function. For example, airway resistance is not significantly different in emphysematous mice compared with the control animals (35, 42). This suggests that parenchymal destruction does not decrease tethering forces critically. In contrast to the marked elevation in functional residual capacity, residual volume (RV) did not change in elastase-treated mice, which is also consistent with the unaltered airway function; however, the crackle sounds recorded during reinflation of the lungs from RV were distributed over a much wider range of transrespiratory pressures than in the control animals, which indicates an enhanced heterogeneity in the peripheral recruitment processes (35).

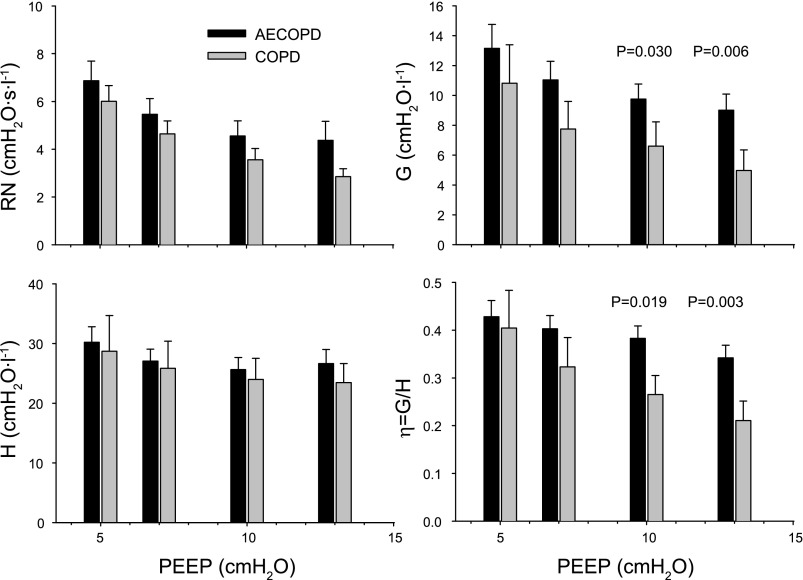
Low-frequency impedance measurements in intubated COPD patients unequivocally reveal elevated lung resistance along with enhanced frequency dependence in both resistance and elastance (25, 26, 47, 53). Although the mechanical heterogeneity associated with this disease and underlying the alterations in the impedance spectrum is very complex, even simple inverse modeling with an airway and constant-phase tissue compartment (Eq. 1) yields insight into basic phenomena. Lorx et al. (53) measured Z_rs in mechanically ventilated patients with earlier diagnosis of COPD and those requiring ventilatory support for acute exacerbation of the disease (AECOPD). Increases in end-expiratory lung volume between 5 and 13 cmH₂O PEEP decreased the Newtonian (airway) resistance in both groups, whereas the improvement in the mechanical homogeneity, as indicated by the decreases in G and η, was significantly stronger in the COPD group (Fig. 4). While extension of the model with distributions in either H or R (i.e., Eqs. 2 and 3, respectively) improved the fit at all PEEP levels, the significant differences between the corresponding parameters disappeared at higher levels of PEEP. However, in a small subgroup of patients in this study, even the extended models failed to result in physiologically interpretable parameter values, indicating that in severe COPD serial and parallel structural inhomogeneities combine in a way that these single-generation periphery models are unable to account for (53).

Fig. 4.

Dependence of respiratory mechanics on positive end-expiratory pressure (PEEP) in chronic obstructive pulmonary disease (COPD) patients mechanically ventilated because of acute exacerbation of the disease (AECOPD) or because of other indications (COPD). Mean values of Newtonian resistance (R_N), tissue damping (G), elastance (H), and hysteresivity (η) at transrespiratory pressures of 5, 7, 10, and 13 cmH₂O. Bars indicate SE. Values of P show the significance of differences between the 2 groups. [Reproduced with permission from Lorx et al. (53).]

CONCLUSIONS

In this paper, we have reviewed the impact of various types of mechanical heterogeneity on the structure-function relationships of mammalian respiratory system, specifically with regard to human pathology and animal models of lung disease. Recent computer modeling studies have demonstrated that the unique architectural constraints of the lung require that pathological alterations “emerge” in heterogeneous patterns rather than occur uniformly. On a global level, the unique frequency-dependent features of the mechanical impedance spectrum of the lung are exquisitely sensitive to detecting and monitoring the progression of this structural heterogeneity. The combination of impedance with inverse modeling further elucidates pathophysiological processes in the airways and parenchyma, as well as their corresponding responses to various treatment protocols. This makes measurements of impedance an ideal diagnostic tool to complement more conventional tests of lung function, such as spirometry or plethysmography (32). Future studies that incorporate imaging with oscillatory mechanics will be necessary to determine how specific heterogeneous alterations in lung structure affect its global dynamic behavior. Such information will validate clinically optimal approaches for ventilator management as well as therapeutic medical and surgical interventions.

GRANTS

This work was supported by National Heart, Lung, and Blood Institute Grant K08 HL-089227 and Hungarian Scientific Research Fund Grant 67700.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).