Structural heterogeneity promotes triggered activity, reflection and arrhythmogenesis in cardiomyocyte monolayers

Non-technical summary

The heartbeat depends on the spread of electrical waves through the cardiac muscle. If that spread becomes disturbed, arrhythmias and death may ensue. Patients with heart disease are predisposed to cardiac arrhythmias by unidentified mechanisms. Using both experiments and computer models we demonstrate that structural defects in the heart leading to contiguous areas of physical narrowing and expansion of the musculature can alter the spread of the waves, in such a way that some waves may return abnormally along the same narrow pathway as the original electrical wave (reflection), leading to extra beats and arrhythmia initiation. The possibility of reflection is enhanced when structural defects combine with alterations in the sodium channels responsible for the electrical waves, such as seen in inherited and acquired cardiac electrical diseases. Our results provide a novel mechanism whereby a substrate (structural heterogeneity) and a trigger (abnormal sodium channel activity) combine to promote life-threatening arrhythmia initiation.

Abstract

Abstract

Patients with structural heart disease are predisposed to arrhythmias by incompletely understood mechanisms. We hypothesized that tissue expansions promote source-to-sink mismatch leading to early after-depolarizations (EADs) and reflection of impulses in monolayers of well-polarized neonatal rat ventricular cardiomyocytes. We traced electrical propagation optically in patterned monolayers consisting of two wide regions connected by a thin isthmus. Structural heterogeneities provided a substrate for EADs, retrograde propagation along the same pathway (reflection) and reentry initiation. Reflection always originated during the action potential (AP) plateau at the distal expansion. To determine whether increased sodium current (I_Na) would promote EADs, we employed adenoviral transfer of Nav1.5 (Ad-Nav1.5). Compared with uninfected and adenoviral expression of green fluorescent protein (Ad-GFP; viral control), Ad-Nav1.5 significantly increased Nav1.5 protein expression, peak and persistent I_Na density, AP upstroke velocity, AP duration, conduction velocity and EAD incidence, as well as reflection incidence (29.2%, n = 48 vs. uninfected, 9.4%, n = 64; and Ad-GFP, 4.8%, n = 21). Likewise, the persistent I_Na agonist veratridine (0.05–3 μm) prolonged the AP, leading to EADs and reflection. Reflection led to functional reentry distally and bigeminal and trigeminal rhythms proximally. Reflection was rare in the absence of structural heterogeneities. Computer simulations demonstrated the importance of persistent I_Na in triggering reflection and predicted that the gradient between the depolarizing cells at the distal expansion and the repolarizing cells within the isthmus enabled retrograde flow of depolarizing electrotonic current to trigger EADs and reflection. A combination of a substrate (structural heterogeneity) and a trigger (increased persistent I_Na and EADs) promotes reflection and arrhythmogenesis.

Introduction

Patients with structural heart diseases have a high incidence of arrhythmias and sudden cardiac death. However, the role of structural heterogeneities in triggering arrhythmias remains poorly understood. The structure of the heart is very heterogeneous, owing to varying wall thickness, fibre orientation, microvasculature, trabeculation, fibrosis, and thin pathways that lead into large expansions, all of which impact the dynamics of impulse propagation (Hocini et al. 2002; Klos et al. 2008). In pathological states, these heterogeneities can be exacerbated by new discontinuties, such as accessory pathways (Schwieler et al. 2008), ischaemic or infarcted tissue (Janse & van Capelle, 1982; de Bakker et al. 1988) and fibrosis (Tanaka et al. 2007), all of which provide a substrate for the initiation of atrial and ventricular arrhythmias.

Most previous work on arrhythmogenesis focused on anatomical or functional reentry. However, little attention was paid to the possible role of reflection as a mechanism for the initiation and maintenance of arrhythmias. Reflection is defined as electrical activity that propagates in the anterograde direction, followed by re-excitation and propagation in the retrograde direction along the same pathway. In the original model of reflection, an area of impaired conduction was a prerequisite (Antzelevitch et al. 1980).

Here we present a new form of reflection that depends on a structural heterogeneity promoting a transient local imbalance between inward and outward currents during the action potential (AP) plateau and early after-depolarization (EAD). We hypothesized that: (1) in the absence of impaired conduction or gradients in ion channel expression, an abrupt structural heterogeneity, where a thin strand of viable tissue (an isthmus) connects two wide regions of tissue, provides the necessary conditions for premature re-excitation, reflection and arrhythmogenesis; and (2) in the presence of changing geometry, increased persistent sodium current (I_Na) during the AP plateau further promotes EADs and reflection.

An increase in persistent I_Na, as seen in acquired and inherited ion channel diseases, disrupts the balance of inward and outward currents, leads to changes in the AP morphology and AP duration (APD), and promotes local re-excitation during the AP plateau (Clancy & Kass, 2005). Increased persistent I_Na has been implicated as the cause of arrhythmogenesis and sudden cardiac death, and even sudden infant death syndrome (Arnestad et al. 2007; Tester et al. 2007). Mutations in the sodium channel (Nav1.5) result in an increase in the persistent I_Na in patients with long-QT syndrome type 3 (LQTS-3). Patients with LQTS-3 are highly susceptible to arrhythmogenesis during rest and bradycardia (Moss & Kass, 2005). The data presented here demonstrate that cardiac structural heterogeneities significantly enhance the role that an increase in persistent I_Na density and EADs has in arrhythmogenesis.

Methods

The methods are presented below in abbreviated form. All experiments were conducted following NIH guidelines. Please see the online Supplemental Material for details on the ethical aspects, experimental methodology, solutions, viral vectors, biochemical assays, and the optical mapping and patch-clamp equipment.

Cultured neonatal rat ventricular myocytes

Neonatal rat ventricular myocytes (NRVMs) were obtained from 1- to 2-day-old Sprague–Dawley rat (Charles River, Wilmington, MA, USA) hearts using enzymatic procedures (Rohr et al. 2003). Following 2 h differential pre-plating, myocytes (1.2 × 10⁶ cells) were plated on 25 mm glass coverslips (Fisher Scientific, Pittsburgh, PA, USA) in 35mm wells, or on cell culture-treated 35 mm plastic dishes (Corning, Corning, NY, USA) coated with collagen type IV. The myocytes were maintained in M199 (Lonzo, Walkersville, MD, USA) supplemented with 10% horse serum (Invitrogen, Carlsbad, CA, USA), bromodeoxyuridine (30 μl ml⁻¹, Sigma Aldrich, St. Louis, MO, USA), 20 units ml⁻¹ of penicillin and 20 μg ml⁻¹ streptomycin. The myocyte monolayers were stored in an incubator (37°C, air supplemented with 5% CO₂, VWR International, Batavia, IL, USA), and all experiments were performed after 4–5 days in culture.

Photolithographic patterning

We used a technique derived from that originally published (Rohr et al. 2003). As shown in Fig. 1A, this technique was used to create the two expansion regions (6 mm long × 9 mm wide), connected by a thin isthmus (6 mm long, and precise widths ranging from 0.1 to 2.0 mm wide).

Figure 1. Excitation frequency dependence of conduction slowing and block at regions of geometrical expansion.

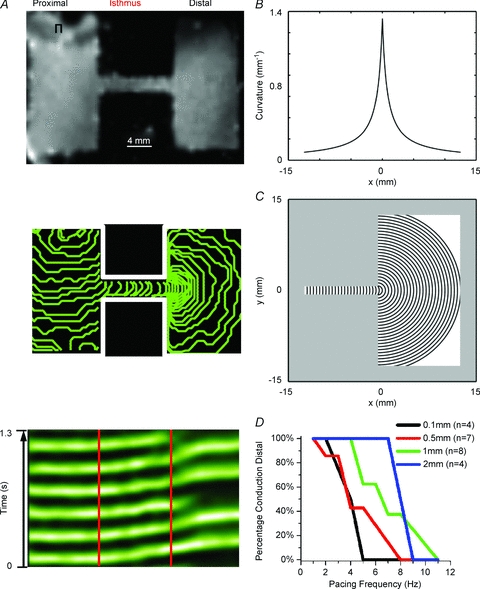
A, top panel, uninfected patterned monolayer (1-mm-wide isthmus). A, middle panel, activation map of a patterned NRVM monolayer with a 1-mm-wide isthmus that was paced at 6 Hz, showing 5 ms isochrone lines. A, bottom panel, average time–space plot (TSP) for pixels along horizontal lines that traversed the isthmus from the same preparation when the excitation frequency was increased to 7 Hz (red lines demark the structural heterogeneity). There was conduction slowing at the distal expansion and subsequent conduction block in a 3:2 pattern of conduction to block distally. B, curvature profile along the cable. C, wavefronts (spaced every 0.5 mm) corresponding to the curvature shown in B. There is a 0.75 mm (r₀) offset between the location of the highest curvature along the 1D cable (B) and the isthmus–expansion interface in the 2D system (C). This relates to the geometrical properties of the wavefront; the wavefront with the highest curvature (thus the smallest radius, r₀) has its right-most point at x₀= 0 (according to B) and its centre at x=−r₀. D, percentage of the preparations at each isthmus width and pacing frequency that sustained propagation into the distal expansion.

Adenoviral transfer

Recombinant adenoviruses encoding the human SCN5a gene and green fluorescent protein (GFP) were applied to myocyte monolayers. The NRVMs were infected after 48 h in culture, and experiments were performed after an additional 48–72 h.

Single-cell electrophysiology

Experiments were carried out using a Multiclamp 700B amplifier and glass pipettes with the appropriate tip resistance. The data were acquired and analysed using pCLAMP 10 (Molecular Devices, Sunnyvale, CA, USA). Whole cell current-clamp experiments were performed in Hanks Balanced Salt Solution with Ca²⁺ and Mg²⁺ (Sigma). The temperature was 37°C. The myocytes were paced at 0.5 Hz and from 1 Hz until loss of 1:1 capture of stimulus to AP response, in 1 Hz increments.

Whole cell voltage clamp was used to measure I_Na. To ensure adequate voltage control, experiments were performed at room temperature (21–22°C) with pipette resistances ≤3 MΩ when filled with the pipette filling solution and 20 mm[NaCl]_o. Appropriate whole-cell capacitance and series resistance compensation (≥70%) was applied, along with leak subtraction.

Optical mapping and experimental protocol

Optical mapping experiments of NRVM monolayers were conducted using a custom-made apparatus, consisting of a high-powered halogen lamp and a high-speed CCD camera (SciMeasure Analytical Systems Inc., Decatur, GA, USA). A bipolar electrode was used to drive the patterned monolayer from the proximal wide area at increasing frequencies, from 1 Hz to the highest frequency that maintained 1:1 propagation distally.

Pharmacological challenges

The following pharmacological agents were used as follows: (1) to block the sodium current, 30 μm tetrotoxin (TTX, Sigma); (2) to increase the persistent I_Na, 0.01–30 μm veratridine (Sigma); and (3) an L-type Ca²⁺ current (I_CaL) agonist, 1 μm Bay K 8644 (CalBioChem, Gibbstown, NJ, USA). We alternated the order of solution delivery with each preparation to rule out potential run down or deterioration of a dish affecting the possibility of reflection.

Statistical analyses

Data are presented as means ± SEM. The χ² test, Fisher's exact test, one-way ANOVA with Tukey's test, and Student's unpaired t test with Welch's correction were used when appropriate. Statistical significance was determined at P < 0.05.

Computer simulations

Extensive details regarding the mathematical derivations and equations for the numerical modelling of the ion channel kinetics and geometrical patterns used in our simulations can be found in the online Supplemental Material. Briefly, cells were modelled using the LR2000 model (Faber & Rudy, 2000), with calcium release triggered by voltage crossing −35 mV and a customized model of I_Na based on a best fit to the patch-clamp data. Simulations were conducted using a one-dimensional (1D) cable (see online Supplemental Material for details) with a single expansion, and a two-dimensional (2D) model simulating an isthmus bridging two identical expansions.

Cable with single expansion

To acquire detailed insights into the interplay among various parameters, we simulated a 1D cable of 500 nodes in length, with each node corresponding to 0.05 mm, with a internodal conductance of 0.00096 mS. The 1D cable was simulated using the following differential equation:

(1)

where D is the diffusion constant, κ is the wavefront curvature (see next paragraph), V_m is the transmembrane voltage, x is a geometrical co-ordinate along the cable, and i_stim and i_ion are, respectively, the stimulation and ionic currents (normalized to cell capacitance). A detailed numerical derivation of eqn (1) can be found in the online Supplemental Material.

The wavefront curvature varied along the cable according to the following equation:

(2)

where x₀ denotes location of the highest curvature along the cable and r₀ is the radius of that highest curvature. When x > x₀ this model directly mimics the conditions experienced by an impulse travelling from the isthmus into the expansion region in which the curvature decays hyperbolically. When x < x₀ the model approximates the effects of the bulk of the expansion region ‘seen’ by the impulse while still in the isthmus via the electrotonic interaction. The changes in curvature at the expansion are illustrated in Fig. 1B and C. Here, curvature is defined by (eqn (2)), assuming x₀= 0 mm and r₀= 0.75 mm, and expressed in terms of curvature. This curvature profile models a 1.5-mm-wide (i.e. twice r₀) isthmus that then expands into a large distal region (Fig. 1C).

The 1D simulations were used to overcome several limitations of 2D modelling. First, as demonstrated by the simulations presented in Fig. 9 and Supplemental Fig. 7, the 1D cable enabled us to examine many curvatures within the same simulation for each persistent-to-peak I_Na condition. As such, we precisely determined the combination of curvature, persistent I_Na and peak I_Na needed for EAD formation and reflection. Second, the 1D cable enabled us to rule out the influence of boundary conditions and to see what effect an abrupt expansion (increased curvature) had upon reflection. Finally, our 1D approach allowed us clearly to rule out micro-reentry. The simulated expansions served to model these same effects reproducibly and to establish a model precisely to dissect out the mechanisms for APD prolongation, EAD formation and reflection.

Figure 9. Fate of an impulse arriving at high-curvature region.

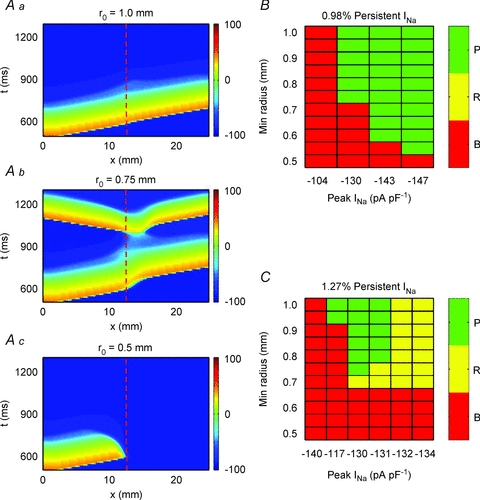
A, time–space plots illustrating three different fates of an impulse propagating through a high curvature region: propagation (a), reflection (b) and block (c). Red dashed lines denote the expansion (increased curvature). B, fate of the wavefront as a function of peak I_Na and isthmus half-width at a low level of persistent I_Na (0.98%). C, fate of the wavefront as a function of peak I_Na and isthmus half-width at a higher level of persistent I_Na (1.27%). P, propagation through the region of high curvature; R, reflection at the region of high curvature; B, block at the region of high curvature.

Patterned two-dimensional model

Two-dimensional simulations were performed at a spatial resolution of 0.1 mm per node, with internodal conductance of 0.00024 mS. The simulated domain was 90 × 45 nodes (9.0 mm × 4.5 mm) in size and composed of a proximal expansion, an isthmus and a distal expansion. Each of those three segments was 3 mm long; and both the proximal and the distal expansions were 4.5 mm wide. The isthmus width was varied to test its effect on impulse propagation.

Results

Source-to-sink mismatch

In Fig. 1A, high-frequency stimulation (6 Hz) was applied to the proximal zone of a patterned monolayer with an isthmus of viable tissue that connected the two wide zones. When the electrical impulse exited the isthmus and encountered the large distal expansion, the velocity of impulse propagation decreased, illustrated by the crowding of the isochrone lines at the distal expansion (middle panel). As expected, in the same preparation when the pacing frequency was further increased to 7 Hz there was intermittent 3:2 conduction block at the distal expansion. As seen in the time–space plot (TSP; bottom panel), in each 3:2 sequence the first two beats propagated through the entire preparation with slowing at the distal expansion (illustrated by an increase in the slope of the green line at the interface). Conduction for the second beat was further prolonged, and the third beat blocked at the interface. This 3:2 pattern repeated as long as the same high stimulation frequency was maintained. In Fig. 1D we quantified the incidence of conduction block for each isthmus width at various pacing frequencies. Patterned monolayers with wide isthmuses (2 mm) responded in a 1:1 manner to higher frequencies before the onset of conduction block, compared with preparations having narrower isthmuses (0.1 mm), thus confirming, as seen previously, the presence of a large electrotonic load at the distal expansion (Cabo et al. 1994; Rohr et al. 1999).

Heterogeneous tissue geometry and vulnerability for reflection

As illustrated in the TSP presented in Fig. 2A (bottom), in contrast to high excitation frequencies, during stimulation at a relatively low frequency (1 Hz), impulses initiated at the proximal wide region propagated across the narrow isthmus and the distal region without major delay, serving to excite the entire preparation.

Figure 2. Structural heterogeneities promote reflection.

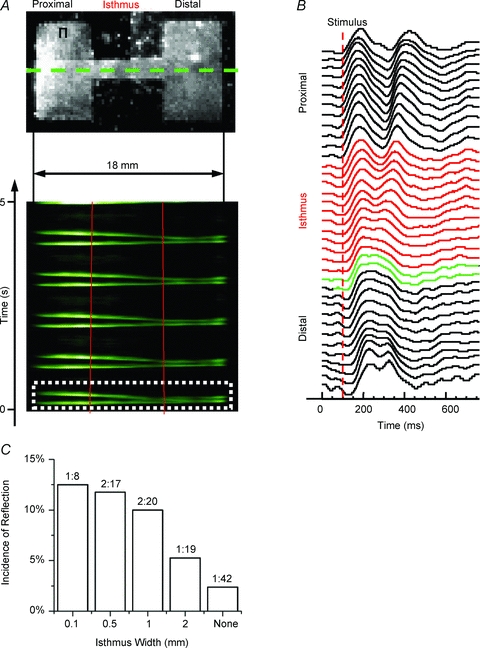
A, top panel, uninfected patterned monolayer (2-mm-wide isthmus) paced at 1 Hz (Π, site of stimulation). A, bottom panel, average TSP for pixels along horizontal lines that traversed the isthmus in A (green dotted line denotes one example). The impulse originates on the upper proximal (left) side and activates the entire preparation distally (right; red lines demark the structural heterogeneity), followed by re-excitation and reflection for each wave. B, optical APs across the preparation for wave 1 (white dotted box in A). Red APs are from pixels within the isthmus and green APs are pixels within the first 500 μm of the distal expansion. C, incidence of reflection at each cable width. Numbers above the bars are the ratio of the number of preparations displaying reflection to the total number of preparations.

Low-frequency stimulation revealed prolongation of the AP plateau at the distal expansion (green APs in Fig. 2B), which led to EADs that propagated retrogradely through the isthmus and gave rise to reflection. As shown by the TSP (Fig. 2A, bottom panel), with each anterograde propagating wave there was re-excitation at the distal expansion and subsequent retrograde propagation along the same pathway. The reflected wave reactivated the entire preparation. The average conduction velocity (CV) for all of the anterograde beats that subsequently led to reflection in this preparation was 24 cm s⁻¹, and 13 cm s⁻¹ for the retrogradely propagating beats. The average CV of anterograde impulses is consistent with the average CV at 1 Hz pacing (point stimulation using a bipolar electrode) of homogeneous monolayers that were 35 mm in diameter (Figure 3E). We set the following strict criteria for quantifying reflection: (1) re-excitation must occur before complete repolarization at the site of reflection (removing the possibility of automatic foci or delayed after-depolarization); and (2) the anterograde wavefront had to successfully propagate through the entire preparation before re-excitation and reflection (ruling out micro-reentry).

Figure 3. Characterization of Ad-Nav1.5 expression.

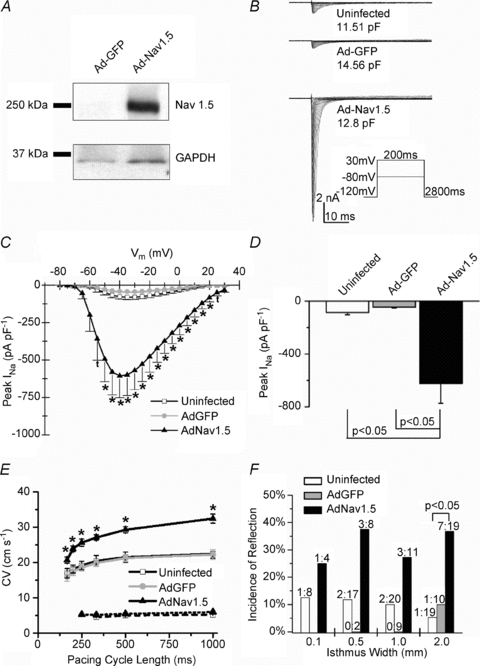
A, representative Ad-Nav1.5 Western blot. Top, Nav1.5 expression; bottom, GAPDH as the loading control. B, representative I_Na family of traces. C, current–voltage relation of I_Na. The I_Na density was significantly larger in the Ad-Nav1.5 group vs. uninfected (t, P < 0.05,) or both uninfected and Ad-GFP (*P < 0.05, N = 6–8, n = 8–12). D, the peak I_Na density in the Ad-Nav1.5 group. E, conduction velocity (CV) in homogenous NRVM monolayers at various pacing cycle lengths. The CV was significantly faster at all cycle lengths in the Ad-Nav1.5 group vs. uninfected and Ad-GFP groups (*P < 0.05, continuous lines, n = 3–8 monolayers). Upon I_Na blockade (30 μm TTX), the CV decreased to 4.5–6.0 cm s⁻¹ in all three groups (dotted lines, one-way ANOVA and Tukey's test). F, incidence of reflection for each isthmus width (P < 0.05, χ² test).

We quantified the susceptibility for reflection as a function of isthmus width. As shown in Fig. 2C, while the incidence of reflection was low, it was greatest for the preparations with the narrowest isthmus and tended to decrease progressively with wider isthmuses (n.s.). Overall, based on our strict criteria, reflection was seen in 6 of 64 patterned uninfected preparations (9.4%). Yet, reflection was extremely rare in structurally homogeneous monolayers (2.4%, 1 of 42).

Upregulated I_Na increases the incidence of reflection in patterned monolayers

Reflection through the narrow isthmus seemed to be closely related to AP prolongation, with EAD formation at or near the distal expansion (Fig. 2B). We therefore surmised that increasing the inward current density during the AP plateau would increase the incidence of EAD formation and reflection. We tested this idea in patterned monolayers adenovirally overexpressing Nav1.5 (Ad-Nav1.5). As seen in Fig. 3A, Ad-Nav1.5 led to a marked increase in Nav1.5 protein expression (∼250 kDa protein band). We repeated these protein blots numerous times (Ad-GFP N = 4 infection experiments, n = 6 preparations; Ad-Nav1.5 N = 4, n = 5) and there was always a dramatic increase in Nav1.5 expression in the Ad-Nav1.5 vs. Ad-GFP group (see also Supplemental Fig. 1D). Next, at the functional level we observed a significant increase in I_Na current density (Fig. 3B–D) and CV (Fig. 3E) in the Ad-Nav1.5 group compared with the uninfected and Ad-GFP preparations. Blockade of I_Na (30 μm TTX) reduced the CV in all three groups to 4.5–6 cm s⁻¹, confirming that the Ad-Nav1.5-induced increase in CV was due to increased I_Na density.

Similar to uninfected preparations, in Ad-Nav1.5 and Ad-GFP monolayers the impulses initiated in the proximal wide region propagated through the isthmus and resulted in EAD formation at the distal expansion, with retrograde propagation. As summarized in Fig. 3F, at each isthmus width the incidence of reflection increased two- to sevenfold in the Ad-Nav1.5 NRVM monolayers compared with the uninfected group (P < 0.05 at 2-mm-wide isthmus).

Infection with Ad-Nav1.5 promotes APD prolongation and EADs in single NRVMs

To assess the ionic mechanism(s) underlying the promotion of reflection by the increased I_Na we performed single-cell voltage- and current-clamp AP recordings to examine the biophysical properties of I_Na and their implications upon the AP morphology and APD. A detailed description of all of the biophysical properties of I_Na in each of the three groups can be found in the online Supplemental Material (Supplemental Figs 2 and 3). Briefly, the normalized current–voltage relations of the endogenous and virally overexpressed I_Na overlapped, and the voltage of peak inward current, as well as the voltage dependence of I_Na activation (V_1/2) and slope factor were all similar in each of the three groups. In addition, the slope factors for the voltage dependence of I_Na availability curves did not differ between groups. In contrast, not unexpectedly (Stocker & Bennett, 2006), the Ad-Nav1.5 V_1/2 of I_Na availability was left shifted compared with the uninfected and Ad-GFP groups. Finally, all three fits for the time dependence of I_Na recovery from inactivation overlapped and were virtually identical.

Following our hypothesis of increasing the depolarizing current during the AP plateau, the TTX-sensitive persistent I_Na (measured at −40 mV) was significantly larger in the Ad-Nav1.5 group (−7.73 ± 1.91 pA pF⁻¹) than in the uninfected (−1.46 ± 0.86 pA pF⁻¹) and Ad-GFP groups (−1.45 ± 0.81 pA pF⁻¹; Fig. 4A and B). However, the persistent I_Na scaled with the peak I_Na in each group (n.s.; Fig. 4C), which suggested that there was no difference in this biophysical property between the three groups and that the increase was due to the increased functional sodium channel density. There was no difference in the absolute or normalized persistent I_Na between the uninfected and Ad-GFP groups.

Figure 4. Persistent I_Na.

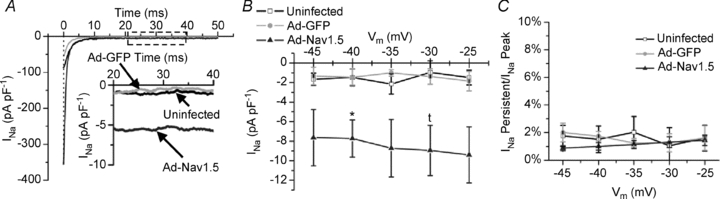
A, representative traces of TTX-sensitive persistent I_Na in each group. B, quantification of the persistent I_Na (N = 2–3, n = 3). C, TTX-sensitive persistent I_Na normalized to the TTX-sensitive peak I_Na for each trace as a percentage. One-way ANOVA and Tukey's test.

As seen by the representative recordings in Fig. 5A, isolated myocytes overexpressing I_Na had appreciably longer APDs and often developed EADs (arrows). In Fig. 5B, the incidence of EADs was significantly greater (fourfold) in the Ad-Nav1.5 group than in both the uninfected and the Ad-GFP groups. The prolonged AP plateau was also observed in Ad-Nav1.5 NRVM monolayers; the average optical APD at 50% repolarization (APD₅₀) was significantly prolonged (Fig. 5C).

Figure 5. Expression of Ad-Nav1.5 promotes APD prolongation and EADs.

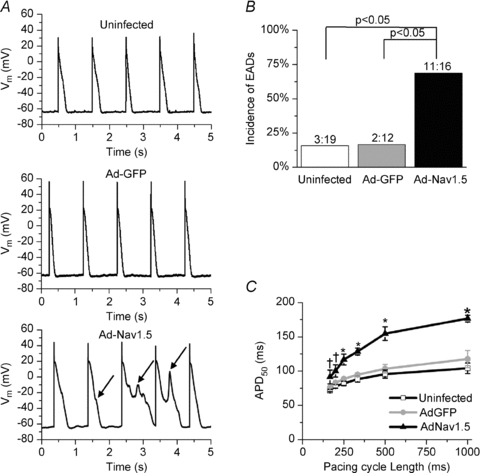
A, representative single-cell current-clamp AP recordings in each group. The AP plateau was prolonged and unstable in the Ad-Nav1.5 group, leading to the frequent occurrence of EADs (arrows). B, incidence of EADs (P < 0.05, χ² test). C, optical APD at 50% repolarization (APD₅₀) was significantly prolonged at all pacing cycle lengths in the Ad-Nav1.5 group vs. uninfected (†) or both uninfected and Ad-GFP (*); one-way ANOVA and Tukey's test (n = 3–18 monolayers).

Heterogeneous structure and low excitation frequency promote EADs and reflection

Overall, in patterned monolayers I_Na overexpression significantly increased the total incidence of reflection (29.2%, n = 48) compared with both the uninfected (9.4%, n = 64) and the Ad-GFP groups (4.8%, n = 21; Fig. 6A). In contrast, in all three groups reflection was extremely rare in the absence of an isthmus. In the Ad-Nav1.5 group, the heterogeneity provided by an isthmus significantly increased the total incidence of reflection from 3.6 to 29.2% (P < 0.05). In the uninfected and the Ad-GFP groups the total incidence of reflection also tended to increase in the presence of heterogeneity (n.s.).

Figure 6. Structural and excitation frequency determinants of reflection.

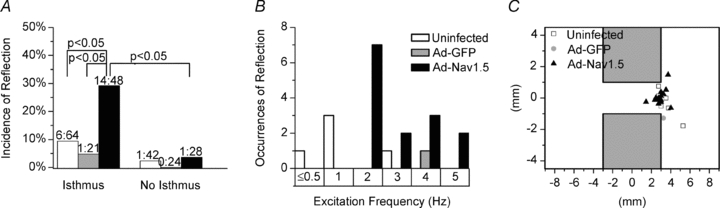
A, total incidence of reflection between each group and in the presence vs. absence of an isthmus; χ² and Fisher's exact test. B, occurrence of reflection at each excitation frequency (rounded to the nearest integer). C, diagram of the monolayer pattern with the site of re-excitation plotted.

As seen in Fig. 6B, the average excitation frequency at which reflection occurred was significantly greater in the Ad-Nav1.5 (2.9 ± 0.3 Hz) vs. the uninfected group (1.3 ± 0.4 Hz, P < 0.05; Student's unpaired t test with Welch's correction). In the Ad-Nav1.5 group, reflection occurred at excitation frequencies of 1.5–5 Hz. In the uninfected group, five of the six cases of reflection occurred at excitation frequencies ≤3 Hz. For the sixth case, the stimulus-to-captured response pattern at the electrode was 3:2, precluding measurement of the excitation frequency. The single instance of reflection in the Ad-GFP group occurred at 3.5 Hz.

In Fig. 6C, the site of re-excitation was plotted; every case of reflection in each of the three groups originated at the interface between the isthmus and distal expansion. In the preparations devoid of the isthmus, the two sole cases of re-excitation and reflection originated from the border of the preparation, which is also a region of structural heterogeneity.

Conditions for reflection of individual wavefronts

Not every propagated wave reflected. As seen in the TSP of Fig. 7A, paced waves labelled 1, 3, 5, 7, 8 and 10 propagated through the entire preparation and ceased upon reaching the distal border. Waves 2, 4, 6 and 9 each resulted in a reflected response. The reflected responses to waves 2 and 9 (e.g. blue dashed box) were followed by two additional impulses that emerged at the distal expansion and propagated from right to left. Following the anterograde wave that activated the entire preparation, there was EAD formation at the distal expansion, which gave rise to reflection. In addition, as the activation map of Fig. 7B illustrates, due to source-to-sink mismatch at the distal expansion the wave that initiated reflection also underwent unidirectional block, giving rise to an anticlockwise rotor that sustained for two full rotations. In Fig. 7C and D, note the prolonged and unstable AP plateau only at the distal expansion for the reflected vs. non-reflected waves. Furthermore, as Fig. 7E and F illustrates in a different preparation, APD prolongation at the distal expansion (green APs) was particularly striking compared with the APs elsewhere.

Figure 7. Reflection in the Ad-Nav1.5 group.

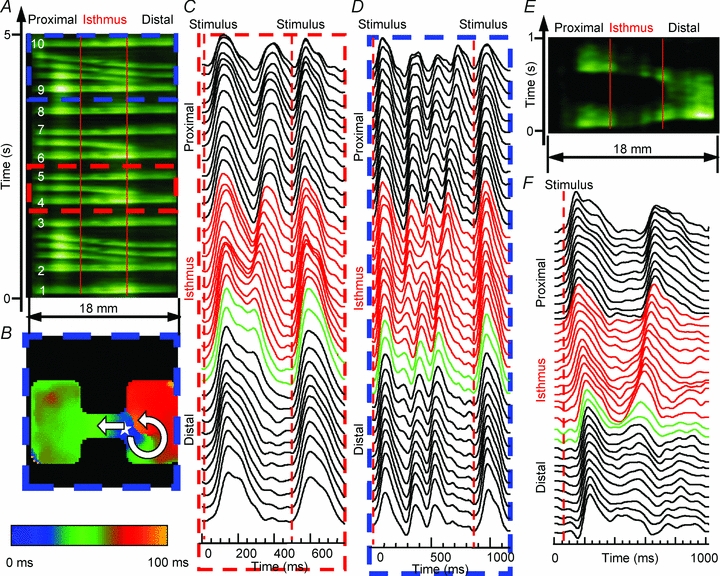
A, average TSP for pixels along horizontal lines that traversed the isthmus from an Ad-Nav1.5 monolayer (2-mm-wide isthmus; red vertical lines demark the structural heterogeneity). Stimulation was at 2 Hz on the proximal (left) side, and the impulse traversed the isthmus and activated the large distal expansion (right), followed by the intermittent occurrence of reflection. Anterograde propagating waves are numbered in white. B, activation map illustrated that re-excitation (star) led to reflection, and a small distal area beneath the expansion was re-excited, which resulted in unidirectional propagation and an anticlockwise rotor. C and D, optical AP recordings during the time period within the red dashed and blue dashed boxes in A, respectively. The red APs are from pixels within the isthmus, and green APs are pixels within the first 500 μm of the distal expansion. E, average TSP from another Ad-Nav1.5 monolayer (0.5-mm-wide isthmus, 3 Hz stimulation) exhibiting reflection. F, optical AP recordings across the preparation in E.

Overall, the reflection patterns varied on a beat-to-beat basis and between preparations. In addition to reflection triggering the initiation of reentry, there were instances of reflection where each paced wave reflected back (e.g. Fig. 2A, bottom), serving to sustain this arrhythmic activity. In other preparations, even at a fixed frequency of stimulation, not every wave would reflect back (i.e. Fig. 7A), resulting in bigeminal and trigeminal rhythms on the proximal side.

The anterogradely propagating waves that led to subsequent reflection took significantly longer to travel from the proximal to the distal side compared with waves from the same recording that failed to reflect back. In the uninfected and Ad-Nav1.5 groups, the total conduction time was 23.2 ± 7.5 and 50 ± 10.3% longer, respectively.

Pharmacological increase in the persistent I_Na

In an effort to expose the contribution of the persistent I_Na in the absence of an increase in the peak I_Na we used veratridine, a commonly used late sodium channel agonist. We administered veratridine at varying concentrations (0.01–30 μm) to single NRVMs, as well as patterned NRVM monolayers. Veratridine increased the persistent I_Na at each drug concentration and returned to control upon washout (Fig. 8A). In contrast, peak I_Na increased less than 9% at 0.15 and 3 μm veratradine, and decreased by 33% at 30 μm veratradine (data not shown). Both the AP plateau duration (Fig. 8B) and APD₈₀ (Fig. 8C) increased with increasing concentrations of veratridine. At 30 μm veratridine, the AP failed to repolarize, presumably due to the massive amount of persistent I_Na. Single-cell EADs were observed at 0.15 and 3 μm veratridine (Fig. 8D and E), but were never observed in the control vehicle solution. Re-excitation always arose during phases 2 and 3 of the AP.

Figure 8. Increased persistent I_Na promotes EADs and reflection.

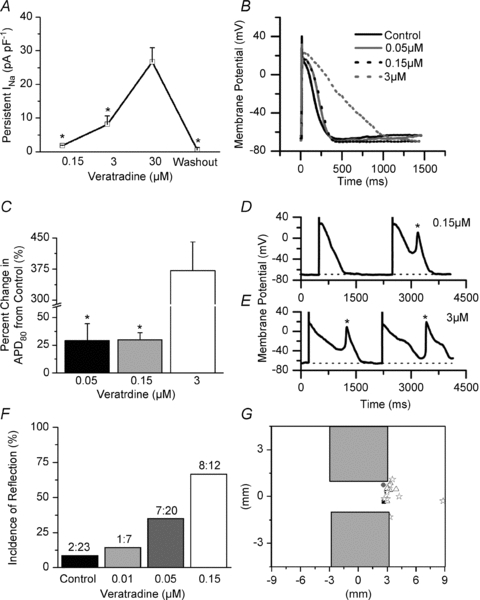
A, change in persistent I_Na (veratridine minus control) in single NRVMs (*P < 0.05 vs. 30 μm, n = 3–7). B, representative APs at each dosage of veratridine. C, quantification of percentage increase in the APD₈₀ from control (*P < 0.05 vs. 3 μm, n = 3–9). D and E, representative APs and EADs at 0.15 and 3 μm veratridine (dotted line denotes baseline). F, incidence of reflection at each concentration of veratridine (P = 0.003, χ² test). G, diagram of the monolayer pattern with the site of re-excitation plotted (black square, control; grey circle, 0.01; white triangle, 0.05 μm; and white star, 0.15 μm). One-way ANOVA and Tukey's test were used in A and C.

Using patterned monolayers (2-mm-wide isthmus) we investigated the effect of increasing the persistent I_Na. In Fig. 8F, the incidence of reflection was low in the control conditions, but increased progressively at increasing veratridine concentrations. At 0.05 μm, the incidence of reflection was the same as that seen in the Ad-Nav1.5 group (Fig. 3F). Most importantly, similar to the results in Fig. 6C, in control conditions and in the presence of veratridine the origin of reflection was localized at the distal expansion. In Fig. 8G, each symbol indicates the site of initiation of reflection for a given episode. Importantly, only at the highest concentration of veratridine (0.15 μm) did we observe one out of eight cases of reflection arising from the boundary of the distal region (star). Taken together with the Nav1.5 overexpression results, these data support our conclusion that the persistent I_Na has an important role in the mechanism of reflection in structurally heterogeneous tissue.

Interplay between wavefront curvature and persistent I_Na at the expansion

Electrical waves propagating through areas of tissue expansion experience significant slowing as a result of source-to-sink mismatch related to increased wavefront curvature (Fig. 1; Cabo et al. 1994; Rohr et al. 1999). However, whether curvature and source-to-sink mismatch also affect the APD has not been investigated. Therefore, we conducted numerical simulations to test whether a change in local curvature simulating a structural heterogeneity, in combination with an increase in persistent I_Na, would result in EADs and reflection. In the simulations presented in Fig. 9, we used a 1D cable of 500 nodes (25 mm) with a resolution of 0.05 mm per node. The cell kinetics were as described in the Methods, Computer simulations. The curvature varied along the cable as in Fig. 1B (eqn (2)) to mimic a wavefront entering a single abrupt expansion. This model is reminescent of the NRVM experimental pattern, as well as of abrupt expansions seen in the normal and pathological heart.

We tested for different levels of persistent I_Na (relative to peak I_Na), level of I_Na expression (measured as peak I_Na) and various curvatures, corresponding to various isthmus widths. Overall, we observed the following three major types of behaviour, as illustrated in Fig. 9A: impulses passing through (Fig. 9Aa), reflection (Fig. 9Ab) and block (Fig. 9Ac).

Clearly, the specific fate of the wavefronts depends on the relation between persistent I_Na and the curvature radius. Figure 9B shows results from simulations at a relatively low level of persistent I_Na (0.98%). The impulses either propagated into the expansion (P, green), with some transient slowing of CV (data not shown) or blocked (red). As expected, successful propagation was seen at low curvatures (large curvature radius, corresponding to wide isthmus) and block was seen at high curvatures (small curvature radius, corresponding to a narrow isthmus). When the level of persistent I_Na was kept constant at 0.98% of peak I_Na, increasing peak I_Na (sodium channel conductance; G_Na) led to increases in the ‘critical’ curvature for successful propagation into the expansion (i.e. narrower and narrower isthmuses were needed to achieve conduction block), but reflection did not occur. Only an extreme increase in G_Na resulted in reflection, which was not dependent on the structure (data not shown).

Figure 9C shows the results obtained at a higher level of persistent I_Na (1.27%). In this case, a new behaviour between P (propagation) and B (block), namely R (reflection) became apparent. As G_Na was increased, smaller curvatures (larger radii) became sufficient to enable reflection. Notably, the transition between block and reflection occurred at a curvature level similar to Fig. 9B, whereas the transition between propagation and reflection depended on the curvature over the same range of peak I_Na (from −130 to −134 pA pF⁻¹). Taken to the extreme, with high levels of G_Na, reflection began to be seen even without curvature (data not shown).

At both levels of persistent I_Na (Fig. 9B and C), extremely high values of G_Na (not shown in the graphs) resulted in reflection independent of curvature (structure). The latter behaviour would be the 1D equivalent of EADs occurring spontaneously in the middle of a 2D preparation.

Reflection in the two-dimensional model

As illustrated in Fig. 10A, 2D simulations were performed with peak I_Na of −152 pA pF⁻¹ and persistent I_Na of 0.98% using a patterned 2D numerical model that closely resembled the experimental preparations. Stimulation was applied to the proximal (left) expansion at 1 Hz. When the isthmus width was four or more nodes (0.4 mm), the impulse propagated through the entire preparation. An isthmus width two or fewer nodes (0.2 mm) led to conduction block at the interface between the isthmus and the distal expansion. Yet, when the isthmus width was three nodes (0.3 mm) the conditions were appropriate for the intermittent appearance of re-excitation at the distal expansion with reflection (Fig. 10A, bottom). Re-excitation arose from the distal expansion region (green APs in Fig. 10B are nodes within the first 600 μm of the distal expansion). These 2D numerical simulation results strongly support our contention based on experimental results (e.g. Fig. 6C) that the distal expansion region provides the critical substrate for EAD formation and reflection.

Figure 10. Two-dimensional simulations.

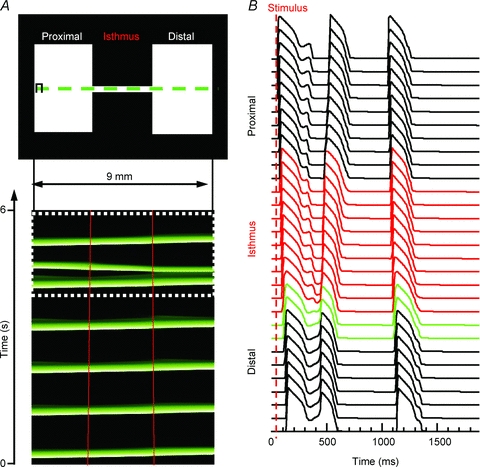
A, top panel, 2D pattern (9 mm × 4.5 mm). A, bottom panel, time–space plot for pixels along the horizontal line that traversed the isthmus in the top panel. The impulse originates on the proximal (left) side and activates the entire preparation distally (right; red lines demark the structural heterogeneitiy). Following the fifth beat, there was re-excitation at the distal expansion region and a retrograde reflected wave. The final beat propagated through the entire preparation without reflection. B, APs across the preparation for the final two beats (white dotted box in A). The red APs are from nodes within the isthmus, and green APs are pixels within the first 600 μm of the distal expansion.

Discussion

We demonstrate for the first time that areas of source-to-sink mismatch, where a narrow isthmus of fully excitable cells connects to a distal expansion, are a substrate for re-excitation, reflection and arrhythmogenesis. Increased I_Na (Ad-Nav1.5 or veratridine) served to prolong the APD, enhance the occurrences of single-cell EADs and promote reflection. Re-excitation always arose during phases 2 and 3 of the AP, in regions of decreased load. Homogeneous preparations, devoid of structural heterogeneity, rarely exhibited reflection.

Original vs. present model of reflection

The original reflection model consisted of a linear cardiac Purkinje fibre placed in a three-chambered tissue bath (sucrose gap; Antzelevitch et al. 1980). A prerequisite for reflection was the presence of an area of depressed excitability between two fully excitable zones. Here we demonstrate that structural heterogeneities provide a substrate for reflection even when the tissues are fully excitable. In both models, an abrupt heterogeneity provides conditions for source-to-sink mismatch and reflection. However, the analogy stops there, because in the original reflection model a central region of low excitability was essential to allow sufficient delay for electrotonically mediated re-excitation at a time when the tissue at the proximal site was fully recovered. In contrast, reflection in the presence of a geometrical expansion was dependent upon prolongation of the AP plateau and EAD formation secondary to increased local curvature at the site of expansion.

Interplay between cardiac structure and I_Na determines the susceptibility for reflection

Previous studies have quantified the effects of geometrical expansions upon local conduction slowing and conduction block (Cabo et al. 1994; Rohr et al. 1999). Importantly, these effects are most prominent at high excitation frequencies, as confirmed in Fig. 1. However, a completely different picture emerged at low excitation frequencies; the conduction delay was relatively small at the expansion. Yet, an abrupt change in local wavefront curvature at the expansion changed the source-to-sink relations, resulting in prolongation of the local AP plateau and consequent EAD formation and reflection (Figs 2, 7, 9 and 10).

In Fig. 11, we present a model illustrating the underlying mechanisms of reflection in the patterned monolayer. As illustrated by the phase map in Fig. 11A, when a wavefront (blue) enters the distal expansion, the depolarizing electrotonic current (the source) disperses into a wide area (the sink). Therefore, impulses initiated proximally at a low frequency that subsequently lead to reflection always take slightly longer to propagate from the isthmus to the distal side, compared with non-reflected waves; this probably provides more time to facilitate the recovery of depolarizing currents in the myocytes upstream of the expansion.

Figure 11. Schematic representation depicting our explanation for the mechanism of re-excitation and reflection at the isthmus.

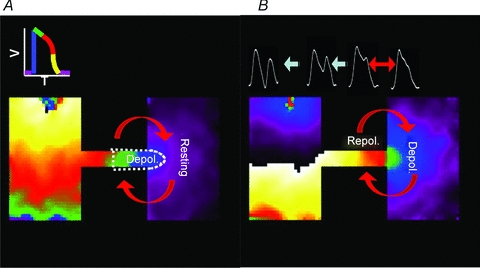
A, as the depolarizing wavefront (blue) enters the distal expansion there is a strong voltage gradient, and repolarizing electrotonic current flows from the expansion into the isthmus, which leads to conduction slowing and block. B, upon depolarization of the distal region, the voltage gradient is reversed because there is a large area at the depolarized state, while the small area within the isthmus is beginning to repolarize, resulting in APD prolongation at the expansion, and depolarizing electrotonic current flows into the cells within the isthmus, which face a high input impedance and membrane resistance. Consequently, there is re-excitation at the distal expansion, which leads to reflection.

When the wavefront activates a sufficiently large number of cells at the distal expanded region, the direction of electrotonic flow reverses, which tends to prolong the APD (Supplemental Fig. 5C). In Fig. 11B there is a large blue region of depolarized cells that is in close apposition to the small region of cells within the isthmus that is beginning to repolarize. Consequently, as confirmed by the numerical simulations, the local wavefront curvature–APD relations are such that there is only a relatively small amount of repolarizing electrotonic current flowing downstream upon the cells within the distal expansion, thus resulting in APD prolongation.

In all the experiments in which we observed reflection, the AP plateau became prolonged at the distal expansion (green APs in Fig. 7F) where the degree of source-to-sink mismatch was greatest. As demonstrated by the simulations presented in Supplemental Fig. 5, the APD depended on the local curvature, which was an indication of the degree of source-to-sink mismatch. The shortest APDs were always found in regions of zero curvature (planar wavefront), and the APD increased in parallel with wavefront curvature. Local EADs ensued at the distal expansion if the AP plateau was sufficiently prolonged and phases 2 and 3 depolarization was enhanced by the presence of a persistent late I_Na (Figs 3F and 8F) and/or I_CaL (Moss & Kass, 2005). Previous studies support this concept and have highlighted APD gradients and prolongation at geometrical expansions and resistive barriers (Janse & van Capelle, 1982; Antzelevitch, 1990; Derksen et al. 2003). In our experiments, the width of the isthmus was narrow and therefore the input impedance in that region should be relatively high compared with the wide regions, particularly during the AP plateau, which is a time of high membrane resistance. Therefore, it was not surprising that the depolarizing electrotonic current, supplied by the distal expansion, was sufficient to result in EADs. In computer simulations, high local curvature not only reduced the CV as expected but also prolonged the APD (Fig. 9A and Supplemental Fig. 5). However, the question remains as to why EADs and reflection occurred so sporadically rather than after every paced wave in constant experimental conditions of isthmus width, Nav1.5 expression and pacing frequency. We surmise that very small beat-to-beat changes in the initial conditions leading to the highly non-linear interaction among the inward and outward membrane currents that maintain the AP plateau tilt the balance in either the depolarizing or repolarizing direction in seemingly unpredictable ways.

Nevertheless, our experiments and simulations clearly demonstrated that the susceptibility for reflection was conditioned by both structural heterogeneities and persistent I_Na density. Computer simulations illustrate that the mechanism depends on the mutual potentiation of persistent/reactivated I_Na and depolarizing electrotonic current at the repolarizing wavetail (Fig. 9 and Supplemental Figs 6 and 7). Consistently, there was a need for a prolongation of the conduction time and the APD to facilitate reflection.

We demonstrate how the interplay between three parameters, namely the level of persistent I_Na, the level of G_Na and the local curvature, determines whether or not EADs and reflection will occur in a structurally heterogeneous medium (Fig. 9). Our simulations predicted that, in the presence of changing curvature, the following three factors contribute to reflection: (1) late I_Na, whose timing depends on the curvature (Fig. 9); (2) I_CaL, which slowly reactivates before the propagated EAD occurs (Supplemental Fig. 6C); and (3) curvature-dependent electrotonic current (Supplemental Fig. 6E). All three factors working together determine the location of reflection in our model. Moreover, all three factors influence each other dynamically. This is illustrated in Supplemental Fig. 6D, which indicates the apparent origin of reflection. First, an EAD resulted from the mutual contribution in time and space of all of the above factors in each of the electrotonically coupled cells. Increased curvature resulted in an increase in the flow of retrograde depolarizing electrotonic current and decreased anterograde flow of repolarizing electrotonic current, which served to prolong the APD. As the APD was prolonged, I_CaL and I_Na reactivated (which is seen as humps). Sufficient prolongation of the APD aggravated this phenomenon to an extent that brought I_CaL and I_Na above the threshold, thus yielding a reflected beat. The feedback also worked in the opposite way; even before I_CaL and I_Na activated to the threshold level, their presence helped to prolong the AP via their electrotonic effect.

Overall, our simulations strongly support the experimentally derived conclusion that reflection is the result of both structural (local curvature) and ionic (I_Na, I_CaL) factors. As predicted by the numerical model (Fig. 9B and C and Supplemental Fig. 7), there is only a small window of parameters allowing for reflection to occur, which explains why the incidence of reflection in the experimental setting was relatively low. The role of APD prolongation was clearly demonstrated in the simulation.

A numerical study by Maoz et al. (2009) predicted that the heterogeneous expression of the transient outward potassium current results in an APD heterogeneity along a one-dimensional cable. In some cases, the APD heterogeneity triggered an EAD and reflection (phase 2 reentry). We have demonstrated that, in the absence of any electrophysiological gradients in ion channel expression or unexcitable regions, curvature effects associated with geometrical expansions can create a substrate for EAD formation and subsequent reflection.

Even in the presence of a structural substrate, there needed to be a sufficient level of excitability to facilitate re-excitation and reflection. Re-excitation and reflection always occurred at long pacing cycle lengths, when there were: (1) longer APDs and a higher incidence of single-cell EADs; and (2) greater availability of depolarizing currents and excitability. The Ad-Nav1.5 expression increased the peak and persistent I_Na density (Figs 3B–D and 4), APD (Fig. 5A and C), incidence of single-cell EADs (Fig. 5B) and incidence of reflection (Figs 3F and 6A). Figure 8 demonstrates that the increased APD, incidence of EADs and incidence of reflection were the result of increased persistent I_Na, in the absence of increased peak I_Na. Computer simulations suggested that the effect was related to the G_Na and the persistent I_Na density (Fig. 9 and Supplemental Fig. 7). Pharmacological activation of I_CaL (1 μm Bay K 8644) did not increase the incidence of reflection, although a role for I_CaL in EAD formation in the patterned monolayers cannot be ruled out. Supplemental Fig. 6C illustrates that reactivation of I_CaL provides additional depolarizing current to facilitate EAD formation.

In numerical simulations, Schwieler et al. (2008) suggested that reflection across a heterogeneous accessory pathway between the atrium and ventricle may lead to the initiation of atrial fibrillation. A novel finding in our study was that reentry was also initiated when a small area of the distal region became re-excited by the reflected wave, which led to wavebreak and functional reentry (Fig. 7B).

Re-excitation of the proximal tissue by a reflected wave was not the result of some type of pacemaker wave, alternative pathway, entrance block with exit conduction or (micro)reentry (Wit et al. 1972; Cranefield et al. 1973). The mechanism of reflection was rather a one-dimensional electrotonically mediated event. As demonstrated in this study, as well as by numerous groups experimentally (Rozanski et al. 1984) and in numerical simulations (Janse & van Capelle, 1982; Cabo & Barr, 1992; Maoz et al. 2009), reflection existed in a one-dimensional cable, ruling out the possibility of reentry. Next, in the present study, reflection was only considered when the entire preparation was activated by the anterograde propagating response prior to re-excitation, and the cells at the region of re-excitation could not have fully repolarized, which rules out reentry, pacemaker activity or delayed afterdeplarization. Therefore, based upon these criteria, reflection does not require a region of conduction block or delayed activation at the distal expansion, or an alternative pathway for conduction. Finally, the occurrence of re-excitation and reflection was greatest at lower excitation frequencies (<5 Hz; Fig. 6B), which was when the APD was most prolonged, there were single-cell EADs and there was a low incidence of conduction block. At the higher excitation frequencies (>5 Hz), there was APD shortening (Fig. 3E), no EADs or reflection (Fig. 6B), and the percentage of the preparations with conduction distally sharply decreased (Fig. 1D).

Clinical perspective

The heart is structurally very heterogeneous, but it does not frequently undergo arrhythmias. Interestingly, when additional pathologies, such as accessory pathways (Schwieler et al. 2008), replacement fibrosis (Coronel et al. 2005; Tanaka et al. 2007) or ischaemic or infarcted tissue (Janse & van Capelle, 1982; de Bakker et al. 1988, 1990) are involved, patients become highly prone to atrial and ventricular arrhythmias. Using a simple biological model that included structural heterogeneity, we obtained mechanistic insights into the initiation of arrhythmias, which may be of high clinical relevance. For instance, in the heart, narrow pathways connecting large tissue expansions may be the result of normal variations in wall thickness, fibre orientation, microvasculature, trabeculations and fibrosis (Hocini et al. 2002; Chang et al. 2007; Klos et al. 2008). In addition, in pathological states these heterogeneities can be exacerbated by other factors, such as the presence of accessory pathways (ie. Wolf–Parkinson–White syndrome; Schwieler et al. 2008), ischaemic or infarcted tissue (Janse & van Capelle, 1982; de Bakker et al. 1988, 1990), fibrosis (Coronel et al. 2005; Tanaka et al. 2007; Awad et al. 2008) and fibro-fatty infiltration (e.g. arrhythmogenic right ventricular cardiomyopathy; Awad et al. 2008). Such abrupt geometrical heterogeneities provide conditions for source-to-sink mismatch that may, depending upon excitability, lead to reflection and ultimately initiate ventricular tachycardia or ventricular fibrillation.

The model provided a new framework to examine the role that cardiac structure and alterations in ion channel expression and function have upon arrhythmogenesis. Results from this study offer insights into which patients may be at the greatest risk of ventricular tachycardia/ventricular fibrillation initiated by reflection.

Limitations

There are differences in ion channel expression and currents that shape the cardiac AP of rat and human hearts. However, despite the fact that adult myocytes can technically be cultured (Westfall et al. 1997), to our knowledge no one has been able to construct confluent electrically coupled monolayers. Thus, NRVM monolayers (even in the absence of t-tubules and reduced repolarization reserve) have become an established model to study electrical impulse propagation and arrhythmogenesis in the presence of structural heterogeneities and alterations in ion channel expression (Rohr et al. 1991; Iravanian et al. 2003; Munoz et al. 2007; Zlochiver et al. 2008).

Conclusions

Fully excitable tissue and abrupt geometrical expansions provided a substrate for local phase 2 and 3 re-excitation at the distal expansion, which led to reflection. Expression of Ad-Nav1.5 served to increase the peak and persistent I_Na density, APD, CV, and the incidence of EADs and reflection. A combination of a substrate (structural heterogeneity) and a trigger (increased I_Na and thus EADs) promoted reflection and arrhythmogenesis.

Glossary

Abbreviations

Ad-GFP

adenoviral expression of GFP, viral control

Ad-Nav1.5

adenoviral expression of human Nav1.5

AF

atrial fibrillation

AP

action potential

APD

action potential duration

CV

conduction velocity

EAD

early after-depolarization

GFP

green fluorescent protein

LQTS

long-QT syndrome

NRVM

neonatal rat ventricular myocytes

TSP

time–space plot

Author contributions

Conception and design, or analysis and interpretation of data: D.S.A., K.R.G., P.B.F., P.Y.S., S.M., J.J.; drafting the article or revising it critically for important intellectual content: D.S.A., K.R.G., J.J.; Final approval of the version to be published: D.S.A., K.R.G., P.B.F., P.Y.S., S.M., J.J.

Supplementary material

OLS Figure 1

OLS Figure 2

OLS Figure 3

OLS Figure 4

OLS Figure 5

OLS Figure 6

OLS Figure 7

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer-reviewed and may be re-organized for online delivery, but are not copy-edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors