Skin Relaxation Predicts Neural Firing Rate Adaptation in SAI Touch Receptors

Abstract

In response to ramp-and-hold indentation, the slowly-adapting type I (SAI) afferent exhibits an exponential decrease in its firing frequency during the hold phase. Such adaptation may be tied to skin relaxation but is neither well understood nor has it been quantitatively modeled. The specific hypothesis of this work is that skin relaxation is a primary contributor to observed changes in firing rate. Double exponential functions were fit to 21 responses from a mouse SAI afferent for both instantaneous firing rate and indenter tip force over time. The model was then generalized by using a linear transformation between fit parameters for force and firing rate data, allowing prediction of firing rates from force. The results show that the generalized model matches the recorded firing rate (R² = 0.65) equally well as fitting a double-exponential function directly to firing rate (R² = 0.67) for a second dataset. When the procedure was repeated with two D-hair fibers, the generalized model matched the recorded firing rate (R² = 0.47) much more poorly compared to the fitted double-exponential function (R² = 0.89). Thus, firing rate adaptation in SAI responses can be predicted by skin relaxation, whereas this factor alone did not adequately describe adaptation in the D-hair.

I. Introduction

Adaptation in neuronal firing rate has classically been explained as a function of the nervous system [1], although for responses from touch receptors, the skin may play a significant role [2]. Many touch-receptor afferents are rapidly adapting, meaning they fire only in response to moving stimuli [3, 4]. Slowly adapting afferents, including slowly-adapting type I (SAI) afferents, are responsive throughout sustained mechanical stimuli in addition to the onset and offset [5–7]. Transduction of skin deformation into action potentials in the SAI receptor occurs at Merkel cell-neurite complexes [8], which comprise a cluster of Merkel cells [9, 10] located in the basal layer of the epidermis with a connecting neuronal afferent [11]. This arrangement suggests that these end organs, and therefore the responsiveness of the SAI afferent, is intimately tied to the skin’s mechanics.

Others have examined how skin mechanics relate to SAI afferent firing characteristics. In particular, Pubols observed that firing rate declines as the skin relaxes in response to held indentation [2, 12, 13]. Such adaptation in the rate of neuronal firing therefore may be a direct consequence of the macro-level relaxation of the skin; however, mechanisms intrinsic to the fiber may also play a role. To fill a gap in the literature regarding the source of adaptation, this work seeks to quantify the relationship between indentation force and firing rate observed in the SAI.

We hypothesized that skin mechanics is a primary determinant of neuronal firing rates in SAI afferents. To test this, we sought to build a model to predict firing rates recorded from intact SAI afferents in an ex vivo skin-nerve preparation with only applied force as the input [14]. The initial efforts are described here, showing a strong dependence of SAI afferent firing on the force adaptation caused by viscoelastic relaxation of the skin.

II. Methods

A. Overview

We sought to build a predictive model that will use force as an input to predict firing rate as an output. Therefore, the objective of this work is twofold: 1) to analyze and fit a descriptive model, using curve fitting and the linear regression method of least squares, of force and firing rate in response to a ramp-and-hold stimulus performed with a mouse SAI afferent, and then 2) to create a generalized predictive model, using matrix algebra and a linear transformation, relating force domain parameters to the firing rate domain parameters. As the model in step 1 was built on training data, the generalized model of step 2 was tested against a recording from a second SAI afferent. This process was then repeated with a second afferent type (D-hair afferents) to test whether skin relaxation has a comparatively larger effect on the phenomena of firing rate adaptation for the SAI afferent compared to the D-hair afferent.

B. Experimental Setup and Procedure

The experiments concerning animals were approved by Institutional Animal Care and Use Committees of Baylor College of Medicine and the Department of Defense. Both male and female mice were used, age 7–15 weeks and weighing 22–24 g.

We used an ex vivo experimental setup, which allows for finer control of experimental conditions than the in vivo preparation described by Pubols [2, 12, 13] and others [15, 16]. We found that afferents responded consistently in this ex vivo preparation for up to 30 stimulations. To avoid fiber rundown [17], stimulation numbers for each afferent were kept under this threshold.

The experimental setup is as described by Wellnitz et al. [14]. A portion of nerve and the hairy skin of the hind paw were dissected and then pinned to a silicone-elastomer substrate (~5 mm thick) coating the bottom of a custom two compartment organ chamber. Synthetic interstitial fluid was perfused beneath the skin while nerve fibers were separated and draped over an electrode for differential recording. Calibrated force fibers were then used to locate the receptive field of single afferents and to estimate their mechanical thresholds. Responses were qualified as an SAI by the following characteristics: conduction velocity, >9 m·s⁻¹; mechanical threshold, <1 mN; punctate receptive field, <0.5 mm in diameter; slow adaptation; irregular firing pattern; low spontaneous firing rate; and no directional sensitivity to stretch [18–20]. Responses were qualified as a D-hair afferent by the following characteristics: conduction velocity, 1–11 m·s⁻¹; large, elongated receptive field (~2 mm); rapid adaptation to low forces with a slowly adapting response to high forces; and a low mechanical threshold, ≤0.4 mN.

Calibrated mechanical displacements were applied to the receptive field of the identified afferent by a custom-built z-stage indenter powered by a linear actuator (Ultra Motion, model D-A.25AB-HT17-2-BR/4.) The stimulus probe was a MACOR cylinder 3.4 mm in diameter with a fillet of radius 0.32 mm, which applied forces on the entire receptive field with minimal edge effects [21]. A load cell (Honeywell model 31) was connected to the probe. Extracellular readings were made using a differential amplifier (A-M systems Model 1800) and recorded with a DT304 A/D card (Data Translation) and SciWorks Experimenter software ver. 6.0 (DataWave). Multidimensional cluster analysis was used to sort individual action potentials.

The indenter applied a constant displacement while the applied force values were measured. The delivered stimuli were chosen to have an average applied force of approximately 500 mN. The indentations accelerated at a rate of 0.00127 mm/ms², reaching their target displacements within 80 ms, and were then held for 5 s. After a 25 s rest period, the indentation was repeated. Twenty-one stimuli with this timing were delivered per afferent.

C. Data Analysis

Extracellular recordings for 84 stimulations [21 stimulations × (2 SAI afferents + 2 D-hair afferents)] were used to calculate the dependent measure, instantaneous firing rate, and the independent measure, force. Both measures were calculated within an analysis window of 2.5 sec beginning at stimulus hold, Fig. 1. Stimulus hold begins when force reaches its peak. In this region the indenter is held at constant displacement, therefore changes in force are a result of skin relaxation.

Figure 1.

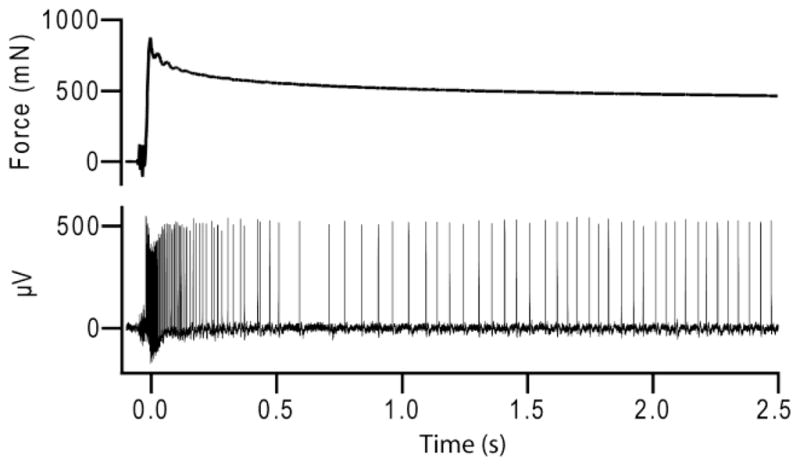
Example traces of force at probe tip and corresponding SAI afferent action potential train to a ramp-and-hold stimulus.

D. Model

We described skin relaxation during the static phase in response to a stimulation of constant displacement. Using the Matlab Curve Fitting Toolbox (Matlab version 7.9.0.529, Curve Fitting Toolbox 2.1), we fit a double-exponential to the aggregate instantaneous firing rate for the 21 stimulations of the first afferent over the 2.5 sec window. Single exponential and power law fits were considered in a pilot study, but had lower R² values than double-exponential models, as has been observed [22]. The double-exponential model is shown in Equation 1,

$$FR(t)=A_{fr}{e}^{-b_{fr}t}+C_{fr}{e}^{-d_{fr}t}$$ (1)

where FR is the instantaneous firing rate as a function of t, time, A_fr and b_fr are parameters fit to the rapid skin relaxation, and C_fr and d_fr are parameters fit to the slow creep relaxation. The firing rate domain parameters resulting from the fit make up the vector B_fr, where B_fr = {A_fr b_fr C_fr d_fr}.

We followed the same procedure to create a double-exponential fit for force, F(t), against time. The force domain parameters resulting from the fit make up the vector A_f, where A_f = {A_f b_f C_f d_f}.

Using matrix algebra, we found a linear transformation f to relate the firing rate domain parameters with the force domain parameters using ratios between the two sets of parameters. The transformation was calculated as shown in Equation 2,

$$f_A=A_{fr}/A_f$$ (2)

and is repeated for parameters b, C, and d. This relationship, shown in Equation 3,

$${\mathbf{B}}_{fr}=f({\mathbf{A}}_f)$$ (3)

connects the relaxation of skin as measured by the load cell to the changing firing rate within the training dataset from an SAI afferent. This model was then validated on a testing dataset from an independent SAI by predicting firing rate over time from recorded force and the linear transformation, f, calculated from the training set (Fig. 2). We then compared the predicted firing rate to the recorded firing rate. This process was also applied to two D-hair responses.

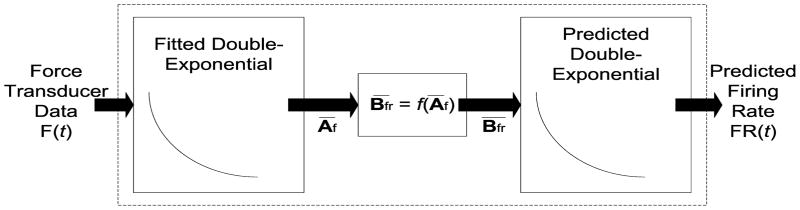
Figure 2.

The model produces firing rate predictions given force over time. Fitting the vectors A_f and B_fr are done in the intermediate step described in the text. The predicted firing rate FR(t) is then compared with the recorded firing rate.

III. Results

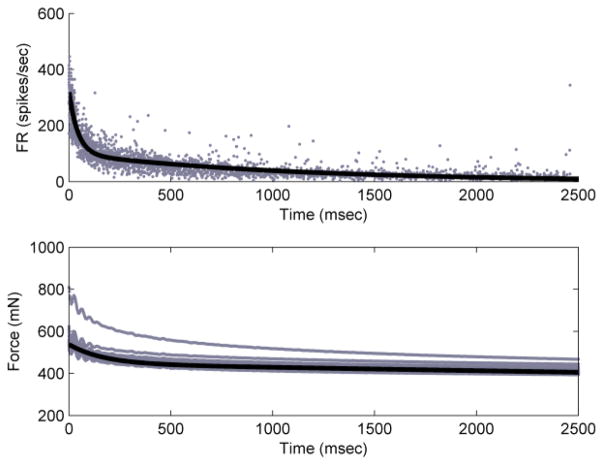
Double-exponential fits for both instantaneous firing rate and force for an SAI afferent were made (Fig. 3). The firing rate domain parameters for the fit were A_fr = 224, b_fr = 2.31*10⁻², C_fr = 99.8, and d_fr = 9.28*10⁻⁴, fit with R² = 0.82. The force domain parameters for the fit are A_f = 92.6, b_f = 5.92*10⁻³, C_f = 445, and d_f = 3.78*10⁻⁵, fit with R² = 0.46. These fits are shown in Fig. 3. The apparent outlier in the force plot is the first indentation, observed because the skin was not pre-conditioned, according to plan.

Figure 3.

Double-exponential fits to the SAI response training data. Top panel shows instantaneous firing rate vs. time (R² = 0.82) and bottom panel shows force vs. time for training SAI (R² = 0.46).

Using these parameters, we found a linear transformation f to relate the force domain parameters with the firing rate domain parameters. The transformation f was calculated to be f_A = 2.42, f_b = 3.90, f_C = 0.224, and f_d = 24.5.

This model was validated with recordings from a second SAI afferent. Using this model to predict the firing rate of this SAI response, we matched the actual data with error R² = 0.65 (Fig. 4). For comparison, fitting a double-exponential directly to the firing rate data provides an R² = 0.67.

Figure 4.

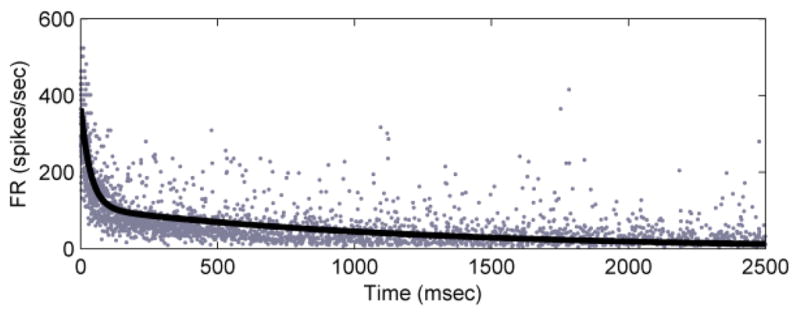
Model prediction of instantaneous firing rate for a second SAI afferent, with force input to the generalized model (R² = 0.65).

We repeated this process with responses from D-hair afferents. For one D-hair afferent (Fig. 5), the firing rate domain parameters for the fit were A_fr = 212, b_fr = 2.43*10⁻², C_fr = 26.5, and d_fr = 5.82*10⁻⁴, fit with R² = 0.72. The force domain parameters for the fit were A_f = 370, b_f = 5.25*10⁻², C_f = 385, and d_f = 4.76*10⁻⁵, fit with R² = 0.80.

Figure 5.

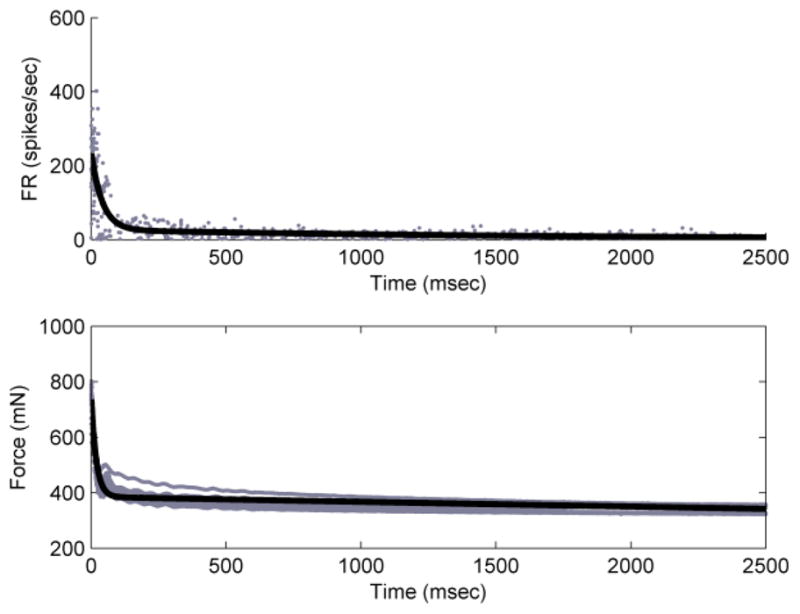
Double-exponential fits to the D-hair response training data. Top panel shows instantaneous firing rate vs. time (R² = 0.72) and bottom panel shows force vs. time for training D-hair (R² = 0.80).

As before, the transformation f was calculated and found to be f_A = 0.574, f_b = 0.463, f_C = 6.88*10⁻², and f_d = 12.2. Using this model to predict the firing rate of a second D-hair afferent we matched the actual data with error R² = 0.47 (Fig. 6). Fitting a double-exponential directly to the firing rate data provides an R² = 0.89.

Figure 6.

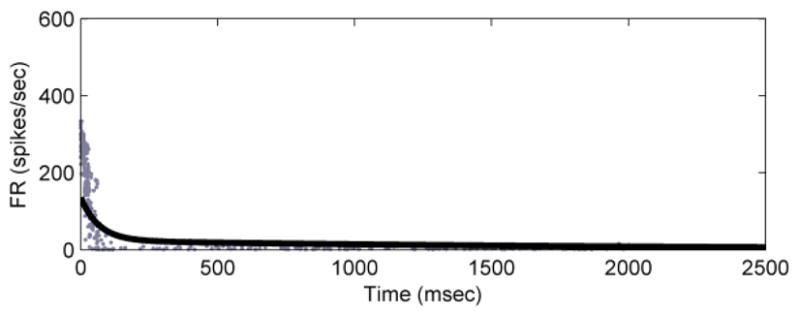
Model prediction of instantaneous firing rate for a second D-hair afferent, with force input to the generalized model (R² = 0.47).

IV. Discussion

We observed that skin relaxation recorded from the load cell closely follows the expected double-exponential function. SAI afferent firing rate follows a similar double-exponential, which is well-predicted by a linear transformation of force. This model is different in detail than that proposed by Pubols, who concluded that the relationship between firing rate and force could best be described with a logarithmic function, but has similar implications about the relationship of force and firing rate. Thus, we preliminarily conclude that skin relaxation is a primary contributor to adaptation in SAI responses.

By contrast, firing responses of D-hair afferents were not well predicted by a simple linear model, though the time course of skin relaxation measured at the probe tip remained the same as for SAI afferents. Although their end organs have not been definitively identified, D-hair afferents are proposed to innervate down hair follicles deep in the dermis. Thus it is possible that force values measured at the epidermal surface do not adequately reflect relaxation at the afferent’s end organ. Additionally, the receptive field of the D-hair afferent is much larger than the SAI, which means there could be more variability in the response due to stimulus placement as compared to the SAI. Alternatively, other factors related to the fiber and/or end organ might play a greater role in determining D-hair response characteristics.

This paper focused on studying the macro-level relaxation of the skin. Adaptation in firing rate is a complex biological phenomenon that is also likely to include factors at the cellular level of the neuron. We will further separate and classify this complex relationship in future work, including detailed modeling using first-principles finite element analysis of skin mechanics.