Abstract
One of the key problems of motor control is the redundancy problem, in particular how the central nervous system (CNS) chooses an action out of infinitely many possible. A promising way to address this question is to assume that the choice is made based on optimization of a certain cost function. A number of cost functions have been proposed in the literature to explain performance in different motor tasks: from force sharing in grasping to path planning in walking. However, the problem of uniqueness of the cost function(s) was not addressed until recently. In this article, we analyze two methods of finding additive cost functions in inverse optimization problems with linear constraints, so-called linear-additive inverse optimization problems. These methods are based on the Uniqueness Theorem for inverse optimization problems that we proved recently (Terekhov et al., J Math Biol 61(3):423–453, 2010). Using synthetic data, we show that both methods allow for determining the cost function. We analyze the influence of noise on the both methods. Finally, we show how a violation of the conditions of the Uniqueness Theorem may lead to incorrect solutions of the inverse optimization problem.
Keywords: Inverse optimization, Optimization, Uniqueness Theorem, Cost function, Grasping, Force sharing
1 Introduction
The problem of motor redundancy, emphasized by Bernstein (1967), remains one of the central in the current motor control and biomechanical studies. One can say that, the problem consists in understanding how the human motor system benefits from the redundant degrees of freedom it possesses. The fact that humans tend to perform the same motor task in very similar manner suggests that the performance is optimal in some sense. In other words, among all possible movements satisfying constraints and goals of a motor task, humans prefer those that minimize a certain cost function. Starting from a pioneering study by Nubar and Contini (1961), this view gained its popularity. It is interesting to mention that the authors suggested as a possible cost function used by the central controller minimization of a ‘muscular effort’, the sum of squared values of muscle moments of force.
The above view of the problem of human movement control has been adopted in a variety of studies. Among them are the control of arm reaching (Biess et al. 2007; Cruse et al. 1990; Engelbrecht 2001; Flash and Hogan 1985; Plamondon et al. 1993; Tsirakos et al. 1997; Hoff and Arbib 1993; Harris and Wolpert 1998; Uno et al. 1989; Ben-Itzhak and Karniel 2008; Plamondon et al. 1993; Berret et al. 2008), walking (Anderson and Pandy 2003; Prilutsky 2000; Prilutsky and Zatsiorsky 2002; Pham et al. 2007; De Groote et al. 2009), standing (Guigon 2010; Martin et al. 2006; Kuo and Zajac 1993), finger manipulation (Zatsiorsky et al. 2002; Pataky et al. 2004; Friedman and Flash 2009; Lee and Zhang 2005; Niu et al. 2009; Aoki et al. 2006; Pataky 2005; O’Sullivan et al. 2009; Crevecoeur et al. 2010) and especially force sharing among the agonist muscles (Crowninshield and Brand 1981; Binding et al. 2000; Ding et al. 2000; Collins 1995; Pandy 2001; Davy and Audu 1987; Prilutsky and Gregory 2000; van Bolhuis and Gielen 1999; Buchanan and Shreeve 1996; Fagg et al. 2002; Happee and der Helm 1995; Kaufman et al. 1991; van Dieën and Kingma 2005; Hughes et al. 1994; Nussbaum et al. 1995; Herzog and Leonard 1991; Prilutsky et al. 1997; Schappacher-Tilp et al. 2009; Ait-Haddou et al. 2000, 2004; Amarantini et al. 2010; Challis 1997; Dul et al. 1984b, a; Heintz and Gutierrez-Farewik 2007; Herzog 1987; Menegaldo et al. 2006; Pedersen et al. 1987; Pierce and Li 2005; Prilutsky et al. 1998; Raikova 2000; Raikova and Aladjov 2002; Hughes and Chaffin 1995; Seth and Pandy 2007; van den Bogert 1994; Vilimek 2007; Zheng et al. 1998; Vigouroux et al. 2007; Czaplicki et al. 2006; Anderson and Pandy 1999; Kuzelicki et al. 2005). In these studies, the researches usually agree on the constraints and the goals of a particular movement, which are often determined by the task itself and the biomechanics of the human body. On the contrary, the consensus on the employed cost function is very rare. The cost functions have usually been proposed based on the intuition of the researcher and common sense.
Adopting the optimization-based view of the motor control has led to new mathematical problem, namely the identification of the cost function based on the experimental data. It can be called the problem of inverse optimization, where the word ‘inverse’ means that the problem is opposite to the common optimization: here the optimal solution is known (recorded movement characteristics), whereas the cost function is not. The problem is usually regarded for a set of known constraints and a set of solutions, i.e. experimental data corresponding to the actually performed movements. Most commonly this problem is approached in ‘cut-and-try’ manner: the researcher guesses what the central nervous system (CNS) might optimize in a particular situation and then validates the guess by comparing predictions of the model with the available experimental data.
In the last years, few more systematic approaches to the problem were proposed (Bottasso et al. 2006; Mombaur et al. 2010; Liu et al. 2005). Similar problem was addressed in the domain of reinforcement learning (Abbeel and Ng 2004). In both cases, the cost function in inverse optimization or the reward function in inverse reinforcement learning was assumed to belong to a known parametrized class. If so, the problem of the inverse optimization can be reduced to finding values of parameters, for which the discrepancies between the experimental data and the cost function-based predictions are minimal. Such approach is an evident step forward if compared to the simple ‘cut-and-try’. However, the proposed methods do not address the question of whether the cost function can be determined uniquely.
To emphasize the importance of this question, we propose the following mental experiment. A subject performs the four-finger pressing task with the requirement of making the total pressing force equal to a target value Ft. Assume that the performance is ideal, i.e. it is optimal and is not subjected to noise of any nature. Moreover, assume that the sharing pattern (percentage of the total force produced by individual fingers) is the same for all values of the target force and hence the individual finger forces Fi, i = 1, …, 4, satisfy the equations:
| (1) |
where ai are the parameters of the force sharing pattern.
The observed force sharing pattern might arise as a solution of the optimization problem:
subject to a constraint
and inequality constraints, reflecting the fact that the finger forces cannot be negative and must stay within the range of physiologically possible values.
Now we would like to determine the cost function J, whose minimization would result in the observed sharing profile (1). It appears that there exist infinitely many essentially different cost functions, satisfying this requirement. For example, one can verify that the functions
and
both can explain the sharing patterns with equal success. Moreover, for any increasing continuously differentiable function g, the cost function
can do that as well.
For given example, there exist infinitely many essentially different cost functions explaining the same experimental data. We would like to note that our mental example is not completely artificial. In fact, as it has been shown by Niu et al. (2009) for prismatic grasps, the normal finger forces tend to scale linearly with the weight of the grasped object, while the force sharing pattern remains relatively unchanged (in this study, the subjects held a vertically oriented object at rest and the required moment of force was zero).
Clearly, any method of solving inverse optimization problems would at most result in one of the infinity of the possible cost functions if applied to the data of our mental experiment. Such a ‘solution’ can hardly be accepted in motor control or biomechanical studies. Indeed, it follows, in particular, that two different methods applied to the same data set may result in significantly different cost functions. As a result, one can expect that for the same motor action various researches would propose a variety of cost functions, each of them being equally good in explaining experimental data. Such a situation was reported for force sharing problem (Collins 1995; Buchanan and Shreeve 1996; van Bolhuis and Gielen 1999), for finger force distribution in prismatic grasping (Zatsiorsky et al. 2002) and for trajectory planning in reaching task (Plamondon et al. 1993) as well as for some other tasks. On the other hand, the same method, when applied to the data sets from different motor tasks, could result in different cost functions, even if the CNS uses the same one for all the tasks.
These considerations illustrate the necessity of formulating the conditions, under which the inverse optimization problem can be solved unambiguously. Recently, we obtained such conditions for inverse optimization problems with additive cost function and linear constraints (Terekhov et al. 2010). Such an optimization problem consists in minimization of a cost function of the kind
| (2) |
subject to linear constraints:
| (3) |
where x is an n-dimensional vector, fi are scalar functions, C is a (k × n) matrix of constraints and b is a k-dimensional vector.
In Terekhov et al. (2010), we presented some results of theoretical analysis of the inverse optimization problem (2) and (3), the most significant of which was Uniqueness Theorem. This theorem gives some conditions, under which the inverse optimization problem can be solved unambiguously. A summary of the results of Terekhov et al. (2010) is provided in the following section. Essentially, the Uniqueness Theorem states that the solution of the inverse optimization problem is unique if optimal solutions are available for every vector b from a domain of the k-dimensional space. This means that if a problem has k linear constraints then in order to find the cost function from experimental recordings the values of all constraints must be varied independently in the experiment.
The conditions of the Uniqueness Theorem are formulated for an ideal situation: when infinitely many experimental observations are available (every possible b from a domain) and those observations are not subjected to any noise (precise values of x are assumed to be available). Clearly, such situation can never happen in practical applications. However, as we show in this article, the obtained conditions of uniqueness do not lose their value because of that.
This article has three following goals: (1) to propose methods of finding an approximation of a cost function given a limited set of noisy experimental data, which relies on the uniqueness conditions reported in Terekhov et al. (2010); (2) to illustrate the fact that these conditions indeed guarantee unambiguous identification of the cost function even in practical situations; and (3) to show that violation of the above conditions may lead to an incorrect solution of the inverse optimization problem.
The article has the following structure. We, first, give a short summary of the theoretical results from Terekhov et al. (2010) obtained for the inverse optimization problems (2) and (3). Then, we propose two methods of solving such problems and compare their efficiency. We illustrate applicability of the methods by analyzing synthetic data. We show that, as long as the uniqueness conditions are satisfied, the methods result in a unique solution. More precisely, we show that if two different parametric classes are used to find two approximations of the same cost function from experimental data, then these two approximations are close even if their symbolic representations are significantly different. Next, we illustrate that violation of each of the conditions of Uniqueness Theorem from Terekhov et al. (2010) may lead to an erroneous solution of the inverse optimization problem.
2 Theoretical considerations
Common sense guides us to conclude that the problem of inverse optimization can never be solved uniquely: if a function J explains given experimental data, so does the function f (J), where f is any strictly increasing function. The cost function can be only determined up to the class of essentially similar cost functions: two functions are said to be essentially similar if under any possible constraints the same values of the arguments bring global minima to both of them.
Consider, for example, two cost functions:
and
Evidently, whatever are the constraints, the vector x is a solution of optimization problem with J1 if and only if it minimizes J2. In other words, with respect to the optimization problems, the essentially similar cost functions are indistinguishable. Thus, one cannot expect to solve inverse optimization problem better than up to the class of essentially similar functions unless additional assumptions are made on the cost function.
The solutions of the optimization problem (2) and (3) for a set of different vectors b form a subset X* of ℝn. Every point of this set is optimal under the constraints with some value b and, consequently, at each point the Lagrange principle must hold. Here and on we assume the function J to be analytic.
The Lagrange principle
For every x* ∈ X*, the function J from (2) satisfies the equation:
| (4) |
where (prime symbol denotes derivative over the variable),
| (5) |
and I is the n × n unit matrix.
The Lagrange principle gives the condition (4), which must be satisfied by the true cost function, i.e. the function which produced the experimental data given the constraints. In other words, it gives necessary condition for a cost function J to be the true one. It appears that in some cases this necessary condition is also sufficient. The latter is formalized in the Uniqueness Theorem.
The Uniqueness Theorem
If two nonlinear functions J1(x) and J2(x) defined on a domain X inside n-dimensional space satisfy the Lagrange principle for every point x in the set X* with the constraints matrix C and
J1 and J2 are additive,
X* is a smooth k-dimensional hypersurface,
the number of constraints k is greater or equal to 2,
the matrix Č defined in (5) cannot be made block-diagonal by simultaneous reordering of the rows and columns with the same indices,1
then
| (6) |
for every x inside the hyper-parallelepiped surrounding the hypersurface X*. The hyper-parallelepiped is defined as follows: , r is a non-zero scalar value and q is an arbitrary k-dimensional vector.
The proofs of these statements can be found in Terekhov et al. (2010).
In other words, the Uniqueness Theorem defines conditions, under which the inverse optimization problem can be solved almost unambiguously. Indeed, it states that if one has a solution of the inverse optimization problem, J1(x), then the true cost function J2(x) is essentially similar to J1(x) up to unknown linear terms qT Cx.
These terms appear because the values qT Cx are predefined by the constraints (3) and are equal to qT b. Resolving this unambiguity requires additional experimental data, obtained under the conditions with different constraint matrices. More precisely, if L additional experimental points x1, …, xL belonging to the hyper-parallelepiped are available, each of them obtained under the constraints with the matrix Cℓ, ℓ = 1, …, L, and if the matrix
| (7) |
has the rank equal to n, then the vector q in (6) can be determined unambiguously.
The Uniqueness Theorem requires that the solutions form a k-dimensional hypersurface, which assumes that they are known for an infinite number of vectors b in (3). This requirement can never be met in practice, and, hence, the cost function can never be determined precisely. It can be only approximated; the approximation may be close to the true cost function.
3 Methods
A typical approach to numerical approximation of a function may consist in defining ad hoc a set of basis functions and then to find the coordinates of the desired function in this basis. For example, if polynomial functions are chosen as basis, one obtains Taylor’s decomposition of a function. If trigonometric functions serve as basis then the decomposition is called Fourier decomposition. The choice of the basis functions is biased to prior expectations of the properties of the desired function. In general, the basis consists of an infinite number of basis functions (for polynomials it can be: 1, x, x2, x3, etc.); however, in practical applications, we can obtain only an approximation of the desired function and consequently we can consider a finite number of basis functions.
The assumption of additivity of the cost function allows one to use scalar functions of scalar arguments as basis for each component fi of the desired cost function (2). For simplicity of notations, we assume that the basis functions are the same for each component. This assumption can be easily removed.
A general form of the approximation of the cost function (2) is given by the formula:
| (8) |
where m is the number of basis functions and h j is the j -th cost function. In other words, we use a weighted sum of the basis functions h j (xi) to approximate the true cost function. The approximation is then defined by the weights ai j. In general, the parameters of the approximation (here weights) are not obliged to occur linearly in the approximation. However, as it is shown below, the chosen form of the approximation significantly facilitates the solution of the inverse optimization problem.
As it was noted above, for a fixed constraints matrix C the solution of the inverse optimization problem can be determined only up to linear terms. This fact makes the linear functions play a special role in finding the cost functions. Here and on we assume that the first basis function is always identity:
| (9) |
In addition, we never include constant function into the basis because the inverse optimization problem can only be solved up to the class of essentially similar cost functions.
Now we can formulate the inverse optimization problem that we are addressing:
Given a finite set of solutions of the optimization problem with additive cost function (2) and linear constraints (3), find coefficients of the best approximation (8) of the true cost function (2). The set of solutions is assumed to be obtained for N different vectors b from (3), such that the linear space spanned over all b has dimension k. Here and on the set of solutions is also called ‘experimental data’.
The words ‘the best approximation’ require additional explanation. It is clear that the best approximation is the one which is the closest to the true cost function. However, since the true cost function is unknown such measure is inaccessible. We use two criteria of what can be considered as ‘the best approximation’. Each of them produces a method of finding the approximation (described in the ensuing sections).
We would like to emphasize that each of the following methods is applicable only when conditions of the Uniqueness Theorem are satisfied, in particular, when the experimental data points tend to lie on a k-dimensional surface.
3.1 Method of nested optimization (NOP)
We borrowed the first method from the work of Bottasso et al. (2006). Evidently, if the approximation of the cost function equals the true cost function, then it must be minimized by the experimental values x*s. If the approximation deviates from the true function, or if the values x*s are not known precisely, then it is minimized by some other values xs, which in general are different from x*s. However, if the deviation is small, the difference between xs and x*s can be expected to be small as well. We can use the distance between xs and x*s as the first criterion of the quality of the approximation. The method then consists in solving the following nested optimization problem.
The outer problem
| (10) |
searches for the parameters of the cost function approximation a11, …, anm, which minimize the discrepancy between the experimental observations x*s and model predictions xs.
The inner optimization problem determines the model predictions xs for the given parameters of the approximation:
subject to the experimental constraints, which in this case are linear:
| (11) |
The presented nested optimization problem is computationally very expensive because for every iteration of the outer minimization it requires solving N inner optimization problems. Bottasso et al. (2006) proposed to transform this nested optimization problem into single optimization problem of higher dimension by substituting the inner optimization problem with necessary conditions of optimality from the Lagrange principle. In our case of linear constraints and additive cost function, the latter can be done rather easily.
The inner optimization problem can be replaced with the equation from the Lagrange principle:
| (12) |
where Č is defined in (5) and
| (13) |
As a result, the nested optimization problem transforms into a single optimization problem with the cost function (10) and constraints (11) and (12).
3.2 Method derived from analytical inverse optimization results (ANIO)
The second criterion is directly based on the analytical findings presented in Terekhov et al. (2010). According to the Lagrange principle for inverse optimization if a cost function Ja reaches its minimum at a point xs then Eq. 12 must be satisfied. In ideal case, we might determine the coefficients a by resolving this equation on the experimental data. However, since the latter usually contain noise, this equation may be inconsistent. Instead, we can demand the equation to be satisfied as well as possible meaning that the solution minimizes the following function:
| (14) |
where J′(x*s) is defined in (13).
3.3 Regularization of the methods
It must be noted that both methods in the form they are currently formulated have infinitely many solutions with respect to the coefficients ai j, among which there are two cases, which must be avoided: (i) when all ai j are equal to zero and (ii) when only ai1 do not vanish, i.e. the approximation is a linear function of xi. Both cases must be avoided, because they violate conditions of the Uniqueness Theorem. In order to make the methods applicable, they must be regularized, so that the singular cases are excluded and there exists unique solution for the problem.
In order to avoid the singular cases, we demand that the coefficients ai j, j = 2, …, m (i.e. coefficients of non-linear functions h j) do not vanish simultaneously. To ensure that the problem has a unique solution, we exclude two sources of ambiguity. The first one comes from the fact that the inverse optimization problem can only be solved up to the class of essentially similar cost functions. As a result, multiplying all coefficients ai j by the same value r does not influence solution of the problem. In order to eliminate this source of ambiguity and to prevent all coefficients in front of non-linear basis functions from vanishing, we introduce rather arbitrary normalizing constraints on all ai j, j = 2, …, m:
| (15) |
Here, we choose the normalizing constraints to be linear, instead of traditionally used quadratic constraints, because linear constraints are easier to satisfy when solving corresponding optimization problem.
The other source of ambiguity is related to the presence of unknown linear terms in Eq. 6. As a consequence, replacing the coefficients of the linear terms a1 = (a11, …, an1)T with a1 + CT q, q ∈ ℝk, does not cause any changes neither in minimized functions (10) and (14) nor in constraints (12). In order to avoid this ambiguity, we require the vector a1 to be the shortest among all a1 + CT q. This requirement corresponds to the equation:
| (16) |
Indeed, for every vector a1, we can define a unique vector q0, which corresponds to the shortest vector among all a1 + CT q:
The solution q0 can be found analytically:
In turn, the shortest vector
and, consequently, the requirement of the vector a1 to be the shortest among all a1 + CT q yields (16).
3.4 About the numeric implementation of the methods
The presented methods require minimization of the criteria (10) or (14) subject to constraints. In both cases, the minimized criteria are quadratic: in NOP, it is quadratic with respect to the model solutions xs, while in ANIO, it is quadratic with respect to the parameters of the approximation ai j. The NOP minimizes the function (10), which depends on n × m parameters of approximation and n × N values of the model solutions xs. The function is minimized subject to k × N linear constraints (11), (n − k) × N nonlinear constraints (12) and common for both problems linear regularization constraints (15) and (16) of total rank k + 1. We do not see an easy way to solve this optimization problem and cannot propose at the moment anything better than to use general methods of optimization for finding its solution. In particular, we used Matlab function fmincon. To facilitate the computations, we provided a Jacobian matrix of the function (10). In our computations, we used the experimental values of x*s as initial values of xs and random numbers between −1 and 1 as initial values for the coefficients a11, …, anm. The minimization was performed 10 times, and then the solution with the smallest value of SI was selected.
The ANIO minimizes the function (14) of n × m parameters of approximation only. Just like NOP, it is subject to k + 1 regularization constraints (15) and (16). The fact that the cost function is quadratic and the constraint equations are linear allows to find the solution of the problem analytically. Particular formulae are presented in Appendix.
For better stability of the methods, it is preferred if the experimental data are normalized, so that they have zero mean and unit standard deviation. We used this normalization when determined the approximations from noisy experimental data in Sect. 4.3. All plots and cost functions in the article are presented in the original scale of the experimental data.
4 Computational experiments
The aims of the current section are: to demonstrate the fact that the methods can correctly find the approximation of the cost functions if the inverse optimization problem satisfies the conditions of the Uniqueness Theorem; to show that unique approximation is impossible if any of the Uniqueness Theorem conditions is violated; to compare the performance of the proposed methods. For these purposes, we build a synthetic optimization problem, for which we know the cost function (true cost function) and can produce as much experimental data as we need. We will apply NOP and ANIO methods to the synthetic experimental data and compare the approximations with the true cost function.
4.1 Synthetic inverse optimization problem
Here, we formulate the synthetic inverse optimization problem, used hereafter. We choose the cost function to be additive, as it is required by the first condition of the Uniqueness Theorem. For simplicity of notation and illustration, we restrict ourselves to the 3D case. We have chosen the following cost function:
| (17) |
where
| (18) |
When choosing the cost function, we required that the function should be convex and sufficiently simple computationally, but at the same time that it could not be approximated by finite number of most typical basis functions: polynomials.
4.1.1 Main set of experimental data
For the selected cost function, we must provide a set of synthetic experimental points, e.g. the solutions of the optimization problem for a set of constraint. We impose the following constraints:
| (19) |
If the values x1, x2, x3 were the forces of three digits, these constraints would correspond to predefined total force of the digits and total moment with respect to the point of the second digit placement. However, we prefer not to focus on any particular interpretation of the synthetic inverse optimization problem we construct.
The readers can verify that the matrix Č of the constraints (19) cannot be made block diagonal by simultaneous reordering rows and columns with the same indices, i.e. the problem is non-splittable. The rank of matrix equals 2, and consequently the conditions 3 and 4 of the Uniqueness Theorem are satisfied.
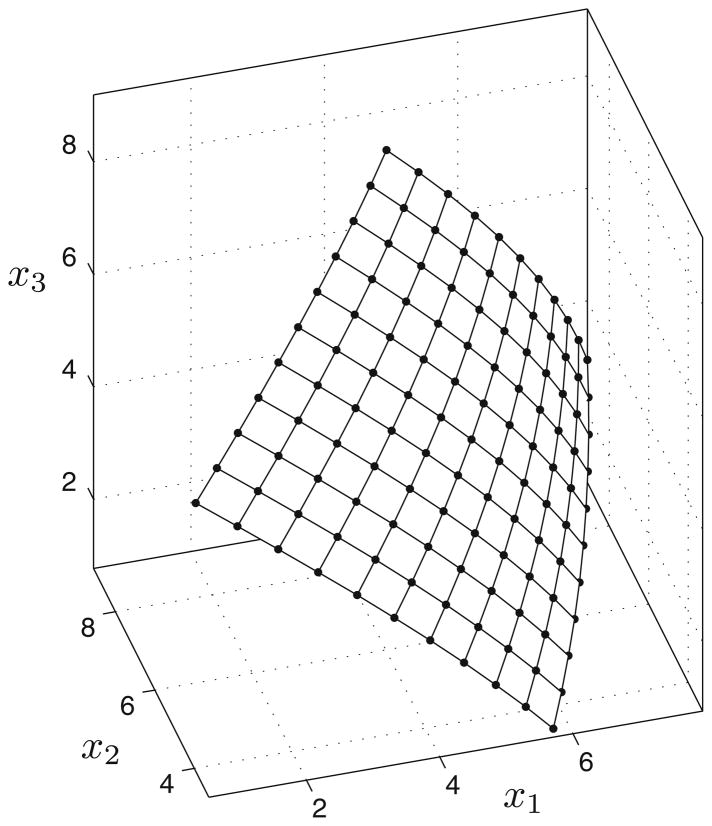
The values b1 and b2 in (19) vary independently in the range 10 ≤ b1 ≤ 20, −5 ≤ b2 ≤ 5 with the step size equal to 1. Corresponding solutions of the optimization problem (17) and (19) are presented in Fig. 1. It can be clearly seen that the solutions tend to form a 2D surface, which allows us to assume that the second condition of the Uniqueness Theorem is satisfied. On the whole, the experimental data count 121 points in 3D space. The set, in which the inverse optimization problem can be solved, lies inside the minimal parallelepiped enclosing the experimental surface and whose facets are parallel to the coordinate planes. For the presented data, the parallelepiped is defined as
Fig. 1.
The surface of solutions of the synthetic optimization problem (17) and (19). The nodes of the lattice correspond to the optimal solutions, and the edges are added exclusively for illustrative purpose
4.1.2 Experimental data for determining linear terms
Presented experimental data are sufficient for finding an approximation of the cost function inside , but only up to unknown linear terms (see details in formulation of Uniqueness Theorem). In order to determine the linear terms, one must provide experimental data, lying inside the parallelepiped , but obtained under new constraints, such that joint matrix Č0 defined in (7) has full rank.
We assume that in addition to solutions of the optimization problem (17) and (19), few data points obtained under the constraints
| (20) |
are available. The value b3 varies in the range 12 ≤ b3 ≤ 24 with the step equal to 4. This results in 4 data points, corresponding to solutions of the optimization problem (17) and (20). The range of variation of b3 is chosen in such a way that the solutions lie inside the parallelepiped .
4.2 Approximation of the cost function
Having sufficient, according to the Uniqueness Theorem, amount of experimental data, we can apply the described methods and obtain an approximation of the cost function (17). The first step to do that is to fix the basis functions. Of course, we might pick the functions f1, f2 and f3 as basis and then approximation would be precise, however, this case represents no interest since in real applications the parametrized class, to which belongs the desired cost function, is rarely known. We use two sets of basis functions. The first one, the most natural, in our opinion, is the class of polynomials. Therefore, we choose:
We don’t use higher powers, because, as we show below, the fourth-order polynomials are able to provide very precise approximation of the desired cost function.
One of our aims is to show that the uniqueness of the approximation in general does not depend on the choice of the basis functions. To do that we use the second set of the basis functions, which we arbitrary pick to be exponential:
Here, we limit the number of the basis functions for the same reason as above.
We would like to emphasize that since linear functions play a special role in linear-additive inverse optimization problems (see Uniqueness Theorem for details), we include them in both sets of basis functions.
We apply NOP and ANIO methods to obtain approximations of the cost function. We use the following schema: we first use the experimental data obtained under the constraints (19) in order to find the approximation containing unknown linear terms, then apply the same method to determine these linear terms from the experimental data, obtained under the constraint (20).
Both methods perform nearly equally good for finding the approximation of the cost function (17). Here, we present results obtained using ANIO; the results for NOP are indistinguishable.
The result of application of the algorithm is the set of parameters and of polynomial Jp and exponential Je approximations of the cost function (17):
As the first test, we determine the ability of the approximations Jp and Je to explain the experimental data, used for their identification. The distances between the experimental data and the data points, obtained by minimizing Jp or Je subject to constraints (19), are very small: the average value equals 0.02 for polynomial approximation and 0.03 for exponential, that corresponds to 0.9 and 1.3% of standard deviation of the experimental data, respectively. We would like to note that absolute coincidence between the experimental and recomputed points is impossible because the cost function (17) cannot be approximated by finite number of basis functions.
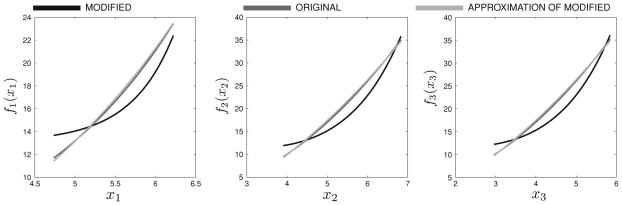
More interesting would be to compare the approximations with the true cost function, e.g. and with fi. However, it is not immediately clear how to do it, because the functions J = f1(x1) + f2(x2) + f3(x3) and J = k(f1(x1) + r1) + k(f2(x2) + r2) + k(f3(x3) + r3) are essentially similar and for the optimization problem they are nothing but two different representations of the same cost function, while if plotted together these functions look differently.
To make the comparison possible, we substitute the approximation with another function, essentially similar to it, but at the same time being as close to the true cost function as possible. More precisely, we substitute the functions with k(fi (·) + ri), where the values k, r1, r2, r3 minimize the difference between the terms of the approximation and the true cost function, defined as follows:
| (21) |
Similarly for
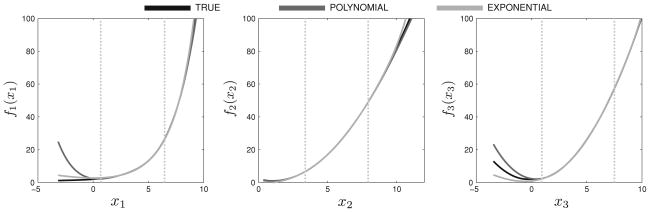
The functions and after the described linear corrections are presented in Fig. 2. As one can see, they are nearly indistinguishable from the true functions fi within the parallelepiped , which borders are denoted by dashed vertical lines in Fig. 2. The latter is not true outside of . Since the experimental data entirely lie within , we have no information about the cost function outside of the parallelepiped. In other words, changing the cost function (17) outside of would not lead to any change in experimental data.
Fig. 2.
The true cost functions and two approximations, obtained using ANIO method: polynomial and exponential. Dashed vertical lines denote minimum and maximum experimental value of the corresponding variable. It can be seen that the approximations fit the true cost functions rather precisely inside the region, denoted by dashed lines, but not outside of this region
The approximations Jp, Je of the cost function (17) after the linear correction are the following:
When written down, the approximations Jp and Je do not resemble at all neither the true cost function J nor each other. At the same time, they approximate the true cost function (17) very precisely.
In addition, it can be seen that in the polynomial approximation, the coefficients for the 3rd and 4th powers of x2 are non-zero, even though the true cost function depends on x2 as the second-order polynomial. Similarly, we would expect that in , all coefficients except for the one in front of ex1/2 would vanish. We think that this inconsistency is observed because in inverse optimization problems one cannot approximate particular component of the cost function, but instead approximates it as a whole. It happens because all components are tightly interdependent through Eq. 4 of the Lagrange principle. Consequently, deviating in one component may lead to better consistency of the cost function as a whole. To confirm this, we determine the functions and under the assumption that equals f2. We performed forward optimization for such approximation and compared the solutions under the constraints (19) with the experimental data. The average distance in this case was approximately 50% larger than in case when no assumptions are made about .
The ANIO method is precise in case when the cost function can be precisely fitted by the basis functions. For example, when the cost function is polynomial, say, of the second order, and the basis functions are polynomials up to the fourth order, the method is capable to find precise values of the coefficients. In particular, in the approximation, like in the original function, all coefficients in front of the third-and fourth-order polynomials are zero. This property reflects the fact that ANIO method has a unique minimum, which in this case coincides with the true solution. In opposite, NOP method usually has a big number of local minima and thus there is no guarantee that it will converge to the precise solution.
4.3 Comparison of the methods
As we have shown in the previous section, the proposed methods could produce rather precise approximation of the cost function using the experimental data. The analysis was performed in an ideal case, when the experimental observations were not subjected to noise of any nature. In applications such situation is impossible, and in addition to purely theoretical applicability of the methods we would like to analyze their performance in more relevant case, when experimental observations are noisy. Thereby two questions arise: how the precision of the approximation depends on the level of noise in the data and which of the proposed methods shows higher robustness to the noise.
In the analysis, we use the synthetic optimization problem with the cost function (17) and two variants of constraints: (19) and (20). We add artificially created noise to the optimal solutions of this problem; the noise has normal distribution and is independent for each axis (has diagonal covariation matrix). The standard deviation of the noise is scaled so that it equals particular percentage of the standard deviation of the experimental data along the corresponding axis. The percentage ranges from 0 to 50% with the step size equal to 2.5%.
We used polynomial approximations of different order: 2, 3 or 4. To evaluate the methods, we use three performance criteria: (i) the difference between the approximation and the true cost function, (ii) the ability of the approximation to explain clean experimental data shown in Fig. 1 and (iii) its ability to explain data of new tests, presented below.
The difference between the approximation and true cost function is defined as the sum of normalized distances between their components:
where is the component of the approximation after the linear correction (see previous section) and f̄i (xi) is the centered value of fi (xi):
The ability of the approximation to explain the clean experimental data is defined as the average Euclidean distance between the true data points, presented on Fig. 1, and the solutions of the optimal problem with the approximation of the true cost function and constraints (19). The Euclidean distance is normalized by the standard deviation of the true experimental data.
For the new data, we use a set of new constraints:
| (22) |
We choose the values in the right-hand side of the equations such that the solutions of the corresponding optimization problem with the true cost function (17) lie inside the parallelepiped . As the measure of the ability to explain new experimental data, we use normalized average Euclidean distance, like before. The standard deviations used in normalization are still computed for the original data presented in Fig. 1.
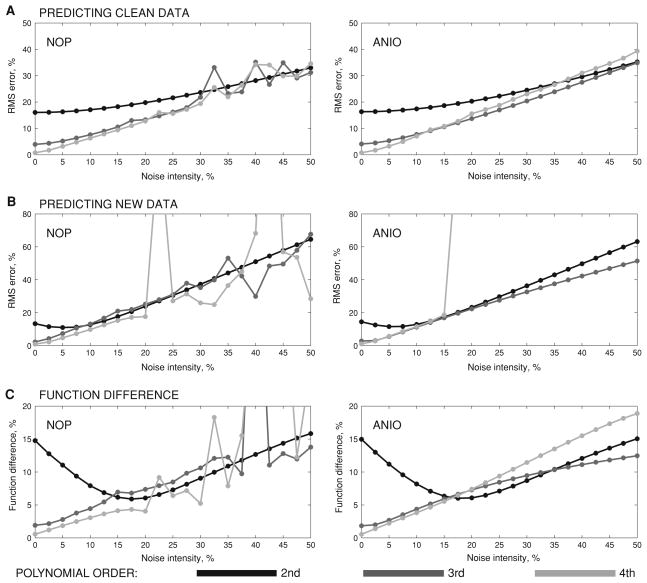
The results are presented in Fig. 3. One can see that the average performance of the methods is more or less the same. The NOP method becomes rather unstable with the increase of the noise amplitude (above 20%) which might signify that the local minima, to which the algorithm converges, are rather distant from the global ones. We would like to emphasize that such behavior is due to the numeric routine used for solving the NOP optimization problem. If we could always find globally optimal solution for the NOP problem, no unstable behavior would be most probably observed. In contrast, ANIO method always converges to a unique global minimum and the dependency of the scores presented in Fig. 3 is rather smooth.
Fig. 3.
Comparison of NOP and ANIO methods performance on noisy experimental data for polynomial approximations of different degree. Comparison is performed based on the criteria a the ability of the approximation to predict clean (noiseless) data, from the noisy version of which it was identified; b the ability of the approximation to predict brand new data obtained under new constraints; and c the difference between the approximation and original cost functions
For all scores, the higher order polynomials are preferable in both methods for low level of noise (15% or less). For more intense noise, the error on the constraints (22) occasionally becomes very high, which implies that the approximation does not have minima inside the parallelepiped . The latter is regularly observed for the fourth order approximation, provided by the ANIO method. Finally, for the noise level above 15%, the error on the new data and the difference of the cost functions are more or less the same independently of the order of the approximating polynomials.
4.4 Violating conditions of the Uniqueness Theorem
In the previous sections, we have shown how unknown cost function can be determined from the experimental data if the conditions of the Uniqueness Theorem are satisfied. After seeing only positive results, one might wonder why satisfaction of the Uniqueness Theorem conditions is emphasized all over the manuscript. To answer this question, we show how violation of these conditions may lead to non-uniqueness of solution and consequently to totally incorrect approximation of the cost function. In all numeric experiments described below, we determine polynomial approximations of the fourth degree, unless specified otherwise.
4.4.1 Violation of additivity
The first condition of the Uniqueness Theorem is the additivity of the desired cost function. Here, we show that if this condition is violated, e.g. the desired cost function is not necessarily additive, then the experimental data, like presented in Fig. 1, are insufficient for finding an approximation of the cost function. To illustrate this fact, we use the synthetic inverse optimization problem presented before. We state that there exist infinitely many non-additive optimization functions, whose minimization subject to the constraints (19) results in the surface presented in Fig. 1.
The surface from Fig. 1 can be defined by a scalar equation:
There exist infinitely many different functions ψ defining this surface. For example, one of them can be derived from the Lagrange principle:
where (Č)1i denotes the i -th element of the first row of the matrix Č.
Let us construct a new cost function J̃ of the form:
where J is the cost function defined in (17), F is an arbitrary positive scalar function having unique minimum at zero and G is an arbitrary function taking a 2D vector as input and returning a scalar value as output.
We state that under the constraints (19), the constructed function J̃1 is minimized by the same set of values as the J. Indeed, the term G(Cx) does not depend on x on the constraints (19) and, consequently, does not influence the optimization. Multiplication by the term F does not change the location of the minima because F is positive and reaches its minimum only on the surface ξ(x1, x2, x3) = 0, e.g. when the function J reaches its minima. Consequently, there exist infinitely many essentially different non-additive cost functions reaching their minima subject to the constraints (19) at the same points as J.
As a consequence, it is impossible to determine the minimized cost function from the experimental data presented in Fig. 1, unless it is known to be additive. Of course, it does not mean that it is also impossible for larger amount of experimental data. Obtaining the conditions of uniqueness for general optimization problem represents a serious problem and stays beyond the scope of this study. However, we would like to notice that the latter would definitely require variation of the constraints matrix C in addition to their values b.
One can see that though there exist infinitely many essentially different non-additive cost functions explaining the same set of data, all of them would probably have rather artificial structure, like the one we presented here. Therefore, we think that in practical applications in human movement study if a particular set of experimental data can be explained by an additive cost function, it gives a rather strong argument in favor of the hypothesis that the observed behavior is governed by an additive cost function.
4.4.2 Insufficiency of experimental data
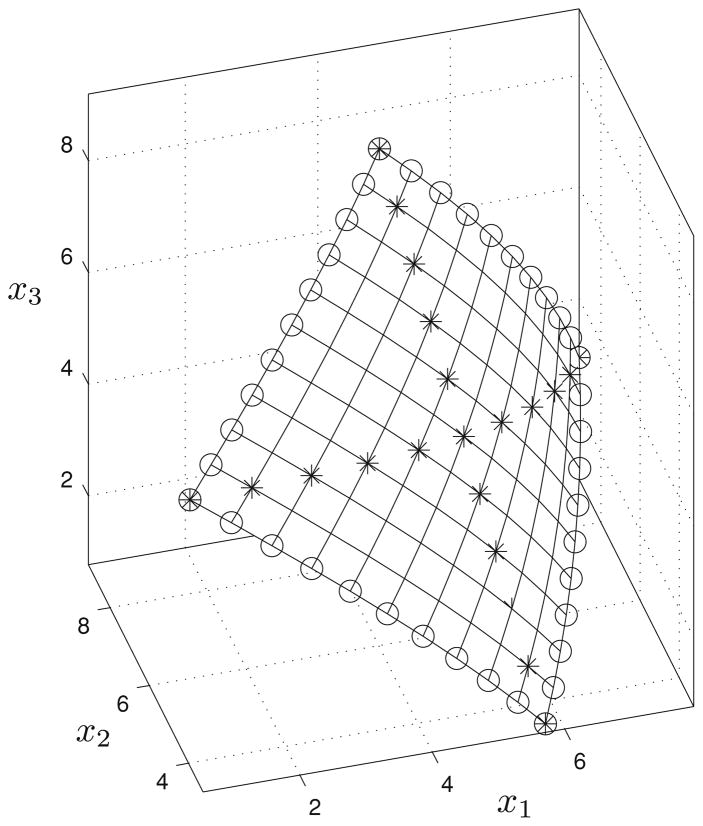
The second condition of the Uniqueness Theorem requires the solutions of the optimization problem to be known in a k-dimensional hypersurface, where k is the number of constraints in the problem. This condition is violated if the solutions lie in a hypersurface of a smaller dimension. For the inverse optimization problem (17) and (19) to be solved correctly, the hypersurface of solutions must be 2D (see Fig. 1). This condition is violated if the solutions lie on a curve instead of the surface. To analyze how important this condition is for finding the correct approximation of the cost function, we perform numerical simulations, in which we replace the original experimental data with a subset of it. In particular, we use two different subsets of the original data, which are illustrated in Fig. 4: (i) the two ‘diagonals’ of the original surface (stars) and (ii) its edge (circles).
Fig. 4.
The two subsets of the original data, to which ANIO method is applied in order to obtain an approximation of the cost function; stars diagonals, circles edge
Interestingly, for both data sets, the approximations determined by ANIO methods are rather close to the original function. More precisely, the score of the difference between the cost functions equals 5.0% for the diagonals and 1.7% for the edge. To check that it does not happen by pure coincidence, we performed the same test for a new cost function derived from the original one by raising each fi (·) into the second power. For this case, we used seventh order approximations. The approximations obtained from incomplete data sets (similar to the ones presented in Fig. 4) were less precise: 9.5% of error for the diagonals and 7.1% for the edge.
It is clear that when we have only a finite number of points, the decision whether they form a surface or a curve is left to the researcher. For example, the data presented in Fig. 1 can be seen as defining either a surface or 22 curves. Similarly, we may consider the data presented in Fig. 4 as defining the surface (but rather poorly) or as defining the curves. According to the results of the computation, for the cost function J from (17), the subsets of data from Fig. 4 can be considered as defining the surface. For another cost function, produced from J by raising its terms fi into the second power, the latter does not hold: precise approximation requires more dense coverage of the surface.
4.4.3 The case of single constraint
The third condition of the Uniqueness Theorem requires that the dimension of constraints must be great or equal 2. This one may seem strange, however, here we show that it is crucial for solving inverse optimization problem.
Let us assume that the inverse optimization problem consists of minimization of the cost function (17) subject to the first constraint of (19), e.g.
| (23) |
The solutions define functions x1(b1), x2(b1) and x3(b1). Let us assume that these functions and the functions f1, f2, f3 are monotonically increasing inside the parallelepiped. One can verify that is true for the considered example. We construct a new cost function
| (24) |
where
We state that there exist infinitely many different functions ϕ such that the cost function J̃3 is minimized by the same values as J under the constraints (23).
The Lagrange principle, applied to the function J and the constraints (23), yields two equations:
| (25) |
which must be satisfied on the curve of the experimental data xi = xi (b1).
In turn, the cost function J̃3 must satisfy:
which after substituting expression for gi gives
Clearly, for any non-zero ϕ(b1), the last equations are satisfied if and only if Eq. 25 holds. As a consequence, ϕ can be always chosen such that the functions J and J̃3 have the same minima.
ANIO fails when applied to the data produced by the problem (17) and (23). The matrix inversion procedure, required by the method, cannot be performed because the matrix to be inverted (see Appendix for details) has zero determinant. This means, in particular, that the problem does not have unique solution. In opposite, when applying NOP method, it converges to one of the possible solutions, which gives rather good approximation of the cost function (17). This finding is rather surprising because, as we have just shown, the problem may have an infinite number of essentially different solutions and the fact that the algorithm converges to the true cost function seems rather strange.
It is unclear whether the unexpectedly good performance of NOP in the considered problem represents a general rule or it is occasional and can be attributed only to this problem. In order to investigate this issue, we constructed the function J̃3 as defined in (24) with the function ϕ(s) = s4. Since necessary calculations can be hardly performed analytically, we computed the values of the functions gi (fi (xi)) and then approximated each of them with a fifth-order polynomial. The resulting functions are shown in Fig. 5. One can notice that they are significantly different from the terms of the original function J.
Fig. 5.
Approximation of the cost function in case of single-dimensional constraint. The NOP method is applied to approximate the modified cost function J̃3, however, the algorithm converges to the approximation, which is closer to the original cost function J given in (17). This example illustrates importance of the condition of Uniqueness Theorem, according to which the dimension of constraints must be ≥ 2
We produced the experimental data for the function J̃3 minimized under the constraint (23). The obtained solutions were very close to those computed for the function J. The average distance was less than 1% of standard deviation for each coordinate. Next we applied the NOP method to these new experimental points in order to find the approximation of the cost function J̃3. Surprisingly, the approximation was very close to J and not to J̃3, which experimental data we used to find the approximation. The terms of the functions J3, J and the approximation computed from the experimental data of J̃3 are given in Fig. 5. This example illustrates how the function can be determined totally incorrectly if the dimension of the constraints is equal to one.
4.4.4 Splittable constraints
The last condition of the Uniqueness Theorem requires that matrix Č cannot be made block-diagonal by simultaneous swapping rows and columns with the same indices. The constraints, satisfying this requirement are called non-splittable (see Terekhov et al. 2010 for details on splittable optimization problems). Here, we show that if the constraints are splittable the cost function cannot be determined correctly.
We use the following constraints:
| (26) |
which differ from those defined in (19) by the sign in the second equation. For these constraints,
and it can be made block-diagonal by swapping the first and the second rows and columns.
For these constraints any cost function of the form
has the same solution. Here ψ(·) is an arbitrary monotonically increasing function. This happens, because according to the constraints (26) x2 = b1 − b2 and, hence, whatever is the function ψ the value of x2 is the same and does not influence the values of x1 and x3.
Like in the previous example, ANIO method fails for the same reason. The NOP method converges to a solution, which is totally arbitrary and does not resemble f2(·) at all.
5 Discussion
This article aimed at three main goals: to propose applied methods of inverse optimization, based on the theoretical considerations from Terekhov et al. (2010); to confirm that when the conditions of Theorem of Uniqueness are satisfied the approximations obtained by the methods are close to the true cost function (i.e. the approximation is unambiguous); and to illustrate how violations of the conditions of Theorem of Uniqueness may lead to incorrect solution of the problem, independently of the employed method. The article deals with the inverse optimization problems, for which it can be assumed that the minimized cost function is additive and the constraints, under which it is minimized, are linear. For such problems, conditions of unambiguous solutions were proposed and corresponding Uniqueness Theorem was proved by Terekhov et al. (2010).
We presented two methods for solving such inverse optimization problems: NOP and ANIO. NOP is based on the method described in Bottasso et al. (2006), which we modified in order to account for possible ambiguity in solutions of inverse optimization problems, reflected in the Uniqueness Theorem. ANIO is derived directly from the Lagrange principle for inverse optimization problems and also accounts for the possible ambiguity. Hence, both methods significantly rely on the theoretical results from Terekhov et al. (2010).
When developing the current methods, we aimed at two relatively vast classes of problems arising in human motor control and biomechanics. The first one includes the problem of choice of the finger forces in various finger manipulations tasks, like grasping and pressing. In such problems, the number of mechanical constraints is typical less than the number of degrees of freedom relevant to the task (Zatsiorsky and Latash 2008). The constraints can be considered linear as long as the locations of the fingertips are fixed, like when grasping an object with the prescribed grasping configuration or when pressing with the fingers at the specified points. Moreover, we believe that it is reasonable to assume that the cost function is close to additive with respect to the finger forces. Some primary results of application of Uniqueness Theorem to these problems are reported in Terekhov et al. (2010) and Park et al. (2010).
Another big class of problems is related to the problem of muscle force distribution. This problem consists in distribution of the forces among the muscles in such a way that altogether they produce prescribed torques at the joints. In isometric force production, i.e. when the limb posture is fixed, the moment arms of the muscles can be considered constant and consequently the constraints can be considered linear. It is reasonable to assume that for each individual muscle there is the cost of its activation and that the total cost function sums the individual costs. This assumption is made in the dominant amount of the studies considering this problem (for example, Crowninshield and Brand 1981; Binding et al. 2000; Prilutsky et al. 1997; Prilutsky and Zatsiorsky 2002, etc.).
In order to analyze the performance of the methods, we built a synthetic inverse optimization problem, for which we knew the true cost function and used this problem to compare the performance of the two methods:
in the case of precise experimental data, we applied the methods to get approximations of the true cost functions on the two classes of basis functions: polynomials and exponential functions;
we found that both methods could provide very precise approximations on both classes of basis functions; the approximations were precise only inside the region, predicted by the Uniqueness Theorem and diverged outside of this region (see Fig. 2);
in the case of noisy experimental data the quality of the approximation depended a lot on the magnitude of noise and the order of the approximating polynomials; for sufficiently intense noise the second-order polynomial approximation is preferable;
in general, the ANIO method works more than 300 times faster and unlike NOP always returns the set of parameters, corresponding to the global minimum of its criterion (14).
The performance of both methods presented in this article was comparable. However, we would recommend ANIO for practical use for two main reasons. First, it is significantly faster than NOP (by about 300 times) that becomes important when large sets of data are considered. Second, it converges always to the unique global minimum of its criterion whenever this minimum exists and it fails when the minimum does not exist. The latter happens when the conditions of the Uniqueness Theorem are coarsely violated. In turn, NOP may converge to a local minimum, which is rather far from the global one, and consequently it may result in wrong approximation of the true cost function. In fact, the main advantage of the ANIO method over to the NOP is that the optimization problem of the ANIO method can be approached analytically, unlike NOP, for which we use a general algorithm, which does not necessarily converge to the global optimal solution. It is quite possible that if one could find a way to solve the NOP problem, this method would show the better performance than ANIO.
We would like to emphasize that when we used two different classes of basis functions, the symbolic representations of the approximating functions differed a lot, while their plots were nearly the same. We think that the latter property is absolutely necessary to check for any method, which claims to address the problem of inverse optimization.
In addition to the demonstration of the applicability of the methods when the conditions of the Uniqueness Theorem were satisfied, we characterized the importance of these conditions for correct approximation of the true cost function:
if the cost function is not assumed additive then for the same set of experimental data there exist infinitely many essentially different non-additive cost functions; however, the fact that the experimental data can be reproduced with the additive cost function may be an argument in favor of the hypothesis that the true cost function is additive;
when the experimental data lie on a curve (or curves) instead of a surface the error of the approximation becomes significant even in absence of noise; the error of the approximation may become small if the curves cover the expected surface sufficiently densely;
if the number of constraints in the inverse optimization problem equals to one, then there exist infinitely many additive cost functions explaining the same set of experimental data (which is a curve in this case); for this reason, it is very unlikely that any algorithm (not only those presented in the paper) will converge to the approximation of the true cost function;
if the constraints of the optimization problem are split-table then only some terms of the cost function can be identified.
It can be seen that not all conditions are equally important for applications. The requirement of additivity, though it is crucial for the theory, in practice can never be insured. However, if all other conditions of the Uniqueness Theorem are satisfied and the experimental data can be explained by an additive objective function then one can expect that the function used by the CNS is additive. Indeed, if a non-additive function were actually used then it would have a very specific structure, illustrated in Sect. 4.4.1, such that it looked like an additive function on the hypersurface of the experimental data.
In opposite, the requirements of the constraints matrix to be non-splittable and to have the rank of 2 or above are very important. In fact, if these requirements are violated the correct approximation of the cost function becomes nearly impossible. This property is intrinsic to the inverse optimization problem and does not depend of the employed method. The same situation may occur when the experimental data are available on the set of lower dimension than the rank of constraints. For example, if in the problem with two constraints the experimental data is available on a curve only the resulting approximation is very likely to be incorrect. However, if this curve covers a surface sufficiently densely the proper approximation may be possible.
We would like to emphasize that the class of additive cost functions, considered in the current study, is significantly vaster than it may seem. As soon as the cost function can be determined only up to essential similarity, any monotonically increasing function of an additive function is also additive. For example, the functions
are additive even though they may not look as such at the first glance. Moreover, the cost function is not obliged to be additive in the whole range of its variables. It can be additive for available range of experimental data, but loose this property when the values of the variables become too large or small.
In general, it must be understood that the cost function can be determined only in the range of the variables, for which experimental data are available. We can only guess what the behavior of the cost function outside of the available range is. As it is clearly shown in Fig. 2, the approximation can be very close to the true cost function in this range, but deviate a lot elsewhere. Without paying proper attention to this matter mistakes and misunderstandings may occur.
There is a rather common tendency to assume that the cost function, used by the CNS, must have ‘nice-looking’ symbolic representation and must contain as few parameters as possible. This tendency is especially evident for the studies modeling human movements from optimal control point of view, where the use of quadratic cost functions prevails. However, in the few studies we know (Körding and Wolpert 2004; Cruse et al. 1990), in which identification of the cost function was performed directly from experimental data, the resultant cost functions were far from being ‘nice-looking’. We see no reasons why the CNS would prefer ‘nice’ cost functions to ‘ugly’ ones. Moreover, as it is illustrated in Sect. 4.2, the same cost function may have both ‘nice’ and ‘ugly’ symbolic representation. Our preference to ‘nice-looking’ functions, biased by the mathematical tools we use, is not necessary applicable to the CNS. In our opinion, one of the reasons, why ‘nice’ cost functions are preferred, is in the ambiguity of solutions of the inverse optimization problems. The requirement of the cost function to be ‘nice-looking’ and free of parameters introduces additional restrictions on the search space and consequently regularize the problem. We hope that the conditions of uniqueness for inverse optimization problem, obtained in Terekhov et al. (2010) and the methods presented here will help relaxing the constraint of ‘nice-looking’ functions and will serve as tools for data-based approximation of the cost function instead of guessing it. Of course, the results of the approximation require interpretation, which can be done only be researchers.
Acknowledgments
The study was in part supported by NIH grants AG-018751, NS-035032 and AR-048563. The authors would like to thank Dr. Dmitri A. Kropotov for his help in the work on the problem, Dr. Mark L. Latash and Dr. Yakov B. Pesin for their valuable comments on the manuscript.
Appendix
Here, we present the solution of the minimization problem corresponding to ANIO method.
We notice that the criterion SI I, defined in (14), is quadratic with respect to the desired coefficients ai j. The minimization of SI I must be performed subject to regularization constraints, which are linear with respect to ai j. This problem can be solved analytically. To find the solution, we rewrite the expression in a more convenient form:
where r is the new index such that r = i + n(j − 1),
and ar = ai j. Consequently,
where a is the vector of the coefficients ordered in such a way that a = (a11, …, a1n, …, am1, …, amn)T.
Substituting the last expression into the function SI I yields:
or, after introducing the matrix ,
| (27) |
The function SI I must be minimized subject to the regularization constraints (15) and (16), which can be rewritten in matrix form:
| (28) |
where 0 and 1 are the matrices of zeros and ones with the specified dimensions.
Applying the Lagrange principle to resulting linear-quadratic optimization problem (27), (28) yields:
| (29) |
where Ď = I − D (D DT) DT.
If the function H has full rank, then the latter equation has the rank equal to n(m−1)−1 and together with the constraints (28) introduces nm linear equations on nm coefficients ai j. If the matrix H does not have full rank then the coefficients ai j cannot be determined uniquely and consequently the conditions of the Uniqueness Theorem are violated.
It is convenient to find the solution using pseudo-inverse matrix. Equations 28 and 29 define the system of linear equations:
where
And since the rank of Z is equal to nm the solution can be expressed as
Footnotes
Such constraints are called non-splittable (Terekhov et al. 2010).
Contributor Information
Alexander V. Terekhov, Email: avterekhov@gmail.com, Institut des Systèmes Intelligents et de Robotique, Université Pierre et Marie Curie-Paris 6, CNRS UMR 7222, 4 Place Jussieu, 75252 Paris Cedex 05, France
Vladimir M. Zatsiorsky, Email: vxz1@psu.edu, Department of Kinesiology, The Pennsylvania State University, Rec.Hall-268N, University Park, PA 16802, USA
References
- Abbeel P, Ng AY. Apprenticeship learning via inverse reinforcement learning. Proceedings of the twenty-first international conference on machine learning; New York: ACM Press; 2004. [Google Scholar]
- Ait-Haddou R, Binding P, Herzog W. Theoretical considerations on cocontraction of sets of agonistic and antagonistic muscles. J Biomech. 2000;33(9):1105–1111. doi: 10.1016/s0021-9290(00)00085-3. [DOI] [PubMed] [Google Scholar]
- Ait-Haddou R, Jinha A, Herzog W, Binding P. Analysis of the force-sharing problem using an optimization model. Math Biosci. 2004;191(2):111–122. doi: 10.1016/j.mbs.2004.05.003. url: http://dx.doi.org/10.1016/j.mbs.2004.05.003. [DOI] [PubMed]
- Amarantini D, Rao G, Berton E. A two-step emg-and-optimization process to estimate muscle force during dynamic movement. J Biomech. 2010;43(9):1827–1830. doi: 10.1016/j.jbiomech.2010.02. 025. url: http://dx.doi.org/10.1016/j.jbiomech.2010.02.025. [DOI] [PubMed]
- Anderson FC, Pandy MG. A dynamic optimization solution for vertical jumping in three dimensions. Comput Methods Biomech Biomed Eng. 1999;2(3):201–231. doi: 10.1080/10255849908907988. [DOI] [PubMed] [Google Scholar]
- Anderson FC, Pandy MG. Individual muscle contributions to support in normal walking. Gait Posture. 2003;17(2):159–169. doi: 10.1016/s0966-6362(02)00073-5. [DOI] [PubMed] [Google Scholar]
- Aoki T, Niu X, Latash ML, Zatsiorsky VM. Effects of friction at the digit-object interface on the digit forces in multi-finger prehension. Exp Brain Res. 2006;172(4):425–438. doi: 10.1007/s00221-006-0350-9. url: http://dx.doi.org/10.1007/s00221-006-0350-9. [DOI] [PMC free article] [PubMed]
- Ben-Itzhak S, Karniel A. Minimum acceleration criterion with constraints implies bang-bang control as an underlying principle for optimal trajectories of arm reaching movements. Neural Comput. 2008;20(3):779–812. doi: 10.1162/neco.2007.12-05-077. url: http://dx.doi.org/10.1162/neco.2007.12-05-077. [DOI] [PubMed]
- Bernstein NA. The coordination and regulation of movements. Pergamon; Oxford: 1967. [Google Scholar]
- Berret B, Darlot C, Jean F, Pozzo T, Papaxanthis C, Gauthier JP. The inactivation principle: mathematical solutions minimizing the absolute work and biological implications for the planning of arm movements. PLoS Comput Biol. 2008;4(10):e1000194. doi: 10.1371/journal.pcbi.1000194. url: http://dx.doi.org/10.1371/journal.pcbi.1000194. [DOI] [PMC free article] [PubMed]
- Biess A, Liebermann DG, Flash T. A computational model for redundant human three-dimensional pointing movements: integration of independent spatial and temporal motor plans simplifies movement dynamics. J Neurosci. 2007;27(48):13,045–13,064. doi: 10.1523/JNEUROSCI.4334-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Binding P, Jinha A, Herzog W. Analytic analysis of the force sharing among synergistic muscles in one- and two-degree-of-freedom models. J Biomech. 2000;33(11):1423–1432. doi: 10.1016/s0021-9290(00)00108-1. [DOI] [PubMed] [Google Scholar]
- Bottasso CL, Prilutsky BI, Croce A, Imberti E, Sartirana S. A numerical procedure for inferring from experimental data the optimization cost functions using a multibody model of the neuro-musculoskeletal system. Multibody Syst Dyn. 2006;16:123–154. [Google Scholar]
- Buchanan TS, Shreeve DA. An evaluation of optimization techniques for the prediction of muscle activation patterns during isometric tasks. J Biomech Eng. 1996;118(4):565–574. doi: 10.1115/1.2796044. [DOI] [PubMed] [Google Scholar]
- Challis JH. Producing physiologically realistic individual muscle force estimations by imposing constraints when using optimization techniques. Med Eng Phys. 1997;19(3):253–261. doi: 10.1016/s1350-4533(96)00062-8. [DOI] [PubMed] [Google Scholar]
- Collins JJ. The redundant nature of locomotor optimization laws. J Biomech. 1995;28(3):251–267. doi: 10.1016/0021-9290(94)00072-c. [DOI] [PubMed] [Google Scholar]
- Crevecoeur F, McIntyre J, Thonnard JL, Lefevre P. Movement stability under uncertain internal models of dynamics. J Neurophysiol. 2010 doi: 10.1152/jn.00315.2010. url: http://dx.doi.org/10.1152/jn.00315.2010. [DOI] [PubMed]
- Crowninshield RD, Brand RA. A physiologically based criterion of muscle force prediction in locomotion. J Biomech. 1981;14(11):793–801. doi: 10.1016/0021-9290(81)90035-x. [DOI] [PubMed] [Google Scholar]
- Cruse H, Wischmeyer E, Brwer M, Brockfeld P, Dress A. On the cost functions for the control of the human arm movement. Biol Cybern. 1990;62(6):519–528. doi: 10.1007/BF00205114. [DOI] [PubMed] [Google Scholar]
- Czaplicki A, Silva M, Ambrsio J, Jesus O, Abrantes J. Estimation of the muscle force distribution in ballistic motion based on a multibody methodology. Comput Methods Biomech Biomed Eng. 2006;9(1):45–54. doi: 10.1080/10255840600603625. url: http://dx.doi.org/10.1080/10255840600603625. [DOI] [PubMed]
- Davy DT, Audu ML. A dynamic optimization technique for predicting muscle forces in the swing phase of gait. J Biomech. 1987;20(2):187–201. doi: 10.1016/0021-9290(87)90310-1. [DOI] [PubMed] [Google Scholar]
- De Groote F, Pipeleers G, Jonkers I, Demeulenaere B, Patten C, Swevers J, De Schutter J. A physiology based inverse dynamic analysis of human gait: potential and perspectives. Comput Methods Biomech Biomed Eng. 2009;12(5):563–574. doi: 10.1080/10255840902788587. url: http://dx.doi.org/10.1080/10255840902788587. [DOI] [PubMed]
- Ding J, Wexler AS, Binder-Macleod SA. Development of a mathematical model that predicts optimal muscle activation patterns by using brief trains. J Appl Physiol. 2000;88(3):917–925. doi: 10.1152/jappl.2000.88.3.917. [DOI] [PubMed] [Google Scholar]
- Dul J, Johnson GE, Shiavi R, Townsend MA. Muscular synergism. II. A minimum-fatigue criterion for load sharing between synergistic muscles. J Biomech. 1984a;17(9):675–684. doi: 10.1016/0021-9290(84)90121-0. [DOI] [PubMed] [Google Scholar]
- Dul J, Townsend MA, Shiavi R, Johnson GE. Muscular synergism. I. On criteria for load sharing between synergistic muscles. J Biomech. 1984b;17(9):663–673. doi: 10.1016/0021-9290(84)90120-9. [DOI] [PubMed] [Google Scholar]
- Engelbrecht S. Minimum principles in motor control. J Math Psychol. 2001;45(3):497–542. doi: 10.1006/jmps.2000.1295. [DOI] [PubMed] [Google Scholar]
- Fagg AH, Shah A, Barto AG. A computational model of muscle recruitment for wrist movements. J Neurophysiol. 2002;88(6):3348–3358. doi: 10.1152/jn.00621.2001. url: http://dx.doi.org/10.1152/jn.00621.2001. [DOI] [PubMed]
- Flash T, Hogan N. The coordination of arm movements: an experimentally confirmed mathematical model. J Neurosci. 1985;5(7):1688–1703. doi: 10.1523/JNEUROSCI.05-07-01688.1985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friedman J, Flash T. Trajectory of the index finger during grasping. Exp Brain Res. 2009;196(4):497–509. doi: 10.1007/s00221-009-1878-2. url: http://dx.doi.org/10.1007/s00221-009-1878-2. [DOI] [PubMed]
- Guigon E. Active control of bias for the control of posture and movement. J Neurophysiol. 2010 doi: 10.1152/jn.00162.2010. url: http://dx.doi.org/10.1152/jn.00162.2010. [DOI] [PubMed]
- Happee R, der Helm FCV. The control of shoulder muscles during goal directed movements, an inverse dynamic analysis. J Bio-mech. 1995;28(10):1179–1191. doi: 10.1016/0021-9290(94)00181-3. [DOI] [PubMed] [Google Scholar]
- Harris CM, Wolpert DM. Signal-dependent noise determines motor planning. Nature. 1998;394(6695):780–784. doi: 10.1038/29528. url: http://dx.doi.org/10.1038/29528. [DOI] [PubMed]
- Heintz S, Gutierrez-Farewik EM. Static optimization of muscle forces during gait in comparison to emg-to-force processing approach. Gait Posture. 2007;26(2):279–288. doi: 10.1016/j.gaitpost.2006.09.074. url: http://dx.doi.org/10.1016/j.gaitpost.2006.09.074. [DOI] [PubMed]
- Herzog W. Individual muscle force estimations using a non-linear optimal design. J Neurosci Methods. 1987;21(2–4):167–179. doi: 10.1016/0165-0270(87)90114-2. [DOI] [PubMed] [Google Scholar]
- Herzog W, Leonard TR. Validation of optimization models that estimate the forces exerted by synergistic muscles. J Biomech. 1991;24(Suppl 1):31–39. doi: 10.1016/0021-9290(91)90375-w. [DOI] [PubMed] [Google Scholar]
- Hoff B, Arbib MA. Models of trajectory formation and temporal interaction of reach and grasp. J Mot Behav. 1993;25(3):175–192. doi: 10.1080/00222895.1993.9942048. [DOI] [PubMed] [Google Scholar]
- Hughes RE, Chaffin DB. The effect of strict muscle stress limits on abdominal muscle force predictions for combined torsion and extension loadings. J Biomech. 1995;28(5):527–533. doi: 10.1016/0021-9290(94)00110-p. [DOI] [PubMed] [Google Scholar]
- Hughes RE, Chaffin DB, Lavender SA, Andersson GB. Evaluation of muscle force prediction models of the lumbar trunk using surface electromyography. J Orthop Res. 1994;12(5):689–698. doi: 10.1002/jor.1100120512. url: http://dx.doi.org/10.1002/jor.1100120512. [DOI] [PubMed]
- Kaufman KR, An KW, Litchy WJ, Chao EY. Physiological prediction of muscle forces. I. Theoretical formulation. Neuroscience. 1991;40(3):781–792. doi: 10.1016/0306-4522(91)90012-d. [DOI] [PubMed] [Google Scholar]
- Körding KP, Wolpert DM. The loss function of sensorimotor learning. Proc Natl Acad Sci USA. 2004;101(26):9839–9842. doi: 10.1073/pnas.0308394101. url: http://dx.doi.org/10.1073/pnas.0308394101. [DOI] [PMC free article] [PubMed]
- Kuo AD, Zajac FE. Human standing posture: multi-joint movement strategies based on biomechanical constraints. Prog Brain Res. 1993;97:349–358. doi: 10.1016/s0079-6123(08)62294-3. [DOI] [PubMed] [Google Scholar]
- Kuzelicki J, Zefran M, Burger H, Bajd T. Synthesis of standing-up trajectories using dynamic optimization. Gait Posture. 2005;21(1):1–11. doi: 10.1016/j.gaitpost.2003.11.004. [DOI] [PubMed] [Google Scholar]
- Lee SW, Zhang X. Development and evaluation of an optimization-based model for power-grip posture prediction. J Biomech. 2005;38(8):1591–1597. doi: 10.1016/j.jbiomech.2004.07.024. url: http://dx.doi.org/10.1016/j.jbiomech.2004.07.024. [DOI] [PubMed]
- Liu CK, Hertzmann A, Popović Z. Learning physics-based motion style with nonlinear inverse optimization. ACM Trans Graph. 2005;24(3):1071–1081. doi: 10.1145/1073204.1073314. [DOI] [Google Scholar]
- Martin L, Cahout V, Ferry M, Fouque F. Optimization model predictions for postural coordination modes. J Biomech. 2006;39(1):170–176. doi: 10.1016/j.jbiomech.2004.10.039. url: http://dx.doi.org/10.1016/j.jbiomech.2004.10.039. [DOI] [PubMed]
- Menegaldo LL, de Toledo Fleury A, Weber HI. A ’cheap’ optimal control approach to estimate muscle forces in musculoskeletal systems. J Biomech. 2006;39(10):1787–1795. doi: 10.1016/j.jbiomech.2005.05.029. url: http://dx.doi.org/10.1016/j.jbiomech.2005.05.029. [DOI] [PubMed]
- Mombaur K, Truong A, Laumond JP. From human to humanoid locomotion—an inverse optimal control approach. Auton Robots. 2010;28(3):369–383. doi: 10.1007/s10514-009-9170-7. [DOI] [Google Scholar]
- Niu X, Latash ML, Zatsiorsky VM. Effects of grasping force magnitude on the coordination of digit forces in multi-finger prehension. Exp Brain Res. 2009;194(1):115–129. doi: 10.1007/s00221-008-1675-3. url: http://dx.doi.org/10.1007/s00221-008-1675-3. [DOI] [PMC free article] [PubMed]
- Nubar Y, Contini R. A minimal principle in biomechanics. Bull Math Biol. 1961;23:377–391. doi: 10.1007/BF02476493. url: http://dx.doi.org/10.1007/BF02476493. [DOI]
- Nussbaum MA, Chaffin DB, Rechtien CJ. Muscle lines-of-action affect predicted forces in optimization-based spine muscle modeling. J Biomech. 1995;28(4):401–409. doi: 10.1016/0021-9290(94)00078-i. [DOI] [PubMed] [Google Scholar]
- O’Sullivan I, Burdet E, Diedrichsen J. Dissociating variability and effort as determinants of coordination. PLoS Comput Biol. 2009;5(4):e1000345. doi: 10.1371/journal.pcbi.1000345. url: http://dx.doi.org/10.1371/journal.pcbi.1000345. [DOI] [PMC free article] [PubMed]
- Pandy MG. Computer modeling and simulation of human movement. Annu Rev Biomed Eng. 2001;3:245–273. doi: 10.1146/annurev.bioeng.3.1.245. url: http://dx.doi.org/10.1146/annurev.bioeng.3.1.245. [DOI] [PubMed]
- Park J, Zatsiorsky VM, Latash ML. Optimality vs. variability: an example of multi-finger redundant tasks. Exp Brain Res. 2010;207(1–2):119–132. doi: 10.1007/s00221-010-2440-y. url: http://dx.doi.org/10.1007/s00221-010-2440-y. [DOI] [PMC free article] [PubMed]
- Pataky TC. Soft tissue strain energy minimization: a candidate control scheme for intra-finger normal-tangential force coordination. J Biomech. 2005;38(8):1723–1727. doi: 10.1016/j.jbiomech.2004.07.020. url: http://dx.doi.org/10.1016/j.jbiomech.2004.07.020. [DOI] [PubMed]
- Pataky TC, Latash ML, Zatsiorsky VM. Prehension synergies during nonvertical grasping. II. Modeling and optimization. Biol Cybern. 2004;91(4):231–242. doi: 10.1007/s00422-004-0506-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pedersen DR, Brand RA, Cheng C, Arora JS. Direct comparison of muscle force predictions using linear and nonlinear programming. J Biomech Eng. 1987;109(3):192–199. doi: 10.1115/1.3138669. [DOI] [PubMed] [Google Scholar]
- Pham QC, Hicheur H, Arechavaleta G, Laumond JP, Berthoz A. The formation of trajectories during goal-oriented locomotion in humans. II. a maximum smoothness model. Eur J Neurosci. 2007;26(8):2391–2403. doi: 10.1111/j.1460-9568.2007.05835.x. [DOI] [PubMed] [Google Scholar]
- Pierce JE, Li G. Muscle forces predicted using optimization methods are coordinate system dependent. J Biomech. 2005;38(4):695–702. doi: 10.1016/j.jbiomech.2004.05.016. url: http://dx.doi.org/10.1016/j.jbiomech.2004.05.016. [DOI] [PubMed]
- Plamondon R, Alimi AM, Yergeau P, Leclerc F. Modelling velocity profiles of rapid movements: a comparative study. Biol Cybern. 1993;69(2):119–128. doi: 10.1007/BF00226195. [DOI] [PubMed] [Google Scholar]
- Prilutsky BI. Coordination of two- and one-joint muscles: functional consequences and implications for motor control. Motor Control. 2000;4(1):1–44. doi: 10.1123/mcj.4.1.1. [DOI] [PubMed] [Google Scholar]
- Prilutsky BI, Gregory RJ. Analysis of muscle coordination strategies in cycling. IEEE Trans Rehabil Eng. 2000;8(3):362–370. doi: 10.1109/86.867878. [DOI] [PubMed] [Google Scholar]
- Prilutsky BI, Zatsiorsky VM. Optimization-based models of muscle coordination. Exerc Sport Sci Rev. 2002;30(1):32–38. doi: 10.1097/00003677-200201000-00007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prilutsky BI, Herzog W, Allinger TL. Forces of individual cat ankle extensor muscles during locomotion predicted using static optimization. J Biomech. 1997;30(10):1025–1033. doi: 10.1016/s0021-9290(97)00068-7. [DOI] [PubMed] [Google Scholar]
- Prilutsky BI, Isaka T, Albrecht AM, Gregor RJ. Is coordination of two-joint leg muscles during load lifting consistent with the strategy of minimum fatigue. J Biomech. 1998;31(11):1025–1034. doi: 10.1016/s0021-9290(98)00116-x. [DOI] [PubMed] [Google Scholar]
- Raikova RT. Some mechanical considerations on muscle coordination. Motor Control. 2000;4(1):89–96. doi: 10.1123/mcj.4.1.89. discussion 97–116. [DOI] [PubMed] [Google Scholar]
- Raikova RT, Aladjov HT. Hierarchical genetic algorithm versus static optimization-investigation of elbow flexion and extension movements. J Biomech. 2002;35(8):1123–1135. doi: 10.1016/s0021-9290(02)00031-3. [DOI] [PubMed] [Google Scholar]
- Schappacher-Tilp G, Binding P, Braverman E, Herzog W. Velocity-dependent cost function for the prediction of force sharing among synergistic muscles in a one degree of freedom model. J Biomech. 2009;42(5):657–660. doi: 10.1016/j.jbiomech.2008.12.013. url: http://dx.doi.org/10.1016/j.jbiomech.2008.12.013. [DOI] [PubMed]
- Seth A, Pandy MG. A neuromusculoskeletal tracking method for estimating individual muscle forces in human movement. J Biomech. 2007;40(2):356–366. doi: 10.1016/j.jbiomech.2005.12.017. url: http://dx.doi.org/10.1016/j.jbiomech.2005.12.017. [DOI] [PubMed]
- Terekhov AV, Pesin YB, Niu X, Latash ML, Zatsiorsky VM. An analytical approach to the problem of inverse optimization with additive objective functions: an application to human prehension. J Math Biol. 2010;61(3):423–453. doi: 10.1007/s00285-009-0306-3. url: http://dx.doi.org/10.1007/s00285-009-0306-3. [DOI] [PMC free article] [PubMed]
- Tsirakos D, Baltzopoulos V, Bartlett R. Inverse optimization: functional and physiological considerations related to the force-sharing problem. Crit Rev Biomed Eng. 1997;25(4–5):371–407. doi: 10.1615/critrevbiomedeng.v25.i4-5.20. [DOI] [PubMed] [Google Scholar]
- Uno Y, Kawato M, Suzuki R. Formation and control of optimal trajectory in human multijoint arm movement. minimum torque-change model. Biol Cybern. 1989;61(2):89–101. doi: 10.1007/BF00204593. [DOI] [PubMed] [Google Scholar]
- van Bolhuis BM, Gielen CC. A comparison of models explaining muscle activation patterns for isometric contractions. Biol Cybern. 1999;81(3):249–261. doi: 10.1007/s004220050560. [DOI] [PubMed] [Google Scholar]
- van den Bogert AJ. Analysis and simulation of mechanical loads on the human musculoskeletal system: a methodological overview. Exerc Sport Sci Rev. 1994;22:23–51. [PubMed] [Google Scholar]
- van Dieën JH, Kingma I. Effects of antagonistic co-contraction on differences between electromyography based and optimization based estimates of spinal forces. Ergonomics. 2005;48(4):411–426. doi: 10.1080/00140130512331332918. url: http://dx.doi.org/10.1080/00140130512331332918. [DOI] [PubMed]
- Vigouroux L, Quaine F, Labarre-Vila A, Amarantini D, Moutet F. Using emg data to constrain optimization procedure improves finger tendon tension estimations during static fingertip force production. J Biomech. 2007;40(13):2846–2856. doi: 10.1016/j.jbiomech.2007.03.010. url: http://dx.doi.org/10.1016/j.jbiomech.2007.03.010. [DOI] [PubMed]
- Vilimek M. Musculotendon forces derived by different muscle models. Acta Bioeng Biomech. 2007;9(2):41–47. [PubMed] [Google Scholar]
- Zatsiorsky VM, Latash ML. Multifinger prehension: an overview. J Mot Behav. 2008;40(5):446–476. doi: 10.3200/JMBR.40.5.446-476. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zatsiorsky VM, Gregory RW, Latash ML. Force and torque production in static multifinger prehension: biomechanics and control. II. Control. Biol Cybern. 2002;87(1):40–49. doi: 10.1007/s00422-002-0320-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zheng N, Fleisig GS, Escamilla RF, Barrentine SW. An analytical model of the knee for estimation of internal forces during exercise. J Biomech. 1998;31(10):963–967. doi: 10.1016/s0021-9290(98)00056-6. [DOI] [PubMed] [Google Scholar]