Abstract
We show that human ability to discriminate the wavelength of monochromatic light can be understood as maximum likelihood decoding of the cone absorptions, with a signal processing efficiency that is independent of the wavelength. This work is built on the framework of ideal observer analysis of visual discrimination used in many previous works. A distinctive aspect of our work is that we highlight a perceptual confound that observers should confuse a change in input light wavelength with a change in input intensity. Hence a simple ideal observer model which assumes that an observer has a full knowledge of input intensity should over-estimate human ability in discriminating wavelengths of two inputs of unequal intensity. This confound also makes it difficult to consistently measure human ability in wavelength discrimination by asking observers to distinguish two input colors while matching their brightness. We argue that the best experimental method for reliable measurement of discrimination thresholds is the one of Pokorny and Smith, in which observers only need to distinguish two inputs, regardless of whether they differ in hue or brightness. We mathematically formulate wavelength discrimination under this wavelength-intensity confound and show a good agreement between our theoretical prediction and the behavioral data. Our analysis explains why the discrimination threshold varies with the input wavelength, and shows how sensitively the threshold depends on the relative densities of the three types of cones in the retina (and in particular predict discriminations in dichromats). Our mathematical formulation and solution can be applied to general problems of sensory discrimination when there is a perceptual confound from other sensory feature dimensions.
Introduction
In a classical wavelength discrimination experiment, the observer views a bipartite
field, one half filled with light of a standard wavelength and the other with light
of a comparison wavelength. The wavelength of the comparison field is changed in
small steps and the observer adjusts the radiance of the comparison field following
each change in an attempt to make the two fields perceptually identical. Wavelength
discrimination threshold is reached when the observer reports that the two fields
always appear different, regardless of the radiance of the comparison [1]. This
discrimination threshold in humans is a “w” shaped function of the
wavelength of the light: it has a central peak at around wavelength
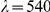 nanometers (nm), minima at
nanometers (nm), minima at 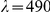 and
and
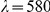 nm, and rises up sharply for
nm, and rises up sharply for 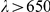 nm and for very short
wavelengths[1]; similar results hold for the macaque monkey and
presumably other old world primates[2].
nm and for very short
wavelengths[1]; similar results hold for the macaque monkey and
presumably other old world primates[2].
This work aims to see if human monochromatic light discrimination thresholds can be understood as optimal decoding of the sensory input using the information available in the cones, regardless of the specific neural mechanisms involved. In particular, we derive and evaluate a photon noise limited ideal observer that performs wavelength discrimination based on the numbers of photons absorbed in the three classes of cone. It is well known that human performance does not approach that of a photon noise limited ideal observer[3], [ 4], [ 5], [ 6], and thus our primary aim here is to determine how well the shape of the human wavelength discrimination function is explained by the ideal observer, regardless of its overall amplitude. If the shape were perfectly explained, then it would imply that the neural mechanisms following the cones are equally efficient for different wavelengths.
Wavelength discrimination of monochromatic lights is one of the visual tasks most suited to ideal observer analysis for the following reasons. Input sampling by the photoreceptors is among the best quantitatively understood process along the visual processing pathway. In particular, the wavelength sensitivities of cones are known, and the stochastic nature of the cone absorption levels can be described by Poisson distributions of absorption levels. The discrimination task is simple because it involves purely chromatic discrimination, so the spatial and temporal aspects of the inputs can be ignored or absorbed by the scale for the total input intensity. Therefore, total cone absorptions by the excited cones can lead to sufficient statistics for analysing the consequent decoding and its uncertainty of the input stimulus.
There have been many previous studies using ideal observer analysis to understand human visual performance[7], [ 3], [ 4], [ 5], [ 8], [ 6]. Geisler[8] in particular used such an analysis to understand many human discrimination tasks based on cone responses. Among these tasks analyzed is our task of monochromatic light discrimination. His work and the current work are both based on the maximum likelihood method which can be used to optimally estimate or discriminate sensory inputs from their evoked neural responses. These two methods are approximately equivalent in the principle of maximum likelihood discrimination of two stimuli. However, this previous work did not identify an important issue that is essential for fully understanding the behavioral data. This issue is that of a confound in perception of multiple sensory features – in particular, human observers can easily confuse an input color change with an input intensity change when monochromatic lights are the inputs; for example a long wavelength input may appear darker when the input wavelength is increased while input intensity is held fixed. This confusion reduces human ability in hue discrimination when observers do not have the full knowledge of input intensities. To fully account for the behavioral data, this confound should be formulated explicitly in the ideal observer analysis.
The current work presents an augmented formulation of the ideal observer analysis to address sensory discrimination under a perceptual confound, and applies it to wavelength discrimination behavior. The sensory input includes both sensory feature dimensions: one is the input wavelength dimension whose discrimination is of interest, and the other is the input intensity dimension which interferes or interacts with wavelength discrimination through the perceptual confound and the experimental methods used. Our mathematical formulation of this problem of sensory discrimination under perceptual confound is general. While it is applied specifically to the wavelength discrimination problem in this paper, it can also be applied elsewhere. It will enable us to identify experimental methods which can provide more reliable measurments of the discrimination performance. From our formulation, we derive how the threshold is related to the cones' wavelength sensitivities and the input light intensity, illustrate how sensitively the predictions depend on the relative densities of the three types of cones in the retina, and analyze why the discrimination threshold varies with the input wavelength in the ways observed. We show that our theoretical predictions from the augmented ideal observer analysis to accommodate the perceptual confound can give a better account of the behavioral data. Furthermore, we show how different sizes of stimuli used by different experiments may explain their different patterns of results. A preliminary report about this work has been presented elsewhere[9].
Methods
The spectral sensitivities of the cones
Let there be three types of cone 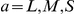 , which are most
sensitive to long, medium, and short wavelengths respectively (they are
sometimes called red, green, and blue cones). They have tuning curves
, which are most
sensitive to long, medium, and short wavelengths respectively (they are
sometimes called red, green, and blue cones). They have tuning curves
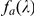 , such that the average cone absorption of a single cone
, such that the average cone absorption of a single cone
 to a monochromatic light of intensity
to a monochromatic light of intensity
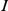 at wavelength
at wavelength 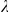 is
is
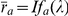 . If
. If 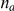 cones of type
cones of type
 are excited by a uniform patch of light, then the
essential quantities for determining input color, regardless of the spatial
shape of the input patch, are the total responses from each of the three cone
types. For the task of color discrimination, it is equivalent to view the
are excited by a uniform patch of light, then the
essential quantities for determining input color, regardless of the spatial
shape of the input patch, are the total responses from each of the three cone
types. For the task of color discrimination, it is equivalent to view the
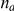 cones of type
cones of type  collectively as a
single giant cone with sensitivity
collectively as a
single giant cone with sensitivity 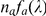 , for this giant
cone's sensitivity provides a sufficient statistic for the task (i.e., this
sensitivity provides all the information relevant to the task) such that viewing
individual cones separately does not provide any additional useful information
for the task. The all-important ratios
, for this giant
cone's sensitivity provides a sufficient statistic for the task (i.e., this
sensitivity provides all the information relevant to the task) such that viewing
individual cones separately does not provide any additional useful information
for the task. The all-important ratios 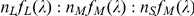 depend on both the
relative densities and the relative sensitivities of the different cone
types.
depend on both the
relative densities and the relative sensitivities of the different cone
types.
According to various experimental data on the responses from and light absorption
by cones [10, 11,
12],  for different
cones should peak to the same peak value, if one ignores the pre-receptor
absorption by the ocular media. We denote this normalized spectral sensitivity
as
for different
cones should peak to the same peak value, if one ignores the pre-receptor
absorption by the ocular media. We denote this normalized spectral sensitivity
as 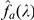 , and will call it the cone fundamental. However,
pre-receptor absorption of the input lights by the ocular media makes
, and will call it the cone fundamental. However,
pre-receptor absorption of the input lights by the ocular media makes
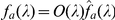 where
where 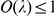 is the
pre-receptor absorption factor. Let
is the
pre-receptor absorption factor. Let 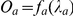 , where
, where
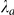 is the wavelength where
is the wavelength where 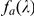 peaks; then
peaks; then
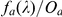 should correspond to the behaviorally measured
(normalized) cone fundamental, and for notation simplicity we still denote it as
should correspond to the behaviorally measured
(normalized) cone fundamental, and for notation simplicity we still denote it as
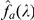 and thus
and thus 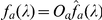 . Meanwhile,
assuming that
. Meanwhile,
assuming that 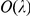 does not change as quickly as
does not change as quickly as
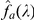 with
with 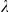 near
near
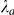 , then
, then 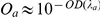 where
where
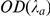 is the optical density of the pre-receptor ocular media
at wavelength
is the optical density of the pre-receptor ocular media
at wavelength  .
.
In our analysis later, we will include the cone density factor
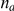 and use the notation
and use the notation 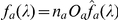 . Furthermore, we
normalize
. Furthermore, we
normalize 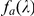 such that Max
such that Max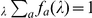 . Given these
normalizations, the total photon absorptions of the cones will also scale with
the size of the input light field (which determines the total number of cones
for each cone type) and the effective input integration time by the viewing of
the observers. These scale factors will be absorbed into the input intensity
parameter
. Given these
normalizations, the total photon absorptions of the cones will also scale with
the size of the input light field (which determines the total number of cones
for each cone type) and the effective input integration time by the viewing of
the observers. These scale factors will be absorbed into the input intensity
parameter 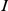 , which also scales with the input radiance. We will see
later that, given
, which also scales with the input radiance. We will see
later that, given 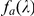 , the shape of the
curve relating the discrimination threshold to wavelength is completely
determined by the optimal decoding, and the parameter
, the shape of the
curve relating the discrimination threshold to wavelength is completely
determined by the optimal decoding, and the parameter
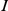 merely scales the threshold.
merely scales the threshold.
As our illustrative starting point, we approximate
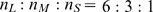 and
and 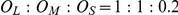 . These numerical
values arise from the following considerations. Firstly, various sources suggest
that S cones are almost absent within 0.3 deg from the center of fovea but their
contribution to the total cone density rises and peaks to 15% around 1
deg from the center[13] and approaches 7–10% in the
periphery[13], [ 14]. Meanwhile, the Pokorny and Smith data[1] were from
experiments using a centrally viewed
. These numerical
values arise from the following considerations. Firstly, various sources suggest
that S cones are almost absent within 0.3 deg from the center of fovea but their
contribution to the total cone density rises and peaks to 15% around 1
deg from the center[13] and approaches 7–10% in the
periphery[13], [ 14]. Meanwhile, the Pokorny and Smith data[1] were from
experiments using a centrally viewed  disc containing
the bipartite field of color inputs. We combine this information to assume that
the S cones contribute 10% to all cones excited by the Pokorny and Smith
stimuli. Secondly, various sources suggest that L cones are about twice as
numerous as the M cones[14], we hence assume that L and M cones contribute
60% and 30%, respectively, of all the excited cones by the
stimuli. This gives us
disc containing
the bipartite field of color inputs. We combine this information to assume that
the S cones contribute 10% to all cones excited by the Pokorny and Smith
stimuli. Secondly, various sources suggest that L cones are about twice as
numerous as the M cones[14], we hence assume that L and M cones contribute
60% and 30%, respectively, of all the excited cones by the
stimuli. This gives us 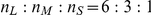 . Thirdly, the
optical density of the pre-receptor ocular media is almost constant in the
medium and long wavelength region, giving
. Thirdly, the
optical density of the pre-receptor ocular media is almost constant in the
medium and long wavelength region, giving  , but rises with
decreasing
, but rises with
decreasing 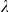 by 0.7 log units when
by 0.7 log units when 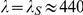 nm[14], giving
nm[14], giving
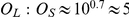 . Additionally, although the cone fundamentals
. Additionally, although the cone fundamentals
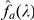 from various literature sources are similar, we use
those from Smith and Pokorny[15] (obtained from the CVRL website (http://www.cvrl.org) by Andrew Stockman), since we will be
fitting their wavelength discrimination data[1]. Combining the
considerations above gives
from various literature sources are similar, we use
those from Smith and Pokorny[15] (obtained from the CVRL website (http://www.cvrl.org) by Andrew Stockman), since we will be
fitting their wavelength discrimination data[1]. Combining the
considerations above gives 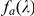 as shown in Fig. 1. It turns out that
these
as shown in Fig. 1. It turns out that
these 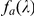 's are not far from those by Vos and Walraven[16], who made
's are not far from those by Vos and Walraven[16], who made
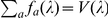 where
where 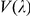 is the luminous
efficiency function, a measure of the visual effectiveness of lights at
different wavelengths for luminosity, normalized such that the maximum value of
is the luminous
efficiency function, a measure of the visual effectiveness of lights at
different wavelengths for luminosity, normalized such that the maximum value of
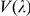 is 1, i.e., Max
is 1, i.e., Max . The biggest
discrepancy between the two sets of
. The biggest
discrepancy between the two sets of 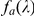 's is that the
S cone contribution is weaker in Vos and Walraven's composition[16] than in ours.
This is not too surprising, as although the relative contributions by different
cone types to luminosity perception are not necessarily the same as their
relative contributions to color perception, they should be related or quite
close to each other, except that S cones may contribute to the luminosity
perception less than suggested by their density[17]. Our analysis and
conclusions do not depend sensitively on our actual approximation for
's is that the
S cone contribution is weaker in Vos and Walraven's composition[16] than in ours.
This is not too surprising, as although the relative contributions by different
cone types to luminosity perception are not necessarily the same as their
relative contributions to color perception, they should be related or quite
close to each other, except that S cones may contribute to the luminosity
perception less than suggested by their density[17]. Our analysis and
conclusions do not depend sensitively on our actual approximation for
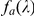 . We will later explore how our results vary
quantitatively when we use other choices for the ratio
. We will later explore how our results vary
quantitatively when we use other choices for the ratio
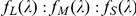 . This ratio depends on cone densities and the optical
density of the pre-receptor ocular media, which both vary substantially between
observers (e.g., by up to one log unit in optical density[14]). This ratio
. This ratio depends on cone densities and the optical
density of the pre-receptor ocular media, which both vary substantially between
observers (e.g., by up to one log unit in optical density[14]). This ratio
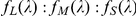 also depends on the cone spectral sensitivities, which
do not vary as substantially between observers but different literature sources
provide slightly different quantitative values for them.
also depends on the cone spectral sensitivities, which
do not vary as substantially between observers but different literature sources
provide slightly different quantitative values for them.
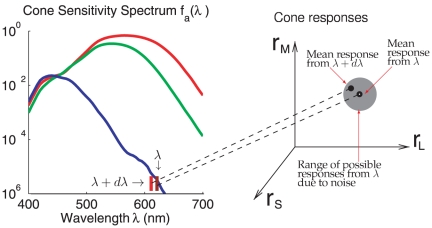
Figure 1. Illustrations of noisy encoding of monochromatic inputs by the cone responses.
On the left is the cone spectral sensitivity
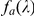 (with
(with
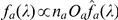 , where
, where
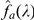 s are
derived from the Smith and Pokorny cone fundamentals[15], the
cone density ratio is
s are
derived from the Smith and Pokorny cone fundamentals[15], the
cone density ratio is 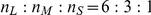 , the
pre-receptor light transmission factors
, the
pre-receptor light transmission factors 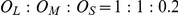 , and
Max
, and
Max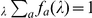 ). A
monochromatic input of wavelength
). A
monochromatic input of wavelength 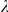 evokes
response
evokes
response 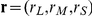 from the
three cones, L, M, and S. Due to input noise, there is a range of
possible responses
from the
three cones, L, M, and S. Due to input noise, there is a range of
possible responses  from this
input. If the mean response to a monochromatic input of nearby
wavelength
from this
input. If the mean response to a monochromatic input of nearby
wavelength 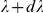 is one of
the typical responses within this range of responses
is one of
the typical responses within this range of responses
 to input
to input
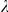 , then it
will be difficult to perceptually distinguish the input
, then it
will be difficult to perceptually distinguish the input
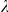 from input
from input
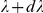 .
.
Stochastic cone absorptions in response to monochromatic light
In this paper, we only consider monochromatic inputs. Hence, we describe our
input stimulus by 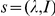 , a vector of two
parameters,
, a vector of two
parameters, 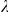 and
and 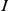 , for the
wavelength and intensity of the input light. The actual cone absorption
, for the
wavelength and intensity of the input light. The actual cone absorption
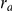 for cone
for cone  is stochastic
following a Poisson distribution with a mean
is stochastic
following a Poisson distribution with a mean 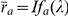
| (1) |
Sometimes we also call 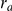 the response of
the cone to the input light. The population response
the response of
the cone to the input light. The population response
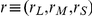 has the probability
has the probability
| (2) |
Fig. 1 shows how an input of
particular wavelength could give rise to many possible responses in the three
dimensional space 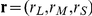 near the mean
response
near the mean
response 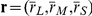 .
.
Maximum likelihood decoding
Given the responses  , one can decode
the input stimulus
, one can decode
the input stimulus 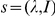 from the
conditional probability
from the
conditional probability 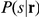 (of
(of
 given
given  ) by finding the
) by finding the
 that makes
that makes 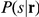 maximum or large.
So the most likely input to evoke
maximum or large.
So the most likely input to evoke  is the one that
maximizes
is the one that
maximizes 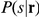 . By Bayes's formula, we have
. By Bayes's formula, we have
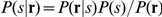 where
where 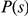 is the prior
probability of input
is the prior
probability of input  and
and
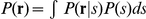 . When the prior probability
. When the prior probability
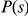 is constant so that it does not favour one
is constant so that it does not favour one
 over another, then
over another, then 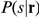 varies with
varies with
 only through
only through 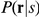 ,
i.e.,
,
i.e.,
| (3) |
Therefore, the input  for responses
for responses
 can be found by maximizing
can be found by maximizing
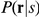 . As
. As 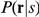 is also called the
likelihood of
is also called the
likelihood of  given
given  , decoding by
maximizing
, decoding by
maximizing  is called maximum likelihood decoding. We will use this
method to understand wavelength discrimination.
is called maximum likelihood decoding. We will use this
method to understand wavelength discrimination.
Decoding for input wavelength when input intensity is known and fixed
When input intensity 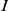 is known and
fixed, knowing the response
is known and
fixed, knowing the response  enables us to
estimate the input wavelength
enables us to
estimate the input wavelength 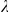 using maximum
likelihood decoding. We call this the simple model of optimal input wavelength
estimation, in the sense that we are not considering the variation of
using maximum
likelihood decoding. We call this the simple model of optimal input wavelength
estimation, in the sense that we are not considering the variation of
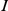 (as in experimental procedure of Pokorny and
Smith[1]) in decoding. With a flat prior expectation that
(as in experimental procedure of Pokorny and
Smith[1]) in decoding. With a flat prior expectation that
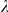 could be any value (within the visible light spectrum),
the best estimate
could be any value (within the visible light spectrum),
the best estimate 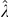 for the input
for the input
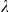 is the one that maximizes the probability
is the one that maximizes the probability
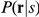 or equivalently its natural logarithm,
or equivalently its natural logarithm,
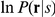 ,
,
 |
(4) |
which we call the log likelihood.
The best estimate 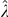 is the value of
is the value of
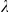 satisfying
satisfying
| (5) |
In a special case, if 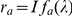 under input
under input
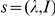 for all three cones (i.e., the response of each cone
type is exactly equal to the mean absorption), then
for all three cones (i.e., the response of each cone
type is exactly equal to the mean absorption), then
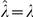 is the value satisfying the above equation. In general,
there is no
is the value satisfying the above equation. In general,
there is no 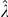 to make
to make 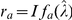 exactly for all
three cones simultaneously, but one can still find a
exactly for all
three cones simultaneously, but one can still find a
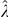 to satisfy the equation above. In any case, given an
input wavelength
to satisfy the equation above. In any case, given an
input wavelength 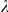 , different
responses
, different
responses  will lead to different estimates
will lead to different estimates
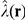 ; most of them will be near to but not equal to the
actual input wavelength
; most of them will be near to but not equal to the
actual input wavelength 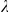 . So if two
different input wavelengths
. So if two
different input wavelengths 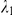 and
and
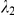 are similar enough, the estimated wavelengths
are similar enough, the estimated wavelengths
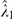 and
and 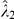 may appear to be
drawn from the same probability distribution. In such a case, these two input
wavelengths would appear perceptually indiscriminable, or within the
discrimination threshold; see Fig.
1.
may appear to be
drawn from the same probability distribution. In such a case, these two input
wavelengths would appear perceptually indiscriminable, or within the
discrimination threshold; see Fig.
1.
With strong enough responses  (effectively
responses collected from enough cones and sufficiently many captured photons),
it is known that the variance of these maximum likelihood decoded
(effectively
responses collected from enough cones and sufficiently many captured photons),
it is known that the variance of these maximum likelihood decoded
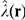 for a given input
for a given input 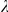 should
approach[18]
should
approach[18]
| (6) |
where 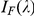 is the Fisher information defined
as
is the Fisher information defined
as
| (7) |
where 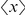 denotes average
denotes average 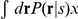 of
of
 over
over 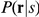 .
Since
.
Since
| (8) |
and 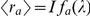 , we have
, we have
| (9) |
As 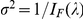 , a larger Fisher information gives a smaller estimation
error
, a larger Fisher information gives a smaller estimation
error  . This estimation error can be expressed
as
. This estimation error can be expressed
as
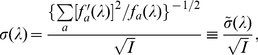 |
(10) |
in which 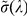 does not depend on intensity
does not depend on intensity
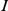 .
.
The estimation error 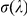 is identified here
as the discrimination threshold, as it characterizes the uncertainty of the
perceived wavelength. Fig. 2
shows this threshold
is identified here
as the discrimination threshold, as it characterizes the uncertainty of the
perceived wavelength. Fig. 2
shows this threshold 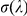 as a function of
as a function of
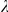 , together with the experimentally observed threshold
, together with the experimentally observed threshold
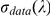 from Pokorny and Smith[1]. Let
from Pokorny and Smith[1]. Let
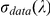 and
and 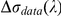 be the mean and
the standard deviation of the wavelength discrimination thresholds of the four
observers in Pokorny and Smith[1]. The input intensity
be the mean and
the standard deviation of the wavelength discrimination thresholds of the four
observers in Pokorny and Smith[1]. The input intensity
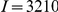 in Fig.
2 is chosen as the one that minimizes the average square
difference:
in Fig.
2 is chosen as the one that minimizes the average square
difference:
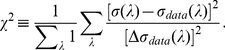 |
(11) |
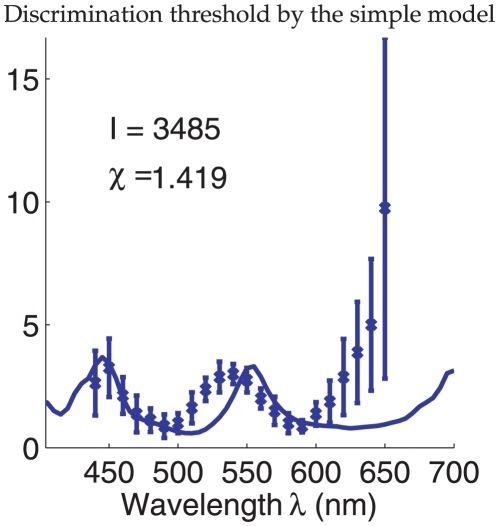
Figure 2. Wavelength discrimination assuming input intensity
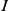 is fixed
and known during color matching.
is fixed
and known during color matching.
It is by maximum likelihood decoding of the cone responses
 using the
simple model. The solid curve plots the discrimination threshold
using the
simple model. The solid curve plots the discrimination threshold
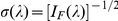 as a
function of
as a
function of 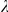 from the
model. The data points with error bars are the mean
from the
model. The data points with error bars are the mean
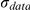 and the
standard deviation
and the
standard deviation 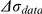 of the
discrimination thresholds of the four observers of Pokorny and
Smith[1]. In fitting the model to the data,
of the
discrimination thresholds of the four observers of Pokorny and
Smith[1]. In fitting the model to the data,
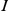 is chosen
such that the quantity
is chosen
such that the quantity 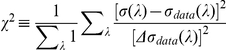 is
minimized.
is
minimized.
The 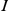 that minimizes
that minimizes 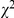 is the one that
gives
is the one that
gives 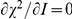 , leading to (since
, leading to (since 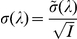 )
)
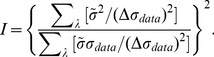 |
(12) |
One can see that the model prediction greatly underestimates the threshold for
long wavelengths 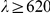 nm. Also, the peak
location near 550 nm is not quite right. This best fit gives
nm. Also, the peak
location near 550 nm is not quite right. This best fit gives
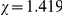 , indiciating that for most data points, the model
predicts a threshold which departs from the data by more than a standard
deviation of the data point.
, indiciating that for most data points, the model
predicts a threshold which departs from the data by more than a standard
deviation of the data point.
The poor fit of the simple model arises because of the following. In Pokorny and
Smith's experiment, observers adjusted the intensity
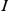 of the comparison input field with wavelength
of the comparison input field with wavelength
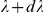 to make it look as perceptually indistinguishable as
possible from the standard input field which has input wavelength
to make it look as perceptually indistinguishable as
possible from the standard input field which has input wavelength
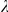 . This adjustment makes the comparison and standard input
fields look indistinguishable until
. This adjustment makes the comparison and standard input
fields look indistinguishable until 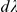 is too large, and
the wavelength discrimination threshold is defined as the
is too large, and
the wavelength discrimination threshold is defined as the
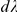 when this matching between the two fields starts to
become impossible, so the comparison field is perceptually discriminable from
the standard field no matter how observers adjust the intensity
when this matching between the two fields starts to
become impossible, so the comparison field is perceptually discriminable from
the standard field no matter how observers adjust the intensity
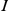 . If the observers somehow had the full knowledge of the
intensities
. If the observers somehow had the full knowledge of the
intensities 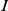 in both fields, they should in principle still be able
to decode and thus discriminate the wavelength to roughly the same accuracy as
predicted by the simple model when the intensity is held fixed and identical in
the two fields. The reason the predictions overestimate the human accuracy is
because one should not assume that the observers know the intensities
in both fields, they should in principle still be able
to decode and thus discriminate the wavelength to roughly the same accuracy as
predicted by the simple model when the intensity is held fixed and identical in
the two fields. The reason the predictions overestimate the human accuracy is
because one should not assume that the observers know the intensities
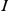 , which also have to be decoded from the same sensory
stimuli used to decode the wavelength. To explain the experimental data, our
model should let
, which also have to be decoded from the same sensory
stimuli used to decode the wavelength. To explain the experimental data, our
model should let 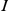 be unknown and
changeable rather than known and fixed. We call this the full model (rather than
the simple model) of optimal wavelength estimation, and this model is explained
next.
be unknown and
changeable rather than known and fixed. We call this the full model (rather than
the simple model) of optimal wavelength estimation, and this model is explained
next.
Sensory discrimination under perceptual confound – wavelength discrimination when input intensity is not fixed
Wavelength discrimination when input intensity is not fixed is just one example
of a general problem of sensory discrimination under perceptual confound:
sensory discrimination along one sensory feature dimension when neural responses
are also affected by feature changes in another feature dimension. In the
wavelength discrimination case, the two feature dimensions are input light
wavelength 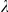 and input intensity
and input intensity 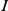 . Here, we
formulate this problem in general, and it will be clear that our result in
equation (20) is general and not specific to our example of monochromatic
wavelength discrimination. Meanwhile, we will use our wavelength discrimination
problem as an example to illustrate this general result.
. Here, we
formulate this problem in general, and it will be clear that our result in
equation (20) is general and not specific to our example of monochromatic
wavelength discrimination. Meanwhile, we will use our wavelength discrimination
problem as an example to illustrate this general result.
Let the sensory input be 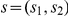 , where
, where
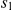 and
and 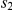 are feature values
in the two feature dimensions, e.g.,
are feature values
in the two feature dimensions, e.g., 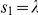 and
and
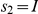 . Let
. Let  be the neural
responses evoked by
be the neural
responses evoked by  with probability
with probability
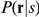 . The maximum likelihood estimation
. The maximum likelihood estimation
 of
of  from
from
 can be arrived at by finding the solution
to
can be arrived at by finding the solution
to
| (13) |
| (14) |
The estimation error is
| (15) |
This error depends on the specific response  in each trial.
Over many trials, these two dimensional errors
in each trial.
Over many trials, these two dimensional errors 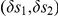 have a covariance,
generalizing from the simple 1-dimensional case above, given
by
have a covariance,
generalizing from the simple 1-dimensional case above, given
by
| (16) |
where 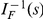 is the matrix inverse of the Fisher information
matrix
is the matrix inverse of the Fisher information
matrix
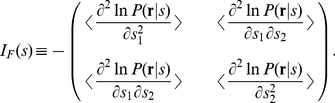 |
(17) |
We note that, when 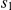 is
is
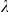 in our example, the matrix element
in our example, the matrix element
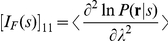 is exactly the Fisher information we had in our simple
model of wavelength discrimination.
is exactly the Fisher information we had in our simple
model of wavelength discrimination.
Let the 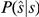 be the probability of obtaining the maximum likelihood
estimate
be the probability of obtaining the maximum likelihood
estimate  when the true input is
when the true input is  . Since the
estimation error
. Since the
estimation error 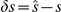 has the covariance
structure in equation (16), we can approximate
has the covariance
structure in equation (16), we can approximate 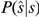 as
as
| (18) |
Note that this approximation makes the error 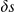 have zero mean and
gives the correct error covariance.
have zero mean and
gives the correct error covariance.
Now the threshold to discriminate 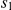 while
while
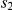 is not fixed is the largest
is not fixed is the largest
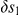 value that can be obtained to maintain
value that can be obtained to maintain
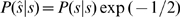 , i.e., to give
, i.e., to give
| (19) |
Applying the above to the example of wavelength discrimination, the threshold for
wavelength 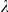 discrimination while
discrimination while 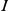 is not fixed is
the largest
is not fixed is
the largest 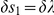 value that can be obtained to maintain
value that can be obtained to maintain
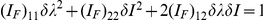 , a particular example of equation (19). This can be
illustrated in Fig. 3. This
figure shows the contour plot of the posterior probability
, a particular example of equation (19). This can be
illustrated in Fig. 3. This
figure shows the contour plot of the posterior probability
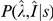 . This probability peaks at the origin
. This probability peaks at the origin
 of the coordinates in this plot. As deviation
of the coordinates in this plot. As deviation
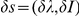 of
of 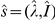 from
from
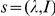 increases, the probability
increases, the probability
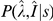 decreases, as indicated by the contours of
probabilities, with larger, darker, contours indicating smaller probabilities.
When
decreases, as indicated by the contours of
probabilities, with larger, darker, contours indicating smaller probabilities.
When 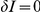 , the largest
, the largest 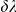 to make
to make
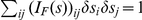 is
is 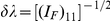 , the color
discrimination threshold in the simple model and indicated by
, the color
discrimination threshold in the simple model and indicated by
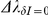 in Fig.
3. If
in Fig.
3. If  , then the largest
wavelength deviation
, then the largest
wavelength deviation 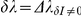 on the contour
on the contour
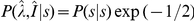 should be larger, as indicated in the figure. This
condition of
should be larger, as indicated in the figure. This
condition of 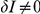 means that the decoding system assumes that
means that the decoding system assumes that
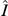 can be different from the default
can be different from the default
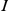 , i.e., the intensity of the comparison field can be
different from the intensity of the standard field in the color matching.
, i.e., the intensity of the comparison field can be
different from the intensity of the standard field in the color matching.
Figure 3. Illustration of 2D decoding in the full model.
Given the true input 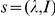 ,
,
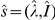 is the
estimated input parameters. This plot illustrates the conditional
probability
is the
estimated input parameters. This plot illustrates the conditional
probability 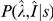 , since a
given
, since a
given  may evoke different responses
may evoke different responses
 leading to
different
leading to
different  . The
wavelength discrimination threshold
. The
wavelength discrimination threshold 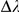 when
when
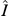 is allowed
to deviate from
is allowed
to deviate from 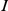 is larger
than otherwise.
is larger
than otherwise.
We can show (detailed derivation in the next subsection after equation (28)) that
the discrimination threshold for feature 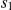 when input feature
when input feature
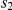 is not fixed (e.g., wavelength discrimination threshold
at wavelength
is not fixed (e.g., wavelength discrimination threshold
at wavelength 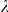 when input intensity
when input intensity 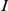 is not fixed)
is
is not fixed)
is
| (20) |
In particular, 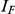 in our wavelength discrimination problem
is
in our wavelength discrimination problem
is
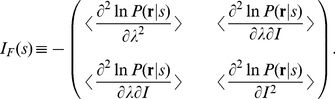 |
(21) |
Since we have
| (22) |
| (23) |
and
| (24) |
| (25) |
| (26) |
then, given 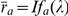 , we have
, we have
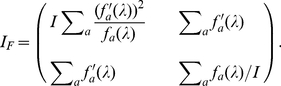 |
(27) |
Plugging the above into equation (20) we have
 |
(28) |
Again, this threshold can be writen as 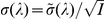 . This predicts
precisely how wavelength discrimination threshold should vary with wavelength
. This predicts
precisely how wavelength discrimination threshold should vary with wavelength
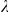 , and that it should scale with
, and that it should scale with
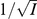 as in the simple model. Like the simple model, the full
model only has one free parameter,
as in the simple model. Like the simple model, the full
model only has one free parameter, 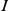 .
.
Mathematical proof of equation (20)
For matrix 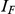 , let us denote its normalized eigenvectors as
, let us denote its normalized eigenvectors as
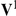 and
and 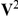 , with
corresponding eigenvalues
, with
corresponding eigenvalues 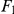 and
and
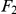 . Note that the two eigenvectors
. Note that the two eigenvectors
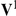 and
and 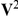 are orthogonal to
each other, since
are orthogonal to
each other, since 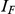 is a symmetric
matrix, so any 2 dimensional vector
is a symmetric
matrix, so any 2 dimensional vector 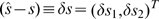 (where the
superscript
(where the
superscript 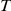 denotes transpose) can be expanded in their basis as
denotes transpose) can be expanded in their basis as
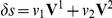 with coefficients
with coefficients 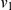 and
and
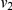 respectively. Then
respectively. Then 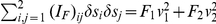 due to the
invariance of this quantity to the bases used. Note that since
due to the
invariance of this quantity to the bases used. Note that since
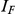 is positive definite,
is positive definite, 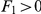 and
and
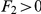 . Defining
. Defining 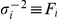 , we
have
, we
have
| (29) |
Analogous to the 1-d case, we find the discrimination threshold by looking at the
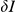 vs.
vs. 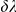 curve such that
curve such that
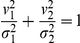 , and find the largest
, and find the largest 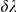 on this curve, and
this largest
on this curve, and
this largest 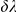 should be the discrmination threshold.
should be the discrmination threshold.
One can always find a parameter 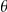 (see Fig. 3), such that the
eigenvectors are
(see Fig. 3), such that the
eigenvectors are
| (30) |
One notes that the dot product 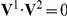 . Then we
have
. Then we
have
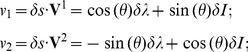 |
(31) |
From these we can solve for 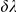 in terms of
in terms of
 and
and 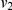 as
as
| (32) |
The values of 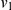 and
and 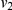 on the curve
on the curve
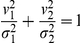 can be described by a parameter
can be described by a parameter
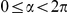 such that
such that
| (33) |
Hence, we can write 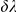 as a function of
as a function of
 as
as
| (34) |
The largest 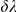 is when
is when 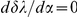 ,
giving
,
giving
| (35) |
The above is satisfied when
| (36) |
and
| (37) |
and since 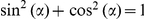 , and
, and
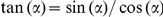 ; then we have
; then we have
| (38) |
Plug equation (36) to equation (34), writing  for this extreme
for this extreme
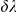 (the discrimination threshold) when
(the discrimination threshold) when
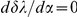 , we have
, we have
| (39) |
or
| (40) |
| (41) |
| (42) |
Noting that, as properties of eigenvectors 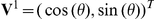 , and
, and
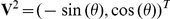 ,
,
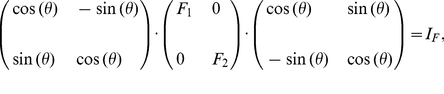 |
(43) |
we
have, equating 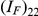 on the right hand
side of the equation to that in the left hand side
on the right hand
side of the equation to that in the left hand side
| (44) |
Also noting that 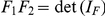 , the determinant
of the
, the determinant
of the 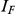 matrix, we have
matrix, we have
| (45) |
Results
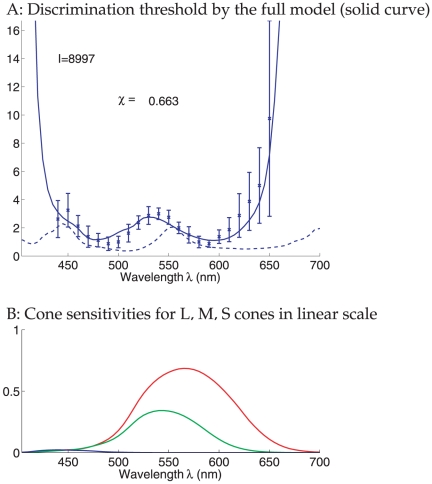
Figure 4 illustrates the full
model's predicted threshold (in equation (28)) fitted to the data. It uses the
optimal 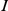 , as in equation (12), such that the summed squared
difference (as in equation (11)) between the predicted and observed thresholds is
minimized. The fitting quality is much better than that by the simple model. In
particular, with
, as in equation (12), such that the summed squared
difference (as in equation (11)) between the predicted and observed thresholds is
minimized. The fitting quality is much better than that by the simple model. In
particular, with 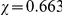 , the predicted threshold is within the standard deviation of
experimental data for most data points. As in the data, the predicted threshold
rises sharply as
, the predicted threshold is within the standard deviation of
experimental data for most data points. As in the data, the predicted threshold
rises sharply as 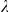 approaches the ends of the spectrum.
approaches the ends of the spectrum.
Figure 4. Wavelength discrimination under input intensity confound.
A: Wavelength discrimination by maximum likelihood decoding of cone inputs
using the full model, assuming that the color matching is done by adjusting
both the input intensity 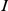 and wavelength
and wavelength
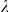 of the comparison field. The solid curve shows the
results from the full model. The parameter
of the comparison field. The solid curve shows the
results from the full model. The parameter 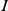 (of the
standard field) is chosen such that the quantity
(of the
standard field) is chosen such that the quantity
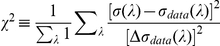 is minimized. The dashed curve shows the results
from the simple model using this same input intensity
is minimized. The dashed curve shows the results
from the simple model using this same input intensity
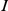 . The data points with error bars are the mean
. The data points with error bars are the mean
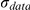 and the standard deviation
and the standard deviation
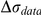 of the discrimination thresholds of the four
observers of Pokorny and Smith[1]. B: cone sensitivities
plotted on a linear scale.
of the discrimination thresholds of the four
observers of Pokorny and Smith[1]. B: cone sensitivities
plotted on a linear scale.
The wavelength-intensity confound and the divergence of threshold near the red and blue ends of the spectrum
The thresholds predicted by the full and simple models differ most towards the
red and blue ends of the spectrum. This is because only one cone type can be
substantially activated at the spectrum ends, making the system practically
color blind, just like in scotopic vision when only the rods are active. For
example, in the red end of the spectrum when the M and S cones are almost
silent, an increase in 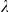 , i.e.,
, i.e.,
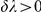 , weakens the L cone response
, weakens the L cone response
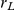 , i.e,
, i.e, 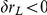 . The simple model
uses
. The simple model
uses 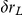 for wavelength discrimination by attributing it to
for wavelength discrimination by attributing it to
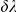 with the relationship
with the relationship 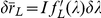 . The full model
however sees this
. The full model
however sees this 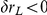 as equally
attributable to a reduced input
as equally
attributable to a reduced input 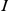 , i.e.,
, i.e.,
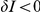 , with
, with 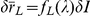 , making it hard to
distinguish whether the input gets redder or darker. This wavelength-intensity
confound for the same
, making it hard to
distinguish whether the input gets redder or darker. This wavelength-intensity
confound for the same 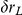 makes wavelength
discrimination difficult. In the procedure of the Pokorny and Smith
experiment[1], it means that an increase in
makes wavelength
discrimination difficult. In the procedure of the Pokorny and Smith
experiment[1], it means that an increase in
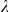 can be easily compensated by an increase in
can be easily compensated by an increase in
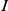 , making the threshold large.
, making the threshold large.
The wavelength-intensity confound is present generally even when all cone types
are substantially activated. Let 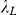 ,
,
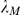 , and
, and 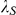 , with
, with
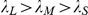 , be the preferred wavelengths of the L, M, and S cones
respectively. This confound is stronger when
, be the preferred wavelengths of the L, M, and S cones
respectively. This confound is stronger when 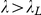 or
or
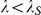 , when the predictions from the simple and full models
differ most (see Fig. 4. In
these wavelength regions, a change
, when the predictions from the simple and full models
differ most (see Fig. 4. In
these wavelength regions, a change 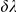 causes response
change
causes response
change 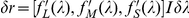 , which either simultaneously increases or simultaneously
decreases the responses from all cone types, just like the response change
, which either simultaneously increases or simultaneously
decreases the responses from all cone types, just like the response change
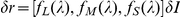 caused by an intensity change
caused by an intensity change
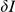 . Although a
. Although a 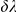 slightly changes
the ratio
slightly changes
the ratio 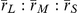 while a
while a 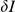 does not, the
difference between the
does not, the
difference between the 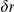 caused by
caused by
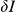 and the
and the 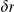 caused by
caused by
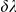 could be submerged under noise such that the two causes
are perceptually indistinguishable.
could be submerged under noise such that the two causes
are perceptually indistinguishable.
This confound is weaker when 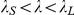 , when a wavelength
change
, when a wavelength
change 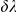 will raise responses from some cone types while lowering
responses from other cone types. In this case, a
will raise responses from some cone types while lowering
responses from other cone types. In this case, a 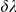 cannot be easily
compensated for by an
cannot be easily
compensated for by an 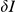 , which raises or
lowers the responses from all cone types simultaneously. Hence, the simple and
full model predict similar thresholds, particularly when
, which raises or
lowers the responses from all cone types simultaneously. Hence, the simple and
full model predict similar thresholds, particularly when
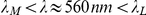 is in between the preferred wavelengths of the two most
numerous cone types, L and M. For
is in between the preferred wavelengths of the two most
numerous cone types, L and M. For 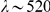 nm, the S cones
are still insensitive, while both the L and M cones prefer larger
nm, the S cones
are still insensitive, while both the L and M cones prefer larger
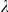 , and the confound is again significant, causing a
substantial difference in the predicted thresholds from the simple and the full
models. This is because a
, and the confound is again significant, causing a
substantial difference in the predicted thresholds from the simple and the full
models. This is because a 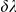 increases or
decreases the responses from the L and M cones simultaneously (while affecting
the S cone response relatively little), and can be easily compensated for by a
increases or
decreases the responses from the L and M cones simultaneously (while affecting
the S cone response relatively little), and can be easily compensated for by a
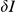 .
.
Implications of the wavelength-intensity confound on the experimental procedures and on the stability of the threshold measurements
The wavelength-intensity confound, especially when
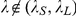 , means that there can be problems with some experimental
methods used to measure wavelength discrimination threshold. In many such
experiments (e.g., [19], [ 20]), the procedure requires adjusting the intensity of
the comparison field such that the brightnesses of the two fields match. The
confound means that, when observers see a difference between the two fields, it
is not easy to tell whether it is a brightness difference or a hue difference.
This is a known difficulty noted in the accompanying discussions of Wright and
Pitt's paper by fellow color vision scientists (pages 469–473 of
[20]).
Supposedly, the threshold is the smallest wavelength difference between the two
fields when observers deem the two fields to differ in hue but not in
brightness. However, whether the observers judge some perceptual difference to
be a brightness or hue difference is likely to be dependent on the following
factors: observers' internal criteria based on their expectations or
biases, specific task instructions given by the experimenters, and perhaps even
the visual environment around the experimental set up. These factors cannot be
predicted straightforwardly from our optimal decoding theory, and could also
cause variabilities between data from different observers and from different
laboratories.
, means that there can be problems with some experimental
methods used to measure wavelength discrimination threshold. In many such
experiments (e.g., [19], [ 20]), the procedure requires adjusting the intensity of
the comparison field such that the brightnesses of the two fields match. The
confound means that, when observers see a difference between the two fields, it
is not easy to tell whether it is a brightness difference or a hue difference.
This is a known difficulty noted in the accompanying discussions of Wright and
Pitt's paper by fellow color vision scientists (pages 469–473 of
[20]).
Supposedly, the threshold is the smallest wavelength difference between the two
fields when observers deem the two fields to differ in hue but not in
brightness. However, whether the observers judge some perceptual difference to
be a brightness or hue difference is likely to be dependent on the following
factors: observers' internal criteria based on their expectations or
biases, specific task instructions given by the experimenters, and perhaps even
the visual environment around the experimental set up. These factors cannot be
predicted straightforwardly from our optimal decoding theory, and could also
cause variabilities between data from different observers and from different
laboratories.
The procedure used by Pokorny and Smith[1] differs from the procedure above. They ask the observers to adjust the intensity of the comparison field until the two fields match in both hue and brightness, and the threshold is the smallest wavelength difference when this match is impossible by any intensity adjustment. This procedure does not require observers to decide whether any perceptual difference is due to brightness or hue, as they simply need to judge whether the two fields differ or not. This makes the threshold data more stable. Therefore, we do not intend to compare our theoretical prediction with data other than those by Pokorny and Smith[1].
The effect of the cone densities and pre-receptor light transmission on wavelength discrimination
It is clear from the analysis that the discrimination threshold depends on the
relative sensitivities 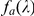 for different cone
types
for different cone
types  . Since our
. Since our  scales with the
relative cone density
scales with the
relative cone density 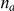 and the relative
pre-receptor transmission factor
and the relative
pre-receptor transmission factor  for each cone
for each cone
 ,
, 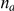 and
and
 should affect discrimination. We remind ourselves that
the cone fundamental
should affect discrimination. We remind ourselves that
the cone fundamental 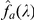 for all cones
for all cones
 have the same peak value
Max
have the same peak value
Max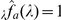 , and we have the normalization
Max
, and we have the normalization
Max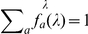 . Let us denote
. Let us denote 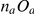 by
by
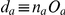 , which could be understood as the effective cone density
for cone type
, which could be understood as the effective cone density
for cone type  . We can rewrite the threshold in equation (28)
as
. We can rewrite the threshold in equation (28)
as
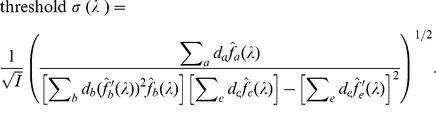 |
(46) |
So 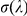 at any particular wavelength
at any particular wavelength
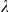 scales roughly with
scales roughly with 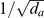 for the cone type
for the cone type
 that dominates at
that dominates at 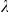 . For example,
increasing the fraction
. For example,
increasing the fraction 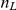 of the L cones
among all cones would relatively lower the discrimination threshold near the red
end of the spectrum, and increasing light absorption by the pre-receptor ocular
media near the short wavelength region would decrease
of the L cones
among all cones would relatively lower the discrimination threshold near the red
end of the spectrum, and increasing light absorption by the pre-receptor ocular
media near the short wavelength region would decrease
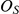 and thus raise the threshold near the blue end of the
spectrum.
and thus raise the threshold near the blue end of the
spectrum.
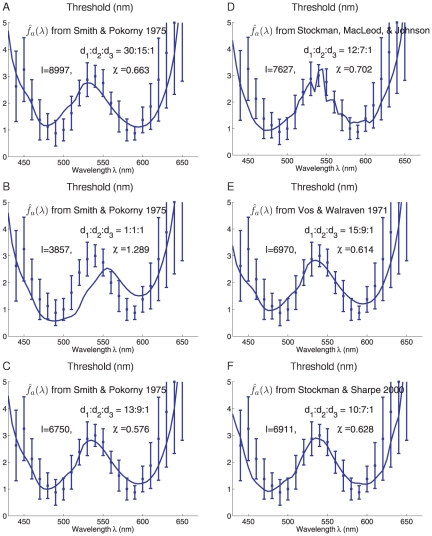
Fig. 5A–C shows the
predictions using Smith and Pokorny cone fundamentals[15]
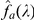 but with different settings for
but with different settings for
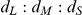 . Fig.
5A is a replot of Fig.
4 with different scales on the axes. Its
. Fig.
5A is a replot of Fig.
4 with different scales on the axes. Its
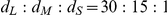 arises from our estimated
arises from our estimated
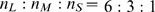 and
and 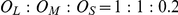 from experimental
data[13],
[ 14]. We
note that its worst predictions are near wavelength
from experimental
data[13],
[ 14]. We
note that its worst predictions are near wavelength
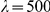 nm, which is in the region where S cones'
sensitivity
nm, which is in the region where S cones'
sensitivity 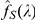 has large slopes
has large slopes 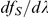 and hence a high
sensitivity to wavelength changes. Fig. 5B has
and hence a high
sensitivity to wavelength changes. Fig. 5B has 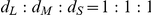 which could be
seen as a situation when all cones have the same density and pre-receptor
optical transmission. It raises the relative density for the S cones way over
the physiological reality, and slightly raises the relative density of the M
cones over the L cones. Consequently, it vastly over-estimates the
discrimination sensitivities near the region
which could be
seen as a situation when all cones have the same density and pre-receptor
optical transmission. It raises the relative density for the S cones way over
the physiological reality, and slightly raises the relative density of the M
cones over the L cones. Consequently, it vastly over-estimates the
discrimination sensitivities near the region 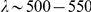 nm, in the domain
of the S and M cone contribution. As a result, it gives a
nm, in the domain
of the S and M cone contribution. As a result, it gives a
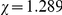 that is substantially worse than the
that is substantially worse than the
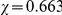 in Fig.
5A. Fig. 5C has a
in Fig.
5A. Fig. 5C has a
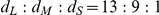 ratio that minimizes
ratio that minimizes 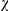 , such that the
predicted thresholds best agree with experimental data. This
, such that the
predicted thresholds best agree with experimental data. This
 ratio is obtained by exhaustively searching all integer
values of
ratio is obtained by exhaustively searching all integer
values of 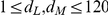 with
with 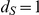 held fixed. With
held fixed. With
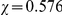 , almost all the data points are within a standard
deviation from the predicted values. Compared with Fig. 5A, Fig. 5C raises the weights for the S cones
(and slightly for the M cones), but not as dramatically as Fig. 5B does. Hence, it corrects the worst
predictions in Fig. 5A near
the
, almost all the data points are within a standard
deviation from the predicted values. Compared with Fig. 5A, Fig. 5C raises the weights for the S cones
(and slightly for the M cones), but not as dramatically as Fig. 5B does. Hence, it corrects the worst
predictions in Fig. 5A near
the 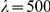 nm region without overshooting the correction.
nm region without overshooting the correction.
Figure 5. Variations of the model predictions due to variations in the cone fundamentals, cone densities, and pre-receptor transmission.
The 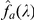 is normalized to the same peak value
Max
is normalized to the same peak value
Max , the cone
factor
, the cone
factor 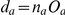 combines
the cone density
combines
the cone density 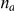 and
pre-receptor transmission factor
and
pre-receptor transmission factor 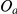 , to
determine the cone sensitivity
, to
determine the cone sensitivity 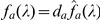 , with
normalizations Max
, with
normalizations Max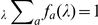 . Each plot
is like Fig. 4A,
having a full model predicted threshold with an optimal
. Each plot
is like Fig. 4A,
having a full model predicted threshold with an optimal
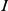 . Each is
labeled with the literature source for
. Each is
labeled with the literature source for 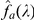 and the
and the
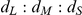 used.
A–C have the Smith and Pokorny cone fundamentals[15] with
different
used.
A–C have the Smith and Pokorny cone fundamentals[15] with
different 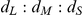 . A is a
modified plot of Fig.
4A. C–F show the best predictions (the
. A is a
modified plot of Fig.
4A. C–F show the best predictions (the
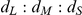 that
minimizes
that
minimizes 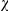 ) for four
different cone fundamentals. Only integer values of
) for four
different cone fundamentals. Only integer values of
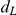 ,
,
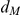 , and
, and
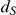 are used
(
are used
(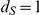 in all
cases).
in all
cases).
Fig. 5D–F show the best
predicted thresholds like Fig.
5C by three other cone fundamentals 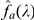 obtained from
different sources in the literature: [21], [16], and [22] (see Andrew
Stockman's webpage http://www.cvrl.org/). Compared
with the predictions when using the Smith and Pokorny cone fundamentals[15] in Fig. 5C, their best predicted
obtained from
different sources in the literature: [21], [16], and [22] (see Andrew
Stockman's webpage http://www.cvrl.org/). Compared
with the predictions when using the Smith and Pokorny cone fundamentals[15] in Fig. 5C, their best predicted
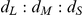 ratios are similar, and so are their goodness of fit
ratios are similar, and so are their goodness of fit
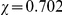 ,
, 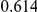 , and
, and
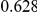 , which are only slightly worse than
, which are only slightly worse than
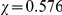 in Fig.
5C. This finding is not so surprising, as the cone fundamentals from
different literature sources are similar to each other. Meanwhile, it may not be
a coincidence that the cone fundamentals of Smith and Pokorny[15] best fitted
the wavelength discrimination data obtained by them. It is likely that different
researchers have different research styles and experimental procedures and hence
different sets of experimental data obtained by the same style are more likely
to be consistent with each other.
in Fig.
5C. This finding is not so surprising, as the cone fundamentals from
different literature sources are similar to each other. Meanwhile, it may not be
a coincidence that the cone fundamentals of Smith and Pokorny[15] best fitted
the wavelength discrimination data obtained by them. It is likely that different
researchers have different research styles and experimental procedures and hence
different sets of experimental data obtained by the same style are more likely
to be consistent with each other.
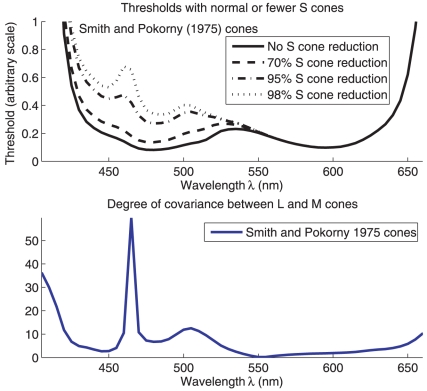
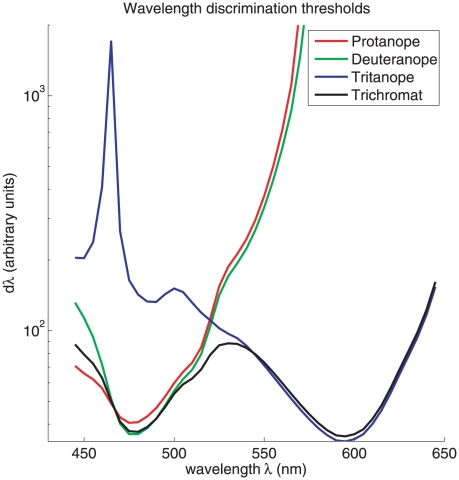
The importance of the S cone minority
Experimental data for wavelength discrimination for
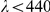 nm are scarse and very variable. These may be caused by
many factors, including the large inter-subject variabilities (e.g., in cone
densities and optical density of the ocular media) in that wavelength region,
the difficulties of delivering stimulus in the short wavelength region, where
light absorption by ocular media is dramatic[14], and, as discussed above,
the wavelength-intensity confound makes some experimental procedures problematic
in that wavelength region. However, Bedford & Wyszecki[19] reported that, as
threshold rises with decreasing
nm are scarse and very variable. These may be caused by
many factors, including the large inter-subject variabilities (e.g., in cone
densities and optical density of the ocular media) in that wavelength region,
the difficulties of delivering stimulus in the short wavelength region, where
light absorption by ocular media is dramatic[14], and, as discussed above,
the wavelength-intensity confound makes some experimental procedures problematic
in that wavelength region. However, Bedford & Wyszecki[19] reported that, as
threshold rises with decreasing 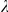 below
below
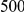 nm, it dips again around
nm, it dips again around  nm before rising
sharply. Wright and Pitt reported in 1934[20] a much shallower dip at a
slightly larger
nm before rising
sharply. Wright and Pitt reported in 1934[20] a much shallower dip at a
slightly larger 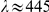 nm. As we argued,
a perceptual confound between wavelength and intensity for
nm. As we argued,
a perceptual confound between wavelength and intensity for
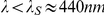 , the most preferred wavelength by S cones, should make
threshold rise continuously with decreasing
, the most preferred wavelength by S cones, should make
threshold rise continuously with decreasing 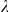 as all three cone
types become less and less sensitive. So it may seem puzzling how this dip could
arise from our full model, which shows a continuous rise of the threshold as
as all three cone
types become less and less sensitive. So it may seem puzzling how this dip could
arise from our full model, which shows a continuous rise of the threshold as
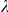 decreases. Bedford and Wyszecki[19] acknowledged and discussed
that the presence of this dip was controversial experimentally. In fact, a dip
in the very long wavelength region was also seen by earlier studies and was then
invalidated by later studies[20], and is no longer seen in modern day data[19], [ 1].
decreases. Bedford and Wyszecki[19] acknowledged and discussed
that the presence of this dip was controversial experimentally. In fact, a dip
in the very long wavelength region was also seen by earlier studies and was then
invalidated by later studies[20], and is no longer seen in modern day data[19], [ 1].
We suggest that the extra dip near 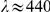 nm may be the side
effect of an extra peak in threshold at
nm may be the side
effect of an extra peak in threshold at 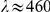 nm caused by too
few blue cones involved in some experiments. We note that Bedford and
Wyszecki[19] used input bipartite fields that were
nm caused by too
few blue cones involved in some experiments. We note that Bedford and
Wyszecki[19] used input bipartite fields that were
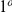 or smaller. This is smaller than the input field
or smaller. This is smaller than the input field
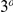 used by Pokorny and Smith[1]. As the density of S cones
drops drastically to zero within
used by Pokorny and Smith[1]. As the density of S cones
drops drastically to zero within 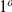 from the center of
the fovea[14],
there are fewer S cones involved if the central viewing color matching fields
are smaller than
from the center of
the fovea[14],
there are fewer S cones involved if the central viewing color matching fields
are smaller than 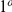 . (Note that
observers in Bedford and Wyszecki's experiment[19] used free viewing for
their task. We consider such free viewing in this attention demanding task as
central viewing since gaze follows attention mandatorily in free viewing[23]). If there
are no S cones, wavelength discrimination relies on L and M cones only. A close
examination of the L and M cone spectral sensitivities reveals that, in a small
region of
. (Note that
observers in Bedford and Wyszecki's experiment[19] used free viewing for
their task. We consider such free viewing in this attention demanding task as
central viewing since gaze follows attention mandatorily in free viewing[23]). If there
are no S cones, wavelength discrimination relies on L and M cones only. A close
examination of the L and M cone spectral sensitivities reveals that, in a small
region of 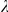 around
around 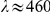 nm,
nm,
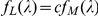 with a scale factor
with a scale factor  that is almost
constant within that region. This means, as
that is almost
constant within that region. This means, as 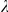 changes in that
region, the responses of the L and M cones co-vary almost completely (except for
noise) so that they act together as if a single rather than two different cone
types. This makes the L+M dichromatic system almost color blind in that
local wavelength region, and consequently the discrimination threshold shoots
up. This covariance of the two cone types can be seen in the signature
changes in that
region, the responses of the L and M cones co-vary almost completely (except for
noise) so that they act together as if a single rather than two different cone
types. This makes the L+M dichromatic system almost color blind in that
local wavelength region, and consequently the discrimination threshold shoots
up. This covariance of the two cone types can be seen in the signature
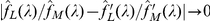 , and we can define a degree of co-variance
as
, and we can define a degree of co-variance
as
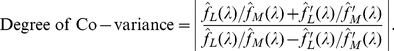 |
(47) |
Mathematically, the 2x2 Fisher
information matrix 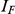 reduces its rank
to 1 when both cones have their
reduces its rank
to 1 when both cones have their  scale with each
other, and thus the two dimensional wavelength-intensity input space is
collapsed into one by the two redundant cone types acting as one. Fig. 6 illustrates how this
Degree of Co-variance between the L and M cones shoots up near
scale with each
other, and thus the two dimensional wavelength-intensity input space is
collapsed into one by the two redundant cone types acting as one. Fig. 6 illustrates how this
Degree of Co-variance between the L and M cones shoots up near
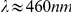 , thus giving a peak in threshold around that wavelength
when there are too few S cones. The exact location of the peak depends slightly
on the
, thus giving a peak in threshold around that wavelength
when there are too few S cones. The exact location of the peak depends slightly
on the 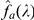 cone fundamentals used, whether it is the[15] cone
fundamentals or other cone fundamentals, but this difference is not big. This
rise in threshold around
cone fundamentals used, whether it is the[15] cone
fundamentals or other cone fundamentals, but this difference is not big. This
rise in threshold around 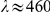 nm can be
prevented by having sufficiently many S cones to remove the collapse of
dimensionality. The dramatically worse discriminability at
nm can be
prevented by having sufficiently many S cones to remove the collapse of
dimensionality. The dramatically worse discriminability at
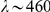 nm with smaller color matching field sizes or in
tritanopic dichromats (who lack S cones) has been observed in previous studies
([24],
[ 25].
nm with smaller color matching field sizes or in
tritanopic dichromats (who lack S cones) has been observed in previous studies
([24],
[ 25].
Figure 6. Illustration of how reducing the density of S cones should create a
threshold peak near 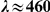 nm.
nm.
Because the L and M cones have their spectral sensitivity co-vary with
each other as 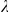 varies
near
varies
near 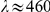 nm, they act as if they are a single cone type
around that
nm, they act as if they are a single cone type
around that  . As
threshold eventually increases when
. As
threshold eventually increases when 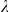 approaches
approaches
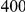 nm, this
local threshold peak at 460 nm creates a threshold dip between
nm, this
local threshold peak at 460 nm creates a threshold dip between
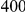 and
and
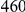 nm.
nm.
Discussion
Our maximum likelihood decoding model can explain the experimental data reasonably
well. This is based on adjusting a single free parameter,
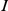 , which characterizes the net effect of the radiance of the
input light, the effective integration time (within the observer's visual
system), and the total area of the input field, etc. Although we did not compute
overall quantum efficiencies (i.e., the ratio between the number of photons needed
by the ideal and human observers for the same task; [7]), they are undoubtedly quite low
(typically they are less than 0.1, [3], [
4], [
5]). Nonetheless, the good agreement between the model and data
shows that, for wavelength discrimination, the efficiency of human color processing
mechanisms is nearly constant over the spectrum (i.e., information is extracted with
equal efficiency at all wavelengths).
, which characterizes the net effect of the radiance of the
input light, the effective integration time (within the observer's visual
system), and the total area of the input field, etc. Although we did not compute
overall quantum efficiencies (i.e., the ratio between the number of photons needed
by the ideal and human observers for the same task; [7]), they are undoubtedly quite low
(typically they are less than 0.1, [3], [
4], [
5]). Nonetheless, the good agreement between the model and data
shows that, for wavelength discrimination, the efficiency of human color processing
mechanisms is nearly constant over the spectrum (i.e., information is extracted with
equal efficiency at all wavelengths).
The best fit between data[1], [
15] and theoretical prediction suggests that the ratios between
effective densities of different cones are 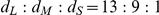 . Here, the effective
density
. Here, the effective
density 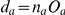 for each cone type
for each cone type  is the actual cone
density
is the actual cone
density 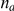 diluted by the pre-receptor optical transmission factor
diluted by the pre-receptor optical transmission factor
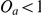 . Meanwhile, evidence suggest that on average
. Meanwhile, evidence suggest that on average
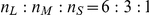 and
and 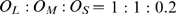 [14], [ 13], giving
[14], [ 13], giving
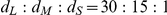 . Since variability in human optical density can give up to a
factor of 10 difference in
. Since variability in human optical density can give up to a
factor of 10 difference in 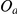 , and a difference in
human
, and a difference in
human 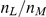 by a factor of 3 seems not unusual[14], our finding of an optimal
by a factor of 3 seems not unusual[14], our finding of an optimal
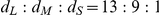 can be seen as within the range of variability of the human
quantities.
can be seen as within the range of variability of the human
quantities.
We analyzed the probable causes of the differences in results across color matching experiments, and how the results could sensitively depend on the experimental procedures and stimulus parameters. It is expected and straightforward to conclude that discrimination threshold should be smaller when color matching is done without adjusting the matching field intensity. Furthermore, we identify that different sizes of the centrally viewed matching fields may cause different findings regarding whether or not there is a dip in discrimination threshold below 450 nm, or a peak around 460 nm. This peak and the resulting dip in particular may arise from small, foveally viewed, fields such that fewer blue cones are excited by the inputs. We also point out that the brightness-hue confound can make some experimental procedures give more accurate and stable results than others. In particular, the procedure used by Pokorny and Smith[1], in which subjects only need to judge whether the two fields differ, is better than other matching procedures in which subjects need to match the brightness of the two fields before judging whether they differ in hue.
The factors responsible for the low overall quantum efficiency of wavelength and other simple discriminations are unknown, but presumably they include photoreceptor inefficiencies, limits in the spatial and temporal integration (by the post-receptor neural mechanisms) of the photoreceptor responses, and neural noise. Any of these factors would tend to reduce overall quantum efficiency while preserving constant relative efficiency[4], [ 6].
Our method in this paper can easily be applied to predict wavelength discrimination by dichromats. Fig. 7 shows that, compared with the trichromats, the protanopes and deuteranopes should have much larger thresholds in the long wavelength region, and the tritanopes should have much larger thresholds in the short wavelength region. These predictions seem to suggest that, for trichromats, wavelength discrimination is mediated by the protanopic/deuteranopic system at short wavelengths and on the tritanopic system at long wavelengths. These theoretical predictions are in line with known observations[25]. They are intuitively expected since color discrimination in the long wavelength region requires the combined activations of both L and M cones, while the S cones are essential for short wavelength discrimination since L and M cones are both only weakly active and co-vary considerably in that wavelength region. These qualitative predictions are insensitive to the actual cone densities used in our formula. These results are arrived at by assuming that the number of L/M cones in a protanope/deuteranope is the same as the total number of L and M cones in a trichromat (as suggested by data from[26]), and that the missing S cones in tritanopes are replaced proportionally by additional L and M cones so that the total number of cones is conserved. The predictions then follow naturally from equation (28) except to replace all summations over three cone types by the corresponding summations over two cone types. One caveat of these predictions is that the large threshold predictions, especially for the dichromats, should be taken as only qualitatively rather than quantitatively trustworthy. This is because our Fisher information formulation for discriminability is based on discriminating two stimuli very close to each other such that a Taylor expansion of log likelihood ratio is a suitable approximation. The suitability of this approximation breaks down when the two stimuli are very different from each other, when the discrimination threshold is too large. This issue has been raised by a previous work on tritanopia[27].
Figure 7. Theoretical preditions of the wavelength discrimination by dichromatics as compared to that by the trichromats.
All these curves are by fixing input intensity
 , while using
, while using 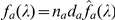 in which
in which
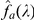 is normalized by Max
is normalized by Max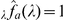 , while
, while
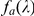 are no longer normalized by
Max
are no longer normalized by
Max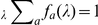 . The values
. The values
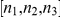 are
are 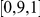 ,
,
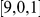 ,
, 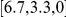 , and
, and
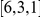 for protanopes, deuteranopes, tritanopes, and
trichromats, respectively.
for protanopes, deuteranopes, tritanopes, and
trichromats, respectively.
Our formulation of an ideal observer analysis for sensory feature discrimination
under perceptual confound is general, and can be used in other sensory
discriminations beyond our example case in this paper. More specifically, let a
sensory world contain two feature dimensions, whose feature values are denoted by
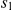 and
and 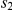 respectively, hence
respectively, hence
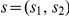 . And suppose we have an experiment to find the minimum
difference in feature
. And suppose we have an experiment to find the minimum
difference in feature 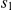 needed to distinguish
a comparison input from a standard input, regardless of the feature
needed to distinguish
a comparison input from a standard input, regardless of the feature
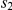 in the comparison input, analogous to the method of Pokorny
and Smith[1]. Let
in the comparison input, analogous to the method of Pokorny
and Smith[1]. Let  be the population
neural responses to the sensory input
be the population
neural responses to the sensory input  with probability
with probability
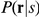 . One can derive Fisher information matrix
. One can derive Fisher information matrix
 as in equation (17) with elements
as in equation (17) with elements
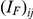 ; then equation (20) gives the discrimination threshold in
; then equation (20) gives the discrimination threshold in
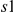 while feature
while feature 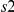 may present a
perceptual confound.
may present a
perceptual confound.
Acknowledgments
Zhaoping would like to thank Prof. Joel Pokorny for private communications for help with references and in explaining their experimental details, and Andrew Stockman for help with references. We would also like to thank the two anonymous reviewers for their very helpful comments.
Footnotes
Competing Interests: The authors have declared that no competing interests exist.
Funding: This work was supported by the Gatsby Charitable Foundation and a Cognitive Science Foresight grant BBSRC #GR/E002536/01. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1.Pokorny J, Smith V. Wavelength discrimination in the presence of added chromatic fields. J Opt Soc America. 1970;69:562–9. doi: 10.1364/josa.60.000562. [DOI] [PubMed] [Google Scholar]
- 2.DeValois R, Jacobs G. Primate color vision. Science. 1968;162:533–40. doi: 10.1126/science.162.3853.533. [DOI] [PubMed] [Google Scholar]
- 3.Barlow H. Measurements of the quantum efficiency of discrimination in human scotopic vision. J Physiology. 1962;160:169–188. doi: 10.1113/jphysiol.1962.sp006839. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Barlow H. Retinal and central factors in human vision limited by noise. In: Barlow HB, Fatt P, editors. Photoreception in Vertebrates. London: Academic Press; 1977. pp. 337–358. [Google Scholar]
- 5.Banks M, Geisler W, Bennett P. The physical limits of grating visibility. Vision Res. 1987;27:1915–24. doi: 10.1016/0042-6989(87)90057-5. [DOI] [PubMed] [Google Scholar]
- 6.Pelli D. The quantum efficiency in vision. In: Blakemore C, editor. Vision: coding and efficiency. Cambridge: Cambridge University Press; 1990. pp. 3–24. [Google Scholar]
- 7.Barlow H. A method of determining the overall quantum efficiency of visual discrimination. J Physiology. 1962;160:155–168. doi: 10.1113/jphysiol.1962.sp006838. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Geisler WS. Sequential ideal-observer analysis of visual discriminations. Psychological Review. 1989;96:267–314. doi: 10.1037/0033-295x.96.2.267. [DOI] [PubMed] [Google Scholar]
- 9.Zhaoping L, May K. Human monochromatic light discrimination explained by optimal signal decoding. Perception. 2010;39:1148–1149. [Google Scholar]
- 10.Naka K, Rushton W. S-potentials from colour units in the retina of fish (cyprinidae). J Physiol. 1966;185:536–555. doi: 10.1113/jphysiol.1966.sp008001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Baylor D, Nunn B, Schnapf J. Spectral sensitivity of cones of the monkey macaca fascicularis. J Physiol. 1987;390:145–160. doi: 10.1113/jphysiol.1987.sp016691. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Bowmaker J, Dartnall H. Visual pigments of rods and cones in a human retina. J Physiol. 1980. pp. 501–511. [DOI] [PMC free article] [PubMed]
- 13.Ahnelt PK, Kolb H, Pflug R. Identification of a subtype of cone photoreceptor, likely to be blue sensitive, in the human retina. Journal of Comparative Neurology. 1987;255:18–34. doi: 10.1002/cne.902550103. [DOI] [PubMed] [Google Scholar]
- 14.Packer O, Williams D. Light, and retinal image, and photoreceptors. Shevell S, editor. The Science of Color, Optical Socieity of America. 2003;41–102 2nd edition. [Google Scholar]
- 15.Smith VC, Pokorny J. Spectral sensitivity of the foveal cone photopigments between 400 and 500 nm. Vision Research. 1975;15:161–171. doi: 10.1016/0042-6989(75)90203-5. [DOI] [PubMed] [Google Scholar]
- 16.Vos JJ, Walraven PL. On the derivation of the foveal receptor primaries. Vision Research. 1971;11:799–818. doi: 10.1016/0042-6989(71)90003-4. [DOI] [PubMed] [Google Scholar]
- 17.Ripamonti C, Woo WL, Crowther E, Stockman A. The s-cone contribution to luminance depends on the m- and l-cone adaptation levels: Silent surrounds? Journal of Vision. 2009;9:3/10/1–16. doi: 10.1167/9.3.10. [DOI] [PubMed] [Google Scholar]
- 18.Dayan P, Abbott L. MIT Press; 2001. Theoretical Neuroscience. [Google Scholar]
- 19.Bedford R, Wyszecki G. Wavelength discrimination for point sources. Journal of Optical Society of America. 1958;48:129–135. doi: 10.1364/josa.48.000129. [DOI] [PubMed] [Google Scholar]
- 20.Wright W, Pitt H. Hue-discrimination in normal colour-vision. Proc Phys Soc. 1934;46:459–473. [Google Scholar]
- 21.Stockman A, MacLeod D, Johnson N. Isolation of the middle- and long-wavelength sensitive cones in normal trichromats. Journal of the Optical Society of America A. 1993;10:2491–2521. doi: 10.1364/josaa.10.002471. [DOI] [PubMed] [Google Scholar]
- 22.Stockman A, Sharpe LT. Spectral sensitivities of the middle- and long-wavelength sensitive cones derived from measurements in observers of known genotype. Vision Research. 2000;40:1711–1737. doi: 10.1016/s0042-6989(00)00021-3. [DOI] [PubMed] [Google Scholar]
- 23.Hoffman JE. Visual attention and eye movements. In: Pashler H, editor. Attention. Psychology Press; 1998. pp. 119–154. [Google Scholar]
- 24.Wright W. The characteristics of tritanopia. J Opt Soc Am. 1952;42:509–521. doi: 10.1364/josa.42.000509. [DOI] [PubMed] [Google Scholar]
- 25.Mollon J, Estevez O, Cavonius C. The two subsystems of colour vision and their roles in wave-length discrimination. In: Blakemore C, editor. Vision: Coding and efficiency. Cambridge University Press; 1990. pp. 119–131. [Google Scholar]
- 26.Cicerone C, Nerger J. The density of cones in the fovea centralis of the human dichromat. Vision Res. 1989;29:1587–95. doi: 10.1016/0042-6989(89)90140-5. [DOI] [PubMed] [Google Scholar]
- 27.Knoblauch K. Theory of wavelength discirmination in tritanopia. J Opt Soc Am A. 1993;10:378–381. doi: 10.1364/josaa.10.000378. [DOI] [PubMed] [Google Scholar]